A dynamical approach to topography estimation in atomic force microscopy based on smooth orthogonal decomposition

Abstract

Atomic force microscope (AFM) is one of the most versatile and powerful devices capable of producing high-resolution images of nanomaterial. Many researchers are widely investigating to improve the scanning speed and image quality of AFM by proposing different techniques. Here, we aim to present a novel approach based on the smooth orthogonal decomposition for the estimation of the surface topography in AFM. The technique proposed in this research not only eliminates the need for a closed-loop controller but also acquires the surface three-dimensional shape (topography) very quickly and accurately. The proposed technique relies on the fact that in the tapping mode of atomic force microscopy, the tip displacements are very fast compared to the topography changes, and the surface topography as a slowly varying parameter can be estimated using the smooth orthogonal decomposition algorithm. To this aim, the state space is reconstructed based on Takens’ theorem and used only the tip displacement measurement data. According to Takens’ theorem, using the delay time and embedding dimension parameters, we are able to create a system in which dynamical behaviors are similar to the original system. The results demonstrate that the proposed estimation approach is robust to noise and does not require large data or computational resources to be implemented. Also, the performance of the proposed method is appropriate for any type of force interactions between the tip and sample.

Appendix

(A) The equations are simplified to dimensionless form using the dimensionless parameters of time ($\tau = \omega_{n} t$) and length ($\frac{1}{L}$). The dimensionless parameters used in LJ potential are as follows:

$$ \xi \left( \tau \right) = \frac{y\left( t \right)}{L} ,\quad \mu_{1} = \frac{{b_{s} }}{{m\omega_{n} }} ,\quad \mu_{2} = \frac{{b_{v} }}{{m\omega_{n} }},\quad \overline{\gamma } = \frac{\gamma }{L} ,\quad \overline{g} = \frac{g}{{L^{3} }} ,\quad \overline{\partial } = \frac{\partial }{L} ,\quad \chi = \frac{{u_{0} }}{L} ,\quad \Omega = \frac{\omega }{{\omega_{n} }} = 1 $$

(A-1)

Using these parameters, the equation of motion can be expressed as:

$$ \begin{aligned} & m\ddot{y} + \left( {b_{{\text{s}}} + b_{{\text{v}}} } \right)\dot{y} + ky = \frac{gk}{{\left( {\gamma - y} \right)^{2} }} - \frac{{g\partial^{6} k}}{{30\left( {\gamma - y} \right)^{8} }} + b_{{\text{s}}} u_{0} \omega \cos \left( {\omega t} \right) + ku_{0} \sin \left( {\omega t} \right) \\ & \quad \Rightarrow m\frac{{{\text{d}}\left( {\frac{{{\text{d}}\left( {L\xi } \right)}}{{{\text{d}}\tau }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}}} \right)}}{{{\text{d}}\tau }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}} + m\omega_{n} \left( {\mu_{1} + \mu_{2} } \right)\frac{{{\text{d}}\left( {L\xi } \right)}}{{{\text{d}}\tau }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}} + kL\xi = \frac{{L^{3} \overline{g}k}}{{L^{2} \left( {\overline{\gamma } - \xi } \right)^{2} }} - \frac{{L^{9} \overline{g}\overline{\partial }^{6} k}}{{30L^{8} \left( {\overline{\gamma } - \xi } \right)^{8} }} \\ & \quad \quad + m\omega_{n}^{2} \mu_{1} L\chi {\Omega }\cos \left( {{\Omega }\tau } \right) + kL\chi \sin \left( {{\Omega }\tau } \right)\mathop \Rightarrow \limits^{{\frac{k}{m} = \omega_{n}^{2} }} mL\omega_{n}^{2} \frac{{{\text{d}}^{2} \left( \xi \right)}}{{{\text{d}}\tau^{2} }} + mL\omega_{n}^{2} \left( {\mu_{1} + \mu_{2} } \right)\frac{{{\text{d}}\left( \xi \right)}}{{{\text{d}}\tau }} \\ & \quad \quad + mL\omega_{n}^{2} \xi = \frac{{mL\omega_{n}^{2} \overline{g}}}{{\left( {\overline{\gamma } - \xi } \right)^{2} }} - \frac{{mL\omega_{n}^{2} \overline{g}\overline{\partial }^{6} }}{{30\left( {\overline{\gamma } - \xi } \right)^{8} }} + mL\omega_{n}^{2} \mu_{1} \chi {\Omega }\cos \left( {{\Omega }\tau } \right) + mL\omega_{n}^{2} \chi \sin \left( {{\Omega }\tau } \right) \\ \end{aligned} $$

(A-2)

By dividing all terms of Eq. (A-2) by $mL{{\omega }_{n}}^{2}$ or $Lk$, the dimensionless form of equation is obtained as follows:

$$ \frac{{{\text{d}}^{2} \left( \xi \right)}}{{{\text{d}}\tau^{2} }} + \left( {\mu_{1} + \mu_{2} } \right)\frac{{{\text{d}}\left( \xi \right)}}{{{\text{d}}\tau }} + \xi = \frac{{\overline{g}}}{{\left( {\overline{\gamma } - \xi } \right)^{2} }} - \frac{{\overline{g}\overline{\partial }^{6} }}{{30\left( {\overline{\gamma } - \xi } \right)^{8} }} + \mu_{1} \chi \Omega \cos \left( {\Omega \tau } \right) + \chi \sin \left( {\Omega \tau } \right) $$

(A-3)

Similarly, the comprehensive tip–sample interaction force model is converted to the dimensionless form as follows:

$$ \frac{{{\text{d}}^{2} \left( \xi \right)}}{{{\text{d}}\tau^{2} }} + \left( {\mu_{1} + \mu_{2} } \right)\frac{{{\text{d}}\left( \xi \right)}}{{{\text{d}}\tau }} + \xi = \overline{{f_{{\text{w}}} }} + \overline{{f_{{\text{r}}} }} + \overline{{f_{{\text{c}}} }} + \overline{{f_{{\text{e}}} }} + + \mu_{1} \chi \Omega \cos \left( {\Omega \tau } \right) + \chi \sin \left( {\Omega \tau } \right) $$

(A-4)

where the dimensionless form of different force terms is given as:

$$ \overline{{f_{{\text{w}}} }} = \frac{{f_{{\text{w}}} }}{Lk} = \left\{ {\begin{array}{*{20}l} {\frac{{\overline{g}}}{{\left( {\overline{\gamma } - \xi_{1} } \right)^{2} }},} \hfill & {\overline{\gamma } - \xi_{1} > \frac{{l_{0} }}{L}} \hfill \\ {\frac{{\overline{g}}}{{\left( {\frac{{l_{0} }}{L}} \right)^{2} }},} \hfill & { \overline{\gamma } - \xi_{1} \le \frac{{l_{0} }}{L}} \hfill \\ \end{array} } \right. $$

(A-5)

$$ \overline{{f_{{\text{r}}} }} = \frac{{f_{{\text{r}}} }}{Lk} = - \frac{{L^{\frac{1}{2}} }}{k}\left\{ {\begin{array}{*{20}l} {0, } \hfill & {\overline{\gamma } - \xi_{1} > \frac{{l_{0} }}{L}} \hfill \\ {\frac{4}{3}E^{*} \sqrt r \left( {\frac{{l_{0} }}{L} - \left( {\overline{\gamma } - \xi_{1} } \right)} \right)^{\frac{3}{2}} ,} \hfill & {\overline{\gamma } - \xi_{1} \le \frac{{l_{0} }}{L}} \hfill \\ \end{array} } \right. $$

(A-6)

$$ \overline{{f_{{\text{c}}} }} = \frac{{f_{{\text{c}}} }}{Lk} = \frac{1}{Lk}\left\{ {\begin{array}{*{20}l} {\frac{{4\pi r\kappa_{{{\text{H}}_{{2}} {\text{O}}}} }}{{1 + \frac{{\overline{\gamma } - \xi_{1} }}{{\frac{{t_{w} }}{L}}}}},} \hfill & {\overline{\gamma } - \xi_{1} > \frac{{l_{0} }}{L}} \hfill \\ {\frac{{4\pi r\kappa_{{{\text{H}}_{{2}} {\text{O}}}} }}{{1 + \frac{{l_{0} }}{{t_{w} }}}},} \hfill & {\overline{\gamma } - \xi_{1} \le \frac{{l_{0} }}{L}} \hfill \\ \end{array} } \right. $$

(A-7)

$$ \overline{{f_{{\text{e}}} }} = \frac{{f_{{\text{e}}} }}{Lk} = \frac{1}{Lk}\left\{ {\begin{array}{*{20}l} {\frac{{\pi \varepsilon_{0} r^{2} V_{0}^{2} }}{{L^{2} \left( {\overline{\gamma } - \xi_{1} } \right)^{2} }},} \hfill & {\overline{\gamma } - \xi_{1} > \frac{r}{L}} \hfill \\ {\frac{{\pi \varepsilon_{0} rV_{0}^{2} }}{{L\left( {\overline{\gamma } - \xi_{1} } \right)}},} \hfill & { \overline{\gamma } - \xi_{1} \le \frac{r}{L}} \hfill \\ \end{array} } \right. $$

(A-8)

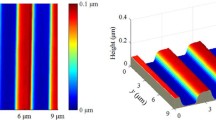
The two topographies, which are used to evaluate the proposed method, are as follows:

$$ \overline{\gamma }_{1} \left( {x_{{\text{s}}} } \right) = 9.2 + \left\{ {\begin{array}{*{20}l} {0.10,} \hfill & { 0 \le x_{{\text{s}}} < 5} \hfill \\ {0,} \hfill & {5 \le x_{{\text{s}}} < 10} \hfill \\ {0.0005\left( {x_{{\text{s}}} - 10} \right)\left( {x_{{\text{s}}} - 20} \right)\left( {x_{{\text{s}}} - 30} \right),} \hfill & {10 \le x_{{\text{s}}} < 30} \hfill \\ { 0.05,} \hfill & { 30 \le x_{{\text{s}}} < 35} \hfill \\ { - 0.0005\left( {x_{{\text{s}}} - 35} \right)\left( {x_{{\text{s}}} - 49} \right)\left( {x_{{\text{s}}} - 50} \right),} \hfill & { 35 \le x_{{\text{s}}} < 50} \hfill \\ {0,} \hfill & {50 \le x_{{\text{s}}} < 55} \hfill \\ {0.05,} \hfill & {55 \le x_{{\text{s}}} \le 60} \hfill \\ \end{array} } \right. $$

(A-9)

$$ \begin{aligned} \overline{\gamma }_{2} \left( {x_{{\text{s}}} } \right) & = 9.2 + \left\{ {\begin{array}{*{20}l} {0,} \hfill & {0 \le x_{s} < 6} \hfill \\ { 0.10,} \hfill & {6 \le x_{{\text{s}}} < 12} \hfill \\ { - 0.05} \hfill & {12 \le x_{{\text{s}}} < 18} \hfill \\ { - 0.10,} \hfill & {18 \le x_{{\text{s}}} < 24} \hfill \\ {0.05,} \hfill & {24 \le x_{{\text{s}}} < 30} \hfill \\ {\overline{ \gamma } ,} \hfill & {30 \le x_{{\text{s}}} \le 60} \hfill \\ \end{array} } \right. \\ \overline{\gamma }^{*} & = 2.25\frac{{\sin \left( {\frac{1}{3}x_{{\text{s}}} - 10} \right)}}{{x_{{\text{s}}} - 30}} + 2.25\frac{{\cos \left( {\frac{1}{2}x_{{\text{s}}} - 15} \right) - 1}}{{x_{{\text{s}}} - 30}} - 0.7e^{{ - \frac{1}{3}\left( {x_{{\text{s}}} - 30} \right)^{2} }} + 0.3e^{{ - \frac{1}{9}\left( {x_{{\text{s}}} - 36} \right)^{2} }} + 0.25e^{{ - \frac{1}{9}\left( {x_{{\text{s}}} - 54} \right)^{2} }} \\ \end{aligned} $$

(A-10)

(B) In this subsection, we aim to demonstrate why the solution of Eq. (13) is equivalent to the solution of Eq. (12). In the mathematics, the Lagrange multiplier approach can be used to solve problems with multiple constraints. Hence, for Eq. (12), the Lagrange function is defined as follows:

$$ L = \varvec{\varphi }^{{\varvec{T}}} \user2{\varphi } - \lambda_{i} \left( {\varvec{d\varphi }} \right)^{{\varvec{T}}} \varvec{d\varphi } = \left( {{\varvec{Pq}}} \right)^{{\varvec{T}}} {\varvec{Pq}} - \lambda_{i} \left( {{\varvec{dPq}}} \right)^{{\varvec{T}}} {\varvec{dPq}} = {\varvec{q}}^{{\varvec{T}}} \left( {{\varvec{P}}^{{\varvec{T}}} {\varvec{P}} - \lambda_{i} \left( {{\varvec{dP}}} \right)^{{\varvec{T}}} {\varvec{dP}}} \right){\varvec{q}} $$

(A-11)

To maximize the Lagrange function (L), its gradient should be determined and set into zero:

$$ \nabla_{{{\varvec{q}}_{{\varvec{i}}} }} L = 0\mathop \Rightarrow \limits^{{{\text{yields}}}} \left( {{\varvec{P}}^{{\varvec{T}}} {\varvec{P}} - \lambda_{i} \left( {{\varvec{dP}}} \right)^{{\varvec{T}}} {\varvec{dP}}} \right){\varvec{q}} = {\mathbf{0}}\mathop \Rightarrow \limits^{{{\text{yields}}}} \left[ {{\varvec{P}}^{{\varvec{T}}} {\varvec{P}}} \right]{\varvec{q}} = \lambda_{i} \left[ {\left( {{\varvec{dP}}} \right)^{{\varvec{T}}} {\varvec{dP}}} \right]{\varvec{q}} $$

(A-12)

(C) In this paper, the mentioned new third-order mapping that uses the current and five next windows is as follows:

where the order of the coefficients is from highest to lowest power. The first row of this matrix is for the current window, the second one is for the next window, and in the same way until the end row that is related to the five ahead window.