1 Introduction

Hydrocarbons have been one of the most powerful drivers for the global economy for almost one century and will continue to be one of the most reliable resources for our human beings for the next several decades. Among the physical properties that are employed for detecting the hydrocarbons beneath the Earth's surface, electrical conductivity (or alternatively its reciprocal, electrical resistivity) is the one that is most sensitive to the different types of fluids residing in the reservoirs. As a result, Archie’s equations (Archie 1942) that relate the electrical conductivity of a reservoir rock to its porosity, to the conductivity of the water saturating its pores, as well as to the degree of water saturation in its pore space, have been widely adopted for the assessments of the volume of hydrocarbon reserves (Gao et al. 2003; Li and Hou 2019).

There are two exponents in Archie’s equations, where the cementation exponent m links the conductivity of the fully water saturated rock (σ0) to the conductivity of the water (σw) and the rock’s porosity (φ), and the saturation exponent n relates the conductivity of the partially water saturated rock (σeff) to that of the fully water saturated rock and the degree of water saturation (Sw) in the pores, in the form of

$$\sigma_{0} = \sigma_{{\text{w}}} \varphi^{m}$$
(1)
$${\text{and }}\sigma_{{\text{eff}}} = \sigma_{0} S_{{\text{w}}}^{n}$$
(2)

respectively. These two exponents are initially regarded as fitting parameters (Archie 1942; Ellis and Singer 2007) and are usually calibrated using a set of experimental data before being applied to the evaluation of the potential of a reservoir. However, a small deviation in the two exponents of real reservoirs from their calibrated values will lead to enormous errors in the estimated reserves (Glover 2017). Naturally, researches have been trying to understand the physical meanings of the exponents with the aim to provide a more accurate prediction of the two exponents (e.g., Adler et al. 1992; Kennedy et al. 2001; Hamamoto et al. 2010; Glover 2010; Bernabé et al. 2011; Soleymanzadeh et al. 2018; Han et al. 2019; Tian et al. 2019).

Unlike cementation exponent, for which a substantial understanding has been obtained through various investigation methods, including theoretical and numerical modeling approaches as well as fractal theories (e.g., Sen et al. 1981; Glover 2009; Han et al. 2015; Tang et al. 2015; Wei et al. 2015; Cai et al. 2017; Yue 2019), there is still no well-accepted physical interpretation for the saturation exponent (Yue et al. 2004, 2009; Glover 2017). The saturation exponent is commonly interpreted qualitatively as some measure of the efficiency for the electrical flow to take place within the water occupying a partially saturated rock (e.g., Sun and Chu 1994; Sun 2008; Li et al. 2012, 2013; Chen et al. 2016). Recently, based on the generalized Archie’s law, Glover (2017) provided a new theoretical interpretation for the saturation exponent in terms of the rate of change of the fractional connectedness with saturation and connectivity within the reference phase. However, the definitions for the ‘connectedness’ and ‘connectivity’ remain qualitative and elusive, and there is still a great need of a more explicit meaning for the saturation exponent.

This work aims to offer a quantitative interpretation of the saturation exponent based on the Maxwell–Wagner theory (Maxwell 1891; Wagner 1914) for the propagation of electromagnetic waves in a two-phase homogeneous system. We first theoretically derive Archie’s equations from the Maxwell–Wagner theory, and the saturation exponent is then related to the aspect ratio of the gas phase in the pores. The commonly used saturation exponent values and their variation with water saturation are finally analyzed and discussed.

2 Quantitative interpretation of the saturation exponent

2.1 Conductivity of a fully water saturated rock

Before deriving the conductivity of a partially water saturated rock, it is helpful to introduce models for the conductivity of a rock with full water saturation, as this will form the basis for the derivation of the conductivity of a rock partially saturated with water.

The model considered here is the Hanai–Bruggeman (HB) equation (Bruggeman 1935; Hanai 1960, 1961) developed based on the Maxwell–Wagner theory and using a differential effective medium algorithm. The HB equation calculates the electrical conductivity (σ0) of a water saturated two-phase rock consisting of water and solid grains with conductivity of σw and σg, respectively, and with porosity of φ (i.e., the volume fraction of the water phase), as follows

$$\varphi = \left( {\frac{{\sigma_{{\text{w}}} }}{{\sigma_{0} }}} \right)^{{\frac{m - 1}{m}}} \left( {\frac{{\sigma_{0} - \sigma_{{\text{g}}} }}{{\sigma_{{\text{w}}} - \sigma_{{\text{g}}} }}} \right)$$
(3)

In the case of insulating grains (i.e., σg = 0), the HB equation reduces to \(\sigma_{0} = \sigma_{{\text{w}}} \varphi^{m}\), which is essentially the Archie’s first equation as given in Eq. 1.

2.2 Conductivity of a partially saturated pore

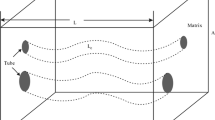
Assume that a partially water saturated rock contains three phases, i.e., the solid grains, the water and the air. It is apparent that both the water and the air phases can only reside in the pore, and therefore, the coexistence of water and air in the pore makes the pore a new two-phase medium (as schematically shown in Fig. 1), where the air in the pore resembles the solid grains in the rock.

In a similar way to the conductivity of a fully water saturated rock (i.e., Eq. 3), the conductivity of a partially saturated pore (σp) is given as

$$S_{{\text{w}}} = \left( {\frac{{\sigma_{{\text{w}}} }}{{\sigma_{{\text{p}}} }}} \right)^{{\frac{{m_{{\text{p}}} - 1}}{{m_{{\text{p}}} }}}} \left( {\frac{{\sigma_{{\text{p}}} - \sigma_{{\text{a}}} }}{{\sigma_{{\text{w}}} - \sigma_{{\text{a}}} }}} \right)$$
(4)

where Sw is the water saturation, σa is the air conductivity and mp is similar to the cementation exponent of the whole rock, but is defined for the ‘rock-like’ pore (see below for further discussion).

When, in the usual and common case, air conductivity is negligible (i.e., σa = 0), the conductivity of a partially saturated pore is finally obtained, as

$$\sigma_{{\text{p}}} = \sigma_{{\text{p}}} S_{{\text{w}}}^{{m_{{\text{p}}} }}$$
(5)

2.3 Conductivity of a partially water saturated rock

Having obtained the conductivity of a partially saturated pore, we proceed to determine the conductivity of a partially water saturated rock. If we assume the air phase is homogeneously distributed in the pore space, it is then reasonable to speculate that the electrical conductivity equals in each pore. Then, a rock with partial water saturation can be regarded as the rock fully saturated with a medium that has a conductivity equivalent to the conductivity of the partially saturated pores. Therefore, the conductivity of a partially water saturated rock (σeff) can be obtained by replacing the water conductivity (σw) with the pore conductivity (σp) in Eq. 1, as

$$\sigma_{{\text{eff}}} = \sigma_{{\text{p}}} \varphi^{m}$$
(6)

Integrating the expression for the electrical conductivity of a partially saturated pore (Eq. 5) into Eq. 6 gives

$$\sigma_{{\text{eff}}} = \sigma_{{\text{w}}} \varphi^{m} S_{{\text{w}}}^{{m_{{\text{}}} }}$$
(7)

Equation 7 is one of the main findings in this work. Comparison between Eq. 7 and the Archie’s equations (Eqs. 1 and 2) indicates that 1) Archie’s equations can be theoretically derived from Maxwell–Wagner theory, which provides a theoretical backup for the empirically obtained Archie’s equations, and 2) the saturation exponent, in essence, is the cementation exponent of the pores (i.e., n = mp), and therefore, whatever physical understanding that has be previously interpreted for the rock’s cementation exponent (e.g., Glover 2009; Zhang et al. 2018) can be now employed to describe the saturation exponent in terms of the gas phase and water in the pores, and the a more explicit and quantitative interpretation of the saturation exponent will be offered in the next section.

2.4 Correlations between saturation exponent and gas aspect ratios

We have demonstrated that the saturation exponent is physically equivalent to the cementation exponent of the pores if we assume each pore to be a new ‘rock-like’ material consisting of randomly orienting spheroidal air bubbles in the connected water background. However, such interpretation of the saturation exponent is still conceptual and qualitative, and we still need a more explicit and quantitative understanding of the saturation exponent.

To arrive at a quantitative interpretation of the saturation exponent, it is necessary to introduce Asami’s equation (Asami 2002) for the electrical conductivity of a two-phase medium, which is also based on the Maxwell–Wagner theory, but instead of using cementation exponent as the geometric factor, approximates the rock ingredients to be spheroids with a specific aspect ratio. The Asami’s equation for the electrical conductivity of a partially saturated pore is given as

$$S_{{\text{w}}} = \left( {\frac{{\sigma_{{\text{w}}} (1 + 3L) + \sigma_{{\text{a}}} (2 - 3L)}}{{\sigma_{{\text{p}}} (1 + 3L) + \sigma_{{\text{a}}} (2 - 3L)}}} \right)^{C} \left( {\frac{{\sigma_{{\text{p}}} - \sigma_{{\text{a}}} }}{{\sigma_{{\text{w}}} - \sigma_{{\text{a}}} }}} \right)\left( {\frac{{\sigma_{{\text{w}}} }}{{\sigma_{{\text{p}}} }}} \right)^{3T}$$
(8)

where C and T are intermediate variables as \(T = \frac{L(1 - 2L)}{{2 - 3L}}\), \(C = \frac{{2(1 - 3L)^{2} }}{(2 - 3L)(1 + 3L)}\), and L is the x-axis depolarization factor (L = Lx = Ly and Lz = 1 ‒ 2L, where Lk is the depolarization factor along the k-axis) that is a function of the air aspect ratio α.

In the case of insulating air bubbles (i.e., σa = 0), Eq. 8 simplifies to

$$S_{{\text{w}}} = \left( {\frac{{\sigma_{{\text{w}}} }}{{\sigma_{{\text{p}}} }}} \right)^{C + 3T - 1}$$
(9)

Substituting the intermediate variables C and T in Eq. 9 with their expressions, where the z-axis depolarization factor of the gas phase is defined as \(L_{{\text{z}}} = \frac{1}{{1 - \alpha^{2} }} - \frac{\alpha }{{\left( {1 - \alpha^{2} } \right)^{3/2} }}\cos^{ - 1} \alpha\) (Asami 2002; see Fig. 2 for the relationship between Lz and aspect ratio of the gas phase), the equality of Eqs. 5 and 9 gives

$$n = m_{{\text{p}}} = \frac{{5 - 3L_{{\text{z}}} }}{{3(1 - L_{{\text{z}}}^{2} )}}$$
(10)

Equation 10 is the other key finding in this work. It quantitatively relates the saturation exponent to the aspect ratio of the air bubbles in the pores and therefore provides an explicit and quantitative interpretation of the saturation exponent.

3 Discussion

We have theoretically derived Archie’s equations from the Maxwell–Wagner theory and related the saturation exponent to the cementation exponent of the pores, which is further correlated with the aspect ratio of the air bubbles in the pores in an explicit and quantitative manner. The derivations and correlations presented in this work are based on the assumption of homogeneous fluid distribution in the thoroughly connected pores, so that the electrical conductivity equals in each partially saturated pore. The air bubbles in the pores are assumed to be ideal spheroids with a specific aspect ratio and to be distributed randomly in the pores. It is also assumed that both the rock grains and the air bubbles are electrically insulating. This implies that the interpretation of the saturation exponent offered in this work is not suitable for clay-rich rocks, where the electrochemical interactions associated with the mineral–water system can give rise to an additional surface conductivity (e.g., Revil and Skold 2011; Revil 2013) that makes the simulation and prediction of the rock conductivity out of the scope of the Maxwell–Wagner theory. The quantitative interpretation of saturation exponent for clay-rich rocks needs further study.

Despite the simplifications and assumptions made in the context, the interpretation of the saturation exponent in terms of its relationship with the aspect ratio of the air bubbles in the pores is reasonable. As mentioned above, the saturation exponent was interpreted as some qualitative measure of the efficiency for the electrical flow to take place within the water in a partially saturated rock, and the higher the efficiency, the lower the saturation exponent. According to the modeling scheme proposed by Ellis et al. (2010), the electrical conductivity and its efficiency are inversely proportional to the increase in the path length taken by an electrical current around the surface of an idealized insulating granular medium. This suggests that a water–air mixture with air bubbles in spherical shapes (i.e., α = 1) will have the highest efficiency for the electrical current to flow and therefore the rock will have the lowest saturation exponent. With a reduction in the aspect ratio of the air bubbles, the efficiency of the current flow decreases and accordingly the saturation exponent of the rock increases. This is consistent with the correlations between the saturation exponent and the air aspect ratio obtained in this work (as shown in Fig. 3).

It is already obvious from the above analyses that the saturation exponent varies with the aspect ratio of the air bubbles in the pores. However, a value of 2 is usually taken for the saturation exponent in the absence of laboratory measurements (e.g., Glover 2017). Why is this the case in a variety of sedimentary rocks? The quantitative relationship between the saturation exponent and the air bubble aspect ratio as shown in Fig. 3 might give a clue. As shown in Fig. 3, the saturation exponent of 2 corresponds to an air aspect ratio of roughly 0.22. On the one hand, an increase in the air aspect ratio from 0.22 to 1 will lead to a decreasing saturation exponent to 1.5, and on the other hand, a reducing air aspect ratio to 0.2 will result in an increasing saturation exponent to 2.1. This means that within the large air aspect ratio range from 0.2 to 1, the saturation exponent varies by only 0.6, and if the real range of the air aspect ratio shrinks, the deviation of the actual saturation exponent from the value of 2 will become smaller. Therefore, the saturation exponent of 2 seems to be a compromising blind estimate for a variety of porous rocks, and it is the same for the cementation exponent of approximately 2 commonly reported for a range of rocks (e.g., Archie 1942) if we replace the saturation exponent and air aspect ratio in Eq. 10 and Fig. 3 with the cementation exponent and grain aspect ratio, respectively.

The saturation exponent of 2 serves only as a rough estimation, and careful laboratory measurements are highly demanded to accurately determine the saturation exponent. However, the saturation exponent can only be estimated by measuring the electrical conductivity of a rock over a broad saturation range, and in fact the changing saturation might have already resulted in a variation in the saturation exponent. Since the saturation exponent is quantitatively related to the aspect ratio of the air bubbles in the pores, with an increase in the air amount (i.e., a reduction in the water saturation), the initial narrow air along the surface of the pores may form more rounded bubbles. This implies that with decreasing water saturation, the air aspect ratio will increase, which in turn leads to a decreasing saturation exponent. This explains the smaller value of saturation exponent experimentally observed at lower degree of water saturation (e.g., Glover 2017).

4 Conclusions

We have derived Archie’s equations from the Maxwell–Wagner theory on the assumption of homogeneous fluid distribution in the pore space of clay-free porous rocks. The saturation exponent was found to be essentially the cementation exponent for the water–air mixture and was further quantitatively and explicitly related to the aspect ratio of the air bubbles in the pores. The results have provided a theoretical backup for the empirically obtained Archie’s equations and have offered a more physical and quantitative interpretation of the saturation exponent.

Fig. 1
figure 1

A schematic diagram showing the coexistence of water (in light blue) and air (in white) in the pore space between solid grains (in gray). The pore is now regarded as a new rock-like medium consisting of randomly distributed air bubbles in the water background.

Full size image
Fig. 2.
figure 2

Relationship between the aspect ratio and z-axis depolarization factor of the gas bubbles.

Full size image
Fig. 3
figure 3

Correlations among the saturation exponent, air bubble aspect ratio and z-axis depolarization in partially water saturated rocks. The two gray dashed lines correspond to the saturation exponent of 2

Full size image