Abstract
We present experimental evidence on the interplay between strategic uncertainty and equilibrium selection in stable matching mechanisms. In particular, we apply a version of risk-dominance to compare the riskiness of “truncation” against other strategies that secure against remaining unmatched. By keeping subjects’ ordinal preferences fixed while changing their cardinal representation, our experimental treatments vary the risk-dominant prediction. We find that both truth-telling and truncation are played more often when they are risk-dominant. In both treatments, however, truncation strategies are played more often in later rounds of the experiment. Our results also shed light on several open questions in market design.





Similar content being viewed by others
Notes
A matching is said to be stable if no agent prefers remaining unmatched to her current allocation and no pair of agents both prefer each other to their current allocations.
Even after removing strategic uncertainty, there is also the possibility of remaining unmatched due to “over-truncation” (i.e., playing the wrong kind of truncation strategy). However, over-truncation is not possible in our experimental set-up. In a related paper, Castillo and Dianat (2016) present evidence that laboratory subjects are less likely to truncate their preferences when the possibility of over-truncation exists.
In this game, firms (computers) have a dominant strategy of truth-telling and workers (subjects) have incentives to misrepresent their preferences to influence the final outcome.
That is, each worker can be matched to either firm at a stable matching.
This is a consequence of the fact that the set of stable matchings has a lattice structure.
Specifically, the NRMP switched from a version of the hospital-proposing deferred acceptance algorithm to a version of the student-proposing deferred acceptance algorithm.
For a survey of this literature, see Camerer (2003).
Although the classical results we present are usually framed in terms of ordinal preferences, the solution concept of risk-dominance is inherently cardinal. Thus, we assume cardinal preferences throughout the analysis.
The assumption that firms play their dominant strategy in the firm-optimal stable mechanism is not entirely innocuous. While the firm-optimal stable mechanism is strategy-proof for the firms, Ashlagi and Gonczarowski (2018) show that it is not obviously strategy-proof in the sense of Li (2017). Furthermore, empirical studies by Rees-Jones (2018) and Hassidim et al. (2017) find that a small fraction of participants fail to play their dominant strategy in strategy-proof matching mechanisms.
This definition is taken from Roth and Rothblum (1999). However, it has been slightly modified such that truthful preference revelation is no longer an “edge case” of a truncation strategy.
The term “dropping strategy” is often used to refer to the act of removing a match partner from the middle of a preference list (rather than from the tail end of a preference list). According to our definitions, a dropping strategy would be classified as a permutation.
The firm-proposing deferred acceptance algorithm is a procedure that generates the firm-optimal stable matching for any preference profile.
In the experiment, the firm-proposing deferred acceptance algorithm is used to illustrate to subjects how reported preferences map to final outcomes.
When firms are unconstrained, there exist other equilibria in which firms play dominated strategies.
For instance, consider the situation facing worker \(w_1\) with preference list \(P_{w_1} = f_2, f_1\). Both permutation strategies (\(Q_{w_1} = f_1, f_2\) and \(Q_{w_1}^\prime = f_1\)) yield the same outcome for all preference reports by the other player. More generally, the equivalence of different permutation strategies need not hold.
Although the two permutation strategies are theoretically equivalent in our experimental set-up, they are not behaviorally equivalent. In the aggregate data, we find that the overwhelming majority of permutations (96%) involve submitting a full-length preference list.
For instance, the binary relation imposed by risk-dominance can fail to be transitive. Morris et al. (1995) provide an example of a \(3\times {3}\) game with three strict Nash equilibria in which the risk-dominance relationship is cyclical.
Since permutation is a weakly dominated strategy, it can never be a strict best-response.
A protective strategy is a refinement of a maxmin strategy. Notice that while both Truth and Permute are maxmin strategies, Truth weakly dominates Permute.
To reduce experimenter demand effects, the terminology of preferences is never used in the experiment. A subject’s true preference list is referred to as a “list of payments” and a subject’s reported preference list is referred to as a “message.”
In the context of stag hunt games, Rankin et al. (2000) also find that laboratory subjects focus on payoff-dominance rather than other solution concepts.
There is a unique action profile that yields an unstable matching: a subject-pair where one subject plays a truncation strategy and the other subject plays a permutation strategy.
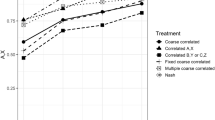
For each treatment, we estimate an OLS regression of a dummy variable for whether the final outcome is the worker-optimal stable matching on the round of the experiment. Standard errors are clustered at the session level.
A protective strategy is a refinement of a maxmin strategy. Notice that while both Truth and Permute are maxmin strategies, Truth weakly dominates Permute.
We use \(s(1) = 10\) and \(s(1) = 100\).
In fact, the computational exercise of Roth and Peranson (1999) has generated a literature on “core convergence” in matching models (e.g. Immorlica and Mahdian 2005; Kojima and Pathak 2009; Lee 2016). Under certain conditions, these papers show that the set of stable matchings shrinks as the size of the market increases.
The NRMP Program Director Survey Reports can be found at the following website: http://www.nrmp.org/report-archives.
Calford and Oprea (2017) make a similar point in the context of continuous-time games in the lab.
If \(\mu _F(w)\) were at the head of any worker’s true preference list, then this contradicts the assumption that all workers have more than one achievable partner.
The proof of this claim closely follows the proof of Theorem 4.15 in Roth and Sotomayor (1992). The only difference is that we allow the preference lists in Q to be of any length.
References
Ashlagi, I., & Gonczarowski, Y. A. (2018). Stable matching mechanisms are not obviously strategy-proof. Journal of Economic Theory, 177, 405–425.
Ashlagi, I., & Klijn, F. (2012). Manipulability in matching markets: Conflict and coincidence of interests. Social Choice and Welfare, 39(1), 23–33.
Barberà, S., & Dutta, B. (1995). Protective behavior in matching models. Games and Economic Behavior, 8(2), 281–296.
Calford, E., & Oprea, R. (2017). Continuity, inertia, and strategic uncertainty: A test of the theory of continuous time games. Econometrica, 85(3), 915–935.
Camerer, C. (2003). Behavioral game theory: Experiments in strategic interaction. Princeton: Princeton University Press.
Castillo, M., & Dianat, A. (2016). Truncation strategies in two-sided matching markets: Theory and experiment. Games and Economic Behavior, 98, 180–196.
Coles, P. A., & Shorrer, R. I. (2014). Optimal truncation in matching markets. Games and Economic Behavior, 87, 591–615.
Cooper, R. W., DeJong, D. V., Forsythe, R., & Ross, T. W. (1990). Selection criteria in coordination games: Some experimental results. American Economic Review, 80(1), 218–233.
Dal Bó, P., & Fréchette, G. R. (2011). The evolution of cooperation in infinitely repeated games: Experimental evidence. American Economic Review, 101(1), 411–429.
Dubins, L. E., & Freedman, D. A. (1981). Machiavelli and the Gale–Shapley algorithm. American Mathematical Monthly, 88(7), 485–494.
Echenique, F., Wilson, A. J., & Yariv, L. (2016). Clearinghouses for two-sided matching: An experimental study. Quantitative Economics, 7, 449–482.
Embrey, M., Fréchette, G. R., & Yuksel, S. (2017). Cooperation in the finitely repeated prisoner’s dilemma. The Quarterly Journal of Economics, 133(1), 509–551.
Erev, I., & Roth, A. E. (1998). Predicting how people play games: Reinforcement learning in experimental games with unique, mixed strategy equilibria. American Economic Review, 88, 848–881.
Featherstone, C. R., Mayefsky, E., & Sullivan, C. D. (2019). Learning to manipulate: Out-of-equilibrium truth-telling in matching markets. Working Paper.
Fischbacher, U. (2007). z-tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178.
Friedman, M. (1953). Essays in positive economics. Chicago: University of Chicago Press.
Gale, D., & Sotomayor, M. (1985). Ms. machiavelli and the stable matching problem. American Mathematical Monthly, 92(4), 261–268.
Hakimov, R., & Kübler, D. (2020). Experiments on centralized school choice and college admissions: A survey. Experimental Economics. https://doi.org/10.1007/s10683-020-09667-7.
Harrison, G. W., & McCabe, K. A. (1996). Stability and preference distortion in resource matching: An experimental study of the marriage market. Research in Experimental Economics, 6, 53–129.
Harsanyi, J. C., & Selten, R. (1988). A general theory of equilibrium selection in games. Cambridge: MIT Press.
Hassidim, A., Marciano, D., Romm, A., & Shorrer, R. I. (2017). The mechanism is truthful, why aren’t you? American Economic Review, 107(5), 220–24.
Healy, P. J. (2017). Epistemic experiments: Utilities, beliefs, and irrational play. Working Paper.
Immorlica, N., & Mahdian, M. (2005). Marriage, honesty, and stability. In Proceedings of the sixteenth annual ACM-SIAM symposium on discrete algorithms (pp. 53–62).
Kartal, M., & Müller, W. (2018). A new approach to the analysis of cooperation under the shadow of the future: Theory and experimental evidence. Working Paper.
Klijn, F., Pais, J., & Vorsatz, M. (2013). Preference intensities and risk aversion in school choice: A laboratory experiment. Experimental Economics, 16(1), 1–22.
Kojima, F. (2006). Risk-dominance and perfect foresight dynamics in n-player games. Journal of Economic Theory, 128(1), 255–273.
Kojima, F., & Pathak, P. A. (2009). Incentives and stability in large two-sided matching markets. American Economic Review, 99(3), 608–627.
Lee, S. M. (2016). Incentive compatibility of large centralized matching markets. Review of Economic Studies, 84(1), 444–463.
Li, S. (2017). Obviously strategy-proof mechanisms. American Economic Review, 107(11), 3257–87.
Morris, S., Rob, R., & Shin, H. S. (1995). p-dominance and belief potential. Econometrica, 63, 145–157.
Rankin, F. W., Van Huyck, J. B., & Battalio, R. C. (2000). Strategic similarity and emergent conventions: Evidence from similar stag hunt games. Games and Economic Behavior, 32(2), 315–337.
Rees-Jones, A. (2018). Suboptimal behavior in strategy-proof mechanisms: Evidence from the residency match. Games and Economic Behavior, 108, 317–330.
Roth, A. E., & Peranson, E. (1999). The redesign of the matching market for American physicians: Some engineering aspects of economic design. American Economic Review, 89(4), 748–780.
Roth, A. E., & Rothblum, U. G. (1999). Truncation strategies in matching markets—In search of advice for participants. Econometrica, 67(1), 21–43.
Roth, A. E., & Sotomayor, M. A. O. (1992). Two-sided matching: A study in game-theoretic modeling and analysis. Cambridge: Cambridge University Press.
Roth, A. E., & Vate, J. H. V. (1991). Incentives in two-sided matching with random stable mechanisms. Economic Theory, 1(1), 31–44.
Van Huyck, J. B., Battalio, R. C., & Beil, R. O. (1990). Tacit coordination games, strategic uncertainty, and coordination failure. American Economic Review, 80(1), 234–248.
Vespa, E., & Wilson, A. J. (2016). Experimenting with equilibrium selection in dynamic games. Working Paper.
Acknowledgements
We thank Ryan Oprea, Leeat Yariv and two anonymous referees for valuable comments. We gratefully acknowledge financial support from the International Foundation for Research in Experimental Economics (IFREE). Prior to conducting the study, the authors obtained ethical approval from the Institutional Review Board (IRB) of both George Mason University and the California Institute of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix
Appendix
1.1 Proof of Proposition 1
Proof
Let T denote the profile of reported preferences in which each worker w truncates her preference list by removing all firms ranked below \(\mu _W(w)\). By Theorem 4.17 of Roth and Sotomayor (1992), T is a Nash equilibrium and it produces the matching \(\mu _W\). Suppose another Nash equilibrium Q payoff-dominates T. Let \(\mu\) denote the matching that is produced by Q. Since Q is a Nash equilibrium, we know by Theorem 4.16 of Roth and Sotomayor (1992) that the matching \(\mu\) is also stable with respect to the true preferences P. Since Q payoff-dominates T, we know that \(u_w(\mu (w)) > u_w(\mu _W(w))\) for all \(w\in {W}\). We have arrived at a contradiction, since \(\mu _W\) is the W-optimal stable matching with respect to P. Thus, there is no other Nash equilibrium that payoff-dominates T. We conclude that T is payoff-dominant. □
1.2 Proof of Proposition 2
Proof
Let Q denote the profile of reported preferences in which each worker w reports a preference list \(Q_w\) that ranks \(\mu _F(w)\) in the first position (regardless of the length of the list). Each preference list \(Q_w\) is clearly a permutation since \(\mu _F(w)\) is not at the head of any worker’s true preference list.Footnote 30 It is straightforward to see that Q produces the matching \(\mu _F\).
We argue that the profile of reported preferences Q constitutes a Nash equilibrium.Footnote 31 To see this, suppose that Q is not a Nash equilibrium. Then, there exists some worker w who can deviate and report a preference list \(Q^\prime _w\), which leads to a new profile of reported preferences \(Q^\prime =(Q_{-w},Q^\prime _w)\) and a new matching \(\mu ^\prime\) such that \(u_w(\mu ^\prime (w)) > u_w(\mu _F(w))\). Let \(f=\mu ^\prime (w)\). Then firm f must have been matched to a worker she prefers to w at \(\mu _F\), otherwise (f, w) would have blocked the matching \(\mu _F\) under the true preferences P. But now firm f and worker \(\mu _F(f)\) block the matching \(\mu ^\prime\) under the reported preferences \(Q^\prime\), which is a contradiction. Therefore, Q is a Nash equilibrium. Furthermore, Q is payoff-dominated by the truncation equilibrium constructed in Proposition 1. □
Rights and permissions
About this article
Cite this article
Castillo, M., Dianat, A. Strategic uncertainty and equilibrium selection in stable matching mechanisms: experimental evidence. Exp Econ 24, 1365–1389 (2021). https://doi.org/10.1007/s10683-021-09702-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10683-021-09702-1