Asymptotic behavior of a discrete-time density-dependent SI epidemic model with constant recruitment

Abstract

We use the epidemic threshold parameter, ${{\mathcal {R}}}_{0}$, and invariant rectangles to investigate the global asymptotic behavior of solutions of the density-dependent discrete-time SI epidemic model where the variables $S_{n}$ and $I_{n}$ represent the populations of susceptibles and infectives at time $n = 0,1,\ldots$, respectively. The model features constant survival “probabilities” of susceptible and infective individuals and the constant recruitment per the unit time interval $[n, n+1]$ into the susceptible class. We compute the basic reproductive number, ${{\mathcal {R}}}_{0}$, and use it to prove that independent of positive initial population sizes, ${{\mathcal {R}}}_{0}<1$ implies the unique disease-free equilibrium is globally stable and the infective population goes extinct. However, the unique endemic equilibrium is globally stable and the infective population persists whenever ${{\mathcal {R}}}_{0}>1$ and the constant survival probability of susceptible is either less than or equal than 1/3 or the constant recruitment is large enough.

1 Introduction

Fatal infectious diseases, such as the ongoing coronavirus (COVID-19) pandemic and Ebola virus diseases, have been part of the human and animal condition since time immemorial. In this paper, we use a discrete-time fatal SI disease model in a variable population, proposed in 2002 by Richard Levine of Harvard School of Public Health, to obtain biologically relevant conditions for the global endemicity (global convergence to a unique interior equilibrium point) of the fatal disease and conditions for the global elimination (global convergence to a unique boundary equilibrium with no infectious individuals) of the disease in the population.

As in [19], we assume that an infectious disease invades and subdivides the target population into two classes: susceptibles (non-infectives) and infectives. Prior to the time of disease invasion, the susceptible population is assumed to have constant recruitment per unit time interval. The transition from susceptible to infective is via a density-dependent “escape” function that depends on the infective population. Our primary focus is on the impact of the survival rates of the susceptibles and infectives on the persistence or control of infectious diseases.

In most discrete-time nonlinear epidemic models, the question of the global stability of the endemic equilibrium or global convergence to a unique interior equilibrium point, when the basic reproduction number, ${\mathcal {R}} _{0}$, is greater than 1, has largely been open. The novelty of our work in this paper, is our use of the method of embedded invariant rectangles to obtain global stability of the unique endemic equilibrium in a nonlinear SI epidemic model, where ${\mathcal {R}}_{0}>1.$ For simplicity, in our fatal SI disease model, we use a Poisson process, a decreasing exponential function of the population of infectious individuals, to describe the escape function of the susceptible individuals from the infectious individuals. Furthermore, in our SI model, we assume that the birth rate or recruitment is constant. However, our methods are general and can be applied to other epidemic models with more general escape and recruitment functions.

The model considered in this paper is one of the first discrete models which studies the effect of recruitment on the resulting epidemics dynamics. In general the presence of recruitment makes mathematical analysis more complicated. The results presented here may also initiate further research in models when the recruitment is non-constant. To prove convergence and stability we use the powerful method of embedded rectangles which takes advantage of monotonicity of transition functions that leads to the problem of solving system of transcendental equations. Such system can be always solved numerically for specific choice of parameters. Thus the convergence to the solution of such system depends on the numerical method used. The precise asymptotic behavior of solutions converging to the equilibrium solution of the model presented can be derived from formulas in [13] or [19] and is given in Theorem 5 of this paper. Our results correct the error in a related paper [11].

The paper is organized as follows. In Sect. 2, we introduce the SI epidemic model for the study. The model, a system of two nonlinear difference equations, describes the population dynamics of the susceptible and infective populations. In Sect. 3, the basic reproductive number, ${\mathcal {R}}_{0}$, is introduced and used to guarantee the existence of the endemic equilibrium. ${\mathcal {R}}_{0}$ is used to predict the local persistence or extinction of the infective population in Sect. 4. In Sect. 5, we use invariant rectangles to obtain global persistence or extinction in the density-dependent SI epidemic model. The implications of our results are discussed in Sect. 6.

2 Density-dependent SI model with constant recruitment

In this section, we construct a simple density-dependent two epidemiological classes discrete-time susceptible-infective $\left( SI\right)$ epidemic process. At each time $n\in \{0,1,...\}$, we let $S_{n}$ denote the population of susceptibles and $I_{n}$ denotes the population of the infected; assumed infectious. We assume that susceptibles and infected individuals respectively survive with constant probabilities $a\in (0,1)$ and $b\in (0,1)$ per generation.

Let $\phi :[0,\infty )\rightarrow [0,1]$ be a monotone concave probability function with $\phi (0)=1,\phi ^{\prime }(I_{n})<0$ and $\phi ^{\prime \prime }(I_{n})>0$ for all $I_{n}\in [0,\infty ).$ We assume the susceptible individuals become infected with nonlinear probability $\left( 1-\phi \left( I_{n}\right) \right)$ per each unit time interval $[n, n+1]$. That is, $\beta$ models the impact of prevalence on $\phi$. When infections are modeled as Poisson processes, then the “escape” function $\phi \left( I_{n}\right) =e^{-\beta I_{n}}$, where $\beta >0$ is the disease transmission rate per each unit time interval [8,9,10,11, 19].

The density dependent discrete-time model implicitly assumes three distinct temporal phases. Per each unit time interval, a fraction of each class is removed; susceptibles become infected; and a constant number of “new” recruits join the susceptible class. This important assumption distinguishes the discrete-time model from a similar continuous-time differential equation model. Typically, continuous-time differential equation models with similar well-defined distinct temporal phases are non-autonomous. Taking into account the temporal ordering of events, we derive our model in the following three steps.

• 1. Death/survival:

  $$\begin{aligned} \left. \begin{array}{lll} S_{n}^{\prime } &{} = &{} aS_{n}, \\ I_{n}^{\prime } &{} = &{} bI_{n}. \end{array} \right\} \end{aligned}$$

  (1)

  That is, after survival (death), $S_{n}^{\prime }$ denotes the susceptible and $I_{n}^{\prime }$ denotes the infected individuals.

• 2. Disease transmission and recovery:

  $$\begin{aligned} \left. \begin{array}{lll} S_{n}^{\prime \prime } &{} = &{} e^{-\beta I_{n}}S_{n}^{\prime }=ae^{-\beta I_{n}}S_{n}, \\ I_{n}^{\prime \prime } &{} = &{} \left( 1-e^{-\beta I_{n}}\right) S_{n}^{\prime }+I_{n}^{\prime }=a\left( 1-e^{-\beta I_{n}}\right) S_{n}+bI_{n}. \end{array} \right\} \end{aligned}$$

  (2)

  After disease transmission, recovery and survival (death), $S_{n}^{\prime \prime }$ denotes the susceptibles and $I_{n}^{\prime \prime }$ denotes the infected individuals.

• 3. Reproduction (constant number of new recruits into S):

  $$\begin{aligned} \left. \begin{array}{lll} S_{n}^{\prime \prime \prime } &{} = &{} S_{n}^{\prime \prime }+B=ae^{-\beta I_{n}}S_{n}+B, \\ I_{n}^{\prime \prime \prime } &{} = &{} I_{n}^{\prime \prime }=a\left( 1-e^{-\beta I_{n}}\right) S_{n}+bI_{n}. \end{array} \right\} \end{aligned}$$

  (3)

  That is, after survival, disease transmission and reproduction, $S_{n}^{\prime \prime \prime }$ denotes the susceptibles and $I_{n}^{\prime \prime \prime }$ denotes the infected individuals.

Our assumptions and notation lead to the following SI epidemic model:

$$\begin{aligned} \left. \begin{array}{lll} S_{n+1} &{} = &{} ae^{-\beta I_{n}}S_{n}+B, \\ I_{n+1} &{} = &{} a\left( 1-e^{-\beta I_{n}}\right) S_{n}+bI_{n}, \end{array} \right\} \end{aligned}$$

(4)

where $0<a,b<1$, $\beta , B>0,$ $S_{0}\ge 0$ and $I_{0}\ge 0$. Any cyclic permutation of the three distinct temporal phases leads to a model that is topologically conjugate to Model (4). However, any non-cyclic permutation of the three distinct temporal phases may lead to models that are not topologically conjugate to Model (4).

Below, we summarize some of the underlying assumptions in Model (4).

(a)	There is no vertical transmission;
(b)	There is no acquired immunity;
(c)	There is no latent period (or it is very short);
(d)	Transmission is density dependent rather than frequency dependent.

Theoretical and empirical investigations have been done on comparing these assumptions. In continuous-time epidemic models, it is known that these assumptions are not universally applicable [6, 19].

Model (4) is a deterministic discrete-time SI epidemic model and has no “probability” of transmission. The assumption of deterministic dynamics is valid in a large population, where stochasticity is unimportant. This assumption places a constraint on the applicability of the model. Stochastic transmission (including a Poisson process) in a small population (close to extinction), for example, would not be described by the SI model. To study the qualitative dynamics of Model (4), we let $\beta I_n = I_n ^{\prime }$. Then Model (4) reduces to the following system of equations:

$$\begin{aligned} \left. \begin{array}{lll} S_{n+1} &{} = &{} a e^{-I_{n}^{\prime }} S_{n}+B, \\ I_{n+1}^{\prime } &{} = &{} a \beta \left( 1-e^{- I_{n}^{\prime }}\right) S_{n}+bI_{n}^{\prime }. \end{array} \right\} \end{aligned}$$

(5)

To simplify the notation, we drop the prime notation so that Model (5) becomes the following system

$$\begin{aligned} \left. \begin{array}{lll} S_{n+1} &{} = &{} a e^{-I_{n}} S_{n}+B, \\ I_{n+1} &{} = &{} a \beta \left( 1-e^{- I_{n}}\right) S_{n}+bI_{n}. \end{array} \right\} \end{aligned}$$

(6)

We will study Model (6) with initial population sizes

$$\begin{aligned} (S_0, I_0) \in [0, \infty )^2. \end{aligned}$$

Model (6) predicts $(S_{n+1}, I_{n+1})$, the vector of population sizes at time $(n+1)$, from knowledge of the vector of population sizes at time n, $(S_{n}, I_{n})$. We will compute the basic reproduction number for model (6), ${\mathcal {R}}_{0}$, and use it to study disease persistence or extinction. Since ${\mathcal {R}}_{0}$ is a dimensionless quantity, without loss of generality, we assume that the unit of time in Model (6) is 1 year.

There are several papers on two dimensional systems of difference equations modelling epidemics such as [2,3,4,5, 8,9,10, 19]. However, most of these papers assume the invariance of the sum of susceptibles and infectives over the course of time. That is, in these studies

$$\begin{aligned} S_{n+1}+I_{n+1}=S_{n}+I_{n}=constant,\quad n=0,1,\ldots . \end{aligned}$$

In this paper we relax this assumption. It is clear that Model (6) satisfies the following equation.

$$\begin{aligned} S_{n+1}+I_{n+1}=aS_{n}\left( (1- \beta ) e^{- I_n} + \beta \right) +bI_{n}+B,\quad n=0,1,\ldots . \end{aligned}$$

It is also clear that

$$\begin{aligned} I_{0}=0\Rightarrow I_{n}=0,\quad n=1,2,\ldots . \end{aligned}$$

Thus, when $I_{0}=0$ then Eq. (5) implies that $S_{n}$ satisfies the linear difference equation

$$\begin{aligned} S_{n+1}=aS_{n}+B,\quad n=0,1,\ldots . \end{aligned}$$

Consequently,

$$\begin{aligned} S_{n}=a^{n}S_{0}+\frac{B}{1-a}\rightarrow \frac{B}{1-a},\quad \text{ as } \;\;n\rightarrow \infty . \end{aligned}$$

In the absence of the disease in Model (6), $I_n=0$ at each time n and

$$\begin{aligned} \lim _{n \rightarrow \infty } S_n={\bar{S}}= \frac{B}{1-a}. \end{aligned}$$

That is, in the absence of the disease, the susceptible population persists on the positive equilibrium point, ${\bar{S}}$. The disease-free equilibrium point of the Model (6) is

$$\begin{aligned} E_{1}= \left( \frac{B}{1-a},0 \right) . \end{aligned}$$

(7)

The paper [11] is a paper wich analyzes similar system with $b=0$ and uses similar methods of analysis but it contains a computational error which makes the main result incorrect. Our model applies also tto the case $b=0$ and it corrects the results in [11].

3 ${\mathcal {R}}_0$ and equilibrium points

Equilibrium points $\left( {\overline{S}},{\overline{I}}\right)$ of Model (6) are solutions of the system of equations

$$\begin{aligned} \left\{ \begin{array}{l} {\overline{S}}=a{\overline{S}}e^{-{\overline{I}}}+B \\ {\overline{I}}=a \beta {\overline{S}}\left( 1-e^{-{\overline{I}}}\right) +b{\overline{I}}. \end{array} \right. \end{aligned}$$

(8)

One disease-free solution of this system is $E_{1}=\left( \frac{B}{1-a} ,0\right)$ for all values of the parameters a, b, and B. Next, we obtain another equilibrium point, an endemic equilibrium.

First equation of System (8) gives

$$\begin{aligned} a {\overline{S}}e^{-{\overline{I}}}={\overline{S}}-B. \end{aligned}$$

(9)

Replacing the left-hand side of (9) in the second equation of (8) we obtain

$$\begin{aligned} {\overline{S}}=\frac{\left( 1-b\right) {\overline{I}}-\beta B}{(a-1) \beta }. \end{aligned}$$

(10)

Taking in account that we are looking for the positive solution $\left( {\overline{S}},{\overline{I}}\right) \in {\mathbf {R}}_{+}^{2}$, (10) implies

$$\begin{aligned} {\overline{I}}<\frac{\beta B}{1-b}. \end{aligned}$$

(11)

Replacing (10) in second equation of system (8) we obtain

$$\begin{aligned} \left( 1-b\right) {\overline{I}}-a\left( \left( 1-b\right) {\overline{I}} -\beta B\right) e^{-{\overline{I}}}-a \beta B=0. \end{aligned}$$

Now, we will show that the last equation has unique positive root ${\overline{I}}$.

In fact, we will show that

$$\begin{aligned} \left( \exists !\;{\overline{I}}>0\right) :\;h\left( {\overline{I}}\right) =0, \end{aligned}$$

(12)

where

$$\begin{aligned} h\left( x\right) =\left( 1-b\right) x-a\left( \left( 1-b\right) x- \beta B\right) e^{-x}-a \beta B. \end{aligned}$$

Notice that

$$\begin{aligned} h\left( 0\right) =0,\quad \underset{x\rightarrow +\infty }{\lim }h\left( x\right) =+\infty . \end{aligned}$$

(*)

To prove (12) it is enough to show that there exists exactly one $x_{0}>0$ where the function $h\left( x\right)$ attains its minimum.

Derivative of $h\left( x\right)$ has the form

$$\begin{aligned} h^{\prime }\left( x\right) =\left( 1-b\right) \left( 1-a\left( 1-x+\frac{\beta B}{ 1-b}\right) e^{-x}\right) . \end{aligned}$$

The critical point of h satisfies:

$$\begin{aligned} e^{x}=a+\frac{a \beta B}{1-b}-a x. \end{aligned}$$

The last equation has a positive solution if and only if

$$\begin{aligned} a+\frac{a \beta B}{1-b}>1. \end{aligned}$$

The basic reproductive number is

$$\begin{aligned} {\mathcal {R}}_{0}=\frac{a \beta B}{\left( 1-a\right) \left( 1-b\right) }. \end{aligned}$$

That is, Model (6) has an endemic equilibrium if and only if ${\mathcal {R}}_{0}>1$.

In ${\mathcal {R}}_{0}$,

$$\begin{aligned} \frac{1}{(1-a)(1-b)}=\frac{1}{1-(a+b-ab)}=1+\left( a+b-ab\right) +\left( a+b-ab\right) ^{2}+\cdot \cdot \cdot \end{aligned}$$

is the product of the average death adjusted infectious period in generations; $a \beta$ is the proportion that can be invaded by the disease; and B is the constant recruitment function per each unit time interval. Thus, ${\mathcal {R}}_{0}$ gives the average number of secondary infections due to small initial infective individuals over their life-time.

Thus, if ${\mathcal {R}}_{0}>1$, there exists $x_{0}>0$ such that $h^{\prime }\left( x_{0}\right) =0$, and consequently there exists unique equilibrium point ${\overline{I}}>0$. Let us check that ${\overline{I}}$ satisfies the condition (11). Otherwise, ${\overline{I}}>\frac{B}{1-b}$ and using the equation $h\left( {\overline{I}}\right) =0$ we obtain

$$\begin{aligned} 0= & {} \left( 1-b\right) {\overline{I}}-a\left( 1-b\right) {\overline{I}}e^{- {\overline{I}}}+a \beta Be^{-{\overline{I}}}-a \beta B\\\ge & {} \beta B-a \beta Be^{-{\overline{I}}}+a \beta Be^{-{\overline{I}}}-a \beta B= \beta B\left( 1-a\right) , \end{aligned}$$

which is a contradiction.

So, Model (6) has a disease-free equilibrium point $E_{1}=\left( \frac{B}{1-a },0\right)$ for all values of parameters $a\in (0,1),b\in (0,1)$, and $B>0$ , and has a unique endemic equilibrium point $E_{2}=\left( {\overline{S}}, {\overline{I}}\right)$, with ${\overline{S}}>0$ and ${\overline{I}}>0$ if and only if ${\mathcal {R}}_{0}>1$. The endemic equilibrium satisfies Eq. (11). We summarize this in the following result.

Lemma 1

In Model (6),

• (a) $E_{1}=\left( \frac{B}{1-a},0\right)$ is the unique disease-free equilibrium point.

• (b) $E_{2}=\left( {\overline{S}},{\overline{I}}\right)$ is the unique endemic equilibrium point if and only if ${\mathcal {R}}_{0}>1$, where ${\overline{S}}>0$ and $0<{\overline{I}}<\frac{\beta B}{1-b}$ are the positive solutions of system (8).

4 Disease extinction versus disease persistence

In this section, we use local stability analysis of the equilibrium points of Model (6) to obtain conditions for disease persistence and extinction [9, 10]. The Jacobian matrix, $J_{T}\left( S,I\right)$, at the arbitrary point (S, I) is

$$\begin{aligned} J_{T}\left( S,I\right) =\left[ \begin{array}{ll} ae^{-I} &{}\quad -aSe^{-I} \\ a \beta \left( 1-e^{-I}\right) &{}\quad a \beta Se^{-I}+b \end{array} \right] . \end{aligned}$$

(13)

The characteristic equation of $J_{T}\left( S,I\right)$ is

$$\begin{aligned} \lambda ^{2}-p\lambda -q=0, \end{aligned}$$

where

$$\begin{aligned} p=ae^{-I}+a \beta Se^{-I}+b,\quad q=-ae^{-I}\left( b+a \beta S\right) . \end{aligned}$$

(14)

Using (13), we obtain that Jacobian matrix evaluated at the equilibrium point $E_{1}=\left( \frac{B}{1-a},0\right)$, is

$$\begin{aligned} J_{T}\left( E_{1}\right) =\left[ \begin{array}{ll} a &{}\quad -\frac{aB}{1-a} \\ 0 &{}\quad \frac{aB}{1-a}+b \end{array} \right] . \end{aligned}$$

The characteristic roots of this equation are

$$\begin{aligned} \lambda _{1}=a\quad \text {and}\quad \lambda _{2}=b+\frac{a \beta B}{1-a}. \end{aligned}$$

This implies the following results.

• (i)
  $$\begin{aligned} \lambda _{2}<1\Leftrightarrow b+\frac{a \beta B}{1-a}<1\Leftrightarrow {\mathcal {R}}_{0}<1, \end{aligned}$$

  in which case the equilibrium $E_{1}$ is locally asymptotically stable.

• (ii)
  $$\begin{aligned} \lambda _{2}>1\Leftrightarrow {\mathcal {R}}_{0}>1, \end{aligned}$$

  in which case the equilibrium $E_{1}$ is not locally asymptotically stable, and more precisely it is a saddle point.

• (iii)
  $$\begin{aligned} \lambda _{2}=1\Leftrightarrow {\mathcal {R}}_{0}=1, \end{aligned}$$

  in which case the equilibrium $E_{1}$ is not hyperbolic.

Local stability analysis for the equilibrium point $E_{2}=({\overline{S}}, {\overline{I}})$ is algebraically complicated. In view of the result on linearized stability, this equilibrium point is locally asymptotically stable if and only if

$$\begin{aligned} \left| \lambda _{1,2}\right|<1\Leftrightarrow \left| p\right|<1-q<2, \end{aligned}$$

(15)

where p and q are given by (14), and $\lambda _{1,2}$ are the zeros of the corresponding characteristic equation.

Next, we express condition (15) in terms of the model parameters and endemic equilibrium point. The straight-forward calculation shows that $\left| p\right| <1-q$ is equivalent to

$$\begin{aligned} \beta \left( 1-a\right) {\overline{S}}^{2}+ \left( 1- b + \beta ((a-1)B +b-1\right) {\overline{S}}-B\left( 1-b\right) <0 \end{aligned}$$

which holds for ${\overline{S}}$ which satisfies

$$\begin{aligned} \overline{S}<S_{+}, \end{aligned}$$

(16)

where

$$\begin{aligned} S_{\pm }=\frac{\left( 1-a\right) B\pm \sqrt{D}}{2\left( 1-a\right) } \end{aligned}$$

(17)

and

$$\begin{aligned} D=\left( 1-b + \beta ((a-1)B + b - 1))\right) ^{2}+4 \beta B\left( 1-a\right) \left( 1-b\right) . \end{aligned}$$

(18)

Thus, $S_{-}<0$ and $S_{+}>0$.

Using the fact that $\overline{S}\in J_{1}=\left[ B,\frac{B}{1-a}\right]$ we obtain

$$\begin{aligned} \overline{S}<\min \left\{ \frac{B}{1-a},S_{+}\right\} . \end{aligned}$$

(19)

Notice that, $q>-1$ is equivalent to $ae^{-\overline{I}}\left( b+a \overline{S}\right) <1$ which in turn is equivalent to $a \beta {\overline{S}}^{2}+\left( b - \beta -a \beta B\right) {\overline{S}}-b B<0.$

The last inequality holds for ${\overline{S}}$ which satisfies

$$\begin{aligned} {\overline{S}}<S_{+}^{*}, \end{aligned}$$

(20)

where

$$\begin{aligned} S_{\pm }^{*}=\frac{a \beta B+\beta -b\pm \sqrt{\Delta }}{2a \beta } \end{aligned}$$

(21)

and

$$\begin{aligned} \Delta =\left( aB+1-b\right) ^{2}+4abB, \end{aligned}$$

(22)

because $S_{-}^{*}<0,$ $S_{+}^{*}>0$.

Again, taking in account ${\overline{S}}\in J_{1}=\left[ B,\frac{B}{1-a}\right]$, condition (20) gives

$$\begin{aligned} {\overline{S}}<\min \left\{ \frac{B}{1-a},S_{+}^{*}\right\} . \end{aligned}$$

(23)

The component of the equilibrium ${\overline{S}}$ must satisfy conditions (19) and (23). Thus, the following should hold

$$\begin{aligned} {\overline{S}}<\min \left\{ \frac{B}{1-a},S_{+},S_{+}^{*}\right\} . \end{aligned}$$

(24)

Notice that the inequality

$$\begin{aligned} \frac{B}{1-a}>S_{+}, \end{aligned}$$

is always satisfied, because it is equivalent to ${\mathcal {R}}_{0}>1$. Now, we check the inequality

$$\begin{aligned} \frac{B}{1-a}<S_{+}^{*} = \frac{a \beta B+ \beta -b+\sqrt{\Delta }}{2a \beta }. \end{aligned}$$

This inequality is equivalent to

$$\begin{aligned} \frac{a \beta B\left( 1+a\right) }{\left( 1-a\right) }-\left( \beta -b\right) <\sqrt{ \Delta }. \end{aligned}$$

(25)

Left hand side of (25) is positive, since otherwise

$$\begin{aligned} \frac{a \beta B\left( 1+a\right) }{\left( 1-a\right) }-\left( \beta -b\right)<0\Rightarrow {\mathcal {R}}_{0}<\frac{1}{a+1}, \end{aligned}$$

which is impossible, in view of Lemma 1. This implies

$$\begin{aligned} 1<{\mathcal {R}}_{0}<\frac{1}{a+1}, \end{aligned}$$

which is a contradiction.

Thus, (24) is equivalent to

$$\begin{aligned} B<\frac{\left( 1-a\right) \left( 1-ab\right) }{a^{2}}. \end{aligned}$$

Using the fact that ${\mathcal {R}}_{0}>1$, we obtain:

$$\begin{aligned} \frac{\left( 1-a\right) \left( 1-b\right) }{a^{{}}}<B<\frac{\left( 1-a\right) \left( 1-ab\right) }{a^{2}}\Rightarrow \frac{B}{1-a}<S_{+}^{*}, \end{aligned}$$

and

$$\begin{aligned} S_{+}<\frac{B}{1-a}<S_{+}^{*}. \end{aligned}$$

In this case, the condition for the local asymptotic stability of the equilibrium point $E_{2}=({\overline{S}},{\overline{I}})$, implies:

$$\begin{aligned} \frac{\left( 1-a\right) \left( 1-b\right) }{a^{{}}}<B<\frac{\left( 1-a\right) \left( 1-ab\right) }{a^{2}}\text { and }{\overline{S}}<S_{+} \text {.} \end{aligned}$$

In addition, we have:

$$\begin{aligned} B>\frac{\left( 1-a\right) \left( 1-ab\right) }{a^{2}}\Rightarrow S_{+}^{*}<\frac{B}{1-a}, \end{aligned}$$

and Eq. (23) has the form:

$$\begin{aligned} {\overline{S}}<\min \left\{ S_{+},S_{+}^{*}\right\} . \end{aligned}$$

(26)

Taking in account that ${\overline{S}}$ is a function of the parameters a, b, and B and that ${\overline{S}}<\frac{B}{1-a}$ that is, ${\overline{S}}=\Phi \left( a,b,B\right)$, we obtain the following result:

Theorem 1

• (a) In Model (6),

  • (i) if ${\mathcal {R}}_{0}<1$, then $E_{1}$ is locally asymptotically stable,

  • (ii) if ${\mathcal {R}}_{0}=1$, then $E_{1}$ is a non-hyperbolic equilibrium point,

  • (iii) if ${\mathcal {R}}_{0}>1$, then $E_{1}$ is an unstable (saddle) equilibrium point.

• (b) Assume that one of the following conditions is satisfied in Model (6).

  • (i) $1<{\mathcal {R}}_{0}<\frac{\left( 1-ab\right) }{a(1-b)}$ and ${\overline{S}}=\Phi \left( a,b,B\right) <S_{+}$ or

  • (ii) ${\mathcal {R}}_{0}>\frac{\left( 1-ab\right) }{a(1-b)}>1$ and ${\overline{S}}=\Phi \left( a,b,B\right) <\min \left\{ S_{+},S_{+}^{*}\right\}$.

  Then $E_{2}$ is locally asymptotically stable and the disease is persistent.

By Theorem 1, ${\mathcal {R}}_{0}<1$ implies local disease extinction while $\mathfrak {R}_{0}>1$ implies local disease persistence. In the next section, we explore conditions for global disease extinction and persistence in Model (6). The relative sensitivities of ${\mathcal {R}}_{0}$ to the survival rates of infectives and susceptibles satisfy

$$\begin{aligned} \frac{\frac{\partial {\mathcal {R}}_{0}}{\partial a}}{\frac{\partial {\mathcal {R}}_{0}}{ \partial b}}=\frac{\left( 1-b\right) }{a(1-a)}\text {.} \end{aligned}$$

Thus, in Model (6), ${\mathcal {R}}_{0}$ is more sensitive to survival rate of the susceptible individuals than to that of the infectives if $(1-b)>a(1-a)$.

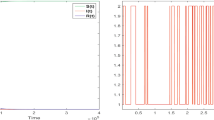
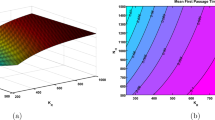
Figure 1 shows plot of the basic reproductive number as a function of a and b for fixed values of $\beta B$. The region where ${\mathcal {R}}_{0}<1$ is larger for smaller values of $\beta B$. Figure 2 shows the typical trajectory of the solutions of Model (6) when ${\mathcal {R}}_{0}>1$, where part (a) shows $S_n$ and $I_n$ as functions of n while part (b) shows the trajectory $(S_n,I_n)$ in the phase plane. Convergence is very fast and it depends on the size of ${\mathcal {R}}_{0}$. See Theorem 5 for precise formulation.

Fig. 1

Graph of ${\mathcal {R}}_{0}$ as a function of a and b versus 1, where a $\beta B=0.5$ and b $\beta B=4$

Fig. 2

a First 10 terms of time series plot of $S_n$ (green) and $I_n$ (red) versus n where $a=0.4, b=0.2, \beta =1, B=5$ and ${\mathcal {R}}_{0}=4.1667$; b Plot of $(S_n,I_n)$ in the phase plane. The convergence is very fast because of the size of ${\mathcal {R}}_{0}$

5 Global disease persistence and invariant rectangles

In this section, we use invariant rectangles of Model (6) to obtain conditions for global disease persistence. An invariant rectangle for the planar system

$$\begin{aligned} \left\{ \begin{array}{l} x_{n+1}=f\left( x_{n},y_{n}\right) \\ y_{n+1}=g\left( x_{n},y_{n}\right) , \end{array} \right. \quad n=0,1,\ldots , \end{aligned}$$

(27)

is a rectangle ${{\mathcal {R}}}=[L_{1},U_{1}]\times [L_{2},U_{2}]$ with the property that if a single point $(x_{N},y_{N})$ of the solution fall in ${{\mathcal {R}}}$ then all the subsequent terms of the solution also belong to ${{\mathcal {R}}}$. In other words, ${{\mathcal {R}}}$ is an invariant rectangle for System (27) if $(x_{N},y_{N})\in {{\mathcal {R}}}$ for some $N\ge 0$, then $(x_{n},y_{n})\in {{\mathcal {R}}}$ for every $n>N$. In this case $[L_{1},U_{1}]$ is an invariant interval for $x_{n}$ and $[L_{2},U_{2}]$ is an invariant interval for $y_{n}$. Similarly, one can define an invariant set in $R^{2}$.

The method of invariant intervals has been widely used to prove the global attractivity in the case of the second order difference equation

$$\begin{aligned} x_{n+1}=f(x_{n},x_{n-1}),\quad n=0,1,\ldots , \end{aligned}$$

see [16,17,18,19] and references therein.

The following theorem gives convergence results in the case when there exists an invariant rectangle and the functions f and g satisfy some additional conditions. This result which appeared first in [18] is a special case of the more general result proved in [17].

Theorem 2

Let [a, b], [c, d] be the intervals of real numbers and assume that

$$\begin{aligned} f : [a,b] \times [c, d] \rightarrow [a, b] \quad \text{ and } \quad g : [a,b] \times [c, d]\rightarrow [c, d] \end{aligned}$$

are continuous functions satisfying the following properties:

• (a) f(x, y) is non-decreasing in $x\in [a, b]$ for each $y\in [c, d]$, and f(x, y) is non-increasing in $y\in [c, d]$ for each $x\in [a, b]$;

• (b) g(x, y) is non-decreasing in each of its arguments;

• (c) If $(m_{1},M_{1},m_{2},M_{2})\in ([a,b]\times [c,d])^{2}$ is a solution of the system

$$\begin{aligned} \left\{ \begin{array}{ll} m_{1}=f(m_{1},M_{2}), &{}\quad M_{1}=f(M_{1},m_{2}) \\ &{} \\ m_{2}=g(m_{1},m_{2}), &{}\quad M_{2}=g(M_{1},M_{2}), \end{array} \right. \end{aligned}$$

(28)

then $m_{1}=M_{1}$ and $m_{2}=M_{2}$.

Then System (27) has a unique positive equilibrium $({\overline{x}},{\overline{y}})\in [a,b]\times [c,d]$ and every solution of System (27) which has one point $(x_{n},y_{n})$ in $[a,b]\times [c,d]$ converges to $({\overline{x}},{\overline{y}})$. In addition $({\overline{x}},{\overline{y}})$ is globally asymptotically stable.

Remark 1

One solution of System (28) is the equilibrium of System (27). So condition (c) of Theorem 2 can be reformulated as the condition which guarantees the uniqueness of the equilibrium of System (27). For any specific choice of the parameters in System (27) one can numerically check the uniqueness of the equilibrium of this system. In many cases one can establish the uniqueness of this equilibrium for the whole range of parameters, as we will do here, see also [17,18,19]. However in some cases of applications of Theorem 2 some authors get incorrect results, see [11]. The convergence analysis of some other interesting discrete systems can be found in papers [1, 12, 14, 15].

Now, we will determine an invariant interval for each component of Model (6) separately. If $\left[ L,U\right]$ is an invariant interval for the $S_{n}$ component, then the following inequalities should hold

$$\begin{aligned} B\le S_{n+1}=aS_{n}e^{-I_{n}}+B\le aS_{n}+B\le aU+B\le U. \end{aligned}$$

This implies $U\ge \frac{B}{1-a}$ and $L\le B$. In particular, an invariant interval for the $S_{n}$ component is

$$\begin{aligned} J_{1}=\left[ B,\frac{B}{1-a}\right] . \end{aligned}$$

(29)

Thus, if $S_{0}\in J_{1}$, then $S_{n}\in J_{1}$$\left( n=1,2,\ldots \right)$.

An invariant interval for the $I_{n}$ component can be determined in a similar way. Denoting this interval by $\left[ L,U\right]$, we see that the following inequalities should be satisfied.

$$\begin{aligned} 0\le I_{n+1}=a \beta S_{n}\left( 1-e^{-I_{n}}\right) +bI_{n}\le a \beta S_{n}+bI_{n}\le a\frac{\beta B}{1-a}+bU\le U. \end{aligned}$$

The endpoints of an invariant interval satisfy $L\ge 0$ and $U\ge \frac{a \beta B }{\left( 1-a\right) \left( 1-b\right) }$. An invariant interval for the $I_{n}$ component is

$$\begin{aligned} J_{2}=\left[ 0,\frac{a \beta B}{\left( 1-a\right) \left( 1-b\right) }\right] . \end{aligned}$$

(30)

Thus, if $I_{0}\in J_{2}$, then $I_{n}\in J_{2},n=1,2,\ldots$ .

Finally, we obtain an invariant set for the Model (6).

$$\begin{aligned} S_{inv}=J_{1}\times J_{2}=\left[ B,\frac{B}{1-a}\right] \times \left[ 0, \frac{a \beta B}{\left( 1-a\right) \left( 1-b\right) }\right] . \end{aligned}$$

(31)

Thus, if $\left( S_{0},I_{0}\right) \in S_{inv}$, then $\left( S_{n},I_{n}\right) \in S_{inv}$ for $n=1,2,\ldots$. Clearly, in view of a method used to obtain the invariant set $S_{inv}$ this set is also an attracting set in the sense that $(S_{n},I_{n})\in S_{inv}$ for $n=1,2,\ldots$.

Theorem 3

Assume that $a\in (0,1)$ and ${\mathcal {R}}_{0}<1$, then $E_{1}$ is globally asymptotically stable. That is, independent of initial population sizes, the disease goes extinct.

Proof

The proof of this statement is straightforward. Indeed, the second equation of (6) implies

$$\begin{aligned} I_{n+1}\le & {} a \beta (1- e^{-I_n})S_n + b I_n < a \beta I_n S_n + b I_n \\\le & {} a \beta \frac{B}{1-a} I_n + b I_n =\left( \frac{a \beta B}{1-a} +b \right) I_n =C I_n, \end{aligned}$$

that is $I_{n+1} < C I_n, n=1,2\ldots$. Straight-forward calculation shows that

$$\begin{aligned} C<1 \Longleftrightarrow {\mathcal {R}}_{0}<1, \end{aligned}$$

which implies $\lim _{n \rightarrow \infty } I_n =0$. This in turn implies $\lim _{n \rightarrow \infty } S_n =\frac{B}{1-a} = {\bar{S}}$. $\square$

Theorem 4

Assume that $a\in (0, \frac{1}{3}]$ and ${\mathcal {R}}_{0}>1$, then $E_{2}$ is globally asymptotically stable. That is, independent of initial population sizes, the disease does not go extinct.

Proof

First, we show that $E_{2}=\left( {\overline{S}},{\overline{I}}\right)$ belongs to the invariant and attracting set

$$\begin{aligned} S_{inv}= \left[ B,\frac{B}{1-a}\right] \times \left[ 0,\frac{a \beta B}{\left( 1-a\right) \left( 1-b\right) }\right] = \left[ B,\frac{B}{1-a}\right] \times [0, {\mathcal {R}}_{0}]. \end{aligned}$$

• (i) ${\overline{I}}$ is a zero of the function

  $$\begin{aligned} h\left( x\right) =\left( 1-b\right) x-a\left[ \left( 1-b\right) x- \beta B\right] e^{-x}-a \beta B. \end{aligned}$$

  That is, $h\left( {\overline{I}}\right) =0$. We need to show that

  $$\begin{aligned} {\overline{I}}<U=\frac{a \beta B}{\left( 1-a\right) \left( 1-b\right) }, \end{aligned}$$

  which is equivalent to

  $$\begin{aligned} {\overline{I}}<U\Leftrightarrow h\left( U\right) >0. \end{aligned}$$

  Now, straight-forward calculation shows that $h(U)>0$ if and only if

  $$\begin{aligned} e^{\frac{a \beta B}{\left( 1-a\right) \left( 1-b\right) }}>\frac{ 2a-1}{a}=2-\frac{1}{a}. \end{aligned}$$

  Using ${\mathcal {R}}_{0}>1$ we obtain

  $$\begin{aligned} e^{\frac{a \beta B}{\left( 1-a\right) \left( 1-b\right) }}=e^{{\mathcal {R}}_{0}}>e>2-\frac{1}{a}, \end{aligned}$$

  which shows that ${\overline{I}}\in \left[ 0,\frac{a \beta B}{\left( 1-a\right) \left( 1-b\right) }\right] =[0,{\mathcal {R}}_{0}].$

• (ii) Clearly

  $$\begin{aligned} {\overline{S}}=\frac{\beta B - \left( 1-b\right) {\overline{I}}}{\beta (1-a)}<\frac{B}{1-a} \end{aligned}$$

  and

  $$\begin{aligned} {\overline{S}}=a{\overline{S}}e^{-{\overline{I}}}+B>B, \end{aligned}$$

  which completes the proof.

Next, we show that the invariant rectangle for system (6) is

$$\begin{aligned} {\mathcal {R}}=[B, U_S] \times [L_I, U_I], \end{aligned}$$

where $U_S, L_I, U_I$ satisfy

$$\begin{aligned} \frac{L_I}{1 - e^{-L_I}} \le \frac{a \beta B}{1-b}, \quad \frac{B}{1 - a e^{-L_I}} \le U_S \le \frac{(1-b) U_I}{a \beta (1 - e^{-U_I})}. \end{aligned}$$

(*)

In view of the fact that

$$\begin{aligned} G(u)=\frac{u}{1 - e^{-u}},\;\, u \ge 0 \end{aligned}$$

is an increasing function which satisfies $G(u)>1, u>0$ the first inequality in (*) implies $a B \beta >1-b$ and consequently ${\mathcal {R}}_{0}>1$.

By using the fact that $S_n \ge B, n=1,2,\ldots$, we obtain

$$\begin{aligned} S_{n+1} = a e^{-I_n} S_n + B \le a e^{-L_I} U_S + B \le U_S, \end{aligned}$$

which implies $\frac{B}{1 - a e^{-L_I}} \le U_S$. Next we have

$$\begin{aligned} L_I\le & {} a \beta B \big (1 - e^{-L_I}\big ) + b L_I \le I_{n+1} = a \beta \big (1 - e^{-I_n}\big ) S_n + b I_n \\\le & {} a \beta \big (1 - e^{-U_I}\big ) U_S + b U_I \le U_I, \end{aligned}$$

which implies the rest of the inequalities (*). Notice that the inequalities (*) are consistent if $\frac{a \beta B}{1-b}>1$ as the function G satisfies $\lim _{x \rightarrow \infty } G(x)= \infty , \lim _{x \rightarrow 0} G(x)=1$ and $U_S \ge \frac{B}{1-a}$. It is also clear that $U_S$ and $U_I$ can be taken as large as we please.

Now, we will apply Theorem 2. In fact we have to check the condition (c) of Theorem 2 which reduces to the system of equations:

$$\begin{aligned} \left\{ \begin{array}{ll} M_1=a M_1 e^{-m_2}+B, &{}\quad m_1=a m_1 e^{-M_2}+B \\ &{} \\ M_2=a \beta M_1\left( 1-e^{-M_2}\right) +bM_2, &{}\quad m_2=a \beta m_1\left( 1-e^{-m_2}\right) +b m_2. \end{array} \right. \end{aligned}$$

(32)

This system gives

$$\begin{aligned} \begin{array}{ll} M_1=\dfrac{\left( 1-b\right) M_2}{a \beta \left( 1-e^{-M_2}\right) },&\quad m_1=\dfrac{\left( 1-b\right) m_2}{a \beta \left( 1-e^{-m_2}\right) } \end{array} \end{aligned}$$

(33)

and

$$\begin{aligned} B=M_1\left( 1-ae^{-m_2}\right) =m_1\left( 1- a e^{-M_2}\right) . \end{aligned}$$

(34)

Replacing (33) in (34) we get

$$\begin{aligned} \frac{M_2}{\left( 1-e^{-M_2}\right) \left( 1-ae^{-M_2}\right) }=\frac{m_2}{\left( 1-e^{-m_2}\right) \left( 1-ae^{-m_2}\right) }. \end{aligned}$$

(35)

Set

$$\begin{aligned} F\left( x\right) =\frac{x}{\left( 1-e^{-x}\right) \left( 1-ae^{-x}\right) }. \end{aligned}$$

(36)

Then (35) can be written as

$$\begin{aligned} F\left( M_2\right) =F\left( m_2\right) . \end{aligned}$$

(37)

Equation (37) implies that $M_2=m_2$ if we show that the function F(x) is an injection. Notice that

$$\begin{aligned} {\lim }_{x\rightarrow 0}F\left( x\right) =\frac{1}{1-a},\quad {\lim } _{x\rightarrow +\infty }F\left( x\right) =+\infty . \end{aligned}$$

Thus we will check if F(x) has an extreme point for $x>0$. In the case where F(x) has no the extreme points for $x>0$ this function is strictly monotone, and consequently an injection.

Derivative of F(x) is

$$\begin{aligned} F^{\prime }\left( x\right) =\frac{\left( 1-e^{-x}\right) \left( 1-ae^{-x}\right) -xe^{-x}\left[ \left( 1-ae^{-x}\right) +a\left( 1-e^{-x}\right) \right] }{\left( 1-e^{-x}\right) ^{2}\left( 1-ae^{-x}\right) ^{2}}. \end{aligned}$$

Straight-forward calculation shows that the function F(x) has a critical point for a which satisfies:

$$\begin{aligned} a=\frac{\left( 1+x\right) e^{x}-e^{2x}}{1+2x-\left( 1+x\right) e^{x}}. \end{aligned}$$

In this case, we consider a as a function of x. The function a(x) is an increasing function of x which satisfies:

$$\begin{aligned} \underset{x\rightarrow -\infty }{\lim } a\left( x\right) =0,\quad \underset{ x\rightarrow 0}{\lim }\; a\left( x\right) =\frac{1}{3},\quad \underset{ x\rightarrow +\infty }{\lim } a\left( x\right) =+\infty , \end{aligned}$$

which implies

$$\begin{aligned} x>0\Rightarrow a>\frac{1}{3},\quad x\le 0\Rightarrow 0<a\le \frac{1}{3}. \end{aligned}$$

Consequently, the function F(x) for $a\in \left( 0, \frac{1}{3}\right]$ has no critical points for $x>0$, which means that F(x) is injection for $x>0$, which in view of (37) implies that $M_2=m_2$. This in view of (34) implies $M_1 = m_1$. $\square$

Corollary 1

Assume that $a\in (0, 1)$, ${\mathcal {R}}_{0}>1$ and $B, L_I \ge a_0=1.2564$, where $a_0$ is the solution of $a=a(x) =1$, then every solution of the Model (6) converges to the positive equilibrium $E_{2}$.

Proof

Notice that the lowest upper bound of the positive critical points of the function F(x) is a solution of $a(x) =1$ that is $x=1.2564\ldots$. This means that the function F(x) is strictly increasing for all $x>1.2564\ldots$, and for all $a\in (0, 1)$. If both lower bounds of invariant rectangle R are greater than or equal to $a_0$ function F(x) is an injection. $\square$

Remark 2

By using the results in [13] we can give precise asymptotic behavior of solutions of Model (6) and so the rate of convergence as well. As it was proven in Theorem 1 of [13] and Theorem 3.1 in [19] this rate depends on the eigenvalues of the matrix of the linearized system at the given equilibrium, which is attractor. In other words the eigenvalues of Jacobian matrix evaluated at the given equilibrium determine the asymptotic behavior and so the rate of convergence. See Corollary 5 in [13] and Theorem 3.1 in [19]. However in epidemic problems the emphasis is on determination of ${\mathcal {R}}_{0}$, and so we will skip the asymptotic of solutions.

Using the same reasoning as in Theorem 3.1 in [19] we obtain the following estimate of the rate of convergence:

Theorem 5

Assume that a solution $\{\left( x_{n},y_{n}\right) \}$ of (6) converges to an equilibrium E. The error vector ${\mathbf {e}}_{n}=\left( \begin{array}{c} e_{n}^{1} \\ e_{n}^{2} \end{array} \right)$ where $e_{n}^{1}=S_n - {\bar{S}}$ and $e_{n}^{2}=I_n - {\bar{I}}$ of every solution of (6) satisfies both of the following asymptotic relations:

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }\root n \of {\left\| {\mathbf {e}} _{n}\right\| }=\left| \lambda _{1,2}J_{T}\left( E\right) \right| , \end{aligned}$$

(1)

and

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }\frac{\left\| {\mathbf {e}}_{n+1}\right\| }{\left\| {\mathbf {e}}_{n}\right\| }=\left| \lambda _{1,2}J_{T}\left( E\right) \right| . \end{aligned}$$

where $\lambda _{1,2}J_{T}\left( E\right)$ are the characteristic roots of the Jacobian matrix $J_{T}\left( E\right)$ evaluated at E.

In view of Theorem 5 and the fact that $\lambda _2(E_1)<1$ if and only if ${\mathcal {R}}_0<1$, we conclude that the rate of convergence depends on ${\mathcal {R}}_0$. If ${\mathcal {R}}_0$ is much larger than 1 convergence is very fast as well as in the case when ${\mathcal {R}}_0$ is very small positive number, which is in accordance with applications. Small basic reproductive number leads to quick disease eradication while large basic reproductive number leads to epidemics persistence. See Figs. 3, 4 and 5 for the plots of $S_n$ and $I_n$ vs. n and the plot of $(S_n,I_n)$ in phase plane.

Based on extensive simulations we formulate the following conjecture.

Conjecture 1

Assume that $a\in (0, 1)$ and ${\mathcal {R}}_{0}>1$. Then every solution of the Model (6) converges to the positive equilibrium $E_{2}=( {\overline{S}},{\overline{I}})$, and the disease is globally persistent. That is, independent of initial population sizes,

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }S_{n}={\overline{S}},\qquad \underset{ n\rightarrow \infty }{\lim }I_{n}={\overline{I}}. \end{aligned}$$

In view of (7), the S-axis is a part of $W^{s}(E_{1})$-the stable manifold of $E_{1}$.

Fig. 3

First 30 terms of System (6) where a time series $S_n$ and $I_n$ vs n. b the phase plot of $(S_n, I_n)$. Here $a=0.2,b=0.8,B=2, \beta =0.42, {\mathcal {R}}_0=1.05$. Convergence is slow because of the size of ${\mathcal {R}}_{0}$

Fig. 4

First 30 terms of System (6) where a time series $S_n$ and $I_n$ versus n. b the phase plot of $(S_n, I_n)$. Here $a=0.2,b=0.8,B=2, \beta =0.42, {\mathcal {R}}_0=1.0$. Convergence is very slow because of the size of ${\mathcal {R}}_{0}$

Fig. 5

First 30 terms of System (6) where a time series $S_n$(green) and $I_n$(red) versus n. b the phase plot of$(S_n, I_n)$. Here $a=0.6,b=0.8,B=0.1, \beta =1, {\mathcal {R}}_0=0.75$

6 Conclusion

In this paper, we use a simple discrete-time density-dependent SI epidemic model with constant recruitment function and non-constant total population to study the impact of the survival rates of the susceptible and infective individuals on disease transmission dynamics. We compute the basic reproductive number, ${\mathcal {R}}_{0}$, and use it to predict the local persistence or extinction of the infective population. The transmission rates of the susceptibles and infectives are critical model parameters for the persistence or control of the disease. We use powerful method of embedded invariant rectangles to obtain conditions for global extinction or persistence of the infective population. Our SI model exhibits a disease-free equilibrium point for all parameter values. Furthermore, the model has an endemic equilibrium point whenever ${\mathcal {R}}_{0}>1$.