1 Introduction

Adhesion plays an important role in contact mechanics at different scales, such as the adhesive ability of natural insects on vertical walls [2, 3], and microelectromechanical systems [4]. As a simple and commonly used approach to adhesive contact mechanics in the Hertzian geometry, the Bradley model assumes that the interaction between the counterfaces is nothing but a Lennard-Jones (LJ) potential [5, 6]. In such a way, assuming that the surface energy is \(\gamma\), and the radius of curvature is R, the pull-off force in athermal case estimated by this model is \(2\pi \gamma R\), which is identical to the estimation of that in the Derjaguin-Muller-Toporov (DMT) model [7].

While it has been demonstrated several times that the DMT model is accurate in the limit of the long-range adhesion and stiff material [8,9,10], this model becomes increasingly inaccurate for large and soft matter, hence different assumptions on the interaction have led to the JKR model [11], in which a singular crack term is assumed near the contact line.

The thermal fluctuation, which is often ignored in most theoretical and numerical studies on contact mechanics, has been demonstrated several times in experiments that can lead to a noticeable reduction of pull-off force [1, 12]. In fact, it has been shown that thermal fluctuations limit the adhesive strength of compliant solids [13]. Therefore, modelling the thermal effects on pull-off force within the framework of JKR model would be worthwhile.

Additionally, in athermal case, the elastic body jumps out of contact when the spring stiffness k is less than the maximum curvature of the potential energy \(V''_{max}\). This mechanism is analogous to that of the friction-velocity relation in the Prandtl model [14,15,16], in which a particle of mass m is dragged through a sinusoidal potential with a driving spring with velocity v. On the other hand, several experimental studies have demonstrated that the velocity can significantly affect the pull-off force [17,18,19]. In light of this fact, we expect that this model to also accurately describe the relation between pull-off force and velocity and further predict the contribution of thermal effects on this relation.

In this study, we set up a loading-unloading experiment in silico, in which a parabolic indenter is fixed in space, a linearly elastic body is placed below the indenter and is connected with an elastic spring, as shown in the inset of Fig. 1. This spring is used to characterize the stiffness of the cantilever and is allowed to move up and down with a constant velocity [20]. The effects of thermal fluctuations can be cast as random forces, which have to satisfy the fluctuation-dissipation theorem (FDT) [21].

The first intention of this study is to validate whether this modified Bradley model can plausibly reproduce the experimental pull-off force distribution. Another intention is to explore the effect of spring velocity on the pull-off force. To discriminate the athermal pull-off force from the thermal pull-off force, the short-hand notation \(F_0\) will be used to indicate the pull-off force in athermal case.

The remainder of this paper is organized as follows: Model and method are introduced in Sect. 2. results are presented in Sect. 3, while conclusions are drawn in Sect. 4.

2 Model and method

2.1 Modified Bradley model

In this model, the Newton’s equation of motion of the elastic solid reads

$$\begin{aligned} m\ddot{u}_{\text{ela}} + m\eta \left( v_{\text{ela}} - v_{\text{spr}}\right) = -\frac{\partial V_{\text{tot}}}{\partial u_{\text{ela}}} + {\Gamma }(t), \end{aligned}$$
(1)

where

$$\begin{aligned} V_{\text{tot}} = \frac{1}{2} k \left( u_{\text{spr}} - u_{\text{ela}}\right) ^2 - \int _0^{u_{\text{ela}}} {\text{d}}u F_{\text{cont}}, \end{aligned}$$
(2)

m is the mass, \(\eta\) is the damping coefficient, k the stiffness of the driving spring, \(u_{\text{ela}}\) and \(u_{\text{spr}}\) represent the displacement of elastic body and driving spring, respectively. \(\Gamma (t)\) is a random force characterizing the thermal fluctuations and thus must satisfy the FDT. \(F_{\text{cont}}\) represents the contact force within the framework of JKR model, which can be determined by

$$\begin{aligned} F_{\text{cont}}&= \frac{4E^*}{3R}a_{\text{c}}^3 - \sqrt{8\pi \gamma E^*}a_{\text{c}}^{3/2} \end{aligned}$$
(3)
$$\begin{aligned} u_{\text{ela}}&= \frac{a_{\text{c}}^2}{R} - \sqrt{\frac{2\pi \gamma }{E^*}}a_{\text{c}}^{1/2} \end{aligned}$$
(4)

jointly, where \(E^*\) is the contact modulus and \(a_{\text{c}}\) the contact area [22]. The pull-off force in athermal case is given by \(F_{\text{JKR}} = 3\pi \gamma R/2\).

Fig. 1
figure 1

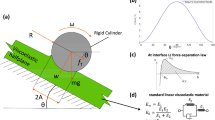
The reduced spring force \(\tilde{F}_{\text{spr}}/\tilde{F}_{\text{JKR}}\) as a function of the reduced spring displacement \(\tilde{u}_{\text{spr}}/ \tilde{u}_0\), where \(\tilde{u}_0\) represents the spring displacement at the pull-off point in athermal case, \(\tilde{F}_{\text{JKR}} = 3\pi \tilde{\gamma }/2\) is the reduced pull-off force in athermal case. Inset shows the schematic illustration of a tip-substrate model for loading-unloading simulations

Full size image

To eliminate the effect of different unit systems, the model should be expressed in a reduced system in which \(\eta\), R and \(E^*\) as well as \(k_B\) are equal to unity. Therefore, the remaining reduced parameters in this model are reduced mass \(\tilde{m} = m \eta ^2/ (E^*R)\), reduced velocity \(\tilde{v} = v / (R\eta )\), reduced stiffness \(\tilde{k} = k / (E^*R)\), reduced thermal energy \(k_B\tilde{T} = k_BT/(E^*R^3)\) and reduced surface energy \(\tilde{\gamma } = \gamma / (E^*R)\). These five independent, dimensional variables can fully determine the performance of this model.

2.2 Simulation method

In molecular dynamics simulation, we apply velocity Verlet algorithm to propagate the equation of motion in Eq. (1), which is a typical Langevin dynamics (LD). The random forces, which are used to characterize the thermal fluctuations, as mentioned before, must satisfy the FDT, which means, the mean and second moment of random forces must obey

$$\begin{aligned} \langle {\Gamma }(t) \rangle&= 0 \end{aligned}$$
(5)
$$\begin{aligned} \langle {\Gamma }(t) {\Gamma }(t')\rangle&= 2m\eta k_B T \delta (t - t') \end{aligned}$$
(6)

respectively, where \(\langle \cdot \rangle\) represents ensemble average and \(\delta (\cdot )\) denotes the Dirac delta function.

In a certain simulation, the random forces are realized by

$$\begin{aligned} {\Gamma }_{\tau } = \sqrt{\frac{6m\eta k_BT}{{\Delta } t}}(2u_{\tau }-1) \end{aligned}$$
(7)

where \(u_{\tau }\) is a (pseudo) random number generator, which can produce random numbers uniformly distributed between [0, 1], \({\Delta } t\) is time step and \(\tau\) is an integer to account the time step. In such a way, the random forces will satisfy the FDT automatically.

Now we must specify the time step \({\Delta }t\). Towards this end, we first determine the value of the mass m, which must be well chosen so that the dynamics is slightly underdamped, specifically, it equals to \(m = 4V_{\text{tot}}''/\eta ^2\). The time step, on one hand, should be fairly small compared to the system period, which is given by \(2\pi \sqrt{m/V_{\text{tot}}''}\). On the other hand, it should be small compared to the retract period, which is given by \(u_{\text{c}}/v_{\text{spr}}\), where \(u_{\text{c}}\) is the distance from unloading position to the jump-out-of-contact position. The expression of \(u_{\text{c}}\) can be determined by Eqs. (3-4) jointly. Therefore, the time step used in our simulation can be written as below,

$$\begin{aligned} {{\Delta } t} = \frac{1}{40}{\text{min}}\left\{ 2\pi \sqrt{ \frac{m}{V_{\text{tot}}''}}, \frac{u_{\text{c}}}{v_{\text{spr}}}\right\} . \end{aligned}$$
(8)

Additionally, the random forces should be separated into two parts, which reads

$$\begin{aligned} {\Gamma }(t) = {\Gamma }_{\text{ela}}(t) + {\Gamma }_{\text{cont}}(t) \end{aligned}$$
(9)

where \({\Gamma }_{\text{ela}}\) is used to simulate the thermal effects on the driving spring, which indicates that it exists throughout the simulation, while \({\Gamma }_{\text{cont}}\) is used to characterize the thermal effects when the elastic body jumps into contact, which follows the spirit of assumptions in the JKR model.

In real experiments, the interaction between the counterfaces results in the vertical deflection of the cantilever. Therefore, the applied force can be deduced from the deflection according to the Hooke’s law [23, 24]. In light of this fact, we measure the spring force \(F_{\text{spr}}\) in simulations, which is given by

$$\begin{aligned} \tilde{F}_{\text{spr}} = -\tilde{k}\left( \tilde{u}_{\text{spr}} - \tilde{u}_{\text{ela}}\right) \end{aligned}$$
(10)

On the other hand, considering that the Langevin dynamics will become inefficient in the case of over-damped simulation as the time step of the simulation \({\Delta } t\) should be very small compared to the damping time \(1/\eta\). This fact motivates us to employ the Brownian dynamics (BD), which can be described as a special case of the Langevin dynamics, that is, the inertia \(m\ddot{u}_{\text{ela}}\) presented in Eq. (1) equals to zero. This allows the Eq. (1) to be reduced to

$$\begin{aligned} 0 = -\frac{\partial V_{\text{tot}}}{\partial u_{\text{ela}}} -m\eta \left( v_{\text{ela}} - v_{\text{spr}}\right) + {\Gamma }(t). \end{aligned}$$
(11)

The equation of motion applied for Brownian dynamics can also be achieved by assuming that the mass m is infinitely small while \(m\eta\) is fixed to non-zero, which corresponds to the over-damped Langevin dynamics. To propagate the simulation, the velocity of the elastic body can be approximated as \(v_{\text{ela}} = (u_{\text{ela}}^{\text{now}} - u_{\text{ela}}^{\text{old}})/{\Delta } t\), as a result, we can write

$$\begin{aligned} u_{\text{ela}}^{\text{now}} = u_{\text{ela}}^{\text{old}} + \frac{{\Delta } t}{m\eta } [m\eta v_{\text{spr}} - \frac{\partial V_{\text{tot}}}{\partial u_{\text{ela}}} + {\Gamma }(t)], \end{aligned}$$
(12)

the time step is chosen as \({\Delta } t = 1 / (20\eta )\) so that it is fairly small compared to the damping time.

3 Results

3.1 Distribution of pull-off forces

In this section, we address the question how thermal fluctuations affect the distribution of pull-off force. As a first glance, Fig. 1 shows a force-displacement hysteresis of a single loading-unloading simulation considering the JKR force and the thermal effects. The reduced parameters which matter this simulation are chosen as \(\tilde{m} = 5.0 \times 10^{-5}\), \(\tilde{v}_{\text{spr}} = 1.0 \times 10^{-4}\), \(\tilde{k} = 2.0 \times 10^{-5}\), \(k_B\tilde{T} = 5.0 \times 10^{-8}\) and \(\tilde{\gamma } = 1.2 \times 10^{-4}\).

In this single loading-unloading hysteresis, it is interesting to observe that the pull-off force is significantly reduced. We would suggest that the adhesive strength is limited in value by thermal fluctuations, which had been noted by Tang et.al [13].

To further study how thermal fluctuations affect the pull-off force, we should firstly demonstrate if our simulation can reasonably reflect the real experiment. Towards this end, we measured the distribution of pull-off force from a mass of loading-unloading simulations, the parameters are well chosen so that they are approximately of the same order as those used in real experiments, which is also applied to simulate the single loading-unloading hysteresis in Fig. 1.

Fig. 2
figure 2

Comparison of experimental data and simulation data on pull-off force distribution. The experimental distribution (grey bars) is obtained from the Fig. 5 of Ref. [1], while the data is renormalized so that the integration equals to unity. The simulation data (red line) is obtained from the method introduced in this study

Full size image

With the choice of parameters, we can map these reduced units to real units, it could be conducted by assuming that \(E^* \approx 20.0~{\text{GPa}}\) and \(R \approx 15.7~{\text{nm}}\). The associated parameters with real unit are \(\gamma = 3.6 \times 10^{-2}~{{\text{J/m}}}^{2}\), \(k = 6.3 \times 10^{-3}~{\text{N/m}}\) and \(T = 288.4~{\text{K}}\). Furthermore, we assume that the mass \(m \approx 1.0 \times 10^{-12}~{\text{kg}}\), which is of the same order as applied in several experimental studies on atomic force microscopy (AFM) contact problems [12, 25], thus it turns out to be a reasonable choice and the resulting velocity of the driving spring is \(v_{\text{spr}} = 196.3~{\text{nm/s}}\).

It should be mentioned that this set of parameters implies that our simulations are most relevant at least in the case of weak interactions, that is, in the case where van der Waals interactions are the only forces at work between the interfaces [26, 27].

Fig. 3
figure 3

Normalized pull-off force distribution with various temperatures. Solid squares represent the simulation results while dashed lines represent fitting curves using the skew-Gaussian probability density function. All pull-off force distributions are obtained from more than 2000 simulations

Full size image

The result is shown in Fig. 2, which is obtained from more than 2000 loading-unloading simulations. To map our simulation to real experiment, this figure is plotted with real units rather than reduced units. The data presented in this figure reveals a good agreement between simulation and the experiment reported in Ref. [1], which follows an asymmetric bell-like curve.

Figure 3 shows reduced pull-off force distributions with different temperatures. The distribution depicted in Fig. 2 is applied as the reference data, while the real units are replaced by reduced units. It indicates that the pull-off force distributions can be fitted reasonably well with the probability density function of skew-Gaussian distribution. Additionally, it confirms that the pull-off force decreases with increasing temperature. Similar results are also observed in the Bradley model simulations by Pinon et al. [12].

3.2 Relation between pull-off forces and velocity

In this section, we investigate how velocity of the driving spring \(\tilde{v}_{\text{spr}}\) affects the pull-off force \(\tilde{F}_{\text{p}}\). Towards this end, both Brownian dynamics and Langevin dynamics are performed to measure the pull-off force with velocity ranging over 5 orders of magnitude at various temperatures. In both dynamics, \(\eta\), \(E^*\) and R as well as \(k_B\) are fixed to unity. The reduced surface energy \(\tilde{\gamma }\) is well chosen such that the depth of the JKR potential equals to unity, which leads to \(\tilde{\gamma }\approx 0.229\).

In terms of the reduced mass, two cases are considered. In one case, it is set to infinity, while the \(m\eta\) is fixed, which leads to overdamped simulation or Brownian dynamics. In another case, the value of the reduced mass is determined such that the simulation is slightly underdamped, in this study, it is fixed to \(\tilde{m} = 0.01\).

Fig. 4
figure 4

Reduced athermal pull-off force \(\tilde{F}_{0}\) as a function of velocity \(\tilde{v}_{\text{spr}}\) for Brownian and Langevin dynamics respectively at different spring stiffness. Open symbols represent the dynamics while dashed lines represent the fitting curves

Full size image

To project the simulations to practical experiments, it is important to map the reduced units to real units. Towards this end, we assume that the contact modulus \(E^* = 1~{\text{GPa}}\), the radius of curvature \(R = 16~{\text{nm}}\) and the mass \(m \approx 10^{-12}~{\text{kg}}\) as used in Ref. [12, 25] is nevertheless a reasonable choice. This makes the velocity \(v_{\text{spr}}\) be roughly located in the range \(64~{\text{nm/s}} \le v_{\text{spr}} \le 3.2~{\text{mm/s}}\), and the velocities used by indenters in several AFM loading-unloading experiments also fall in this range [17, 28].

Since this study considers the effects of thermal fluctuations on pull-off force, it is expected to separate the pull-off force into two parts, which reads,

$$\begin{aligned} \tilde{F}_{\text{p}}(\tilde{v}_{\text{spr}}, k_B\tilde{T}) = \tilde{F}_0(\tilde{v}_{\text{spr}}, 0) - \tilde{F}_{\text{t}}(\tilde{v}_{\text{spr}}, k_B\tilde{T}) \end{aligned}$$
(13)

where \(\tilde{F}_0\) is the pull-off force in athermal case, while \(\tilde{F}_{\text{t}}\) represents the thermal-induced reduction on pull-off force.

Figure 4 compares Brownian and Langevin dynamics for various spring stiffness at athermal case. \(\tilde{F}_0(v_{\text{spr}})\) relation differs noticeably at large velocity for underdamped and overdamped simulations. Nevertheless, both simulations show similar trend, that is, \(\tilde{F}_0(v_{\text{spr}})\) is enhanced with increasing velocity, and it can be fit very well over an extended velocity range \(10^{-5} \le \tilde{v}_{\text{spr}} \le 0.5\) with expression

$$\begin{aligned} \tilde{F}_0(\tilde{v}_{\text{spr}}, 0) = \tilde{F}_{\text{JKR}}\left\{ 1 + \left( \frac{\tilde{v}_{\text{spr}}}{v_0}\right) ^ {\alpha _0}\right\} ^{\beta _0}, \end{aligned}$$
(14)

where \(v_0\), \(\alpha _0\) and \(\beta _0\) are dimensionless parameters.

Furthermore, it is interesting to note that the exponent \(\beta _0\) is remarkably reduced from 0.134 to 0.005 when \(\tilde{k}\) is decreased from 0.8 to 0.1 for Langevin dynamics, similar reduction is also observed for Brownian dynamics. This implies that for compliant spring, the velocity can barely affect the athermal pull-off force \(\tilde{F}_0\). In practical AFM loading-unloading curve, a compliant spring is generally applied to identify the pull-off force in order to obtain precise results [29,30,31]. Therefore, it is more attractive to identify how velocity affects the pull- off force in the case of compliant spring.

Fig. 5
figure 5

Thermal-induced reduction of pull-off force \(\tilde{F}_{t}\) as a function of velocity \(\tilde{v}_{\text{spr}}\) for Langevin dynamics at various temperatures. Lines are fits according to the fitting function as given in Eq. (15). The spring stiffness is fixed to \(\tilde{k} = 0.1\)

Full size image

Figures 5 and 6 show how velocity \(\tilde{v}_{\text{spr}}\) affects the thermal-induced reduction on pull-off force \(\tilde{F}_{\text{t}}\) for \(\tilde{k} = 0.1\) in Langevin and Brownian dynamics respectively. All simulations are performed in an extended velocity range \(10^{-5} \le \tilde{v}_{\text{spr}} \le 0.5\) and can be fitted very well with expression

$$\begin{aligned} \tilde{F}_{\text{t}}(\tilde{v}_{\text{spr}}, k_B\tilde{T}) = \xi \left\{ 1 + \alpha _{\text{t}}\exp \left[ -\left( \frac{{\tilde{v}}_{\text{spr}}}{v_{\text{t}}}\right) ^{\beta _{\text{t}}}\right] \right\} , \end{aligned}$$
(15)

where \(\xi\), \(v_{\text{t}}\), \(\alpha _{\text{t}}\) and \(\beta _{\text{t}}\) are dimensionless parameters which varies with different temperatures.

Fig. 6
figure 6

Thermal-induced reduction of pull-off force \(\tilde{F}_{t}\) as a function of velocity \(\tilde{v}_{\text{spr}}\) for Brownian dynamics at various temperatures. Lines are fits according to the fitting function as given in Eq. (15). The spring stiffness is fixed to \(\tilde{k} = 0.1\)

Full size image

When \(\tilde{v}_{\text{spr}}\) is increased, the reduction of pull-off force is noticeably decreased, which as a result leads to an increment of the pull-off force \(\tilde{F}_{\text{p}}\). In addition, when \(\tilde{k} = 0.1\), the velocity dependence of athermal pull-off force \(\tilde{F}_0(\tilde{v}_{\text{spr}})\) is quite weak as the exponent \(\beta _0\) is extremely small, which indicates that the increment in pull-off force is principally attributes to the effects of the thermal fluctuations.

It can also be observed in these two figures that with increasing temperature, the thermal-induced reduction in pull-off force will approach the athermal pull-off force and eventually cancels it out.

4 Conclusions

In this study, a modified Bradley model, in which the LJ interaction was replaced by the JKR contact force, was presented to study how thermal fluctuations affect the pull-off force. It was demonstrated that this model reasonably reproduced real AFM loading-unloading curve. At a given temperature, a skewed pull-off force distribution was observed by collecting a large number of simulation results. With appropriate parameters, the simulated distribution can be in plausible agreement with the experimental results, and can be fitted reasonably well with the skew Gaussian distribution. Increasing temperature leads to a reduction on pull-off force while a broadening of the distribution.

We also investigated the relation between pull-off force and the driving spring velocity when the thermal effects are considered. Towards this end, the pull-off force was separated into two contributions, namely, the athermal pull-off force and the thermal-induced reduction on pull-off force. When the value of the spring stiffness is fairly small, the athermal pull-off force has a weak dependence on velocity, in which case the thermal-induced reduction term dominate the velocity dependence of pull-off force. It is also observed that the pull-off force decreases as the temperature increases. The main reason for this reduction is that the increase in temperature leads to an enhancement in the value of thermal-induced reduction.