1 Introduction

Composite materials, especially endless fibre reinforced plastics, show a high lightweight potential. Therefore, they are used in high-tech applications, requiring outstanding structural performance at minimum weight. Exemplary domains where fibre reinforced plastics are used, due to high sensitivity of the products regarding weight, are aerospace, sports and automotive. While many applications aim at products with low volumes, modern design tools, exemplarily presented in [1,2,3,4,5], simplify the design process of complex composite parts. In combination with advanced manufacturing technologies, steps towards the use of FRP-parts in high-volume products are made.

For high-volume products, deviations and uncertainties, occurring in the different steps from the design to the manufactured part, have to be considered more carefully during the product development process. Different approaches like robust design and tolerance management address this topic. While robust design tries to design a product to be insensitive to deviations, tolerance management defines tolerances within which the deviating parameters must lie in order to obtain a functioning part. In the following, a novel approach to define such tolerances for laminate and ply parameters of composite structures is presented.

Therefore, the paper is structured as follows. The second chapter begins with an introduction to uncertainty quantification in composite structures with a focus on design parameters, followed by an overview of tolerance management and optimisation in the context of endless fibre reinforced plastics. Due to high computational effort of finite element analyses (FEA), the use of metamodels in the context of FRP parts is regarded. The identification of the research gap and the aim of the novel approach conclude the state of the art section. In the third chapter, the novel method with the aim of optimising tolerances for laminate design parameters is presented. The method is applied to two use cases in chapter four. Finally, a conclusion is drawn and an outlook given.

2 Uncertainties during the design process of composite structures

Considering uncertainties during the design process of high-volume products is essential. This chapter therefore gives insights to occurring uncertainties with a focus on composite design parameters. Furthermore, the state of the art of tolerance management regarding endless fibre reinforced plastics shows current approaches to consider the uncertainties, resulting in the research gap.

2.1 Uncertainty quantification in endless fibre reinforced plastics

Uncertainties are distinguished between epistemic and aleatory uncertainties. Epistemic uncertainties appear due to incomplete or lack of information and knowledge, for example calculation model uncertainties. Aleatory uncertainty, in contrast, describes random physical uncertainty and is often also called variation or deviation [6,7,8].

Modeling uncertainty during the design process of the composite structure is performed on different scales. According to [7, 9, 10], it is differentiated between microscale, mesoscale and macroscale. On the one hand, the smaller the scale on which uncertainties are considered, the more detailed are the insights, on the other hand, the higher the scale, the more uncertainties can be considered in the used model. On the microscale, exemplary uncertainties are deviating material properties, like the Young’s modulus of matrix and fibre, the fibre volume fraction or misalignment of the fibres resulting from the manufacturing process [7]. On the mesoscale, uncertainties on the ply level are investigated, such as improper stack up or position deviation and incomplete curing resulting from the manufacturing process [7, 9, 11]. Finally, on the macrolevel, investigations of entire laminates are the focus of the uncertainty analyses. Table 1 includes typical parameters which are subject to variations and the referred scale.

Table 1 Exemplary parameters subject to uncertainties classified to the containing scale in accordance with [7, 9, 11,12,13,14,15,16,17]
Full size table

Numerous researchers worked on the analyses of uncertainties and variations of the parameters from Table 1. On the ply level (mesoscale), Arao et al. experimentally scrutinised the effect of ply angle misalignments and moisture absorption on the out of plane curvature and compared the results to simulative studies based on laminate theory [18]. Sarangapani and Ganguli perform Monte-Carlo simulations on the ply level to investigate the influence of uncertainties in symmetric as well as in non-symmetric laminates on the coupling terms of the stiffness matrix [12]. Whereas the aforementioned publications mainly concentrate on coupling effects, the influence of ply level uncertainties on reliability and failure is investigated in [16] and [19]. The different considered mechanisms of ply thickness variations in [16] show how complex the concentration on one scale is. The variation of thickness can be subdivided to fibre dominated or matrix dominated variation. Matrix dominated thickness variation can be expressed using correlated thickness and fibre volume fraction variables on the microscale. The influence of these mechanisms on the microscale on the macroscopic structural behaviour is scrutinised in [20].

Further research on uncertainties on the macroscopic behaviour is performed experimentally in [21] and simulatively in [22]. In both the influence of uncertainties on different scales (micro and meso) on the buckling loads of thin walled FRP cylinders is analysed. Tolerance management research mainly focuses on the mesoscale and macroscale. In [23], the influence of varying ply properties, i.e. angles and thicknesses, in an automotive assembly underlying further variations is scrutinised using Monte-Carlo simulations. The results showed that the ply variations do not significantly influence the overall variations and therefore can be considered as additional uncertainty on the geometry of the part. Nonetheless, the question raises whether these observations are applicable to optimised and local reinforced parts. The focus on assemblies is as well found in [24] and [25] where variations of composite parts (namely spring-in) are considered during joining an assembly by glueing. The work shows how the parts interact and transfer the part variations to a resulting geometrical deviation of the assembly.

Further approaches try to consider uncertainties at all three scales and to calculate or transfer uncertainties from one scale to a different scale [7, 11]. In [13], sensitivity analyses are performed considering parameters subject to deviations of all scales using a demonstrator of industrial complexity.

Beside the influence of uncertainties on the structural behaviour and therefore on the design of the composite structures, there is also research investigating the influence on the manufacturability of the structures [26].

Not only the analysis of the influences and the effects of deviations resulting from uncertainties should be scrutinised. Furthermore, uncertainties should be considered during the design of composite parts to support quality management, as suggested by Sriramula in [9]. Tolerances for the deviation of these parameters should be allocated guaranteeing the functionality of the part.

2.2 Handling uncertainties in the context of FRP

In order to handle uncertainties in the design of composite structures, robust design optimisation approaches can be applied, which aim at minimising the effect of deviations in the input parameters, e.g. ply angles, on the output parameter, e.g. deformation or stresses. In this context, there is a wide variety of research on the topic of robust design of composite structures. The authors therefore refer to [27,28,29,30,31].

The consequent step to robust design is the specification and allocation of tolerances to the part, which are supposed to ensure functional key characteristics (FKC) of the assembly. These tolerances are commonly described as design tolerances, e.g. geometrical (flatness, position, parallelism, angularity, etc.) and dimensional (part dimensions, feature dimensions, etc.) tolerances. The assigned tolerances must be met after manufacturing. Therefore, they are an instrument for the design engineer to define the limits of occurring deviations in the manufacturing process and to measure part quality for quality control. The design tolerances can be achieved in manufacturing through a set of manufacturing tolerances [32]. At this point, composite materials differ from classical materials like metals or plastics. Due to their layered structure, endless fibre reinforced laminates have a high number of additional design parameters subject to deviations during the manufacturing process. Deviations of the laminate design parameters have extensive consequences. For example, they influence the thermo-mechanical as well as the mechanical behaviour of the part. This results in deviation of the curing distortion and therefore the beforementioned geometrical and dimensional tolerances can be violated. Furthermore, deviations of the structural behaviour occur, which can influence the functionality of the part, e.g. deformations resulting from structural load.

In [33] and [34], a first, detailed study was performed scrutinising the geometrical deviations, like spring-in and warpage, resulting from the manufacturing process and regarded those deviations in dimension variation analysis of assemblies via the structural tree model. In [35], an extension was presented to predict stresses resulting from the part deviations in an assembly. Further studies of deviations in this context have been performed in [36] by Steinle. He therefore investigated how deviations in the fibre reinforced composite material, as well as deviations of the manufacturing process, namely the resin transfer moulding, influence the geometrical variation, the spring-in deformation, of the part.

However, while design tolerances are typically specified for the non-loaded case, it was shown in [37] that dimensional variations and variations in the material properties can have strong influence on the structural behaviour of parts with isotropic materials. This applies to composites in particular, due to the high number of different possible deviating parameters, which sum up to a wide variety of resulting variations, e.g. unexpected deformation behaviour through coupling effects, areas with decreased strength resulting from gaps or misaligned layers or just an increased deformation because of decreased stiffness.

The usage of composite materials challenges the geometrical variation management. New variational parameters and new manufacturing process simulation methods need adapted workflows in order to consider the specific characteristics of composites. [38]

2.3 Manufacturing tolerance optimisation for composite laminate parameters

The need for tolerancing of the design parameters of the laminate has been already stated. Nonetheless, it leads to new problems in handling CFRP-related uncertainties, as the laminate design parameters can be seen on a level between the classical (geometrical) design tolerances of a part and the manufacturing tolerances. As variations of the laminate design parameters may influence the geometrical design tolerances and the structural behaviour, tolerance values for the laminate parameters should be set to guarantee the functionality of the part. For this purpose, techniques known from tolerance-cost optimisation (see a detailed review on this topic in [32]) can be adopted.

Tolerance optimisation typically aims at minimising the costs resulting from the tolerance ranges while ensuring a maximum allowed variation of the FKCs as a constraint. To optimise the costs resulting from the tolerances of the laminate design parameters, the methods of tolerance optimisation can be used and adapted to the needs of composite parts. Generally the most common types of tolerance optimisation objectives are distinguished to least cost, best quality and multi-objective optimisation [32], which is as well widely used in composite design [39, 40]. Differences of tolerance optimisation of composite structures to common tolerance optimisation are the lack of data for tolerance costs and the difference in the scrutinised design parameters. Furthermore, in the following work, the structural functionality of the part will be evaluated beside the geometrical functionality. First attempts have already been made towards allocation of manufacturing tolerances for the parameters on the smaller scales.

In [41], manufacturing tolerances are considered during the optimisation of the layup of a plate under a buckling load. The manufacturing tolerances are not used as design variables. However, the simulative study has been performed on how the stacking sequence and the buckling load changes when the manufacturing tolerances of the ply angles are set to discrete values between 1 and 5∘. The deviations of the fibre angles lead to a significant decrease of the buckling load as well as to different stacking sequences. Similar investigations are performed in [42] where ply thickness variations are considered instead of the layer angle variations. Both publications do not specifically set the tolerance values and therefore can be classified as robust design optimisation studies. Nonetheless, because they perform studies for different tolerance ranges, they can be seen as a first step to tolerance optimisation.

In [39], an optimisation approach for local reinforcements out of continuous fibre tapes is presented. All simulation results computed during the optimisation using a genetic algorithm are combined to a heat-map which represents how important different areas of the part are. In doing so, the influence of the different tape positions on the objective function can be visualised.

In [43], Kristinsdottir et al. developed an optimisation method for structural optimisation which is split into two steps. First the optimisation algorithm considers defined variations of the design parameters through a margin of safety, which is very similar to other robust design approaches. In a second step, the precise size of the acceptable variations, the design tolerances of the layer angles, to obtain a feasible design, is calculated via a bi-sectioning algorithm.

2.4 Metamodels in the context of FRP

Since tolerance optimisation often needs an high amount of simulations, e.g. FE-simulations, surrogate models, in the following depicted as metamodels, can be used to decrease the high computational effort [44]. An extensive review on the use of metamodels to predict the structural behaviour of composite structures can be found in [45] by Dey et al. They review several metamodels, e.g. polynomial regression or response surface method, radial basis functions and support vector machines, on their precision compared to FEA results as well as on their computational effort. Beside these metamodels, artificial neural networks (ANN) are the most recent approach to model complex behaviour, like the prediction of densities of recycled composite material [46]. Furthermore, ANN provide the possibility to model the local behaviour of parts, e.g. the forming behaviour in sheet-bulk metal forming [47] or draping effects during forming of composite materials [48].

Considering their advantages, such as their high computational efficiency and their ability to gain deeper insights into the relation of input and output parameters [49], and disadvantages, such as the need for high-quality training data and careful result analysis, metamodels have their strengths in tasks where a high number of calculations are needed, e.g. in stochastic evaluation of systems. Applications of metamodels in the context of composite structures can be found in [50] where the metamodels are used to predict structural behaviour, e.g. vibration analysis of plates. Another example for the application of metamodels in composite structures is the modelling of the adhesive layer between carbon fibre reinforced plastics and metals [51].

2.5 Research gap

The introduction showed that there is an important need for the management and handling of uncertainties and tolerances in the design and manufacturing of composite materials and structures. However, especially concerning the tolerance allocation and optimisation for laminate design parameters, there is only few research. Nonetheless, especially variations of the laminate parameters can strongly influence on the one hand the dimensional variations of the structure and on the other hand the structural behaviour. Therefore, an approach to allocate and optimise manufacturing tolerances for the laminate design parameters is required. The importance of manufacturing tolerances increases with the use of optimisation routines during the design phase as all deviations will lead to worse performance of the part.

To overcome these shortcomings, the presented novel approach addresses the following objectives:

  • Development of a tolerance optimisation approach for the allocation of tolerances to laminate design parameters

  • Applicability of the approach to designs with a homogenous ply stack up, as well as to optimised structures including local reinforcements

  • Reduction of the computational effort by using surrogate models during the optimisation

3 Method for optimising the manufacturing tolerances of laminate design parameters

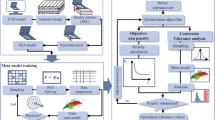
The developed method considers the objectives from Section 2.5, and it optimises the tolerance values for laminate design parameters to fulfil defined FKCs for different load cases. Therefore, the method consists of three main steps, which are shown in Fig. 1 including the corresponding chapter. The first step is the model preparation, followed by the training of the metamodel. Using the trained metamodel, in the next step, the tolerance optimisation is performed.

Fig. 1
figure 1

Flow chart for the metamodel-based manufacturing tolerance optimisation of FRP parts and the related section numbers

Full size image

3.1 Model preparation

The basis of the presented tolerance optimisation routine is a finite element simulation model of the part, including the layup as well as the different load cases applied to it. The simulation model consists of shell elements with a quadratic element formulation, which are capable of a layered formulation to simulate the ply stack up of the laminate.

The method can be applied to homogenous ply stack ups for the whole part, as well as to optimised laminates with local reinforcements, resulting from the optimisation algorithm presented in [2, 3, 52]. In order to use the simulation model for the optimisation routine, it needs to be parametrised. In the presented work, the fibre angles exemplarily are considered as the varying design parameters for which tolerance ranges should be set. This aims to guarantee the functionality of the part under variations. As deviations of the fibre angles lead to highly non-linear changes in the stiffness, they are the most complex parameter to be modelled by the metamodel. The approach is applicable to further laminate design parameters, like ply thickness or fibre volume fraction.

Beside the input parameters, the output parameters, which define the functionality of the part, need to be defined and parametrised as well. Within this work, different measures will be used. The first type of measures is the maximum nodal deformations of the part. Additionally to the total deformation, it is possible to evaluate the directional deformations. The second type of measures is geometrical tolerances. They are used to evaluate the geometrical accuracy after manufacturing simulation, as well as the geometrical accuracy in the loaded state. They are calculated using the coordinates of the deformed nodes. The third type of output parameters is strength criteria. In the presented work, the Puck strength criterion [53, 54] and the Tsai Wu criterion [55, 56] are used. The maximum value occurring in the part is chosen as output value.

As stated before, the fulfilment of different FKCs under variations is important for the product developer. Therefore, the presented method is capable of considering multiple load cases. In the presented work, linear elastic structural and thermal load cases are investigated.

3.2 Metamodel training

To minimise the computational effort of the optimisation, the use of surrogate models is intended. Metamodels show good performance while keeping the computation times relatively low. The training process of the metamodel consists of four different steps, which are shown in Fig. 2. As a first step, the design space of the input parameters which needs to be covered has to be defined, wherein a sampling procedure is performed. A latin hypercube sampling (LHS) is used to cover the complete design space in an efficient way [57]. Especially for optimised parts, the efficiency is important because of the high number of design parameters coming from the local reinforcements. The samplesize N needed for a good fit of the metamodel strongly depends on the number of design parameters. Since the samplesize is a decisive parameter which has to be adapted for every new problem, it needs to be set by the user.

Fig. 2
figure 2

Flow chart of the metamodel training

Full size image

The single samples contain the varying input parameters of the model. By solving all samples utilising the parametrised simulation model for all load cases, the related output values can be calculated and prepared for the training of the metamodel.

The presented method uses a Gaussian process regression (GPR) model, also known as Kriging. It allows to model complex relations of input and output data and therefore is appropriate to model the non-linear behaviour of angle deviations, which are considered in the presented work. Furthermore, the GPR is well suited for deterministic applications, like the used training data from FE-simulations [49].

Gaussian processes are a generalisation of a Gaussian distribution which rely on a mean function m(x) and a covariance function \(k(\boldsymbol {x},\boldsymbol {x^{\prime }})\) with x being the vector containing the design variables [58]. For the mean values a basis function, defined by hyperparameters is used. The covariance function is approximated using a kernel function. During the training process, the hyperparameters of the basis and kernel function are optimised by maximum likelihood to fit the training data. The first one which is chosen in this work is that there is no noise in the training data, and the standard deviation is set to σ2 = 0 in the sample points. The second option is that there is some uncertainty in the data.

The basis function of the used Gaussian process regression model is set to a constant value:

$$ \boldsymbol{H} = 1 $$
(1)

with the length N which is the number of observations used for the training. The basis function is added to the model in the form H ⋅β, where β is a vector of the length N containing the basis coefficients. The kernel function to describe the covariance is a rational quadratic function:

$$ k(x_{i},x_{j}|\theta) = {\sigma_{f}^{2}}\left( 1+\frac{r^{2}}{2{\alpha\sigma_{l}^{2}}}\right)^{-\alpha} $$
(2)

with r being the euclidean distance between the design points xi and xj, the standard deviation σf of the training data, a scale mixture parameter α > 0 and the characteristic length scale σl > 0.

Since the Gaussian process regression model is a probabilistic model, it is possible to calculate confidence intervals for all predictions and therefore evaluate the quality of the prediction.

The quality of the metamodel is evaluated using the normalised root mean square error (NRMSE) which calculates from the root mean square error (RMSE) and the range of the output values in the training data set:

$$ \text{NRMSE} = \frac{\text{RMSE}}{y_{\mathrm{train,max}}-y_{\mathrm{train,min}}} $$
(3)

with the RMSE being

$$ \text{RMSE} = \sqrt{\frac{{\sum}_{n=1}^{N}\left( y_{\text{pred},n}-y_{\text{train},n}\right)^{2}}{N}} $$
(4)

Furthermore, the coefficient of prognosis (COP) as introduced in [59] is used as a second measure for metamodel quality.

$$ \text{COP} = 1 - \frac{{\sum}_{n=1}^{N}\left( y_{n}-y_{\text{pred},n}\right)^{2}}{{\sum}_{n = 1}^{N}\left( y_{n}-\mu_{Y}\right)^{2}} $$
(5)

The COP is calculated similar to the coefficient of determination (COD) but is based on a separate data set for which the simulations and predictions are calculated. The value of the COP lies in between the bounds 0 < COP < 1 and can be interpreted as the prediction quality of the metamodel [59].

Since there is no generally valid definition of quality limits for metamodels in literature, individual values are defined. For the NRMSE, values up to 10% are defined to be acceptable. The COP values have to exceed 80%. If the quality of the metamodel violates these values, there are two possibilities. First the settings for the training of the metamodel can be adjusted and second a new set of training data can be calculated.

3.3 Tolerance optimisation

After the quality of the metamodel is acceptable, the tolerance optimisation can be performed. The tolerance optimisation follows the procedure depicted in Fig. 3. It consists of two major components, the objective function which is minimised and the constraint, which has to be fulfilled. It is formulated as a minimisation problem of the following form:

$$ \begin{array}{ll} \min \quad C_{\text{tot}} =& \sum\limits_{i = 1}^{I} C_{i}(t_{i}) \\ s.t. \quad S_{\text{tot}} =& 1 - \frac{{\sum}_{j=1}^{N}{\prod}_{lc = 1}^{LC}{\prod}_{k=1}^{K}q_{j,lc,k}(Y_{j,lc,k})}{N} \leq S_{\max} \\ t_{\min} \ <&\ t_{i}\ <\ t_{\max} \end{array} $$
(6)

with the measure of FKC boundary value violation:

$$ \begin{array}{ll} q_{j,lc,k} = \begin{cases} 1, & \text{if } Y_{j,lc,k}(\boldsymbol{t}) \leq B_{lc,k}\\ 0, & \text{if } Y_{j,lc,k}(\boldsymbol{t}) > B_{lc,k}\end{cases} \end{array} $$
(7)
Fig. 3
figure 3

Flow chart of the tolerance optimisation using metamodels

Full size image

The objective of the optimisation problem is to minimise the total costs Ctot with respect to the tolerance ranges t of the I design parameters, herein the ply angles. Furthermore, the optimisation considers the functionality of the part subject to variations. Therefore, the constraint function applies tolerance analysis to measure the total scrap rate Stot respect to the tolerance ranges t. Since the distribution of the FKCs is not known and expected to follow no particular distribution, sampling-based tolerance analysis has to be applied [60]. The total scrap rate Stot is estimated empirically considering a sample of the size N. Therefore, the FKC values Yj,lc,k of each sample j are predicted using the metamodels. All violations of the boundary values Blc,k are counted as non-conform samples with the quality measure qj,lc,k = 0. All conform samples are counted as qj,lc,k = 1. To avoid multiple counting of a non-conform sample, logical disjunction according to [61] is used. The formulation of the quality constraint considers a sample as non-conform if at least one boundary value Blc,k of the K FKCs is violated by the FKC value Yj,lc,k. The violation of different FKC boundary values at the same time is still regarded as a single non-conform design in the scrap rate. To consider multiple load cases, a further logical disjunction over all LC load cases is needed, in order to count a sample violating boundary values in different load cases only once. The non-conform samples are summarised over the N samples. The total scrap rate Stot should not exceed the maximum scrap rate \(S_{\max \limits }\). Tolerance ranges are limited by a lower boundary \(t_{\min \limits }\) and an upper boundary \(t_{\max \limits }\) which are defined by the technological capabilities of the manufacturing process.

Objective function

Since to the knowledge of the authors there is no data of tolerance cost curves for composite parts available, the costs have to be seen as a penalty term. The purpose of the penalty function is to force the optimisation algorithm to change the tolerances so they are as narrow as needed and as wide as possible. Different cost functions, e.g. linear, polynomial, exponential or reciprocal, have been presented in literature [32]. In the presented work, an exponential penalty function is used which calculates the penalty Ci(ti) with respect to the tolerance range ti and the coefficients a, b and c.

$$ C_{i}(t_{i}) = a + b \cdot e^{-c \cdot t_{i}} $$
(8)

The function, respect to the tolerance, can be seen in Fig. 4. Due to different occurring tolerance ranges for different design parameters, like the ply angle and the thickness, the penalty function from Equation 8 needs to be adapted for each type of parameter.

Fig. 4
figure 4

Cost function for the angle tolerance range

Full size image

Constraint function

Due to few informations on the distributions of the laminate design parameters, they are assumed to be normally distributed around their nominal values. The tolerance value which gets optimised for each design parameter relates to the distribution of the variation like presented in Fig. 5. The tolerance value, e.g. ± 5∘, defines the range from − 3σ to + 3σ. This range includes ca. 99.7% of the observations of a parameter. The tolerance analysis begins with the generation of a sampling. The sampling has to consider the tolerances and their distributions provided by the optimisation algorithm. Therefore, a LHS with N samples is created. The distributions including the standard deviations σ, resulting from the tolerances t, are fitted to the LHS design. To predict the FKC values Yj,lc,k, the before trained metamodels are used during the tolerance analysis. The metamodels predict the FKC values for all N samples from the LHS design. In the following step, the predicted FKC values Yj,lc,k are analysed whether they violate the boundaries Blc,k of the FKCs. If the total scrap rate Stot exceeds the predefined maximum scrap rate \(S_{\max \limits }\), the tolerance values result in a non-valid solution and have to be adjusted by the optimisation algorithm.

Fig. 5
figure 5

Relation between the distribution of fibre angles and tolerance range

Full size image

To solve the minimisation problem from Eq. 6, an optimisation algorithm has to be applied. Whereas a huge number of different optimisation algorithms exist, the optimisation problem limits the applicable algorithms. Due to the non-linearity and non-continuity of the constraint function as well as the possibility of a non-convex objective function with several local minima, metaheuristic optimisation algorithms are best suited to find the optimal solution [32]. A commonly used algorithm in tolerance cost optimisation is the genetic algorithm, which is used in the following. It mimics the natural behaviour of evolution where the fittest individuals of a population survive. Through mutation, crossover and elite count, new individuals emerge. Due to the stochastic component in the mutation and crossover process, the genetic algorithm is more likely to find the global minimum and get out of local minima, compared to mathematical algorithms which use gradient information.

The optimisation results in optimised tolerance values for the laminate design parameters. These tolerance values can be assigned to the nominal design parameters by the product developer in order to define the limits for manufacturing and quality control.

4 Use cases

The presented method is now applied to two use cases. Both share the same geometry, an omega-shaped stiffener with round cutouts to save weight. The geometry is shown in Fig. 6. The presented method is implemented in Mathworks Matlab. This includes all steps except the solution of the FE analysis. The FEA solutions, which are needed for the metamodel training, are solved utilising Ansys Mechanical via batch scripts. In the first use case, the application to multiple load cases is shown. In the second use case, the application to an optimised, locally reinforced layup is presented.

Fig. 6
figure 6

Geometry and tolerances of the omega-shaped stiffener

Full size image

4.1 Use case 1—multiple load cases

The first use case uses the omega stiffener with multiple load cases, but a simple laminate layup. The layup consists of 8 layers of a unidirectional composite material with a thickness of 0.25 mm. The layer angles are depicted in Fig. 7. The variations of the layer angles are used as design parameters. Therefore, for each layer angle, a tolerance value ti is defined. The material properties can be obtained from Table 2. The demonstrator part gets loaded with three different load cases. In load case 1, a bending load is applied to the part according to Fig. 8a. The ends of the stiffener are connected to the remote points RP1 and RP2 via rigid beam elements. The force F is applied to the red marked surfaces. In the second load case, Fig. 8b, the stiffener is loaded with a tension force while it is fixed via a remote point like in the first load case. The third load case, depicted in Fig. 8c, is a temperature cool down from 180 to 20∘C. The cool down is used as simplified load case to substitute a manufacturing process simulation. Especially a first indication of deformation and warpage due to asymmetry in the layup can be made. The part is supported with an isostatic fixture, which enables the free movement coming from the cool down. The total deformations for the nominal design are presented in Fig. 9.

Fig. 7
figure 7

Layup of use case 1

Full size image
Table 2 Mechanical and thermal properties
Full size table
Fig. 8
figure 8

Loads and boundary conditions for the three scrutinised load cases; (a) Bending load; (b) Tension load; (c) Thermal load

Full size image
Fig. 9
figure 9

Deformations for the three scrutinised load cases; (a) Bending load; (b) Tension load; (c) Thermal load

Full size image

The FKCs of the part can be obtained from Tables 5, 6 and 7. They are subdivided into maximum total and directional deformations, the strength criteria and the geometrical tolerances which are depicted in Fig. 6. The FKC values for the nominal design parameters are included to give a reference for the boundary values which should not be exceeded during the tolerance optimisation.

For the training of the metamodels, a data set with 1000 samples is used. The size was chosen based on the experiences of pre-studies and is a compromise between computational cost and the training results. The size of the training set has to increase with increasing number of parameters. Each of the three load cases is solved for every sample with FEA. The training data are distributed uniformly in between ± 15∘ for each layer angle. For each FKC and each load case, a metamodel is trained. The results of the training data can be seen in Tables 5, 6 and 7. The variations of the FKCs within the training data (sample max. and sample min.) of the load case 1 and 2 compared to the values of the nominal design are moderate and range in the same magnitude like the nominal values. The results of the thermal load case show very high variations, compared to their nominal values. Especially the maximum total deformation with 34.10 mm reaches nearly 20 times the deformation in the nominal design. Such high variations occur through strong asymmetries in the laminate which results in strong coupling deformations and warpage. Figure 10 compares the nominal design (a) with a strongly asymmetric design (b) and shows the twisting which leads to the high deformation values and the high tolerance values.

Fig. 10
figure 10

Total deformations of nominal design (a) and variational design (b) for the thermal load case

Full size image

This proceeds in the quality of the trained metamodels. For the calculation of the COP, a test set consisting of 100 samples has been solved. The NRMSE is calculated from the far bigger training data set with 1000 samples. While the structural load cases 1 and 2 show very good results for the metamodels, with COP values greater than 90% and small values for the NRMSE, the thermal load case shows high variations in the FKC values. These effects are very difficult for the metamodels to predict, which results in the low values of the COP of 83.73 to 94.41% and NRMSE values of 5.02 to 7.66%. The NRMSE does not exceed the limit of 10%. The training and prediction data for the flatness of LC3, with the worst COP and NRMSE values, can be seen in Fig. 11. The data is distributed around the diagonal with slight errors, which compared to the variation range is acceptable. The histograms show a concentration around the minimal value. Based on the observations, the trained metamodels will be used for the following optimisation. Nonetheless, the thermal load case has to be regarded sceptically and interpreted as an indication of the influences of the manufacturing process.

Fig. 11
figure 11

Datapoints of the training data set and the corresponding predicted values for the flatness in use case one for the third load case

Full size image

In the next step, the tolerance optimisation is performed. The optimisation and tolerance analysis settings can be found in Tables 3 and 4. The boundary values for the FKCs can be obtained from Tables 5, 6 and 7 for the different load cases.

Table 3 Optimisation settings
Full size table
Table 4 Tolerance analysis settings
Full size table
Table 5 Boundary values of the FKCs for load case one of use case one
Full size table
Table 6 Boundary values of the FKCs for load case two of use case one
Full size table
Table 7 Boundary values of the FKCs for load case three of use case one
Full size table

The optimisation results in the tolerance values of the ply angles. Figure 12a shows the tolerance values. The plies on the top and bottom side show slightly tighter tolerance values while the middle layers show higher values. Variations in the ± 45∘ layers therefore are of higher importance to the FKC values. These layers bear the shear forces in the angled sections of the part. Furthermore, their effect on coupling deformations is higher since large areas are oriented in the load directions. Additionally they are the outer layers of the laminate with higher moment of inertia of area compared to the inner layers. In contrast, the 90∘ layers, which are oriented in the load direction in the horizontal faces, are of no higher importance, what implies a strong influence of the coupling effects.

Furthermore, the tolerance values show a tendency to a symmetric behaviour. Nonetheless deviations from a full symmetry can have different reasons. On the one hand, the optimisation algorithm and its stochastic components, as well as the used samplesize and sample-set can have substantial influence on the results. On the other hand, the influences can be asymmetric due to the geometry and the position of the layer and the load conditions there.

The optimisation converges in only six generations to a result where the change in the objective function value is below the defined limit of 1 ⋅ 10− 7. The resulting cost value, which is 1357.95, and the convergence history are shown in Fig. 12. This fast convergence stems from the internal handling of the optimisation algorithm with non-linear restrictions. For every individual of a generation, a Lagrangian subproblem is generated which approximates the actual optimisation problem. The subproblems themselves get optimised. This leads to a fast convergence within few generations but at the same time to a higher number of function evaluations. In the first use case, 9390 function evaluations have been performed, which in combination with the three load cases with eleven function values for load case one and two and eight function values for load case three and 10000 samples results in nearly 2.8 ⋅ 109 metamodel predictions during the whole optimisation, which would not be possible to calculate with FEA in an acceptable time. For the investigation and comparison of the times needed for computation a small study has been performed. The FEA model showed an average time of 46.48 s per solution from a total of 60 solutions, including the manipulation of the model, solving and importing the results. The solutions of the metamodel under the same conditions took an average time of 9.67 ⋅ 10− 5s calculated from a total of 30000 observations. This leads to a speed up of ca. 500000 times.

Fig. 12
figure 12

Optimisation results of use case one: (a) Optimised tolerance ranges for the three load cases; (b) Optimisation history

Full size image

The constraints of the resulting tolerances are shown in Fig. 13. The maximum scrap rate, which allows ten violations, is perfectly met. Violations of the boundary values occur in the first and third load case. Furthermore, no sample violates two functions at the same time. For the second load case, no violation occurs. The optimisation therefore leads to suitable results.

Fig. 13
figure 13

Constraint values for the resulting tolerance ranges for use case one

Full size image

4.2 Use case 2—optimised locally reinforced layup

The second use case originates from the same geometry and uses the same bending load case. The difference to the first use case is an optimised laminate design. The model gets optimised with the approach presented in [2, 3, 52, 62]. The result is an optimised symmetric laminate consisting of two thin base layers and 14 local reinforcements, in the following called patches. While for a layup like in the first use case, the product developer might intuitively know the important layers based on experience. In contrast, such optimised and locally reinforced layups result in a high number of design variables and difficult to evaluate influences on the structural behaviour of the part.

The stiffener geometry including all the patches and their surroundings is depicted in Fig. 14. The base layers covering the whole part as well as the patches consist of the same material, with its material properties given in Table 2. The base layers are oriented in a 90∘ and 0∘ direction regarding to the reference direction from Fig. 7 with a thickness of 0.10 mm. The patch reinforcements are oriented as shown in Fig. 14 with a thickness of 1.00 mm. In the second use case, only the bending load from Fig. 8a is applied. The FKCs from use case one are used, but with slightly different values due to the changed layup which can be obtained from Table 8. Furthermore, the angularity is not considered during the tolerance optimisation.

Fig. 14
figure 14

Optimised laminate design with local reinforcements P1–P14

Full size image
Table 8 Boundary values of the FKCs for use case 2
Full size table

Analogous to use case one, the layer and patch angles are the design variables for which a tolerance value should be calculated and optimised. Therefore, the angle variation range is parametrised, which results in 32 tolerance values. The metamodels are trained with 1200 samples. The fibre angles are uniformly distributed in a range of ± 15∘. The training results in acceptable NRMSE and COP values, which can be seen in Table 8. Only the COP values for the strength criteria show moderate values, while having acceptable NRMSE values. The optimisation uses the same settings as in use case one, depicted in Table 3.

The optimisation finishes after six iterations, Fig. 15, due to low change in the objective value. The resulting tolerance values are shown in Fig. 16. No regularities, like symmetry in the tolerances, e.g. for patch P1 and P1 sym or P10 and P10 sym, can be observed in the results. Due to the layup including the local reinforcements, a high number of design parameters, as well as a segmentation of highly loaded areas into several smaller areas with optimised fibre orientations emerged. This reduces the influence of the variations of a single patch. Furthermore, the results get more difficult to interpret, the more FKC values/constraints, the structure has to fulfil. While for the maximum deformation, the patch P1 has a high influence, the influence of the same patch on the strength criteria is rather low. The convergence history is presented in Fig. 15. Similar to the first use case, a fast convergence can be observed which results in the optimised cost value of 6255.86 (Fig. 16). While in the beginning, differences between the different individuals can be observed, after iteration 4, the variations of the 30 individuals are very low.

Fig. 15
figure 15

Optimisation history of the use case 2

Full size image
Fig. 16
figure 16

Optimised tolerance ranges for all patches Pi and base layers Bi

Full size image

The violations of the constraints in Fig. 17 show the most violations for the maximum Tsai Wu values. Furthermore, single violations of the maximum total deformation can be observed.

Fig. 17
figure 17

Constraint values for the resulting tolerance ranges for use case 2

Full size image

5 Discussion and outlook

The presented tolerance optimisation approach calculates tolerance values for laminate design parameters in order to guarantee the functionality of the part after manufacturing as well as during the structural load cases. The computational effort is reduced through the use of surrogate models, namely Gaussian process regression. The approach has been applied to two use cases with different laminate layups. First it was applied to an omega stiffener with a simple laminate consisting of eight unidirectional layers subject to three load cases. The resulting tolerance values are discussed regarding the functionality and the optimisation history. The second use case bases on the same geometry but with an optimised laminate design with local reinforcements for the structural load cases. The second use case shows the applicability to locally reinforced parts.

The advantages of the presented approach are the possibility of calculating optimal tolerance values for layups which are constant in the complete part, as well as for layups with local reinforcements. The tolerance values can help to increase the quality of composite structures and serve as a measure for quality control. It allows the product developer to precisely define the specification limits of a composite part. Furthermore, the approach is very easily extendable to further laminate parameters, e.g. position and dimensions of the local reinforcements, as well as to further FKCs and load cases. The approach should generally be applicable to non-linear simulation models, but further research has to go into the effect on the training of the metamodels.

Beside the advantages, there are some downsides. The main disadvantage is the computational effort to generate the training data for the metamodels. This step has to be redone for every new geometry. Advances in the speed of FEA calculations are needed to reduce times to an amount acceptable by industry.

Future research has to tackle different topics. On the one hand, the variety of design parameters is especially for locally reinforced laminates very high. Further parameters like position and dimensions of the patches should be considered as well. Furthermore, problems can occur when having double curved geometries where draping effects occur. Additionally the question rises whether the degree of detail is good enough? Deviations from the nominal design values can as well occur on different length scales, which could be considered with more advanced modelling, e.g. via Fourier series.

On the other hand, the current state of the problem formulation is limited to single parts. To cover more complex problems, an extension to assemblies is of highest interest. Few topics on variations in assemblies are already scrutinised by current research mainly focusing on the manufacturing process and the effects on geometry. Especially the consideration of variations on the part/laminate level on the structural behaviour and the prestressing of composite assemblies bears huge potentials for future research.