1 Introduction

Time dependent adaptive mesh refinement (AMR) [1, 3, 27], i.e. where a computational mesh is modified dynamically during the course of a simulation, is a popular and extremely useful technique to reduce the cost of complex modeling tasks involving many types of partial differential equations (PDE). By adding more computational nodes in one region and/or removing nodes in another, local changes in solution characteristics over time can be accounted for, leading to a more efficient use of computer resources. See e.g. [2, 11, 17, 24] for a selection of historical applications of AMR techniques.

One of the core aspects of AMR is the transfer of numerical solutions values from the previous mesh to the next using interpolation. If AMR is applied after each or every few time steps, e.g. in order to track a moving solution profile, the accuracy and formal stability properties of such interpolations become important considerations. In this paper we set out to formulate a general framework for stable and accurate AMR interpolation. This new framework is explicitly intended to be used together with the energy method, focusing on semi-bounded semi-discretizations and especially those resulting from the use of discrete operators with a formal summation-by-parts (SBP) property [4, 9, 25].

Inner product preserving (IPP) interpolation has recently emerged as a powerful framework for locally adapting the refinement level of a computational mesh with the use of hanging nodes. Developed for numerical methods ranging from finite difference (FD) [20], mass-lumped discontinuous Galerkin (dG) [7] as well as finite volume and various hybrid methods [14, 18], the framework of IPP is ideally suited to be used in conjunction with the energy method in order to prove stability of interpolation based interface coupling conditions between general blocks or elements in space. The successful use of IPP operators in the references cited above rely heavily on the interplay between the IPP concept and an underlying formal SBP framework for numerical differentiation on each of the individual blocks or element.

The kind of abrupt and repeated modification to the mesh associated with time-dependent AMR generates a sequence of so called transmission problems [22], i.e. semi-discretized systems of equations coupled in time using interpolation. Focusing on the example of numerical filters in [19], it was demonstrated that the stability of transmission problems in general is tightly linked to the IPP concept discussed above. In this work, we will therefore consider the use of IPP type operators for time dependent AMR interpolation. We develop a general methodology allowing for both explicit and implicit implementations. In terms of available IPP type operator that can be used for this purpose, we note that in the element based dG case, the same type of \(L_2\) projection operators traditionally used for couplings in space [12, 13, 21] can be shown to satisfy the IPP framework [7]. Hence these operators can also be used in the AMR context of this paper. In the FD case however, new operators must in general be constructed.

The remainder of this paper is organized as follows. In Sect. 2 we outline a general theory of AMR stability based on IPP operators, mirroring and expanding some of the key results for numerical filters in [19]. In Sect. 3 we relate these theoretical findings to the theory of SBP operators. In particular, we discuss and compare the accuracy limitations inherent to both types of operators, and how these relate to the total accuracy of numerical simulations using AMR. In Sect. 4 we discuss IPP interpolation operator design for FD calculations with moving non-collocated interfaces in a multi-block environment. In Sect. 5 we present numerical calculations using both FD and dG methods, investigating convergence rates as well as demonstrating practical benefits of the formal stability associated with the developed AMR interpolation schemes. Finally, in Sect. 6 we draw conclusions.

2 General Stability Theory

As our starting point we let \({\mathcal {D}}= {\mathcal {D}}(X,U)\) denote a general semi-discretized non-linear PDE operator, posed on a given mesh of computational nodes denoted by X. That is, after imposing homogeneous boundary conditions, we consider the semi-discrete system of equations

$$\begin{aligned} U_t = {\mathcal {D}}(X,U). \end{aligned}$$
(1)

We shall henceforth only consider operators \({\mathcal {D}}\) with a semi-bounded property, i.e. for a general vector \(\varPhi \) defined on the mesh, we have

$$\begin{aligned} \left( \varPhi ,{\mathcal {D}}(\varPhi ,X)\right) _{{\mathcal {P}}(X)} = \varPhi ^T{\mathcal {P}}(X){\mathcal {D}}(\varPhi ,X) \le 0 \end{aligned}$$
(2)

for some quadrature \({\mathcal {P}}(X)\) which defines a discrete \(L_2\) inner product and norm on the mesh (i.e. \({\mathcal {P}}\) is a diagonal matrix with positive quadrature weights inserted along the diagonal).

Note that (2) implies that the solution U to (1) is non-growing in the discrete \(L_2\) norm, and this can typically be seen as an analogue of the same property of the continuous PDE. In other words, semi-boundedness simply means that numerical stability follows from the energy method for a specific quadrature norm. Hence, (1) encompasses a great number of different PDE problems (as well as related numerical methods) of both hyperbolic and parabolic type. See e.g. [9] for a comprehensive introduction to the topics of semi-boundedness and energy stability.

2.1 AMR as a Transmission Problem

Now suppose that we wish to refine and/or coarsen the computational mesh locally after n time steps, and then interpolate the solution to the new mesh before carrying out time step number \(n+1\). Let \(X^n\), \(X^{n+1}\) denote the two meshes at \(t = t^n\) and \(t=t^{n+1}\) respectively. Note that the mesh does not change continuously between the two time steps. In general, even the dimensionality changes abruptly as the mesh is refined and/or coarsened locally.

On the semi-discrete level, we consider a single AMR operation at time \(t=t^n\) as a transmission problem [19, 22]

$$\begin{aligned} \begin{aligned} U_t^{n}&= {{\mathcal {D}}^n(X^n,U^n)}, \quad t \le t^n \\ U_t^{n+1}&= {{\mathcal {D}}^{n+1}(X^{n+1},U^{n+1})}, \quad t > t^n \\ U^{n+1}(t^n)&= \mathcal {F} \left[ U^{n}(t^n),U^{n+1}(t^n)\right] . \end{aligned} \end{aligned}$$
(3)

The symbol \(\mathcal {F}\) is used here to represent the interpolation procedure of either implicit or explicit form, red where in the latter case \(\mathcal {F}\) simplifies into \(\mathcal {F} \left[ U^{n},U^{n+1}\right] =\mathcal {F} (U^{n})\). The design goal of \(\mathcal {F}\), apart from interpolating solution values accurately from one mesh to the other, is to preserve the stability of the underlying schemes due to semi-boundedness (2). To achieve this, we hence require that \(\mathcal {F}\) satisfies the following contractivity condition with respect to the same quadratures

$$\begin{aligned} \varPsi = \mathcal {F}(\varPhi ,\varPsi ) \quad \Rightarrow \quad \Vert \varPsi \Vert _{{\mathcal {P}}^{n+1}} \le \Vert \varPhi \Vert _{{\mathcal {P}}^n}, \end{aligned}$$
(4)

thus ensuring that the solution to (3) remains non-growing.

2.2 Inner Product Preserving Interpolation

A pair of IPP interpolation operators between the two meshes \(X^n\) and \(X^{n+1}\) with respect to the quadratures in (2) are defined by

$$\begin{aligned} (\varPsi , {\mathcal {I}}_{FW}\varPhi )_{{\mathcal {P}}^{n+1}} = ({\mathcal {I}}_{BW}\varPsi , \varPhi )_{{\mathcal {P}}^{n}}, \ \ \text {i.e.} \quad {\mathcal {P}}^{n+1}{\mathcal {I}}_{FW}={\mathcal {I}}_{BW}^T{\mathcal {P}}^{n}, \end{aligned}$$
(5)

where the subscript FW indicates forward interpolation from the previous to the new mesh, and BW denotes backward interpolation in the opposite direction. Note that in the case of an explicit AMR implementation, only \({\mathcal {I}}_{FW}\) has to be implemented. Even in this case however, the backward operator \({\mathcal {I}}_{BW}\) as defined by (5) must be accurate, as we will show below.

We consider accuracy relations of the type

$$\begin{aligned} {\mathcal {I}}_{FW} {\varvec{\varphi }} (X^n) =&\ {\varvec{\varphi }}(X^{n+1}) \end{aligned}$$
(6)
$$\begin{aligned} {\mathcal {I}}_{BW} {\varvec{\varphi }}(X^{n+1}) =&\ {\varvec{\varphi }} (X^n) \end{aligned}$$
(7)

for all polynomials \(\varphi \) up to (and including) a certain order p, where \({\varvec{\varphi }}(X^n)\), \({\varvec{\varphi }}(X^{n+1})\) are vectors with the value of \(\varphi \) in each node. For the reader’s convenience we restate below the central accuracy result for IPP operators originally proven in [18].

Proposition 1

Let \({\mathcal {I}}_{FW}\) and \({\mathcal {I}}_{BW}\) be a pair of IPP interpolation operators, defined in (5). If both (6) and (7) are satisfied for all polynomials \(\varphi \) of order up to p, then

$$\begin{aligned} {\varvec{\varphi }}(X^{n+1})^T{\mathcal {P}}^{n+1} {\varvec{\varphi }}(X^{n+1}) = {\varvec{\varphi }}(X^{n})^T{\mathcal {P}}^{n} {\varvec{\varphi }}(X^{n}) \end{aligned}$$
(8)

also holds for all polynomials up to order p.

In terms of practical operator construction, this result infers an upper theoretical limit to the formal accuracy of \({\mathcal {I}}_{FW}\) and \({\mathcal {I}}_{BW}\) based on properties of the quadratures \({\mathcal {P}}^n\) and \({\mathcal {P}}^{n+1}\) in (2). A more in-depth discussion of the accuracy restrictions following from Proposition 1 in the AMR context will follow later in Sect. 3.

2.3 Explicit Implementation

To start with, we consider the most straightforward, explicit implementation of an interpolation operator \({\mathcal {I}}_{FW}\) in the AMR procedure, i.e. let

$$\begin{aligned} \mathcal {F}(\varPhi ,\varPsi ) = {\mathcal {I}}_{FW} \varPhi . \end{aligned}$$
(9)

The following so-called transmission condition, first formulated for problems of the type (3) in [22], can be shown to imply the contractivity condition (4)

$$\begin{aligned} {\mathcal {I}}_{FW}^T{\mathcal {P}}^{n+1}{\mathcal {I}}_{FW}-{\mathcal {P}}^{n}\le 0 . \end{aligned}$$
(10)

This condition was also considered for stationary non-collocated interfaces of dissipative type in [20].

We are now ready to state our first main new result, providing a link between IPP operator theory and the explicit transmission condition (10).

Proposition 2

Consider a forward interpolation operator \({\mathcal {I}}_{FW}\) satisfying (6) for polynomials up to order p, and assume furthermore that the mesh quadratures satisfy (8) for polynomials up to order p. Then, in order for the transmission condition (10) to hold, it is necessary that also the IPP backward operator \({\mathcal {I}}_{BW}\) (5) satisfies (7) for polynomials up to order p.

Proof

We start by assuming (6) and (8) for some value p, as stated in the premise. Now let \(\varphi \) be any polynomial of order up to p. We then have, defining \({\varvec{\varphi }}_{n}=\varphi (X^n)\) and \({\varvec{\varphi }}_{n+1}=\varphi (X^{n+1})\),

$$\begin{aligned} \begin{aligned} {\varvec{\varphi }}_{n}^T ( {\mathcal {I}}_{FW}^T{\mathcal {P}}^{n+1}{\mathcal {I}}_{FW} - {\mathcal {P}}^n ) {\varvec{\varphi }}_{n}&= ({\mathcal {I}}_{FW}{\varvec{\varphi }}_{n})^T {\mathcal {P}}^{n+1} ({\mathcal {I}}_{FW}{\varvec{\varphi }}_{n}) - {\varvec{\varphi }}_{n}^T{\mathcal {P}}^n{\varvec{\varphi }}_{n} \\&= {\varvec{\varphi }}_{n+1}^T{\mathcal {P}}^{n+1}{\varvec{\varphi }}_{n+1} - {\varvec{\varphi }}_{n}^T{\mathcal {P}}^n{\varvec{\varphi }}_{n} = 0 , \end{aligned} \end{aligned}$$

where we have used both (6) and (8). It now follows from Lemma 14 in [23] that the matrix \({\mathcal {I}}_{FW}^T{\mathcal {P}}^{n+1}{\mathcal {I}}_{FW}-{\mathcal {P}}^n\) is indefinite unless we also have

$$\begin{aligned} ({\mathcal {I}}_{FW}^T{\mathcal {P}}^{n+1}{\mathcal {I}}_{FW}-{\mathcal {P}}^n){\varvec{\varphi }}_{n} = 0 \end{aligned}$$

for all polynomials \(\varphi \) of order up to p. After again inserting (6), using the definition of \({\mathcal {I}}_{BW}\) in (5) and multiplying through with the inverse of \({\mathcal {P}}^n\), we find

$$\begin{aligned} {\mathcal {I}}_{BW}{\varvec{\varphi }}_{n+1} ={\varvec{\varphi }}_{n}. \end{aligned}$$
(11)

Hence, \({\mathcal {I}}_{BW}\) satisfies (7) up to order p, which concludes the proof.

We note that Proposition 2 above can be seen as a straightforward extension of Proposition 1 in [19], which relates to explicit filtering procedures. In the context of filters however, we have \({\mathcal {P}}^{n+1}={\mathcal {P}}^n\), which makes the assumption that (8) holds superfluous. Hence, Proposition 2 is a more general result which applies to all types of IPP operators.

2.4 Implicit Implementation

From a pure operator construction perspective, it is more convenient to only consider the IPP property (5), which is a linear constraint on the coefficients in \({\mathcal {I}}_{FW}\) and \({\mathcal {I}}_{BW}\), rather than also the additional non-convex eigenvalue constraint in (10). As an alternative to the explicit AMR implementation considered above, we add an implicit correction term to (9)

$$\begin{aligned} \mathcal {F}(\varPhi ,\varPsi ) = {\mathcal {I}}_{FW} \varPhi - {\mathcal {I}}_{FW} \left( {\mathcal {I}}_{BW}\varPsi -\varPhi \right) . \end{aligned}$$
(12)

We can now directly prove that the IPP property (5) is sufficient for contractivity (4), i.e. without the need for the additional constraint (10).

Proposition 3

Consider the implicit AMR implementation \(\varPsi = \mathcal {F}(\varPhi ,\varPsi )\) in (12), and let \({\mathcal {I}}_{FW}\) and \({\mathcal {I}}_{BW}\) be IPP as in (5). Then

$$\begin{aligned} \Vert \varPsi \Vert _{{\mathcal {P}}^{n+1}}^2 = \Vert \varPhi \Vert _{{\mathcal {P}}^{n}}^2 - \Vert \varPhi -{\mathcal {I}}_{BW}\varPsi \Vert _{{\mathcal {P}}^{n}}^2 \end{aligned}$$

holds, i.e. the operation is contractive (4).

Proof

First note that \(\varPsi = \mathcal {F}(\varPhi ,\varPsi )\) in (12) gives, \(({\mathcal {I}}+{\mathcal {I}}_{FW}{\mathcal {I}}_{BW})\varPsi = 2 \, {\mathcal {I}}_{FW} \varPhi \). Multiplying with \(\varPsi ^T{\mathcal {P}}^{n+1}\) from the left, we get

$$\begin{aligned} \Vert \varPsi \Vert _{{\mathcal {P}}^{n+1}}^2 + (\varPsi ,{\mathcal {I}}_{FW}{\mathcal {I}}_{BW}\varPsi )_{{\mathcal {P}}^{n+1}} = 2( \varPsi ,{\mathcal {I}}_{FW} \varPhi )_{{\mathcal {P}}^{n+1}}. \end{aligned}$$

From (5), this becomes

$$\begin{aligned} \Vert \varPsi \Vert _{{\mathcal {P}}^{n+1}}^2 + \Vert {\mathcal {I}}_{BW}\varPsi \Vert _{{\mathcal {P}}^{n}}^2 = 2({\mathcal {I}}_{BW} \varPsi , \varPhi )_{{\mathcal {P}}^{n}}. \end{aligned}$$

After adding and subtracting \(\Vert \varPhi \Vert _{{\mathcal {P}}^{n}}^2\) on the right hand side, we finally get

$$\begin{aligned} \begin{aligned} \Vert \varPsi \Vert _{{\mathcal {P}}^{n+1}}^2&= \Vert \varPhi \Vert _{{\mathcal {P}}^{n}}^2 - \Vert \varPhi \Vert _{{\mathcal {P}}^{n}}^2 - \Vert {\mathcal {I}}_{BW}\varPsi \Vert _{{\mathcal {P}}^{n}}^2 + 2({\mathcal {I}}_{BW}\varPsi , \varPhi )_{{\mathcal {P}}^{n}} \\&= \Vert \varPhi \Vert _{{\mathcal {P}}^{n}}^2 - \Vert \varPhi -{\mathcal {I}}_{BW}\varPsi \Vert _{{\mathcal {P}}^{n}}^2, \end{aligned} \end{aligned}$$

which concludes the proof.

The analogous result for filtering procedures with \({\mathcal {P}}^{n+1}={\mathcal {P}}^n\) was given in [19].

3 Accuracy Considerations

In terms of accuracy, we have seen in Proposition 1 that IPP interpolation operators and their underlying quadratures rules are interrelated through the conditions (6), (7) and (8). Recall that these quadrature rules in turn relate to the underlying semi-discrete schemes through the property of semi-boundedness (2). In this section we will discuss accuracy in more depth, and in particular how Proposition 1 relates to the underlying schemes.

3.1 Differentiation and Integration

We consider a discrete first derivative operator \({\mathcal {D}}_{x_i}\), for the coordinate direction \(x_i\) on a mesh denoted by X. The accuracy relations on a Cartesian mesh are of the type

$$\begin{aligned} {\mathcal {D}}_{x_i} {\varvec{\varphi }}(X) = \frac{\partial }{\partial x_i} {\varvec{\varphi }}(X), \end{aligned}$$
(13)

for polynomials \(\varphi \) of order up to (and including) s.

Semi-boundedness (2) can e.g. be achieved by formally postulating a SBP operator structure of all partial derivative approximations. By the use of compatibility conditions, the accuracy of such operators can be shown to be interrelated with their respective quadrature rules in a similar way that IPP operators are due to Proposition 1 [10, 15, 16]. In particular, a simple 1D analysis reveals that if differentiation is carried out to accuracy order s (13), then the associated quadrature must be exact for mesh polynomials up to order \(2s-1\), see [16].

In order to relate this and similar results to the condition (8) in Proposition 1, we note first that the integrand \(\varphi ^2\) in (8) is a polynomial of even order. Hence, if a quadrature \({\mathcal {P}}\) is exact for all polynomials up to order \(2s-1\), we then have

$$\begin{aligned} {\varvec{\varphi }}(X)^T{\mathcal {P}} {\varvec{\varphi }}(X) = \int _{\Omega } \varphi ^2 d\Omega \end{aligned}$$
(14)

for all polynomials \(\varphi \) up to order \(s-1\).

3.2 IPP Interpolation

If the quadratures in (8) are known to satisfy the integration conditions (14) already from properties of the semi-discretization, then the significance of Proposition 1 can be better understood by the following corollary.

Corollary 1

Consider the case where (14) is satisfied up to order \(s-1\), but where neither (14) nor (8) holds to order s or higher. Then an IPP operator pair \({\mathcal {I}}_{FW}\) and \({\mathcal {I}}_{BW}\) can not simultaneously satisfy (6) and (7) for any p larger than \(s-1\). In other words, at most one of them can be satisfied for \(p=s\).

Proof

The premise is that (8) is true for all polynomials \(\varphi \) up to order \(s-1\) (since this follows from (14)), but not for all \(\varphi \) of order s. Moreover, Proposition 1 states that (6) and (7) together implies (8). Thus, if both (6) and (7) would hold for \(p=s\), then this would lead to a contradiction since we have already established that (8) does not hold up to s.

Remark 1

Recall that the upper limit of \(s-1\) in (14) is related to the use of SBP operators of order s (13). In light of this, the upper accuracy limit of \(p=s-1\) given by Corollary 1 should be seen as a serious limitation. By Taylor’s theorem, interpolating a smooth function on the mesh results in errors of order s. As a comparison, in the absence of AMR interpolation, the expected convergence rate of a finite difference SBP scheme is \(s+1\) [25, 26]. This observation suggests that a numerical solution loses one order of accuracy even after a single AMR operation, since the interpolation adds on a new error of order s which is independent of the order of the scheme.

If AMR is applied frequently (after each or every few time steps), the effect on solution accuracy is harder to predict, especially if the region in space where AMR interpolation is applied is small and/or moving. However, some level of error accumulation over time must in general be expected, possibly leading to a further reduction in convergence order.

In the case of finite difference operators, a solution to this suboptimal accuracy constraint resulting from Proposition 1 was proposed in [6]. By increasing the number of boundary nodes and modifying the associated quadrature weights for each grid size, the order of polynomials in (14) could be increased to s, thus removing the constraint of \(s-1\) in Corollary 1. This is a rather specialized approach however, and for standard SBP finite difference operators with fixed boundary closure coefficients, no such fix is possible [16].

3.3 Explicit AMR Interpolation

In the explicit implementation (9) of AMR, we only apply one of the two interpolation operators in an IPP pair, i.e. the forward operator \({\mathcal {I}}_{FW}\). In this case, Corollary 1 does not rule out the possibility of maintaining an accuracy of \(p=s\), as long as \({\mathcal {I}}_{BW}\) (which is not used) has the lower value \(p=s-1\). However, even this is not always possible, as the following result shows.

Corollary 2

Consider the premises of Corollary 1. If we assume that \({\mathcal {I}}_{BW}\) satisfies (7) for \(p=s-1\), and \({\mathcal {I}}_{FW}\) satisfies (6) for \(p=s\), then for (10) to hold we need to additionally have

$$\begin{aligned} {\varvec{\varphi }}_{n+1}^T {\mathcal {P}}^{n+1}{\varvec{\varphi }}_{n+1} \le {\varvec{\varphi }}_{n}^T {\mathcal {P}}^n {\varvec{\varphi }}_{n} \end{aligned}$$
(15)

for all polynomials \(\varphi \) of order s.

Proof

First note that (15) is automatically satisfied with equality up to order \(s-1\) due to (14). For the case of order s, consider the quadratic form of the left hand side in (10) with respect to \({\varvec{\varphi }}_{n}\)

$$\begin{aligned} {\varvec{\varphi }}_{n}^T \left( {\mathcal {I}}_{FW}^T{\mathcal {P}}^{n+1}{\mathcal {I}}_{FW}-{\mathcal {P}}^{n}\right) {\varvec{\varphi }}_{n} \le 0. \end{aligned}$$

Now, since we have assumed that (6) holds up to order s, this condition exactly reduces to (15).\(\square \)

Remark 2

To understand the nature of the constraint (15) better, it is instructive to consider the special case of \({\mathcal {P}}^{n}\) and \({\mathcal {P}}^{n+1}\) representing a trapezoidal rule on two different meshes \(X^n\) and \(X^{n+1}\). If the integration is exact for all polynomials up to order \(2s-1\) due to compatibility conditions, i.e. (14), we may without loss of generality only consider a single monomial of order s in (15), i.e. the highest order term of the polynomial. The integrand \(\varphi ^2\) is then a convex positive function, implying that the piecewise linear trapezoidal segments will systematically overestimate the real integral value. The coarser the mesh, the more pronounced this overestimation becomes, which means that (15) is satisfied if the new mesh \(X^{n+1}\) is a refinement of \(X^{n}\), but not the other way around.

This property of the trapezoidal rule carry over to higher order quadrature rules as well. In other words, as long as the mesh is refined and not coarsened, condition (2) holds, making it possible to construct a forward interpolation operator \({\mathcal {I}}_{FW}\) of order \(p=s\).

3.4 Comments Regarding Explicit Versus Implicit AMR

As already mentioned, one advantage with the implicit implementation (12) of AMR interpolation is the simplicity gained from only requiring a pair of IPP operators (5), whereas the additional transmission condition (10) required in the explicit case is more complicated to achieve. However, we have seen in Corollary 2 and Remark 2 that the explicit implementation is potentially more accurate (raising the order from \(s-1\) to s) in the case of refinement, i.e. adding nodes locally. It is also more straightforward to implement. We will make practical comparisons of solution accuracy using the two approaches in the numerical section of this paper.

4 Finite Difference Application with a Moving Interface

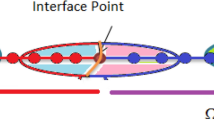
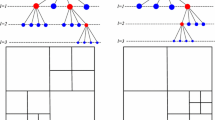
In this section we discuss one application of the AMR theory outlined above. As a model, we consider a two-block FD grid with an advancing front between two areas of different grid resolution. The situation is illustrated in Fig. 1 for the 1D case and in Fig. 2 for the 2D case. Note that these two figures will also be explained in more detail in Sects. 4.1 and 4.2, respectively. In both cases, the interface is moved in a step-wise manner between times \(t^n\) and \(t^{n+1}\) by adding two nodes to the \(x-\)direction of the fine grid, and removing one from the coarse grid. In 2D or 3D, if the resulting interfaces are non-collocated in space, they must be handled weakly by the underlying scheme, with penalty terms included in \({\mathcal {D}}^{n}\) and \({\mathcal {D}}^{n+1}\).

4.1 Operators in One Dimension

Figure 1 illustrates the various components of an AMR operation in 1D. The fine region in both grids are associated with quadratures \(P_f^n\) and \(P_f^{n+1}\), and the coarse regions with \(P_c^n\) and \(P_c^{n+1}\). For interpolation between \(t^n\) and \(t^{n+1}\), we only need to consider a smaller set of nodes, and do nothing outside of the interface region. In other words, we are only interested in a small subset of the quadrature weights, given by

Fig. 1
figure 1

Schematic of AMR interpolation in 1D

Full size image

and we also divide \(P_f^{n+1}\), \(P_c^{n+1}\) in the same way. Correspondingly, we consider interpolation operators of the form

The IPP property (5) thus reduces to

$$\begin{aligned} {\hat{P}}^{n+1}{\hat{I}}_{FW}={\hat{I}}_{BW}^T{\hat{P}}^{n} , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {\hat{P}}^n&= \begin{pmatrix} {\hat{P}}_f^n \\ &{} {\hat{P}}_c^n \end{pmatrix},&{\hat{P}}^{n+1}&= \begin{pmatrix} {\hat{P}}_f^{n+1} \\ &{} {\hat{P}}_c^{n+1} \end{pmatrix}. \end{aligned} \end{aligned}$$

Next, we will show how AMR operators designed in this way for one space dimension can be applied to higher dimensional grids.

4.2 Operators in Two Dimensions

To illustrate the extension of the 1D AMR procedure above into two space dimensions, see Fig. 2 where we simply extrude the 1D example grid from Fig. 1 in the vertical direction.

Fig. 2
figure 2

Schematic of AMR interpolation in 2D. The top part describes the big picture view of refinement with a moving interface, while the bottom part describes the steps involved in more detail

Full size image

In doing this, we introduce new sets of quadrature weights \(P_c\) and \(P_f\) along the whole length of the interface. Corresponding to these, we consider a pair of IPP interpolation operators

$$\begin{aligned} P_f I_{c2f} = I_{f2c}^TP_c. \end{aligned}$$

In the horizontal direction, we will make use of the 1D operators \({\hat{I}}_{FW}\) and \({\hat{I}}_{BW}\) already introduced. As before, we let the complete AMR interpolation operators (here denoted by \({\mathcal {I}}_{FW}\) and \({\mathcal {I}}_{BW}\)) be given by identity outside of the indicated interface region.

Consider a block-wise \(x-\)major lexicographical ordering of all nodes inside the interface region. By the use of Kronecker products, we may thus collect the full set of 2D nodal quadrature weights into the matrices

$$\begin{aligned} \begin{aligned} \hat{{\mathcal {P}}}^n&= \begin{pmatrix} {\hat{P}}_f^{n} \otimes P_f \\ &{} {\hat{P}}_c^{n} \otimes P_c \end{pmatrix},&\hat{{\mathcal {P}}}^{n+1}&= \begin{pmatrix} {\hat{P}}_f^{n+1} \otimes P_f \\ &{} {\hat{P}}_c^{n+1} \otimes P_c \end{pmatrix}. \end{aligned} \end{aligned}$$

The complete IPP procedure for a non-collocated interface in 2D can be divided into a sequence of 1D operations using Kronecker products. For the forward in time operation \({\mathcal {I}}_{FW}\), those steps are described below, and also illustrated in Fig. 2.

  1. 1.

    First, the coarse grid is refined in the vertical direction in order to make the two grids collocated. With respect to the whole interface region, this amounts to applying the operator

    $$\begin{aligned} \begin{pmatrix} {\hat{I}}_f^{n}\otimes I_f \\ &{} {\hat{I}}_c^{n} \otimes I_{c2f} \end{pmatrix}, \end{aligned}$$

    where \({\hat{I}}_c^n\), \({\hat{I}}_f^n\) and \(I_f\) denote identity matrices of the same dimensions as \({\hat{P}}_c^n\), \({\hat{P}}_f^n\) and \(P_f\), respectively. In the lower part of Fig. 2, this step corresponds to moving from the first to the second grid from left to right.

  2. 2.

    At this point, all grid points in the interface region are aligned along horizontal lines. However, before applying the 1D AMR interpolation operators with the use of Kronecker products, we formally have to reorder the nodes between the original block-wise into a complete lexicographical node ordering. For this purpose we let \(\tilde{E}^{n}\) denote the permutation operator which reorders all nodes according to ascending \(y-\)values. This step is only of a virtual book-keeping nature and is not shown explicitly in Fig. 2.

  3. 3.

    We can now extend the AMR interpolation operator in 1D into 2D using a Kronecker product

    $$\begin{aligned} \left( {\hat{I}}_{FW} \otimes I_f \right) . \end{aligned}$$

    This step corresponds to moving from the second to the third grid in the lower part of Fig. 2.

  4. 4.

    Before proceeding, we have to reorder the nodes back into block-wise lexicographical ordering. We let this permutation operation be denoted with \((\tilde{E}^{n+1})^T\).

  5. 5.

    Finally, the right grid is coarsened along the vertical direction to make the interface non-collocated again

    $$\begin{aligned} \begin{pmatrix} {\hat{I}}_f^{n+1}\otimes I_f^{n+1} \\ &{} {\hat{I}}_c^{n+1} \otimes I_{f2c} \end{pmatrix}. \end{aligned}$$

    This step corresponds to moving from the third to the fourth grid in Fig. 2.

It can easily be shown that the successive application of several IPP operators is always an IPP operation in itself, see Lemma 1 in [18]. Thus, since each step above involves the use of an IPP operator, it follows that the whole sequence is IPP with respect to the reverse operation. In the same way, the condition (10) of contractivity is also preserved if each one of the individual steps is contractive.

The complete five step procedure in both directions can be written out compactly as

$$\begin{aligned} \begin{aligned} \hat{{\mathcal {I}}}_{FW} =&\, \begin{pmatrix} {\hat{I}}_f^{n+1}\otimes I_f^{n+1} \\ &{} {\hat{I}}_c^{n+1} \otimes I_{f2c} \end{pmatrix} (\tilde{E}^{n+1})^T \left( {\hat{I}}_{FW} \otimes I_f \right) \tilde{E}^n \begin{pmatrix} {\hat{I}}_f^{n}\otimes I_f^{n} \\ &{} {\hat{I}}_c^{n} \otimes I_{c2f} \end{pmatrix} \\ \hat{{\mathcal {I}}}_{BW} =&\, \begin{pmatrix} {\hat{I}}_f^{n}\otimes I_f^{n} \\ &{} {\hat{I}}_c^{n} \otimes I_{f2c} \end{pmatrix} (\tilde{E}^{n})^T \left( {\hat{I}}_{BW} \otimes I_f \right) \tilde{E}^{n+1} \begin{pmatrix} {\hat{I}}_f^{n+1}\otimes I_f^{n+1} \\ &{} {\hat{I}}_c^{n+1} \otimes I_{c2f} \end{pmatrix} , \end{aligned} \end{aligned}$$

which describes the two operators \({\mathcal {I}}_{FW}\) and \({\mathcal {I}}_{BW}\) inside the interface region.

5 Numerical Results

We test the stability and convergence properties of the new AMR framework, by conducting numerical experiments using a set of both linear and non-linear hyperbolic model problems. The IPP operator coefficients that we have used in conjuction with the novel FD methodology of Sect. 4 are listed in Appendix A. In line with Remark 2, the order of accuracy is \(p=s\) in the forward direction of the schematic in Fig. 1, and \(p=s-1\) in the backward direction.

5.1 One Dimension

For our one-dimensional test cases we consider the model problem

$$\begin{aligned} \begin{aligned} u_t +u_x =&0, \quad -2\le x\le 2, \quad t\ge 0 \\ u(x,0) =&f(x). \end{aligned} \end{aligned}$$
(16)

A time dependent finite difference block discretization is applied, consisting of a moving finely resolved interior block surrounded by two coarser blocks, with a refinement ratio of 1/2 between the coarse and the fine grids. The interior block moves with a constant speed of 1 from a starting point given by \(-1\le x \le 0\) at \(t=0\).

Again relating to Remark 2 and the schematic in Fig. 1, we note that the order of forward AMR interpolation \({\mathcal {I}}_{FW}\) (and thus of the explicit AMR implementation) is \(p=s-1\) at the left block interface, and \(p=s\) at the right interface, while for implicit AMR we have \(p=s-1\) at both interfaces. In order to study the effect of AMR on solution accuracy at these two types of interfaces separately, we will consider two different Gaussian profiles as exact solutions to (16), both moving with the same unit speed as the interior block. The moving block structure as well as the two exact solution profiles are illustrated in Figs. 3 and 4 respectively, where the fine interior block is indicated with dotted red lines in the solution curves.

Fig. 3
figure 3

Gaussian profile with center in the left part of the fine grid

Full size image
Fig. 4
figure 4

Gaussian profile with center in the right part of the fine grid

Full size image

We stress that the only purpose with the numerical tests in this section are to study the asymptotic convergence rates resulting from AMR interpolation around the two types of block interfaces. Hence, we have deliberately placed the two solution profiles such that gradients are relatively large at these two interfaces, respectively, i.e. so that the contribution from AMR interpolation dominates the error. In real world applications one would of course aim to do the exact opposite, i.e. to place active AMR interfaces as far away from steep solution gradients as possible.

5.1.1 Left Interface Treatment

In (16) we first consider the exact solution

$$\begin{aligned} u(x,t) = \mathrm {exp}\left( \frac{-(x+5/7-t)^2}{2(1/7)^2}\right) , \end{aligned}$$

which we have plotted at \(t=0\) and \(t=1\) in Fig. 3, together with the moving multi-block grid structure. Note that in the initial configuration, this Gaussian is centered at \(x=-5/7\), i.e. some distance to the left of the fine block center at \(x=-1/2\). By placing the Gaussian in this way, solution gradients are much steeper at the left interface, and we thus highlight the contribution to the numerical error from the left interface (i.e. where \(p=s-1\) for both the implicit and explicit AMR implementations), while the contribution from the right interface treatment can be neglected.

Fig. 5
figure 5

Error profiles using an implicit AMR implementation

Full size image

In Fig. 5 we show the error profile at \(t=1\) for two different mesh resolutions, using a classical SBP FD scheme with \(s=2\) (i.e. fourth order interior accuracy), together with an implicit AMR implementation. The grid parameter N denotes the number of nodes in the interior fine grid, and we have used the classical fourth order explicit Runge-Kutta scheme for time marching with \(\varDelta t = (1/8) (1/N)\). Consequently, AMR has been applied after each 8 time steps in order for the block interface to move with the correct speed. The same time stepping strategy will be used for all subsequent numerical tests as well.

Already from the two plots in Fig. 5, a slower converge in the region immediately surrounding the left interface can be surmised. To study this effect in more detail, in Tables 1 and 2 we list the obtained convergence rates (using a standard definition of \(p=\mathrm {log}_2(\Vert e(N)\Vert /\Vert e(N/2)\Vert \)) with respect to the maximum (\(L_\infty \)) norm of the error for the explicit and implicit AMR implementations, respectively. Asymptotically, the convergence rates appear to stabilize at an order of \(s-1/2\) in both the explicit and the implicit case, to be compared with the general rate of \(s+1\) for the basic FD schemes, and to order s of the interpolation operators. Note that the interpolation scheme is applied \(\mathcal {O}(N)\) times to track the moving solution profile. Thus, since the observed convergence rate is lower by one half order compared to the interpolation scheme itself, we conclude that this must be due to AMR interpolation errors accumulating over time, as previously predicted in Remark 1. The \(L_2\) convergence rates in the explict and implicit cases are shown in Tables 3 and 4, pointing to a general rate of s, i.e. a loss of one order compared to the case with no AMR interpolation.

Table 1 \(L_\infty \) norm convergence for test case 1 using explicit AMR
Full size table
Table 2 \(L_\infty \) norm convergence for test case 1 using implicit AMR
Full size table
Table 3 \(L_2\) norm convergence for test case 1 using explicit AMR
Full size table
Table 4 \(L_2\) norm convergence for test case 1 using implicit AMR
Full size table

5.1.2 Right Interface Treatment

For the second test case, we use as exact solution in (16) the following Gaussian profile located to the right of the fine block center

$$\begin{aligned} u(x,t) = \mathrm {exp}\left( \frac{-(x+2/7-t)^2}{2(1/7)^2}\right) . \end{aligned}$$

See again Fig. 4 for an illustration. In this way, we thus highlight the contribution to the numerical error from the right interface (i.e. where \(p=s-1\) the implicit and \(p=s\) for the explicit AMR implementation), while the contribution from the left interface treatment can be neglected.

In Fig. 6 we show the error profile for two different mesh resolutions, again using the classical SBP-FD method with \(s=2\) (fourth order interior accuracy), this time with an explicit AMR implementation. Moreover, we quantify the convergence rates obtained in Tables 5 and 6 in the \(L_\infty \) and \(L_2\) norm, respectively. The asymptotic rates are not as easy to interpret in this case, but appear in general to lie somewhere between s and \(s+1/2\) for the \(L_\infty \) norm, and between \(s+1/2\) and \(s+1\) for the \(L_2\) norm. Compared to the previous case, the accuracy is thus approximately between one half and one order higher, which reflects the higher order of AMR interpolation as noted earlier.

Fig. 6
figure 6

Error profiles using an explicit AMR implementation

Full size image
Table 5 \(L_\infty \) norm convergence for test case 2 using explicit AMR
Full size table
Table 6 \(L_2\) norm convergence for test case 1 using explicit AMR
Full size table

5.2 Two Dimensions

We generalize the 1D test case discussed above and consider the moving block mesh drawn in Fig. 7 at \(t=0\) and \(t=1\). The model problem is given by

$$\begin{aligned} \begin{aligned} u_t+u_x+u_y =&0, \quad -2\le x,y\le 2, \quad t\ge 0 \\ u(x,0) =&f(x,y), \end{aligned} \end{aligned}$$

again amended with a Gaussian exact solution profile (described below for the two cases).

In terms of AMR, there are essentially two new features which come into play in the 2D case. Firstly, we need a pair of interpolation operators \(I_{f2c}\) and \(I_{c2f}\) acting in the tangent direction of each mesh refinement interface. Secondly, there are no less than 8 moving interfaces with the same mesh refinement level on both sides. Both of these features require new interpolation operators. We will only study qualitative aspects of the 2D AMR interpolation, and we restrict our attention to the classical SBP FD case with \(s=2\) (i.e. using fourth order interior accuracy). A novel pair of IPP 1D interpolation operators to handle the 8 collocated mesh interfaces is given in Appendix 1, where the accuracy is given by \(p=2\) in both directions.

5.2.1 Left/Bottom Interface Treatment

We generalize the setup from Sect. 5.1.1 and thus consider a Gaussian profile positioned close to the lower left corner of the fine interior grid

$$\begin{aligned} u(x,y,t) = \mathrm {exp}\left( \frac{-(x+5/7-t)^2-(y+5/7-t)^2}{2(1/7)^2}\right) . \end{aligned}$$

We now compare the result of using a mildly unstable AMR procedure compared to a stable one. For this purpose, we will first use the same \(I_{f2c}\) and \(I_{c2f}\) operators that were presented in [18]. These are IPP, but do not satisfy the explicit transmission condition (10). Hence, an explicit AMR procedure using these operators should be unstable. The results for \(N=64\) are shown in Fig. 8, where the explicit case clearly shows elevated error levels compared to the stable implicit implementation. These higher levels are located at the bottom left corner of the fine grid. Since the same operators are used in both cases, the qualitatively different results observed can probably be ascribed to a developing instability in the explicit case.

Fig. 7
figure 7

Block mesh

Full size image
Fig. 8
figure 8

Absolute error levels around the bottom left corner of the fine grid. Operators are used which are IPP but not strictly contractive. Note the different scalings of the color bars

Full size image
Fig. 9
figure 9

Absolute error levels around the bottom left corner of the fine grid. Operators are used which are both IPP and strictly contractive

Full size image

In order to compare these results to a setup where also the explicit implementation is stable, we have slightly modified the operators \(I_{c2f}\) and \(I_{f2c}\) to make them both IPP and contractive, see 1. The new results are shown in Fig. 9, and this time there is no qualitative difference between the two implementations.

This example illustrates the vital importance of making sure that the AMR implementation procedure is strictly stable. Despite the inherent accuracy limitations involved with such schemes, we can not do better by ignoring the issue of stability.

5.2.2 Right/Top Interface Treatment

We also consider the case where the Gaussian profile is close to the upper right corner of the fine grid, i.e.

$$\begin{aligned} u(x,y,t) = \mathrm {exp}\left( \frac{-(x+2/7-t)^2-(y+2/7-t)^2}{2(1/7)^2}\right) . \end{aligned}$$

Just as in the 1D case, we benefit from a more accurate explicit implementation by using only the forward AMR operator \({\mathcal {I}}_{FW}\). However, the operators \(I_{c2f}\) and \(I_{f2c}\) still exhibit the lower accuracy level \(p=1\) at corner points, and hence we expect the errors at the upper right corner to dominate on a fine enough grid. We confirm that this is the case by showing error plots for two different grid parameters in Fig. 10.

Fig. 10
figure 10

Result of refinement for an explicit implementation of a coarse to fine AMR case in 2D. Asymptotically, the errors are dominated by the lower accuracy of \(I_{f2c}\) and \(I_{c2f} \) at the corner point

Full size image

5.3 A Non-linear Example

As a final demonstration, we study the inviscid non-linear Burger’s equation with an initial sinusoidal solution,

$$\begin{aligned} \begin{aligned} u_t + uu_x =&\, 0 , \quad -\pi \le x\le \pi , \quad 0< t < 1,\\ u(x,0) =&\sin (x). \end{aligned} \end{aligned}$$

The initial function has a unit slope at \(x=0\), meaning that a discontinuity will develop at t approaches 1. Our goal with this experiment is to demonstrate how AMR can be used to smoothly resolve the solution up until the very moment of shock formation, using a high order, non-dissipative scheme.

To solve the non-linear problem numerically with no dissipation, we employ a skew-symmetric splitting with SBP operators, see [5] for details of this approach. As discrete operators we use Galerkin element SBP operators with Gauss-Lobatto collocation [8]. For example, using third order polynomials (corresponding to \(s=2\) in (13) and (14)), the elemental operators we use are

$$\begin{aligned} \begin{aligned} \hat{{\mathcal {P}}} =&\varDelta x \begin{pmatrix} 1/6 \\ &{} 2/3 \\ &{}&{} 1/6 \end{pmatrix}, \\ \hat{{\mathcal {D}}}_x =&\hat{{\mathcal {P}}}^{-1} \int _0^1{\mathcal {L}}{\mathcal {L}}_\xi ^T \ d\xi = \hat{{\mathcal {P}}}^{-1} \begin{pmatrix} -1/2 &{} 2/3 &{} -1/6 \\ -2/3 &{} 0 &{} 2/3 \\ 1/6 &{} -2/3 &{} 1/2 \end{pmatrix}, \end{aligned} \end{aligned}$$

where \({\mathcal {L}}\) is the vector containing the Lagrange basis

$$\begin{aligned} {\mathcal {L}} = \begin{pmatrix} 2(\xi -1/2)(\xi -1)&4\xi (\xi -1)&2\xi (\xi -1/2) \end{pmatrix}^T. \end{aligned}$$

For inter-element couplings, we use the non-dissipative version of the inviscid interface treatment in [5]. In this way, we ensure that the scheme is strictly energy conserving.

Fig. 11
figure 11

Top: initial sinus solution on a uniform grid with \(N=32\) elements (inter-element boundaries are not indicated in the figure). Middle: numerical solution after two full cycles of AMR refinement. Bottom: solution after 10 cycles of refinement

Full size image
Table 7 \(L_\infty \) convergence at \(t=7/8\) as a function of the number of starting elements
Full size table

For time integration we use the classical fourth order explicit Runge-Kutta method, with a time step size given by

$$\begin{aligned} \varDelta t = (2/\pi ) \varDelta x. \end{aligned}$$

The AMR refinement process will involve splittings of individual elements into two new ones. Using \(L_2\) projections [12, 13], the AMR operator corresponding to locally refining a single element is as follows

$$\begin{aligned} \hat{{\mathcal {I}}}_{FW} = \begin{pmatrix} \hat{{\mathcal {P}}}^{-1}\int _0^1 {\mathcal {L}}(\xi ){\mathcal {L}}(\xi /2)^T \ d\xi \\ \hat{{\mathcal {P}}}^{-1}\int _0^1 {\mathcal {L}}(\xi ){\mathcal {L}}(1/2 + \xi /2)^T \ d\xi \end{pmatrix}= \begin{pmatrix} 1 &{} 0 &{} 0 \\ 3/8 &{} 3/4 &{} -1/8 \\ 0 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ -1/8 &{} 3/4 &{} 3/8 \\ 0 &{} 0 &{} 1 \end{pmatrix}, \end{aligned}$$

where the integration sign above is carried out numerically using the quadrature weights in \(\hat{{\mathcal {P}}}\). Note that the accuracy is given by \(s=2\) in (6), which is in line with the discussion in Remark 2. We can also verify explicitly that this interpolation operator is contractive in the sense of (10), which enables an explicit implementation. We thus define

$$\begin{aligned} {\hat{P}}^n =\hat{{\mathcal {P}}}, \quad {\hat{P}}^{n+1}= \frac{1}{2}\begin{pmatrix} \hat{{\mathcal {P}}} \\ &{} \hat{{\mathcal {P}}} \end{pmatrix} = \frac{\varDelta x}{2} \begin{pmatrix} 1/6 \\ &{} 2/3 \\ &{}&{} 1/6 \\ &{}&{}&{} 1/6 \\ &{}&{}&{}&{} 2/3 \\ &{}&{}&{}&{}&{} 1/6 \end{pmatrix}, \end{aligned}$$

leading to

$$\begin{aligned} \hat{{\mathcal {I}}}_{FW}^T {\hat{P}}^{n+1}\hat{{\mathcal {I}}}_{FW} -{\hat{P}}^n =-\frac{1}{32}\begin{pmatrix} 1 &{} -2 &{} 1\\ -2 &{} 4 &{} -2 \\ 1 &{} -2 &{} 1 \end{pmatrix} = -\frac{1}{32}\begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix} \begin{pmatrix} 1&-2&1 \end{pmatrix} \le 0. \end{aligned}$$

As the solution profile starts to steepen around \(x=0\), we refine the mesh by adding more elements locally in a controlled way. Here, we are not mainly interested in investigating the best refinement strategy, but rather to demonstrate the robust implementation of a given such strategy. Since the solution behavior is predictable in a qualitative sense, we choose for simplicity to carry out refinement according to a predefined schedule, as described below.

We start from a uniform mesh as in the top graph of Fig. 11, where all element nodes are indicated with blue dots, and for simplicity the inter-element boundaries are not explicitly indicated. We describe the refinement process below only for the positive part (\(x>0\)) of the domain, and note that the negative part follows from symmetry. We start by refining the element whose left boundary is at \(x=0\), i.e. where the solution gradients are steepest. After every second time step, one more element is refined, proceeding outward towards the domain boundary. This continues until \(t=1/2\), at which point exactly half of the domain has been refined. The same process is now repeated on the newly refined part of the domain, thus creates an even finer mesh on the innermost quarter of the domain.

After each cycle of refinement in space, the time step size is correspondingly reduced by one half to keep the ratio between \(\varDelta t\) and \(\varDelta x\) constant, and the resulting total simulation time is \(t=1/2\), 3/4, 7/8, etc. after the first, second and third cycle, etc. The result of this refinement strategy is a process where the simulation time approaches \(t=1\), but in theory could go on indefinitely using smaller and smaller time steps. See Fig. 11 for the result at a few different points in time, starting from a relatively coarse mesh. We are able to capture the solution in a smooth way with high accuracy, even as we are approaching the point of discontinuity.

In absolute terms, the error still increases as we approach the discontinuity, as can be inferred from the clearly visible jump in the discontinuous solution at \(x=0\), in the bottom graph of Fig. 11. As a final test, we confirm that the solution converges with a high order of accuracy at any point in time, i.e. after any given number of AMR refinement cycles. In Table 7 we show the convergence at \(t=7/8\), i.e. after three cycles of refinement, where we have estimated the maximum error to be the jump in solution value at \(x=0\). Asymptotically, the convergence rate is \(s+1=3\).

6 Conclusions

We have developed a provably stable dynamical adaptive mesh refinement procedure, where computational nodes can be added or removed as needed during a simulation. The method is based on inner product preserving interpolation, and can be applied to various classes of numerical methods. Stability was analyzed within the framework of transmission problems, coupling a sequence of semi-discrete computations in time. To illustrate and evaluate the procedure, we have designed new interpolation operators for finite difference applications using moving non-collocated block interfaces. We have also applied \(L_2\) projection operators for Galerkin elements with Gauss-Lobatto collocation.

In terms of performance we found that, due to the accuracy limitations inherent in the inner product preserving approach, the mesh should only be modified in places where the solution gradients are significantly smaller than in the more finely resolved region of interest. Moreover, in terms of interpolation accuracy, we found that adding more computational nodes to a mesh is a less sensitive operation (by an order of magnitude) than to remove nodes. Finally, we have demonstrated with a numerical example the key importance of satisfying the transmission stability definition strictly. Hence, despite the accuracy limitations, we can not hope to do better by abandoning the inner product preserving approach.