A guide to Monte Carlo simulation concepts for assessment of risk-return profiles for regulatory purposes

Abstract

Various regulatory initiatives (such as the pan-European PRIIP-regulation or the German chance-risk classification for state subsidized pension products) have been introduced that require product providers to assess and disclose the risk-return profile of their issued products by means of a key information document. We will in this context outline a concept for a (forward-looking) simulation-based approach and highlight its application and advantages. For reasons of comparison, we further illustrate the performance of approximation methods based on a projection of observed returns into the future such as the Cornish–Fisher expansion or bootstrap methods.

1 Simulation and its role in regulatory issues

The importance of funded private or occupational old age provision will increase due to demographic changes and the resulting challenges for government-run pay-as-you-go systems. Retail investors and advisors therefore need reliable methodologies to match offered products and investors’ needs and risk appetite.

Regulatory issues nowadays typically require the aggregation of the risk of a company, of an investment strategy, a certificate, a pension product or even a short living financial product into a single number. This number might be a fully specified measure such as the variance or the value-at-risk of the final outcome of the investment (just to name two popular such quantities) or a classification into risk classes or chance-risk classes.

Examples for this are the calculation of the Solvency Capital Requirement for an insurance undertaking, the assessment of a product’s risk-return profile for packaged retail and insurance-based investment products (so-called ”PRIIPs”), or the chance-risk classification of pension products from a retail investor’s point of view by the so-called PIA (“Produkt Informationsstelle Altersvorsorge”) in Germany.

As the terms chance and risk already imply, the outcome of the corresponding financial transaction is not exactly predictable. Thus, a stochastic modelling of this outcome is the appropriate task. The full probabilistic information about the outcome is contained in its probability distribution. However, as the explicit form of this probability distribution is often unknown, various approximation methods have been used/suggested in the past such as

• Monte Carlo simulation, i.e. the use of suitably distributed random numbers to imitate the uncertainty inherent in the capital markets combined with a suitable transformation or discretization to either achieve or approximate the aimed distribution,

• approximation via an expansion of the distribution function such as the Delta-Gamma-method or the Cornish–Fisher expansion,

• bootstrap methods or historical simulation, i.e. the use of past market data for future predictions of the performance of financial positions.

The purpose of this article is to demonstrate that of all the above mentioned methods a forward-looking Monte Carlo simulation framework is the most appropriate concept. For this we will present the necessary steps to set up a simulation framework, demonstrate its flexibility and performance potential, and compare it with various approximation methods in real life applications and challenges in the following sections.¹

Before we present the suggested concept in more detail, we will start by commenting on some often raised reservations against the use of Monte Carlo simulation approaches.

Rumour 1: Simulation is technically involved  Simulation consists of the choice of an underlying model (including the parameters determining it) followed by the generation of suitable random numbers. Then, the quantities of interest can be simulated and the corresponding measures—such as risk or chance measures—will be inferred from the simulation. To underline this well-structured concept, we will give a toy example realization of it in the next section followed by a well-established application for chance-risk classification in Sect. 3.

Rumour 2: Simulation needs a huge computing infrastructure   It is often understood that simulations necessary to perform for regulatory issues require the use of huge computing clusters and then result in endless computing times. While this might be true for a naive nested Monte Carlo approach to the calculation of the Solvency Capital of an insurance company (see e.g. Krah et al. [13] for methods and numbers), this definitely is not the case if we consider the risk assessments necessary for PRIIP- or PIA-calculations. There, on the one side instead of an individualized assessment, the calculation is only required for a prototypical customer and on the other side many parts of the simulation can be done offline. Further, the number of the underlying variables that correspond to random numbers are usually very low. In total, typically not more than an ordinary laptop is needed. Although it is in general not required for the chance-risk assessment task in the PIA-calculations, we remark that for particular products a speed-up of the Monte Carlo simulation can be achieved by e.g. incorporating variance reduction methods (see e.g. Korn et al. [10], Chapter 3, for a survey on variance reduction methods or see Korn et al. [12] for an example of speeding up Monte Carlo pricing of a cliquet option that is popular in some insurance products by using the control variate technique).

Rumour 3: Simulation is not accurate  Although Monte Carlo simulation is based on a repeated performance of random experiments the law of large numbers ensures the strong convergence of Monte Carlo estimators for expectations. The Glivenko-Cantelli theorem ensures the uniform convergence if the distribution function of a random event has to be approximated by Monte Carlo simulation. On top of that the availability of confidence intervals often adds information on the accuracy of the simulation-based estimates that other methods cannot provide.

Rumour 4: Simulation as a service is costly  The simulation-based chance-risk classification of German pension products leads to surprisingly low costs per classified product, typically lower than the sales costs of the corresponding product for the therein considered four maturities of 12, 20, 30 and 40 years.

As our guiding—but by far not the only—example where simulation is used in an efficient way, we have chosen the chance-risk-classification of state subsidized German pension products performed by PIA. The underlying approach and the models applied will be introduced in Sect. 3. However, before considering this methodology, Sect. 2 will provide an introduction to the fundamental aspects of model-based simulation. Section 4 will then be devoted to analyze currently required approximation methods by the PRIIP-regulation (cf. European Commission [4] and European Commission [5]) to assess financial products’ risk-return profiles and highlight their weaknesses compared to an approach based on (forward-looking) simulation. Finally, Sect. 5 concludes.

2 Simulation as a universal tool for risk assessment

Model-based simulation always yields an estimation of the distribution function of the desired object, the so-called empirical distribution. Thus, all kinds of assessment (e.g. a classification into different risk classes) or risk measures (e.g. value-at-risk, expected shortfall) can be inferred from it. A theoretical justification for this is the famous Glivenko-Cantelli theorem that states the uniform convergence of the empirical distribution function towards the distribution function of the simulated object. Of course, an appropriate choice of the model for the underlying object is crucial.

We will below describe the general framework for model-based simulation with applications to risk assessment. It typically consists of four steps:

Step 1: Choice of the underlying stochastic model  When judging a financial position, a suitable stochastic model of the underlying capital market is the basis for model-based simulation. As a toy example, we consider the task of calculating the value-at-risk of a European call option on a (non-dividend paying) stock with maturity T at time $T_1 < T$.

For this task, the classical model for the underlying market is the Black–Scholes model. It consists of the evolution of a money market account B(t) with constant interest rate and of the stock price S(t) given by a geometric Brownian motion. I.e. we have the two price evolutions

$$\begin{aligned} B(t) = e^{rt} , \ \ S(t) = S(0) e^{\left( \mu -\frac{1}{2}\sigma ^2\right) t + \sigma W(t)} \end{aligned}$$

for constants $r,\mu ,\sigma$ with $\sigma >0$, W(t) a one-dimensional Brownian motion.

Why not a more sophisticated model? Although the Black–Scholes model is a workhorse of the finance industry, some researchers might question it, particularly for very short running options with e.g. just some days to maturity. They might suggest adding jump components to the stock price or looking at more complicated driving processes than the Brownian motion. While there can be real statistical evidence for those models to describe the stock price evolution (in the risk-neutral setting of $\mu =r$ for reasons of option pricing), there are some fundamental issues with the choice of a more complicated model:

• Practicality vs. state of the art  The market participants have to be able to understand and to implement the chosen model. This in particular means that a typical IT infrastructure is sufficient to come up with accurate results in a reasonable time.

• Complexity vs. gain in accuracy  A more complex model needs more parameters. It will only lead to an improvement in accuracy if the additional parameters can be estimated in an accurate way, a fact that is often not considered when advertising more complex models.

• Task specific issues  Depending on the task, i.e. pricing, risk assessment or internal calculations for portfolio optimization, a simple model can be sufficient or there might be good reasons for using a more sophisticated one.

Who decides on the model to use?  And finally, there has to be some institution that decides on the model choice. Depending on the actual task this can be the financial entity (e.g. a bank, an insurance company, ...) itself in cases of calculating a price for a financial product or an official institution (such as e.g. EIOPA or the European Parliament) in cases such as the Solvency II or the Basel III regulations.

An example where the companies have wide choices is the use of internal models in the ORSA process. This typically leads to the technically involved and realistic models on one hand and simplistic rules that are designed to be conservative with regard to risk issues on the other hand.

Step 2: Calibration—How to obtain the model parameters?  This step consists in fully specifying all the parameters that enter into the model. In our Black–Scholes model example these are the constant riskless rate r, the mean rate of stock return $\mu$ and the stock price volatility $\sigma >0$.

One often chooses r as the spot rate, i.e. the equivalent constant interest rate that delivers the price of a riskless zero bond with maturity T. $\mu$ is very hard to estimate. While it is not needed for reasons of pricing, we need it for risk assessment or portfolio optimization decisions. Using an expert opinion for $\mu$ is a popular choice. $\sigma$ is typically calibrated to market prices of at-the-money call and put options (i.e. those options where the strike is close to the current stock price).² I.e. we choose that value of $\sigma$ such that the sum of squared differences between the market prices of e.g. a set of (European) call options and their theoretical counterparts given by the Black–Scholes formula is minimized.This procedure is also called calibration of the volatility (see e.g. Hull [8], Section 23.14 for a description of a comparable task).

Step 3: Simulation of the underlying stochastic model  The way the model is simulated depends on the actual task. In our example, we only need to know the stock price at time $T_1$ to obtain the call option price at time $T_1$ by the Black–Scholes formula (see Black and Scholes [1]), i.e. we only have to simulate a sequence $Z_1,...,Z_N$ of independent, standard normally distributed random numbers to obtain the corresponding sequences of stock prices

$$\begin{aligned} S^{(k)}(T_1)= S(0)e^{(\mu -\frac{1}{2}\sigma ^2)T_1 + \sigma \sqrt{T_1} Z_k},\ k=1,...,N . \end{aligned}$$

From this, we obtain the sequence $H^{(1)},...,H^{(N)}$ of corresponding call option prices at time $T_1$:

$$\begin{aligned} H^{(k)}&= {} S^{(k)}(T_1)\varPhi \left( d_1(T_1)\right) - K e^{-r(T-T_1)}\varPhi \left( d_2(T_1)\right) , \\ d_1(t)&= \frac{\ln \left( \frac{S^{(k)}(t)}{K}\right) +(r+\frac{1}{2}\sigma ^2)(T-t)}{\sigma \sqrt{T-t}},\quad d_2(t)=d_1(t)-\sigma \sqrt{T-t}\ . \end{aligned}$$

Remark 1

(Two important comments)  (a) The stock price evolves over time in the physical world, i.e. we have to apply the drift parameter $\mu$ to simulate its price at time $T_1$. This is then used as an input for the Black–Scholes formula to calculate the corresponding call option price.

(b)  The number N of simulation runs depends on the actual task, but should in general never be below 10,000. The reason for this is that the MC estimator is unbiased and its standard deviation decreases as $1/\sqrt{N}$. Thus, a choice of $N=10{,}000$ ensures an accuracy of the 1-percent order (see Korn et al. [10], Chapter 3 for more details).

Step 4: Inferring the final risk assessment  As all the necessary simulations are performed, we only have to order the obtained option prices at time $T_1$. Then, the value-at-risk for a given level $0<\alpha <1$ is obtained as the corresponding $\alpha$-quantile of the ordered call option prices.

Example 1

To illustrate the performance of the Monte Carlo approach we consider a European call option with a strike of $K=S(0)=100$ and parameters $r=0$, $\mu =0.03$, $\sigma =0.2$. We want to calculate the $95\%$-quantile of the call price at time $T_1<T$ for various values of $T,T_1$. We therefore consider the plain Monte Carlo method, the so-called Delta-Gamma-approximation (see e.g. Korn et al. [10]), both with 10,000 simulation runs and compare it to the exact solution that we obtain by putting the $95\%$-quantile of $S(T_1)$ as input into the Black–Scholes formula to obtain the call price at time $T_1$. The results are displayed in Table 1.

Table 1 Comparison of the $95\%$-quantile of call option prices obtained by different methods

The Monte Carlo method shows a remarkable accuracy for just 10,000 simulation runs. The Delta-Gamma-approximation performs very good for a small value of $T_1$, but clearly looses accuracy with increasing $T_1$.

3 A simulation concept for chance-risk classification

As a part of ”pre-contractual” customer information, since 2017 every state subsidized pension product sold in Germany has to be assigned to a so-called chance-risk class (CRC). By law, the decision for the classification of a particular pension product has to be based on the simulated contract wealth at the end of the accumulation phase. We will describe this now well-established application of Monte Carlo simulation methods in detail below.

The choice of the underlying capital market model and the chance and risk measures, the development of the software concept for the simulation and the actual computations (including the calibration of the market parameters and the simulation of the contract wealth in all classified products) have been performed by the Fraunhofer Institute for Industrial Mathematics ITWM in Kaiserslautern, Germany. The final assignment of the CRC is then done by PIA.

Note, an approach similar to the methodology introduced in this section has also been implemented by the Austrian and German insurance market as “a robust and well recognized industry and regulatory standard” in the context of the PRIIP-regulation (cf. Sect. 4).

Further, we discuss the specific implementation of the four steps of the previous section and look at various decisions and alternatives that have to be considered within the task of CRC assignment step by step.

Step 1: The underlying stochastic market model   The choice of the capital market model underlying the simulation is a fundamental decision with regard to the simulation effort, the realism of the simulations and the relevance of the CRC. As pensions are long-term products and also German life insurers typically invest a large fraction of the incoming premia into bonds, it is of high relevance to have a good model for the interest rate evolution. To be able to classify both participating life insurance contracts and bank savings plans, a two-factor Hull–White model in the so-called G2++ variant (see Brigo and Mercurio [2]) has been chosen. This model has the advantage of being well understood by both practitioners and academics. As a two factor model, it can explain random influences that are relevant for short-term interest rates and also those that are relevant for long-term rates. Due to the normally distributed short rate, it can also model negative interest rates. On top of that, it allows for a perfect fit to the initial yield curve, a fact that will be explained in detail in Step 2.

The resulting model for the short rate $r^\star (t)$ under the risk-neutral measure ${\mathbb {Q}}$ is given by the following set of equations

$$\begin{aligned} dx\left( t\right)&= {} -ax\left( t\right) dt + \sigma dW_1\left( t\right) , \\ dy\left( t\right)&= {} -by\left( t\right) dt + \eta \left( \rho dW_1\left( t\right) +\sqrt{1-\rho ^2}dW_2\left( t\right) \right) , \\ r^\star \left( t\right)&= {} x\left( t\right) +y\left( t\right) +\psi \left( t\right) \end{aligned}$$

with $W_i(t)$ independent one-dimensional Brownian motions. The function

$$\begin{aligned} \psi \left( t\right)&= {} {f}^{M}\left( 0,t \right) +\tfrac{{{\sigma }^{2}}}{2{{a}^{2}}}{{\left( 1-{{e}^{-at}} \right) }^{2}}\nonumber \\&\ \ +\tfrac{{{\eta }^{2}}}{2{{b}^{2}}}{{\left( 1-{{e}^{-bt}} \right) }^{2}} +\rho \tfrac{\sigma \eta }{ab}\left( 1-{{e}^{-at}} \right) \left( 1-{{e}^{-bt}} \right) \end{aligned}$$

contains additional drift parts and the deterministic function ${f}^{M}\left( 0,t\right)$, the so-called initial market forward yield curve (see Step 2 for details).

As a second basic asset a reference stock index with dynamic evolution given by a generalized Black–Scholes model is introduced as

$$\begin{aligned} S\left( t \right) =S(0)\exp \left( \int \limits _{0}^{t}{r\left( s \right) ds}+\left( \lambda _S -0,5\,{{\sigma }_{S}}^{2} \right) t+{{\sigma }_{S}}W\left( t\right) \right) \end{aligned}$$

where the Brownian motion W(t) can be correlated to $W_i(t)$, $i=1,2$.

Of course, there are technically more involved stock price models and interest rate models available in the literature, but the above choices are a good compromise between realism, acceptance and accessibility by the insurance market.

Step 2: Parameter calibration  We will need different methods to obtain all required model parameters. As a first step, we consider the initial market forward rate curve $f^M(0,t)$ which in theory has the task to ensure equality between the initial model prices P(0, t) for zero bonds and the observed market prices $P^M(0,t)$. As this is only possible theoretically, a popular parameterization in terms of the the Nelson-Siegel-Svensson (cf. Svensson [14]) is applied. We obtain its actual form at time 0 by

$$\begin{aligned} f^{M}(0,t)&= {} \beta _0 +\beta _1 \frac{\theta _1}{t} \left( 1 - e^{ - t/\theta _1}\right) \nonumber \\&\quad + \beta _2 \frac{\theta _1}{t} \left( 1 - e^{- t/\theta _1} \left( 1 + \frac{t}{\theta _1} \right) \right) + \beta _3 \frac{\theta _2}{t} \left( 1 - e^{- t/\theta _2} \left( 1 + \frac{t}{\theta _2} \right) \right) \end{aligned}$$

for parameters $\beta _0,\beta _1,\beta _2, \theta _1, \theta _2$ with $\theta _1\ge 0$ and $\theta _2\ge 0$ that are publicly available from the German Bundesbank. The advantage of this choice is obvious as the German Bundesbank is a neutral and respected institution.

The remaining parameters $a,b,\eta ,\sigma \ge 0$ and $\rho \in [-1,1]$ are also obtained from market prices. As the bond prices are already used to obtain the Nelson-Siegel-Svensson curve, we calibrate $a,b,\eta ,\sigma$ and $\rho$ to market prices of interest rate caps and interest rate swaptions. I.e. we choose those values such that the sum of squared deviations of market prices of interest rate caps and swaptions from their theoretical counterparts at time 0 are minimal.

As the simulations for classification purposes have to be performed under a real-world measure ${\mathbb {P}}$, we have to add a suitable risk premium (not necessarily a positive one!) to obtain the final short rate process r(t) under ${\mathbb {P}}$. For reasons of conceptual compatibility, we want to stay in the G2++ model class, and modify $x_t$ and $y_t$ by introducing additional drift parameters $\lambda _x$ and $\lambda _y$ to obtain

$$\begin{aligned} \begin{aligned} dx(t)&= a \left( \lambda _x - x(t)\right) dt+ \sigma dW_1(t),\ \ x(0)=0\ , \\ dy(t)&= b \left( \lambda _y - y(t)\right) dt+ \eta \left( \rho dW_1(t) +\sqrt{1-\rho ^2} dW_2(t)\right) ,\ \ y(0)=0\ . \end{aligned} \end{aligned}$$

and where for simplicity of notation we kept the names of the two Brownian motions, i.e. we now assume that they are Brownian motions under ${\mathbb {P}}$. To determine the risk premia $\lambda _x, \lambda _y$, one needs predictions of the future evolution of the short rate. For this, we use the annual predictions by the OECD on the expected future development of the interest rate market.

To specify the parameters $\lambda _S$ and $\sigma _S$ of the evolution of a stock index, we choose yet another approach. As the Euro area is an attractive market for German insurance companies, the EuroStoxx 50 is a relevant reference index. From historical time series data, the choice of $\sigma =0.2$ is a reasonable value. As we only perform relative comparisons in the classification task, there is no need to obtain a pseudo accuracy (such as $\sigma =0.19867$) in this case. Historical data also suggest the use of a risk premium of $\lambda _S = 0.04$.

To simulate another index or a stock that has a volatility of $\sigma$, we assign it a risk premium $\lambda$ via the relation

$$\begin{aligned} \lambda = \lambda _S \frac{\sigma }{\sigma _S} . \end{aligned}$$

Remark 2

(More assets)   If one wants to introduce diversification effects on the stock side, one can introduce a second stock price ${\tilde{S}}(t)$ with log-returns that are correlated (but not linearly dependent!) to those of the first stock, a volatility of $\sigma _{{\tilde{S}}}$ and a risk premium of $\lambda _{{\tilde{S}}}$. Of course, the introduction of this second stock comes along with uncertainty about the volatility and the risk premium of the second stock and the correlation $-1< \rho _{S{\tilde{S}}}< 1$ of the log-returns of the stocks.

Another issue arises to simulate assets of a mixed type. An example for this is a defaultable bond which typically contains characteristics of both (riskless) bonds and stocks. To deal with those assets a mapping approach can be introduced that uses a portfolio of riskless bonds (of a certain duration) and a stock (of a certain volatility) as a model for assets of mixed type.

Step 3: Simulation of the capital market and of the contract values  We simulate 10,000 paths of the short rate process and of the basic stock index price for e.g. 40 years. More precisely, we use a monthly discretization and first simulate

$$\begin{aligned} \begin{aligned} x^{(k)}((i+1)/12)&= a \left( \lambda _x - x^{(k)}(i/12)\right) /12 + \sigma \sqrt{1/12} Z^{(k)}(i+1),\ \ x^{(k)}(0)=0\ , \\ y^{(k)}((i+1)/12)&= b \left( \lambda _y - y^{(k)}(i/12)\right) /12 \\&\quad + \eta \sqrt{1/12}\left( \rho Z^{(k)}(i+1) + \sqrt{1-\rho ^2}{\tilde{Z}}^{(k)}(i+1)\right) ,\ \ y^{(k)}(0)=0\ \end{aligned} \end{aligned}$$

for $k=1,...,10{,}000$, $i=0,...,479$. Here, $(Z^{(k)}(i),{\tilde{Z}}^{(k)}(i))$ are independent pairs of independent standard normally distributed random variables. From these simulated paths, we directly obtain the 10,000 short rate paths, but can also derive values of zero bond prices or yield curve dynamics over time.

For the simulation of the basic stock index fund we use the generated short rate paths $r^{(k)}(i/12)$ and obtain the corresponding stock price paths via

$$\begin{aligned} S^{(k)}\left( \frac{i+1}{12}\right)&= {} S^{(k)}\left( \frac{i}{12}\right) \exp \left( \left( r^{(k)}\left( \frac{i+1}{12}\right) + \lambda _S -0,5\,{{\sigma }_{S}}^{2} \right) \frac{1}{12}\right) \nonumber \\&\cdot\quad \exp \left( {{\sigma }_{S}}\frac{{\hat{Z}}^{(k)}(i+1)}{\sqrt{12}} \right) \; . \end{aligned}$$

The standard normally distributed and independent random variables ${\hat{Z}}^{(k)}(i+1)$ are also independent from the Z- and ${\tilde{Z}}$-variables.

Remark 3

(Simulation basis) It is worth to point out that this is already the full simulation of the basic capital market. The evolution of all (!) other possible ingredients (such as stocks, bonds, defaultable bonds, ...) are now a consequence of the simulated paths of the x-,y- and S-processes.

Remark 4

(The prototypical customer) The next task is the actual simulation of the evolution of a customer’s contract value over time. To standardize this, one has introduced a prototypical customer that contributes 100 Euro at the beginning of each month until the end of the accumulation phase. In particular, it is assumed that the customer survives the accumulation phase.

We now have the basis for generating the paths of the evolution of the prototypical customer’s contract value by additionally including the different types of costs and the way that profits are generated, assigned and shared between the policy holders and the insurer.

Remark 5

(Product specific simulation) For each (!) product classified in Germany, there exists a corresponding implementation to perform the required simulation task. However, this simulation is only performed once a year assuming the prototypical customer and not per individualized constellation. The latter would have resulted in an enormous simulation effort.

Step 4: Calculating the chance and risk measures and assigning the CRC  Having simulated 10,000 contract values $V^{(k)}(T)$ for a pension product hold by the prototypical customer at the end of the accumulation phase T, $T\in \left\{ 12, 20, 30, 40 \right\}$, we get the chance measure as the (largest) solution C(T) of the equation

$$\begin{aligned} 100\left( 1+C(T)/12\right) \frac{{{\left( 1+C(T)/12 \right) }^{12T}}-1}{C(T)/12}=\frac{1}{10{,}000}\sum \limits _{k=1}^{10{,}000}{V^{(k)}(T)}\ . \end{aligned}$$

(1)

I.e. C(T) is the constant interest rate such that a riskless investment of the contributions of the prototypical customer leads to a wealth at time T that equals the mean of the above simulated 10,000 final contract values.

To obtain the risk measure R(T), we order the contract values at the end of the accumulation phase, take the smallest 2.000 of the values, and solve the corresponding version of Eq. (1). It is clear that we have

$$\begin{aligned} R(T) \le C(T)\ . \end{aligned}$$

Note further that a lower value of R(T) indicates a higher risk (for a bad performance) of the pension product.

Based on the performance of five benchmark portfolios without costs, a decomposition of ${\mathbb {R}}^2$ in five areas is calculated³. The CRC of a product is then a direct consequence of the above calculated pair (C(T), R(T)). In addition, there are necessary side constraints for CRC 1 and 2 (a money back guarantee for CRC 2, and a money back guarantee plus a strictly increasing value process after costs for CRC 1). The decomposition of ${\mathbb {R}}^2$ is time dependent which allows for different CRC for the same product for different durations of the accumulation phase. Details on the form of the benchmark portfolios are publicly available to the product providers.

Remark 6

(Annual recalculation and calibration) To be in line with actual market developments, the market coefficients are recalibrated annually. As this leads to a change of the pairs (C(T), R(T)) and the decomposition of ${\mathbb {R}}^2$ that defines the different CRC, there is an annual reclassification.

4 Simulation vs. approximation methods: some explicit examples in the context of PRIIPs

Since ${1}\mathrm{st}$ of January 2018, providers of packaged retail and insurance-based investment products (so-called PRIIPs) have to disclose a key-information document (so-called KID) following regulation EU 1286/2014 issued by the European Commission (cf. European Commission [4]). This key information document has to be provided to the customer in good time before the actual purchase of the considered product and contains among others an indication of products’

• risk by means of a summary risk indicator,

• return by means of so-called performance scenarios,

• costs by means of a summary cost indicator.

For deriving the required figures on risk, return and costs, the European Commission issued additional regulatory technical standards (RTS) by European Commission [5] and assigns each product subject to the PRIIP-regulation to one of four different product categories which are briefly summarized as follows: Category 1 comprises derivative-like products, products with a less than monthly price assessment and products where the retail investor may loose more than her invested premiums. Further, Category 2 covers products which provide a linear exposure to their underlying assets whereas Category 3 encompasses products with non-linear exposure to their underlying investments. Finally, Category 4 contains products whose “values depend in part on factors not observed in the market” (cf. European Commission [5]) and especially includes insurance-based investment products that are equipped with some profit participation which is generally not directly observed in the market.

In this section, we will focus on the performance scenarios which—following European Commission [5]—shall represent a “stress scenario, an unfavourable scenario, a moderate scenario and a favourable scenario.” Further, the unfavourable, moderate and favourable scenario shall correspond to the ${10}\mathrm{th}$-, ${50}\mathrm{th}$- and ${90}\mathrm{th}$-percentile of the PRIIP’s probability distribution of returns.⁴

For deriving these percentiles European Commission [5] proposes different calculation methodologies for the different product categories considered. A so-called Cornish–Fisher approximation (cf. Cornish and Fisher [3]) shall be applied for products of Category 2, whereas a simulation by means of a bootstrap shall be performed for Category 3 type products. Concerning products of Category 4, no actual methodology is defined, but a “robust and well recognized industry and regulatory standard” (e.g. the one introduced in Sect. 3) shall be applied instead to derive the required figures. For products of Category 1, no calculations concerning the performance-scenarios shall be performed at all, but the possible derivative-like structure of this type of products (such as e.g. a call-option) shall be indicated graphically instead.

We will now analyze how the different methodologies—especially those for Categories 2 and 3—perform. For doing so, we will assume a simple Black–Scholes model equipped with drift $\mu$ and volatility $\sigma$ and analyze the results when the Cornish–Fisher approximation and the bootstrap methodology as required by European Commission [5] are applied to this model. Both proposed methodologies essentially build on the considered underlying assets’ historically observed returns⁵ and then basically project these returns into the future. Note, assuming a Black–Scholes model as an underlying model for the considered time series, we are able to derive analytical solutions for the true performance scenarios, i.e. the true 10th-, 50th and 90th-percentile of returns and are hence able to compare the results obtained by the Cornish–Fisher approximation and the bootstrap methodology to the true values actually provided by the model. These analyses will show that an application of the currently proposed methodologies for Category 2 or 3 which essentially projects observed past returns into the future, may yield very unintended results since the product’s true performance potential may be significantly under- respectively overestimated. Therefore, an approach based on (forward-looking) simulations as e.g. introduced in Sect. 3 may in our view yield much more stable results when the product’s probability distribution of (future) returns is assessed for a disclosure of the required key information document.

4.1 Sketch of the Cornish–Fisher approximation and the bootstrap methodology

The Cornish–Fisher approximation and the bootstrap methodology as introduced by European Commission [5] base their projection of the required performance scenarios on (preferably daily) observed log-returns over the last 5 years of the underlying time series considered.⁶

Therefore, let $\left\{ r_i,i=1,\ldots M_0 \right\}$ denote a collection of $M_0$ historically observed daily log-returns over the period of the last 5 years. The Cornish–Fisher approximation (cf. Sect. 4.1.1) provides an analytical assessment of the future performance scenarios based on some estimation of the moments of $\left\{ r_i\right\}$ whereas the bootstrap methodology (cf. Sect. 4.1.2) builds on sampling future returns from the historically observed ones to assess the required performance scenarios.

4.1.1 Cornish–Fisher approximation

We use the notation as introduced in European Commission [5] in what follows to describe the application introduced by Cornish and Fisher [3] to estimate percentiles of a distribution based on its (centralized) moments. Considering $\left\{ r_i\right\}$ we obtain an estimate for

• the expected return or first moment $M_1$

  $$\begin{aligned}M_1:=\frac{1}{M_0}\sum _{i=1}^{M_0}{r_i}\end{aligned}$$

• the $j{\mathrm{th}}$-centralized moment $M_j,j=,2,\ldots ,4$

  $$\begin{aligned}M_j:=\frac{1}{{M_0}}\sum _{i=1}^{M_0}{\left( r_i-M_1 \right) ^j}\end{aligned}$$

• the volatility

  $$\begin{aligned}\sigma :=\sqrt{M_2}\end{aligned}$$

• the skewness

  $$\begin{aligned}\mu _1:=\frac{M_3}{\sigma ^3}\end{aligned}$$

• the excess kurtosis

  $$\begin{aligned}\mu _2:=\frac{M_4}{\sigma ^4}-3\end{aligned}.$$

Let us consider a product with a maturity⁷ of T years and further assume N trading days within this period. The annualized log-returns in the unfavourable, moderate and favourable performance scenario are then given as (cf. European Commission [5]):

• unfavourable scenario

  $$\begin{aligned}\frac{1}{T} \left( M_1 N +\sigma \sqrt{N} \left( -1.28 + 0.017 \frac{\mu _1}{\sqrt{N}} + 0.0724\frac{\mu _2}{N} - 0.0611 \frac{\mu _1^2}{N} \right) -0.5\sigma ^2 N \right) \end{aligned}$$

• moderate scenario

  $$\begin{aligned}\frac{1}{T} \left( M_1 N - \sigma \frac{\mu _1}{6} -0.5\sigma ^2 N \right) \end{aligned}$$

• favourable scenario

  $$\begin{aligned}\frac{1}{T} \left( M_1 N +\sigma \sqrt{N} \left( 1.28 + 0.017 \frac{\mu _1}{\sqrt{N}} - 0.0724\frac{\mu _2}{N} + 0.0611 \frac{\mu _1^2}{N} \right) -0.5\sigma ^2 N \right) \end{aligned}.$$

Note, Graf [7] shows that these formulae contain technical errors—that is the term $-0.5\sigma ^2N$ should actually be removed—and hence postulates modified versions of the unfavourable, moderate and favourable performance scenario as

• modified unfavourable scenario

  $$\begin{aligned}\frac{1}{T} \left( M_1 N +\sigma \sqrt{N} \left( -1.28 + 0.017 \frac{\mu _1}{\sqrt{N}} + 0.0724\frac{\mu _2}{N} - 0.0611 \frac{\mu _1^2}{N} \right) \right) \end{aligned}$$

• modified moderate scenario

  $$\begin{aligned}\frac{1}{T} \left( M_1 N - \sigma \frac{\mu _1}{6}\right) \end{aligned}$$

• modified favourable scenario

  $$\begin{aligned}\frac{1}{T} \left( M_1 N +\sigma \sqrt{N} \left( 1.28 + 0.017 \frac{\mu _1}{\sqrt{N}} - 0.0724\frac{\mu _2}{N} + 0.0611 \frac{\mu _1^2}{N} \right) \right) \end{aligned}.$$

Remark 7

(When will the Cornish–Fisher approximation fail?) Note, the Cornish–Fisher approximation introduced here might fail to accurately estimate the product’s true unfavourable, moderate or favourable scenario for at least two reasons:

• The assumptions underlying the original expansion as introduced by Cornish and Fisher [3] prove to be wrong (cf. Jaschke [9] for some more insight how wrong the assumptions and their impact could be).

• The actual estimates for $M_1, \sigma , \mu _1, \mu _2$ derived from the observed returns of the last five years prove to be inaccurate. Section 4.2 shows how inaccurate these estimates can actually be, even when the Cornish–Fisher-approximation should—if its parameters were correctly known—provide an accurate estimate for the required performance scenarios in this setup.

4.1.2 Bootstrap methodology

Whereas the Cornish–Fisher approximation as introduced in the previous section provides an analytical approximation of the performance scenarios by a parametric approach based on the observed returns $\left\{ r_i,i=1,\ldots ,M_0\right\}$, the bootstrap methodology required for products of Category 3 relies on re-sampling these observed returns to assess the future performance potential. Note, in a practical application for products of Category 3 $\left\{ r_i\right\}$ would not resemble the observed returns of the actual product itself, but rather the observed returns of the product’s underlying assets. When products of Category 3 are considered, a non-linear relationship between the product’s and its underlying performance is generally assumed and hence a bootstrapping methodology on the underlying returns is proposed. However, in order to assess if the bootstrap approach delivers appropriate results, we directly assess the underlying and neglect any further non-linear relationships to the performance potential of the considered product.

In order to derive the unfavourable, moderate and favourable performance scenario for a product with maturity T years and N trading days within this period, the bootstrap methodology as stated by European Commission [5] proposes the following approach:

• Project one future trajectory of the product by

  • 1. sample the product’s daily (log-)return by randomly picking $r_s \in \left\{ r_i, i=1, \ldots , M_0 \right\}$,

  • 2. add this return to the product’s total return so far,

  • 3. repeat N times.

• Repeat this projection at least 10,000 times.

• Estimate the required percentiles (10th-, 50th-, 90th-percentile) from the simulated trajectories.

Remark 8

(When will the bootstrap methodology fail?) Compared to the Cornish–Fisher approach introduced previously, the bootstrap methodology may fail to accurately estimate the product’s true unfavourable, moderate or favourable scenario if the observed returns $\left\{ r_i\right\}$ fail to appropriately reproduce the underlying’s true probability distribution of returns. Since, naturally the bootstrap approach will only apply those returns that have actually been observed in the past again and just rearrange them somehow.

4.2 Numerical analyses of the Cornish–Fisher approximation and the bootstrap methodology and comparison with a Monte Carlo simulation

After a brief sketch of the Cornish–Fisher approximation and the bootstrap methodology, we will now analyze whether these approaches are able to appropriately estimate the future performance scenarios in case we do know the true underlying probability distribution and further compare results obtained by means of Monte Carlo.

We assume S(t) to follow a Black–Scholes model with drift $\mu$ and volatility $\sigma$, i.e. $S\left( t\right) = e^{(\mu -\frac{1}{2}\sigma ^2)t + \sigma W(t)}$ with W(t) denoting a Brownian motion in what follows. This model will on the one side be used as a data-generating model for the required time series of observed returns. Thus, we will sample 5 years of realized log-returns $\left( \ln {\frac{S(t+\varDelta t)}{S(t)}}\right)$ on a daily basis, assuming 252 trading days per year and hence set $\varDelta t = \frac{1}{252}$. On the other side, the model will also be the underlying of our considered product for which the future performance scenarios should be estimated. Since S(t) follows a log-normal distribution its probability distribution of returns is easily assessed in closed form. Assuming $\mu =0.06$ and $\sigma =0.2$ we consider a product with maturity $T=20$ years and hence obtain the true future performance scenarios in terms of annualized log-returns as summarized in Table 2.

Table 2 True log-returns (p.a.) for the different performance scenarios

Next, we analyze how the Cornish–Fisher approximation and the bootstrap methodology perform when observations of daily log-returns of the considered model serve as the required historical basis $\left\{ r_i\right\}$. For doing so, we generate 10,000 streams of observed daily log-returns from the underlying model, i.e. we obtain a set

$$\begin{aligned} {\mathcal {R}}:=\left\{ \mathbf {r_k}, k=1, \ldots ,10{,}000 \quad \text { with } \mathbf {r_k}:=\left\{ r_{k,i}, i=1,\ldots , M_0\right\} \right\} \end{aligned}$$

of 5-year observed log-returns with $M_0=5\cdot 252$. Then, we analyze the results of the Cornish–Fisher approximation and the bootstrap methodology if we set the underlying time series of observed returns to $\mathbf {r_k}, k=1, \ldots , 10{,}000$. For each $\mathbf {r_k} \in {\mathcal {R}}$, we estimate $M_1, \sigma , \mu _1, \mu _2$ for the Cornish–Fisher approximation and perform a bootstrap re-sampling (based on 10,000 trajectories each) vice versa. These calculations finally provide us with 10,000 realizations of the projected performance scenarios when both proposed methodologies are applied. The Monte Carlo simulation also builds on 10,000 trajectories (“inner simulations”) of the underlying Geometric Brownian motion assuming a monthly time step. From this inner simulations we then estimate the unfavourable, moderate and favourable scenario as respective percentiles. This procedure is then repeated 10,000 times (“outer simulations”) which allows to derive an estimate for the empirical probability distribution of the different performance scenarios for the Monte Carlo exercise as well.

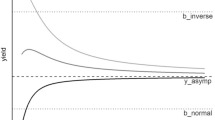
Figures 1,  2 and 3 show the results of the empirical probability distributions of projected performance scenarios by depicting some estimated percentiles. First, it is worthwhile noting that in this case the Cornish–Fisher approximation should be able to accurately estimate the underlying probability distribution—when the parameters were known—since the log-returns are normally distributed and hence perfectly fit to the Cornish–Fisher approximation’s assumptions. However, taking the results of Fig. 1 into account, the considered approach might tremendously over-respectively underestimate the product’s true performance scenarios even when a corrected version of the Cornish–Fisher formulae (cf. modified results) is applied. The Cornish–Fisher approximation only on average delivers appropriate estimates of the performance scenarios and hence is subject to a very high parameter risk. This issue is reasoned with the fact that it is very hard (if not impossible) to derive an appropriate estimate for the required parameters (especially regarding the expected return $M_1$) from just one realized path of observation.⁸

Taking the parameter risk of the Cornish–Fisher approximation into account, it is not surprising that the bootstrap methodology is generally prone to the same issues and may—due to good or bad luck observed in the considered time series—yield to a severe over- respectively underestimation of the product’s true performance potential (cf. Fig. 2).

Finally, Fig. 3 in our view clearly shows the advantage of the Monte Carlo method both taking bias and a possible variability into account. Note, the key take away here is that—although the data-generating model’s distributional characteristics would in this case allow the Cornish–Fisher approximation and bootstrap methodology to deliver appropriate estimates for the required percentiles—both methodologies face severe “parameter risk” and can utterly fail, since their underlying parameters are derived from just one observed trajectory. Naturally, this is overcome by the Monte Carlo method where one “only” faces the risk of a Monte-Carlo error when applying a certain number (here 10,000) of trajectories.

To be clear, only to assess the resulting Monte-Carlo error depicted in Fig. 3, we repeated the Monte-Carlo exercise 10,000 times and hence in total used 100 million sample paths to derive the empirical probability distribution. Then, we were able to conclude that already one set of 10,000 trajectories is enough to yield a much better result than the Cornish–Fisher approximation or the bootstrap methodology in terms of stability and robustness.

Fig. 1

Performance scenarios’ estimated log-returns (p.a.) applying the Cornish–Fisher approximation

Fig. 2

Performance scenarios’ estimated log-returns (p.a.) via the bootstrap methodology

Fig. 3

Performance scenarios’ estimated log-returns (p.a.) via Monte Carlo simulation

Further, Tables 3 and 4 show percentiles of the unfavourable respectively favourable performance scenario for the different methodologies when our sample ${\mathcal {R}}$ of observed time series and the outer Monte Carlo simulations are considered.

Table 3 Percentiles of estimated log-returns (p.a.) for the unfavourable performance scenario

Table 4 Percentiles of estimated log-returns (p.a.) for the favourable performance scenario

Note, taking the true performance scenarios of the underlying model into account (cf. Table 2), there is—due to the mentioned parameter risk—a chance of $25\%\,(10\%)$ that the approximated unfavourable scenario delivers higher returns than the actually true moderate (favourable) performance scenario. In contrast, there also is a chance of $25\%\,\left( 10\%\right)$ that the approximated favourable scenario gives lower returns than the actually true moderate (unfavourable) performance scenario. Further, very high projections for the favourable scenario (e.g. twice as high as the actual true value) may also be observed with a significant probability.

Of course a forward-looking simulation as e.g. the one introduced in Sect. 3 will still only constitute a modelling approach and hence should not claim to exactly produce or deliver the true probability distribution of future returns. However, such an approach if appropriately calibrated does not suffer from the above issues and therefore provides stable instead of rather random results on the assessment of possible future performance scenarios for different financial products (cf. Tables 3 and 4).

5 Conclusion

In this work we have presented some basics of simulation approaches and a fully developed simulation framework in detail that is successfully used in Germany for chance-risk classification of pension products. We have further highlighted some disadvantages of the use of moment based approximations such as the Delta–Gamma-method or the Cornish–Fisher expansion on the one side and also on bootstrapping historically observed returns on the other side and especially commented on their application in the PRIIPs regulatory framework. Their performance is particularly bad for assessing the risk-return profile of long-term financial products, even for much simpler ones than typical pension products.

In contrast to the performance of these approximations, simulation approaches can be tailored to an actual application such that any degree of desired accuracy can be obtained. However, to make use of their full potential in a general setting, it needs a clear and detailed concept for their application. As the chance-risk classification approach in Germany—which also serves as a basis for some ”robust and well recognized industry and regulatory standards” used in the context of PRIIPs—has shown this can be done in a satisfying way for insurance companies, customers and political decision makers.

As a conclusion of the examples and concepts presented in our work, we want to summarize some important advantages of simulation methods for risk assessment:

Flexibility  Simulation approaches can easily be modified to deal with tasks that have not been present at the time of their conception. Examples are the risk assessment of novel products or of novel risk mitigation techniques and investment strategies.

Accuracy  Given a good model choice, simulation approaches can deliver every desired degree of accuracy via increasing the number of simulation runs.

Past and future—Using the best of both worlds  Simulation approaches use the essential information of the past data to calibrate the model parameters, but allow for much more possible future scenarios as just repeating what has been observed in the past. Thus, even economic scenarios that have been unexpected given past performance can enter the result of the simulations. This mainly avoids being caught by surprise.

Customer relevant information by a forward looking approach  Simulation approaches are forward-looking, i.e. the simulations of future evolutions are based on parameters inferred from the actual market situation. They therefore provide relevant information for the customer, a feature that static approaches solely based on historic data do not have. This is especially true when markets have changed recently as is the case with the current low interest rate environment.

Raising the standards  Our experience has shown that the presence of a model-based simulation approach has forced the providers to actually deal with this approach. This then also leads to a more detailed understanding of the own product’s properties. Further, the simulation approach also proved to be beneficial for product design.

Summing up all the conceptual considerations and examples presented above, we believe that there are convincing arguments for considering a well-specified model-based Monte Carlo simulation concept as a highly suitable tool for risk assessment in various applications, especially those related to pension products.