Introduction

Heat engines are the fundamental building blocks of modern technology. These were invented primarily to convert heat into mechanical work. To lay a theoretical framework and to uncover the laws governing the processes in the engines, the thermodynamics was empirically developed1. Later, it has been founded on statistical mechanics2 assuming that the systems are large and composed of an asymptotically large number of particles (N → ∞) interacting with even larger baths, where the average fluctuation in energy approaches zero. This is termed usually as the asymptotic regime.

However, the situation changes completely for the systems of a finite, but moderate or even small number of quantum particles (N ≪ ∞) where the standard thermodynamics is not applicable. In such cases, from the very beginning, the fluctuations may play a much more important role. The situations may be classified in two regimes: many-shot finite-size regime, where repeated measurements (in time) are allowed on a system, is made up of moderate or a small number of particles, and one-shot finite-size regime, where only one-shot measurements are allowed on a system, composed of a single or a moderate number of particles. In the last decades, enormous efforts have been put forward to extend thermodynamics to these regimes, leading to two major approaches.

The first approach is based on fluctuation theorems, exploiting statistical mechanics and open quantum systems dynamics3,4,5. The other one is based on the quantum information theory6,7,8,9,10,11,12,13,14,15,16,17,18,19. Among others, the latter leads to a resource theory of quantum systems out of thermal equilibrium, which is commonly termed as the resource theory of quantum thermodynamics (RTQTh)6,8,10. The RTQTh stands out among the other approaches, as it exploits a rigorous mathematical framework similar to the resource theory of entanglement. Recently, the approaches based on fluctuation theory and resource theory have been interconnected for some cases20,21,22. All these investigations are majorly limited to the situations, where the quantum system is interacting with only one thermal bath at a fixed temperature. Apart from some efforts to quantify extractable work and engine efficiency in few special cases, and to study the finite-size effects and the quantum signatures23,24,25,26,27,28,29,30,31,32, there has been no major progress, so far, in formulating a resource theory for quantum heat engines.

One of the striking features is that the engines operating in the one-shot finite-size regime can only deliver fluctuating work8,10 and the lesser the fluctuation lesser becomes the extractable deterministic or one-shot work. Further, a heat engine operating in this regime cannot in general achieve reversible transformation. As a consequence, it is not possible to attain the maximum allowed heat-to-work conversion efficiency (i.e., the Carnot efficiency) in a Carnot engine, unless the system interacting with the baths is made up of an asymptotically large number of particles where Carnot efficiency may at most be achieved on average.

In this work, we present quantum and nanoscale heat engines that attain the maximum possible heat-to-work conversion efficiency, i.e., the Carnot efficiency, in the one-shot finite-size regime. These engines are superior in work extraction efficiency compared to the traditional engines. To prove our results and to address quantum thermodynamics in the one-shot finite-size regime in general, we formulate a resource theory for quantum heat engines (see Supplementary Information) in which a system with few quantum particles interacts with two or multiple thermal baths. With the precise characterization of thermodynamic operations by introducing a first law for engines, we derive the second laws for quantum state transformation in presence two or multiple baths at different temperatures by using information-theoretic tools. The newly introduced engine operations are more general in the sense that the system interacts with the baths simultaneously. We term these engine operations as “semi-local thermal operations” (SLTOs). The SLTOs not only enable us to build a Carnot heat engine operating with a one-step cycle but also enhances the work extraction efficiency in the one-shot finite-size regime—in this sense, the SLTOs are more powerful than the ones considered earlier. As revealed by this resource theoretic framework, the state transformations in the quantum engine are fundamentally irreversible and must obey many second laws. As an important result of this framework, we design a reversible engine transformation that attains the maximum possible efficiency for work extraction, i.e., the Carnot efficiency, there by demonstrating the supremacy of quantum heat engines.

Results

A typical (Carnot) heat engine comprised two heat baths B1 and B2 with the inverse temperatures β1 = 1/T1 and β2 = 1/T2, respectively, and a working system S, as shown in the Fig. 1. We assume β1 < β2 throughout this article. In our proposed quantum heat engine, we define a new engine operation where a working system (S12) is composed of two non-interacting subsystems S1 and S2. The Hamiltonian is \({H}_{{S}_{12}}={H}_{{S}_{1}}+{H}_{{S}_{2}}\equiv {H}_{{S}_{1}}\otimes {{\mathbb{I}}}_{{S}_{2}}+{{\mathbb{I}}}_{{S}_{1}}\otimes {H}_{{S}_{2}}\). The Hamiltonians of the baths B1 and B2 are denoted as \({H}_{{B}_{1}}\) and \({H}_{{B}_{2}}\) respectively. The subsystems S1 and S2 semi-locally interact with the baths B1 and B2, respectively. With this, the number of steps in the Carnot engine is reduced. For instance, consider that the subsystems S1 and S2 are in the states ρ and σ, respectively. Then the isothermal steps (C1) and (C3) can be combined to one step, as

$$(\rho \otimes \sigma,\,{H}_{{S}_{1}}+{H}_{{S}_{2}})\to (\sigma \otimes \rho,\,{H}_{{S}_{1}}+{H}_{{S}_{2}}),$$

where the \({H}_{{S}_{1}}=H\) and the \({H}_{{S}_{2}}={H}^{\prime}\). In this step, the subsystems swap their states without changing their Hamiltonian. Further, both the adiabatic steps (C2) and (C4) can be performed in one step as well, i.e.,

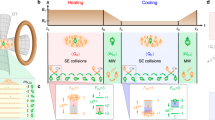
$$(\sigma \otimes \rho,\,{H}_{{S}_{1}}+{H}_{{S}_{2}})\to (\sigma \otimes \rho,\,{H}_{{S}_{1}}^{\prime}+{H}_{{S}_{2}}^{\prime}),$$

where the \({H}_{{S}_{1}}^{\prime}={H}^{\prime}\) and \({H}_{{S}_{2}}^{\prime}=H\). Here, the subsystems swap their local Hamiltonians without modifying their states. In fact, the four steps in a Carnot heat engine can be further reduced to just one step (see Fig. 2), which enables one to attain maximum possible heat-to-work conversion efficiency, as we shall discuss later.

Fig. 1: A schematic of the operations in a traditional Carnot heat engine.
figure 1

The horizontal and vertical axes are the thermodynamic entropy (S) and the temperature (T). The engine is made up of one working system and two heat baths with inverse temperatures β1 = 1/T1 and β2 = 1/T2, where β1 < β2. The engine operates in a cycle composed of four thermodynamically reversible steps: (C1) First, an isothermal transformation (ρ, H) → (σ, H) in interaction with the bath B1 at inverse temperature β1, where the state changes (ρ → σ) without updating the system Hamiltonian H. (C2) Second, an adiabatic transformation \((\sigma,H)\to (\sigma,{H}^{\prime})\) without any contact with the baths, where state remain unchanged but the system Hamiltonian modifies to \(H\to {H}^{\prime}\). (C3) Third, an isothermal transformation \((\sigma,H^{\prime})\to (\rho,{H}^{\prime})\) in interaction with the bath B2 at inverse temperature β2, only changing the state. (C4) Finally, an adiabatic transformation \((\rho,{H}^{\prime})\to (\rho,H)\) without any interaction with the baths and updating only the system Hamiltonian \({H}^{\prime}\to H\). The steps (C1)–(C4) constitute a cycle and the engine operates repeating the cycle many times. The important point is that, in the steps (C1) and (C2), the working system interacts with one bath at a time.

Full size image

Semi-local thermal operations

Let us now introduce the general form of thermodynamically allowed (semi-local) operations that a (bipartite) quantum system S12 undergoes in a quantum heat engine, where the bipartite system S12 can be in an arbitrary state. Even, the states may possess strong correlation, e.g., quantum entanglement, shared by the subsystems S1 and S2.

Definition 1. SLTOs. In a quantum heat engine, the thermodynamic operations on system S12 in a state \({\rho }_{{S}_{12}}\) are defined as

$${{{\Lambda }}}_{{S}_{12}}\left({\rho }_{{S}_{12}}\right)={{\rm{Tr}}}_{{B}_{1}{B}_{2}}\left[U({\gamma }_{{B}_{1}}\otimes {\gamma }_{{B}_{2}}\otimes {\rho }_{{S}_{12}}){U}^{\dagger }\right],$$
(1)

with the condition that the global unitary U satisfies the commutation relations

$$\left[U,\ {H}_{{B}_{1}}+{H}_{{S}_{1}}+{H}_{{B}_{2}}+{H}_{{S}_{2}}\right]=0,$$
(2)
$$\left[U,\,{\beta }_{1}\,({H}_{{B}_{1}}+{H}_{{S}_{1}})+{\beta }_{2}\,({H}_{{B}_{2}}+{H}_{{S}_{2}})\right]=0,$$
(3)

where the thermal states of the baths are denoted by \({\gamma }_{{B}_{x}}=\frac{{e}^{-{\beta }_{x}{H}_{{B}_{x}}}}{{\rm{Tr}}[{e}^{-{\beta }_{x}{H}_{{B}_{x}}}]}\) for x = 1, 2.

The resultant operations on the system S12 are semi-local in the sense that, even though the subsystems (S1 and S2) “selectively” interact with the baths (B1 and B2), the unitary U still allows certain interactions among them with the constraints (2) and (3). It should be noted that the commutation relations (2) and (3) together constitute the first law for quantum heat engines. The relation (2) guarantees strict conservation of the total energy E12 = E1 + E2, where E1 and E2 are the energies of the B1S1 and B2S2 composites, respectively. In addition, the relation (3) ensures strict conservation of the total weighted-energy \({E}_{12}^{{\beta }_{1}{\beta }_{2}}={\beta }_{1}{E}_{1}+{\beta }_{2}{E}_{2}\) and it signifies that any change in (one-shot) entropy of B1S1, due to an exchange of energy between B1S1 and B2S2, must be compensated by a counter change in (one-shot) entropy of B2S2. It is interesting to note that the SLTOs converge to the (local) thermal operations that are introduced in the resource theory of quantum states beyond thermal equilibrium presented in refs. 6,8,10, when both the baths are of the same temperature, i.e., for β1 = β2. Several useful properties of SLTOs possess are outlined in the “Methods.”

The SLTOs can be further generalized with an access to a bipartite catalyst C12 composed of two non-interacting subsystems C1 and C2 and the Hamiltonian \({H}_{{C}_{12}}={H}_{{C}_{1}}+{H}_{{C}_{2}}\). The C1 is clubbed with the subsystem S1 to form the composite S1C1. Similarly, the C2 is clubbed with the S2 to form S2C2. Then, the composites S1C1 and S2C2 interacts with the baths B1 and B2 via SLTOs. Such operations are called catalytic semi-local thermal operations (cSLTOs) that satisfy

$${{{\Lambda }}}_{{S}_{12}{C}_{12}}({\rho }_{{S}_{12}}\otimes {\rho }_{{C}_{12}})\to {\sigma }_{{S}_{12}}\otimes {\rho }_{{C}_{12}},$$
(4)

where \({\rho }_{{C}_{12}}\) is a state of the catalyst. Note, the catalyst remains unchanged before and after the process. These catalytic operations form a larger set of thermodynamically allowed operations compared to SLTOs and respect all the properties satisfied by the SLTOs. The cSLTOs are the allowed thermodynamic operation in a quantum heat engine and constitute the free operation for the resource theory developed to prove the results presented in this article (see Supplementary Information).

When the subsystems are locally in thermal equilibrium with the baths they are semi-locally interacting with, the joint uncorrelated state of the system S12 becomes \({\gamma }_{{S}_{12}}={\gamma }_{{S}_{1}}\otimes {\gamma }_{{S}_{2}}\), where \({\gamma }_{{S}_{x}}={e}^{-{\beta }_{x}{H}_{{S}_{x}}}/{Z}_{x}\) with the partition functions \({Z}_{x}={\rm{Tr}}[{e}^{-{\beta }_{x}{H}_{{S}_{x}}}]\) for x = 1, 2. We term these states as the semi-Gibbs states. The set of all such semi-Gibbs states is denoted by the set \({{\mathcal{T}}}_{{S}_{12}}\ni {\gamma }_{{S}_{12}}\). The cSLTOs map the set \({{\mathcal{T}}}_{{S}_{12}}\) onto itself. The cSLTOs and the semi-Gibbs states are the precursors of a resource theory of heat engines that we develop in the Supplementary Information.

Engine with one-step cycle, second laws, and work extraction

The first important result of this work is that the cSLTOs can be utilized to implement the cycle in a Carnot engine in one step, as shown in Fig. 2. At the end of a cycle, the initial state of the system is returned. Such a one-step engine cycle involves the transformation

$$\left({\rho }_{{S}_{12}},\,{H}_{{S}_{12}}\right)\longrightarrow \left({\sigma }_{{S}_{12}}^{\prime},\,{H}_{{S}_{12}}^{\prime}\right).$$
(5)

Here, the system Hamiltonian is modified to \({H}_{{S}_{12}}={H}_{{S}_{1}}+{H}_{{S}_{2}}\to {H}_{{S}_{12}}^{\prime}={H}_{{S}_{1}}^{\prime}+{H}_{{S}_{2}}^{\prime}\) and satisfies the conditions \({\sigma }_{{S}_{12}}^{\prime}={U}_{{S}_{1}\leftrightarrow {S}_{2}}^{SWAP}\left({\rho }_{{S}_{12}}\right),\,\,{H}_{{S}_{1}}^{\prime}={H}_{{S}_{2}},\,\,\,\text{and}\,\,\,{H}_{{S}_{2}}^{\prime}={H}_{{S}_{1}}\), where the unitary \({U}_{{S}_{1}\leftrightarrow {S}_{2}}^{SWAP}\) swaps the subsystems S1 and S2. The next cycle starts by inter-changing the interactions between subsystems and baths. In other words, the first engine cycle starts with the (semi-local) interactions as B1S1 − S2B2, where the subsystems S1 and S2 semi-locally interact with the baths B1 and B2, respectively. In the next cycle, engine interchanges the interactions as B1S2 − S1B2, where the subsystem S1 and S2 semi-locally interact with the baths B2 and B1, respectively, via a cSLTO, and the cycles continue.

Fig. 2: Generalized one-step engine operation.
figure 2

Consider initial state and the non-interacting Hamiltonian of the working system are \({\rho }_{{S}_{12}}\) and \({H}_{{S}_{12}}={H}_{{S}_{1}}+{H}_{{S}_{2}}\), respectively. The sub-systems S1 and S2 semi-locally interact with the baths B1 and B2 with inverse temperatures β1 and β2, respectively, where β1 < β2. The engine operates in a cycle by implementing the step \(\left({\rho }_{{S}_{12}},\,{H}_{{S}_{12}}\right)\longrightarrow \left({\sigma }_{{S}_{12}}^{\prime},\,{H}_{{S}_{12}}^{\prime}\right)\), with the modified system Hamiltonian \({H}_{{S}_{12}}^{\prime}={H}_{{S}_{1}}^{\prime}+{H}_{{S}_{2}}^{\prime}\), so that it satisfies the conditions \({\sigma }_{{S}_{12}}^{\prime}={U}_{{S}_{1}\leftrightarrow {S}_{2}}^{SWAP}\left({\rho }_{{S}_{12}}\right),\,\,{H}_{{S}_{1}}^{\prime}={H}_{{S}_{2}},\,\,\,\text{and}\,\,\,{H}_{{S}_{2}}^{\prime}={H}_{{S}_{1}}\), where the unitary \({U}_{{S}_{1}\leftrightarrow {S}_{2}}^{SWAP}\) performs a SWAP operation between sub-systems S1 and S2. It is noteworthy that all four steps in the traditional Carnot engine (comprising the steps (C1)–(C4) in Fig. 1) can be performed in one stroke with \({\rho }_{{S}_{12}}=\rho \otimes \sigma\), which is just a special case of above general operation.

Full size image

Here we restrict ourselves to the states \({\rho }_{{S}_{12}}\), which are block-diagonal in the energy eigenbases of the system Hamiltonian \({H}_{{S}_{12}}\), i.e., \([{\rho }_{{S}_{12}},{H}_{{S}_{12}}]=0\). The cSLTOs are time-translation symmetric with respect to the time translation driven by \({H}_{{S}_{12}}\), and that is why the cSLTOs monotonically decrease the superpositions between different energy eigenbases (see Appendix). For a heat engine operates in an arbitrarily large number of cycles, it is therefore safe to assume that an arbitrary state will dephase to its block-diagonal form after some cycles. Then, the second laws that provide the necessary and sufficient conditions for such transformations are given in the theorem below. This theorem is proven, even for more general transformation, in the Supplementary Information.

Theorem 2. Second laws for engines. Under cSLTOs, the transformation in Eq. (5) is possible if, and only if,

$${S}_{\alpha }\left({\rho }_{{S}_{12}},{\gamma }_{{S}_{1}}\otimes {\gamma }_{{S}_{2}}\right)\ge {S}_{\alpha }\left({\sigma }_{{S}_{12}}^{\prime},{\gamma }_{{S}_{1}}^{\prime}\otimes {\gamma }_{{S}_{2}}^{\prime}\right),\,\,\forall \alpha \ge 0,$$
(6)

where the α-free entropy of \({\rho }_{{S}_{12}}\) (and similarly for \({\sigma }_{{S}_{12}}^{\prime}\)) is defined, for all α ∈ [−∞, ∞], as

$${S}_{\alpha }({\rho }_{{S}_{12}},{\gamma }_{{S}_{1}}\otimes {\gamma }_{{S}_{2}})={D}_{\alpha }\left({\rho }_{{S}_{12}}\parallel {\gamma }_{{S}_{1}}\otimes {\gamma }_{{S}_{2}}\right)-\mathrm{log}\,{Z}_{1}{Z}_{2},$$
(7)

with the thermal states \({\gamma }_{{S}_{x}}=\frac{{e}^{-{\beta }_{x}{H}_{{S}_{x}}}}{{Z}_{x}}\) and \({\gamma }_{{S}_{x}}^{\prime}=\frac{{e}^{-{\beta }_{x}{H}_{{S}_{x}}^{\prime}}}{{Z}_{x}^{\prime}}\), and the partition functions \({Z}_{x}={\rm{Tr}}[{e}^{-{\beta }_{x}{H}_{{S}_{x}}}]\) and \({Z}_{x}^{\prime}={\rm{Tr}}[{e}^{-{\beta }_{x}{H}_{{S}_{x}}^{\prime}}]\) for x = 1, 2. Here, the Rényi α-relative entropy is given by \({D}_{\alpha }(\rho \parallel \gamma)=\frac{\,\text{sgn}\,(\alpha)}{\alpha -1}\mathrm{log}\,{\rm{Tr}}[{\rho }^{\alpha }\,{\gamma }^{1-\alpha }]\).

The α-free entropies quantify the thermodynamic resource present in the system S12 and it vanishes for the semi-Gibbs states. Therefore, any transformation among the block-diagonal states under the cSLTOs must respect the above monotonic relation for the α-free entropies for all α. It is noteworthy that the second laws leading to these monotonic relations can also be derived for more general state transformations as allowed by non-cyclic engine operations (see Supplementary Information). Apart from dictating state transformations, the Theorem 2 delimits the amount of thermodynamic resource, i.e., free entropy or work, can be extracted using a state transformation in an engine. It also quantifies the amount of the free entropy required to be expended to make a transformation possible. For this, a bipartite battery W12 is introduced that stores work in the form of pure energy. It is attached with the system S12 and then jointly evolved with cSLTOs, as shown in Fig. 3. Now the free-entropy distance is introduced in Theorem 3 to quantify the extractable free entropy or the free-entropy cost in the one-shot finite-size regime, in terms of the works that can be stored in a battery. This in turn also quantifies the maximum extractable deterministic work from a quantum engine or the minimum deterministic work required to execute a refrigeration process.

Fig. 3: Extraction of free entropy.
figure 3

A battery \({S}_{{W}_{12}}\), with two sub-systems \({S}_{{W}_{1}}\) and \({S}_{{W}_{2}}\) and the non-interacting Hamiltonian \({H}_{{S}_{{W}_{12}}}={H}_{{S}_{{W}_{1}}}+{H}_{{S}_{{W}_{2}}}\) is attached with the system S12 to store free entropy (or work) once extracted. Without loss of generality, the battery subsystems are considered to be two-level systems with the Hamiltonians \({H}_{{S}_{{W}_{1}}}={W}_{1}\left|{W}_{1}\right\rangle {\left\langle {W}_{1}\right|}_{{S}_{{W}_{1}}}\) and \({H}_{{S}_{{W}_{2}}}={W}_{2}\left|{W}_{2}\right\rangle {\left\langle {W}_{2}\right|}_{{S}_{{W}_{2}}}\), and these are restricted to remain in the eigenstates of the Hamiltonians always. The \({S}_{{W}_{1}}\) is tagged with subsystem S1 and similarly the \({S}_{{W}_{2}}\) is with S2. The initial battery state is chosen to be the zero-energy state \({\rho }_{{S}_{{W}_{12}}}^{i}=\left|0\right\rangle {\left\langle 0\right|}_{{S}_{{W}_{1}}}\otimes \left|0\right\rangle {\left\langle 0\right|}_{{S}_{{W}_{2}}}\). The composites \({S}_{1}{S}_{{W}_{1}}\) and \({S}_{2}{S}_{{W}_{2}}\) interact with the baths B1 and B2 (at different inverse temperatures β1 and β2), respectively, through semi-local thermal operations, so that the overall transformation is \(\left({\rho }_{{S}_{12}}\otimes {\rho }_{{S}_{{W}_{12}}}^{i},\,{H}_{{S}_{12}}+{H}_{{S}_{{W}_{12}}}\right)\to \left({\sigma }_{{S}_{12}}^{\prime}\otimes {\rho }_{{S}_{{W}_{12}}}^{f},\,{H}_{{S}_{12}}^{\prime}+{H}_{{S}_{{W}_{12}}}\right)\), where the final state of the battery is \({\rho }_{{S}_{{W}_{12}}}^{f}=\left|{W}_{1}\right\rangle {\left\langle {W}_{1}\right|}_{{S}_{{W}_{1}}}\otimes \left|{W}_{2}\right\rangle {\left\langle {W}_{2}\right|}_{{S}_{{W}_{2}}}\). It is noteworthy that the battery Hamiltonian remains unchanged in the transformation. The values of W1 and W2 depend on the very cSLTO under which the transformation happens.

Full size image

Theorem 3. Free-entropy distance in each engine cycle. For the transformation in Eq. (5) via a cSLTO, the free-entropy distance between the initial and final states of the system is given by

$$\begin{array}{lll}{S}_{d}\left({\rho }_{12}\right.\,{\to} \,\left.{\sigma }_{12}^{\prime}\right)={\beta }_{1}{W}_{1}+{\beta }_{2}{W}_{2},\\ \qquad\qquad\quad\qquad =\, \mathop{\mathrm{inf}}\limits_{\alpha \ge 0}\left[{S}_{\alpha }({\rho }_{{S}_{12}},{\gamma }_{{S}_{1}}\otimes {\gamma }_{{S}_{2}})-{S}_{\alpha }({\sigma }_{{S}_{12}}^{\prime},{\gamma }_{{S}_{1}}^{\prime}\otimes {\gamma }_{{S}_{2}}^{\prime})\right].\end{array}$$
(8)

We refer to the Supplementary Information for the proof. As per the second laws, if the initial state possesses larger free entropy than the final one, i.e., \({S}_{\alpha }\left({\rho }_{{S}_{12}},{\gamma }_{{S}_{1}}\otimes {\gamma }_{{S}_{2}}\right)\ge {S}_{\alpha }\left({\sigma }_{{S}_{12}}^{\prime},{\gamma }_{{S}_{1}}^{\prime}\otimes {\gamma }_{{S}_{2}}^{\prime}\right)\) for all α ≥ 0, the transformation can take place spontaneously under cSLTOs. This we term as the forward process. Then, the guaranteed one-shot extractable work from the process is

$${W}_{ext}={W}_{1}+{W}_{2}\,>\,0,$$
(9)

where W1 > 0 and W2. To perform the reverse transformation \(({\sigma }_{{S}_{12}}^{\prime},{H}_{{S}_{12}}^{\prime})\to ({\rho }_{{S}_{12}},{H}_{{S}_{12}})\), as for a refrigeration process, the Theorem 3 constrains that the minimum one-shot free entropy to be supplied to ascertain the transformation is \({S}_{d}({\sigma }_{12}^{\prime}\to {\rho }_{12})\). It is important to note that the free-entropy distance of a forward process is not in general equal to its reverse process and \({S}_{d}({\rho }_{12}\to {\sigma }_{12}^{\prime})\le -{S}_{d}({\sigma }_{12}^{\prime}\to {\rho }_{12})\), where the equality holds for a few special cases. Therefore, the thermodynamic reversibility is no longer respected in the one-shot finite-size regime.

The one-step engine cycle also enables an engine to operate exclusively utilizing inter-system correlations. This is the second important result of this work. Consider that the subsystem S1 (and S2) is made up of two parties M1 and N1 (and M2 and N2) with Hamiltonian \({H}_{{S}_{1}}={H}_{{M}_{1}}+{H}_{{N}_{1}}\) (and \({H}_{{S}_{2}}={H}_{{M}_{2}}+{H}_{{N}_{2}}\)). We further assume \({H}_{{M}_{1}}={H}_{{M}_{2}}\) and \({H}_{{N}_{1}}={H}_{{N}_{2}}\). The cycle starts with the state \({\rho }_{{S}_{12}}=\rho \otimes \sigma\), where the state ρ of S1 has no correlation between M1 and N2, i.e., \(\rho ={\rho }_{{M}_{1}}\otimes {\rho }_{{N}_{1}}\) with \({\rho }_{{M}_{1}}={{\rm{Tr}}}_{{N}_{1}}\rho\) and \({\rho }_{{N}_{1}}={{\rm{Tr}}}_{{M}_{1}}\rho\). However, the state σ of S2 has non-vanishing correlation between M2 and N2, i.e., \(\sigma\, \ne \,{\sigma }_{{M}_{2}}\otimes {\sigma }_{{N}_{2}}\) with \({\sigma }_{{M}_{2}}={{\rm{Tr}}}_{{N}_{2}}\sigma\) and \({\sigma }_{{N}_{2}}={{\rm{Tr}}}_{{M}_{2}}\sigma\). The one-step engine cycle that exclusively utilizes correlation is \(\left({\rho }_{{S}_{12}},\,{H}_{{S}_{12}}\right)\to \left({\sigma }_{{S}_{12}},\,{H}_{{S}_{12}}\right)\), where \({\sigma }_{{S}_{12}}=\sigma \otimes \rho\). Then, in each cycle, the extractable free-entropy distance is \({S}_{d}({\rho }_{{S}_{12}}\to {\sigma }_{{S}_{12}})={\beta }_{1}{W}_{1}^{c}+{\beta }_{2}{W}_{2}^{c}\), and the extractable work is \({W}_{ext}^{c}={W}_{1}^{c}+{W}_{2}^{c}\).

It is known that the inter-system correlation can store thermodynamic work potential and can lead to "anomalous” heat flow - a spontaneous heat transfer from a cooler to a warmer body14. However, the studies were restricted to the asymptotic regime. Now, we are able to characterize such thermodynamic potential and its role in anomalous heat flow in the one-shot finite-size regime. For instance, consider a system state \({\rho }_{{S}_{12}}\), which has non-vanishing correlation shared by the subsystems S1 and S2, i.e., \({\rho }_{{S}_{12}}\,\ne \,{\rho }_{{S}_{1}}\otimes {\rho }_{{S}_{2}}\), where \({\rho }_{{S}_{1}}={{\rm{Tr}}}_{{S}_{2}}[{\rho }_{{S}_{12}}]\) and \({\rho }_{{S}_{2}}={{\rm{Tr}}}_{{S}_{1}}[{\rho }_{{S}_{12}}]\). Then, a (non-cyclic) state transformation \(\left({\rho }_{{S}_{12}},\,{H}_{{S}_{12}}\right)\to \left({\rho }_{{S}_{1}}\otimes {\rho }_{{S}_{2}},\,{H}_{{S}_{12}}\right)\) leads to the free-entropy distance \({S}_{d}({\rho }_{{S}_{12}}\to {\rho }_{{S}_{1}}\otimes {\rho }_{{S}_{2}})={\beta }_{1}{W}_{1}+{\beta }_{2}{W}_{2}\) and the extractable work Wext = W1 + W2. In fact, this work is responsible for the anomalous heat from or, equivalently, the refrigeration process.

Attaining Carnot efficiency

The state transformations in the one-shot finite-size regime are very restrictive as these need to obey many second laws simultaneously. Moreover, thermodynamics is irreversible in general. This raises the question if there can be a heat engine that attains the maximum possible heat-to-work conversion efficiency (i.e., the Carnot efficiency) in the one-shot finite-size regime. Here we give an affirmative answer to this question that also vindicates the superiority of the quantum heat engines operating in the one-step cycle using SLTOs. The Carnot efficiency of a work extraction process is attained when the transformations occurring in an engine are reversible. In the one-shot finite-size regime, such a reversible engine transformation can be achieved if we consider initial and final states of the (working) system to be the energy eigenstates of the Hamiltonian.

Let us present one such engine transformation that attains maximum possible heat-to-work conversion efficiency, i.e., the Carnot efficiency. Without loss of generality, we consider a two-qubit (working) system S12 with the Hamiltonian \({H}_{{S}_{12}}={H}_{{S}_{1}}+{H}_{{S}_{2}}\). The subsystem Hamiltonians are given by \({H}_{{S}_{1}}=a\left|1\right\rangle \ {\left\langle 1\right|}_{{S}_{1}}\) and \({H}_{{S}_{2}}=a\left|1\right\rangle \ {\left\langle 1\right|}_{{S}_{2}}\). The engine undergoes a one-step cycle following the transformation \(({\rho }_{{S}_{12}},{H}_{{S}_{12}})\to ({\sigma }_{{S}_{12}},{H}_{{S}_{12}})\) using SLTO, where the initial and final states, respectively, are

$${\rho }_{{S}_{12}}=\left|0\right\rangle \ {\left\langle 0\right|}_{{S}_{1}}\otimes \left|1\right\rangle \ {\left\langle 1\right|}_{{S}_{2}}\,\,\,\text{and}\,\,\,{\sigma }_{{S}_{12}}=\left|1\right\rangle \ {\left\langle 1\right|}_{{S}_{1}}\otimes \left|0\right\rangle \ {\left\langle 0\right|}_{{S}_{2}}.$$
(10)

The Hamiltonians of the subsystems S1 and S2 do not change under this transformation. The transformation is reversible because α-free entropies for such pure states are α independent. As a consequence, free-entropy distances satisfy \({S}_{d}({\rho }_{{S}_{12}}\to {\sigma }_{{S}_{12}})={S}_{d}({\rho }_{{S}_{12}}\leftarrow {\sigma }_{{S}_{12}})\), where

$${S}_{d}({\rho }_{{S}_{12}}\to {\sigma }_{{S}_{12}})={\beta }_{2}a-{\beta }_{1}a={\beta }_{1}{W}_{1}+{\beta }_{2}{W}_{2}\, > \,0.$$
(11)

The net extracted work in each engine cycle is given by Wext = W1 + W2 > 0. Recall, β1 < β2.

To understand the conversion of heat into work and how it attains the Carnot efficiency, let us explore the state transformation in the engine considering baths-system-battery composite all together. As the system battery \({S}_{12}{S}_{{W}_{12}}\) is in a block-diagonal state, the initial state of baths-system-battery composite can be expressed in the block-diagonal form as

$${\gamma }_{{B}_{1}}\otimes {\gamma }_{{B}_{2}}\otimes {\rho }_{{S}_{12}}\otimes {\rho }_{{S}_{{W}_{12}}}=\bigoplus _{{E}_{1}+{E}_{2}}{[{\gamma }_{{B}_{1}}\otimes {\gamma }_{{B}_{2}}\otimes {\rho }_{{S}_{12}}\otimes {\rho }_{{S}_{{W}_{12}}}]}_{{E}_{1}+{E}_{2}},$$

where \({[{\gamma }_{{B}_{1}}\otimes {\gamma }_{{B}_{2}}\otimes {\rho }_{{S}_{12}}\otimes {\rho }_{{S}_{{W}_{12}}}]}_{{E}_{1}+{E}_{2}}\) is the part of the global state that resides in the total energy block E1 + E2. Here \({E}_{1}={E}_{{S}_{1}}+{E}_{{B}_{1}}\) is the sum of energies belonging to S1 and B1, and similarly for \({E}_{2}={E}_{{S}_{2}}+{E}_{{B}_{2}}\). A global unitary U is applied jointly on the composite conserves total energy and the total weighted-energy of the baths-system composite due to the constraints (2) and (3), and has the block-diagonal structure, given by \(U{ = \bigoplus }_{{E}_{1}+{E}_{2}}{U}_{{E}_{1}+{E}_{2}}\) (see Supplementary Information). The unitary \({U}_{{E}_{1}+{E}_{2}}\) applies to the total energy block E1 + E2 and is allowed transfer populations within the block so that total weighted-energy β1E1 + β2E2 is strictly conserved. In the block of total energy E1 + E2, the transformation becomes

$${[{\gamma }_{{B}_{1}}\otimes {\gamma }_{{B}_{2}}\otimes {\rho }_{{S}_{12}}]}_{{E}_{1}+{E}_{2}}\otimes {\rho }_{{S}_{{W}_{12}}}^{i}\to {[{\sigma }_{{B}_{1}{B}_{2}{S}_{12}}]}_{{E}_{1}^{\prime}+{E}_{2}^{\prime}}\otimes {\rho }_{{S}_{{W}_{12}}}^{f},$$

where \({\rho }_{{S}_{{W}_{12}}}^{i}=\left|0\right\rangle \ {\left\langle 0\right|}_{{S}_{{W}_{1}}}\otimes \left|0\right\rangle \ {\left\langle 0\right|}_{{S}_{{W}_{2}}}\) is the initial battery state, \({\rho }_{{S}_{{W}_{12}}}^{f}=\left|{W}_{1}\right\rangle \ {\left\langle {W}_{1}\right|}_{{S}_{{W}_{1}}}\otimes \left|{W}_{2}\right\rangle \ {\left\langle {W}_{2}\right|}_{{S}_{{W}_{2}}}\) is the final battery state, and \({{\rm{Tr}}}_{{B}_{1}{B}_{2}}{\sigma }_{{B}_{1}{B}_{2}{S}_{12}}={\sigma }_{{S}_{12}}\). Here, the bipartite battery Hamiltonian is \({H}_{{S}_{{W}_{12}}}={H}_{{S}_{{W}_{1}}}={W}_{1}\left|1\right\rangle \ {\left\langle 1\right|}_{{S}_{{W}_{1}}}+{W}_{2}\left|1\right\rangle \ {\left\langle 1\right|}_{{S}_{{W}_{2}}}\). Now the conservation of the total weighted-energy and the total energy ensure that

$${\beta }_{1}{E}_{1}+{\beta }_{2}{E}_{2}={\beta }_{1}({E}_{1}^{\prime}+{W}_{1})+{\beta }_{2}({E}_{2}^{\prime}+{W}_{2}),$$
(12)
$${E}_{1}+{E}_{2}={E}_{1}^{\prime}+{E}_{2}^{\prime}+{W}_{1}+{W}_{2},$$
(13)

where \({E}_{1}={E}_{{B}_{1}}\), \({E}_{2}={E}_{{B}_{2}}+a\), \({E}_{1}^{\prime}={E}_{{B}_{1}}^{\prime}+a\), and \({E}_{2}^{\prime}={E}_{{B}_{2}}^{\prime}\). The Eqs. (12) and (13), along with Eq. (11), lead to

$${\beta }_{1}({E}_{{B}_{1}}-{E}_{{B}_{1}}^{\prime})+{\beta }_{2}({E}_{{B}_{2}}-{E}_{{B}_{2}}^{\prime})={\beta }_{1}{Q}_{1}+{\beta }_{2}{Q}_{2}=0,$$
(14)
$${W}_{\mathrm{ext}}={W}_{1}+{W}_{2}={Q}_{1}+{Q}_{2}\,>\,0,$$
(15)

where we have identified the heat as the change in energy of the bath B1 given by \({Q}_{1}={E}_{{B}_{1}}-{E}_{{B}_{1}}^{\prime}\) and similarly \({Q}_{2}={E}_{{B}_{2}}-{E}_{{B}_{2}}^{\prime}\) for bath B2. The Eq. (14) represents the Clausius equality for the cyclic process. The Eq. (15) quantifies the extracted work in each one-step cycle. The other total energy blocks will result in identical Clausius equality and the same amount of extracted work. Therefore, the efficiency for the heat-to-work conversion is now reduced to

$${\eta }_{C}=\frac{{W}_{ext}}{{Q}_{1}}=1-\frac{{\beta }_{1}}{{\beta }_{2}},$$
(16)

which is exactly the Carnot efficiency. As a result, the Carnot’s efficiency can be attained for an engine operating in the one-shot finite-size regime. A refrigerator can also be constructed just by reversing engine cycle, i.e., \(({\sigma }_{{S}_{12}},{H}_{{S}_{12}})\to ({\rho }_{{S}_{12}},{H}_{{S}_{12}})\), and that achieves maximum possible coefficient of performance in the one-shot finite-size regime. The example for the two-qubit system we have considered above can automatically be generalized to arbitrary dimensional (working) systems where the subsystems are also allowed to update their Hamiltonians. The only requirement to attain the Carnot efficiency is that the initial and final states of the system have to be in the eigenstates of the initial and final Hamiltonians.

Discussion

In this work, we have designed a heat engine that attains Carnot efficiency in the one-shot finite-size regime. These engines are superior in work extraction compared with the other engines so far considered in the literature. To prove our result, we have developed a resource theory of quantum heat engines to systematically study thermodynamics in the presence of two or more baths in the finite-size one-shot regime (see Supplementary Information). We stress that the earlier works focus on how the a-thermal (or out-of-equilibrium) properties of a system transform into thermodynamic work and do not consider the conversion of heat into work. For such considerations, one thermal bath is sufficient. On the contrary, the resource theory developed for quantum heat engines, with two or more thermal baths, is the only framework to systematically address how and to what extent the heat can be converted into work in the quantum heat engines operating in the one-shot finite-size regime.

We have proceeded with the precise characterizations of thermodynamic operations, i.e., the SLTOs, by introducing the first law for engines, where the system simultaneously interacts with both the baths. In addition to strict total energy conservation, the first law also ensures a strict weighted-energy conservation. Then, we have defined semi-Gibbs states as resource-free states and free entropies as the measure of thermodynamic resource applicable in the one-shot finite-size regime. With this, we have formulated the second laws for state transformations in a quantum engine. Our formulation reveals that the state transformations in a quantum engine are irreversible, in general, and are dictated by many second laws (see Supplementary Information). In addition, the framework enables us to design a Carnot heat engine operating with a one-step cycle that can enhance work extraction efficiency in the one-shot finite-size regime (see “Methods”). Most importantly, we have presented the reversible engine operations that result in the maximum possible heat-to-work conversion efficiency, i.e., the Carnot efficiency, in the one-shot finite-size regime.

Although the framework for resource theory of heat engines is mathematically rigorous and clean in the theoretical sense, the SLTOs are difficult to implement in experiments. It is noteworthy that there have been various proposals exploring possible physical realizations of (local) thermal operations in the presence of a single bath, see for example33,34,35. Following a similar track, it can also be possible to implement SLTOs. In particular, the proposed engine operation that results in higher efficiency in the conversion of heat into work can be implemented without much difficulties. This will certainly open up the possibility to experimentally realize quantum heat engines operating in a one-step cycle with higher one-shot efficiencies in the finite-size regime, even a possibility of attaining Carnot efficiency.

In summary, our work achieves:

  • An engine with a one-step cycle leading to higher heat-to-work conversion efficiency, even attaining Carnot efficiency in the one-shot finite-size regime for the first time. The results in turn demonstrate the superiority of the proposed engines over other engines operating in the one-shot finite-size regime.

  • A quantum heat engine that converts heat into work by exclusively utilizing inter-system correlations.

  • A fundamental gain, i.e., a concrete mathematical framework leading to a resource theory and a novel theoretical understanding of quantum and nanoscale heat engine, and, in particular, the conversion of heat into work in quantum heat engines operating in the one-shot finite-size regime and the role of inter-system correlations in such processes.

  • Possibilities of new experimental avenues for quantum heat engines that attain higher or even Carnot efficiency in the one-shot finite-size regime.

Methods

Characterization of the SLTOs

The SLTOs, introduced in the Definition 1, possess several important properties. We outline them below.

(P1) For an arbitrary initial semi-Gibbs state \({\gamma }_{{S}_{12}}\in {{\mathcal{T}}}_{{S}_{12}}\), the SLTOs satisfy \({{{\Lambda }}}_{{S}_{12}}\left({\gamma }_{{S}_{12}}\right)\in {{\mathcal{T}}}_{{S}_{12}}\). Therefore, the SLTOs map semi-Gibbs states onto itself. This is a consequence of the very definition of operation in Definition 1, in particular the constraint (3). If the local states of the subsystems S1 and S2 are in thermal equilibrium, the SLTOs cannot bring them away from their local equilibrium, despite the fact that the SLTOs are semi-local in nature and allow an exchange of energy among the subsystems. This happens despite the fact that the operation is global in nature and justifies the semi-local character of the SLTOs. Therefore, under the SLTOs, the semi-Gibbs states represent the fixed points. This is one of the required properties the allowed operations should possess to formulate a resource theory.

(P2) Action of an operation that satisfies \({{{\Lambda }}}_{{S}_{12}}\left({\gamma }_{{S}_{12}}\right)\in {{\mathcal{T}}}_{{S}_{12}}\), on a system state \({\rho }_{{S}_{12}}\) can be simulated by an SLTO, given that \([{\rho }_{{S}_{12}},{H}_{{S}_{12}}]=0\). A detailed proof is given in the Supplementary Information. It is noteworthy that these operations are termed as the semi-Gibbs preserving operations and form a larger set of operation than that of the SLTOs.

(P3) The SLTOs can implement the changes in the system Hamiltonians. For instance, an initial non-interacting Hamiltonian of S12 can be updated to a new one, as \({H}_{{S}_{12}}={H}_{{S}_{1}}+{H}_{{S}_{2}}\to {H}_{{S}_{12}}^{\prime}={H}_{{S}_{1}}^{\prime}+{H}_{{S}_{2}}^{\prime}\), with the help of clocks (see Supplementary Information). These operations are nothing but the (semi-local) adiabatic transformations in a typical heat engine.

(P4) It is interesting to note that the SLTOs, as well as the cSLTOs, are time-translation symmetric operations with respect to the time evolution generated by the Hamiltonian \({H}_{{S}_{12}}={H}_{{S}_{1}}+{H}_{{S}_{2}}\). In other words, if there is a time translation of the system driven by unitary \(V(t)={e}^{-it{H}_{{S}_{12}}/\hslash }\) for any given time t, then

$$V(t)\left[{{{\Lambda }}}_{{S}_{12}}({\rho }_{{S}_{12}})\right]{V}^{\dagger }(t)={{{\Lambda }}}_{{S}_{12}}\left[V(t)({\rho }_{{S}_{12}}){V}^{\dagger }(t)\right],$$
(17)

i.e., the order of the time-translation operations and the SLTO commute. Because of this symmetric property, the SLTOs monotonically decrease the superpositions between different eigenbases of \({H}_{{S}_{12}}\) or, in other words, among the energy eigenbases. It is worth noting that the SLTOs are also time-translation symmetric with respect to the system’s weighted Hamiltonian \({H}_{{S}_{12}}^{{\beta }_{1}{\beta }_{2}}={\beta }_{1}{H}_{{S}_{1}}+{\beta }_{2}{H}_{{S}_{2}}\), as \([{H}_{{S}_{12}}^{{\beta }_{1}{\beta }_{2}},{H}_{{S}_{12}}]=0\).

Equation (17) further implies that the SLTOs commute with the dephasing operations in the eigenbases of the Hamiltonian of the system \({H}_{{S}_{12}}={\sum }_{i,j}({E}_{i}^{{S}_{1}}+{E}_{j}^{{S}_{2}})\left|ij\right\rangle \left\langle ij\right|\), i.e.,

$${{{\Lambda }}}_{{S}_{12}}\circ {P}_{{S}_{12}}({\rho }_{{S}_{12}})={P}_{{S}_{12}}\circ {{{\Lambda }}}_{{S}_{12}}({\rho }_{{S}_{12}}),$$
(18)

where \({P}_{{S}_{12}}({\rho }_{{S}_{12}})={\sum }_{ij}\left\langle ij| {\rho }_{{S}_{12}}| ij\right\rangle \left|ij\right\rangle \ \left\langle ij\right|\) is the dephasing operation. Also the dephasing operation can be achieved by time-averaging time-translated state for a long enough time T,

$${P}_{{S}_{12}}({\rho }_{{S}_{12}})=\frac{1}{T}{\int\nolimits_{0}^{T}}V(t)\,({\rho }_{{S}_{12}})\,V(t)dt.$$
(19)

Equation (18) signifies that the diagonal elements in the eigenbases of \({H}_{{S}_{12}}\), i.e., \({P}_{{S}_{12}}({\rho }_{{S}_{12}})\), evolve independently of the off-diagonal elements. Further, the amount of asymmetry present in a state due to the superposition between different energy eigenbases monotonically decreases under the SLTOs. We use these properties to understand the free-entropy locking in superpositions and to add more conditions to supplement the second laws for state transformations (see Supplementary Information).

More extractable work using cSLTOs

Here we show how the semi-local character in the cSLTOs can lead to a higher amount of extractable work compared to the engine that operates using (local) thermal operations. Consider that the working system is initially in an uncorrelated state \({\rho }_{{S}_{12}}=\rho \otimes \sigma\) in an engine. Then the one-step engine transformation, given in Eq. (5), reduces to

$$(\rho \otimes \sigma,\,{H}_{{S}_{12}})\to (\sigma \otimes \rho,\,{H}_{{S}_{12}}^{\prime}).$$
(20)

In this transformation, there are two sub-transformations happening simultaneously via a cSLTO: (i) forward sub-transformation, \((\rho,{H}_{{S}_{1}})\to (\sigma,{H}_{{S}_{2}})\), in presence of the bath B1 at inverse temperature β1, and (ii) the reverse sub-transformation \((\sigma,{H}_{{S}_{2}})\to (\rho,{H}_{{S}_{1}})\) while interacting with bath B2 at inverse temperature β2.

For the uncorrelated state ρ12 = ρ ⊗ σ, the α-free entropy becomes additive \({S}_{\alpha }(\rho \otimes \sigma,{\gamma }_{{S}_{1}}\otimes {\gamma }_{{S}_{2}})={S}_{\alpha }(\rho,{\gamma }_{{S}_{1}})+{S}_{\alpha }(\sigma,{\gamma }_{{S}_{2}})\), where \({S}_{\alpha }({\rho }_{{S}_{x}},{\gamma }_{x})={D}_{\alpha }\left({\rho }_{{S}_{x}}\parallel {\gamma }_{{S}_{x}}\right)-\mathrm{log}\,{Z}_{x}\). The \({S}_{\alpha }({\rho }_{{S}_{x}},{\gamma }_{x})/{\beta }_{x}\) is the accessible α-free energy stored in the system \({\rho }_{{S}_{x}}\) and can be converted into work using a (local) thermal operation in presence of a bath at inverse temperature βx10. The second laws, considering the sub-transformations (i) and (ii) simultaneously occur via a cSLTO, imply

$${\beta }_{1}{W}_{1}^{(\alpha)}+{\beta }_{2}{W}_{2}^{(\alpha)}\ge 0,\,\,\forall \alpha \ge 0,$$
(21)

where the \({W}_{x}^{(\alpha)}\) quantifies the change in α-work due to the transformation in the presence of the bath at inverse temperature βx. In terms of the α-free energies10, we express these α-works as

$${W}_{1}^{(\alpha)}=\frac{1}{{\beta }_{1}}\left[{S}_{\alpha }\left(\rho,{\gamma }_{{S}_{1}}\right)-{S}_{\alpha }\left(\sigma,{\gamma }_{{S}_{1}}^{\prime}\right)\right],$$
(22)
$${W}_{2}^{(\alpha)}=\frac{1}{{\beta }_{2}}\left[{S}_{\alpha }\left(\sigma,{\gamma }_{{S}_{2}}\right)-{S}_{\alpha }\left(\rho,{\gamma }_{{S}_{2}}^{\prime}\right)\right],$$
(23)

where \({\gamma }_{{S}_{x}}=\frac{{e}^{-{\beta }_{x}{H}_{{S}_{x}}}}{{\rm{Tr}}[{e}^{-{\beta }_{x}{H}_{{S}_{x}}}]}\) for x = 1, 2, \({\gamma }_{{S}_{1}}^{\prime}=\frac{{e}^{-{\beta }_{1}{H}_{{S}_{2}}}}{{\rm{Tr}}[{e}^{-{\beta }_{1}{H}_{{S}_{2}}}]}\), and \({\gamma }_{{S}_{2}}^{\prime}=\frac{{e}^{-{\beta }_{2}{H}_{{S}_{1}}}}{{\rm{Tr}}[{e}^{-{\beta }_{2}{H}_{{S}_{1}}}]}\). Given β1 < β2 and a spontaneous engine cycle, Eq. (21) guarantees that \({W}_{ext}^{(\alpha)}={W}_{1}^{(\alpha)}+{W}_{2}^{(\alpha)}\, > \,0,\,\forall \alpha \ge 0\).

Let us now show that the one-shot efficiency of the Carnot engine operating via cSLTOs is larger, in general, compared to the case considered in Fig. 1, where the system locally interacts with individual baths at a time. Suppose that the system locally interacts with the baths using local thermal operations6,8,10 and undergoes two sub-transformations (i) and (ii) in separate steps to complete the Carnot cycle, as discussed earlier. For these sub-transformations (i) and (ii), the one-shot extractable work and the work cost under local thermal operations, respectively, are

$${\bar{W}}_{1}=\mathop {\mathrm{inf}}\limits_{\alpha \ge 0}[{W}_{1}^{(\alpha)}]\le {W}_{1},\,\,\,\,\text{and}\,\ \ \ {\bar{W}}_{2}=\mathop {\mathrm{sup}}\limits_{\alpha \ge 0}[{W}_{2}^{(\alpha)}]\ge {W}_{2}.$$
(24)

The net one-shot extracted work using local thermal operations is \({\bar{W}}_{\mathrm{ex}t}={\bar{W}}_{1}+{\bar{W}}_{2}\), where \({\bar{W}}_{1}\ge 0\) and \({\bar{W}}_{2}\le 0\). It is easy to check that \({W}_{\mathrm{ext}}\ge {\bar{W}}_{\mathrm{ext}}\) which is satisfied for arbitrary engine cycle in general.