A new perspective on static bifurcations in the presence of viscoelasticity

Abstract

This manuscript explores the effect of viscoelasticity on static bifurcations: such as pitchfork, saddle-node, and transcritical bifurcations, of a single-degree-of-freedom mechanical oscillator. The viscoelastic behavior is modeled via a differential form, where the extra degree of freedom represents the internal force provided by the viscoelastic element. The governing equations are derived from a simplified lumped parameter model consisting of a rigid rod incorporating a viscoelastic element and subjected to axial and transverse forces at the free end, in addition to an external time-varying moment applied to the rod. In order to study the effect of viscoelasticity on bifurcation diagrams, the equations of motion are non-dimensionalized. Next, a review of static bifurcations in the absence of viscoelasticity is conducted, followed by an examination of the effect of viscoelasticity on the bifurcation diagrams. Finally, this paper investigates the effects of viscoelasticity on the transient behavior of the oscillator. Results show that the Deborah number, which measures the ratio of the viscoelastic time constant to the natural periodic time of the system, controls the duration of time needed to maintain oscillations around an unstable point before jumping to a stable equilibrium point.

Appendix

This appendix converts the linear standard viscoelastic element from stress–strain form to a force–displacement form. It presents an internal variable formulation of the governing equations of the system.

Fig. 13

Viscoelastic linear standard model with internal variable

1.1 Stress to force

In this work, the additional degree of freedom is the viscoelastic force in the system. Recall the viscoelastic relationship in the linear standard model can be written as

$$\begin{aligned} \frac{1}{E_1}{\dot{\sigma }}+\frac{1}{\mu }\sigma =\frac{E_1+E_2}{E_1}{\dot{\epsilon }}+\frac{E_2}{\mu }\epsilon . \end{aligned}$$

(A.1)

where $E_1$ and $E_2$ denote the modulus of the element and $\mu$ is the viscosity. Now if the moduli $E_1$ and $E_2$ are parameterized as $E_1=(1-\beta )E$ and $E_2=\beta E$, where E is a base elastic modulus and $\beta$ is a constant, the strain $\epsilon =L\sin \theta /b$ where A and b are the cross section area of length of the viscoelastic element, and $\sigma =f_\mathrm{v}A$, Eq. (A.1) can be written as

$$\begin{aligned}&\frac{{\dot{f}}_\mathrm{v}}{(1-\beta )k}+\frac{f_\mathrm{v}}{\eta }=\frac{\dot{\bar{\delta }}}{(1-\beta )}+\left( \frac{\beta k }{\eta }\right) \bar{\delta }, \nonumber \\&\text {where}~\bar{\delta }=L\sin \theta ,~k=EA/b,\text {and}~\eta =\mu A/b. \end{aligned}$$

(A.2)

1.2 Internal variable description

An alternate description can be obtained using the internal strain in the system. In this description the viscoelastic stress can be written as

$$\begin{aligned}&\sigma =(E_1+E_2)\epsilon -E_1\bar{\epsilon }, \end{aligned}$$

(A.3)

$$\begin{aligned}&\mu \dot{\bar{\epsilon }}+E_1(\bar{\epsilon }-\epsilon )=0, \end{aligned}$$

(A.4)

where $\bar{\epsilon }$ is the internal strain [36] and is shown in Fig. 13. These two descriptions are equivalent. This can be shown by taking the derivative of Eq. (A.3) to yield

$$\begin{aligned}&{\dot{\sigma }}=(E_1+E_2){\dot{\epsilon }}-E_2\dot{\bar{\epsilon }}. \end{aligned}$$

(A.5)

Now, Eqs. (A.5) and (A.3) can be plugged into Eq. (A.4) to yield

$$\begin{aligned} \frac{1}{E_1}{\dot{\sigma }}+\frac{1}{\mu }\sigma =\frac{E_1+E_2}{E_1}{\dot{\epsilon }}+\frac{E_2}{\mu }\epsilon . \end{aligned}$$

The additional dynamics of the system to viscoelasticity can be represented as $\sigma$ or $\bar{\epsilon }$.

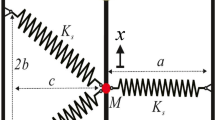
The equation motion of the system in Fig. 2b can be written in terms of internal displacements ${\bar{x}}$ as

$$\begin{aligned}&I\ddot{\theta }+{\bar{M}}(\theta ;k_1,k_2,k_3) \end{aligned}$$

(A.6)

$$\begin{aligned}&\quad =\beta k L {\bar{x}} \cos \theta -kL^2\cos \theta \sin \theta + \nonumber \\&F_CL \sin \theta -PL\cos \theta +M \cos \varOmega t,\nonumber \\&\quad \eta \dot{{\bar{x}}}\beta k ({\bar{x}}-L\sin \theta )=0; \end{aligned}$$

(A.7)

when the functions $\sin \theta$ and $\cos \theta$ are expanded using a Taylor series, the equations of motion for the system can be written as

$$\begin{aligned}&I\ddot{\theta }+(k_1-F_CL)\theta +k_2\theta ^2+k_3\theta ^3\nonumber \\&\quad = kL(\beta x_i-L\theta )-PL+M \cos \varOmega t,\end{aligned}$$

(A.8)

$$\begin{aligned}&\eta {\dot{x}}_i+\beta k (x_i-L\theta )=0. \end{aligned}$$

(A.9)

Equations  in (A.8) and  (A.9) are the internal displacement equivalents of Equations (3) and (4).

1.3 Characteristic polynomial

The characteristic polynomial for the Jacobian defined in Eq. 14 can be written as

$$\begin{aligned} \varLambda ^3+a_0\varLambda ^2+a_1\varLambda +a_2=0, \end{aligned}$$

(A.10)

where

$$\begin{aligned} a_0&=1-\beta ,\end{aligned}$$

(A.11)

$$\begin{aligned} a_1&=\frac{1}{D_e^{-2}}\left( 1+\alpha _2 x_{01} +3\alpha _3^2 x_{01}-\lambda \right) ,~\text {and}\end{aligned}$$

(A.12)

$$\begin{aligned} a_2&=+\frac{1}{D_e^{-2}} \left( \beta \lambda - \alpha \beta ^2-\lambda \right) . \end{aligned}$$

(A.13)