Managing liquidity with portfolio staleness

Abstract

Liquidity is a risk factor of primary relevance that can significantly affect the asset allocation decisions of investors. In this paper, we introduce the concept of portfolio staleness and propose a simple framework to manage portfolio liquidity, intended as the cost needed to liquidate the portfolio. Within this framework, the traditional minimum variance problem is solved under the additional constraint that portfolio staleness must be smaller than a given threshold. We show that a dynamic asset allocation strategy based on the staleness constrained portfolio can significantly enhance portfolio liquidity over the standard minimum variance solution. Meanwhile, the increase in portfolio risk is limited, generating large liquidity gains per unit of risk.

1 Introduction

The Markowitz (1952) mean–variance framework is at the core of modern asset allocation. In this setting, an investor optimally allocates wealth across risky assets caring only about the mean and the variance of portfolio returns. Although theoretically sound, the mean–variance framework has not reached widespread consensus in the finance industry. Among the causes of what Michaud (1989) defines “the Markowitz optimization enigma”, he identifies the fact that mean–variance portfolios ignore factors, such as liquidity, that are important for investment decisions. The relevance of liquidity in the asset allocation problem is widely recognized in the financial economics literature. For instance, Canner et al. (1997) show that portfolios recommended by four popular financial advisors are not on the mean–variance efficient frontier and consider assets marketability among the possible explanatory factors. Similarly, Ghysels and Pereira (2008), Hodrick and Moulton (2009) and Bazgour et al. (2016) find that fund managers are sensitive to liquidity while achieving their targets in the portfolio allocation decision. Despite these empirical evidences, few efforts have been devoted to understanding how investors can manage liquidity within the mean–variance framework.

Since the last financial crisis, both regulators and investors have expressed concerns about the worsening conditions of liquidity in the markets. First, the regulatory restructuring related to the traditional activities of banks and financial intermediaries tightened capital requirements, reducing their ability to supply liquidity. Funding constraints and higher margins can force liquidity suppliers to liquidate their positions in case of redemption pressures, thus raising market illiquidity (Gromb and Vayanos 2002; Chiu et al. 2012). Second, the growth of the ETF industry is raising concerns for a possible liquidity crisis.¹ In case of investor redemption, passive (index-tracking) funds following similar strategies can induce coordinated liquidations of securities (Scharfstein and Stein 1990), depressing market prices and thus leading to “liquidity spirals” (Brunnermeier and Pedersen 2008; Hameed et al. 2010). These premises warrant the development of a methodological framework to manage portfolio liquidity.

In this paper, we consider an investor who uses the minimum-variance framework² to allocate funds across stocks, and pursuits a volatility timing strategy (Fleming et al. 2001, 2003). The portfolio is rebalanced on a daily basis, and the solution of the optimization problem is a sequence of optimal weights that vary exclusively according to changes in the conditional covariances of the assets held in the portfolio. Using this framework, we aim to answer the following questions: how can we include liquidity in the dynamic portfolio optimization problem? How can we measure portfolio liquidity? Can we consistently generate portfolio liquidity gains selecting portfolios that are close to the minimum-variance portfolio?

The traditional approach to portfolio construction in the presence of illiquid assets entails the modeling of the transaction costs and the solution of a dynamic portfolio strategy. Some examples are given by Constantinides (1986), Gârleanu (2009) and Gârleanu and Pedersen (2013). A similar route is adopted in the literature on asset pricing with transaction costs (Amihud and Mendelson 1986; Acharya and Pedersen 2005; Vayanos 1998; Vayanos and Vila 1999) and in that on optimal trade execution (Bertsimas and Lo 1998; Almgren and Chriss 2000). Modeling and estimating the transaction costs is a difficult task. Commissions fees, bid–ask spreads, funding costs, price-impact are all relevant components of the transaction costs that may not be directly available to the investor. For this reason, a set of simplifying assumptions are typically imposed on the transaction cost function, and the existence of a closed-form or numerically tractable solution crucially relies on these assumptions.

The approach adopted in this paper is deliberately different. Our goal is to include the liquidity dimension in the standard Markowitz framework without explicitly modeling the transaction costs. To be more specific, we look for a synthetic and easy-to-compute measure which reflects the main determinants of portfolio illiquidity. In doing so, we try to conciliate the need for sufficiently liquid portfolios with parsimony and computational efficiency.

Bandi et al. (2017) show that asset prices observed at high-frequency update less frequently than what assumed in standard continuous time models of asset pricing. They introduce an economic indicator, named idle time, that estimates the probability of observing a zero return (or a stale price, whence the nomenclature adopted in this manuscript) at a given sampling frequency. Idle time provides information on the extent of liquidity of an asset, and it is related to both transaction costs and absence of volume (Bandi et al. 2020). We extend this notion to a portfolio of assets by defining the concept of portfolio staleness: on a given day, portfolio staleness is computed as the weighted average of assets’ idle times, using the corresponding portfolio weights. This measure has several attractive features: (a) is easy to compute, as idle time solely requires data on transaction prices to be implemented; (b) has a clear economic interpretation, as idle time can be regarded as an illiquidity proxy within a model of price formation with transaction costs and asymmetric information; (c) being idle time a probability, it naturally ranges between zero and one, allowing to easily compare and rank portfolios.

Building upon these considerations, our first contribution is to propose a tractable framework where the liquidity dimension is integrated into the portfolio selection problem. This is done by imposing an additional constraint (henceforth referred to as staleness constraint) on the minimum-variance portfolio optimization that limits the degree of portfolio staleness. The intuition behind this approach is straightforward: a portfolio with lower staleness places larger weights on assets with lower idle time. To the extent that idle time proxies illiquidity, the new portfolio is expected to give larger weights to liquid assets than the standard minimum-variance portfolio. On the other side, a very tight upper bound on the level of staleness for the assets included in the allocation will unavoidably result in a less-diversified portfolio. These considerations naturally lead to wonder to what extent such a staleness constrained asset allocation delivers a more liquid portfolio. Several definitions and measures of liquidity are available for individual securities, but the literature offers little guidance toward defining and assessing portfolio liquidity. Here, we adopt the economically motivated measure of portfolio liquidity of Pastor et al. (2017) to evaluate the degree of liquidity of an asset allocation strategy. Pastor et al. (2017) argue that the liquidity of a portfolio should depend not only on the liquidities of the stocks held in the portfolio, but also on the degree of portfolio diversification. The intuition underlying this argument is that a more diversified portfolio can lead to lower trading costs.³ Similarly, when the total value of the assets in the portfolio relative to the market capitalization of the assets is large, trading is more expensive. They formalize this intuition in a simple economic setting and derive the following portfolio liquidity measure:

$$\begin{aligned} {\mathbb {L}}= \left( \sum _{i=1}^{N} \frac{\omega _i^2}{m_i} \right) ^{-1} \end{aligned}$$

(1)

where N is the number of assets held in the portfolio, $\omega _i$ is the portfolio weight of stock i, and $m_i$ denotes the weight of asset i in a market-cap-weighted benchmark portfolio. Note that ${\mathbb {L}}$ takes values between 0 and 1. It can be shown that the portfolio with lowest ${\mathbb {L}}$ is the one fully invested in the stock with smallest market capitalization, and that the portfolio with largest ${\mathbb {L}}$ is the one coinciding with the benchmark portfolio, for which ${\mathbb {L}}=1$. In addition, Pastor et al. (2017) show that ${\mathbb {L}}$ factorizes into the product of two components: (1) the average of individual liquidities, defined as a function of the stock market capitalization; (2) a measure of the degree of diversification, related to the number of stocks held in the portfolio and to the Herfindahl index of portfolio weights.

Our second contribution is to show empirically that an appropriate choice of the staleness constraint leads to significant liquidity gains over the standard minimum-variance portfolio, as quantified by the measure of Pastor et al. (2017). Moreover, we show that gains in portfolio liquidity are much larger than the unavoidable increase in portfolio variance. Noteworthy, the risk profile of the staleness constrained portfolio is found to be very close to that of the minimum-variance portfolio. This result is somewhat consistent with the evidence in Canner et al. (1997) that investors do not choose portfolios on the efficient frontier, but are not too far from it.

Finally, our third contribution is to show how the proposed asset allocation strategy can be implemented in practice in an out-of-sample exercise. Given that idle time significantly changes over time, the portfolio staleness constraint must be adapted dynamically to the evolving market conditions. We show that this can be done with a simple rule based on forecasts of portfolio staleness. As before, we find that staleness constrained portfolios are significantly more liquid than minimum-variance portfolios, and that the liquidity-risk tradeoff is definitely in favor of portfolio liquidity.

Our paper is closely related to the works of Michaud (1989) and Lo et al. (2003), but it substantially differs in at least three aspects. First, we work in a dynamic setting, as the portfolio is rebalanced on a daily basis; second, we use an economically motivated measure of portfolio liquidity (i.e. portfolio staleness) to assess the degree of liquidity of the constrained portfolio; third, we show how to set the portfolio staleness constraint to obtain out-of-sample liquidity gains. Our paper is also related to the literature on shrinkage of portfolio weights (Jagannathan and Ma 2003; DeMiguel et al. 2009). However, instead of reducing the uncertainty on the estimated covariance matrix, our aim is to shrink portfolio weights towards more liquid assets.

As a robustness check, we replicate our analysis using, in place of portfolio staleness, the weighted average of inverse daily trading volume and the weighted average of daily bid–ask spreads. We show that bounds on these illiquidity measures provide liquidity-volatility profiles similar to those obtained through portfolio staleness. However, we discuss why portfolio staleness is more suited within the portfolio optimization framework.

The paper is organized as follows: Sect. 2 introduces the methodology and describes the staleness constrained portfolio; Sect. 3 provides details on the econometric modeling and forecasting of portfolio staleness and realized covariances; Sect. 4 reports the results of the empirical analysis and provides a comparison with common liquidity proxies; Sect. 5 concludes. Supplementary analyses are relegated to “Appendix”.

2 Framework

Let us consider a portfolio of N assets. Let $t=s_{n,0}<s_{n,1}<\cdots <s_{n,n}=t+1$ be a sampling partition of $n+1$ points of the time interval $[t,t+1]$, which can be thought of as representing one trading day. Let us also denote by $\Delta _{n,j}=s_{n,j}-s_{n,j-1}$ the lengths of the n sub-intervals and let $s\in [t,t+1]$. The vector of logarithmic efficient price processes ${\mathbf {X}}_s=\left( X_{s}^{(1)},\ldots ,X_{s}^{(N)}\right)$ is assumed to follow a Brownian semimartingale

$$\begin{aligned} d{\mathbf {X}}_s= \varvec{\mu }_s \hbox {d}s + \varvec{\sigma }_s \hbox {d}\mathbf{W }_s \end{aligned}$$

(2)

where $\varvec{\mu }_s$ is an N-dimensional drift process, $\varvec{\sigma }_s$ is an $N\times N$ matrix and $\mathbf{W }_s$ is an N-dimensional standard Brownian motion. The assumptions on the sub-interval lengths $\Delta _{n,j}$ and on the drift and diffusion coefficients $\varvec{\mu }_s, \varvec{\sigma }_s$ are the same as in Bandi et al. (2017). Following Bandi et al. (2017, (2020), we assume that, due to illiquidity frictions, the observed (on the sampling partition) logarithmic price processes $Y_{s_{n,j}}^{(i)}, i=1,\ldots ,N$, differ from the efficient logarithmic price paths. More precisely, $Y_{s_{n,j}}^{(i)}$ is assumed to be driven by the following recursive equation

$$\begin{aligned} {\left\{ \begin{array}{ll} Y_{s_{n,0}}^{(i)} = X_{s_{n,0}}^{\left( i\right) }\\ Y_{s_{n,j}}^{(i)} = (1-B_{j,n}^{(i)})X_{s_{n,j}}^{(i)} + B_{j,n}^{(i)}Y_{s_{n,j-1}}^{(i)} \end{array}\right. } \end{aligned}$$

(3)

where $B_{j,n}^{(i)}$ is a triangular array of measurable Bernoulli variates so that

$$\begin{aligned} \sum _{j=1}^n\Delta _{n,j}B_{j,n}^{(i)}\xrightarrow [n\rightarrow \infty ]{p} p_i \end{aligned}$$

Here, $p_i\in ]0,1]$ represents a random asymptotic probability, which we will address as “probability of stale price”. The Bernoulli variates are pairwise independent,⁴ that is, for all $i_1\ne i_2, {\mathbb {P}}[B_{j,n}^{(i_1)}=a,B_{k,n}^{(i_2)}=b]={\mathbb {P}}[B_{j,n}^{(i_1)}=a]{\mathbb {P}}[B_{k,n}^{(i_2)}=b]$, for all $j,k=1,\ldots ,n$. The key idea behind the modeling in Eq. (3) is that it allows for the possibility of no trade, hence capturing inhibition of the trading activity. As in Bandi et al. (2017), we further assume that the supremum of the number of consecutive flat trades, denoted by $K_n^{(i)}$, diverges at a rate slower than the number of observations

$$\begin{aligned} \frac{K_n^{(i)}}{n}\xrightarrow [n\rightarrow \infty ]{p}0 \end{aligned}$$

(4)

for $i=1,\ldots ,N$. Such assumption is necessary for the development of the asymptotic theory of the idle time estimator described in Sect. 3.2; see Bandi et al. (2017). In what follows, we will denote by $p_{i,t}$ the asymptotic probability of stale price of asset i on day t. Note that the above assumptions allow the Bernoulli variates to be correlated with the efficient price process, temporally dependent and non identical distributed.

Finally, it is worth mentioning that the relationship between the Bernoulli variates and the efficient price process can be understood in a context of a micro-founded model of price formation. We refer the interested reader to the model described in Bandi et al. (2017).

Let $\varvec{\Sigma }_t=\int _{t}^{t+1}\varvec{\sigma }_s\cdot \varvec{\sigma }_s^{T}\,\hbox {d}s$ denote the $N\times N$ integrated covariance matrix of the vector of efficient prices ${\mathbf {X}}$, on day t. Let ${\mathfrak {p}}_t=(p_{1,t},\ldots ,p_{N,t})'$ be the $N\times 1$ vector of stale price probabilities. Denoting by $\varvec{\omega }_t=(\omega _{1,t},\ldots ,\omega _{N,t})'$ the portfolio weights, we define the portfolio staleness on day t as the weighted average of stale price probabilities

$$\begin{aligned} \text {S}_t = \varvec{\omega }_t^{\prime }\, {\mathfrak {p}}_t=\omega _{1,t}\,p_{1,t}+\cdots +\omega _{N,t}\,p_{N,t}. \end{aligned}$$

(5)

For each day t, the investor solves the following quadratic optimization:

$$\begin{aligned} \begin{aligned}&\text {min} \; \varvec{\omega }_t^{\prime } \varvec{\Sigma }_t \varvec{\omega }_t\\ \text {s.t.}\quad&\mathbb {1}_N\varvec{\omega }_t \ge {\varvec{0}}_N \\&\varvec{\omega }_t^{\prime } \varvec{\iota } = 1 \\&\text {S}_t \le {\overline{\text {S}}}_t \end{aligned} \end{aligned}$$

(6)

where $\mathbb {1}_N$ is the $N\times N$ identity matrix, ${\varvec{0}}_N$ is an $N\times 1$ vector of zeros, $\varvec{\iota }$ is an $N\times 1$ vector of ones and ${\overline{\text {S}}}_t$ is a cap on the portfolio staleness $S_t$. The problem in equations (6) extends the classical minimum-variance (henceforth MV) Markowitz problem⁵ by including the linear constraint $\text {S}_t \le {\overline{\text {S}}}_t$.

Since, as empirically proved in Bandi et al. (2020), asset staleness measures illiquidity (along several dimensions), it is natural to impose the constraint $S_t\le {\overline{S}}_t$ for the purpose of putting larger weights on more liquid assets. As a consequence, the resulting portfolio composition is expected to be more liquid than that of the classical MV portfolio. We notice that the optimization problem (6) incorporates a liquidity constrain with the minimal set of input data: portfolio staleness $S_t$ can be obtained as soon as transaction prices are available, as it happens for the variance–covariance matrix $\varvec{\Sigma }_t$.

By looking at the equations in (6), it is clear that the proposed framework differs from the literature on portfolio construction with transaction costs (Constantinides 1986; Gârleanu 2009; Gârleanu and Pedersen 2013) in at least two aspects. First, portfolio illiquidity is captured by portfolio staleness to the same extent that the transaction costs of the individual assets are captured by idle time. Therefore, no explicit modelization of the multiple components of the transaction costs (commissions fees, bid–ask spreads, funding costs, price-impact) is required. Second, the optimization problem is a simple quadratic problem with linear constraints. It is thus readily implementable by financial institutions that aim to conciliate the request of lower trading costs with computational efficiency.

A more general framework would include a further constraint on portfolio expected returns. However, the latter are notoriously difficult to estimate and measurement errors can lead to overweight (underweight) securities with large (small) expected returns (Jorion 1985; Garlappi et al. 2006). Since our aim is to evaluate the improvement of portfolio liquidity for every unit of risk, we avoid to target expected returns. However, the methodology remains unchanged for mean–variance portfolios.

3 Portfolio allocation model

Given the information available at time t, the quadratic minimization problem (6), which returns the weights of the SC portfolio, can be solved based on one-step ahead forecasts of the integrated covariance matrix ${\widehat{\varvec{\Sigma }}}_{t+1}$ and of the vector of stale price probabilities ${\widehat{{\mathfrak {p}}}}_{t+1}$. In addition, the cap ${\overline{\text {S}}}_{t+1}$ that defines the staleness constraint must be chosen. In this section, we describe the forecasting models adopted to obtain the predictions ${\widehat{\varvec{\Sigma }}}_{t+1}$ and ${\widehat{{\mathfrak {p}}}}_{t+1}$ and show how to set a dynamic portfolio staleness constraint ${\overline{\text {S}}}_{t+1}$.

3.1 Covariance matrix estimation

Since the seminal works of Andersen et al. (2003) and Barndorff-Nielsen and Shephard (2004), realized measures constructed from high-frequency returns have became the preferential tool to estimate covariances. We model time-series of realized covariance matrices using the dynamic HAR-DRD specification of Oh and Patton (2016). Let $r_{j,n}^{(i)} = Y_{s_{n,j}}^{(i)}-Y_{s_{n,j-1}}^{(i)}$ be the jth intraday return of the ith asset on day t. We consider the $N\times 1$ vector of returns ${\varvec{r}}_{j,n} = (r_{j,n}^{(1)},\ldots ,r_{j,n}^{(N)})'$ and compute the realized covariance matrix on day t as

$$\begin{aligned} \mathbf{RC }_t = \sum ^{n}_{j=1} {\varvec{r}}_{j,n}{\varvec{r}}_{j,n}' \end{aligned}$$

Similarly to the DCC (Engle 2002) parameterization of the conditional covariance matrix, Oh and Patton (2016) factorize the realized covariance matrix in terms of realized variances and realized correlations

$$\begin{aligned} \mathbf{RC }_t = [\text {diag}(\mathbf{RV }_t)]^{1/2} \varvec{\rho }_t [\text {diag}(\mathbf{RV }_t)]^{1/2}, \end{aligned}$$

where $\text {diag}(\mathbf{RV }_t)$ is an $N \times N$ diagonal matrix of realized variances and $\varvec{\rho }_t$ is an $N \times N$ matrix of realized correlations. Individual variances are modeled through the HAR model of Corsi (2009)

$$\begin{aligned} \log \left( \mathbf{RV }_{i,t}\right)= & {} \phi ^{(c)}_i + \phi ^{(d)}_i\log \left( \mathbf{RV }_{i,t-1}\right) + \phi ^{(w)}_i\frac{1}{4}\sum ^{5}_{j=2}\log \left( \mathbf{RV }_{i,t-j}\right) \nonumber \\&+ \phi ^{(m)}_i\frac{1}{15}\sum ^{20}_{j=6}\log \left( \mathbf{RV }_{i,t-j}\right) + \varepsilon _{i,t} \end{aligned}$$

(7)

where $i=1,\ldots ,N, \mathbf{RV }_{i,t}$ denotes the ith element of $\mathbf{RV }_t$ and $\varepsilon _{i,t}$ are idiosyncratic innovations. Correlations are modeled through an analogous HAR specification

$$\begin{aligned} {\text {vech}}(\varvec{\rho }_t) = \varvec{\theta }^{(c)} + \theta ^{(d)} {\text {vech}}(\varvec{\rho }_{t-1}) + \theta ^{(w)} \frac{1}{4} \sum ^{5}_{j=2} {\text {vech}}(\varvec{\rho }_{t-j}) + \theta ^{(m)} \frac{1}{15} \sum ^{20}_{j=6} {\text {vech}}(\varvec{\rho }_{t-j}) + \varvec{\eta }_t, \end{aligned}$$

(8)

where ${\text {vech}}\left( \varvec{\rho }_t\right)$ indicates the operator stacking in a column the lower triangular part of $\varvec{\rho }_t$ and $\varvec{\theta }^{(c)} = {\overline{\varvec{\rho }}} (1-\theta ^{(d)} - \theta ^{(w)} - \theta ^{(m)} )$, with ${\overline{\varvec{\rho }}} = \frac{1}{T}\sum _{t=1}^{T} {\text {vech}}\left( \varvec{\rho }_t\right)$, while the elements $\eta _{i,t}$ of the vector $\varvec{\eta }_t$ are idiosyncratic innovations. Estimation of the parameter vectors $\left( \phi ^{(c)}_i, \phi ^{(d)}_i, \phi ^{(w)}_i, \phi ^{(m)}_i\right) ^N_{i=1}$ and $\left( \theta ^{(c)}, \theta ^{(d)}, \theta ^{(w)}, \theta ^{(m)}\right)$ is easily achieved through standard OLS, without requiring to specify a distribution for the error terms $\varepsilon _{i,t}$ and $\eta _t$. From Eqs. (7)–(8), it is straightforward to derive the one-step-ahead forecast of the covariance matrix

$$\begin{aligned} {\widehat{\varvec{\Sigma }}}_{t+1} ={\mathbb {E}}_t[\text {diag}(\mathbf{RV }_{t+1})]^{1/2} {\mathbb {E}}_t[\varvec{\rho }_{t+1}] {\mathbb {E}}_t[\text {diag}(\mathbf{RV }_{t+1})]^{1/2} \end{aligned}$$

(9)

where ${\mathbb {E}}_{t}[\text {diag}(\mathbf{RV }_{t+1})]$ is the $N\times N$ matrix with the predicted realized variances on the main diagonal and ${\mathbb {E}}_{t}[\varvec{\rho }_{t+1}]$ is obtained by re-arranging the predicted correlations into an $N\times N$ matrix. Theorem 2 in Oh and Patton (2016) provides conditions under which ${\widehat{\varvec{\Sigma }}}_{t+1}$ is positive definite.

3.2 Estimating the probability of stale prices

As anticipated in the introduction, following Bandi et al. (2020), we estimate the probabilities of stale price through the percentage of zero-returns at a given frequency. For this purpose, we define the idle time for the ith asset on day t as

$$\begin{aligned} \text {IT}_{i,t} = \frac{1}{n}\sum ^{n}_{j=1}\mathbb {1}_{\left\{ r_{j,n}^{(i)}=0\right\} } \end{aligned}$$

where $\mathbb {1}_{\{\cdot \}}$ denotes the indicator function. $\text {IT}_{i,t}$ is easily interpretable as the percentage of zero returns at a given sampling frequency. Time series of idle times of equity stocks exhibit strong serial dependence. As an example, consider Fig. 1, which shows the sample autocorrelation function of idle time of Goldman Sachs (GS) and Altria Group (MO). This empirical evidence supports the adoption of the following HAR (Corsi 2009) specification for the dynamics of daily idle times:

$$\begin{aligned} \text {IT}_{i,t} = \psi ^{(c)}_i + \psi ^{(d)}_i \text {IT}_{i,t-1} + \psi ^{(w)}_i \frac{1}{4}\sum ^{5}_{j=2} \text {IT}_{i,t-j} + \psi ^{(m)}_i \frac{1}{15}\sum ^{20}_{j=6} \text {IT}_{i,t-j} + \xi _{i,t}, \end{aligned}$$

(10)

which, in all our applications, is estimated through OLS. Similarly to the case of the variance–covariance matrix in Eq. (9), the t-conditional vector of stale price probabilities predicted for the day $t+1$ is obtained as

$$\begin{aligned} {\widehat{{\mathfrak {p}}}}_{t+1} = \left( {\mathbb {E}}_{t}\left[ \text {IT}_{1,t+1}\right] , \ldots , {\mathbb {E}}_{t}\left[ \text {IT}_{N,t+1}\right] \right) ^{\prime }. \end{aligned}$$

(11)

To conclude this section, we remark that we did not specify whether the forecasts are performed in-sample or out-of-sample. Since both cases will be considered, we postpone the remaining implementation details to Sect. 4.

Fig. 1

Realized variance and idle time. The time series of 1-min realized variance (upper-left panel) and 1-min idle time (upper-right panel). Bottom left and bottom right panels show, respectively, their corresponding autocorrelation functions. Black and red lines correspond to the tickers Goldman Sachs (GS) and Altria Group (MO), respectively (color figure online)

3.3 Portfolio staleness constraint

Since idle time changes significantly over time, the portfolio staleness cap ${\overline{\text {S}}}_t$, that appears in the minimization problem (6), needs to be set adaptively in order to be meaningful. More specifically, at each day t, the staleness constraint is required to lie in the interval between the lowest and the highest daily forecast of asset stale price probabilities. Indeed, a constraint lower than the lowest asset staleness will not be satisfied, and a constraint higher than the highest asset staleness will return a solution for the staleness constrained portfolio equal to the MV. We overcome this issue by choosing, given the information at time t, the staleness cap ${\overline{\text {S}}}_{t+1}$ as the $\alpha$-quantile of t-conditional idle time predictions. In formula, if ${\mathcal {Q}}_{\alpha }(\cdot )$ denotes the empirical quantile function⁶ at quantile level $\alpha$, then we set the staleness constraint as ${\overline{\text {S}}}_{t+1} = {\mathcal {Q}}_{\alpha }({\widehat{{\mathfrak {p}}}}_{t+1})$. Hence, $\alpha$ is a choice variable designed to trade-off liquidity and diversification, which are the two liquidity components of the portfolio liquidity measure in Eq. (1). In fact, setting a tight constraint on portfolio staleness (i.e. a value of $\alpha$ close to zero) imposes to concentrates funds on more liquid assets, reducing the benefits derived from diversification. In contrast, loosening the portfolio staleness constraint (i.e. a value of $\alpha$ close to one) makes the portfolio converge toward that of minimum variance, thus loosing the benefits from the highly liquid assets.

Table 1 Summary statistics

4 Empirical analysis

Our dataset consists of transactions prices of 50 NYSE assets and covers $T=2244$ business days, from 03-01-2006 to 31-12-2014. The time resolution is the minute. We select trades occurring between 9:30 and 16:00, leading to 390 timestamps. Summary statistics for the assets in the sample are reported in Table 1. In order to assess the effectiveness of our methodology at different dimensions, we build three groups of 10, 25 and 50 assets, respectively. The stocks included in the 10- and 25-sized groups are randomly selected, while the 50-sized group includes all the assets in the dataset.

Both $\text {IT}_{i,t}$ and $\mathbf{RC }_t$ are computed at the same sampling frequency of 1 min.⁷ We perform both an in-sample and an out-of-sample analysis. The in-sample analysis is made on the whole dataset and is aimed to provide empirical evidence that SC portfolios are significantly more liquid than standard MV portfolios. Portfolio liquidity is assessed through the measure of Pastor et al. (2017) in Eq. (1). In particular, we use the weight of each asset i in the S&P500 to obtain a proxy for the weight $m_i$ that appears in Eq. (1). The out-of-sample analysis is performed through a rolling window of 1000 days. Our dynamic HAR models are re-estimated on a daily basis and then used to construct a sequence of SC portfolios based on one-step-ahead forecasts of $\mathbf{RC }_t$ and $\text {IT}_{i,t}$. Similarly to the in-sample analysis, we show that out-of-sample SC portfolios feature larger liquidity. Moreover, we provide guidelines on how to set in practice the quantile level $\alpha$ of the staleness constraint.

4.1 In-sample analysis

In the in-sample analysis the HAR models (7), (8) and (10) are estimated using the whole sample available. We solve the SC problem for twenty equally distant values of the quantile level $\alpha$, obtaining a sequence of optimal solutions $\widehat{\varvec{\omega }}^{\text {SC}_{\alpha }}_t$ of the minimization problem (6).

To assess to which extent the SC portfolio is more liquid than its MV counterpart, we compute the portfolio liquidity measure ${\mathbb {L}}_t$ defined in Eq. (1) for both the MV and SC portfolios, for every day t of the sample. Figure 2 reports (in percentage) the average relative difference

$$\begin{aligned} \frac{1}{T}\sum _{t=1}^{T} \frac{{\mathbb {L}}^{\text {SC}_{\alpha }}_t - {\mathbb {L}}^{\text {MV}}_t}{{\mathbb {L}}^{\text {MV}}_t} \end{aligned}$$

(12)

between the liquidity ${\mathbb {L}}^{\text {SC}_{\alpha }}_t$ of the SC portfolio at quantile level $\alpha$ and the liquidity ${\mathbb {L}}^{\text {MV}}_t$ of the MV portfolio. A grey area delimits the $95\%$ confidence bands, obtained with a block bootstrap of 12 lags based on 1000 resamplings of the differences in portfolio liquidities. The plots in Figure 2 show that, for the three groups of assets, there exist several choices of $\alpha$ for which the corresponding SC portfolios are significantly more liquid than their MV counterparts. In particular, the plots show that portfolio liquidity presents an inverse U-shaped pattern. Setting a tight portfolio staleness constraint allows to concentrates funds on more liquid assets, but does not allow to benefit from diversification. In contrast, increasing the portfolio staleness constraint beyond a certain threshold makes the portfolio converge toward the MV portfolio, thus loosing the benefits from the highly liquid assets. This result shows that there is a tradeoff between the two liquidity components of the portfolio liquidity measure in (1), and highlights how portfolio staleness can be effectively used to manage portfolio liquidity. We also notice that, at the optimal $\alpha$, the SC portfolio is considerably more liquid than the MV portfolio. Indeed, the average relative difference of portfolio liquidities between the two can be as high as $110\%$ for $N=10, 40\%$ for $N=25$ and $22\%$ for $N=50$.

Fig. 2

In-sample portfolio liquidity. The red line corresponds to the average percentage relative difference in portfolio liquidity between the SC portfolio at the quantile level $\alpha$ and the MV portfolio, i.e. $\left( 1/T\right) \,\sum _{t=1}^{T} \left( {\mathbb {L}}^{\text {SC}_{\alpha }}_t - {\mathbb {L}}^{\text {MV}}_t\right) /{\mathbb {L}}^{\text {MV}}_t$. Grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding the horizontal dashed-blue line signal a statistically significant improvement in portfolio liquidity of the SC portfolio over the MV (color figure online)

The volatility of the SC portfolio is expected to be higher than that of the MV portfolio. To complete our empirical analysis, it is thus necessary to assess the cost of liquidity gains in terms of deterioration of portfolio risk. We estimate the SC portfolio volatility (${\mathbb {V}}_t^{\text {SC}_{\alpha }}$) and the MV portfolio volatility (${\mathbb {V}}_t^{\text {MV}}$) as

$$\begin{aligned} {\mathbb {V}}_t^{\text {SC}_{\alpha }} = \sqrt{\left( {\widehat{\varvec{\omega }}}_t^{\text {SC}_{\alpha }}\right) ^{\prime } \,\mathbf {{\widehat{\Sigma }}}_t\,{\widehat{\varvec{\omega }}}_t^{\text {SC}_{\alpha }}},\quad {\mathbb {V}}_t^{\text {MV}} = \sqrt{\left( {\widehat{\varvec{\omega }}}_t^{\text {MV}}\right) ^{\prime } \,\mathbf {{\widehat{\Sigma }}}_t \,{\widehat{\varvec{\omega }}}_t^{\text {MV}}} \end{aligned}$$

where ${\widehat{\varvec{\omega }}}^{\text {SC}_{\alpha }}$ and ${\widehat{\varvec{\omega }}}_t^{\text {MV}}$ indicates the corresponding portfolio weights. Figure 3 reports, in percentage and as a function of $\alpha$, the average relative difference $\left( 1/T\right) \sum _{t=1}^T\left( {\mathbb {V}}_t^{\text {SC}_{\alpha }}-{\mathbb {V}}_t^{\text {MV}}\right) /{\mathbb {V}}_t^{\text {MV}}$, along with the $95\%$ bootstrap confidence bands. The SC portfolios are always more volatile than the MV portfolio but, for large enough values of $\alpha$, the difference between the two portfolio volatilities becomes very small.

Fig. 3

In-sample portfolio volatility. The red line corresponds to the average percentage relative difference in portfolio volatility between the SC portfolio at the quantile level $\alpha$ and the MV portfolio, i.e. $\left( 1/T\right) \,\sum _{t=1}^{T}({\mathbb {V}}^{\text {SC}_{\alpha }}_t - {\mathbb {V}}^{\text {MV}}_t)/{\mathbb {V}}^{\text {MV}}_t$. Grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding zero signal a statistically significant deterioration in portfolio volatility of the SC portfolio with respect to MV (color figure online)

In order to quantify how much the increase in portfolio variance is compensated by the increase in portfolio liquidity, we compute a volatility-adjusted measure of liquidity, defined as

$$\begin{aligned} \mathbb {AL}_t^{\text {SC}_{\alpha }} = \frac{{\mathbb {L}}_t^{\text {SC}_{\alpha }}}{{\mathbb {V}}_t^{\text {SC}_{\alpha }}},\quad \mathbb {AL}_t^{\text {MV}} = \frac{{\mathbb {L}}_t^{\text {MV}}}{{\mathbb {V}}_t^{\text {MV}}} \end{aligned}$$

(13)

for both the SC and the MV portfolios. Figure 4 reports, in percentage and as a function of $\alpha$, the average of the relative difference

$$\begin{aligned} \frac{\mathbb {AL}_t^{\text {SC}_{\alpha }}- \mathbb {AL}_t^{\text {MV}}}{\mathbb {AL}_t^{\text {MV}}} \end{aligned}$$

(14)

along with $95\%$ bootstrap confidence bands. Similarly to Fig. 2, we find an inverse U-shaped pattern. This implies that the tradeoff between the two liquidity components of the portfolio liquidity measure (1) is still present after controlling for portfolio volatility. In particular, we can find values of $\alpha$ for which gains in portfolio liquidity are significantly greater than the increase in portfolio volatility. This finding further corroborates the use of portfolio staleness as a tool to manage portfolio liquidity.

Fig. 4

In-sample adjusted portfolio liquidity. The red line corresponds to the average percentage relative difference in the adjusted portfolio liquidity between the SC portfolio at the quantile level $\alpha$ and the MV portfolio, i.e. $\left( 1/T\right) \,\sum _{t=1}^{T}\left( \mathbb {AL}^{\text {SC}_{\alpha }}_t - \mathbb {AL}^{\text {MV}}_t\right) /\mathbb {AL}^{\text {MV}}_t$. Grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding the dashed-blue line signal a statistically significant improvement of the volatility-adjusted portfolio liquidity of the SC portfolio over the MV (color figure online)

To conclude this section, we observe that the minimization problem in Eq. (6) could be solved by directly imposing a cap on the measure of portfolio liquidity in Eq. (1). In other words, we could limit the degree of portfolio illiquidity as quantified by the Pastor et al. (2017) measure ${\mathbb {L}}_t$ rather than the portfolio staleness $S_t$. While this is theoretically possible, due to the highly nonlinear dependence of ${\mathbb {L}}_t$ on the weights, the corresponding optimization problem can only be solved numerically and it may lead to unstable and irregular portfolio configurations. For this reason, we implement the linear portfolio staleness constraint and use the Pastor et al. (2017) measure as an independent proxy to assess and compare the level of liquidity of the constructed portfolios.

4.2 Out-of-sample analysis

The results discussed in Sect. 4.1 show that it is possible to appropriately choose the staleness constraint to achieve statistically significant in-sample gains in terms of volatility-adjusted liquidity. We now question whether these results can be extended to an out-of-sample framework.

For this purpose, we design an out-of-sample asset allocation strategy in which we adopt a rolling window of $T_0=1000$ observations, leaving the remaining $T_1=1244$ days as a validation sample. We estimate, for each day $t>T_0$ and in the time window $[t-T_0+1,t]$, the dynamic models (7) and (8) for the covariance matrices and the model (10) for the idle times. The output of the estimation are the one-day-ahead forecasts ${\widehat{\varvec{\Sigma }}}_{t+1}$ and ${\widehat{{\mathfrak {p}}}}_{t+1}$. These predictions are then used to solve the SC and MV optimization problems, obtaining the portfolio weights $\widehat{\varvec{\omega }}^{\text {SC}_{\alpha ^{*}}}_{t+1}$ and $\widehat{\varvec{\omega }}^{\text {MV}}_{t+1}$, respectively. The quantile level $\alpha ^*$ is chosen following a simple optimization procedure: first, the estimated covariance and stale price probabilities corresponding to the last day of the rolling window are used to solve the SC optimization problem with 20 different constraints, as in Sect. 4.1; then, we choose the $\alpha ^{*}$ that maximizes the volatility-adjusted liquidity measure $\mathbb {AL}_t^{\text {SC}_{\alpha }}$ in Eq. (13) and set ${\overline{\text {S}}}^{*}_{t+1} = {\mathcal {Q}}_{\alpha ^*}({\widehat{{\mathfrak {p}}}}_{t+1})$ as a constraint in the out-of-sample portfolio problem.

For each day of the validation sample, we compute the volatility-adjusted liquidity measure in Eq. (13), for both SC and MV portfolios. Figure 5 reports the percentage relative differences, defined in Eq. (14), together with 95% bootstrap confidence bands under the null hypothesis of zero difference. The plots show that these differences tend to be positive over the whole validation sample, suggesting that the volatility-adjusted liquidity of the out-of-sample SC portfolios is significantly larger than that of the MV portfolio.

The results of this empirical study suggest that the introduction of a portfolio staleness constraint in the Markowitz framework can significantly enhance out-of-sample portfolio liquidity without jeopardizing the portfolio risk profile.

Fig. 5

Out-of-sample adjusted portfolio liquidity. Percentage relative differences in the volatility-adjusted liquidity measure, defined in Eq. (14), between the SC and MV portfolios (red line), their average (blue line), and the 95% bootstrap confidence bands (grey-shaded area) under the null hypothesis of zero difference (color figure online)

4.3 Robustness check: comparison with other liquidity measures

The outcome of Sect. 4 naturally leads to wonder whether similar results may have been obtained imposing a constraint on other illiquidity proxies and, in case, what are the advantages of relying on portfolio staleness.

In order to answer this question, we perform an empirical analysis identical to that proposed in Sect. 4, with the notable difference that the constraint on portfolio staleness is substituted with a constraint on different, commonly used, illiquidity proxies. Formally, let $\varvec{\ell }_t = \left( \ell _{1,t}, \ldots , \ell _{N,t} \right) '$ be a vector of illiquidity proxies at time t. We solve the following portfolio optimization problem

$$\begin{aligned} \begin{aligned}&\text {min} \; \varvec{\omega }_t^{\prime } \varvec{\Sigma }_t \varvec{\omega }_t \\ \text {s.t.}\quad&\mathbb {1}_N\varvec{\omega }_t \ge {\varvec{0}}_N \\&\varvec{\omega }_t^{\prime } \varvec{\iota } = 1 \\&\varvec{\omega }_t '\varvec{\ell }_t\le {\overline{\ell }}_t \end{aligned} \end{aligned}$$

(15)

where ${\overline{\ell }}_t$ is a cap on the portfolio illiquidity $\varvec{\omega }_t '\varvec{\ell }_t$. For each day t, we consider, as illiquidity proxies, the inverse of the total daily trading volume and the daily average relative bid–ask spread. Daily volumes and average relative bid–ask spreads for the ith asset, $i=1,\ldots ,N$, are defined as

$$\begin{aligned} V_{i,t}= & {} \sum ^{n_{i,t}}_{s = 1} N_{i,s} \end{aligned}$$

(16)

$$\begin{aligned} S_{i,t}= & {} \frac{1}{n_{i,t}}\sum ^{n_{i,t}}_{s = 1} \frac{A_{i,s} - B_{i,s}}{B_{i,s}} \end{aligned}$$

(17)

where $n_{i,t}$ is the number of transactions on day $t, N_{i,s}$ is the number of shares traded at the sth transaction of day $t, A_{i,s}$ and $B_{i,s}$ denote, respectively, the best ask and the best bid prevailing at the sth transaction.

The results of the analysis are reported in Appendix A. They are similar to those obtained with SC portfolios, which further corroborates the interpretation of idle time as a proxy of illiquidity. However, it is worth pointing out that the use of idle time in a portfolio selection problem provides several advantages.

First, idle time can be computed using solely transaction data. This is convenient from a practical perspective, given that order book data related to bid–ask spreads or other micro-structural variables are not generally available to investors. Second, idle time has solid economic foundations. In a price formation model featuring transaction costs and agents with different degrees of information, it is correlated with relevant illiquidity factors, such as bid–ask spreads, asymmetric information and delays in the incorporation of the information flow into the assets’ prices (Bandi et al. 2017). In contrast, common liquidity measures computed with high-frequency data are not easy to interpret once aggregated at the daily level. For instance, bid–ask spread is a very informative liquidity measure, well-suited to derive the optimal trading positioning minimizing the transaction costs. However, it looses its natural interpretation when aggregated over the day. Finally, idle time is formally a probability and thus can be compared across assets without normalization. In a portfolio setting, standard liquidity measures need some sort of normalization to be compared. For example, the bid–ask spread is naturally larger for stocks with larger prices, but this does not imply that these stocks are less illiquid. To circumvent this issue, one needs to normalize the aggregated daily measures of liquidity in order to make them comparable in the asset allocation procedure (Lo et al. 2003). Of course, this practice introduces some form of arbitrariness in the optimization strategy that instead is absent when using idle time.

5 Conclusions

Building upon the interpretation of idle time as an illiquidity proxy, we introduced the concept of portfolio staleness and showed that it can be effectively used to manage liquidity in a standard minimum-variance framework. A staleness constrained portfolio leads to significant improvements in terms of individual asset liquidities and to lower price impact due to a better degree of diversification. Interestingly, the unavoidable deterioration of portfolio risk due to the staleness constraint is much less important than the corresponding liquidity gain. Using transaction data of a cross section of NYSE assets, we showed how to properly select the staleness constraints in a real-life out-of-sample portfolio choice problem.

The proposed approach can be viewed as an “econometric framework” to manage liquidity in a standard minimum-variance problem. At each time period, the user of our methodology computes one-step-ahead forecasts of the relevant econometric variables (covariances and idle times) in order to recover the portfolio weights. The optimization problem is solved in closed form without explicitly modeling the multiple components of the transaction costs (commissions fees, bid–ask spreads, funding costs, price-impact). In this perspective, the methodology differs substantially from the methods based on direct inclusion of transaction costs in the investor’s objective function, which lead to more complex dynamic programming optimization problems.

Robustness checks: inverse of total trading volume and average relative bid–ask as illiquidity proxies

We solve the portfolio problem (15) for 20 equally spaced quantile levels $\alpha$, using the procedure outlined in Sect. 3.3. Figure 6 reports the average relative difference

$$\begin{aligned} \frac{1}{T}\sum _{t=1}^{T} \frac{{\mathbb {L}}^{\text {VC}_{\alpha }}_t - {\mathbb {L}}^{\text {MV}}_t}{{\mathbb {L}}^{\text {MV}}_t} \end{aligned}$$

(A.1)

between the inverse-volume constrained liquidity portfolio ${\mathbb {L}}^{\text {VC}_{\alpha }}_t$ and the its MV counterpart ${\mathbb {L}}^{\text {MV}}_t$. The former is obtained solving the optimization problem (15) with $\varvec{\ell }_t=\left( 1/V_{1,t},\ldots ,1/V_{N,t}\right)$ where $V_{i,t}$ is the liquidity measure defined in Eq. (16), i.e. the total daily trading volume for asset i. Similarly, Figure 7 shows the average relative difference

$$\begin{aligned} \frac{1}{T}\sum _{t=1}^{T} \frac{{\mathbb {L}}^{\text {BAC}_{\alpha }}_t - {\mathbb {L}}^{\text {MV}}_t}{{\mathbb {L}}^{\text {MV}}_t} \end{aligned}$$

between the bidask-spread constrained liquidity portfolio ${\mathbb {L}}^{\text {BAC}_{\alpha }}_t$ and the its MV counterpart ${\mathbb {L}}^{\text {MV}}_t$. The former is obtained solving the optimization problem (15) with $\varvec{\ell }_t=\left( S_{1,t},\ldots ,S_{N,t}\right)$ where $S_{i,t}$ is the illiquidity measure defined in Eq. (17), i.e. the daily average relative spread for asset i. We adopt, in both cases, the same groups of $N=10, N=25$ and $N=50$ assets considered in the analysis with constrains on portfolio staleness. Gray shaded areas correspond to $95\%$ bootstrap confidence bands. We note that both the inverse-volume and the bidask-spread constrained portfolios provide significant liquidity gains over MV portfolios, in a similar fashion to staleness constrained portfolios.

Fig. 6

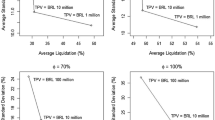
Liquidity of inverse-volume constrained portfolios. Average percentage relative difference in portfolio liquidity between the inverse-volume constrained portfolio, at the quantile level $\alpha$, and the MV portfolio (red line). The grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding the dashed-blue line signal an improvement of portfolio liquidity over the MV portfolio (color figure online)

Fig. 7

Liquidity of bidask-spread constrained portfolios. Average percentage relative difference in portfolio liquidity between the bidask-spread constrained portfolio, at the quantile level $\alpha$, and the MV portfolio (red line). The grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding the dashed-blue line signal an improvement of portfolio liquidity over the MV portfolio (color figure online)

In order to assess the increase in volatility, we plot in Figs. 8 and 9 the average relative differences between volatilities of, respectively, inverse-volume and bidask-spread constrained portfolios and MV portfolios. As expected, these differences are positive and statistically significant, and similar in magnitude to those observed for the SC portfolios.

Fig. 8

Volatility of inverse-volume constrained portfolios. Average percentage relative difference in portfolio volatility between the inverse-volume constrained portfolio, at the quantile level $\alpha$, and the MV portfolio (red line). The grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding zero signal a statistically significant deterioration in portfolio volatility with respect to the MV portfolio (color figure online)

Fig. 9

Volatility of bidask-spread constrained portfolios. Average percentage relative difference in portfolio volatility between the bidask-spread constrained portfolio, at the quantile level $\alpha$, and the MV portfolio (red line). The grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding zero signal a statistically significant deterioration in portfolio volatility with respect to the MV portfolio (color figure online)

Fig. 10

Volatility-adjusted liquidity of inverse-volume constrained portfolios. Average percentage relative difference in the adjusted portfolio liquidity between the inverse-volume constrained portfolio, at the quantile level $\alpha$, and the MV portfolio (red line). The grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding the dashed-blue line signal an improvement of adjusted portfolio liquidity over the MV portfolio (color figure online)

Fig. 11

Volatility-adjusted liquidity of bidask-spread constrained portfolios. Average percentage relative difference in the adjusted portfolio liquidity between the bidask-spread constrained portfolio, at the quantile level $\alpha$, and the MV portfolio (red line). The grey-shaded area delimits the 95% bootstrap confidence bands. Values of the red line exceeding the dashed-blue line signal an improvement of adjusted portfolio liquidity over the MV portfolio (color figure online)

Fig. 12

Out-of-sample volatility-adjusted liquidity of inverse-volume constrained portfolios. Percentage relative (with respect to the MV portfolio) differences in volatility-adjusted liquidity between the inverse-volume constrained and MV portfolios (red line), their average (blue line), and the 95% bootstrap confidence bands (grey-shaded area) under the null hypothesis of zero difference (color figure online)

Fig. 13

Out-of-sample volatility-adjusted liquidity of bidask-spread constrained portfolios. Percentage relative (with respect to the MV portfolio) differences in volatility-adjusted liquidity between the bidask-spread constrained and MV portfolios (red line), their average (blue line), and the 95% bootstrap confidence bands (grey-shaded area) under the null hypothesis of zero difference (color figure online)

We also evaluate whether portfolio liquidity gains can justify the increased volatility. Figure 10 (resp. Fig. 11) reports the (percentage) average of the relative differences in volatility-adjusted liquidity, defined analogously to those in Eq. (14), between the inverse-volume (resp. the bidask-spread) constrained portfolios and the MV portfolios, for the three portfolio dimensions considered here. Also in this case, considerable gains in the liquidity/volatility trade-off can be obtained for suitable choices of $\alpha$.

As a final robustness check, we replicate the out-of-sample analysis of Sect. 4.2 for the inverse-volume and bidask-spread constrained portfolios. The same groups of $N=10, N=25$ and $N=50$ assets are used. The illiquidity caps ${\overline{\ell }}_t$ for the inverse volume and the average relative spread portfolios are adaptively chosen each day, using the same procedure adopted in the case of the staleness constrained minimization. We compute the volatility-adjusted liquidity measure in Eq. (13) for the inverse-volume and bidask-spread constrained portfolios and report, respectively, in Figs. 12 and 13 the (percentage) relative differences with respect to the MV portfolio (defined analogously to those defined in Eq. (14) for the staleness constrained portfolio). We note that these differences are significantly positive in most of the days of the sample.