Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T01:12:43.171Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal two-parameter 𝒲∞-algebra and vertex algebras of type 𝒲(2, 3, …, N)

Part of: Lie algebras and Lie superalgebras Groups and algebras in quantum theory

Published online by Cambridge University Press:  10 February 2021

Andrew R. Linshaw
Andrew R. Linshaw*
Affiliation:
Department of Mathematics, University of Denver, 2390 S. York St., Denver, CO80208, USAandrew.linshaw@du.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the longstanding physics conjecture that there exists a unique two-parameter 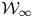${\mathcal {W}}_{\infty }$-algebra which is freely generated of type 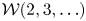${\mathcal {W}}(2,3,\ldots )$, and generated by the weights 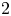$2$ and 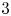$3$ fields. Subject to some mild constraints, all vertex algebras of type 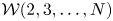${\mathcal {W}}(2,3,\ldots , N)$ for some 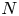$N$ can be obtained as quotients of this universal algebra. As an application, we show that for 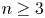$n\geq 3$, the structure constants for the principal 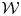${\mathcal {W}}$-algebras 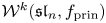${\mathcal {W}}^k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ are rational functions of 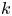$k$ and 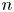$n$, and we classify all coincidences among the simple quotients 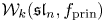${\mathcal {W}}_k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ for 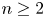$n\geq 2$. We also obtain many new coincidences between 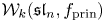${\mathcal {W}}_k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ and other vertex algebras of type 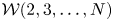${\mathcal {W}}(2,3,\ldots , N)$ which arise as cosets of affine vertex algebras or nonprincipal 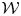${\mathcal {W}}$-algebras.

Keywords

vertex algebra𝒲-algebranonlinear Lie conformal algebracoset construction

MSC classification

Primary: 17B67: Kac-Moody (super)algebras; extended affine Lie algebras; toroidal Lie algebras 17B68: Virasoro and related algebras 17B69: Vertex operators; vertex operator algebras and related structures 81R10: Infinite-dimensional groups and algebras motivated by physics, including Virasoro, Kac-Moody, $W$-algebras and other current algebras and their representations
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 1 , January 2021 , pp. 12 - 82
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by grants $\#$318755 and $\#$635650 from the Simons Foundation.

References

Adamović, D., Representations of the vertex algebra ${\mathcal {W}}_{1+\infty }$ with a negative integer central charge, Comm. Algebra 29 (2001), 3153–3166.Google Scholar
Adamović, D., A construction of admissible $A^{(1)}_1$-modules of level $-\frac {4}{3}$, J. Pure Appl. Algebra 196 (2005), 119–134.CrossRefGoogle Scholar
Adamović, D., Creutzig, T., Genra, N. and Yang, J., The vertex algebras ${\mathcal {R}}^{(p)}$ and ${\mathcal {V}}^{(p)}$, Preprint (2020), arXiv:2001.08048.Google Scholar
Adamović, D. and Perše, O., Fusion rules and complete reducibility of certain modules for affine Lie algebras, J. Algebra Appl. 13 (2014), 1350062.CrossRefGoogle Scholar
Adler, M., On a trace functional for formal pseudo differential operators and the symplectic structure of the Korteweg-de Vries type equations, Invent. Math. 50 (1978), 219–248.CrossRefGoogle Scholar
Adler, M., Shiota, T. and van Moerbeke, P., From the $w_{\infty }$-algebra to its central extension: a $\tau$-function approach, Phys. Lett. A 194 (1994), 33–43.CrossRefGoogle Scholar
Alday, L., Gaiotto, D. and Tachikawa, Y., Liouville correlation functions from four-dimensional gauge theories, Lett. Math. Phys. 91 (2010), 167–197.CrossRefGoogle Scholar
Arakawa, T., Rationality of Bershadsky-Polyalov vertex algebras, Comm. Math. Phys. 323 (2013), 627–633.CrossRefGoogle Scholar
Arakawa, T., Associated varieties of modules over Kac-Moody algebras and $C_2$-cofiniteness of ${\mathcal {W}}$-algebras, Int. Math. Res. Not. IMRN 2015 (2015), 11605–11666.Google Scholar
Arakawa, T., Rationality of ${\mathcal {W}}$-algebras: principal nilpotent cases, Ann. Math. (2) 182 (2015), 565–694.CrossRefGoogle Scholar
Arakawa, T., Creutzig, T., Kawasetsu, K. and Linshaw, A., Orbifolds and cosets of minimal $\mathcal {W}$-algebras, Comm. Math. Phys. 355 (2017), 339–372.CrossRefGoogle Scholar
Arakawa, T., Creutzig, T. and Linshaw, A., Cosets of Bershadsky-Polyakov algebras and rational $\mathcal {W}$-algebras of type $A$, Selecta Math. (N.S.) 23 (2017), 2369–2395.CrossRefGoogle Scholar
Arakawa, T., Creutzig, T. and Linshaw, A., W-algebras as coset vertex algebras, Invent. Math. 218 (2019), 145–195.CrossRefGoogle Scholar
Arakawa, T. and Frenkel, E., Quantum Langlands duality of representations of ${\mathcal {W}}$-algebras, Compos. Math. 155 (2019), 2235–2262.CrossRefGoogle Scholar
Arakawa, T., Lam, C. H. and Yamada, H., Parafermion vertex operator algebras and ${\mathcal {W}}$-algebras, Trans. Amer. Math. Soc. 371 (2019), 4277–4301.CrossRefGoogle Scholar
Arakawa, T. and Moreau, A., Lectures on ${\mathcal {W}}$-algebras, Preprint (2016).Google Scholar
Arakawa, T. and Moreau, A., Joseph ideals and lisse minimal W-algebras, J. Inst. Math. Jussieu 17 (2018), 397–417.CrossRefGoogle Scholar
Arbesfeld, N. and Schiffmann, O., A presentation of the deformed ${\mathcal {W}}_{1+\infty }$ algebra, in Symmetries, integrable systems and representations, Springer Proceedings in Mathematics & Statistics, vol. 40 (Springer, Heidelberg, 2013), 1–13.Google Scholar
Awata, H., Fukuma, M., Matsuo, Y. and Odake, S., Character and determinant formulae of quasifinite representation of the ${\mathcal {W}}_{1+\infty }$ algebra, Comm. Math. Phys. 172 (1995), 377–400.CrossRefGoogle Scholar
Bais, F. A., Bouwknegt, P., Surridge, M. and Schoutens, K., Extension of the Virasoro algebra constructed from Kac-Moody algebra using higher order Casimir invariants, Nuclear Phys. B 304 (1988), 348–370.CrossRefGoogle Scholar
Bais, F. A., Bouwknegt, P., Surridge, M. and Schoutens, K., Coset construction for extended Virasoro algebras, Nuclear Phys. B 304 (1988), 371–391.CrossRefGoogle Scholar
Bakalov, B. and Vac, V., Field algebras, Int. Math. Res. Not. IMRN 2003 (2003), 123–159.CrossRefGoogle Scholar
Bakas, I. and Kiritsis, E., Beyond the large N limit: nonlinear ${\mathcal {W}}_{\infty }$ as symmetry of the $SL(2,R)/U(1)$ coset model, in Infinite analysis, Kyoto, 1991, Advanced Series in Mathematical Physics, vol. 16 (World Scientific, River Edge, NJ, 1992), 55–81.Google Scholar
Blumenhagen, R., Eholzer, W., Honecker, A., Hornfeck, K. and Hubel, R., Coset realizations of unifying $\mathcal {W}$-algebras, Int. J. Modern Phys. Lett. A10 (1995), 2367–2430.CrossRefGoogle Scholar
Blumenhagen, R., Flohr, M., Kliem, A., Nahm, W., Recknagel, A. and Varnhagen, R., ${\mathcal {W}}$-algebras with two and three generators, Nuclear Phys. B 361 (1991), 255.CrossRefGoogle Scholar
Borcherds, R., Vertex operator algebras, Kac-Moody algebras and the monster, Proc. Natl. Acad. Sci. USA 83 (1986), 3068–3071.CrossRefGoogle Scholar
Bouwknegt, P. and Schoutens, K., ${\mathcal {W}}$-symmetry in conformal field theory, Phys. Rep. 223 (1993), 183–276.CrossRefGoogle Scholar
Bowcock, P., Quasi-primary fields and associativity of chiral algebras, Nuclear Phys. B 356 (1991), 367.CrossRefGoogle Scholar
Braverman, A., Finkelberg, M. and Nakajima, H., Instanton moduli spaces and ${\mathcal {W}}$-algebras, Astérisque 385 (2016).Google Scholar
Cordova, C. and Shao, S. H., Schur indices, BPS particles, and Argyres-Douglas theories, J. High Energy Phys. 2016(01) (2016), Article 40.CrossRefGoogle Scholar
Creutzig, T., ${\mathcal {W}}$-algebras for Argyres-Douglas theories, Eur. J. Math. 3 (2017), 659–690.CrossRefGoogle Scholar
Creutzig, T. and Gaiotto, D., Vertex algebras for S-duality. Comm. Math. Phys. 379 (2020), 785–845.CrossRefGoogle Scholar
Creutzig, T., Kanade, S., Linshaw, A. and Ridout, D., Schur-Weyl duality for Heisenberg cosets, Transform. Groups 24 (2019), 301–354.CrossRefGoogle Scholar
Creutzig, T. and Linshaw, A., The super ${\mathcal {W}}_{1+\infty }$ algebra with integral central charge, Trans. Amer. Math. Soc. 367 (2015), 5521–5551.CrossRefGoogle Scholar
Creutzig, T. and Linshaw, A., Cosets of the ${\mathcal {W}}^k({\mathfrak s}{\mathfrak l}_4, f_{\text {subreg}})$-algebra, in Vertex algebras and geometry, Contemporary Mathematics, vol. 711 (American Mathematical Society, Providence, RI, 2018), 105–117.CrossRefGoogle Scholar
Creutzig, T. and Linshaw, A., Cosets of affine vertex algebras inside larger structures, J. Algebra 517 (2019), 396–438.CrossRefGoogle Scholar
Creutzig, T., Ridout, D. and Wood, S., Coset constructions of logarithmic $(1,p)$ models, Lett. Math. Phys. 104 (2014), 553–583.CrossRefGoogle Scholar
De Sole, A. and Kac, V., Freely generated vertex algebras and non-linear Lie conformal algebras, Comm. Math. Phys. 254 (2005), 659–694.CrossRefGoogle Scholar
De Sole, A. and Kac, V., Finite vs affine ${\mathcal {W}}$-algebras, Jpn. J. Math. 1 (2006), 137–261.CrossRefGoogle Scholar
De Sole, A., Kac, V. and Valeri, D., Adler-Gelfand-Dickey approach to classical ${\mathcal {W}}$-algebras within the theory of Poisson vertex algebras, Int. Math. Res. Not. IMRN 2015 (2015), 11186–11235.CrossRefGoogle Scholar
Dickey, L., Soliton equations and integrable systems, Advanced Series in Mathematical Physics, vol. 12 (World Scientific, Singapore, 1991).Google Scholar
Dong, C., Lam, C. and Yamada, H., ${\mathcal {W}}$-algebras related to parafermion algebras, J. Algebra 322 (2009), 2366–2403.CrossRefGoogle Scholar
Dong, C., Li, H. and Mason, G., Compact automorphism groups of vertex operator algebras, Int. Math. Res. Not. IMRN 1996 (1996), 913–921.CrossRefGoogle Scholar
Drinfeld, V. and Sokolov, V., Lie algebras and equations of Korteweg-de Vries type, in Current problems in mathematics, Itogi Nauki i Tekhniki, Akad. Nauk SSSR, vol. 24 (Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1984), 81–180.Google Scholar
Fateev, V. and Lukyanov, S., The models of two-dimensional conformal quantum field theory with $Z_n$ symmetry, Internat. J. Modern Phys. A 3 (1988), 507–520.CrossRefGoogle Scholar
Feigin, B., Lie algebras ${\mathfrak g}{\mathfrak l}(\lambda )$ and cohomology of a Lie algebra of differential operators, Uspekhi Mat. Nauk 43 (1988), 157–158; translation in Russian Math. Surveys 43 (1988), 169–170.Google Scholar
Feigin, B. and Frenkel, E., Quantization of the Drinfeld-Sokolov reduction, Phys. Lett. B 246 (1990), 75–81.CrossRefGoogle Scholar
Feigin, B., Jimbo, M., Miwa, T. and Mukhin, E., Branching rules for quantum toroidal ${\mathfrak g}{\mathfrak l}_n$, Adv. Math. 300 (2016), 229–274.CrossRefGoogle Scholar
Feigin, B. and Semikhatov, A., ${\mathcal {W}}_n^{(2)}$ algebras, Nuclear Phys. B 698 (2004), 409–449.CrossRefGoogle Scholar
Frenkel, E., Langlands correspondence for loop groups, Cambridge Studies in Advanced Mathematics, vol. 103 (Cambridge University Press, Cambridge, 2007).Google Scholar
Frenkel, E. and Ben-Zvi, D., Vertex algebras and algebraic curves, Mathematical Surveys and Monographs, vol. 88 (American Mathematical Society, Providence, RI, 2001).Google Scholar
Frenkel, E. and Gaiotto, D., Quantum Langlands dualities of boundary conditions, D-modules, and conformal blocks. Commun. Number Theory Phys. 14 (2020), 199–313.CrossRefGoogle Scholar
Frenkel, I. B., Huang, Y-Z and Lepowsky, J., On axiomatic approaches to vertex operator algebras and modules, Mem. Amer. Math. Soc. 104 (1993).Google Scholar
Frenkel, E., Kac, V., Radul, A. and Wang, W., ${\mathcal {W}}_{1+\infty }$ and ${\mathcal {W}}(gl_N)$ with central charge $N$, Comm. Math. Phys. 170 (1995), 337–358.CrossRefGoogle Scholar
Frenkel, E., Kac, V. and Wakimoto, M., Characters and fusion rules for ${\mathcal {W}}$-algebras via quantized Drinfeld-Sokolov reduction, Comm. Math. Phys. 147 (1992), 295–328.CrossRefGoogle Scholar
Frenkel, I. B., Lepowsky, J. and Meurman, A., Vertex operator algebras and the monster (Academic Press, New York, NY, 1988).Google Scholar
Frenkel, I. B. and Zhu, Y. C., Vertex operator algebras associated to representations of affine and Virasoro algebras, Duke Math. J. 66 (1992), 123–168.CrossRefGoogle Scholar
Gaberdiel, M. R. and Gopakumar, R., An AdS$_3$ dual for minimal model CFTs, Phys. Rev. D 83 (2011), 066007.CrossRefGoogle Scholar
Gaberdiel, M. R. and Gopakumar, R., Triality in minimal model holography, J. High Energy Phys. 2012(7) (2012), Article 127.CrossRefGoogle Scholar
Gaberdiel, M. R. and Hartman, T., Symmetries of holographic minimal models, J. High Energy Phys. 2011(05) (2011), Article 031.Google Scholar
Gaiotto, D. and Rapčák, M., Vertex algebras at the corner, J. High Energy Phys. 2019(1) (2019), Article 160.CrossRefGoogle Scholar
Gaitsgory, D., The master chiral algebras, talk at Perimeter Institute, https://www.perimeterinstitute.ca/videos/master-chiral-algebra.Google Scholar
Gaitsgory, D., Quantum Langlands correspondence, Preprint (2016), arXiv:1601.05279.Google Scholar
Gelfand, I. and Dickey, L., A family of Hamiltonian structures connected with integrable nonlinear differential equations, Preprint 136, Akademiya Nauk SSSR. Institut Prikladnoĭ Matematiki (1978).Google Scholar
Genra, N., Screening operators for ${\mathcal {W}}$-algebras, Selecta Math. (N.S.) 23 (2017), 2157–2202.CrossRefGoogle Scholar
Goddard, P., Kent, A. and Olive, D., Virasoro algebras and coset space models, Phys. Lett. B 152 (1985), 88–93.CrossRefGoogle Scholar
Gorelik, M. and Kac, V., On simplicity of vacuum modules, Adv. Math. 211 (2007), 621–677.CrossRefGoogle Scholar
Hornfeck, K., ${\mathcal {W}}$-algebras with set of primary fields of dimensions $(3,4,5)$ and $(3,4,5,6)$, Nuclear Phys. B 407 (1993), 237–246.CrossRefGoogle Scholar
Hornfeck, K., ${\mathcal {W}}$-algebras of negative rank, Phys. Lett. B 343 (1995), 94–102.CrossRefGoogle Scholar
Kac, V., Vertex algebras for beginners, University Lecture Series, vol. 10 (American Mathematical Society, Providence, RI, 1998).CrossRefGoogle Scholar
Kac, V. and Peterson, D., Spin and wedge representations of infinite-dimensional Lie algebras and groups, Proc. Natl. Acad. Sci. USA 78 (1981), 3308–3312.CrossRefGoogle ScholarPubMed
Kac, V. and Radul, A., Quasi-finite highest weight modules over the Lie algebra of differential operators on the circle, Comm. Math. Phys. 157 (1993), 429–457.CrossRefGoogle Scholar
Kac, V. and Radul, A., Representation theory of the vertex algebra $\mathcal {W}_{1+\infty }$, Transform. Groups 1 (1996), 41–70.CrossRefGoogle Scholar
Kac, V., Roan, S. and Wakimoto, M., Quantum reduction for affine superalgebras, Comm. Math. Phys. 241 (2003), 307–342.CrossRefGoogle Scholar
Kac, V. and Wakimoto, M., Classification of modular invariant representations of affine algebras, in Infinite-dimensional Lie algebras and groups, Luminy-Marseille, 1988, Advanced Series in Mathematical Physics, vol. 7 (World Scientific, Teaneck, NJ, 1989), 138–177.Google Scholar
Kac, V. and Wakimoto, M., Branching functions for winding subalgebras and tensor products, Acta Appl. Math. 21 (1990), 3–39.CrossRefGoogle Scholar
Kac, V. and Wakimoto, M., Quantum reduction and representation theory of superconformal algebras, Adv. Math. 185 (2004), 400–458.CrossRefGoogle Scholar
Kac, V. and Wakimoto, M., On rationality of ${\mathcal {W}}$-algebras, Transform. Groups 13 (2008), 671–713.CrossRefGoogle Scholar
Kac, V. and Wakimoto, M., A remark on boundary level admissible representations, C. R. Math. Acad. Sci. Paris 355 (2017), 128–132.CrossRefGoogle Scholar
Kausch, H. G. and Watts, G. M. T., A study of ${\mathcal {W}}$-algebras using Jacobi identities, Nuclear Phys. B 354 (1991), 740.CrossRefGoogle Scholar
Kawasetsu, K., ${\mathcal {W}}$-algebras with non-admissible levels and the Deligne exceptional series, Int. Math. Res. Not. IMRN 3 (2018), 641–676.Google Scholar
Khesin, B. and Malikov, F., Universal Drinfeld-Sokolov reduction and matrices of complex size, Comm. Math. Phys. 176 (1996), 113–134.CrossRefGoogle Scholar
Khesin, B. and Zakharevich, I., Poisson-Lie group of pseudodifferential symbols, Comm. Math. Phys. 171 (1995), 475–530.CrossRefGoogle Scholar
Kostant, B., On Whittaker vectors and representation theory, Invent. Math. 48 (1978), 101–184.CrossRefGoogle Scholar
Li, H., Symmetric invariant bilinear forms on vertex operator algebras, J. Pure Appl. Algebra 96 (1994), 279–297.CrossRefGoogle Scholar
Li, H., Local systems of vertex operators, vertex superalgebras and modules, J. Pure Appl. Algebra 109 (1996), 143–195.CrossRefGoogle Scholar
Li, H., Vertex algebras and vertex Poisson algebras, Commun. Contemp. Math. 6 (2004), 61–110.CrossRefGoogle Scholar
Lian, B. and Zuckerman, G., Commutative quantum operator algebras, J. Pure Appl. Algebra 100 (1995), 117–139.CrossRefGoogle Scholar
Linshaw, A., Invariant theory and the ${\mathcal {W}}_{1+\infty }$ algebra with negative integral central charge, J. Eur. Math. Soc. 13 (2011), 1737–1768.Google Scholar
Linshaw, A., The structure of the Kac-Wang-Yan algebra, Comm. Math. Phys. 345 (2016), 545–585.CrossRefGoogle Scholar
Mason, G., Vertex rings and their Pierce bundles, in Vertex algebras and geometry, Contemporary Mathematics, vol. 711 (American Mathematical Society, Providence, RI, 2018), 45–104.CrossRefGoogle Scholar
Maulik, D. and Okounkov, A., Quantum groups and quantum cohomology, Astérisque 408 (2019).Google Scholar
Premet, A., Special transverse slices and their enveloping algebras, Adv. Math. 170 (2002), 1–55.CrossRefGoogle Scholar
Procházka, T., Exploring ${\mathcal {W}}_{\infty }$ in the quadratic basis, J. High Energy Phys. 2015(9) (2015), Article 116.CrossRefGoogle Scholar
Procházka, T., ${\mathcal {W}}$-symmetry, topological vertex, and affine Yangian, J. High Energy Phys. 2016(10) (2016), Article 77.CrossRefGoogle Scholar
Procházka, T. and Rapčák, M., Webs of ${\mathcal {W}}$-algebras, J. High Energy Phys. 2018(11) (2018), Article 109.CrossRefGoogle Scholar
Schiffmann, O. and Vasserot, E., Cherednik algebras, ${\mathcal {W}}$-algebras and the equivariant cohomology of the moduli space of instantons on $\textbf {A}^2$, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 213–342.CrossRefGoogle Scholar
Thielemans, K., A Mathematica package for computing operator product expansions, Int. J. Modern Phys. C 2 (1991), 787–798.CrossRefGoogle Scholar
Tsymbaliuk, A., The affine Yangian of ${\mathfrak g}{\mathfrak l}_1$ revisited, Adv. Math. 304 (2017), 583–645.CrossRefGoogle Scholar
Wang, W., $\mathcal {W}_{1+\infty }$ algebra, $\mathcal {W}_3$ algebra, and Friedan-Martinec-Shenker bosonization, Comm. Math. Phys. 195 (1998), 95–111.CrossRefGoogle Scholar
Weyl, H., The classical groups: their invariants and representations (Princeton University Press, Princeton, NJ, 1946).Google Scholar
Yu, F. and Wu, Y. S., Nonlinearly deformed $\hat {{\mathcal {W}}}_{\infty }$-algebra and second hamiltonian structure of KP hierarchy, Nuclear Phys. B 373 (1992), 713–734.CrossRefGoogle Scholar
Zamolodchikov, A. B., Infinite extra symmetries in two-dimensional conformal quantum field theory (in Russian), Teoret. Mat. Fiz. 65 (1985), 347–359.Google Scholar
Zhu, C. J., The complete structure of the nonlinear $W_4$ and $W_5$ algebras from quantum Miura transformation, Phys. Lett. B 316 (1993), 264–274.CrossRefGoogle Scholar
Zhu, Y., Modular invariants of characters of vertex operators, J. Amer. Math. Soc. 9 (1996), 237–302.CrossRefGoogle Scholar