Outer approximation for global optimization of mixed-integer quadratic bilevel problems

Abstract

Bilevel optimization problems have received a lot of attention in the last years and decades. Besides numerous theoretical developments there also evolved novel solution algorithms for mixed-integer linear bilevel problems and the most recent algorithms use branch-and-cut techniques from mixed-integer programming that are especially tailored for the bilevel context. In this paper, we consider MIQP-QP bilevel problems, i.e., models with a mixed-integer convex-quadratic upper level and a continuous convex-quadratic lower level. This setting allows for a strong-duality-based transformation of the lower level which yields, in general, an equivalent nonconvex single-level reformulation of the original bilevel problem. Under reasonable assumptions, we can derive both a multi- and a single-tree outer-approximation-based cutting-plane algorithm. We show finite termination and correctness of both methods and present extensive numerical results that illustrate the applicability of the approaches. It turns out that the proposed methods are capable of solving bilevel instances with several thousand variables and constraints and significantly outperform classical solution approaches.

1 Introduction

Bilevel optimization problems are used in various applications, e.g., in energy markets [9, 12, 20, 29, 31, 34, 39], in critical infrastructure defense [11, 16], or in pricing problems [15, 40] to model hierarchical decision processes. As such, they embed one optimization problem, the so-called lower-level problem, into the constraints of a so-called upper-level problem. This leads to inherent nonconvexities, which render already linear bilevel problems with a linear upper- and lower-level problem NP-hard; see, e.g., [14, 32, 35].

In this work, we study mixed-integer quadratic bilevel problems of the form

$$\begin{aligned} \min _{x, {\bar{y}}} \quad&q_u(x, {\bar{y}})= \frac{1}{2} x^\top H_ux + c_u^\top x + \frac{1}{2} {\bar{y}}^\top G_u{\bar{y}}+ d_u^\top {\bar{y}}\nonumber \\ \text {s.t.} \quad&A x + B {\bar{y}}\ge a, \nonumber \\&x_i \in \mathbb {Z}\cap [x_i^-,x_i^+] \quad \text {for all }i \in I {{:}{=}}\{1,\ldots ,|I|\}, \nonumber \\&x_i \in \mathbb {R}\quad \text {for all }i \in R {{:}{=}}\{|I| + 1,\ldots ,{n_x}\}, \nonumber \\&{\bar{y}}\in {{\,\mathrm{arg\,min}\,}}_{y} \bigg \{ \begin{array}{l} q_l(y)= \frac{1}{2} y^\top G_ly + d_l^\top y : C x_I + D y \ge b,\ y \in \mathbb {R}^{{n_y}} \end{array}\bigg \}, \end{aligned}$$

(1)

where $H_u\in \mathbb {R}^{{n_x}\times {n_x}}$, $G_u\in \mathbb {R}^{{n_y}\times {n_y}}$, and $G_l\in \mathbb {R}^{{n_y}\times {n_y}}$ are symmetric and positive semidefinite matrices. Furthermore, we have vectors $c_u\in \mathbb {R}^{n_x}$, $d_u, d_l\in \mathbb {R}^{n_y}$, matrices $A \in \mathbb {R}^{{m_u}\times {n_x}}$, $B \in \mathbb {R}^{{m_u}\times {n_y}}$, $C \in \mathbb {R}^{{m_l}\times |I|}$, $D\in \mathbb {R}^{{m_l}\times {n_y}}$, as well as right-hand side vectors $a\in \mathbb {R}^{m_u}$ and $b\in \mathbb {R}^{m_l}$. The variables $x=(x_I, x_R)$ denote the integer ($x_I$) and continuous ($x_R$) upper-level variables and y denotes the (continuous) lower-level variables. Note that we w.l.o.g. ordered the integer and continuous upper-level variables for the ease of presentation. In this setup, the upper-level problem is a convex mixed-integer quadratic problem (MIQP) and for fixed integer upper-level variables $x_I$, the lower level is a convex quadratic problem (QP), i.e., it is a parametric convex QP. In total, we are facing an MIQP-QP bilevel problem with the following key properties:

• (i) All upper-level integer variables $x_I$ are bounded.

• (ii) All linking variables, i.e., upper-level variables that appear in the lower-level constraints, are integer.

We note that in Problem (1), we implicitly assume that all integer upper-level variables are linking variables. However, this formulation also contains the more general case of integer upper-level variables that do not appear in the lower-level problem by setting some columns in the matrix C to zero.

The main motivation of this work is to exploit the two properties above to develop a multi- and a single-tree solution approach for Problem (1) based on outer approximation for convex mixed-integer nonlinear problems (MINLP) [18, 25]. The above-mentioned two properties are required by many other state-of-the-art algorithms for linear bilevel problems with purely integer linear (ILP-ILP) or mixed-integer linear upper- and lower-level problems (MILP-MILP); see, e.g. [21, 23, 43, 50, 54]. These methods successfully use bilevel-tailored branch-and-bound or branch-and-cut methods to solve quite large instances of hundreds or thousands of variables and constraints. However, they cannot directly deal with continuous lower-level problems and/or have not yet been extended to the convex-quadratic case—if this is possible at all. An extension of [54] to the general class of mixed-integer nonlinear bilevel problems with integer linking variables is proposed in [41] but the computational study therein only covers mixed-integer linear bilevel problems. In [3], the authors use multi-parametric programming techniques to solve bilevel problems with convex MIQPs on both levels. This algorithm explicitly allows for continuous linking variables. The backbone of the approach is the computation of the optimal solutions of the lower-level problem as a function of the upper-level decisions. This step is very costly and, according to the authors, it is evident that this algorithm is not intended for the solution of larger problems. The computational study included in the paper deals with problems up to 65 variables. In addition, the algorithm is only applicable for problems that possess unique lower-level solutions.

Aside from mixed-integer bilevel problems, algorithms for various classes of continuous convex-quadratic bilevel problems have been proposed. However, in contrast to algorithms for mixed-integer bilevel problems, reported numerical results for continuous convex-quadratic bilevel problems seem to cover only rather small instances. A branch-and-bound algorithm for bilevel problems with a convex upper-level problem and a strictly convex lower-level problem is proposed in [5]. The author demonstrates the effectiveness of his method for problems with up to 15 variables and 20 constraints on each level. In [6], a convex-quadratic lower-level problem is replaced by its Karush–Kuhn–Tucker (KKT) conditions and then a branching on the complementarity constraints is applied. The authors report results for problems with up to 60 upper-level and 40 lower-level variables. This approach is generalized from linear upper-level to convex upper-level problems in [19]. Two different descent algorithms for bilevel problems with a strictly convex lower level and a concave or convex upper level are proposed in [53]. However, the authors do not provide computational results. Recently, also neural networks are used to tackle continuous convex-quadratic bilevel problems; see [33, 42].

To the best of our knowledge, tailored algorithms for mixed-integer quadratic bilevel problems of the form (1) are neither reported nor has their efficiency been demonstrated in a comprehensive computational study. In fact, there exist no code packages that can be used as a benchmark for our proposed solution techniques. Thus, we use well-known single-level reformulations based on KKT conditions and strong duality as a benchmark in our computational study in Sect. 4.

Our contribution is the following. We consider bilevel problems with a mixed-integer convex-quadratic upper level and a convex-quadratic lower level. For this nonconvex problem class, we provide an equivalent reformulation to a convex MINLP that uses strong duality of the lower level; see Sect. 2. Further, in Sect. 3 we propose a multi- and a single-tree solution approach that are both inspired by outer-approximation techniques for convex MINLPs. We prove the correctness of the methods and discuss further extensions. We are not aware of any other work that applies outer-approximation techniques from the area of convex MINLP to mixed-integer bilevel programming. In Sect. 4, we evaluate the effectiveness of the proposed approaches in an extensive numerical study, in which we solve instances with up to several thousand variables and constraints. We conclude in Sect. 5.

2 A convex single-level reformulation

Most solution techniques for bilevel problems rely on a reformulation of the bilevel problem to a single-level problem [14]. For problems with a convex lower level, the lower-level problem can be replaced by its nonconvex KKT conditions. Especially for problems with linear lower-level constraints, this approach is very popular, because it allows for a mixed-integer linear reformulation of the KKT complementarity conditions using additional binary variables and big-M values; see, e.g., [26]. With this approach the bilevel problem (1) can be equivalently transformed to the following mixed-integer single-level problem

$$\begin{aligned} \min _{x,y,v,\lambda } \quad&q_u(x,y) \end{aligned}$$

(2a)

$$\begin{aligned} \text {s.t.} \quad&Ax + By \ge a, \quad x_i \in \mathbb {Z}\cap [x_i^-,x_i^+] \quad \text {for all }i \in I, \end{aligned}$$

(2b)

$$\begin{aligned}&Cx_I + Dy \ge b, \end{aligned}$$

(2c)

$$\begin{aligned}&G_ly + d_l= D^T \lambda , \quad \lambda \ge 0, \end{aligned}$$

(2d)

$$\begin{aligned}&v \in \{0,1\}^{{m_l}}, \quad Cx_I + Dy - b \le M_1 v, \quad \lambda \le M_2 (1-v), \end{aligned}$$

(2e)

where Constraints (2b) and (2c) model primal feasibility of the upper and lower level, respectively. Constraint (2d) models dual feasibility of the lower-level problem with dual lower-level variables $\lambda \in \mathbb {R}^{m_l}_{\ge 0}$. Constraints (2e) ensure KKT complementarity via additional binary variables $v_j$ and sufficiently large numbers $M_1$ and $M_2$. Similarly, a strong-duality-based reformulation can be derived by replacing KKT complementarity (2e) by the strong-duality equation of the lower level. This approach is significantly less used in practice because even for linear bilevel problems one obtains nonconvex bilinear terms due to products of primal upper-level and dual lower-level variables. These terms can only be linearized if all linking variables are integer. Recently, in [55], a numerical study is provided that compares the KKT approach with the strong-duality approach for linear bilevel problems with integer linking variables and continuous lower-level problems. The authors conclude that the strong-duality reformulation works significantly better than the KKT reformulation for problems with large lower-level problems. Other contributions that successfully apply the strong-duality reformulation to linear bilevel problems include, e.g., [2, 27, 28, 30, 40, 44]. Except from Bard, who briefly sketches the idea in [5], we are not aware of any works that use strong duality for bilevel problems with quadratic lower levels. One reason might be that the resulting strong-duality equation is quadratic. Opposed to the linearized KKT reformulation, the strong-duality-based reformulation thus yields a quadratically constrained program. Despite this drawback, we derive such a strong-duality-based single-level reformulation after introducing some notation.

2.1 General notation

The bilevel constraint region is denoted by

$$\begin{aligned} P\,\, {{:}{=}}\,\, \{(x,y): Ax+By\ge a,\ Cx_I+Dy\ge b,\ x_i \in \mathbb {Z}\cap [x_i^-,x_i^+]\ \text {for all } i \in I \}. \end{aligned}$$

Throughout this paper, we assume that P is bounded. This set corresponds to the set obtained by relaxing the optimality of the lower-level problem. Its projection onto the decision space of the upper level is given by

$$\begin{aligned} P_u\,\, {{:}{=}}\,\, \{x:\exists \, y \text { such that } (x,y) \in P\}. \end{aligned}$$

For fixed $\bar{x}=(\bar{x}_R,\bar{x}_I) \in P_u$, the lower-level feasible region is given by

$$\begin{aligned} P_l(\bar{x}_I) = \{y:Dy \ge b - C \bar{x}_I\} \end{aligned}$$

and the rational reaction set of the lower level reads

$$\begin{aligned} M(\bar{x}_I)&= \mathop {{{\,\mathrm{arg\,min}\,}}}\limits _{y} \, \{q_l(y) : y \in P_l(\bar{x}_I)\}. \end{aligned}$$

Since $G_l$ is semidefinite, the lower level may not have a unique solution, i.e., $M(\bar{x}_I)$ may not be a singleton. In such a case, we assume the optimistic bilevel solution, i.e., ${\bar{y}}\in M(\bar{x}_I)$ is chosen in favor of the upper level; see, e.g., Chapter 1 in [14]. In Problem (1), this is indicated by “$\min _{x,{\bar{y}}}$” in the upper-level objective, i.e., the upper-level minimizes over x and ${\bar{y}}$. We emphasize that single-level reformulations, like, e.g., Problem (2), implicitly assume the optimistic bilevel solution, such that there is no need to distinguish between y and ${\bar{y}}$. Further, note that our solution approach explicitly allows for $M(\bar{x}_I)=\emptyset$ for some $\bar{x} \in P_u$. Finally, the bilevel feasible set is given by

$$\begin{aligned} \mathcal {F}&= \{(x,{\bar{y}}):x \in P_u, \, {\bar{y}}\in M(\bar{x}_I)\}. \end{aligned}$$

If $\mathcal {F}= \emptyset$, then Problem (1) is infeasible.

2.2 Strong-duality-based nonconvex single-level reformulation

We now use strong duality of the lower-level problem to transform Problem (1) into an equivalent nonconvex single-level problem. The parametric Lagrangian dual problem of the parametric lower level

$$\begin{aligned} \min _y \quad q_l(y) \quad \mathrm {s.t.}\quad Dy \ge b - C x_I \end{aligned}$$

(3)

with parameter $x_I$ is given by

$$\begin{aligned} \max _{\lambda \ge 0} \quad g(x_I;\lambda ) \end{aligned}$$

(4)

with $g(x_I;\lambda )= \inf _y \mathcal {L}(x_I;y,\lambda )$; see [10]. In our setup, the Lagrangian $\mathcal {L}$ reads

$$\begin{aligned} \mathcal {L}(x_I;y, \lambda ) = \frac{1}{2} y^\top G_ly + d_l^\top y - \lambda ^\top (C x_I+Dy-b). \end{aligned}$$

(5)

Since $\mathcal {L}(x_I;y,\lambda )$ is convex and differentiable in y, the infimum is given by

$$\begin{aligned} \nabla _y \mathcal {L}(x_I;y,\lambda ) = G_ly + d_l- D^\top \lambda = 0. \end{aligned}$$

(6)

In order to denote the Lagrangian dual problem in its general form (4), we could use Expression (6) to obtain $y = G_l^{-1}(D^\top \lambda - d_l)$. This can then be used to substitute the primal variable y in the Lagrangian (5) to obtain

$$\begin{aligned} g(x_I;\lambda ) = -\frac{1}{2} (D^\top \lambda - d_l)^\top G_l^{-1} (D^\top \lambda - d_l) - (C x_I -b)^\top \lambda . \end{aligned}$$

However, this only works if $G_l$ is regular, e.g., if $G_l$ is strictly definite. In the more general case of semidefinite matrices, we can explicitly keep the primal variable y and substitute $D^\top \lambda = G_ly + d_l$ in the Lagrangian (5). This yields the dual problem

$$\begin{aligned} \begin{aligned} \max _{y, \lambda } \quad&\bar{g}(x_I;y,\lambda ) = -\frac{1}{2} y^\top G_ly - (Cx_I -b)^\top \lambda \\ \mathrm {s.t.}\quad&G_ly + d_l= D^\top \lambda , \quad \lambda \ge 0. \end{aligned} \end{aligned}$$

(7)

Note that $\bar{g}(x_I;\cdot )$ is a concave-quadratic function in y and $\lambda$ because $G_l$ is positive semidefinite. Thus, the dual problem (7) is a parametric concave-quadratic maximization problem over affine-linear constraints. Since Problem (7) does not involve the inverse $G_l^{-1}$, we use formulation (7) also in the case when $G_l$ is strictly positive definite.

In the following, we only consider $x \in P_u$, i.e., upper-level variables for which the parametric lower-level problem is feasible. The parametric lower-level problem (3) is a convex-quadratic minimization problem over affine-linear constraints. Consequently, duality conditions apply without requiring additional constraint qualifications; see Chapter 5.2.3 in [10] and Theorem 24.1 in [52]. For every primal-dual feasible point $(y,\lambda )$, i.e., $y \in P_l(x_I)$ and $\lambda \ge 0$ that fulfill $G_ly + d_l= D^\top \lambda$, weak duality

$$\begin{aligned} q_l(y) \ge \bar{g}(x_I;y,\lambda ) \end{aligned}$$

(8)

holds. Furthermore, for optimal primal-dual points $({y}^{*}, {\lambda }^{*})$, strong duality holds, i.e., $q_l({y}^{*}) = \bar{g}(x_I;{y}^{*},{\lambda }^{*})$. Together with weak duality (8), strong duality can be enforced by the constraint $q_l(y) - \bar{g}(x_I;y,\lambda ) \le 0$, i.e.,

$$\begin{aligned} \begin{aligned} c(x_I,y,\lambda )\,\, {{:}{=}}\,\, q_l(y) - \bar{g}(x_I;y,\lambda ) = y^\top G_ly + d_l^\top y - b^\top \lambda + \lambda ^\top C x_I \le 0. \end{aligned} \end{aligned}$$

(9)

This strong-duality inequality is convex in y but the bilinear term $\lambda ^\top C x_I$ is nonconvex. Using (9), the bilevel problem (1) can be recast as the equivalent single-level nonconvex mixed-integer quadratically constrained quadratic program (MIQCQP):

$$\begin{aligned} \begin{aligned} \min _{x,y,\lambda } \quad&q_u(x,y) \\ \mathrm {s.t.}\quad&(x,y) \in P, \\&G_ly + d_l= D^\top \lambda , \quad \lambda \ge 0, \\&c(x_I,y,\lambda ) \le 0. \end{aligned} \end{aligned}$$

(10)

2.3 Convexification of the strong-duality constraint

The only nonconvexity in the strong-duality inequality (9) is the bilinear product $\lambda ^\top C x_I$. Since the variables $x_I$ are integer, this product can be reformulated using a binary expansion. For the ease of presentation, we w.l.o.g. assume in the following that $x_i^- = 0$ for all $i \in I$. The products of binary and continuous variables can then be linearized by several techniques. According to the numerical study in [55], the following approach works best in a bilevel context. We express the integer variables $x_j$ with the help of $\bar{r}_j = \lfloor \log _2(x_j^+) \rfloor + 1$ many auxiliary binary variables $s_{jr}$:

$$\begin{aligned} s_{jr}&\in \{0,1\},&j \in I,\ r \in [\bar{r}_j], \end{aligned}$$

(11a)

$$\begin{aligned} x_j&= \sum _{r=1}^{\bar{r}_j} 2^{r-1} s_{jr},&j \in I. \end{aligned}$$

(11b)

With this we obtain

$$\begin{aligned} \lambda ^\top Cx_I = \sum _{i=1}^{m_l}\sum _{j=1}^{|I|} c_{ij} \lambda _i x_j = \sum _{i=1}^{m_l}\sum _{j=1}^{|I|} \sum _{r=1}^{\bar{r}_j} 2^{r-1} c_{ij} \lambda _i s_{jr} = \sum _{j=1}^{|I|} \sum _{r=1}^{\bar{r}_j} 2^{r-1} s_{jr} \sum _{i=1}^{m_l}c_{ij} \lambda _i. \end{aligned}$$

Now, we replace the binary-continuous products $s_{jr} \sum _{i=1}^{{m_l}} c_{ij} \lambda _i$ by introducing auxiliary continuous variables $w_{jr}$ and enforce

$$\begin{aligned} w_{jr} = s_{jr} \sum _{i=1}^{{m_l}} c_{ij} \lambda _i \end{aligned}$$

(12)

by the additional constraints

$$\begin{aligned} w_{jr}&\le \overline{\lambda }_j s_{jr},&j \in I,\ r \in [\bar{r}_j], \end{aligned}$$

(13a)

$$\begin{aligned} w_{jr}&\le \sum _{i=1}^{{m_l}} c_{ij} \lambda _i + \underline{\lambda }_j (s_{jr} - 1),&j \in I,\ r \in [\bar{r}_j], \end{aligned}$$

(13b)

$$\begin{aligned} w_{jr}&\ge \underline{\lambda }_j s_{jr},&j \in I,\ r \in [\bar{r}_j], \end{aligned}$$

(13c)

$$\begin{aligned} w_{jr}&\ge \sum _{i=1}^{{m_l}} c_{ij} \lambda _i + \overline{\lambda }_j (s_{jr} - 1),&j \in I,\ r \in [\bar{r}_j]. \end{aligned}$$

(13d)

In this formulation, we need bounds $\overline{\lambda }_j \ge \sum _{i=1}^{{m_l}} c_{ij} \lambda _i$, and $\underline{\lambda }_j \le \sum _{i=1}^{{m_l}} c_{ij} \lambda _i$ which are, in practice, often derived by some suitable big-M. The need for such bounds is also a major drawback in the KKT-based reformulation (2). In [46], it is shown that wrong big-Ms can lead to suboptimal solutions or points that are actually bilevel infeasible. Unfortunately, even verifying that the bounds are correctly chosen is, in general, at least as hard as solving the original bilevel problem; see [37]. Thus, if possible, big-Ms should be derived using problem-specific knowledge. However, we point out that our solution approaches introduced in Sect. 3 compute bilevel-feasible points independent of the big-Ms. Thus, in case of too small big-Ms, our algorithms may terminate with a suboptimal solution but never compute bilevel-infeasible points. We discuss this also later in Sect. 3.3.

Using (11) and (13), we rewrite Constraint (9) as

$$\begin{aligned} \hat{{c}}(y,\lambda ,w) \,\,{{:}{=}}\,\, y ^\top G_ly + d_l^\top y - b^\top \lambda + \sum _{j=1}^{|I|} \sum _{r=1}^{\bar{r}_j} 2^{r-1} w_{jr} \le 0, \end{aligned}$$

(14)

which is convex in y and linear in $\lambda$ and $w$. Note that $2^{r-1} \le x_j^+$ holds, i.e., for reasonable bounds $x_j^+$, the exponential coefficients $2^{r-1}$ can be considered as numerically stable.

Finally, the single-level problem (10) can be stated equivalently as

$$\begin{aligned} \begin{aligned} \min _{x,y,\lambda ,w,s} \quad&q_u(x,y) \\ \mathrm {s.t.}\quad&(x,y) \in P,\\&G_ly + d_l= D^\top \lambda , \quad \lambda \ge 0, \\&\lambda ^\top Cx_I \text { linearization: } (11), (13), \\&\text {Strong duality: }(14). \end{aligned} \end{aligned}$$

(15)

This is a convex MIQCQP that has more binary variables and constraints compared to the nonconvex MIQCQP (10). We denote the feasible set of Problem (15) by $\Omega$, feasible points by $z=(x,y,\lambda ,w,s) \in \Omega$ and optimal points by ${z}^{*}$. By construction of Problem (15), we have the following equivalence result.

Lemma 1

The feasible set of Problem (15) projected on the (x, y)-space equals the bilevel feasible set of the bilevel Problem (1), i.e., $\mathcal {F}= {{\,\mathrm{Proj}\,}}_{(x,y)}(\Omega )$ holds. In addition, for every global optimal solution ${z}^{*}=({x}^{*}, {y}^{*}, {\lambda }^{*}, {w}^{*}, {s}^{*})$ of Problem (15), $({x}^{*},{y}^{*})$ is a global optimal solution for Problem (1) and every global optimal solution $({x}^{*}, {y}^{*})$ of Problem (1) is part of an optimal solution ${z}^{*}$ of Problem (15).

3 Two outer-approximation solution approaches

Problem (15) is an MIQCQP in which the single quadratic constraint is convex. Such problem classes can be solved, e.g., directly by modern solvers like Gurobi or CPLEX. On the other hand, Problem (15) belongs to the broader class of convex MINLPs. For such problems, a variety of approaches exist, e.g., nonlinear branch-and-bound or multi- and single-tree methods based on outer approximation, generalized Benders decomposition, and extended cutting-planes; see [7] for a detailed survey of these methods. In this section, we introduce outer-approximation techniques that are tailored for mixed-integer quadratic bilevel problems. The general idea is to relax the convex-quadratic strong-duality inequality (14) of the lower level in Problem (15) to obtain an MIQP. Strong duality is then resolved by iteratively adding linear outer-approximation cuts. In its simplest form, this is a direct application of Kelley’s cutting-planes approach [36], which would add linear outer-approximation cuts until the strong-duality inequality (14) is satisfied up to a certain tolerance. Our preliminary numerical results indicate that this requires an enormous amount of iterations. We thus discuss a more sophisticated multi-tree approach and its single-tree variant in Sects. 3.1 and 3.2.

3.1 A multi-tree outer-approximation approach

The well-known multi-tree outer approximation for convex MINLPs was first proposed in [18] and has been enhanced in [8, 25]. It alternatingly solves a mixed-integer linear master problem and a convex nonlinear problem (NLP) as a subproblem. The master problem is a mixed-integer linear relaxation of the original convex MINLP and is tightened subsequently by adding linear outer-approximation cuts for the convex nonlinearities. The convex nonlinear subproblem results from fixing all integer variables to the solution of the master problem in the original convex MINLP. Under suitable assumptions, every feasible integer solution of the master problem is visited at most once, and the algorithm terminates after a finite number of iterations with the correct solution. The algorithm proposed in this subsection is very much inspired by this scheme. The master problem that we solve in every iteration $p\ge 0$ is given by

where $\bar{c}(\bar{y}^\ell ;y, \lambda , w) \le 0$ is the linear outer-approximation cut that is added to the master problem after every iteration. Thus, in iteration $p$, the master problem ($\text {M}^{p}$) contains $p$ outer-approximation cuts. We shed some more light on $\bar{c}$ later, but first emphasize that Problem ($\text {M}^{p}$) is a convex MIQP. This is in contrast to the standard outer-approximation literature, where the objective function is relaxed and iteratively approximated as well, resulting in a mixed-integer linear master problem. The rationale is that, in our implementation, the main working horse is a state-of-the-art solver like Gurobi or CPLEX. In recent years, these solvers made significant progress in solving convex MIQPs effectively. Thus, we want to exploit these highly evolved solvers as much as possible.

Now, we give some more details on the linear function $\bar{c}$, which is derived using the first-order Taylor approximation of the convex strong-duality inequality (14). For a general convex function h(v), the first-order Taylor approximation at $\bar{v}$ reads

$$\begin{aligned} h(\bar{v}) + \nabla _v h(\bar{v})^\top (v - \bar{v}). \end{aligned}$$

Applied to (14), this gives

$$\begin{aligned} \bar{c}(\bar{y};y,\lambda , w) {{:}{=}}2 \bar{y}^\top G_ly + d_l^\top y - b^\top \lambda + \sum _{j\in I} \sum _{r=1}^{\bar{r}_j} 2^{r-1} w_{jr} - \bar{y} ^\top G_l\bar{y}. \end{aligned}$$

(16)

Since $\hat{{c}}(y,\lambda ,w)$ is linear in $\lambda$ and $w$, the first-order Taylor approximation (16) is parameterized solely by $\bar{y}$. The effectiveness of the proposed outer-approximation approach will depend on the actual selection of $\bar{y}$, but $\bar{c}(\bar{y};y,\lambda , w) \le 0$ is a valid inequality no matter how $\bar{y}$ is obtained. This is shown in the following lemma, in which $\mathcal {M}^p$ denotes the feasible set of ($\text {M}^{p}$).

Lemma 2

For every iteration $p\ge 1$, $\Omega \subseteq \mathcal {M}^p\subseteq \mathcal {M}^{p-1}$ holds.

The consequence of Lemma 2 is that every master problem ($\text {M}^{p}$) is a relaxation of the single-level reformulation (15).

Proof

Let $z=(x,y,\lambda ,w,s) \in \Omega$ be a feasible point of Problem (15). In particular, z fulfills strong duality, i.e., $\hat{{c}}(y,\lambda ,w) = 0$. Obviously, $z \in \mathcal {M}^0$ holds because $\mathcal {M}^0$ corresponds exactly to $\Omega$ without the strong-duality inequality (14). In addition, since $\hat{{c}}$ is convex, its first-order Taylor approximation is a global underestimator at any point $\bar{y}$, i.e.,

$$\begin{aligned} \bar{c}(\bar{y};y,\lambda ,w) \le \hat{{c}}(y,\lambda , w) = 0. \end{aligned}$$

This holds in particular for the choice $\bar{y}=\bar{y}^\ell$ for any $\ell =1,\ldots ,p$ and $p\ge 1$. Hence, $z \in \mathcal {M}^p$. Further, $\mathcal {M}^p\subseteq \mathcal {M}^{p-1}$ follows by construction. $\square$

In the following, we give details on how to select the linearization points $\bar{y}$. We therefore assume that the master problem ($\text {M}^{p}$) is solvable and denote its solution by $z^p=(x^p, y^p, \lambda ^p, w^p, s^p)$. According to Kelley’s cutting plane approach [36], one would add an outer-approximation cut (16) at the solution of the master problem, i.e., one would add the inequality $\bar{c}(y^p;y,\lambda , w) \le 0$. Kelley has shown that this yields a convergent approach. However, in many cases this will turn out to be inefficient, because these cuts are rather weak. The outer-approximation methods in the spirit of [8, 18, 25] additionally solve a convex nonlinear subproblem that results from fixing the integer variables in the original convex MINLP (or an auxiliary feasibility problem if the subproblem is infeasible) to obtain suitable linearization points $\bar{y}$. In our context, the subproblem is given by fixing $x_I=x_I^p$ and $s=s^p$ in the convex MINLP (15), which yields the convex quadratically constrained quadratic problem (QCQP):

We denote the feasible set of ($\text {S}^p$) by $\mathcal {S}^p$ and first assume $\mathcal {S}^p\ne \emptyset$. The infeasible case is discussed afterward. Let $(\bar{x}_R^p, \bar{y}^p, \bar{\lambda }^p, \bar{w}^p)$ be the solution of the subproblem ($\text {S}^p$). For the correctness of our proposed algorithms, we need a technical assumption that is also used in [8, 18, 25].

Assumption 1

For every feasible subproblem ($\text {S}^p$), the Abadie constraint qualification holds at the solution $(\bar{x}_R^p, \bar{y}^p, \bar{\lambda }^p, \bar{w}^p)$, i.e., the tangent cone and the linearized tangent cone coincide at $(\bar{x}_R^p, \bar{y}^p, \bar{\lambda }^p, \bar{w}^p)$.

A formal description of standard cones in nonlinear optimization along with the corresponding theory that is also required in the proof of the following lemma can be found, e.g., in [45]. In theory, Assumption 1 is crucial for the termination of the methods described in this section. An indication that this assumption is not fulfilled in practice is cycling, i.e., a certain integer solution is computed more than once. In our preliminary numerical tests, cycling hardly ever occurred for any of the proposed approaches, such that we disabled an expensive cycling detection (e.g., storing all integer solutions and adding a no-good-cut if an integer solution is computed for the second time) in our computations.

We now show that it is indeed a good idea to linearize the strong-duality inequality (14) at the solution of the subproblem $\bar{y}^p$ instead of at the solutions of the master problem $y^p$.

Lemma 3

Let $z^{p}=(x_I^p,x_R^p, y^p, \lambda ^p, w^p, s^p)$ be an optimal solution of the master problem ($\text {M}^{p}$) and assume that the subproblem ($\text {S}^p$) is feasible and has the optimal solution $(\bar{x}_R^p, \bar{y}^p, \bar{\lambda }^p, \bar{w}^p)$. Suppose further that Assumption 1 holds and consider the new master problem that is obtained by adding the outer-approximation cut $\bar{c}(\bar{y}^{p};y,\lambda , w) \le 0$ to ($\text {M}^{p}$). Then, for any feasible point of the form $z=(x_I^p, x_R, y,\lambda ,w,s^p)$ of this problem the following holds:

$$\begin{aligned} q_u(x_I^{p}, x_R, y) \ge q_u(x_I^p, \bar{x}_R^p, \bar{y}^p). \end{aligned}$$

Proof

We consider $x_I^p$ and $s^p$ fixed and assume that ($\text {S}^p$) is feasible with optimal solution $(\bar{x}_R^p, \bar{y}^{p},\bar{\lambda }^{p}, \bar{w}^p)$. Thus, $(\bar{y}^{p},\bar{\lambda }^{p}, \bar{w}^p)$ fulfills the convex strong-duality inequality (14). Since weak duality holds anyway, we obtain $\hat{{c}}(\bar{y}^p, \bar{\lambda }^p, \bar{w}^p) = 0$. Now, let $z=(x_I^p, x_R, y,\lambda ,w,s^p)$ be feasible for ($\text {M}^{p}$) and let $\bar{c}(\bar{y}^p; y, \lambda , w) \le 0$, i.e., z is feasible for a suitably chosen master problem in iteration $p+ 1$. In the following, we abbreviate the vector $v=(y,\lambda , w)$ for the ease of presentation. Then, we have

$$\begin{aligned} 0 \ge \bar{c}(\bar{y}^p; v) = \hat{{c}}(\bar{v}^p) + \nabla _v \hat{{c}}(\bar{v}^p) (v - \bar{v}^{p}) = \nabla _{v} \hat{{c}}(\bar{v}^{p})^\top (v - \bar{v}^{p}), \end{aligned}$$

i.e., $\nabla _{v} \hat{{c}}(\bar{v}^{p})^\top (v - \bar{v}^{p}) \le 0,$ which means that $(v - \bar{v}^p)$ is in the linearized tangent cone ${T}^{\mathrm {lin}}_{\mathcal {S}^p}(\bar{v}^p)$. Due to Assumption 1, ${T}^{\mathrm {lin}}_{\mathcal {S}^p}(\bar{v}^p)$ equals the tangent cone ${T}_{S^p}(\bar{v}^p)$, which gives $(v - \bar{v}^p) \in {T}_{S^p}(\bar{v}^p)$. For all directions $d \in {T}_{S^p}(\bar{v}^p)$, we know that the property

$$\begin{aligned} \nabla _v q_u(x_I^p, \bar{x}_R^p, \bar{y}^p)^\top d \ge 0 \end{aligned}$$

(17)

holds. Thus, we have

$$\begin{aligned} q_u(x_I^p, x_R, y) \ge q_u(x_I^p, \bar{x}_R^p, \bar{y}^p) + \nabla _v q_u(x_I^p, \bar{x}_R^p, \bar{y}^p)^\top (v - \bar{v}^p) \ge q_u(x_I^p, \bar{x}_R^p, \bar{y}^p). \end{aligned}$$

The first inequality follows because $q_u$ is convex, i.e., its first-order Taylor approximation is a global underestimator. The second inequality follows from Inequality (17). $\square$

In contrast to the slightly different setting in [25], using the solution of the subproblem ($\text {S}^p$) as the linearization point of the outer-approximation inequality (14) does not explicitly cut off the related integer solution $x_I^p$. The reason is our modified master problem, that does not linearize and approximate the convex objective function. Nevertheless, Lemma 3 lets us conclude that every integer assignment $x_I$ that yields a feasible subproblem ($\text {S}^p$) needs to be visited only once, because the objective cannot be improved by visiting such a solution for a second time. This will be one of the key properties to prove finite termination of our algorithm.

We now consider the case of an infeasible subproblem ($\text {S}^p$). In [18], it is argued that in order to eliminate $x_I^p$ from further consideration, an integer no-good-cut must be introduced. In our application, this is a straightforward task. The subproblem ($\text {S}^p$) is fully parameterized by fixed upper-level variables $x_I^p$. For these variables we have a binary expansion available anyway (the variables $s$) so that a simple binary no-good-cut on $s$ can be used. However, such no-good-cuts are known to cause numerical instabilities. As a remedy, in [25], it is proposed to derive cutting planes from an auxiliary feasibility problem that indeed cut off the integer solution $x_I^p$. The feasibility problem minimizes the constraint violations of the infeasible subproblem in some suitable sense, e.g., via the $\ell ^1$- or the $\ell ^\infty$-norm. Recap that $z^p$ is a solution of the master problem ($\text {M}^{p}$). In particular, $(y^p,\lambda ^p)$ is primal-dual feasible for the lower-level problem (3) with fixed $x_I^p$. Thus, the latter problem also has an optimal solution that fulfills strong duality. Since the subproblem ($\text {S}^p$) is infeasible, this optimal solution must be infeasible for the upper-level constraints. On the other hand, $z^p$ must be feasible for the subproblem ($\text {S}^p$) without the strong-duality inequality, because $z^p$ is feasible for Problem ($\text {M}^{p}$). Thus, a simple feasibility problem in the sense of [25] is given by

whose objective value is strictly greater than zero, since otherwise the subproblem ($\text {S}^p$) would be feasible. For a solution of ($\text {F}^p$), we obtain the following lemma by adapting Lemma 1 of [25].

Lemma 4

Let $z^p$ be a solution of the master problem ($\text {M}^{p}$), let the subproblem ($\text {S}^p$) be infeasible, and let $(\bar{x}_R^p, \bar{y}^p, \bar{\lambda }^{p}, \bar{w}^{p})$ be a solution of the feasibility problem ($\text {F}^p$). Then, $\hat{{c}}(\bar{y}^p, \bar{\lambda }^p, \bar{w}^p) > 0$ and every $z=(x_I^p, x_R, y, \lambda , w, s^p) \in \mathcal {M}^p$ is infeasible for the constraint

$$\begin{aligned} \bar{c}(\bar{y}^p; y, \lambda , w) \le 0. \end{aligned}$$

(18)

Proof

Consider a fixed $x_I^p$ and assume ($\text {S}^p$) to be infeasible, which means that ($\text {F}^p$) has an optimal solution $(\bar{x}_R^p, \bar{y}^p, \bar{\lambda }^p, \bar{w}^p)$ with $\hat{{c}}(\bar{y}^p, \bar{\lambda }^p, \bar{w}^p) > 0$. For the ease of presentation, we again use the abbreviation $v=(y,\lambda , w)$ and we rewrite the linear constraint set of ($\text {F}^p$) to obtain

$$\begin{aligned} \min _{x_R, v} \quad \hat{{c}}(v) \quad \mathrm {s.t.}\quad \tilde{A}x_R + \tilde{B} v \le \tilde{b},\ \tilde{D} v = \tilde{d}. \end{aligned}$$

(19)

Problem ($\text {F}^p$), and hence Problem (19), minimizes a convex function over affine-linear constraints. Thus, $(\bar{x}_R^p,\bar{v}^p)$ fulfills the KKT conditions of Problem (19), i.e., primal feasibility, stationarity, non-negativity of multipliers $\alpha$ of inequality constraints, and complementarity. With $\delta$ denoting the multipliers of the equality constraints, the KKT conditions read

$$\begin{aligned} \tilde{A} \bar{x}_R^p+ \tilde{B} \bar{v}^p\le \tilde{b}, \ \tilde{D} \bar{v}^p&= \tilde{d}, \end{aligned}$$

(20a)

$$\begin{aligned} \tilde{A}^\top \alpha&= 0, \end{aligned}$$

(20b)

$$\begin{aligned} - \tilde{B}^\top \alpha - \tilde{D}^\top \delta&= \nabla _{v} \hat{{c}}(\bar{v}^p), \end{aligned}$$

(20c)

$$\begin{aligned} \alpha&\ge 0, \end{aligned}$$

(20d)

$$\begin{aligned} \alpha ^\top \tilde{A} \bar{x}_R^p+ \alpha ^\top \tilde{B} \bar{v}^p&= \alpha ^\top \tilde{b}. \end{aligned}$$

(20e)

We recap that $\bar{c}$ is derived from the first-order Taylor approximation, i.e., it holds

$$\begin{aligned} \bar{c}(\bar{y}^p;v) = \hat{{c}}(\bar{v}^p) + \nabla _v \hat{{c}}{(\bar{v}^p})^\top ( v - \bar{v}^p). \end{aligned}$$

This can be expanded to

$$\begin{aligned} \bar{c}(\bar{y}^p;v)&= \hat{{c}}(\bar{v}^p) - (\tilde{B}^\top \alpha + \tilde{D} ^\top \delta )^\top ( v - \bar{v}^p) \end{aligned}$$

(21a)

$$\begin{aligned}&= \hat{{c}}(\bar{v}^p) - \alpha ^\top \tilde{B}v + \alpha ^\top \tilde{B} \bar{v}^p- \delta ^\top (\tilde{D} v - \tilde{D} \bar{v}^p) \end{aligned}$$

(21b)

$$\begin{aligned}&= \hat{{c}}(\bar{v}^p) - \alpha ^\top ( \tilde{B} v - \tilde{b}) - \delta ^\top (\tilde{D} v - \tilde{d}), \end{aligned}$$

(21c)

by using KKT stationarity (20c) (for (21a)) and re-ordering the terms (for (21b)). Further, we replaced $\alpha ^\top \tilde{B} \bar{v}^p$ by $\alpha ^\top \tilde{b}$ according to (20e) and (20b) and $\tilde{D} \bar{v}^p$ by $\tilde{d}$ according to (20a) to obtain (21c). Now, let $z=(x_I^p, x_R, v, s^p) \in \mathcal {M}^p$. This implies that v must be feasible for ($\text {F}^p$), respectively (19). In particular, we know that $\tilde{B}v - \tilde{b} \le - \tilde{A}x_R$ and $\tilde{D} v - \tilde{d} = 0$. Applying this to (21) and using (20b) yields

$$\begin{aligned} \bar{c}(\bar{y}^p;v) \ge \hat{{c}}(\bar{v}^p) + \alpha ^\top \tilde{A}x_R = \hat{{c}}(\bar{v}^p) > 0. \end{aligned}$$

Thus, v violates (18). $\square$

We recap that, with the last lemma, we can derive cutting planes that cut off $x_I^p$ if the subproblem ($\text {S}^p$) is infeasible. This is another key property for the finite termination of our approach. With this result, we are ready to present the multi-tree outer approximation in Algorithm 1.

In every iteration $p$, Algorithm 1 first solves the master problem ($\text {M}^{p}$) to obtain a solution $z^p$. According to Lemma 2, $\mathcal {M}^p\subseteq \mathcal {M}^{p- 1}$ and we can update the lower bound $\phi$ by $q_u(x_I^p, x_R^p, y^p)$. Next, either the subproblem ($\text {S}^p$) or, in case of infeasibility, the feasibility problem ($\text {F}^p$) is solved. If the subproblem is feasible with solution $(\bar{x}_R^p, \bar{y}^p, \bar{\lambda }^p, \bar{w}^p)$, then the point $(x_I^p, \bar{x}_R^p, \bar{y}^p, \bar{\lambda }^p, \bar{w}^p, s^p)$ is feasible for the convex single-level reformulation (15) and the upper bound is updated if $q_u(x_I^p, \bar{x}_R^p, \bar{y}^p) < \Phi$. In this case, also ${z}^{*}$ is updated. We terminate when $\phi \ge \Phi$ is achieved and return the best solution ${z}^{*}$. We now show the correctness of this approach.

Theorem 1

Algorithm 1 terminates after a finite number of iterations at an optimal solution of Problem (1) or with an indication that the problem is infeasible.

The following proof is adapted from [25].

Proof

First of all, note that all master problems are bounded since P is assumed to be bounded. We next show finiteness of Algorithm 1. If Problem (1) is feasible, then we can follow from Lemma 3 that at most one integer solution is visited twice. Whenever an integer solution is visited for a second time, $\phi \ge \Phi$ holds and the algorithm terminates. On the other hand, if Problem (1) is infeasible, then every subproblem ($\text {S}^p$) is infeasible. According to Lemma 4, the integer solution $x_I^p$ is infeasible for the master problem in iteration $p+ 1$, which results in an infeasible master problem after a finite number of iterations. Thus, finiteness follows from the finite number of integer solutions for Problem (1).

Second, we show that Algorithm 1 always terminates at a solution of Problem (1), if it is feasible. We denote a (possibly non-unique) optimal solution of Problem (1) by $({x}^{*}_I, {x}^{*}_R, {y}^{*})$ with objective function value $q_u^*=q_u({x}^{*}_I, {x}^{*}_R, {y}^{*})$. Now assume that Algorithm 1 terminates with a solution $(x_I^\prime , x_R^\prime , y^\prime , \lambda ^\prime , w^\prime , s^\prime )$ and objective function value $\Phi = q_u(x_I^\prime , x_R^\prime , y^\prime )$. It is obvious that $(x_I^\prime , x_R^\prime , y^\prime , \lambda ^\prime )$ is feasible for the nonconvex single-level reformulation (10). According to Lemma 1, $(x_I^\prime , x_R^\prime , y^\prime )$ is then feasible for the original bilevel problem, which gives $q_u^*\le \Phi = q_u(x_I^\prime , x_R^\prime , y^\prime )$. On the other hand, Lemma 2 together with Lemma 1 state that every master problem ($\text {M}^{p}$) is a relaxation of the original bilevel problem (1), i.e., $\phi \le q_u^*$. Since Algorithm 1 only terminates when $\phi \ge \Phi$, we obtain $q_u({x}^{*}_I, {x}^{*}_R, {y}^{*}) = q_u(x_I^\prime , x_R^\prime , y^\prime )$. $\square$

In the remainder of this subsection we discuss some enhancements of Algorithm 1.

Additional outer-approximation cuts:

Since the outer-approximation cuts of the form of (16) are globally valid, we can add cuts also for points other than the solution of the subproblem. One point that comes for free is the solution $z^p$ of the master problem, i.e., we can add a cut (16) for the point $y^p$. This is an outer-approximation cut in the sense of Kelley [36]. Further, we can add outer-approximation cuts for all feasible solutions that are encountered in the process of solving the master problem.

Early termination of the master problem:

It is sufficient for the correctness of the entire algorithm that the master problem provides a new integer-feasible point. Since the outer-approximation cuts are constructed in a way that already visited integer solutions of the previous iterations have an objective value worse or equal to the incumbent $\Phi$, we can stop the master problem with the first improving integer-feasible solution, i.e., a solution that has an objective value better than the incumbent $\Phi$; see also [25]. This strategy mimics the single-tree approach that is stated in Sect. 3.2.

Warmstarting the master problem:

Warmstarting mixed-integer problems can be a very effective strategy because it may produce a tight initial upper bound and help to keep the branch-and-bound trees small. Since the incumbent solution $z^*$ is feasible for every master problem, it is reasonable to warmstart the master problems with this solution.

The performance of the plain Algorithm 1 as well as the effectiveness of the mentioned enhancements is evaluated in Sect. 4.

3.2 A single-tree outer-approximation approach

The multi-tree outer-approximation approach from Sect. 3.1 can also be cast into a single branch-and-bound tree. In the context of general convex MINLPs, this approach is known as LP/NLP-based branch-and-bound (LP/NLP-BB) and was first introduced in [47]. LP/NLP-BB avoids the time-consuming solution of subsequently updated mixed-integer master problems by branching on the integer variables of an initial master problem and solving continuous relaxations of the subsequently updated master problem at every branch-and-bound node. Whenever such a relaxation results in a new integer solution with a better objective value than the incumbent, the solution process is interrupted. In this event the convex nonlinear subproblem with fixed integer variables is solved and the master problem is updated by an outer-approximation cut derived from the solution of the subproblem. In this view, LP/NLP-BB can be interpreted as a branch-and-cut algorithm that requires the solution of NLPs to separate cuts. For additional implementation details we refer to [1, 8].

If we apply such a single-tree approach to our setup, the initial master problem is given by Problem ($\text {M}^{p}$) for $p=0$, i.e., this corresponds exactly to the initial multi-tree master problem. In this view, the problem that is solved at every branch-and-bound node is the continuous relaxation of Problem ($\text {M}^{p}$) with bounds $\ell ,u \in \mathbb {R}^{|I|}$ on the integer variables, i.e., the QP:

The index $p$ in ($\text {N}^p(l, u)$) corresponds to the number of added strong-duality cuts. The specific values for l and u follow from branching. As opposed to the textbook LP/NLP-BB that solves an LP at every branch-and-bound node, we solve a QP. Thus, we rather perform a QP/NLP-BB.

We now state a tailored single-tree approach for bilevel problems of the form (1) in Algorithm 2.

The rationale is the following. The algorithm subsequently solves QPs of the form ($\text {N}^p(l, u)$), starting with the root-node problem for $p=0$, $l=x^-$, and $u=x^+$. Whenever such a QP is infeasible or its objective function value can not improve the incumbent, then this problem can be removed from the set of open problems $\mathcal {O}$ once and for all. In case the solution of Problem ($\text {N}^p(l, u)$) is integer feasible, then the corresponding subproblem ($\text {S}^p$)—or the feasibility problem ($\text {F}^p$) if the subproblem is infeasible—is solved. One key difference of LP/NLP-BB compared to a standard branch-and-bound is that this solved subproblem must not be pruned but needs to be updated with an appropriate outer-approximation cut. Moreover, all other open problems in $\mathcal {O}$ need to be updated as well. Finally, if Problem ($\text {N}^p(l, u)$) is feasible but the solution is not integer feasible, one branches on a fractional integer variable to obtain two new open problems. Similar to the multi-tree approach, only one integer assignment—the optimal one—is computed twice during the solution process. Finiteness follows again from the finite number of possible integer assignments. At some point all problems in the set $\mathcal {O}$ are infeasible, $\mathcal {O}$ is emptied, and the algorithm terminates. If all subproblems turned out to be infeasible, then ${z}^{*}$ is never updated and the infeasibility of the bilevel problem is correctly detected. All together, we obtain the following correctness theorem.

Theorem 2

Algorithm 2 terminates after a finite number of iterations with an optimal solution of Problem (1) or with an indication that the problem is infeasible.

Since all arguments mainly follow from the proof of Theorem 1, we refrain from a formal proof of Theorem 2. We close this subsection by discussing some possible enhancements of Algorithm 2.

Additional outer-approximation cuts:

Similar to the multi-tree approach, we can enhance Algorithm 2 by adding outer-approximation cuts for all integer-feasible solutions $z^{l,u}$ with $q_u(x^{l,u},y^{l,u}) \ge \Phi$, i.e., integer-feasible solutions that do not fulfill the if-condition in Line 7 in Algorithm 2. This can be done, e.g., by storing these non-improving integer-feasible solutions and adding outer-approximation cuts for these solutions together with the cut that is added in Line 13.

Advanced initialization:

Initializing the single-tree approach with a bilevel-feasible solution may be beneficial for various reasons. First, in the initial master problem ($\text {M}^{p}$) for $p=0$, the constraints for the binary expansion (11) and for the linearization (13) are redundant, because they are not yet coupled by any outer-approximation cut. When the master problem is equipped with an initial outer-approximation cut, however, then all parts of the model are coupled and the solver can effectively presolve the entire model before solving the root-node problem, i.e., ($\text {N}^p(l, u)$) for $p=0$, $l=x^-$, and $u=x^+$. In addition, this initial outer-approximation cut results in a tighter root-node problem.

Second, an initial bilevel-feasible solution can be used to pass an incumbent solution $z^*$ to Algorithm 2 and to compute an initial upper bound $\Phi$. This may allow to prune parts of the search tree right in the beginning. An initial bilevel-feasible point can be obtained, e.g., by finding a feasible or optimal point for Problem ($\text {M}^{p}$) for $p=0$ and solving the corresponding subproblem. This mimics the first iteration of the multi-tree approach.

We evaluate the plain Algorithm 2 and these enhancements in Sect. 4.

3.3 Exploiting the bilevel structure

The two outer-approximation algorithms stated in the previous sections are an application of the approaches in [8, 25] and [47], respectively. The effectiveness of both algorithms will depend, among other aspects, on the following properties:

• (i) The ability to solve the master problem(s) effectively.

• (ii) The number of integer-feasible solutions of the master problem that need to be evaluated.

• (iii) The ability to solve the subproblems effectively.

Aspect (i) is addressed by the various enhancements stated in Sects. 3.1 and  3.2, respectively. For the latter two aspects, we can exploit the specific bilevel structure of Problem (1). We explain this on the example of the multi-tree method in Algorithm 1, but the same explanations hold for the single-tree approach in Algorithm 2 as well.

We first discuss aspect (ii). In general, the number of integer-feasible solutions of the master problem coincides with the number of subproblems that need to be solved. In the worst case, the algorithm needs to consider every integer-feasible solution of the initial master problem. However, for bilevel problems of the form (1), there is hope that one needs to evaluate only a few subproblems. The hypothesis is the following. Both the upper- and the lower-level objective functions are convex-quadratic in y and are to be minimized. This means that explicit min-max problems for which the upper level minimizes a function that the follower maximizes, cannot arise for quadratic bilevel problems of the form (1), unless all matrices $H_u$, $G_u$, and $G_l$ are 0. Thus, the solution of the early master problems (that mainly abstract from lower-level optimality) might already be a good estimate of the optimal lower-level solution, depending on how competitive the two objective functions are. As a consequence, it might be quite likely that the first few solutions of the master problem already contain a close-to-optimal or even optimal integer upper-level decision $x_I$. Hence, the solution of the respective subproblem already provides a very tight upper bound $\Phi$. This is, of course, instance-specific and we discuss this in more detail in Sect. 4.6.

We now turn to aspect (iii). Both Algorithm 1 and Algorithm 2 require the solution of the subproblem ($\text {S}^p$). It is easy to see that the variables $w$ can be eliminated in this convex QCQP. The resulting problem is then equivalent to fixing $x_I=x_I^p$ directly in the original nonconvex MINLP (10). Note that for fixed integer variables, (10) is a convex QCQP as well. While the full subproblem ($\text {S}^p$) is more in line with the standard literature on outer approximation for convex MINLPs and makes it easier to proof correctness, it is better to use Problem (10) with fixed integer variables in the actual implementation for the following reasons. First, Problem (10) is smaller than ($\text {S}^p$). Second, and more importantly, Problem (10) does not contain any big-M. As already discussed in Sect. 2, a wrong big-M can result in terminating with points that are actually bilevel-infeasible or suboptimal. When using Problem (10) as the subproblem, the former case can never appear. This is an huge advantage compared to solving the two single-level reformulations (2) and (15) directly, which may indeed terminate with points that are actually bilevel-infeasible.

Further, we can replace the subproblem ($\text {S}^p$) (respectively Problem (10) with fixed integers) by two easier problems. For the parametric lower-level problem (3), the optimal value function is given by

$$\begin{aligned} q_l^*(x_I)\,\, {{:}{=}}\,\, \min _{y} \, \{ q_l(y):y \in P_l(x_I)\}. \end{aligned}$$

(22)

It is well known that the bilevel problem (1) can be reformulated as an equivalent single-level problem using the optimal value function (22); see, e.g., [13, Chapter 5.6]:

$$\begin{aligned} \min _{x_I, x_R, y} \quad&q_u(x_I, x_R, y) \end{aligned}$$

(23a)

$$\begin{aligned} \mathrm {s.t.}\quad&(x_I, x_R, y) \in P, \end{aligned}$$

(23b)

$$\begin{aligned}&q_l(y) \le q_l^*(x_I). \end{aligned}$$

(23c)

It thus follows directly from Lemma 1 that Problem (15) and Problem (23) are equivalent in the following sense.

Lemma 5

The feasible set of Problem (15) projected on the (x, y)-space coincides with the feasible set of Problem (23). In addition, for every global optimal solution ${z}^{*}=({x}^{*}, {y}^{*}, {\lambda }^{*}, {w}^{*}, {s}^{*})$ of Problem (15), $({x}^{*},{y}^{*})$ is a global optimal solution for Problem (23) and every global optimal solution $({x}^{*}, {y}^{*})$ of Problem (23) can be extended to a global optimal solution ${z}^{*}$ of Problem (15).

This enables to solve the subproblem in a bilevel-specific way as follows.

Remark 1

We can replace Step 9 of Algorithm 1 (or Step 8 of Algorithm 2) by first solving the parametric lower-level problem (3) with fixed integer linking variables $x_I=x_I^p$ to obtain a (possibly ambiguous) lower-level solution $\tilde{y}^p$ and the corresponding objective function value $q_l(\tilde{y}^p) = q_l^*(x_I^p)$. Then, we solve Problem (23) with fixed $x_I=x_I^p$, which is a convex QCQP, to obtain an optimistic bilevel solution $(x_I^p, \bar{x}_R^p, \bar{y}^p)$. In other words, instead of solving subproblem ($\text {S}^p$), we can solve a convex QP and a convex QCQP that is considerably smaller than ($\text {S}^p$).

In case the lower-level problem has a unique solution, Remark 1 can be strengthened.

Remark 2

If the matrix $G_l$ is positive definite, then the lower-level problem has a unique solution and $M(\bar{x}_I)$ is a singleton. In this case we can replace Step 9 of Algorithm 1 (or Step 8 of Algorithm 2) by subsequently solving the parametric lower-level QP (3) with fixed integer upper-level variables $x_I^p$ to obtain the unique lower-level solution $\bar{y}^p$, and solving the upper-level problem

$$\begin{aligned} \min _{x_R} \quad q_u(x_I^p, x_R, \bar{y}^p) \quad \mathrm {s.t.}\quad A\left( \begin{array}{l}x_I^p\\ x_R\end{array}\right) + B\bar{y}^p\ge a, \end{aligned}$$

(24)

in which all integer upper-level variables are fixed to $x_I^p$ and all lower-level variables are fixed to the unique solution $\bar{y}^p$. Problem (24) is a convex QP as well.

With this remark, the large QCQP ($\text {S}^p$) can be replaced by two considerably easier QPs. We discuss the effectiveness of Remarks 1 and 2 in Sect. 4.

4 Computational study

In this section, we provide detailed numerical results for the methods proposed in the previous sections. Besides mean and median running times and counts of solved subproblems, the evaluations and comparisons rely on performance profiles according to [17]. For every test instance i we compute ratios $r_{i,s}= t_{i,s} / \min \{t_{i,s} : s \in S\}$, where S is the set of the solution approaches and $t_{i,s}$ is the running time of a solver s for instance i, given in wall-clock seconds. Each performance profile in this section shows the percentage of instances (y-axis) for which the performance ratio $r_{i,s}$ of approach s is within a factor $\tau \ge 1$ (log-scaled x-axis) of the best possible ratio. Before we go into the details, we provide some information on the computational setup in Sect. 4.1. We then specify the test set that we use throughout the study in Sect. 4.2. We also compare the two benchmark approaches of solving the KKT-based reformulation (2) and the strong-duality-based reformulation (15) in this section. In Sects. 4.3 and 4.4, we evaluate the results for different variants of the multi- and the single-tree approach, respectively. In Sect. 4.5, we compare both methods and also test their performance against the benchmark. Finally, we evaluate the impact of different modifications of the test set on running times in Sect. 4.6.

4.1 Computational setup

We implemented all solution approaches using C++-11 and used GCC 7.3.0 as the compiler. All optimization problems, i.e., all convex (MI)(QC)QP problems, are solved by Gurobi 9.0.1 using its C interface.¹ The single-tree approach of Sect. 3.2 is realized using lazy constraint callbacks of Gurobi that are invoked whenever a new integer-feasible solution with an objective value better than the bilevel incumbent is found. Note however that using Gurobi’s lazy constraint callbacks requires to set the parameter LazyConstraints to 1, which avoids certain reductions and transformations during the presolve that are incompatible with lazy constraints. For all solution approaches we set the NumericFocus parameter to a value of 3, which results in increased numerical accuracy. Further, we tightened Gurobi’s integer feasibility tolerance from its default value $10^{-5}$ to $10^{-9}$ throughout all computations. The rationale is to prevent numerical inaccuracies caused by products of binary variables and big-M values, e.g., in the Constraints (13). All big-M values are fixed to $10^5$. For each solution attempt, we set a time limit of ${3600}{\hbox {s}}$. The computational experiments have been executed on a compute cluster using compute nodes with Xeon E3-1240 v6 CPUs with 4 cores, ${3.7}{\hbox { GHz}}$, and ${32}{\hbox { GB}}$ RAM; see [49] for more details.

4.2 Selection of the test set and evaluation of the benchmarks

Our test set is based on a subset of the MIQP-QP test set used in [38], but is extended by the additional instance classes DENEGRE, INTER-ASSIG, and INTER-KP, which turned out to be too easy for the local optimality considerations in [38]. On the other hand, some of the instance classes used in [38] are too hard to be solved to global optimality, i.e., for most instances of the respective instance class, every tested solver exceeds the time limit. For this reason, we excluded the instance classes GENERALIZED, GK, KP, MIPLIB2010, MIPLIB2017, and OR from our test set. All instances used in this paper are based on MILP-MILP instances from the literature; see the “Ref” column in Table 1 for a reference to the original MILP-MILP test set. The MIQP-QP instances were generated by relaxing all integrality conditions in the lower-level problem and by enforcing continuous linking variables to be integer. Further, we added quadratic terms to both objective functions. To this end, we randomly generated quadratic matrices Q, R, and S of suitable sizes and entries in $[-\root 4 \of {\sigma }, \root 4 \of {\sigma }]$ with $\sigma = \max \{\Vert c_u\Vert _{\infty }, \Vert d_u\Vert _{\infty }\}$ (or $\sigma = \Vert d_l\Vert _{\infty }$). We then set $H_u=Q^\top Q$, $G_u=R^\top R$, and $G_l=S^\top S + D$, where D is a diagonal matrix with entries in $[1, \root 4 \of {\Vert d_l\Vert _{\infty }}]$. This approach renders $H_u$ and $G_u$ positive semidefinite and $G_l$ positive definite.² This allows to evaluate both Remarks 1 and 2 on the full test set. Note that for the sake of completeness, we also provide results for semidefinite matrices $G_l$ in Sect. 4.6. The full test set $\mathcal {I}^\mathrm {full}$ contains 757 instances, which is—to the best of our knowledge—the largest test set of MIQP-QP bilevel problems considered for approaches that compute global optimal solutions of these models. Before we thin out this test set to compare the various methods on a more balanced set, we first compare the two benchmark approaches introduced in Sect. 2 on the full test set $\mathcal {I}^\mathrm {full}$.

We therefore briefly recap the two methods. The first approach (KKT-MIQP) solves a reformulated and linearized single-level problem, in which the lower level is replaced by its KKT conditions. The KKT complementarity conditions are linearized with a big-M formulation. This yields the convex MIQP (2), which can be solved directly using solvers such as Gurobi or CPLEX. This approach is very popular and widely used in applied bilevel optimization. Similarly, using strong duality of the lower level and convexifying the strong-duality inequality yields the convex MIQCQP (15). We call this approach SD-MIQCQP in the following. Instead of applying outer-approximation algorithms to this problem as proposed in Sect. 3, one can also solve this problem directly. Solvers like Gurobi then either apply a linear outer approximation or solve a continuous QCP relaxation at every branch-and-bound node. The exact method can be set via the MIQCPMethod parameter that we left at its default value $-1$. This setting automatically chooses the best strategy. In rare cases (5 instances) this resulted in unsolved node relaxations and thus a suboptimal termination. We count these instances as unsolved by SD-MIQCQP. We also emphasize again, that KKT-MIQP and SD-MIQCQP make use of a big-M value. This may result in bilevel-infeasible “solutions”, which is not the case for the proposed outer-approximation algorithms. Thus, we implemented an ex-post sanity check that computes the relative strong-duality error of the lower level for a given solution $(x,y,\lambda )$:

$$\begin{aligned} \chi (x,y,\lambda )\, {{:}{=}}c(x_I, y, \lambda )/|q_l(y)|. \end{aligned}$$

Whenever the error $\chi (x,y,\lambda )$ exceeds the tolerance of $10^{-4}$, we consider the instance as unsolved for the respective solver. This never occurred for KKT-MIQP but happened in 19 cases for SD-MIQCQP.

Fig. 1

Log-scaled performance profiles for the benchmark approaches KKT-MIQP and SD-MIQCQP on those instances in $\mathcal {I}^\mathrm {full}$ that at least one of the two approaches solves (left) and on those instances in $\mathcal {I}^\mathrm {full}$ that both approaches solve (right)

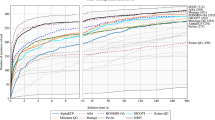
In Fig. 1 (left) we compare the running times of KKT-MIQP and SD-MIQCQP on those 561 instances in $\mathcal {I}^\mathrm {full}$ that at least one of the two benchmark approaches solves. It is obvious that SD-MIQCQP is the better and more reliable approach. It solves around ${95}\%$ of the instances of the subset and is the faster method for most of these instances. In contrast, KKT-MIQP is only capable of solving around ${60}\%$ of the instances. Figure 1 (right) compares the running times of KKT-MIQP and SD-MIQCQP on the subset of 310 instances that both benchmark approaches solve. Also on this subset, SD-MIQCQP is the dominating approach. This is interesting, since the KKT reformulation is the most used approach in applied bilevel optimization. Note that these results are in line with the study in [55], which reveals that a strong-duality-based reformulation outperforms a KKT-based reformulation for mixed-integer linear bilevel problems with integer linking variables and considerably large lower-level problems. Due to this clear dominance, we exclude KKT-MIQP from our further considerations.

We now thin out the test set $\mathcal {I}^\mathrm {full}$ to obtain a more balanced set for the outer-approximation methods that we evaluate in the following and for SD-MIQCQP. We remove 7 instances that exceed the memory limit for all above-mentioned approaches and 1 instance that is proven to be infeasible by all approaches. Further, we exclude 177 instances that are too easy, i.e., that all approaches solve within ${1}{\hbox {s}}$. In addition, we also exclude 149 instances that cannot be solved to global optimality by any of the approaches within the time limit of ${3600}{\hbox {s}}$. The resulting final test set $\mathcal {I}$ contains $|\mathcal {I}|=423$ instances with up to several thousand variables and constraints. Note that we checked that the objective function values and best bounds provided by different approaches are consistent for each instance. This is not guaranteed due to possibly wrong big-M values. All instances in $\mathcal {I}$ passed this ex-post optimality check. More details on the instances in $\mathcal {I}$ can be found in Table 1.

Table 1 Details of the test set $\mathcal {I}$ per instance class

Besides the resulting size of each instance class (“Size”), we also specify the minimum and maximum number of upper-level and lower-level variables (${n_x}, {n_y}$) and constraints (${m_u}, {m_l}$), as well as the minimum and maximum number of linking variables ($|I|$) and of the maximum upper bound of the linking variables ($\max _{i \in I} x_i^+$). The densities of the objective function matrices $H_u$, $G_u$, and $G_l$ of the instances in $\mathcal {I}$ are displayed in Fig. 2.

Fig. 2

Sizes ${n_x}$ resp. ${n_y}$ (x-axis) and densities (y-axis) of the matrices $H_u\in \mathbb {R}^{{n_x}\times {n_x}}$, $G_u\in \mathbb {R}^{{n_y}\times {n_y}}$, and $G_l\in \mathbb {R}^{{n_y}\times {n_y}}$ for the instances in set $\mathcal {I}$

Finally, we mention that we later also analyze the performance of the various methods on the instance set $\mathcal {I}^\text {hard}$ that contains those 149 instances that none of the tested approaches can solve within the time limit.

4.3 Evaluation of the multi-tree approach

We now evaluate the following different parameterizations of the multi-tree approach as described in Sect. 3.1:

MT:

A basic variant without any enhancements, i.e., the plain Algorithm 1.

MT-K:

Like MT but additional Kelley-type cutting planes (“K”) are used.

MT-K-F:

The master problem terminates as soon as a first (“F”) improving integer-feasible solution is found and after every iteration additional Kelley-type cutting planes are added for every non-improving integer-feasible solution found by the master problem.

MT-K-F-W:

Like MT-K-F but every master problem is warmstarted (“W”) using the best available bilevel-feasible solution.

Since $G_l$ is positive definite for the test set $\mathcal {I}$, we use Remark 2 as the default method for solving the subproblem, which dominates the method proposed in Remark 1. Later, we also compare the best setting among these four variants with an equivalent setting that uses the standard subproblem ($\text {S}^p$), i.e., Problem (10) with fixed integer variables; see the discussion in Sect. 3.3. Note that we assess Remark 1 on instances with positive semidefinite matrices $G_l$—an instance class, for which Remark 2 is not applicable—separately in Sect. 4.6.

Figure 3 (left) shows the performance profile of the four variants on the 406 instances in $\mathcal {I}$ that at least one of the four methods can solve.

Fig. 3

Log-scaled performance profiles for different variants of the multi-tree approach that use Remark 2 on the instances in $\mathcal {I}$ that at least one multi-tree approach solves (left) and for the best multi-tree approach that uses Remark 2 compared to when the standard subproblem ($\text {S}^p$) is used on the instances in $\mathcal {I}$ that at least one of the two approaches solves (right)

It turns out that MT-K clearly outperforms MT, which means that adding Kelley-type cutting planes improves the performance. In addition, MT-K-F dominates MT-K in terms of reliability, i.e., it solves more instances. MT-K-F in turn is dominated by MT-K-F-W, which obviously outperforms all other tested variants. In fact, MT-K-F-W is the fastest method for almost ${50}\%$ of the instances. Further, it is the most reliable approach and solves almost every instance that any of the multi-tree approaches solves. Overall, according to Fig. 3 (left), MT-K-F-W is the winner among the four tested variants. It is noteworthy, however, that the performance profiles suggest that the difference in MT-K, MT-K-F, and MT-K-F-W mostly lies in the reliability of the approaches, i.e., in the number of solved instances.

In Fig. 3 (right), we compare the “winner setting” MT-K-F-W with a variant with the same settings than the former approach but that uses the “standard outer-approximation” subproblem ($\text {S}^p$) instead of the bilevel-tailored strategy proposed in Remark 2. We label the latter approach by MT-STD as an abbreviation for MT-K-F-W-STD. Note that the underlying instance set covers those 404 instances in $\mathcal {I}$ that can be solved by at least one of the two methods. The performance profile shows that MT-STD is clearly dominated by MT-K-F-W, which is the faster method for around ${85}\%$ of the instances. This highlights the usefulness of applying Remark 2 to solve the subproblem in a bilevel-tailored way.

Table 2 Running times (in sec), number of solved subproblems, and time spent in the subproblems for all tested multi-tree variants on the subset of instances in $\mathcal {I}$ that every multi-tree approach solves

The conclusions drawn from the performance profiles are underlined by the mean and median running times displayed in Table 2. Note that, in order to have a fair comparison, we used for the computation of the numbers in Table 2 the 339 instances in $\mathcal {I}$ that every multi-tree solver can solve. It can be seen that MT-K, MT-K-F, and MT-K-F-W have considerably shorter mean and median running times than MT. The differences across the former three approaches are however negligible. This supports the conclusion drawn from the performance profiles in Fig. 3 (left): The algorithmic enhancements mainly yield an increased number of solved instances but, on the instances that all approaches can solve, no significant differences can be observed. In fact, MT-K-F-W neither has the shortest mean running time nor the shortest median running time. Table 2 also shows the mean and median number of solved subproblems (or feasibility problems), which corresponds to the number of evaluated integer-feasible solutions (or to the number of iterations minus 1, since per construction, the last iteration computes a specific integer solution for the second time). The table reveals that adding Kelley-type outer-approximation cuts reduces the number of solved subproblems by almost ${75}\%$ in the mean (MT-K vs. MT). On the other hand, terminating the master problem early increases the number of solved subproblems again by almost ${300}\%$ in the mean (MT-K-F vs. MT-K). This is expected and these additional iterations are obviously overcompensated by a reduction in the running time per iteration, i.e., the master problem terminates much faster. Note that the number of solved subproblems is more or less identical for MT-K-F-W and MT-STD. This is expected, since apart from the solution routine for the subproblem, the algorithmic setting is the same for these two approaches. However, the time spent for solving the subproblems drastically increases, if the standard subproblem is used. The mean and median times spent in the subproblems clearly justify the bilevel-tailored solution of the subproblems as proposed in Remark 2.

4.4 Evaluation of the single-tree approach

We now analyze the single-tree approach described in Sect. 3.2 in the following variants:

ST:

A basic variant without any enhancements as stated in Algorithm 2.

ST-K:

Additional Kelley-type cutting planes (“K”) are added for every non-improving integer-feasible solution found.

ST-K-C:

Like ST-K but an initial bilevel-feasible solution is computed (if available) to add an initial outer-approximation cut (“C”).

ST-K-C-S:

Like ST-K-C but the initial bilevel-feasible solution is used to set start values (“S”) for $z^*$ and $\Phi$.

Again, all these variants apply Remark 2 to solve the subproblems. Later, we compare the winner setting to an equivalent setting that uses subproblem ($\text {S}^p$) instead, i.e., Problem (10) with fixed integer variables; see the discussion in Sect. 3.3.

We compare the running times of the four variants using the performance profiles in Fig. 4 (left) on those 409 instances in $\mathcal {I}$ that can be solved by at least one of the four approaches.

Fig. 4

Log-scaled performance profiles for different variants of the single-tree approach that use Remark 2 on the instances in $\mathcal {I}$ that at least one single-tree approach solves (left) and for the best single-tree approach that uses Remark 2 compared to when the standard subproblem ($\text {S}^p$) is used on the instances in $\mathcal {I}$ that at least one of the two approaches solves (right)

The first observation is that the plots for ST and ST-K almost match. This means that additional Kelley-type cutting planes for all non-improving integer-feasible solutions do not make a significant difference, which is in contrast to the results for the multi-tree approach. One explanation might be that the performance boost that is observed in the multi-tree method is mainly due to more effective presolving of the individual master problems when additional cuts are added. This is, of course, not possible in the single-tree approach. On the contrary, adding an initial outer-approximation cut is very beneficial. The methods without this initial cut, ST and ST-K, are clearly dominated by ST-K-C. The latter is in turn slightly dominated by ST-K-C-S, the variant that also sets starting values according to the initial bilevel-feasible solution. ST-K-C-S is the fastest method for around ${50}\%$ of the instances and it solves more instances than any other single-tree variant. Thus, ST-K-C-S is the “winner setting” for the single-tree approach.

In Fig. 4 (right), we compare this winner setting to a variant with the same settings but that uses the “standard outer-approximation” subproblem ($\text {S}^p$). We use the label ST-STD as an abbreviation for ST-K-C-S-STD for this variant. The underlying instance set consists of the 401 instances in $\mathcal {I}$ that can be solved by ST-K-C-S or ST-STD. The performance profile shows that ST-K-C-S is the faster method for around ${80}\%$ of the instances and it also solves more instances than ST-STD. This suggests, that it clearly makes sense to solve the subproblem in a bilevel-tailored way.

Table 3 Running times (in sec), number of solved subproblems, and time spent in the subproblems for all tested single-tree variants on the subset of instances in $\mathcal {I}$ that every single-tree approach solves

The conclusions drawn from the performance profiles in Fig. 4 are also visible in Table 3, which displays statistics on running times and on the number of solved subproblems. The instances underlying the analysis in Table 3 consist of the 359 instances in $\mathcal {I}$ that all single-tree variants (including ST-STD) solve. Note that this renders a comparison of Tables 2 and 3 invalid, because the underlying instance sets are different. Looking at the running times in Table 3, we see that ST-K-C-S has the lowest mean running time, which is almost half of the mean running time of ST. Additionally, the median running times are dominated by ST-K-C-S, which supports the conclusion drawn from Fig. 4 (left): ST-K-C-S is the best parameterization of the single-tree approach. Looking at the number of solved subproblems, it is interesting to see that the additional Kelley-type cutting planes decrease the mean number of solved subproblems significantly, although in terms of running times only a slightly positive effect can be observed (ST-K vs. ST). This may indicate that there is a handful of instances that require to solve many subproblems when no additional Kelley-type cutting planes are added. In contrast, the other two algorithmic enhancements show hardly any effect on the number of solved subproblems (ST-K-C and ST-K-C-S vs. ST-K). Since ST-STD is set up in the same way as ST-K-C-S, it is clear that the mean and median numbers of solved subproblems are similar. However, the time spent for the subproblems significantly increases when ($\text {S}^p$) is used (ST-STD vs. ST-K-C-S), such that ST-STD has significantly longer running times in the mean and median. Again, this justifies the bilevel-tailored solution of the subproblems as proposed in Remark 2.

4.5 Comparison of the multi- and single-tree approaches with the benchmark

We now compare the best parameterizations of the multi- and single-tree approach (MT-K-F-W and ST-K-C-S) with the benchmark approach SD-MIQCQP. Figure 5 (left) shows performance profiles of the running times for those 419 instances that at least one of the three methods solves. Obviously, both outer-approximation approaches dominate the benchmark SD-MIQCQP. They are more reliable and solve around ${95}\%$ of the 419 instances compared to around ${85}\%$ solved by SD-MIQCQP. The outer-approximation methods are also the faster methods. In particular, ST-K-C-S is the fastest approach for more than ${60}\%$ of the instances and is the dominating approach according to the performance profiles.

Fig. 5

Log-scaled performance profile for the winner configurations of the multi-tree and single-tree approaches compared to the benchmark SD-MIQCQP on the instances in $\mathcal {I}$ that at least one of the three methods solves (left) and an ECDF plot of the gaps on the instances in $\mathcal {I}^\text {hard}$ (right)

Table 4 Running times (in sec), number of solved subproblems, and time spent in the subproblems for the best outer-approximation approaches and the benchmark on the subset of instances in $\mathcal {I}$ that all the considered approaches solve

We analyze this in more detail by looking at mean and median running times displayed in Table 4. This table is based on those 338 instances in $\mathcal {I}$ that all three approaches can solve. Restricted to these instances, SD-MIQCQP is a factor of around 1.7 slower compared to MT-K-F-W in the mean, but it is slightly the faster method in the median. However, as seen in Fig. 5 (left), MT-K-F-W is the more reliable method. In contrast, SD-MIQCQP is a factor of more than 2 slower in the mean and almost 2.5 in the median compared to ST-K-C-S—without taking the 55 instances into account that SD-MIQCQP cannot solve within the time limit but that are solved by ST-K-C-S. Compared to MT-K-F-W, the single-tree method is almost 3 times faster in the median, although it needs to solve more subproblems in the mean and median and thus significantly spends more time in the subproblems. The reason for that may simply lie in the nature of the methods: The single-tree approach needs to search only one branch-and-bound tree. Overall, the single-tree approach ST-K-C-S is the winner approach on the test set $\mathcal {I}$. For a more detailed evaluation of the three methods, we provide performance profiles and mean and median running times per instance class as well as tables with running times and gaps per instance in Appendix 1. The figures and tables therein underline the observations discussed in this subsection.

We also evaluate the performance of the three methods on the hard instances $\mathcal {I}^\text {hard}$ that none approach can solve within the time limit. Therefore, we show plots of the empirical cumulative distribution functions (ECDF) of the optimality gaps of each method obtained after the time limit in Fig. 5 (right). The x-axis shows the gap in percent while the y-axis shows the percentage of instances. The figure reveals that after ${3600}{\hbox {s}}$, ST-K-C-S has the smallest optimality gap and is thus the preferable method also on the instances in $\mathcal {I}^\text {hard}$. In addition, the two outer-approximation variants are more robust in the sense that they provide gaps within ${100}\%$ for more instances than SD-MIQCQP does. However, the differences between the three methods are not very pronounced.

The effectiveness of our methods is also underlined in that extent that the charm of solving the MIQCQP (15) directly, i.e., applying SD-MIQCQP, lies, among other things, in the exploitation of the numerical stability of modern solvers. This contains, e.g., an elaborate numerical polishing of the outer-approximation cuts and managing these cuts in cut pools—numerical details that we mostly abstracted from in our implementation. Incorporating such aspects in our implementation would certainly not harm our results, but it can be expected that a more elaborated implementation would lead to an even greater domination of our approaches compared to the benchmark approaches.

4.6 Sensitivity on specific test set properties

Finally, we analyze the performance of the outer-approximation algorithms MT-K-F-W and ST-K-C-S in comparison to the benchmark SD-MIQCQP under three different modifications of the test set $\mathcal {I}$.

First, we adapt the matrix $G_l$ to be positive semidefinite instead of positive definite for every instance in $\mathcal {I}$. We label this adapted test set by $\mathcal {I}^\text {psd}$. Note that with this modification, all instances in $\mathcal {I}^\text {psd}$ may have ambiguous lower-level solutions such that Remark 2 is not applicable anymore. We thus equip the multi- and single-tree approaches with the subproblem routine according to Remark 1 and label these approaches by MT-R1 and ST-R1 as abbreviations for MT-K-F-W-R1 and ST-K-C-S-R1, respectively. Note that MT-STD and ST-STD, i.e., MT-K-F-W and ST-K-C-S equipped with the standard subproblem, as well as the benchmark approach SD-MIQCQP, are also applicable for the instance set $\mathcal {I}^\text {psd}$. We thus compare these five methods on the 417 instances in $\mathcal {I}^\text {psd}$ that at least one of the five methods solves using the performance profiles shown in Fig. 6.

Fig. 6

Log-scaled performance profile for MT-R1, MT-STD, ST-R1, and ST-STD compared to the benchmark SD-MIQCQP on the instances in $\mathcal {I}^\mathrm{{psd}}$ that at least one of the five approaches solves

It can be seen that the single-tree methods are still the dominating ones among the tested approaches, both in terms of running times and also in terms of reliability. Further, the multi-tree approaches still dominate the benchmark SD-MIQCQP. Thus, the outer-approximation methods outperform the benchmark, although not as pronounced as for the standard test set $\mathcal {I}$. The maximum factor $\tau$ is approximately 14 in Fig. 6 compared to 100 in Fig. 5 (left). This can be expected, since the subproblem routines are more expensive compared to approaches that make use of Remark 2. Figure 6 also suggests that using Remark 1 is not beneficial over simply using the standard outer-approximation subproblem. Thus, for instances with ambiguous lower-level solutions, ST-STD is the method of choice. This is underlined by mean and median running times as well as the numbers of solved subproblems that are shown in Table 5.

Table 5 Running times (in sec), number of solved subproblems, and time spent in the subproblems for MT-R1, MT-STD, ST-R1, ST-STD, and the benchmark SD-MIQCQP on the subset of instances in $\mathcal {I}^\mathrm{{psd}}$ that all five approaches solve

The table reveals also another interesting aspect. While the mean and median number of solved subproblems is very comparable for ST-R1 and ST-STD (as well as for MT-R1 vs. MT-STD), the mean and median times spent in the subproblems differ significantly. While the first aspect can be expected due to the same algorithmic setting, the latter aspect is interesting. ST-STD spends more than twice the time of ST-R1 in the subproblems in the mean, but it only spends half of the time of ST-R1 in the subproblem in the median. Thus, there seem to be few instances for which the standard subproblem ($\text {S}^p$) is very challenging, but for the most instances it is much easier to solve than subsequently solving the two problems (3) and (23) as proposed by Remark 1.

Second, we choose the entries of the matrices Q, R, S, and D to be in $[-\root 2 \of {\sigma }, \root 2 \of {\sigma }]$ respectively $[1, \sqrt{\sigma }]$ with $\sigma = \max \{\Vert c_u\Vert _{\infty }, \Vert d_u\Vert _{\infty }\}$ (or $\sigma = \Vert d_l\Vert _{\infty }$) instead of $[-\root 4 \of {\sigma }, \root 4 \of {\sigma }]$. In this setting, the coefficients of the resulting matrices $H_u=Q^\top Q$, $G_u=R^\top R$, and $G_l=S^\top S + D$ have larger absolute values and an analysis of the resulting matrices revealed that also the size of the spectrum, i.e., the range between the smallest and largest eigenvalue, increases compared to the matrices described in Sect. 4.2. We label this modified test set as $\mathcal {I}^\mathrm{{lc}}$ and compare the methods MT-K-F-W, ST-K-C-S, and SD-MIQCQO. Performance profiles of those 400 instances in $\mathcal {I}^\mathrm{{lc}}$ that can be solved by at least one of the three methods is shown in Fig. 7.

Fig. 7

Log-scaled performance profile for MT-K-F-W, ST-K-C-S, and the benchmark SD-MIQCQP on the instances in $\mathcal {I}^\mathrm{{lc}}$ that at least one of the three approaches solves

In comparison to the standard test set $\mathcal {I}$, see Fig. 5, the dominance of the outer-approximation approaches is even more pronounced. The reason for this behavior is that the outer-approximation methods need to solve significantly less subproblems on the test set $\mathcal {I}^\mathrm{{lc}}$; see Table 6.

Table 6 Running times (in sec), number of solved subproblems and time spent in the subproblems for MT-K-F-W, ST-K-C-S, and the benchmark SD-MIQCQP on the subset of instances in $\mathcal {I}^\mathrm{{lc}}$ that all three approaches solve

In fact, for at least half of the instances in $\mathcal {I}^\mathrm{{lc}}$ the outer-approximation methods need to solve only 1 subproblem; see the median numbers of solved subproblems in Table 6. In addition, there is not much difference between the multi- and the single-tree method; see Fig. 7 and the mean and median running times in Table 6. One possible explanation follows the discussion in Sect. 3.3. For many instances, the linear parts in the upper- and lower-level objective functions model a min-max structure. This structure cannot be “purely” present in our quadratic setting. Thus, choosing larger coefficients in the quadratic parts reduces the min-max structure and the two objective functions are more aligned, such that the first or second integer solution $x_I$ of the master problem already yields the bilevel optimal solution. Overall, the properties of the involved matrices of the quadratic terms seem to have a significant impact on the effectiveness of the outer approximation algorithms.

Third, we highlight that for almost all instance classes in $\mathcal {I}$, the linking variables are binary. The reason is that most of these instances originate from MILP-MILP interdiction instances, in which the integer variables are binary by nature. In addition, for many instances in XUWANG and XULARGE that have lower and upper bounds of 0 and 10, the implied bounds are in fact 0 and 1, because the right-hand side values of these randomly generated instances limit the feasible region of the linking variables. In [54] it is pointed out that enlarging the feasible set of the original MILP-MILP instances by changing the right-hand side vectors renders the instances very hard to solve. We observed the same pattern for the MIQP-QP variants in a preliminary numerical test. In our notation, all entries in A, B, a, C, D, and b are non-positive. Decreasing the right-hand side vectors renders most of the instances too hard to be solved by any of the proposed outer-approximation or benchmark methods. On the one hand, this underlines the general hardness of MIQP-QP bilevel problems with general integer (i.e., not binary) linking variables. On the other hand, the instances XUWANG and XULARGE are randomly generated and it is not clear whether these observations generalize to “real-world” bilevel instances.

5 Conclusion

In this paper, we considered bilevel problems with a convex-quadratic mixed-integer upper level and a convex-quadratic lower level. Further, all linking variables are assumed to be bounded integers. For such problems, we proposed an equivalent transformation to a single-level convex MINLP and developed a multi- and a single-tree outer-approximation algorithm that we derived from algorithms for general convex MINLPs. We further proposed enhancements of these algorithms that exploit the bilevel-specific structure of the problem. Finally, we proved the correctness of the methods and carried out an extensive numerical study.

The study revealed that the two proposed outer-approximation algorithms outperform known benchmark approaches. For bilevel problems with unique lower-level solutions, the proposed bilevel-tailored solution of the subproblem turned out to be very effective. Even for instances with ambiguous lower-level problems, the novel algorithms perform better than the benchmark approaches. In general, the single-tree outer approximation implementation performs better than the multi-tree counterpart and is, in our opinion, the preferred method.

For both methods several questions remain open. Following the discussion in Sect. 4.6, the impact of the objective function matrices and their spectra as well as the performance on instances with non-binary linking variables needs further assessment. Up to know, this is however not possible due to a lack of bilevel instances with such properties. An interesting direction for future research can be to drop the integrality condition on the linking variables. This would require, e.g., spatial branching on linking variables but may also introduce some pitfalls like unattainable bilevel solutions; see [43]. Another question is whether one can introduce integer variables to the lower level, i.e., considering MIQP-MIQP bilevel problems. Certainly, the strong-duality-based reformulation for convex lower-level problems would not be applicable anymore, but one could use a more general single-level reformulation like the value-function reformulation, as it is done, e.g., for MILP-MILP bilevel problems in [21].

Appendix A: Detailed results

In this section, we provide more detailed results for the benchmark approach SD-MIQCQP as well as for MT-K-F-W and ST-K-C-S. For each instance class specified in Table 1, we provide

• (i) performance profiles for all instances of the class that can be solved by at least one of the three methods;

• (ii) a table with mean and median running times and number of solved subproblems for all instances of the class that could be solved by all three approaches;

• (iii) a table with the exit status, gap, and running time of each solver for each instance of the class.

In the latter tables, a status “optimal” means that the instance has been solved to global optimality, “time limit” specifies that the time limit has been reached, “suboptimal” indicates a suboptimal termination due to unsolved node relaxations, and “numerics” denotes numerical issues detected in an ex-post feasibility check. Note that the last status is only relevant for SD-MIQCQP. For each instance, we mark the best running time using bold font.

1.1 Results for CLIQUE

Figure 8, Tables 7 and 8 show the results for the instance class CLIQUE.

Fig. 8

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class CLIQUE that can be solved by at least one approach

Table 7 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class CLIQUE that can be solved by every approach

Table 8 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class CLIQUE

1.2 Results for DENEGRE

Figure 9, Tables 9 and  10 show the results for the instance class DENEGRE.

Fig. 9

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class DENEGRE that can be solved by at least one approach

Table 9 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class DENEGRE that can be solved by every approach

Table 10 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class DENEGRE

1.3 Results for IMKP

Figure 10, Tables 11 and  12 show the results for the instance class IMKP.

Fig. 10

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class IMKP that can be solved by at least one approach

Table 11 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class IMKP that can be solved by every approach

Table 12 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class IMKP

1.4 Results for INT0SUM

Figure 11, Tables 13 and  14 show the results for the instance class INT0SUM.

Fig. 11

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class INT0SUM that can be solved by at least one approach

Table 13 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class INT0SUM that can be solved by every approach

Table 14 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class INT0SUM

1.5 Results for INTER-ASSIG

Figure 12, Tables 15 and 16 show the results for the instance class INTER-ASSIG.

Fig. 12

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class INTER-ASSIG that can be solved by at least one approach

Table 15 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class INTER-ASSIG that can be solved by every approach

Table 16 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class INTER-ASSIG

1.6 Results for INTER-CLIQUE

Figure 13, Tables 17 and 18 show the results for the instance class INTER-CLIQUE.

Fig. 13

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class INTER-CLIQUE that can be solved by at least one approach

Table 17 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class INTER-CLIQUE that can be solved by every approach

Table 18 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class INTER-CLIQUE

1.7 Results for INTER-FIRE

Figure 14, Tables 19 and 20 show the results for the instance class INTER-FIRE.

Fig. 14

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class INTER-FIRE that can be solved by at least one approach

Table 19 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class INTER-FIRE that can be solved by every approach

Table 20 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class INTER-FIRE

1.8 Results for INTER-KP

Figure 15, Tables 21 and 22 show the results for the instance class INTER-KP.

Fig. 15

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class INTER-KP that can be solved by at least one approach

Table 21 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class INTER-KP that can be solved by every approach

Table 22 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class INTER-KP

1.9 Results for MIPLIB

Figure 16, Tables 23 and 24 show the results for the instance class MIPLIB.

Fig. 16

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class MIPLIB that can be solved by at least one approach

Table 23 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class MIPLIB that can be solved by every approach

Table 24 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class MIPLIB

1.10 Results for XULARGE

Figure 17, Tables 25 and 26 show the results for the instance class XULARGE.

Fig. 17

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class XULARGE that can be solved by at least one approach

Table 25 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class XULARGE that can be solved by every approach

Table 26 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class XULARGE

1.11 Results for XUWANG

Figure 18, Tables 27 and 28 show the results for the instance class XUWANG.

Fig. 18

Log-scaled performance profile for the instances in $\mathcal {I}$ belonging to the class XUWANG that can be solved by at least one approach

Table 27 Running times (in sec), number of solved subproblems and time spent in the subproblems (in sec) for the instances in $\mathcal {I}$ belonging to the class XUWANG that can be solved by every approach

Table 28 Exit status, gap, and running time for every instance in $\mathcal {I}$ belonging to the class XUWANG