Abstract
We consider gradient fields on \({\mathbb {Z}}^d\) for potentials V that can be expressed as
This representation allows us to associate a random conductance type model to the gradient fields with zero tilt. We investigate this random conductance model and prove correlation inequalities, duality properties, and uniqueness of the Gibbs measure in certain regimes. We then show that there is a close relation between Gibbs measures of the random conductance model and gradient Gibbs measures with zero tilt for the potential V. Based on these results we can give a new proof for the non-uniqueness of ergodic zero-tilt gradient Gibbs measures in dimension 2. In contrast to the first proof of this result we rely on planar duality and do not use reflection positivity. Moreover, we show uniqueness of ergodic zero tilt gradient Gibbs measures for almost all values of p and q and, in dimension \(d\ge 4\), for q close to one or for \(p(1-p)\) sufficiently small.
Similar content being viewed by others
1 Introduction
Gradient fields are a statistical mechanics model that can be used to model phase separation or, in the case of vector valued fields, solid materials. Formally they can be defined as a random field \((\varphi _x)_{x\in {\mathbb {Z}}^d}\in {\mathbb {R}}^{{\mathbb {Z}}^d}\) with distribution
Here \(\mathrm {d}\varphi (x)\) denotes the Lebesgue measure, \(V:{\mathbb {R}}\rightarrow {\mathbb {R}}\) a measurable symmetric potential, and \(x\sim y\) indicates the sum over unordered pairs of neighbouring sites of \({\mathbb {Z}}^d\). We can give a meaning to the formal expression (1.1) using the DLR-formalism. The DLR-formalism defines equilibrium distributions usually called Gibbs measure for this type of models as measures \(\mu \) on \({\mathbb {R}}^{{\mathbb {Z}}^d}\) such that the conditional probability of the restriction to any finite set is as above. In the setting of gradient interface models in general no Gibbs measure exists in dimension \(d\le 2\) [33]. Therefore one often considers gradient Gibbs measures [20]. This means that attention is restricted to the \(\sigma \)-algebra generated by the gradient fields
Then infinite volume measures exist if V(s) grows sufficiently fast (linearly is sufficient) as \(s\rightarrow \pm \infty \). Gradient Gibbs measures are also useful to model tilted surfaces. For a translation invariant gradient Gibbs measure \(\mu \) the tilt vector \(u\in {\mathbb {R}}^d\) is defined by
where \(\nabla \varphi (x)\in {\mathbb {R}}^d\) denotes the discrete derivative, i.e., the vector with entries \(\nabla _i\varphi (x)=\varphi (x+e_i)-\varphi (x)\) with \(e_i\) denoting the ith standard unit vector. If the gradient Gibbs measure is ergodic the tilt corresponds to the asymptotic average inclination of almost every realisation of the gradient field.
Gradient interface models have been studied frequently in the past years. In particular the discrete Gaussian free field with \(V(s)=s^2\) where the fields are Gaussian caught considerable attention. Many of the results obtained in this case were generalized to the class of strictly convex potentials satisfying \(c_1\le V''(s)\le c_2\) for some \(0<c_1<c_2\) and all \(s\in {\mathbb {R}}\). Let us only mention two results for convex potentials and refer to the literature in particular the reviews [19, 30] for all further results and references. Funaki and Spohn showed in [20] that for every tilt vector u there exists a unique translation invariant gradient Gibbs measure. Moreover, the scaling limit of the model is a massless Gaussian field as shown by Naddaf and Spencer [28] for zero tilt and generalised to arbitrary tilt by Giacomin et al. [22]. In contrast for non-convex potentials far less is known because all the techniques seem to rely on convexity in an essential way. For potentials of the form \(V=U+g\) where U is strictly convex and \(g''\in L^q\) for some \(q\ge 1\) with sufficiently small norm the problem can be led back to the convex theory by integrating out some degrees of freedom. This way many results from the convex case can be proved in particular uniqueness and existence of the Gibbs measure for every tilt and that the scaling limit is Gaussian [11, 12, 15]. This setting corresponds to the high temperature phase. For low temperatures which correspond to non-convexities far away from the minimum of V it was shown that the surface tension is strictly convex and the scaling limit is Gaussian [1, 2, 24].
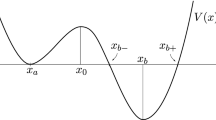
For intermediate temperatures where the potentials can be very non-convex no robust techniques are known. All results to date are restricted to the special class of potentials introduced by Biskup and Kotecky in [6] that can be represented as
where \(\rho \) is a non-negative Borel measure on the positive real line. Biskup and Kotecky mostly considered the simplest nontrivial case, denoting the Dirac measure at \(x\in {\mathbb {R}}\) by \(\delta _x\),
where \(p\in [0,1]\) and \(q\ge 1\). They show that in dimension \(d=2\) and for \(q>1\) sufficiently large there exist two ergodic zero-tilt gradient Gibbs measures. Later, Biskup and Spohn showed in [7] that nevertheless the scaling limit of every zero-tilt gradient Gibbs measure is Gaussian if the measure \(\rho \) is compactly supported in \((0,\infty )\). In [34] their result was recently extended by Ye to potentials of the form \(V(s)=(1+s^2)^\alpha \) with \(0<\alpha <\frac{1}{2}\) which can be written as in (1.4) for some \(\rho \) with unbounded support.
Our main results concern the phase diagram at zero tilt for this class of potentials. Although our techniques would apply to general \(\rho \) we restrict our attention to the simplest case where \(\rho \) is as in (1.5) and the potential can be written as
For this class of potentials we show uniqueness of the ergodic zero tilt gradient Gibbs measures for almost all p and q and, in dimension \(d\ge 4\) for \(p(1-p)\) or \(q-1\) small. Moreover, we give a new proof for the result that for large q there exists a p such that there are two distinct ergodic gradient Gibbs measures without the use of reflection positivity. For a detailed statement of our main results we refer to Sect. 2. Note that one major drawback is the restriction to zero tilt that applies here and to all earlier results for this model.
The main reason to study this class of potentials is that they are much more tractable because the variable \(\kappa \) can be considered as an additional degree of freedom using the representation (1.4). This leads to extended gradient Gibbs measures which are given by the joint law of \((\eta _{e},\kappa _{e})_{e\in {\mathbf {E}}({\mathbb {Z}}^d)}\). These extended gradient Gibbs measures can be represented as a mixture of non-homogeneous Gaussian fields with bond potential \(\kappa _{e}\eta ^2/2\) for every edge \(e\in {\mathbf {E}}({\mathbb {Z}}^d)\) and \(\kappa _{e}\in {\mathbb {R}}_+\). This implies that for a given \(\kappa \) the distribution of the random field is Gaussian with covariance given by the inverse of the operator \(\Delta _\kappa \) where
In all the works mentioned before this structure is frequently used, e.g. in [7] it is proved that the resulting \(\kappa \)-marginal of the extended gradient Gibbs measure is ergodic so that well known homogenization results for random walks in ergodic environments can be applied.
The main purpose of this note is to investigate the properties of the \(\kappa \)-marginal of extended gradient Gibbs measures in a bit more detail. The starting point is the observation that the \(\kappa \)-marginal of an extended gradient Gibbs measures with zero tilt is itself a Gibbs measure for a specification of a certain random conductance model. Moreover, the ergodic Gibbs measures of the random conductance model are in a one to one relation with the ergodic gradient Gibbs measures with zero tilt. In particular, we can lift results about the (simpler) random conductance model to results about gradient Gibbs measures. Let us mention that massive \({\mathbb {R}}\)-valued random fields have been earlier connected to discrete percolation models to analyse the existence of phase transitions [35]. For gradient models the setting is slightly different because we consider a random conductance model on the bonds with long ranged correlations while for massive models one typically considers some type of site percolation with quickly decaying correlations.
The random conductance model is simpler than the corresponding gradient interface model in at least three aspects. Firstly, it has a compact single spin state space which is actually just \(\{1,q\}\) in our main case of interest. Secondly, it satisfies strong correlation inequalities in particular the FKG-inequality while there are no such results for gradient interface models with non-convex interactions. The proofs of the correlation inequalities are further simplified by the observation that the random conductance model is closely related to determinantal processes and they then follow immediately from similar results for the weighted spanning tree. Finally, duality takes a much clearer form for the random conductance model. It was already observed in [6] that in dimension \(d=2\) the gradient interface model with potential \(V_{p,q}\) exhibits a duality property when defined on the torus. Moreover, there is a self dual point \(p_{\mathrm {sd}}=p_{\mathrm {sd}}(q)\in (0,1)\) satisfying the equation
where the model agrees with its own dual and two Gibbs measures exist for large q. For the random conductance model duality can be stated for arbitrary planar graphs and similarly to the coexistence proof for the Ising model this duality can be used to show the existence of two distinct Gibbs measures at \(p_{\mathrm {sd}}\). We remark that many of our techniques and results for the random conductance model originated in the study of the Potts model and the random cluster model and we conjecture further similarities. To avoid confusion between the terms random cluster model and random conductance model we will use the term FK random cluster model in the following.
This paper is structured as follows. In Sect. 2 we give a precise definition of gradient Gibbs measures and state our main results. Then, in Sect. 3 we introduce and motivate the random conductance model and its relation to extended gradient Gibbs measures. We prove properties of the random conductance model in Sects. 4 and 5. Finally, in Sect. 6 we use the duality of the model to reprove the phase transition result. Two technical proofs and some results about regularity properties of discrete elliptic equations are delegated to appendices.
2 Model and main results
2.1 Specifications
Let us briefly recall the definition of a specification because the concept will be needed in full generality for the random conductance model (see Sect. 4). We consider a countable set S (mostly \({\mathbb {Z}}^d\) or the edges of \({\mathbb {Z}}^d\)) and a measurable state space \((F,{{\mathcal {F}}})\) (mostly either \(|F|=2\) or \((F,{{\mathcal {F}}})= ({\mathbb {R}},{\mathcal {B}}({\mathbb {R}}))\)). Random fields are probability measures on \((F^S,{{\mathcal {F}}}^S)\) where \({{\mathcal {F}}}^S\) denotes the product \(\sigma \)-algebra. The set of probability measures on a measurable space \((X,{\mathcal {X}})\) will be denoted by \({\mathcal {P}}(X,{\mathcal {X}})\). For any \(\Lambda \subset S\) we denote by \(\pi _\Lambda :F^S\rightarrow F^\Lambda \) the canonical projection. We often consider the \(\sigma \)-algebra \({{\mathcal {F}}}_\Lambda =\pi _\Lambda ^{-1}({{\mathcal {F}}}^\Lambda )\) of events depending on the set \(\Lambda \). Recall that a probability kernel \(\gamma \) from \((X,{\mathcal {B}})\) to \((X,{\mathcal {X}})\), where \({\mathcal {B}}\subset {\mathcal {X}}\) is a sub-\(\sigma \)-algebra, is called proper if \(\gamma (B,\cdot )={\mathbb {1}}_B\) for \(B\in {\mathcal {B}}\).
Definition 2.1
A specification is a family of proper probability kernels \(\gamma _\Lambda \) from \({{\mathcal {F}}}_{\Lambda ^\mathrm {c}}\) to \({{\mathcal {F}}}_{S}\) indexed by finite subsets \(\Lambda \subset S\) such that \(\gamma _{\Lambda _1}\gamma _{\Lambda _2} =\gamma _{\Lambda _1}\) if \(\Lambda _2\subset \Lambda _1\). We define the set of Gibbs measures for the specification \(\gamma \) by
We call measures in \({\mathcal {G}}(\gamma )\) specified by \(\gamma \)
Remark 2.2
There is a well known equivalent definition of Gibbs measures. A cofinal set I is a subset of subsets of S with the property that for any finite set \(\Lambda _0\subset S\) there is \(\Lambda \in I\) such that \(\Lambda _0\subset \Lambda \). Then \(\mu \in {\mathcal {G}}(\gamma )\) if and only if \(\mu \gamma _{\Lambda }=\mu \) for \(\Lambda \in I\) where I is a cofinal subset of subsets of S. See Remark 1.24 in [21] for a proof.
2.2 Gradient Gibbs measures
We introduce the relevant notation and the definition of Gibbs and gradient Gibbs measures to state our results. For a broader discussion see [21, 30]. In this paragraph we consider real valued random fields indexed by a lattice \(\Lambda \subset {\mathbb {Z}}^d\). We will denote the set of nearest neighbour bonds of \({\mathbb {Z}}^d\) by \({\mathbf {E}}({\mathbb {Z}}^d)\). More generally, we will write \({\mathbf {E}}(G)\) and \({\mathbf {V}}(G)\) for the edges and vertices of a graph G. To consider gradient fields it is useful to choose on orientation of the edges. We orient the edges \(e=\{x,y\}\in {\mathbf {E}}({\mathbb {Z}}^d)\) from x to y iff \(x\le y\) (coordinate-wise), i.e., we can view the graph \(({\mathbb {Z}}^d,{\mathbf {E}}({\mathbb {Z}}^d))\) as a directed graph but mostly we work with the undirected graph.
To any random field \(\varphi :{\mathbb {Z}}^d\rightarrow {\mathbb {R}}\) we associate the gradient field \(\eta =\nabla \varphi \in {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) given by \(\eta _{e}=\varphi _y-\varphi _x\) if \(\{x,y\}\in {\mathbf {E}}({\mathbb {Z}}^d)\) are nearest neighbours and \(x\le y\). We formally write \(\eta _{x,y}=\eta _e=\varphi _y-\varphi _x\) and \(\eta _{y,x}=-\eta _e=\varphi _x-\varphi _y\). The gradient field \(\eta \) satisfies the plaquette condition
for every plaquette, i.e., nearest neighbours path \(x_1,x_2,x_3,x_4,x_1\). Vice versa, given a field \(\eta \in {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) that satisfies the plaquette condition there is a up to constant shifts a unique field \(\varphi \) such that \(\eta =\nabla \varphi \) (the antisymmetry of the gradient field is contained in our definition). We will refer to those fields as gradient fields and denote them by \({\mathfrak {X}}\subset {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}\). To simplify the notation we write \(\varphi _\Lambda \) for \(\Lambda \subset {\mathbb {Z}}^d\) and \(\eta _{E}\) for \(E\subset {\mathbf {E}}({\mathbb {Z}}^d)\) for the restriction of fields and gradient fields. We usually identify a subset \(\Lambda \subset {\mathbb {Z}}^d\) with the graph generated by it and as before we write \({\mathbf {E}}(\Lambda )\) for the bonds with both endpoints in \(\Lambda \).
For a subgraph \(H\subset G\) we write \(\partial H\) for the (inner) boundary of H consisting of all points \(x\in {\mathbf {V}}(H)\) such that there is an edge \(e=\{x,y\}\in {\mathbf {E}}(G){\setminus } {\mathbf {E}}(H)\). In the case of a graph generated by \(\Lambda \subset G\) we have \(x\in \partial \Lambda \) if there is \(y\in \Lambda ^{\mathrm {c}}\) such that \(\{x,y\}\in {\mathbf {E}}(G)\). We define \(\Lambda ^\circ =\Lambda {\setminus } \partial \Lambda \). For a finite subset \(\Lambda \subset {\mathbb {Z}}^d\) we denote by \(\mathrm {d}\varphi _\Lambda \) the Lebesgue measure on \({\mathbb {R}}^\Lambda \).
We define for \(\omega \in {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}_{g} \) and \(\Lambda \) finite and simply connected (i.e., \(\Lambda ^\mathrm {c}\) connected) the following a priori measure on gradient configurations
where \({\tilde{\varphi }}\) is a configuration such that \(\nabla {\tilde{\varphi }}=\omega \) and \(\nabla _*\) the push-forward of this measure along the gradient map \(\nabla :{\mathbb {R}}^{{\mathbb {Z}}^d}\rightarrow {\mathfrak {X}}\). The shift invariance of the Lebesgue measure implies that this definition is independent of the choice of \({\tilde{\varphi }}\) and it only depends on the restriction \(\omega _{{\mathbf {E}}(\Lambda )^{\mathrm {c}}}\) since \(\Lambda ^\mathrm {c}\) is connected. For a potential \(V:{\mathbb {R}}\rightarrow {\mathbb {R}}\) satisfying some growth condition we define the specification \(\gamma _\Lambda \)
where the constant \(Z_\Lambda (\omega _{{\mathbf {E}}(\Lambda )^{\mathrm {c}}})\) ensures the normalization of the measure. We introduce the notation \({\mathcal {E}}_{E}=\pi _E^{-1}(\mathcal {B}({\mathbb {R}})^E)\) for \(E\subset {\mathbf {E}}({\mathbb {Z}}^d)\) for the \(\sigma \)-algebra of events depending only on E. In accordance with Definition 2.1 measures that are specified by the specification \(\gamma \), i.e., measures \(\mu \) that satisfy for simply connected \(\Lambda \subset {\mathbb {Z}}^d\)
will be called gradient Gibbs measures for the potential V.
For \(a\in {\mathbb {Z}}^d\) we define the shifts \(\tau _a:{\mathbb {Z}}^d\rightarrow {\mathbb {Z}}^d\) and \(\tau _a:{\mathbf {E}}({\mathbb {Z}}^d)\rightarrow {\mathbf {E}}({\mathbb {Z}}^d)\) (always using the same symbol \(\tau _a\) for shifts) by
We also consider the extension \(\tau _a:{\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}\rightarrow {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) to gradient fields which is defined by
A measure is translation invariant if \(\mu (\tau _a^{-1}(A))=\mu (A)\) for all a and \(A\in {\mathcal {B}}({\mathbb {R}})^{{\mathbf {E}}({\mathbb {Z}}^d)}\). An event is translation invariant if \(\tau _a(A)=A\) for all \(a\in {\mathbb {Z}}^d\). A gradient measure is ergodic if \(\mu (A)\in \{0,1\}\) for all translation invariant A.
2.3 Main results
Our main results concern the uniqueness and non-uniqueness of gradient Gibbs measures with zero tilt for potentials as in (1.6). Our first main result shows that the shift invariant gradient Gibbs measures are unique for almost all values of p and q.
Theorem 2.3
For every q and \(d\ge 2\) there is an at most countable set \(N(q,d)\subset [0,1]\) such that for any \(p\in [0,1]{\setminus } N(q,d)\) there is a unique shift invariant ergodic gradient Gibbs measure \(\mu \) with zero tilt for the potential \(V_{p,q}\).
This theorem is proved in Sect. 5 below the proof of Theorem 5.1. Moreover, we reprove the non-uniqueness result originally shown in [6] for this type of potential.
Theorem 2.4
There is \(q_0\ge 1\) such that for \(d=2\), \(q\ge q_0\), and \(p=p_{\mathrm {sd}}(q)\) the solution of (1.8), there are at least two shift invariant gradient Gibbs measures with 0 tilt.
The proof of this theorem is given at the end of Sect. 6. Moreover we prove uniqueness for ’high temperatures’ and dimension \(d\ge 4\). This corresponds to the regime where the Dobrushin condition holds.
Theorem 2.5
Let \(d\ge 4\). For any \(q\ge 1\) there exists \(p_0=p_0(q,d)>0\) such that for all \(p\in [0,p_0)\cup (1-p_0,1]\) there is a unique shift invariant ergodic gradient Gibbs measure with zero tilt for the potential \(V_{p,q}\). Moreover, there exists \(q_0=q_0(d)>1\) such that for any \(q\in [1,q_0]\) and any \(p\in [0,1]\) there is a unique shift invariant ergodic gradient Gibbs measure with zero tilt for the potential \(V_{p,q}\).
The proof of this Theorem is given in Sect. 5 below the proof of Theorem 5.6.
The main tool in the proofs of these theorems is the fact that the structure of the potentials V in (1.4) allows us to consider \(\kappa \) as a further degree of freedom and we consider the joint distribution of the gradient field \(\eta \) and \(\kappa \). We show that the law of the \(\kappa \)-marginal can be related to a random conductance model. The analysis of this model then translates back into the theorems stated before. We will make those statements precise in the next section. Let us end this section with some remarks.
Remark 2.6
-
1.
For spin systems with finite state space and bounded interactions there are general results that show that phase transitions, i.e., non-uniqueness of the Gibbs measure are rare, see, e.g., [21]. Theorem 2.3 establishes a similar result for a specific class of potentials for a unbounded spin space where no general results are known. As discussed in more detail at the end of Sect. 5 we expect that for every \(q\ge 1\) the Gibbs measure is unique for all \(p\in [0,1]\) except possibly for \(p=p_c\) for some critical value \(p_c=p_c(q)\). Hence, Theorem 2.3 is far from optimal but we hope that the results provided in this paper prove useful to establish stronger results.
-
2.
Let us compare the results to earlier results in the literature. For \(p/(1-p)<1/q\) the potential \(V_{p,q}\) is strictly convex so that uniqueness of the translation invariant, ergodic Gibbs measures is well known and holds for every tilt. The two step integration used by Cotar and Deuschel extends the uniqueness result to the regime \(p/(1-p)<C/\sqrt{q}\) (see Section 3.2 in [11]). In particular the case \(p\in [0,p_0)\) in Theorem 2.5 is included in earlier results. However, the potential becomes very non-convex (has a very negative second derivative at some points) for p close to 1 and the uniqueness result for \(p\in (1-p_0,1]\) and \(d\ge 4\) appears to be new. In this regime the only known result seems to be convexity of the surface tension as a function of the tilt which was shown in [2] (see in particular Proposition 2.4 there). Their results apply to p very close to one, \(q-1\) very small, and \(d\le 3\). The results in [1] remove the restrictions on q and d.
-
3.
The restriction to dimension \(d\ge 4\) arises from the fact that the Green function for inhomogeneous elliptic operators in divergence form decays slower than in the homogeneous case.
3 Extended gradient Gibbs measures and random conductance model
3.1 Extended gradient Gibbs measure
In this work we restrict to potentials of the form introduced in (1.4). As already discussed in more detail in [6, 7] it is possible to use the special structure of V to raise \(\kappa \) to a degree of freedom. Let \(\mu \) be a gradient Gibbs measure for V. For a finite set \(E\subset {\mathbf {E}}({\mathbb {Z}}^d)\) and Borel sets \({\mathbf {A}}\subset {\mathbb {R}}^E\) and \({\mathbf {B}}\subset {\mathbb {R}}_+^E\) we define the extended gradient Gibbs measure as in [6] by
It can be checked that this is a consistent family of measures and thus we can extend \({\tilde{\mu }}\) to a measure on \(({\mathbb {R}}\times {\mathbb {R}}_+)^{{\mathbf {E}}({\mathbb {Z}}^d)}\). It was explained in [6] that \(\tilde{\mu }\) is itself a Gibbs measure for the specification \({\tilde{\gamma }}_\Lambda \) defined by
Note that the distribution \((\mathrm {d}{\bar{\eta }},\mathrm {d}{\bar{\kappa }})_{{\mathbf {E}}(\Lambda )}\) actually only depends on \(\eta _{{\mathbf {E}}(\Lambda )^{\mathrm {c}}}\) and is independent of \(\kappa \). Let us add one remark concerning the notation. In this work we essentially consider three strongly related viewpoints of one model. The first viewpoint are gradient Gibbs measures that are measures on \({\mathfrak {X}}\). They will be denoted by \(\mu \) and the corresponding specification is denoted by \(\gamma \). Then there are extended gradient Gibbs measures for a specification \({\tilde{\gamma }}\). They are measures on \({\mathfrak {X}}\times {\mathbb {R}}_+^{{\mathbf {E}}({\mathbb {Z}}^d)}\) and will be denoted by \({\tilde{\mu }}\). The \(\eta \)-marginal of \({\tilde{\mu }}\) is a gradient Gibbs measure \(\mu \). Finally there is also the \(\kappa \)-marginal of \({\tilde{\mu }}\) which is a measure on \({\mathbb {R}}_+^{{\mathbf {E}}({\mathbb {Z}}^d)}\) and will be denoted by \({\bar{\mu }}\). An important result here is that \({\bar{\mu }}\) is a Gibbs measure for a specification \({\bar{\gamma }}\) if \(\rho \) is a measure as in (1.5). In this case \({\bar{\mu }}\) is a measure on the discrete space \(\{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\). We expect that this result can be extended to far more general measures \(\rho \) but we do not pursue this matter here. To keep the notation consistent we denote objects with single spin space \({\mathbb {R}}\), e.g., gradient Gibbs measures without symbol modifier, objects with single spin space \(\{1,q\}\), e.g., the \(\kappa \)-marginal with a bar, and objects with single spin space \(\{1,q\}\times {\mathbb {R}}\), e.g., extended Gibbs with a tilde.
It was already remarked in [6] that this setting resembles the situation for the Potts model that can be coupled to the FK random cluster model via the Edwards–Sokal coupling measure.
3.2 The random conductance model
As explained before our strategy is to analyse the \(\kappa \)-marginal of extended gradient Gibbs measures and then use the results to deduce properties of the gradient Gibbs measures for \(V_{p,q}\). The key observation is that the \(\kappa \)-marginal of extended gradient Gibbs measures is given by the infinite volume limit of a strongly coupled random conductance model. To motivate the definition of the random conductance model we consider the \(\kappa \)-marginal of the extended specification \(\tilde{\gamma }\) defined in (3.2). For zero boundary value \({\bar{0}}\in {\mathfrak {X}}\) with \({\bar{0}}_e=0\) and \(\lambda \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) we obtain
We write \(\Lambda ^w=\bar{\Lambda }/\partial \Lambda \) for the graph where the entire boundary is collapsed to a single point (this is called wired boundary conditions and we will discuss this below in more detail). We denote the lattice Laplacian with conductances \(\lambda \) and zero boundary condition outside of \(\Lambda ^\circ \) by \(\tilde{\Delta }_{\lambda }^{{\Lambda }^w}\), i.e., \(\tilde{\Delta }_{\lambda }^{{\Lambda }^w}\) acts on functions \(f:{\Lambda ^\circ }\rightarrow {\mathbb {R}}\) by \(\tilde{\Delta }_{\lambda }^{{\Lambda }^w}f(x) =\sum _{y\sim x} \lambda _{\{x,y\}}(f(x)-f(y))\) where we set \(f(y)=0\) for \(y\notin \Lambda ^\circ \). The definition (3.2) and an integration by parts followed by Gaussian calculus then imply
It simplifies the presentation to introduce the random conductance model of interest in a slightly more general setting. We consider a finite and connected graph \(G=(V,E)\). The combinatorial graph Laplacian \(\Delta _c\) associated with a set of conductances \(c:E\rightarrow {\mathbb {R}}_+\) is defined by
for any function \(f:V\rightarrow {\mathbb {R}}\). Note that we defined the graph Laplacian as a non-negative operator which is convenient for our purposes and common in the context of graph theory. In the following we view the Laplacian \(\Delta _c\) as a linear map on the space \(H_0=\{f:V\rightarrow {\mathbb {R}}: \sum _{x\in V} f(x)=0\}\) of functions with vanishing average. We define \(\det \Delta _c\) as the determinant of this linear map. By the maximum principle the Laplacian is injective on \(H_0\), hence \(\det \Delta _c>0\). Sometimes we clarify the underlying graph by writing \(\Delta _c^G\).
Remark 3.1
In the general setting it is more natural to let the Laplacian act on \(H_0\) instead of fixing a point to 0 as in the definition of \(\tilde{\Delta }_{\lambda }^{{\Lambda }^w}\) above where this corresponds to Dirichlet boundary conditions. It would also be possible to fix a point \(x\in {\mathbf {V}}(G)\) and consider \(\tilde{\Delta }_c^G\) acting on functions \(f:{\mathbf {V}}(G){\setminus } \{x_0\}\rightarrow {\mathbb {R}}\) defined by \(({\tilde{\Delta }}_c^Gf)(x)=\sum _{y\sim x} c_{\{x,y\}} f(x)-f(y)\) for \(x\in {\mathbf {V}}(G){\setminus } \{x_0\}\) where we set \(f(x_0)=0\). It is easy to see using, e.g., Gaussian calculus and a change of measure that the determinant of \({\tilde{\Delta }}_c^G\) is independent of \(x_0\) and
Note that the Gibbs property is harder to verify when restricting the average.
Motivated by (3.4) we fix a real number \(q> 1\) and consider the following probability measure on \(\{1,q\}^E\)
where \(Z=Z^{G,p}\) denotes a normalisation constant such that \({\mathbb {P}}^{G,p}\) is a probability measure. In the following we will often drop G and p from the notation and we will always suppress q. We restrict our attention to \(q\ge 1\) because by scaling the model with conductances \(\{1,q\}\) has the same distribution as a model with conductances \(\{\alpha ,\alpha q\}\) for \(\alpha >0\) so that we can set the smaller conductance to 1. Let us state a remark concerning the relation to the FK random cluster model.
Remark 3.2
-
1.
We chose the notation such that the similarity to the FK random cluster model is apparent. Both models have an a priori distribution given by independent Bernoulli distribution with parameter p on the bonds that is then correlated by a complicated infinite range interaction depending on q. For \(q=1\) the FK random cluster model reduces to Bernoulli percolation. Similarly, as \(q\rightarrow 1\) the pushforward of the distribution of the random conductance model under the map \(\{1,q\}\rightarrow \{0,1\}\) converges to the Bernoulli percolation measure. At the end of Sect. 5 we state a couple of conjectures about the behaviour of this model that show that we expect similarities with the in many more aspects.
-
2.
While there are several close similarities to the FK random cluster model there is also one important difference that seems to pose additional difficulties in the analysis of this model. The conditional distribution in a finite set depends on the entire configuration of the conductances outside the finite set (not just a partition of the boundary as in the FK random cluster model). In particular the often used argument that the conditional distribution of a random cluster model in a set given that all boundary edges are closed is the free boundary FK random cluster distribution has no analogue in our setting.
-
3.
We refer to the model as a random conductance model since we will (not very surprisingly) use tools from the theory of electrical networks. Note that in the definition of the potential V the parameters correspond to different (random) stiffness of the bonds.
4 Basic properties of the random conductance model
4.1 Preliminaries
As before we consider a connected graph \(G=(V,E)\). To simplify the notation we introduce for \(E'\subset E\) and \(\kappa \in \{1,q\}^E\) the notation
for the number of hard and soft edges respectively and we define \(h(\kappa )=h(\kappa ,E)\) and \(s(\kappa )=s(\kappa ,E)\). Let us introduce the weight of a subset of edges \({\varvec{t}}\subset E\) by defining
We will denote the set of all spanning trees of a graph by \(\mathrm {ST}(G)\). We identify spanning trees with their edge sets. In the following, we will frequently use the Kirchhoff formula
for the determinant of a weighted graph Laplacian (cf. [32] for a proof). Let us remark that the Kirchhoff formula is frequently used in statistical mechanics and has also been used in the context of gradient interface models for some potentials as in (1.4) in [9].
Remark 4.1
Note that Eq. (4.4) remains true for graphs with multi-edges and loops. Indeed, loops have no contribution on both sides and multi-edges can be replaced by a single edge with the sum of the conductances as conductance.
4.2 Correlation inequalities
We will now show correlation inequalities for the measures \({\mathbb {P}}={\mathbb {P}}^{G,p}\). We start by recalling several of the well known correlation inequalities. To state our results we introduce some notation. Let E be a finite or countable infinite set. Let \(\Omega =\{1,q\}^E\) and \({\mathcal {F}}\) the \(\sigma \)-algebra generated by cylinder events. We consider the usual partial order on \(\Omega \) given by \(\omega _1\le \omega _2\) iff \((\omega _1)_e\le (\omega _2)_e\) for all \(e\in E\). A function \(X:\Omega \rightarrow {\mathbb {R}}\) is increasing if \(X(\omega _1)\le X(\omega _2)\) for \(\omega _1\le \omega _2\) and decreasing if \(-X\) is increasing. An event \(A\subset \Omega \) is increasing if its indicator function is increasing. We write \({\bar{\mu }}_1\succsim {\bar{\mu }}_2\) if \({\bar{\mu }}_1\) stochastically dominates \({\bar{\mu }}_2\) which is by Strassen’s Theorem equivalent to the existence of a coupling \((\omega _1,\omega _2)\) such that \(\omega _1\sim {\bar{\mu }}_1\) and \(\omega _2\sim {\bar{\mu }}_2\) and \(\omega _1\ge \omega _2\) (see [31]). We introduce the minimum \(\omega _1 \wedge \omega _2\) and the maximum \(\omega _1\vee \omega _2\) of two configurations given by \((\omega _1 \wedge \omega _2)_e=\min ( (\omega _1)_e, (\omega _2)_e)\) and \((\omega _1 \vee \omega _2)_e=\max ((\omega _1)_e, (\omega _2)_e)\) for any \(e\in E\). We call a measure \({\bar{\mu }}\) on \(\Omega \) strictly positive if \({\bar{\mu }}(\omega )>0\) for all \(\omega \in \Omega \). Finally we introduce for \(f,g\in E\) and \(\omega \in \Omega \) the notation \(\omega _{fg}^{\pm \pm }\in \Omega \) for the configuration given by \((\omega _{fg}^{\pm \pm })_e=\omega _e\) for \(e\notin \{f,g\}\) and \((\omega _{fg}^{+ *})_f= q\), \((\omega _{fg}^{-*})_f = 1\), \((\omega _{fg}^{*+})_g= q\), \((\omega _{fg}^{*-})_g = 1\) and similarly for g. We define \(\omega _f^{\pm }\) similarly. We sometimes drop the edges f, g from the notation. We write \({\bar{\mu }}(\omega )={\bar{\mu }}(\{\omega \})\) for \(\omega \in \Omega \) and \({\bar{\mu }}(X)=\int _{\Omega }X\,\mathrm {d}{\bar{\mu }}\) for \(X:\Omega \rightarrow {\mathbb {R}}\).
Theorem 4.2
(Holley inequality) Let \(\Omega =\{1,q\}^E\) be finite and \({\bar{\mu }}_1\), \({\bar{\mu }}_2\) strictly positive measures on \(\Omega \) that satisfy the Holley inequality
Then \({\bar{\mu }}_1\precsim {\bar{\mu }}_2\).
Proof
The original proof appeared in [25], a simpler proof can be found , e.g., in [23, Theorem 2.1]. \(\square \)
A strictly positive measure is called strongly positively associated if it satisfies the FKG lattice condition
Theorem 4.3
A strongly positively associated measure \({\bar{\mu }}\) satisfies the FKG inequality, i.e., for increasing functions \(X,Y:\Omega \rightarrow {\mathbb {R}}\)
Proof
A proof can be found in [23, Theorem 2.16]. \(\square \)
The next theorem provides a simple way to verify the assumptions of Theorems 4.2 and 4.3. Basically it states that it is sufficient to check the conditions when varying at most two edges.
Theorem 4.4
Let \(\Omega =\{1,q\}^E\) be finite and \({\bar{\mu }}_1\), \({\bar{\mu }}_2\) strictly positive measures on \(\Omega \). Then \({\bar{\mu }}_1\) and \({\bar{\mu }}_2\) satisfy (4.5) iff the following two inequalities hold
In particular, (4.8) and (4.9) together imply \({\bar{\mu }}_1\precsim {\bar{\mu }}_2\).
Proof
See [23, Theorem 2.3]. \(\square \)
We state one simple corollary of the previous results.
Corollary 4.5
Let \({\bar{\mu }}_1\), \({\bar{\mu }}_2\) be strictly positive measures on \(\Omega =\{1,q\}^E\) such that at least one of the measures \({\bar{\mu }}_1\), \({\bar{\mu }}_2\) is strongly positively associated. Then
implies \({\bar{\mu }}_1\precsim {\bar{\mu }}_2\).
Proof
Assuming that \({\bar{\mu }}_1\) is strongly positively associated we find using first the assumption (4.10) and then (4.6)
Now Theorem 4.4 implies the claim. The proof if \({\bar{\mu }}_2\) is strictly positively associated is similar. \(\square \)
It is convenient to derive the following correlation results for the measures \({\mathbb {P}}^{G,p}\) from corresponding results for the weighted spanning tree measure. The weighted spanning tree measure on a connected weighted graph \((G,\kappa )\) is a measure on \(\mathrm {ST}(G)\) with distribution
This model has been studied extensively, see [4] for a survey. An important special case is the uniform spanning tree corresponding to constant conductances \(\kappa \) that assigns equal probability to every spanning tree.
The following lemma provides the basic estimate to check the condition (4.9) for the measures \({\mathbb {P}}^{G,p}\).
Recall the notation \(\kappa ^{\pm \pm }_{fg}\) introduced before Theorem 4.2 and also the shorthand \(\kappa ^{\pm \pm }\).
Lemma 4.6
For a finite graph G and \(\kappa \in \{1,q\}^E\) as above
Remark 4.7
The proof in fact extends to any \(\kappa \in {\mathbb {R}}_+^E\) and \((\kappa ^{\pm \pm }_{fg})_f=c_f^{\pm }\), \((\kappa ^{\pm \pm }_{fg})_g=c_g^{\pm }\) with \(c_f^-\le c_f^+\) and \(c_g^-\le c_g^+\).
Proof
The lemma can be derived from the fact that the weighted spanning tree has negative correlations. It is well known (see, e.g., [4]) that for all positive weights \(\kappa \) on a finite graph G the measure \(\mathbb {Q}_\kappa ^G\) has negative edge correlations
Simple algebraic manipulations show that this is equivalent to
We introduce the following sums that depend on f, g, and \(\kappa \)
With this notation multiplication by \((A_{fg}+A_f+A_g+A)^2\) shows that (4.15) is equivalent to
It remains to show that the statement in the lemma can be deduced from (4.17) (actually the statements are equivalent). Clearly we can assume \(\kappa =\kappa ^{--}\), i.e., \(\kappa _f=\kappa _g=1\). Using the Kirchhoff formula (4.4) we find the following expression
In the second step we split the sum into four terms depending on whether \(f\in {\varvec{t}}\) and \(g \in {\varvec{t}}\) and use the shorthand introduced in (4.16). Hence we obtain
Subtracting those two identities we find that only the cross-terms between \(A_f,A_g\) and between \(A_{fg}, A\) do not cancel and we get
We can conclude using (4.17). \(\square \)
The previous lemma directly implies that the measures \({\mathbb {P}}^{G,p}\) are strongly positively associated.
Corollary 4.8
The measure \({\mathbb {P}}^{G,p}\) satisfies the FKG lattice condition for any \(\kappa _1,\kappa _2\in \{1,q\}^E\)
and the FKG inequality
for any increasing functions \(X,Y:\{1,q\}^E\rightarrow {\mathbb {R}}\).
Proof
Lemma 4.6 and the trivial observation that \(h(\kappa ^{++})+h(\kappa ^{--})=h(\kappa ^{+-})+h(\kappa ^{-+})\) imply for any \(\kappa \in \{1,q\}^E\) and \(f,g\in E\) the lattice inequality
Then Theorem 4.4 applied to \({\bar{\mu }}_1={\bar{\mu }}_2={\mathbb {P}}^{G,p}\) implies that the FKG lattice condition (4.21) holds and therefore by Theorem 4.3 also the FKG inequality (4.22). \(\square \)
Let us first state a trivial consequence of this corollary.
Corollary 4.9
The measures \({\mathbb {P}}^{G,p}\) and \({\mathbb {P}}^{G,p'}\) satisfy for \(p\le p'\)
Proof
Using Corollaries 4.8 and 4.5 we only need to check whether (4.10) holds for \({\bar{\mu }}_1={\mathbb {P}}^{G,p}\) and \({\bar{\mu }}_2={\mathbb {P}}^{G,p'}\). This is clearly the case if \(p\le p'\). \(\square \)
The next step is to show correlation inequalities with respect to the size of the graph. More specifically we show statements for subgraphs and contracted graphs. This will later easily imply the existence of infinite volume limits. Moreover, we can bound infinite volume states by finite volume measures in the sense of stochastic domination. Let \(F\subset E\) be a set of edges. We define the contracted graph G/F by identifying for every edge \(f\in F\) the endpoints of f. Similarly for a set \(W\subset V\) of vertices we define the contracted graph G/W by identifying all vertices in W. The resulting graphs may have multi-edges. We also consider connected subgraphs \(G'=(V',E')\) of G. Recall the notation \(\kappa ^{\pm }=\kappa _f^\pm \) for \(f\in E\). We use the notation \(\Delta _\kappa ^{G'}\) for the graph Laplacian on \(G'\) where we restrict the conductances \(\kappa \) to \(E'\) and we denote by \(\Delta _\kappa ^{G/F}\) the graph Laplacian on G/F. The following lemma relates the determinants of the different graph Laplacians.
Lemma 4.10
With the notation introduced above we have for \(\kappa \in \{1,q\}^E\)
Remark 4.11
The lemma again extends to \(\kappa \in {\mathbb {R}}_+^E\) and \(\kappa ^\pm _f\) with \((\kappa _f^+)_f=c_+>c_-=(\kappa _f^-)_f\).
Proof
The proof is similar to the proof of Lemma 4.6. We derive the statement from a property of the weighted spanning tree model. For graphs as above and \(e\in E'\) the estimate
holds (see Corollary 4.3 in [4] for a proof). We can rewrite (assuming again \(\kappa _f=1\), i.e., \(\kappa =\kappa ^-\))
Note that
and therefore (using \(\kappa =\kappa ^-\))
Similar statements hold for the graphs G/F and \(G'\). Hence (4.26) implies (4.25). \(\square \)
Let us remark that the probability \({\mathbb {Q}}^G_\kappa (f\in {\varvec{t}})\) can also be expressed as a current in a certain electrical network. In order to avoid unnecessary notation at this point we kept the weighted spanning tree measure and we will only exploit this connection when necessary below.
Again, the previous estimates imply correlation inequalities for the measures \({\mathbb {P}}^{G,p}\). In the following we consider a fixed value of p but different graphs so that we drop only p from the notation but we keep the graph G. We introduce the distribution under boundary conditions for a connected subgraph \(G'=(V',E')\) of G. For \(\lambda \in \{1,q\}^E\) we define the measure \({\mathbb {P}}^{G,E',\lambda }\) on \(\{1,q\}^{E'}\) by
where \((\lambda ,\kappa )\in \{1,q\}^E\) denotes the conductances given by \(\kappa \) on \(E'\) and by \(\lambda \) on \(E{\setminus } E'\). This definition implies that we have the following domain Markov property for \(\omega \in \{1,q\}^{E'}\)
Since the measure \({\mathbb {P}}^G\) is strongly positively associated, (4.31) and Theorem 2.24 in [23] imply that the measure \({\mathbb {P}}^{G,E',\lambda }\) is strongly positively associated. We now state the consequences of Lemma 4.10 on stochastic ordering.
Corollary 4.12
For a finite graph \(G=(V,E)\), a connected subgraph \(G'=(V',E')\), an edge subset \(F\subset E\), and configurations \(\lambda _1, \lambda _2\in \{1,q\}^E\) such that \(\lambda _1\le \lambda _2\) the following holds
More generally, we have for \(\lambda \in \{1,q\}^E\) and \(E''\subset E'\) or \(E''\cap F=\emptyset \) respectively
Proof
From Lemma 4.10 we obtain for \(f\in E'\) and any \(\kappa \in \{1,q\}^{E'}\)
Similarly, Lemma 4.10 implies for \(f\in E{\setminus } F\) and \(\kappa \in \{1,q\}^{E{\setminus } F}\)
Then the strong positive association of \({\mathbb {P}}^G\) and Corollary 4.5 imply the first and the last stochastic orderings claimed in (4.32). The stochastic domination result in the middle of (4.32) follows from (4.31) and a general result for strictly positive associated measures (see [23, Theorem 2.24]). The proof of (4.33) is similar. \(\square \)
4.3 Infinite volume measures
The definition of the measure \({\mathbb {P}}\) shows that it is a finite volume Gibbs measure for the energy \(E(\kappa )=\ln (\det \Delta _\kappa )/2\) and a homogeneous Bernoulli a priori measure. We would like to define infinite volume limits for the measures \({\mathbb {P}}^G\) and define a notion of Gibbs measures in infinite volume. This requires some additional definitions. The \(\sigma \)-algebras \({\mathcal {F}}_E\) for \(E\subset {\mathbf {E}}(G)\) are defined as the \(\sigma \)-algebra generated by \((\kappa _e)_{e\in E}\) and we write \({\mathcal {F}}={\mathcal {F}}_{{\mathbf {E}}(G)}\).
An event \(A\subset {\mathcal {F}}\) is called local if it measurable with respect to \({\mathcal {F}}_E\) for some finite set E, i.e., A depends only on finitely many edges. Similarly we define a local function as a function that is measurable with respect to \({\mathcal {F}}_E\) for a finite set E. We say that a sequence of measures \({\bar{\mu }}_n\) on \(\{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) converges in the topology of local convergence to a measure \({\bar{\mu }}\) if \({\bar{\mu }}_n(A)\rightarrow {\bar{\mu }}(A)\) for all local events A. For a background on the choice of topologies in the context of Gibbs measures we refer to [21]. The construction of the infinite volume states proceeds similarly to the construction for the Potts model by defining a specification and introducing the notion of free and wired boundary conditions. For simplicity we restrict the analysis to \({\mathbb {Z}}^d\) but the generalisation to more general graphs is straightforward. First, we define infinite volume limits of the finite volume distributions with wired and free boundary conditions. Let us denote by \(\Lambda _n=[-n,n]\cap {\mathbb {Z}}^d\) the ball with radius n in the maximum norm around the origin and we denote by \(E_n={\mathbf {E}}(\Lambda _n)\) the edges in \(\Lambda _n\). We introduce the shorthand \(\Lambda _n^w=\Lambda _n/\partial \Lambda _n\) for the box with wired boundary conditions. We define
for the measures \({\mathbb {P}}\) on \(\Lambda _n\) with free and wired boundary conditions respectively. From Corollary 4.12 and Eq. (4.31) we conclude that for any increasing event A depending only on edges in \(E_n\)
We conclude that for any increasing event A depending only on finitely many edges the limits \(\lim _{n\rightarrow \infty } {\bar{\mu }}_{n,p}^0(A)\) and similarly \(\lim _{n\rightarrow \infty } {\bar{\mu }}_{n,p}^1(A)\) exist. Using standard arguments we can write every local event A as a union and difference of increasing local events and we conclude that \(\lim _{n\rightarrow \infty } {\bar{\mu }}_{n,p}^{0}(A)\) and \(\lim _{n\rightarrow \infty } {\bar{\mu }}_{n,p}^{1}(A)\) exist. It is well known (see [5]) that this implies convergence of \({\bar{\mu }}_{n,p}^{0}\) and \({\bar{\mu }}_{n,p}^1\) to a measure on \(\{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) in the topology of local convergence. We denote the infinite volume measures by \({\bar{\mu }}_p^{0}\) and \({\bar{\mu }}_p^1\).
Lemma 4.13
The measure \({\bar{\mu }}_p^0\) and \({\bar{\mu }}_p^1\) satisfy the FKG-inequality and for \(0\le p\le p'\le 1\) the relations
Moreover they are invariant under symmetries of the lattice and ergodic with respect to translations.
Proof
We refer to the proof of Theorem 4.17 and Corollary 4.23 in [23] for a detailed proof for the FK random cluster model which essentially also applies to the model considered here. For the proof of shift invariance and ergodicity our proof is closer to Lemma 1.11 in [17].
The first part of the lemma is a consequence of Corollaries 4.8, 4.9, and 4.12 and a limiting argument.
The invariance under rotations of the lattice follows from the invariance of the finite volume measures under rotations. We now prove the shift invariance of \({\bar{\mu }}^1_p\), i.e.,
Recall that \(\tau _x e = e+x \) for \(e\in {\mathbf {E}}({\mathbb {Z}}^d)\) and \((\tau _x \eta )_e=\eta _{\tau _{-x}e}\) for gradient fields. As before it is sufficient to show shift invariance for increasing local events. Let \(x\in {\mathbb {Z}}^d\) and suppose \(x\in \Lambda _k\) for some \(k>0\). Let A be an increasing local event. Let n be large enough such that A only depends on the edges in \(\Lambda _{n-2k}\). From the relation \(\Lambda _{n-k}\subset \tau _x\Lambda _n \subset \Lambda _{n+k}\) and Corollary 4.12 we conclude that
Taking the limit \(n\rightarrow \infty \) we conclude that \(\lim _{n\rightarrow \infty } {\mathbb {P}}^{\tau _x \Lambda _n}(\tau _x A)={\bar{\mu }}^0(\tau _x A)\). Translation invariance of \({\bar{\mu }}^0\) now follows from
We prove ergodicity of \({\bar{\mu }}^0\) by showing that it is even mixing, i.e., \({\bar{\mu }}^0\) satisfies for all local events A and B
Again, it is sufficient to show this for all decreasing local events. The FKG inequality stated in Corollary 4.8 and translation invariance imply that for all \(x\in {\mathbb {Z}}^d\)
It remains to show the reverse inequality for \(|x|\rightarrow \infty \). We assume that A, B only depend on the edges in \(\Lambda _k\) for some k. Let n and m be integers such that \(n+k< |x|_\infty < m -k \). Then we can write the measure \({\mathbb {P}}^{\Lambda _m}(\cdot \vert \tau _xB)\) as a mixture of measures \({\mathbb {P}}^{\Lambda _m, E_n, \lambda }\) such that \(\lambda \in \tau _xB\) (here we use that \(\tau _x B\) does not depend on the edges in \(E_n\)). By the first statement of Corollary 4.12 the stochastic ordering \({\mathbb {P}}^{\Lambda _m, E_n, \lambda }\succsim {\mathbb {P}}^{\Lambda _n}\) holds true for all \(\lambda \) and therefore (note that A is decreasing)
Sending first \(m\rightarrow \infty \), then \(|x|\rightarrow \infty \) and \(n\rightarrow \infty \) we conclude that
Thus \({\bar{\mu }}^0\) is mixing. The fact that \({\bar{\mu }}^1\) is also translation invariant and mixing can be shown with similar arguments. \(\square \)
4.4 Infinite volume specifications
We now introduce the concept of infinite volume Gibbs measures for this model. We first consider the case of a finite connected graph G. For \(E\subset {\mathbf {E}}(G)\) we consider the finite volume specifications \({\bar{\gamma }}^G_{E}:{\mathcal {F}}\times \{1,q\}^{{\mathbf {E}}(G)}\rightarrow {\mathbb {R}}\)
where the normalisation \(Z_\lambda \) ensures that \({\bar{\gamma }}^G_{E}(\cdot ,\lambda )\) is a probability measure. A careful calculation shows that \({\bar{\gamma }}^G\) is indeed a specification, i.e., \({\bar{\gamma }}^G_{E}\) are proper probability kernels that satisfy for \(E\subset E'\)
Let us remark for readers familiar with the theory of Gibbs measures that this specification is actually a modification of the independent specification with \(\uplambda =p\delta _q+(1-p)\delta _1\) and one can also use Proposition 1.30 in [21] to verify that \({\bar{\gamma }}\) defines a specification. Since \({\bar{\gamma }}_{E}^G(\cdot , \lambda )\) is concentrated on a finite set it is convenient to use the notation \({\bar{\gamma }}_{E}^G(\kappa ,\lambda )={\bar{\gamma }}_{E}^G(\{\kappa \},\lambda )\). The measure \({\mathbb {P}}^{G}\) is a finite volume Gibbs measure, i.e., it satisfies
or put differently for \(\kappa ,\lambda \in \{1,q\}^{E}\)
We would like to call \(\mu \) a Gibbs measure on \(\{1,q\}^{{\mathbb {Z}}^d}\) for the random conductance model if
holds for all \(E\subset {\mathbf {E}}({\mathbb {Z}}^d)\) finite. However, \({\bar{\gamma }}^{G}_E\) is a priori only well defined for finite graphs so that we use an approximation procedure for infinite graphs. Let G be a connected infinite graph. We are a bit sloppy with the notation and do not distinguish between \({\bar{\gamma }}^H_{E}\) for a subgraph H of G and its proper extension to \({\mathcal {F}}\times \{1,q\}^{{\mathbf {E}}(G)}\), i.e., we define for \(\kappa ,\lambda \in \{1,q\}^{{\mathbf {E}}(G)}\)
We denote for \(f\in {\mathbf {E}}(G)\) and \(\kappa \in \{1,q\}^{{\mathbf {E}}(G)}\) by \(\kappa ^+\) and \(\kappa ^-\) as before the configurations such that \(\kappa _e^+=\kappa ^-_e\) for \(e\ne f\) and \(\kappa _f^-=1\), \(\kappa ^+_f=q\).
In the following we assume \(p\in (0,1)\). For \(p\in \{0,1\}\) the measures \({\mathbb {P}}^{G,p}\) agree with the Dirac measure on the constant 1 or constant q configuration. Since we assume that E is finite the specification \({\bar{\gamma }}^H_{E}\) can be uniquely characterized by the following two conditions: Firstly, the kernels \({\bar{\gamma }}^H_E\) are proper and secondly they satisfy for all \(\kappa ,\lambda \in \{1,q\}^{{\mathbf {E}}(H)}\) with \(\kappa _{E^{\mathrm {c}}}=\lambda _{E^{\mathrm {c}}}\)
where we used (4.29) in the second step. We show that we can give meaning to this expression in infinite volume. For this we sketch the definition of spanning trees in infinite volume but we refer to the literature for details (see [4]). A monotone exhaustion of an infinite graph G is a sequence of subgraphs \(G_n\) such that \(G_n\subset G_{n+1}\) and \(G=\bigcup _{n\ge 1} G_n\). It can be shown that for any finite sets \(E_1\subset E_2\subset {\mathbf {E}}(G)\) the limit \(\lim _{n\rightarrow \infty } {\mathbb {Q}}^{G_n}_\kappa ({\varvec{t}}\cap E_2=E_1)\) exists. In fact this is a consequence of (4.26) and the arguments we used for \({\bar{\mu }}_n^0\) above. Hence it is possible to define a measure \({\mathbb {Q}}_\kappa ^{G,0}\) on \(2^{{\mathbf {E}}(G)}\), the power set of \({\mathbf {E}}(G)\) which will be called the weighted free spanning forest on G (as the name suggest the measure is supported on forests but not necessarily on trees, i.e., on connected subsets of edges). Similarly, we can define the wired spanning forest \({\mathbb {Q}}_\kappa ^{G,1}\) replacing the subgraphs \(G_n\) by the contracted graphs \(G_n/\partial G_n\). By definition those measures satisfy
for any \(f\in E\). Then it is possible to define two families of proper probability kernels \({\bar{\gamma }}^{G,0}_{E}\) and \({\bar{\gamma }}^{G,1}_{E}\) for \(E\subset ({\mathbf {E}}(G))\) finite by the property that for \(f\in E\) and \(\kappa ,\lambda \in \{1,q\}^{{\mathbf {E}}(G)}\) such that \(\kappa _{E^{\mathrm {c}}}=\lambda _{E^{\mathrm {c}}}\)
From and (4.52) and (4.52) we conclude that \({\bar{\gamma }}^{G,0}\) and \({\bar{\gamma }}^{G,1}\) are well defined. Moreover we obtain that this family of probability kernels satisfy for \(\lambda ,\kappa \in \{1,q\}^{{\mathbf {E}}(G)}\)
Note that the concatenation for \({\bar{\gamma }}^{G,0}\) for \(E',E\subset {\mathbf {E}}({\mathbb {Z}}^d)\) is given by
in particular it only involves a finite sum in the case of a finite spin space. We conclude using (4.57) and (4.58) that \({\bar{\gamma }}^{G,0}_E\) and \({\bar{\gamma }}^{G,1}_E\) define two specifications on G.
Suppose the wired and the free uniform spanning forests on G agree. This implies that also the weighted wired and free spanning forests \({\mathbb {Q}}^{G,0}_\kappa \) and \({\mathbb {Q}}^{G,1}_\kappa \) on G agree if the conductances \(\kappa _e\) are contained in a compact subset of \((0,\infty )\) (see Theorem 7.3 and Theorem 7.7 in [4]). Thus \({\bar{\gamma }}^{G,1}_{E}={\bar{\gamma }}^{G,0}_{E}\) in this case. In particular we obtain that \({\bar{\gamma }}^{{\mathbb {Z}}^d,0}_{E}={\bar{\gamma }}^{{\mathbb {Z}}^d,1}_{E}\) because the free and the wired uniform spanning forests on \({\mathbb {Z}}^d\) agree (Corollary 6.3 in [4]). In the following we will denote this specification by \({\bar{\gamma }}_{E}\). To ensure consistency with the earlier definition of \({\tilde{\gamma }}\) we define for a connected subset \(\Lambda \subset {\mathbb {Z}}^d\) that \({\bar{\gamma }}_{\Lambda }={\bar{\gamma }}_{{\mathbf {E}}(\Lambda )}\). We can now give a formal definition of Gibbs measures for the random conductance model.
Definition 4.14
A measure \({\bar{\mu }}\in {\mathcal {P}}(\{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)})\) is an infinite volume Gibbs measure for the random conductance model if it is specified by \({\bar{\gamma }}_E\), i.e., a Gibbs measure in the sense of Definition 2.1 for the specification \({\bar{\gamma }}_E\).
As one would expect the infinite volume measures \({\bar{\mu }}_p^0\) and \({\bar{\mu }}_p^1\) are Gibbs measures.
Lemma 4.15
The measures \({\bar{\mu }}_p^0\) and \({\bar{\mu }}_p^1\) are Gibbs measures as defined in Definition 4.14. Moreover any Gibbs measure \({\bar{\mu }}\) satisfies \({\bar{\mu }}_p^0\precsim {\bar{\mu }}\precsim {\bar{\mu }}_p^1\).
Proof
By Eq. (4.48) we have for \(E\subset E_n\)
We show that both sides converge in the topology of local convergence as \(n\rightarrow \infty \). Let A be an increasing event depending on a finite number of edges. We have seen in (4.37) that \(\mu _n^0(A)\) is an increasing sequence and converges by definition to \(\mu ^0(A)\). We derive the convergence of the left hand side of equation (4.60) from the following three observations. First, we conclude from (4.32) and (4.49) that \({\bar{\gamma }}^{\Lambda _n}_E(A,\cdot )\) is an increasing function. Second, using (4.33) and (4.49) we obtain \({\bar{\gamma }}^{\Lambda _{n+1}}_E(A,\kappa )\ge {\bar{\gamma }}^{\Lambda _n}_E(A,\kappa _{E_n})\) for all \(\kappa \in \{1,q\}^{E_{n+1}}\). The third observation is that (4.37) can also be applied to an increasing function instead of an increasing event. These three facts imply
On the other hand, we obtain for any \(m\in \mathbb {N}\)
Sending \(m\rightarrow \infty \) we get
Hence, we have shown that
holds for any increasing and local event A. Using standard arguments (4.64) holds for all local events. Therefore \(\mu ^0\) is a Gibbs measure. The proof for \(\mu ^1\) is similar based on the identity
Finally, a limiting argument and the comparison of boundary conditions show that \({\bar{\mu }}_p^0\precsim {\bar{\mu }}\precsim {\bar{\mu }}_p^1\) for any Gibbs measure \(\mu \) (see [23, Proposition 4.10]). \(\square \)
Let us briefly introduce the class of quasilocal specifications which is a natural and useful condition for a specification. For an extensive discussion we refer to the literature [21]. A quasilocal function on a general state space is a bounded function \(X:F^S\rightarrow {\mathbb {R}}\) that can be approximated arbitrarily well by local functions, i.e.,
A specification \(\gamma \) is called quasilocal if \(\gamma _{\Lambda } X\) is a quasilocal function for every local function X. We will show that the specification \({\bar{\gamma }}_{E}\) is quasilocal. This will be a direct consequence of the following result that shows uniform convergence of \({\bar{\gamma }}^{\Lambda _n^w}_E\) to \({\bar{\gamma }}_E\). This convergence will be of independent use later.
Lemma 4.16
The specifications \({\bar{\gamma }}_{E_n}\) and \({\bar{\gamma }}_{E_n}^{\Lambda _N^w}\) satisfy
Proof
First, we claim that it is sufficient to show that
Indeed, using (4.68) in (4.52) we obtain
Since \(E_n\) is finite this implies the claim.
It remains to prove (4.68). This is a consequence of the transfer current theorem (see Theorem 4.1 in [4]) that states in the special case of the occupation property that for \(f=\{x,y\}\in {\mathbf {E}}(G)\)
where the expression \(I_f(f)\) denotes the current through the edge f when 1 unit of current is induced respectively removed at the two ends of f. In the last step we used that \(I_f(f)\) can be calculated by applying the inverse Laplacian to the sources to obtain the potential which can be used to calculate the current through f. Now (4.68) follows from the display (4.70) and Lemma B.3. \(\square \)
Corollary 4.17
The specification \({\bar{\gamma }}_E\) is quasilocal.
Proof
Let X be a local function. We need to show that \({\bar{\gamma }}_EX\) is quasilocal. Lemma 4.16 implies that the local functions \({\bar{\gamma }}^{\Lambda _N^w}_EX\) satisfy
\(\square \)
4.5 Relation to extended gradient Gibbs measures
In this paragraph we state the results that relate the random conductance model to extended gradient Gibbs measure. This is finally the justification to consider this model. The proofs of the results in this paragraph are deferred to Appendix A. The first Proposition establishes that the \(\kappa \)-marginal of extended gradient Gibbs measures are Gibbs states for the random conductance model.
Proposition 4.18
Let \(\tilde{\mu }\) be an extended gradient Gibbs measure associated to a translation invariant and ergodic gradient Gibbs measure \(\mu \) with zero tilt. Then the \(\kappa \)-marginal \(\bar{\mu }\) of \(\tilde{\mu }\) is a Gibbs measure in the sense of Definition 4.14.
The second main result in this paragraph is a reverse of Proposition 4.18, namely that it is possible to obtain an extended Gibbs measure with zero tilt for the potential \(V_{p,q}\), given a Gibbs measure \({\bar{\mu }}\) for the random conductance model with parameters p, q.
Proposition 4.19
Let \({\bar{\mu }}\) be a Gibbs measure in the sense of Definition 4.14 for parameters p and q and \(\kappa \sim {\bar{\mu }}\). Let \(\varphi ^\kappa \) be the random field that for given \(\kappa \) is a Gaussian field with zero average, \(\varphi ^\kappa (0)=0\), and covariance \((\Delta _\kappa )^{-1}\), i.e., \(\varphi ^\kappa \) satisfies for \(f:{\mathbb {Z}}^d\rightarrow {\mathbb {R}}\) with finite support and \(\sum _{x} f(x)=0\)
Let \({\tilde{\mu }}\) be the joint law of \((\kappa ,\nabla \varphi ^\kappa )\). Then \({\tilde{\mu }}\) is an extended Gibbs measure for the potential \(V_{p,q}\) with zero tilt, in particular its \(\eta \)-marginal is a gradient Gibbs measure with zero tilt.
As a last result in this direction we state a very useful result from [7] that characterizes the law of \(\varphi \) given \(\kappa \) for extended gradient Gibbs measures if \(\varphi \) is distributed according to a gradient Gibbs measure.
Proposition 4.20
Let \(\mu \) be a translation invariant, ergodic gradient Gibbs measure with zero tilt and \({\tilde{\mu }}\) the corresponding extended gradient Gibbs measure. Then the conditional law of \(\varphi \) given \(\kappa \) is \({\tilde{\mu }}\)-almost surely Gaussian. It is determined by its expectation
and the covariance given by \((\Delta _\kappa )^{-1}\), i.e., for \(f:{\mathbb {Z}}^d\rightarrow {\mathbb {R}}\) with finite support and \(\sum _{x} f(x)=0\)
Proof
This is Lemma 3.4 in [7]. \(\square \)
In particular those results establish the following. Assume that \(\mu \) is an ergodic zero tilt gradient Gibbs measure. Let \({\bar{\mu }}\) be the \(\kappa \)-marginal of the corresponding extended gradient Gibbs measure \({\tilde{\mu }}\) (which by Proposition 4.18 is Gibbs for the random conductance model). We can use Proposition 4.19 to construct an extended gradient Gibbs measure \({\tilde{\mu }}'\). Using the definition of \({\tilde{\mu }}'\) in Propositions 4.19 and 4.20 we conclude that we get back the extended gradient Gibbs measure we started from, i.e., \({\tilde{\mu }}={\tilde{\mu }}'\).
5 Further properties of the random conductance model
In this section we state and prove more results about the random conductance model considered in this work and use the results from the previous section to derive corresponding results for the associated gradient interface model. We end this section with some conjectures and open questions.
5.1 Uniqueness results for the random conductance model
We start by proving \({\bar{\mu }}_p^0={\bar{\mu }}_p^1\) for \(d\ge 2\) and almost all values of p which will in particular implies uniqueness of the Gibbs measure for those p.
Theorem 5.1
For every \(q\ge 1\) there are at most countably many \(p\in [0,1]\) such that \({\bar{\mu }}_p^1\ne {\bar{\mu }}_p^0\).
Proof
It is a standard consequence of the invariance under lattice symmetries and \({\bar{\mu }}_{p}^0\precsim {\bar{\mu }}_{p}^1\) that \({\bar{\mu }}_p^1={\bar{\mu }}_p^0\) is equivalent to \({\bar{\mu }}_p^1(\kappa _e=q)={\bar{\mu }}_p^0(\kappa _e=q)\) for one and therefore any \(e\in {\mathbf {E}}({\mathbb {Z}}^d)\) (see, e.g, Proposition 4.6 in [23]). Lemma 5.3 below implies for \(e\in {\mathbf {E}}({\mathbb {Z}}^d)\)
for any \(p'>p\). In particular, we can conclude that \({\bar{\mu }}_p^0={\bar{\mu }}_p^1\) holds for all points of continuity of the map \(p\mapsto {\bar{\mu }}^0_p(\kappa _e=q)\). Since this map is increasing by Corollary 4.9 it has only countably many points of discontinuity. \(\square \)
We are now in the position to prove Theorem 2.3.
Proof of Theorem 2.3
We note that a translation invariant zero tilt Gibbs measure exists for any p and q, e.g., as a limit of torus Gibbs states (see the proof of Theorem 2.2 in [6]). It remains to show uniqueness. Consider p such that \(\bar{\mu }^1_p=\bar{\mu }^0_p\) which is true for all but a countable number of \(p\in [0,1]\) by Theorem 5.1 above. Let \(\mu _1\) and \(\mu _2\) be ergodic zero tilt gradient Gibbs measures for \(V=V_{p,q}\). By Proposition 4.18 the corresponding \(\kappa \)-marginals \({\bar{\mu }}_1\) and \({\bar{\mu }}_2\) of the extended Gibbs measures \({\tilde{\mu }}_1\) and \({\tilde{\mu }}_2\) are Gibbs measures in the sense of Definition 4.14 and therefore equal. Using Proposition 4.20 we conclude that since \(\mu _1\) and \(\mu _2\) are ergodic zero tilt gradient Gibbs measures their laws are determined by \({\bar{\mu }}_1\) and \({\bar{\mu }}_2\), hence \(\mu _1=\mu _2\). \(\square \)
Remark 5.2
Similar arguments for this model appeared already in the proof of Theorem 2.4 in [6] where they use the convexity of the pressure to show that the number of q-bonds on the torus is concentrated around its expectation in the thermodynamic limit. However, this is not sufficient to conclude uniqueness.
The key ingredient in the proof of Theorem 5.1 is the following lemma that compares \({\bar{\mu }}_p^1(\kappa _e=q)\) with \({\bar{\mu }}_{p'}^0(\kappa _e=q)\) for \(p<p'\). Intuitively the reason for this result is that a change of p is a bulk effect of order \(|\Lambda |\) while the effect of the boundary conditions is of order \(|\partial \Lambda |\).
Lemma 5.3
For any \(p<p'\) we have
Proof
The proof follows the proof of Theorem 1.12 in [17] where a similar result for the FK random cluster model is shown. The only difference is that the comparison between free and wired boundary conditions is slightly less direct. We define \(a= {\bar{\mu }}_{p'}^0(\kappa _e=q)\) and \(b= {\bar{\mu }}_{p}^1(\kappa _e=q)\). Comparison between boundary condition implies \({\bar{\mu }}_{n,p'}^0(\kappa _e=q)\le {\bar{\mu }}_{p'}^0(\kappa _e=q)=a\) for any \(e\in E_n\). Recall that \(h(\kappa )=| \{e\in {\mathbf {E}}(G):\kappa _e=q\} |\) denotes the number of q-bonds and \(s(\kappa )\) similarly the number of 1-bonds. The definition of a and b implies for \(0<\varepsilon <1-a\)
Similarly for \(0<\varepsilon <b\)
Our goal is to show that \(b-\varepsilon \le a+\varepsilon \). We denote by \(\Delta ^0\) and \(\Delta ^1\) the graph Laplacian on \(\Lambda _n\) with free and wired boundary conditions respectively. To compare the boundary conditions we denote by \(T_1=\mathrm {ST}(\Lambda _n^w)\) the set of wired spanning trees on \(\Lambda _n\) and by \(T_0=\mathrm {ST}(\Lambda _n)\) the set of spanning trees on \( \Lambda _n\) with free boundary conditions. There is a map \(\Phi :T_0 \rightarrow T_1\) such that \(\Phi ({\varvec{t}}){\restriction _{\Lambda _{n-1}}}={\varvec{t}}{\restriction _{\Lambda _{n-1}}}\). Indeed, removing all edges in \(E_n{\setminus } E_{n-1}\) from \({\varvec{t}}\) we obtain an acyclic subgraph of \(\Lambda _n^w\), hence we can find a tree \(\Phi ({\varvec{t}})\) such that \({\varvec{t}}{\restriction _{\Lambda _{n-1}}}\subset \Phi ({\varvec{t}})\subset {\varvec{t}}\). The observation \(|{\varvec{t}}{\setminus } \Phi ({\varvec{t}})|=|\partial \Lambda _n|-1\) implies that \(w(\kappa ,{\varvec{t}})\le w(\kappa ,\Phi ({\varvec{t}}))q^{|\partial \Lambda _n|-1}\). Since \(\Phi \) does not change the edges in \(E_{n-1}\) each tree \({\varvec{t}}\in T_1\) has at most \(2^{|E_n{\setminus } E_{n-1}|}\) preimages. We obtain that
Similarly, there is an injective mapping \(\Psi :T_1\rightarrow T_0\) such that \({\varvec{t}}\subset \Psi ({\varvec{t}})\). Indeed, we fix a tree \({\varvec{t}}_b\) in the graph \((\Lambda _n{\setminus } \Lambda _{n-1}, {\mathbf {E}}(\Lambda _n{\setminus } \Lambda _{n-1})\) and define \(\Psi ({\varvec{t}})={\varvec{t}}\cup {\varvec{t}}_b\in T_0\). We get
Inserting the bound \(|E_n{\setminus } E_{n-1}|\le 2d|\partial \Lambda _n|\) we infer from the definition (3.7) for any \(\kappa \in \{1,q\}^{E_n}\)
We define the constant \(\alpha =p'(1-p)/(p(1-p'))>1\). Simple manipulation show that for any function \(X:\{1,q\}^{E_n}\rightarrow {\mathbb {R}}\)
Therefore we obtain
From (5.3) and (5.4) we conclude
which implies \(a-b+2\varepsilon \ge 0\) as \(n\rightarrow \infty \) since \(\alpha >1\) and \(|E_n|/|\partial \Lambda _n|\rightarrow \infty \). The lemma follows as \(\varepsilon \rightarrow 0\). \(\square \)
The next result is a non-uniqueness result for the random conductance model.
Theorem 5.4
In dimension \(d=2\) and for \(q>1\) sufficiently large there are two distinct Gibbs measures \({\bar{\mu }}_{p_{\mathrm {sd}}}^1\ne {\bar{\mu }}_{p_{\mathrm {sd}}}^0\) at the self-dual point defined by Eq. (1.8).
The proof uses duality of the random conductance model and can be found in Sect. 6. This result easily implies Theorem 2.4.
Proof of Theorem 2.4
Using Proposition 4.19 we infer from Theorem 5.4 the existence of two translation invariant extended gradient Gibbs measures \(\tilde{\mu }_0\) and \(\tilde{\mu }_1\) constructed from \({\bar{\mu }}_{p_{\mathrm {sd}}}^0\ne {\bar{\mu }}_{p_{\mathrm {sd}}}^1\). Their \(\eta \)-marginals \(\mu _0\) and \(\mu _1\) are not equal since then the \(\kappa \)-marginals \({\bar{\mu }}_1\) and \({\bar{\mu }}_2\) would agree. They both have zero tilt by Proposition 4.19 and the definition of \({\tilde{\mu }}\) shows that \({\tilde{\mu }}\) is translation invariant if \({\bar{\mu }}\) is translation invariant. \(\square \)
Remark 5.5
A proof similar to Lemma 3.2 in [7] shows that ergodicity of \({\bar{\mu }}_1\) and \({\bar{\mu }}_2\) implies that \(\mu _0\) and \(\mu _1\) are themselves ergodic. The only difference is that \(\eta \) given \(\kappa \) is not independent (while \(\kappa \) given \(\eta \) is). Instead one has to rely on the decay of correlations for Gaussian fields stated in Appendix B.
Theorem 5.6
For \(d\ge 4\) there is \(q_0>1\) such that for \(p\in [0,1]\) and \(q\in [1,q_0)\) the Gibbs measure for the random conductance model is unique. Similarly, for \(d\ge 4\) and \(q\ge 1\) there is a \(p_0=p_0(q,d)>0\) such that the Gibbs measure is unique for \(p\in [0,p_0)\cup (1-p_0,1]\).
Proof
We are going to apply Dobrushin’s criterion (see, e.g., [21, Theorem 8.7]. The necessary estimate is basically a refined version of the proof of Lemma 4.6. Fix two edges \(f,g\in {\mathbf {E}}({\mathbb {Z}}^d)\). Recall the notation \(\lambda ^{\pm \pm }=\lambda ^{\pm \pm }_{fg}\) and \(\lambda ^\pm =\lambda ^\pm _f\) introduced above Theorem 4.2. We will write \({\bar{\gamma }}_f={\bar{\gamma }}_{\{f\}}\) in the following. Note that (4.52) and \({\bar{\gamma }}_{f}(\lambda ^{+},\lambda )+{\bar{\gamma }}_{f}(\lambda ^{-},\lambda )=1\) imply that
where \({\mathbb {Q}}_{\lambda ^-}\) denotes the weighted spanning forest measure on \({\mathbb {Z}}^d\) with conductances \(\lambda ^-\). We need to bound the entries of the Dobrushin interdependence matrix given by
Since the derivative of the map \(x\mapsto p/(p+(1-p)\sqrt{x})\) is bounded by \(p(1-p)\) for \(x\ge 1\) we conclude that
To simplify the notation we assume \(\lambda =\lambda ^{--}\). We can express \(\mathbb {Q}_{\lambda ^{-+}}(f\in {\varvec{t}})\) through the measure \(\mathbb {Q}_{\lambda ^{--}}=\mathbb {Q}_\lambda \) as follows
A sequence of manipulations then shows that
The numerator can be rewritten using the transfer-current Theorem for two edges (see [4, Page 10] and equation below 4.3 in [27])
where \(I_f^\kappa (g)\) denotes the current through g in a resistor network with conductances \(\kappa \) when 1 unit of current is inserted (respectively removed) at the ends of f (using a fixed orientation of the edges here, e.g., lexicographic). Altogether we have shown that
Using electrical network theory we can express for \(f=(x,x+e_i)\) and \(g=(y,y+e_j)\)
where \(G_\kappa \) denotes the inverse of the operator \(\Delta _\kappa \) which exists in dimension \(d\ge 3\) and whose derivative exists in dimension \(d\ge 2\). The second derivative of the Green function can be bound using Nash–Moser theory. It is shown in Lemma B.2 that there are constants \(C_3(q,d), \alpha (q,d)>0\) depending on the ellipticity contrast of the operator \(\Delta _\kappa \) and and the dimension such that
Combining this bound with (5.17) and (5.18) we conclude for \(f\in {\mathbf {E}}({\mathbb {Z}}^d)\) that
In dimension \(d\ge 4\) the sum is finite. Now, for fixed q, the sum becomes smaller than 1 for p sufficiently close to 0 or 1. Therefore there is \(p_0=p_0(q,d)\) such that the Gibbs measure is unique for \(p\in [0,p_0)\cup (1-p_0,1]\). On the other hand, the constant \(C_3(q,d)\) from Lemma B.2 is decreasing in q. Therefore we can estimate uniformly for \(p\in [0,1]\) and for \(q\le 2\)
Hence the Dobrushin criterion is satisfied for q sufficiently close to 1 and all \(p\in [0,1]\).
\(\square \)
Remark 5.7
-
1.
Note that the gradient-gradient correlations in gradient models at best only decay critically with \(|x|^{-d}\) (which is the decay rate for the discrete Gaussian free field). In particular, the sum of the covariances \(\sum _{g\in {\mathbf {E}}({\mathbb {Z}}^d)} \mathrm {Cov}(\eta _f,\eta _g)\) diverges in this type of model. We use crucially in the previous theorem that the decay of correlations is better for the discrete model: They decay with the square of the gradient-gradient correlations.
-
2.
The averaged (annealed) second order derivative of the Green function decays with the optimal decay rate \(|x|^{-d}\) as shown in [14]. For the application of the Dobrushin criterion we, however need deterministic bounds which are weaker.
-
3.
To extend the uniqueness result for q close to 1 to dimensions \(d=3\) and \(d=2\) one would need estimates for the optimal Hölder exponent \(\alpha \) depending on the ellipticity contrast of discrete elliptic operators. Here the ellipticity contrast can be bounded by q. There do not seem to be any results in this direction in the discrete setting. In the continuum setting the problem is open for \(d\ge 3\), but has been solved for \(d=2\) in [29]. In this case \(\alpha \rightarrow 1\) as the ellipticity contrast converges to 1. A similar result in the discrete setting would imply uniqueness of the Gibbs measure for small q in dimension 2.
Note that we can again lift the uniqueness result for the Gibbs measure of the random conductance model to a uniqueness result for the ergodic gradient Gibbs measures with zero tilt.
Proof of Theorem 2.5
The proof follows from the uniqueness of the discrete Gibbs measure proven in Theorem 5.6 in the same way as the proof of Theorem 2.3 which can be found above Remark 5.2. \(\square \)
5.2 Open questions
Let us end this section by stating one further result and two conjectures regarding the phase transitions of this model. They are most easily expressed in terms of percolation properties of the model even though the interpretation as open and closed bonds is somehow misleading in this context. We write \(x\leftrightarrow y\) for \(x,y\in {\mathbb {Z}}^d\) and \(\kappa \) if there is a path of q-bonds in \(\kappa \) connecting x and y and similarly for sets. Observe that the results of [18] can be applied to the model introduced here and we obtain the existence of a sharp phase transition.
Theorem 5.8
For every q the model undergoes a sharp phase transition in p, i.e., there is \(p_c(q,d)\) such that the following two properties hold. On the one hand there is a constant \(c_1>0\) such that for \(p>p_c\) sufficiently close to \(p_c\)
On the other hand, for \(p<p_c\) there is a constant \(c_p\) such that
Proof
The proof of Theorem 1.2 in [18] for the FK random cluster model applies to this model. Indeed, it only relies on \(\mu _{n,p}^1\) being strongly positively associated and a certain relation for the p derivative of events stated in Theorem 3.12 in [23] which is still true since the p-dependence is the same as for the FK random cluster model. \(\square \)
Remark 5.9
For \(d=2\) the self dual point defined in (1.8) and the critical point agree: \(p_c=p_{\mathrm {sd}}\). This can be seen based on Theorem 1.5 and the arguments used in the proof of Theorem 1.4 in [18] for the FK random cluster model.
In the FK random cluster model the most interesting phenomena happen for \(p=p_c\) and the subcritical and supercritical phase are much simpler to understand (in particular in \(d=2\)). Due to the differences explained in Remark 3.2 those questions seem to be harder for our random conductance model. Nevertheless we conjecture the following stronger version of Theorems 5.1 and 5.6.
Conjecture 5.10
For \(p\ne p_c\) there is a unique Gibbs measure.
Note that the sharpness result Theorem 5.8 shows that the probability of subcritical q-clusters to be large is exponentially small. Nevertheless it is not clear how this can be used to show uniqueness of the Gibbs measure in our setting.
The behaviour at \(p_c\) is also very interesting. A phase transition is called continuous if \(\mu _{p_c}^1(0\leftrightarrow \infty )=0\) and otherwise it is discontinuous. For the FK random cluster model in dimensions \(d=2\) the phase transition is continuous for \(q\le 4\) and otherwise discontinuous. Moreover, the uniqueness of the Gibbs measure at \(p_c\) is equivalent to a continuous phase transition. We do not know whether the same is true for the random conductance model considered here. But we expect the general picture to be true also for the random conductance and we make this precise in a second conjecture.
Conjecture 5.11
There is a \(q_0=q_0(d)\) such that for \(q> q_0\) there is non-uniqueness of Gibbs measures \({\bar{\mu }}_{p_c,q}^1\ne {\bar{\mu }}_{p_c,q}^0\) at the critical point while for \(q<q_0\) the Gibbs measures agree, i.e., \({\bar{\mu }}_{p_c,q}^1={\bar{\mu }}_{p_c,q}^0\).
A partial result in the direction of this conjecture is Theorem 5.4 that states non-uniqueness for large q in dimension \(d=2\) and Theorem 5.6 that shows uniqueness for q close to 1 and \(d\ge 4\).
6 Duality and coexistence of Gibbs measures
In this section we are going to prove that \(\mu ^0_{p_{\mathrm {sd}}}\ne \mu ^1_{p_{\mathrm {sd}}}\) for large q which implies the non-uniqueness of gradient Gibbs measures stated in Theorem 2.4. This is a new proof for the result in [6]. They consider conductances \(q_1\), \(q_2\) with \(q_1q_2=1\) which makes the presentation slightly more symmetric.
In contrast to their work we do not rely on reflection positivity but instead we exploit the planar duality that is already used in [6] to find the location of the phase transition. Therefore it is not possible to extend the argument given here to \(d\ge 3\) while the proof using reflection positivity is in principle independent of the dimension (note that the spin wave calculations in [6] can be simplified substantially and generalised to \(d\ge 3\) using the Kirchhoff formula cf. [10, Section 5.7]). In addition to planar duality we rely on the properties proved in Sect. 4, in particular on the Kirchhoff formula. Similar arguments were developed in the context of the FK random cluster model and we refer to [23, Sections 6 and 7].
We proceed now by stating the duality property in our setting. For a planar graph \(G=(V,E)\) we denote its dual graph by \(G^*=(V^*,E^*)\). The dual graph has the faces of G as vertices and the vertices of G as faces and each edge has a corresponding dual edge. For a formal definition of the dual of a graph and the necessary background we refer to the literature, e.g., [32].
For any configuration \(\kappa :E\rightarrow \{1,q\}\) we define its dual configuration \(\kappa ^*\in \{1, q\}^{E^*}\) by \(\kappa ^*_{e^*}=1+q-\kappa _e\) where \(e^*\in E^*\) denotes the dual edge of an edge \(e\in E\). More generally we denote for \(E_1\subset E\) by \(E_1^*=\{e^*\,:e\in E_1\}\) the dual edges of the edges \(E_1\). We also introduce the notation \(E_1^{\mathrm {d}}=\{e^*\in E^*: e\notin E_1\}=(E_1^\mathrm {c})^*\) for \(E_1\subset E\) for the dual set of an edge subset.
From now on we restrict our attention to finite graphs G except when stated otherwise. Note that \(E_1\) is acyclic if and only if \(E_1^{\mathrm {d}}\) is spanning, i.e., every two points \(x^*, y^*\in V^*\) are connected by a path in \(E_1^{\mathrm {d}}\). In particular, \({\varvec{t}}\subset E\) is a spanning tree in G if and only if \({\varvec{t}}^{\mathrm {d}}\) is a spanning tree in \(G^*\) and the map \({\varvec{t}}\mapsto {\varvec{t}}^d\) is an involution and in particular bijective from \(\mathrm {ST}(G)\) to \(\mathrm {ST}(G^*)\).
Recall that \(h(\kappa ,{\varvec{t}})=| \{e\in {\varvec{t}}: \kappa _e=q\} |\) denotes the number of q-bonds in the set \(t\subset {\mathbf {E}}(G)\) of \(\kappa \) and the similar definition of \(s(\kappa ,{\varvec{t}})\) for the number of soft 1-bonds in \({\varvec{t}}\). The definitions imply that
The last two identities follow from the observation that \(s(\kappa ^*,{\varvec{t}}^{\mathrm {d}})=h(\kappa , E{\setminus } {\varvec{t}})\) and similarly for s and h interchanged. We calculate the distribution of \(\kappa ^*\) if \(\kappa \) is distributed according to \({\mathbb {P}}^{G,p}\)
This implies that if \(\kappa \) is distributed according to \({\mathbb {P}}^{G,p}\) the dual configuration \(\kappa ^*\) is distributed according to \({\mathbb {P}}^{G^*, p^*}\) where \(q^*=q\) and
Note that the self dual point \(p_{\mathrm {sd}}\) defined by \(p_{\mathrm {sd}}^*=p_{\mathrm {sd}}\) is given by the solution of
We will now restrict our attention to \({\mathbb {Z}}^2\). Let us mention that detailed proofs of the topological statements we use can be found in [26].
We can identify the dual of the graph \(({\mathbb {Z}}^2,{\mathbf {E}}({\mathbb {Z}}^2))\), which will be denoted by \((({\mathbb {Z}}^2)^*,{\mathbf {E}}({\mathbb {Z}}^2)^*)\), with \({\mathbb {Z}}^2\) shifted by the vector \(w=(\tfrac{1}{2},\tfrac{1}{2})\). We also consider the set of directed bonds \(\mathbf {{\mathbf {E}}}({\mathbb {Z}}^2)\) and \(\mathbf {{\mathbf {E}}}({\mathbb {Z}}^2)^*\). For a directed bond \(\mathbf {e}=(x,y)\in {\mathbf {E}}({\mathbb {Z}}^2)\) we define its dual bond as the directed bond \(\mathbf {e}^*=(\tfrac{1}{2}(x+y+(x-y)^\perp ),\tfrac{1}{2} (x+y+(y-x)^\perp )\) where \(\perp \) denotes counter-clockwise rotation by \(90^\circ \), i.e., the linear map that satisfies \(e_1^\perp =e_2\), \(e_2^\perp =-e_1\). In other words, the dual of a directed bond \(\mathbf {e}\) is the bond whose orientation is rotated by \(90^\circ \) counter-clockwise and crosses \(\mathbf {e}\).
Every point \(x\in {\mathbb {Z}}^2\) determines a plaquette with corners \(z_1,z_2,z_3,z_4\in ({\mathbb {Z}}^2)^*\) where \(z_i\) are the four nearest neighbours of x in \(({\mathbb {Z}}^2)^*\) and the plaquette has faces \(e_1^*,e_2^*, e_3^*, e_4^*\in {\mathbf {E}}({\mathbb {Z}}^2)^*\) where \(e_i^*\) are the dual bonds of the four bonds \(e_i\) that are incident to x. Vice versa every point \(z\in ({\mathbb {Z}}^2)^*\) determines a plaquette in \({\mathbb {Z}}^2\). We write \({\mathbf {P}}({\mathbb {Z}}^2)\) for the set of plaquettes of \({\mathbb {Z}}^2\).
For a bond \(e=\{x,y\}\) we define the shifted dual bond \(e+w=\{x+w,y+w\}\). Similarly, we define \(E+w=\{e+w\in {\mathbf {E}}({\mathbb {Z}}^2)^*\,: \,e\in E\}\) for a set \(E\subset {\mathbf {E}}({\mathbb {Z}}^2)\). For a subgraph \(G\subset {\mathbb {Z}}^2\) we denote by \({\mathbf {P}}(G)=\{P\in {\mathbf {P}}({\mathbb {Z}}^2): \text {all faces of } P \text { are in } {\mathbf {E}}(G)\}\) the plaquettes of G. A subgraph \(G\subset {\mathbb {Z}}^2\) is called simply connected if the union of all vertices \(v\in {\mathbf {V}}(G)\), all edges \(\{x,y\}\in {\mathbf {E}}(G)\) which are identified with the line segment from x to y in \({\mathbb {R}}^2\) and all plaquettes \({\mathbf {P}}(G)\) is a simply connected subset of \({\mathbb {R}}^2\). An important tool in the analysis of planar models from statistical mechanics is the use of contours which are suitably defined circuits. Below we provide a notion of contours adapted to our setting that is slightly more complicated than for the FK random cluster model. We consider closed paths \(\gamma =(x_1^*,\ldots ,x_n^*,x_1^*)\) with \(x_i^*\in ({\mathbb {Z}}^2)^*\) (not necessarily all distinct) along pairwise distinct directed dual bonds \(\mathbf {b}_1^*=(x_1^*,x_2^*),\ldots , \mathbf {b}_n^*=(x_n^*,x_1^*)\). We denote the vertices of the path by \({\mathbf {V}}(\gamma )^*=\{ x_i^*\, :\, 1\le i\le n\}\) and the bonds by \(\mathbf {{\mathbf {E}}}(\gamma )^*=\{\mathbf {b}_i^*\,:\, 1\le i\le n\}\). Similarly we write \(\mathbf {{\mathbf {E}}}(\gamma )=\{\mathbf {b}_i\,:\, 1\le i\le n\}\) for the corresponding primal bonds. We also consider the underlying sets of undirected bonds \({\mathbf {E}}(\gamma )\) and \({\mathbf {E}}(\gamma )^*\). Finally, we denote the heads and tails of \(\mathbf {b}_i\) by \(y_i\) and \(z_i\), i.e., \(\mathbf {b}_i=(z_i,y_i)\).
Definition 6.1
A contour \(\gamma \) is a closed path in the dual lattice without self-crossings in the sense that there is a bounded connected component \(\mathrm {int}(\gamma )\) of the graph \(({\mathbb {Z}}^2,{\mathbf {E}}({\mathbb {Z}}^2){\setminus } {\mathbf {E}}(\gamma ))\) such that \(\partial (\mathrm {int}(\gamma ))=\{z_i\,:\, 1\le i\le n\}\). We denote the union of the remaining connected components by \(\mathrm {ext}(\gamma )\) and we define the length \(|\gamma |\) of the contour as the number of (directed) bonds it contains, i.e., \(|\gamma |=|\mathbf {{\mathbf {E}}}(\gamma )|=n\).
Note that \(\mathrm {ext}(\gamma )\) is not necessarily connected and that \(\{x,y\}\in {\mathbf {E}}(\gamma )\) if \(x\in \mathrm {int}(\gamma )\) and \(y\in \mathrm {ext}(\gamma )\) (see Fig. 1).
Examples of q-contours. In the second example there are two nested q-contours. Curly bonds indicate soft bonds with \(\kappa _e=1\) and straight bonds indicate hard bonds with \(\kappa _e=q\). In red the dual bonds of the contours are shown. The horizontal curly bond in the top middle connects two point in \(\mathrm {int}\,\gamma \) (colour figure online)
Contours are a suitable notion to define interfaces between hard and soft bonds.
Definition 6.2
A contour \(\gamma \) is a q-contour for \(\kappa \) if the following two conditions hold. First, the primal bonds \(b\in {\mathbf {E}}(\gamma )\) are soft, i.e., \(\kappa _{b}=1\). Moreover, for every plaquette with centre \(x^*\in {\mathbf {V}}(\gamma )^*\) all its faces b such that \(b\in {\mathbf {E}}(\mathrm {int}(\gamma ))\) are hard, i.e., satisfy \(\kappa _b=q\).
Our goal is to show that q-contours are unlikely for large values of q and \(p\le p_{\mathrm {sd}}\). We now fix a contour \(\gamma \) and introduce some useful notation and helpful observations for the proof of the following theorem. We use the shorthand \(G_\mathrm {int}=\mathrm {int}(\gamma )\) and \(E_\mathrm {int}={\mathbf {E}}(\mathrm {int}(\gamma ))\). We observe that \(G_\mathrm {int}\) is simply connected because \(\gamma \) is connected and without self-crossings. Therefore the faces of \(G_\mathrm {int}\) consist of plaquettes in \({\mathbb {Z}}^2\) and one infinite face. We also consider the graph G with edges \(E=E_\mathrm {int}\cup {\mathbf {E}}(\gamma )\) and endpoints of edges as vertices. Let \({\bar{1}}\in \{1,q\}^{E}\) denote the configuration given by \({\bar{1}}_e=1\) for all \(e\in E\). We write \(G^w=G/\partial G=G/ \mathrm {ext}(\gamma )\) for the graph G with wired boundary conditions. Moreover we introduce the graph \(H^*\) with edges \(E_\mathrm {int}^*\) and their endpoints as vertices. We claim that \(H^*/\partial H^*\) agrees with the graph theoretic dual of \(G_\mathrm {int}\). To show this we need to prove that we identify all vertices that lie in the same face of \(G_\mathrm {int}\). First we note that every point in \({(H^\circ )}^*=H^*{\setminus } \partial H^*\) determines a plaquette in \({\mathbf {P}}(G_\mathrm {int})\) and this is a bijection. Then it remains to show that all vertices in \(\partial H^*\) lie in the infinite face of \(G_\mathrm {int}\). This follows from the observation
To show the observation we note that if \(x^*\in \partial H^*\) then there are edges \(e^*_1 \notin {\mathbf {E}}(H^*)\) and \(e^*_2\in {\mathbf {E}}(H^*)\) incident to \(x^*\). This implies that there is a face \(e'=\{z_1,z_2\}\) of the plaquette with centre \(x^*\) such that \(z_1\in {\mathbf {V}}(G_\mathrm {int})\) but \(e'\notin {\mathbf {E}}(G_\mathrm {int})\). Then \(e\in {\mathbf {E}}(\gamma )\) and therefore \(x^*\in {\mathbf {V}}(\gamma )^*\) because \(x^*\) is an endpoint of \(e^*\in {\mathbf {E}}(\gamma )^*\). This ends the proof of the inclusion ‘\(\subset \)’. Now we note that if \(x^*\in {\mathbf {V}}(H^*)\cap {\mathbf {V}}(\gamma )^*\) there is an edge \(e^*\in {\mathbf {E}}(\gamma )^*\) incident to \(x^*\) which is not contained in \({\mathbf {E}}(H^*)\) and therefore \(x^*\in \partial H^*\).
Finally we remark that if \(\gamma \) is a q-contour for \(\kappa \) then
Indeed, we argued above that if \(e^*\in {\mathbf {E}}(H^*)\) is incident to \( \partial H^*\) then \(x^*\in {\mathbf {V}}(\gamma )^*\). Thus \(e\in E_\mathrm {int}\) is a face of the plaquette with centre \(x^*\) so that the definition of q-contours implies that \(\kappa _{e}=q\).
Theorem 6.3
Let \(\gamma \) be a contour and let \(G=G(\gamma )\) and \(E_\mathrm {int}=E_\mathrm {int}(\gamma )\) be defined as above. The probability that \(\gamma \) is a q-contour under the measure \({\mathbb {P}}^{G^w, E_IN,{\bar{1}}}\) for \(p=p_{\mathrm {sd}}\) is bounded by
Remark 6.4
The general idea of the proof is the same as when proving similar estimates for the Ising model. One tries to find a map from configurations where the contour is present to configurations where this is not the case and then estimates the corresponding probabilities. The more similar argument for the FK random cluster model can be found, e.g., in Theorem 6.35 in [23]. For an illustrated version see [17].
Proof
We denote the set of all \(\kappa \in \{1,q\}^{E}\) such that \(\gamma \) is a q-contour for \(\kappa \) by \(\Omega _\gamma \).
Step 1 We define a map \(\Phi :\Omega _\gamma \rightarrow \{1,q\}^{E}\) with \(\Phi (\kappa )=\kappa ^\#\) as follows. Recall the definition of the dual configuration \(\kappa ^*\) on \(E^*\subset {\mathbf {E}}({\mathbb {Z}}^2)^*\) and define for \(e\in E\)
We claim that
By definition of \(\kappa ^{\#}\), we only need to consider the case \(e-w\in {E_\mathrm {int}}^*={\mathbf {E}}(H^*)\). We will show a slightly more general statement. Let us introduce the set \({\tilde{E}}={\mathbf {E}}(H^*)+w=E_\mathrm {int}^*+w\subset E\) and the graph \({{\tilde{G}}} \) consisting of the edges \({{\tilde{E}}}\) and their endpoints as vertices. See Fig. 2 for an illustration of this construction. We remark that \({\tilde{G}}\) agrees with \(H^*\) shifted by w, which we denote by \({\tilde{G}}=H^*+w\). Equation (6.7) implies that
because then \(e-w\in {\mathbf {E}}(H^*)\) is incident to \(\partial H^*\). It remains to show that all edges \(e\in E\cap {\tilde{E}}{\setminus } E_\mathrm {int}\) are incident to \(\partial {\tilde{G}}\). From \(e\in E{\setminus } E_\mathrm {int}\) we conclude that \(e\in {\mathbf {E}}(\gamma )\). The edge \(e-w\) has a common endpoint with \(e^*\in {\mathbf {E}}(\gamma )^*\) and is therefore incident to \({\mathbf {V}}(\gamma )^*\) in this case. Using the observation (6.6) this implies that \(e-w\in {\mathbf {E}}(H^*)\) is incident to \(\partial H^*\).
(Left) The dashed line indicates a q-contour for the depicted configuration. In red the dual configuration on \(E^*\) for the edges E is shown. (Right) The configuration \(\kappa ^\#\) for \(\kappa \) depicted on the left. The red edges are the shifted dual edges forming the set \({\tilde{E}}\) (colour figure online)
Our goal is to compare the probabilities of \({\mathbb {P}}^{G^w,E_\mathrm {int},{\bar{1}}}(\kappa _{E_\mathrm {int}})\) and \({\mathbb {P}}^{G^w,E_\mathrm {int},{\bar{1}}}(\kappa ^{\#}_{E_\mathrm {int}})\). To achieve this we use a strategy similar to the proof of Lemma 5.3.
Step 2 We define a map \(\Psi :\mathrm {ST}(G^w)\rightarrow \mathrm {ST}(G^w)\) with \(\Psi ({\varvec{t}}^{\#})= {\varvec{t}}\) in the following steps
-
1.
We choose deterministically a subset \({\tilde{{\varvec{t}}}}\subset {\varvec{t}}^{\#}{\restriction }_{{\tilde{E}}}\) such that \({\tilde{{\varvec{t}}}}\) is a spanning tree on \({\tilde{G}}/\partial {{\tilde{G}}}\) and all edges in \({\varvec{t}}^\#{\restriction }_{{\tilde{E}}}{\setminus } {\tilde{{\varvec{t}}}}\) are incident to \(\partial {\tilde{G}}\).
-
2.
We set \(\Psi ({\varvec{t}}^\#){\restriction }_{E_\mathrm {int}}=\{e\in E_\mathrm {int}\, :\, e^*\notin {\tilde{{\varvec{t}}}}-w\}= (\tilde{{\varvec{t}}}-w)^d\) (as a subset of \(E_\mathrm {int}^*\)).
-
3.
We consider a fixed \(b\in {\mathbf {E}}(\gamma )\) that is incident to \(\mathrm {int}(\gamma )\) and \(\mathrm {ext}(\gamma )\) and we define \({\varvec{t}}=\Psi ({\varvec{t}}^\#)=\Psi ({\varvec{t}}^\#){\restriction }_{E_\mathrm {int}}\cup b\)
See Fig. 3 for an illustration of the construction.
We have to show that this construction is possible, in particular that \(t\in \mathrm {ST}(G^w)\). We start with the first step. The relation \({\tilde{G}}\subset G\) implies
Hence \({\tilde{G}}/\partial {\tilde{G}}\) agrees with \((G/\partial G)/({{\tilde{G}}}^{\mathrm {c}}\cup \partial {\tilde{G}})\) up to self loops. This implies that \({\varvec{t}}^{\#}{\restriction }_{{\tilde{E}}}\) is spanning in \({{\tilde{G}}}/\partial {{\tilde{G}}}\) if \({\varvec{t}}^{\#}\in \mathrm {ST}(G^w)\). We consider the subset \({\varvec{t}}'\subset {\varvec{t}}^{\#}{\restriction }_{{\tilde{E}}}\) consisting of all edges \(e\in {\varvec{t}}^{\#}{\restriction }_{{\tilde{E}}}\) that are not incident to \(\partial {{\tilde{G}}}\). The set \({\varvec{t}}'\) contains no cycles because \({\varvec{t}}^{\#}\in \mathrm {ST}(G^w)\) and no edge in \({\varvec{t}}'\) is incident to \(\partial G\) by (6.12). Therefore we can select a spanning tree \({\tilde{{\varvec{t}}}}\) in \({\tilde{G}}/\partial {{\tilde{G}}}\) with \({\varvec{t}}'\subset {\tilde{{\varvec{t}}}}\subset {\varvec{t}}^{\#}{\restriction }_{{\tilde{E}}}\) deterministically, e.g., using Kruskal’s algorithm.
We now argue that the second and third step yield a spanning tree in \(G^w\). Clearly it is sufficient to show that \(\Psi ({\varvec{t}}^\#){\restriction }_{E_\mathrm {int}}\in \mathrm {ST}(G_\mathrm {int})\). We note that the relation between \({\tilde{G}}\) and \(H^*\) implies that \(\tilde{{\varvec{t}}}-w\) is a spanning tree on \(H^*/\partial H^*\). As shown before the theorem \(H^*/\partial H^*\) agrees with the dual of \(G_\mathrm {int}\) and thus \((\tilde{{\varvec{t}}}-w)^d \in \mathrm {ST}(G_\mathrm {int})\).
Step 3 The next step is to consider \(\kappa ^\#=\Phi (\kappa )\) and \({\varvec{t}}=\Psi ({\varvec{t}}^\#)\) and compare the weights \(w(\kappa ^\#,{\varvec{t}}^\#)\) and \(w(\kappa ,{\varvec{t}})\). First we argue that
Since \(\tilde{{\varvec{t}}}\subset {\varvec{t}}^\#\) it is sufficient to show that \({\varvec{t}}^\#{\setminus } {\tilde{{\varvec{t}}}}\) contains only edges e such that \(\kappa ^\#_e=1\). Indeed, let e be an edge in \({\varvec{t}}^\#{\setminus } {\tilde{{\varvec{t}}}}\). For \(e\notin {{\tilde{E}}}\) we have \(\kappa ^\#_e=1\) by definition. Let us now consider
By construction of \({\tilde{{\varvec{t}}}}\) the edge e is incident to a vertex \(v\in \partial {\tilde{G}}\). This implies that \(e-w\in {\mathbf {E}}(H^*)\) is incident to \(v-w\in \partial H^*\subset {\mathbf {V}}(\gamma )^*\). Using (6.7) we conclude that
For the trees \(\tilde{{\varvec{t}}}\) and \(\Psi ( {\varvec{t}}^\#){\restriction }_E\) we can apply the usual duality relations stated before. Using (6.2) and as before \(\kappa ^\#=\Phi (\kappa )\) and \({\varvec{t}}=\Psi ({\varvec{t}}^\#)\) we obtain
We compute
In the last step we used that \({\varvec{t}}\cap E_\mathrm {int}\) is a free spanning tree on \(G_\mathrm {int}\) and therefore has \(|{\mathbf {V}}(G_\mathrm {int})|-1\) edges.
Step 4 We bound the number of preimages of a tree \({\varvec{t}}\) under \(\Psi \). Note that \(\Psi \) factorizes into two maps \({\varvec{t}}^\#\rightarrow {\tilde{{\varvec{t}}}}\rightarrow {\varvec{t}}\). The second map is injective since we only pass to the dual tree which is an injective map and we add one additional edge. For the first map we observe that we only delete edges e incident to \(\partial {{\tilde{G}}}\). However, for \(x\in \partial {{\tilde{G}}}\) the point \(x-w\in \partial H^*\) is contained in the contour by (6.6). Therefore there are at most \(4|\gamma |\) such edges. We conclude that
for every \({\varvec{t}}\in \mathrm {ST}(G^w)\). The displays (6.17) and (6.18) imply
Step 5 We can now estimate the probabilities of the patterns \(\kappa \) and \(\kappa ^\#=\Psi (\kappa )\) under \({\mathbb {P}}^{G^w,E_\mathrm {int},{\bar{1}}}\) using (6.19) and \(\kappa ^\#_e=1={\bar{1}}_e\) for \(e\in E{\setminus } E_\mathrm {int}\)
where we used Eq. (6.5) of \(p_{\mathrm {sd}}\) in the last step. The definition of \(\kappa ^\#\) implies that \(h(\kappa ^\#,E_\mathrm {int})=h(\kappa ^\#,{\tilde{E}})=s(\kappa ,E_\mathrm {int})\) and we get
Now we observe that \(4|{\mathbf {V}}(G_\mathrm {int})|-2|{\mathbf {E}}(G_\mathrm {int})|=|\mathbf {{\mathbf {E}}}(\gamma )| =|\gamma |\). We end up with the estimate
Conclusion Note that the map \(\Phi \) is injective, hence
\(\square \)
Using correlation inequalities we can derive the following stronger version of the previous theorem. For a simply connected subgraph \(H\subset {\mathbb {Z}}^2\) we say that \(\gamma \) is contained in H if all faces of plaquettes with centre \(x^*\) for \(x^*\in {\mathbf {V}}(\gamma )^*\) are contained in \({\mathbf {E}}(H)\).
Corollary 6.5
For any \(p\le p_{\mathrm {sd}}\), any finite simply connected subgraph \(H\subset {\mathbb {Z}}^2\), and a contour \(\gamma \) that is contained in H the probability that \(\gamma \) is a q-contour can be estimated by
Proof
We estimate
For the measure \({\mathbb {P}}^{H,{\mathbf {E}}(H){\setminus } {\mathbf {E}}(\gamma ),{\bar{1}}}\) the bonds crossing the contour are fixed to the correct value. Hence the event that \(\gamma \) is a q-contour for \(\kappa \) is increasing, such that the stochastic domination results proved in Corollaries 4.9 and 4.12 imply that
where G denotes the graph corresponding to \(\gamma \) as introduced above Theorem 6.3. Theorem 6.3 implies the claim. \(\square \)
We can now give a new proof for the coexistence result stated in Theorem 2.4.
Proof of Theorem 5.4
First we note that the duality between free and wired boundary conditions in finite volume implies that \(\mu ^0_{p_{\mathrm {sd}}}\) and \(\mu ^1_{p_{\mathrm {sd}}}\) are dual to each other in the sense that if \(\kappa \sim \mu ^0_{p_{\mathrm {sd}}}\) then \(\kappa ^*\sim \mu ^1_{p_{\mathrm {sd}}}\) (on \(({\mathbb {Z}}^2)^*)\)). The proof is the same as for the FK random cluster model, see, e.g., [23, Chapter 6]. Hence, it is sufficient to show that \(\mu ^0_{p_{\mathrm {sd}}}(\kappa _e=q)<1/2\) because then we can conclude that
whence \({\bar{\mu }}_{p_{\mathrm {sd}}}^1\ne {\bar{\mu }}_{p_{\mathrm {sd}}}^0\).
Note that if \(\kappa _e=q\) and there is any contour \(\gamma \) such that \(e\in {\mathbf {E}}(\mathrm {int}(\gamma ))\) and \(\kappa _b=1\) for \(b\in {\mathbf {E}}(\gamma )\) then there is a q-contour surrounding e. We can thus estimate for \(e\in E_n\)
where as before \({\bar{1}}_e=1\) for all e. The shortest contour \(\gamma \) that surrounds the edge e has length 6 so the bound in Corollary 6.5 implies that \({\mathbb {P}}^{\Lambda _{n+1},E_n,{\bar{1}}}(\gamma \text { is a } q\text {-contour})\le C/q^{\frac{1}{4}}\) for any \(\gamma \) surrounding e. Using Corollary 4.12 we can compare boundary conditions to obtain the relation \({\bar{\mu }}_n^0\precsim {\mathbb {P}}^{\Lambda _{n+1},E_n,{\bar{1}}}\). This and a standard Peierls argument imply for q sufficiently large
Taking the limit \(n\rightarrow \infty \) we obtain \({\bar{\mu }}_{p_{\mathrm {sd}}}^0(\kappa _e=q)\le \tfrac{1}{4}\). \(\square \)
References
Adams, S., Buchholz, S., Kotecký, R., Müller, S.: Cauchy-born rule from microscopic models with non-convex potentials. arXiv preprint arXiv:1910.13564v1 (2019)
Adams, S., Kotecký, R., Müller, S.: Strict convexity of the surface tension for non-convex potentials. arXiv preprint arXiv:1606.09541 (2016)
Armstrong, S., Kuusi, T., Mourrat, J.-C.: Quantitative Stochastic Homogenization and Large-Scale Regularity, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 352. Springer, Cham (2019)
Benjamini, I., Lyons, R., Peres, Y., Schramm, O.: Uniform spanning forests. Ann. Probab. 29(1), 1–65 (2001)
Billingsley, P.: Convergence of Probability Measures. Wiley Series in Probability and Statistics: Probability and Statistics, 2nd edn. Wiley, New York (1999)
Biskup, M., Kotecký, R.: Phase coexistence of gradient Gibbs states. Probab. Theory Relat. Fields 139(1–2), 1–39 (2007)
Biskup, M., Spohn, H.: Scaling limit for a class of gradient fields with nonconvex potentials. Ann. Probab. 39(1), 224–251 (2011)
Brascamp, H.J., Lieb, E.H.: On extensions of the Brunn–Minkowski and Prékopa–Leindler theorems, including inequalities for log concave functions, and with an application to the diffusion equation. J. Funct. Anal. 22(4), 366–389 (1976)
Brydges, D.C., Spencer, T.: Fluctuation estimates for sub-quadratic gradient field actions. J. Math. Phys. 53(9), 095216, 5 (2012)
Buchholz, S.: Renormalisation in discrete elasticity. Dissertation, University of Bonn (2019)
Cotar, C., Deuschel, J.-D.: Decay of covariances, uniqueness of ergodic component and scaling limit for a class of \(\nabla \phi \) systems with non-convex potential. Ann. Inst. Henri Poincaré Probab. Stat. 48(3), 819–853 (2012)
Cotar, C., Deuschel, J.-D., Müller, S.: Strict convexity of the free energy for a class of non-convex gradient models. Commun. Math. Phys. 286(1), 359–376 (2009)
Delmotte, T.: Inégalité de Harnack elliptique sur les graphes. Colloq. Math. 72(1), 19–37 (1997)
Delmotte, T., Deuschel, J.-D.: On estimating the derivatives of symmetric diffusions in stationary random environment, with applications to \(\nabla \phi \) interface model. Probab. Theory Relat. Fields 133(3), 358–390 (2005)
Deuschel, J.-D., Nishikawa, T., Vignaud, Y.: Hydrodynamic limit for the Ginzburg–Landau \(\nabla \varphi \) interface model with non-convex potential. Stoch. Process. Appl. 129(3), 924–953 (2019)
Devroye, L., Mehrabian, A., Reddad, T.: The total variation distance between high-dimensional Gaussians. arXiv preprint arXiv:1810.08693 (2018)
Duminil-Copin, H.: Lectures on the Ising and Potts Models on the Hypercubic Lattice, Random Graphs, Phase Transitions, and the Gaussian Free Field. Springer Proceedings in Mathematics and Statistics, vol. 304, pp. 35–161. Springer, Cham (2020)
Duminil-Copin, H., Raoufi, A., Tassion, V.: Sharp phase transition for the random-cluster and Potts models via decision trees. Ann. Math. (2) 189(1), 75–99 (2019)
Funaki, T.: Stochastic Interface Models, Lectures on Probability Theory and Statistics. Lecture Notes in Mathematics, vol. 1869, pp. 103–274. Springer, Berlin (2005)
Funaki, T., Spohn, H.: Motion by mean curvature from the Ginzburg–Landau \(\nabla \phi \) interface model. Commun. Math. Phys. 185(1), 1–36 (1997)
Georgii, H.-O.: Gibbs Measures and Phase Transitions. de Gruyter Studies in Mathematics, vol. 9, 2nd edn. Walter de Gruyter & Co., Berlin (2011)
Giacomin, G., Olla, S., Spohn, H.: Equilibrium fluctuations for \(\nabla \phi \) interface model. Ann. Probab. 29(3), 1138–1172 (2001)
Grimmett, G.: The Random-Cluster Model, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 333. Springer, Berlin (2006)
Hilger, S.: Scaling limit and convergence of smoothed covariance for gradient models with non-convex potential. arXiv preprint arXiv:1603.04703 (2016)
Holley, R.: Remarks on the \({\rm FKG}\) inequalities. Commun. Math. Phys. 36, 227–231 (1974)
Kesten, H.: Percolation Theory for Mathematicians, Progress in Probability and Statistics, vol. 2. Birkhäuser, Boston (1982)
Lyons, R., Peres, Y.: Probability on Trees and Networks, Cambridge Series in Statistical and Probabilistic Mathematics, vol. 42. Cambridge University Press, New York (2016)
Naddaf, A., Spencer, T.: On homogenization and scaling limit of some gradient perturbations of a massless free field. Commun. Math. Phys. 183(1), 55–84 (1997)
Piccinini, L.C., Spagnolo, S.: On the Hölder continuity of solutions of second order elliptic equations in two variables. Ann. Scuola Norm. Sup. Pisa (3) 26, 391–402 (1972)
Sheffield, S.: Random surfaces, Astérisque, no. 304, vi+175 (2005)
Strassen, V.: The existence of probability measures with given marginals. Ann. Math. Stat. 36, 423–439 (1965)
Tutte, W.T.: Graph Theory, Encyclopedia of Mathematics and its Applications, vol. 21. Cambridge University Press, Cambridge (2001). With a foreword by Crispin St. J. A. Nash-Williams, Reprint of the 1984 original
Velenik, Y.: Localization and delocalization of random interfaces. Probab. Surv. 3, 112–169 (2006)
Ye, Z.: Models of gradient type with sub-quadratic actions. J. Math. Phys. 60(7), 073304, 26 (2019)
Zahradník, M.: Contour Methods and Pirogov–Sinai Theory for Continuous Spin Lattice Models, On Dobrushin’s Way, From Probability Theory to Statistical Physics. American Mathematical Society Translations: Series 2, vol. 198, pp. 197–220. American Mathematical Society, Providence (2000)
Acknowledgements
This work was supported by the CRC 1060 The mathematics of emergent effects and by the Hausdorff Center for Mathematics (GZ 2047/1, Projekt-ID 390685813) through the Bonn International Graduate School of Mathematics. The author would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme Scaling limits, rough paths, quantum field theory where work on this paper was undertaken. This work was supported by EPSRC Grant No. EP/K032208/1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Proofs of Propositions 4.18 and 4.19
In this section we pay the last remaining debt of proving two propositions from Sect. 2.
Proof of Proposition 4.18
For \(\lambda \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) and \(E\subset {\mathbf {E}}({\mathbb {Z}}^d)\) finite we define the cylinder event
With a slight abuse of notation we drop the pullback from the notation when we consider the set \(\pi _2^{-1}({\mathbf {A}}(\lambda _E))\subset {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}\times \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\). Since all local cylinder events in \({\mathcal {F}}\) can be written as a union of events of the form \({\mathbf {A}}(\lambda _{E_L})\) it is by Remark 2.2 sufficient to show
for all \(L,n\ge 0\) and all \(\lambda \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\). Using the quasilocality of \({\bar{\gamma }}\) stated in Corollary 4.17 and Remark 4.21 in [21] it is sufficient to consider \(L=n\) and we will do this in the following. We are going to show the claim in a series of steps.
Step 1 We investigate the distribution of the \(\kappa \)-marginal conditioned on \(\omega {_{E_N^{\mathrm {c}}}}\).
Since \({\tilde{\mu }}\) is a gradient Gibbs measure we know by (3.2) that for \(\omega \in {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}_g\) and \(\kappa \in \{1,q\}^{{\mathbf {E}}(\Lambda )}\)
where Z is the normalisation and
denotes the partition function corresponding to the configuration \(\kappa \). Let \(\varphi \in {\mathbb {R}}^{{\mathbb {Z}}^d}\) be the configuration such that \(\nabla \varphi =\omega \) and \(\varphi (0)=0\). We denote by \(\chi _\kappa \) the corrector of \(\kappa \), i.e., the solution of \(\nabla ^*\kappa \nabla \chi _\kappa =0\) with boundary values \(\varphi _{\Lambda ^{\mathrm {c}}}\). A shift of the integration variables and Gaussian calculus implies [see also (3.4)]
where \({\bar{0}}\) is the configuration with vanishing gradients, i.e., \({\bar{0}}_e=0\) for \(e\in {\mathbf {E}}({\mathbb {Z}}^d)\). The necessary calculation to obtain (A.5) basically agrees with the calculation that shows that the discrete Gaussian free field can be decomposed in a zero boundary discrete Gaussian free field and a harmonic extension. We now restrict our attention to \(\Lambda =\Lambda _N=[-N,N]^d\cap {\mathbb {Z}}^d\) for \(N\in \mathbb {N}\). We introduce the law of the \(\kappa \)-marginal for wired non-constant boundary conditions for \(\kappa \in \{1,q\}^{E_N}\) by
Note that \({\bar{\mu }}^{1,{\bar{0}}}_N={\bar{\mu }}^{1}_N\) where \({\bar{\mu }}^{1}_N\) was defined in (4.36).
Step 2 In this step we are going to show that for every \(\varepsilon >0\) there is \(N_0\in \mathbb {N}\) depending on n and \(\varepsilon \) such that for \(N\ge N_0\) and uniformly in \(\lambda \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\)
i.e., the boundary effect is negligible. We start by showing that typically the difference between the corrector energies for configurations \(\kappa \) and \({\tilde{\kappa }}\) that only differ in \(E_n\) will be small. This will allow us to estimate the difference between \({\bar{\mu }}^1_N\) and \({\bar{\mu }}^{1,\omega }_N\) conditioned to agree close to the boundary.
Recall that we consider the case that \(\Lambda =\Lambda _N\) is a box. The Nash–Moser estimate stated in Lemma B.1 combined with the maximum principle for the equation \(\nabla ^*\kappa \nabla \chi _\kappa =0\) imply for \(b\in E_n\) and some \(\alpha =\alpha (q)>0\)
We introduce the event \(\varvec{M}(N)=\{\omega : \max _{x\in \partial \Lambda _N}\varphi (x)-\min _{y\in \partial \Lambda _N}\varphi (y)\le (\ln N)^3\}\). Consider configurations \(\kappa , {\tilde{\kappa }}\in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) such that \(\kappa _e={\tilde{\kappa }}_e\) for \(e\notin E_n\). Using the fact that the corrector is the minimizer of the quadratic form \((\nabla \chi _\kappa ,\kappa \nabla \chi _\kappa )_{E_N}\) with given boundary condition we can estimate
From (A.8) we infer that for \(N\ge 2n\) and \(\varphi \in {\mathbf {M}}(N)\)
By choosing \(N_1\ge 2n\) sufficiently large we can ensure that for \(N\ge N_1\), \(\varphi \in {\mathbf {M}}(N)\), and uniformly in \(\kappa , {\tilde{\kappa }}\) as before
Using this in (A.5) we conclude that for \(N\ge N_1\vee 2n\), \(\omega \in {\mathbf {M}}(N)\), \(\varepsilon <1/3\), and \(\lambda \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\)
This implies
From Lemma A.1 below and Proposition 4.20 we infer that for an extended gradient Gibbs measure \({\tilde{\mu }}\) associated to an ergodic zero tilt Gibbs measure \(\mu \) and any \(\lambda \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\)
for all \(N\ge N_2\) and \(N_2\) sufficiently large. We conclude that for \(N\ge N_0:= N_1\vee N_2\vee 2n\)
Step 3 Using the previous results we can now finish the proof. We rewrite
The identity above and the fact that \({\bar{\gamma }}_{E_n}\) is proper imply adding and subtracting the same term
We continue to estimate the right hand side of this expression. We start with the first term. Since \({\bar{\mu }}^1_{\Lambda _N}\) is a finite volume Gibbs measure [see (4.60)] we have for \({\mathbf {A}}\in {\mathcal {F}}_{E_N}\)
Using this and the bound (A.7) we obtain for \(N\ge N_0\)
We now address the second term on the right hand side of (A.17). By Lemma 4.16 there is \(N_3\) such that for \(N\ge N_3\) and any \(\lambda ,\sigma \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\)
This implies for \(N\ge N_3\)
Using (A.17), (A.19), and (A.21) we conclude that for any \(\varepsilon >0\)
This ends the proof. \(\square \)
The following simple lemma was used in the proof of Proposition 4.18.
Lemma A.1
Let \(\lambda \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) and denote by \(\varphi ^\lambda \) the centred Gaussian field on \({\mathbb {Z}}^d\) with \(\varphi (0)=0\) and covariance \(\Delta _\lambda ^{-1}\). Then \(\varphi ^\lambda \) satisfies
Proof
We use the notation \({\bar{1}}\in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) for the configuration given by \({\bar{1}}_e=1\) for \(e\in {\mathbf {E}}({\mathbb {Z}}^d)\). The Brascamp–Lieb inequality (see [8, Theorem 5.1]) implies for the centred Gaussian fields \(\varphi ^\lambda \) and \(\varphi ^{{\bar{1}}}\) that
It is well known that for a centred Gaussian random vector \(X\in {\mathcal {P}}({\mathbb {R}}^m)\) with \(\mathbb {E}(X_i^2)\le \sigma ^2\) the expectation of the maximum is bounded by
Indeed, this bound can be established by noting that for any t we have using Jensen’s inequality
Taking the logarithm and setting \(t=\sqrt{2\ln m}/\sigma \) we get (A.25).
We use (A.25) for the Gaussian field \(\varphi ^\lambda \) and conclude that
A simple Markov bound implies that there is \(C=C(d)>0\) such that
\(\square \)
It remains to provide a proof of Proposition 4.19. We will only sketch the argument.
Proof of Proposition 4.19
Let us denote the law of the Gaussian gradient field \(\nabla \varphi ^\kappa \) on \({\mathfrak {X}}\) by \(\mu _{\varphi ^\kappa }\) (recall that \({\mathfrak {X}}\subset {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) denotes the set of gradient fields). We first remark that the law of \((\kappa , \nabla \varphi ^\kappa )\) is a Borel-measure on \(\{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\times {\mathfrak {X}}\). This follows from Carathéodory’s extension theorem and the observation that for a local event \({\mathbf {A}}\in {\mathcal {E}}_E\) with \(E\subset {\mathbf {E}}({\mathbb {Z}}^d)\) finite the function \(\kappa \mapsto \mu _{\varphi ^\kappa }({\mathbf {A}})\) is continuous (this can be shown using Lemma B.3). By Remark 2.2 it is sufficient to prove that \({\tilde{\mu }}{\tilde{\gamma }}_{\Lambda _n}={\tilde{\mu }}\) for all n. To prove this we use an approximation procedure. We fix n and define for \(N>n\) a measure \({\tilde{\mu }}_N\) on \( \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\times {\mathfrak {X}}\) as follows. The \(\kappa \)-marginal of \({\tilde{\mu }}_N\) is given by \({\bar{\mu }}_N={\bar{\mu }}{\bar{\gamma }}_{E_n}^{\Lambda _N^w}\) where as before we extended \({\bar{\gamma }}_{E_n}^{\Lambda _N^w}\) to a proper probability kernel on \(\{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\).
For given \(\kappa \), let \(\varphi ^\kappa \) be the centred Gaussian field with zero boundary data outside of \(\Lambda _N^\circ \) and covariance \((\tilde{\Delta }_{\kappa _{E_N}}^{\Lambda _N^w})^{-1}\) where \(\tilde{\Delta }_{\kappa _{E_N}}^{\Lambda _N^w}\) was defined in Sect. 3. The measure \({\tilde{\mu }}_N\) is the joint law of \((\kappa ,\varphi ^\kappa )\) where \(\kappa \) has law \({\bar{\mu }}_N\). We claim that for \(N>n\)
We prove this by showing the statement for the measures \({\tilde{\mu }}_N\big (\cdot |{\mathbf {A}}(\lambda _{E_N{\setminus } E_n})\big )\) for every configuration \(\lambda \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\). To shorten the notation we write \({\tilde{\mu }}_N^{\lambda }={\tilde{\mu }}_N\big (\cdot |{\mathbf {A}}(\lambda _{E_N{\setminus } E_n})\big )\). By definition of \({\tilde{\mu }}_N\) the \(\varphi \)-field conditioned on \(\kappa \) has density \(\exp (-\frac{1}{2} (\varphi ,\tilde{\Delta }_{\kappa }^{\Lambda _N^w}\varphi ))/\sqrt{\det 2\pi (\tilde{\Delta }_\kappa ^{\Lambda _N^w}})^{-1}\,\mathrm {d}\varphi _{\Lambda _N^\circ }\) where \(\mathrm {d}\varphi _\Lambda =\prod _{x\in \Lambda }\mathrm {d}\varphi _x\) denotes the Lebesgue measure. This implies for \({\mathbf {B}}\in \mathcal {B}({\mathbb {R}}^{\Lambda _N})\) and \(\sigma \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) such that \(\sigma _{E_N{\setminus } E_n}=\lambda _{E_N{\setminus } E_n}\)
We use the definition of \({\tilde{\mu }}_N\) and the fact that specifications are proper to rewrite
Note that
The last three displays, a summation by parts, and (3.6) lead us to
Combining this with the definition (3.2) we conclude that for \(\sigma '\in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) such that \(\sigma '_{E_N{\setminus } E_n}=\lambda _{E_N{\setminus } E_n}\) and \(\omega \in {\mathfrak {X}}\) such that \(\omega _{E_N^\mathrm {c}}=0\)
This implies \({\tilde{\mu }}_N^\lambda {\tilde{\gamma }}_{\Lambda _n}={\tilde{\mu }}_N^\lambda \) and (A.29) follows directly.
It remains to pass to the limit in Eq. (A.29), i.e., we show that the right hand side converges in the topology of local convergence to \({\tilde{\mu }}\) and the left hand side to \({\tilde{\mu }}{\tilde{\gamma }}_{\Lambda _n}\) thus finishing the proof. We only sketch the argument. Since \({\tilde{\gamma }}(A,\cdot )\) is a measurable, local, and bounded function if A is a local event it is sufficient to show that \({\tilde{\mu }}_N\) converges to \({\tilde{\mu }}\) locally in total variation, that is for every \(\Lambda \subset \subset {\mathbb {Z}}^d\)
Where we used the \(\sigma \)-algebra \({\mathcal {A}}_E\) on \({\mathfrak {X}}\times \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) defined in Sect. 3 as the product of the pullbacks of \({\mathcal {E}}_E\) and \({\mathcal {F}}_E\). We first consider the \(\kappa \)-marginals of \({\tilde{\mu }}_N\) and \({\tilde{\mu }}\). They are given by \({\bar{\mu }}_N={\bar{\mu }}{\bar{\gamma }}_{E_n}^{\Lambda _N^w}\) and \({\bar{\mu }}={\bar{\mu }}{\bar{\gamma }}_{E_n}\) where we use that \({\bar{\mu }}\) is a Gibbs measure. We can estimate the total variation of those two measures by
In the second step we used that the specifications are proper thus we can assume \(A\subset {\mathbf {A}}(\kappa _{E_n^{\mathrm {c}}})\) and use that \(|{\mathbf {A}}(\kappa _{E_n^{\mathrm {c}}})|\le 2^{|E_n|}\). Using Lemma 4.16 we conclude
We address the \(\eta \)-marginals of the measures \({\tilde{\mu }}\) and \({\tilde{\mu }}_N\). We write \({\tilde{\mu }}(\cdot \mid \kappa ), {\tilde{\mu }}_N(\cdot \mid \kappa )\in \mathcal {P}({\mathfrak {X}})\) for the conditional distribution of the \(\eta \)-field for a given \(\kappa \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\). From the construction this is well defined for every \(\kappa \). We define the centred Gaussian field \(\varphi ^\kappa \) by \(\varphi ^\kappa (0)=0\) and its covariance \((\Delta _\kappa )^{-1}\) and the centred fields \(\varphi _N^\kappa \) pinned to 0 outside of \(\Lambda _N^\circ \) with covariance \((\tilde{\Delta }_\kappa ^{\Lambda _N^w})^{-1}\) and we denote their gradients by \(\eta ^\kappa =\nabla \varphi ^\kappa \) and \(\eta _N^\kappa =\nabla \varphi _N^\kappa \). Note that by definition of \({\tilde{\mu }}\) and \({\tilde{\mu }}_N\) the law of \(\eta ^\kappa \) and \(\eta _N^\kappa \) coincides with \({\tilde{\mu }}(\cdot \mid \kappa )\) and \({\tilde{\mu }}_N(\cdot \mid \kappa )\). Fix an integer L. We introduce the Gaussian vectors \(X^\kappa =(\varphi ^\kappa (x)-\varphi ^\kappa (0))_{x\in \Lambda _L}\) and \(X_N^\kappa =(\varphi ^\kappa _N(x)-\varphi _N^\kappa (0))_{x\in \Lambda _L}\). Note that given \(X^\kappa \), \(X_N^\kappa \) the gradient field \(\eta ^\kappa {\restriction _{{\mathbf {E}}(\Lambda _{L})}}\) respectively \(\eta _N^\kappa {\restriction _{{\mathbf {E}}(\Lambda _{L})}}\) can be expressed as a function of \(X^\kappa \) and \(X^\kappa _N\) respectively. This implies that
Theorem 1.1 in [16] states that the total variation distance between two centred Gaussian vectors \(Z_1\), \(Z_2\) with covariance matrices \(\Sigma _1\) and \(\Sigma _2\) can be bounded by \(\tfrac{3}{2}|\Sigma _1^{-1}\Sigma _2-{\mathbb {1}}|_F\) where \(|\cdot |_F\) denotes the Frobenius norm. Using this theorem and the uniform convergence of the covariance of \(\eta _N^\kappa \) to the covariance of \(\eta ^\kappa \) stated in Lemma B.3 we conclude that
We denote for a set \(A\in {\mathcal {A}}\) and \(\kappa \in \{1,q\}^{{\mathbf {E}}({\mathbb {Z}}^d)}\) by \(A_\kappa \) the intersection of A and the line through \(\kappa \), i.e., \(A_\kappa =\{\eta \in {\mathbb {R}}^{{\mathbf {E}}({\mathbb {Z}}^d)}\,:\, (\eta ,\kappa )\in A\}\). Using disintegration, (A.37), (A.39), and the dominated convergence theorem we estimate
We conclude that for any local event A
\(\square \)
Estimates for discrete elliptic equations
In this appendix we collect some regularity estimates for discrete elliptic equations. We consider as before uniformly elliptic \(\kappa :{\mathbf {E}}({\mathbb {Z}}^d)\rightarrow {\mathbb {R}}_+\) with \(0<c_-\le \kappa _e\le c_+<\infty \) for all \(e\in {\mathbf {E}}({\mathbb {Z}}^d)\). We denote corresponding set of conductances by \(M(c_-,c_+)=[c_-,c_+]^{{\mathbf {E}}({\mathbb {Z}}^d)}\).
Next we state a discrete version of the well known Nash–Moser estimates for scalar elliptic partial differential equations with \(L^\infty \) coefficients.
Lemma B.1
Let \(0<c_-<c_+<\infty \), \(\Lambda \subset {\mathbb {Z}}^d\), and \(\kappa \in M(c_-,c_+)\). Let \(u:\Lambda \rightarrow {\mathbb {R}}\) be a solution of
Then there are constants \(\alpha =\alpha (c_-,c_+,d)\) and \(C_1=C(c_-,c_+,d)\) such that the following estimate holds for \(x,y\in \Lambda \)
Proof
This is Proposition 6.2 in [13]. \(\square \)
Moreover, we state some consequences for the Green function of uniformly elliptic operators in divergence form. We define the Green function \(G_\kappa :{\mathbb {Z}}^d\times {\mathbb {Z}}^d\rightarrow {\mathbb {R}}\) as the inverse of \(\Delta _\kappa \), i.e., \(G_\kappa \) satisfies for \(d\ge 3\)
It is well known that such a Green function does not exist in dimension 2, however the derivative \(\nabla _{x,i}G_\kappa \) does exist in dimension 2, in particular one can make sense of expressions as \(G_\kappa (x_1,y)-G_\kappa (x_2,y)\). Formally one can define \(\nabla G_\kappa \) by adding a mass \(m^2\) to the Laplace operator, i.e., consider the Green function of \(\Delta _\kappa +m^2\) and then send \(m^2\rightarrow 0\). The following estimates hold for the Green function.
Lemma B.2
For any \(d\ge 3\) and \(\kappa \in M(c_-,c_+)\) the estimate
holds where the constant \(C_2\) depends only on \(c_-\), \(c_+\), and d. Moreover there exist \(\alpha >0\) depending on \(c_+/c_-\) and d and \(C_3\) depending on \(c_-\), \(c_+\), and d such that for \(d\ge 2\)
Proof
These estimates are well known. Estimates for the corresponding parabolic Green function are called Nash–Aronson estimates and they can be found, e.g., in Proposition B.3 in [22]. Integrating the bound for the parabolic Green function implies (B.4). The estimates (B.5) and (B.6) follow for \(d> 2\) from (B.4) and Lemma B.1. For \(d=2\) one can bound the oscillation of the Green function using Nash–Aronson estimates and the parabolic Nash–Moser estimate. In particular as shown, e.g., in [3, Chapter 8] there is a constant \(C=C(c_-,c_+, d)\) such that for all \(r>0\)
Lemma B.1 then implies (B.5) and (B.6). \(\square \)
The previous results allow us to bound the difference between the Green function in a set with Dirichlet boundary conditions and the Green function on whole space. We define the Green function \(G^{\Lambda ^w}_\kappa :\Lambda \times \Lambda \rightarrow {\mathbb {R}}\) with Dirichlet boundary values in finite volume by
For clarity we write \(G^{{\mathbb {Z}}^d}_\kappa =G_\kappa \) in the following.
Lemma B.3
Let \(0<c_-<c_+<\infty \) and \(R>0\), then
Remark B.4
Note that the two scalar products can be equivalently written as \(\nabla _{x,i}\nabla _{y,j}G_\kappa ^{\Lambda _n^w }(x,y)\) and \(\nabla _{x,i}\nabla _{y,j}G_\kappa ^{{\mathbb {Z}}^d }(x,y)\). This expression agrees with the gradient correlations of a Gaussian field:
A similar equation holds when \(\Lambda _n^w\) is replaced by \({\mathbb {Z}}^d\). Thus the lemma implies local uniform convergence of the covariance matrix of those two gradient Gaussian fields.
Proof
In \(d>2\) the difference of the Green functions can be expressed through the corrector function \(\varphi _{\kappa ,n,y}:\Lambda _n\rightarrow {\mathbb {R}}\) that is defined by
Using the definition of the Green function we obtain that the corrector satisfies
The estimate (B.4) in Lemma B.2 now implies
for \(z\in \partial \Lambda _n\). By the maximum principle for \(\Delta _\kappa \) the bound extends to all \(z\in \Lambda _n\). The claim then follows from
The extension to dimension \(d=2\) is again slightly technical. We can define
The corrector satisfies
Using (B.7) we can bound for \(y\in B_{n/2}(0)\)
Lemma B.1 implies \(\nabla \varphi _{\kappa ,n,y}(x)\le Cn^{-\alpha }\) for \(x\in \Lambda _{n/2}\) and we can conclude using (B.14). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Buchholz, S. Phase transitions for a class of gradient fields. Probab. Theory Relat. Fields 179, 969–1022 (2021). https://doi.org/10.1007/s00440-020-01021-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-020-01021-5