Skip to main content
SpringerLink
Log in

Information processing and thermodynamic properties of microtubules

  • Published:
Pramana Aims and scope Submit manuscript

Abstract

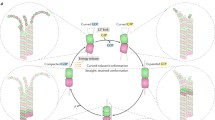
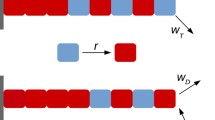
The Shannon entropy dependence on temperature, dipole moment and thermodynamic properties of microtubules (MTs) have been investigated using the Landau–Ginzburg phenomenological theory through continuum Boltzmann distribution function. By minimising the loss in energy, we found that there is a possibility that MTs formed from the heterodimers can process information over a long time at higher temperature. We also found that multiple heterodimers under the influence of dipole moment, has the tendency to process information whenever the amount of information stored or transferred decreases with increasing electronegativity of the system. We analyse the dynamic instability phenomenon that infinitely occurs in polymerisation and depolymerisation processes in MTs. Also, under physiological conditions, temperature dependence of thermodynamic properties was investigated and our results exhibited critical behaviour of heat capacity and chemical potential giving room for phase transitions around 302 K.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. S R Hameroff and R Penrose, Toward a science of consciousness (MIT Press, Cambridge, 1996)

    Book  Google Scholar 

  2. S R Hameroff and R Penrose, The hard problem (MIT Press, Cambridge, USA, 1998)

    MATH  Google Scholar 

  3. M Tegmark, Phys. Rev. E 61, 4194 (2000)

    Article  ADS  Google Scholar 

  4. S Hagan, S R Hameroff and J A Tuszynski, Phys. Rev. E 65, 061901 (2002)

    Article  ADS  Google Scholar 

  5. L P Rosa and J Faber, Phys. Rev. E 70, 031902 (2004)

    Article  ADS  Google Scholar 

  6. N J Woolf, The frontiers collection (Springer, Berlin, Heidelberg, 2006)

  7. H Li, D J DeRosier, W V Nicholson, E Nogales and K H Downing, Structure 10(10), 1317 (2002)

    Article  Google Scholar 

  8. Stuart Hameroff and Jack Tuszynski, Energy and information transfer in biological systems: How physics could enrich biological understanding (World Scientific, 2003)

  9. T J A Craddock and J A Tuszynski, J. Biol. Phys. 36, 53 (2010)

  10. T J A Craddock, C Beaucheminb and J A Tuszynski, BioSystems 97, 28 (2009)

    Article  Google Scholar 

  11. S R Hameroff, S Rasmussen and F T Hong, Molecular electronics (Springer, Boston, MA, 1989)

    Google Scholar 

  12. Stuart R Hameroff and Richard C Watt, J. Theor. Biol. 98, 549 (1982)

  13. J Shaffer, Front. Psychol. 7, 1 (2016)

    Article  Google Scholar 

  14. S Hameroff and R Penrose, Phys. Life Rev. 11(1), 39 (2014)

    Article  ADS  Google Scholar 

  15. A Bandyopadhyay, Experimental studies on a single microtubule (Google Workshop on Quantum Biology, 2011)

  16. J A Tuszynski, J A Brown and P Hawrylak, Philos. Trans. R. Soc. London A 356, 1897 (1998)

  17. Jean Faber, Renato Portugal and Luiz Pinguelli, 10.1016/j.biosystems.2005.06.011 (Elsevier Ireland Ltd, 2006)

  18. R J DiPerna and P-L Lions, Ann. Math. 130(2), 321 (1989)

  19. Alexander I Nesterov, Mónica F Ramírez, Gennady P Berman and Nick E Mavromatos, Phys. Rev. E 93, 062412 (2016)

  20. J A Tuszynski, B Trpisova, D Sept and M V Sataric, Biosystems 42, 153 (1997)

    Article  Google Scholar 

  21. J A Tuszynski, S R Hameroff, M V Sataric, B Trpisova and M L A Nip, J. Theor. Biol. 174, 371 (1995)

    Article  Google Scholar 

  22. J A Tuszynski, J A Brown, E Crawford, E J Carpenter, M L A Nip, J M Dixon and M V Satari, Mathematical and computer modelling (Elsevier Ltd, 2005)

  23. G M Alushin, G C Lander, E H Kellogg, R Zhang, D Baker and E Nogales, Cell 157(5), 1117 (2014)

    Article  Google Scholar 

  24. J C Tolédano and P Tolédano, The Landau theory of phase transitions (World Scientific Publishing, Singapore, 1987)

  25. M F C Fobasso, A J Fotue, S C Kenfack and L C Fai, Physica E  118, 113941 (2020)

    Article  Google Scholar 

  26. A T Ayoub, M Klobukowski and J A Tuszynski, PLoS Comput. Biol.  11, 1 (2015)

    Article  Google Scholar 

  27. M Katsuki and D R Drummond, Nat. Commun. 5 (2014)

  28. Yasar Demirel, Entropy  16, 1931 (2014)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mesoscopic and Multilayers Structures Laboratory, Department of Physics, Faculty of Science, University of Dschang, P.O. Box 479, Dschang, Cameroon

    M C Ekosso, A J Fotue & L C Fai

  2. Laboratory of Electronics and Signal Processing, Department of Physics, Faculty of Science, University of Dschang, P.O. Box 67, Dschang, Cameroon

    H Fotsin

Authors
  1. M C Ekosso
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A J Fotue
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. H Fotsin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. L C Fai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A J Fotue.

Appendices

Appendix A

The Shannon entropy is given by

$$\begin{aligned} \int \nolimits _{-\infty }^{+\infty } {g\left( {P} \right) \log g\left( { P} \right) \text{ d }{ P}=\langle I\rangle }, \end{aligned}$$
(A.1)

knowing that

$$\begin{aligned} \int \nolimits _{-\infty }^{+\infty } {g\left( {P} \right) { P}\text{ d }{P}=\langle {P}\rangle }. \end{aligned}$$
(A.2)

The suitable use of eq. (A.2) allow us to write

$$\begin{aligned} \langle I\rangle =\left\langle \frac{\ln Z}{\ln 2}\right\rangle +\frac{N_{0} A}{2kT\ln 2}\langle {P}^{2}\rangle +\frac{N_{0} b}{4kT\ln 2}\langle { P}^{4}\rangle . \end{aligned}$$
(A.3)

Assuming \(A=a\left( {T-T_{C} } \right) \), we compute the expression of the partition function Z, the mean square \(\langle { P}^{2}\rangle \) and mean quadratic \(\langle { P}^{4}\rangle \) of polarisation as

$$\begin{aligned} Z= & {} \sqrt{\frac{a\left( {T-T_{C} } \right) }{2b}} \text{ e}^{{{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}}/ {{8bkT}}}\nonumber \\&\times \text{ Bessel }K\left[ {-\dfrac{1}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \end{aligned}$$
(A.4)
$$\begin{aligned}&\langle { P}^{2}\rangle =\int \nolimits _{-\infty }^{+\infty } {g\left( { P} \right) { P}^{2}\text{ d }{ P}=} -\!\frac{\pi \text{ e}^{^{\frac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}}}}{4Zb\sqrt{a\left( {T-T_{C} } \right) b} }\nonumber \\&\times \left( {\begin{array}{l} a^{2}N_{0} \left( {T-T_{C} } \right) ^{2} \text{ Bessel }I\left[ {-\dfrac{1}{4},\dfrac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] \\ -\left( {a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}+4bkT} \right) \\ \times \text{ Bessel }I\left[ {\dfrac{1}{4},\dfrac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] +a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}\\ \left( \text{ Bessel }I\left[ {\dfrac{3}{4},\dfrac{a^{2}N_{0} \left( \! {T\!-\!T_{C} } \right) ^{2}}{8bkT}} \right] \right. \left. -\text{ Bessel }I\left[ \! {\dfrac{5}{4},\dfrac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] \right) \\ \end{array}} \!\!\!\right) \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$
(A.5)
$$\begin{aligned}&\langle {{P}}^{\text{4 }}\rangle =\int \nolimits _{-\infty }^{+\infty } {g\left( {P} \right) {{P}}^{2}\text{ d }{ P}=} \frac{\text{ e}^{{{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }}/ {{8bkT}}}}{2\sqrt{2} N_{0} Z\sqrt{\frac{b^{5}}{a\left( {T-T_{C} } \right) }} }\nonumber \\&\quad \times \left( {\begin{array}{l} -a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} \text{ Bessel }K\\ \left[ {-\dfrac{5}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \\ +\left( {a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} +6bkT} \right) \text{ Bessel }K\\ \times \left[ {-\dfrac{1}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \\ \end{array}} \right) .\nonumber \\ \end{aligned}$$
(A.6)

The final expression of the Shannon entropy is expressed as

$$\begin{aligned} \langle I\rangle= & {} \frac{\ln \left[ {\sqrt{\frac{a\left( {T-T_{c} } \right) }{2b}} *\text{ exp }\left[ {\frac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \text{ Bessel }K\left[ {-\frac{1}{4},\frac{a^{2}\left( {T-T_{c} } \right) ^{2}N_{0} }{8bkT}} \right] } \right] }{\ln 2} -\frac{\pi N_{0} a*\text{ exp }\left[ {\frac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] }{8kbTZ\ln 2\sqrt{a\left( {T-T_{C} } \right) b} }\\&\times \left( \begin{array}{l} a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}\text{ Bessel }I\left[ {-\dfrac{1}{4},\dfrac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] \\ -\left( {a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}+4bkT} \right) \text{ Bessel }I\left[ {\dfrac{1}{4},\dfrac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] \\ +a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}\left( \text{ Bessel }I\left[ {\dfrac{3}{4},\dfrac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] \right. \left. -\text{ Bessel }I\left[ {\dfrac{5}{4},\dfrac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] \right) \\ \end{array} \right) \\&-\frac{b*\mathrm{exp}\left[ {\frac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] }{8kT\sqrt{2} Z\ln 2\sqrt{\frac{b^{5}}{a\left( {T-T_{C} } \right) }} }\left( {\begin{array}{l} -a^{2}\left( {T-T_{C} } \right) ^{2}N_{0}\ \text{ Bessel }K\left[ {-\dfrac{5}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] + \\ +\left( {a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} +6bkT} \right) \text{ Bessel }K\left[ {-\dfrac{1}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \\ \end{array}} \right) . \\ \end{aligned}$$

Appendix B

Heat capacity is expressed as

$$\begin{aligned} C= & {} \frac{a_{0}^{2} }{2b}T_{C} -\frac{T}{2^{8}b^{2}kT^{3}\left( {T-T_{C} } \right) ^{2}\text{ Bessel }K\left[ {-\frac{1}{4},\frac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] ^{2}} \\&\left( \begin{array}{l} a^{4}N_{0}^{2}\left( {T-T_{C} } \right) ^{4}\left( {T+T_{C} } \right) ^{2}\text{ Bessel }K\left[ {-\dfrac{5}{4},\dfrac{a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}}{8bkT}} \right] ^{2} \\ -a^{4}N_{0}^{2} \left( {T-T_{C} } \right) ^{4}\left( {T+T_{C} } \right) ^{2}\text{ Bessel }K\left[ {-\dfrac{9}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \\ *\text{ Bessel }K\left[ {-\dfrac{1}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] + \text{ Bessel }K\left[ {-\dfrac{1}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] ^{2}\\ \times \left( {\begin{array}{l} -2^{7}b^{2}k^{2}T^{4}-2^{6}a^{2}N_{0} bkT^{5}-2a^{4}N_{0}^{2} T^{6}\\ +2^{8}b^{2}k^{2}T^{3}T_{C} +2^{7}N_{0} bkT^{4}T_{C}\\ +2^{2}a^{4}N_{0}^{2} T^{5}T_{C} -2^{6}a^{2}N_{0} bkT^{3}T_{C}^{2}\\ +2a^{4}N_{0}^{2} T^{4}T_{C}^{2} -2^{3}a^{4}N_{0}^{2} T^{3}T_{C}^{3}\\ +2a^{4}N_{0}^{2} T^{2}T_{C}^{4} +2^{2}a^{4}N_{0}^{2} TT_{C}^{5} -2^{2}a^{4}N_{0}^{2}T_{C}^{6} \\ \end{array}} \right) \\ +\text{ Bessel }K\left[ {-\dfrac{1}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] *\text{ Bessel }K\left[ {\dfrac{3}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \\ \times \left( 2^{5}a^{2}bkN_{0} T^{5}-2^{6}a^{2}bkN_{0} T^{4}T_{C}\right. \left. +2^{5}a^{2}bkN_{0} T^{3}T_{C}^{2} \right) + \text{ Bessel }K\left[ {\dfrac{3}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] ^{2}\\ \times \left( a^{4}N_{0}^{2} T^{6}-2a^{4}N_{0}^{2} T^{5}T_{C} -a^{4}N_{0}^{2} T^{4}T_{C}^{2}\right. \\ +2^{2}a^{4}N_{0}^{2} T^{3}T_{C}^{3} -a^{4}N_{0}^{2} T^{2}T_{C}^{4}\\ \left. -2a^{4}N_{0}^{2} TT_{C}^{5} +a^{4}N_{0}^{2} T_{C}^{6} \right) + 2a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}\text{ Bessel }K\left[ {-\dfrac{5}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \\ \times \left( 2^{4}bkT^{3}\text{ Bessel }K\left[ {-\dfrac{1}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \right. \\ \left. +a^{2}N_{0} \left( {T-T_{C} } \right) ^{2}\text{ Bessel }K\left[ {\dfrac{3}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \right) \\ + \text{ Bessel }K\left[ {-\dfrac{1}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] *\text{ Bessel }K\left[ {\dfrac{7}{4},\dfrac{a^{2}\left( {T-T_{C} } \right) ^{2}N_{0} }{8bkT}} \right] \\ \left( -a^{4}N_{0}^{2} T^{6}+2a^{4}N_{0}^{2} T^{5}T_{C} +a^{4}N_{0}^{2} T^{4}T_{C}^{2} -2^{2}a^{4}N_{0}^{2} T^{3}T_{C}^{3}\right. \\ \left. +a^{4}N_{0}^{2} T^{2}T_{C}^{4} +2a^{4}N_{0}^{2} TT_{C}^{5} -a^{4}N_{0}^{2} T_{C}^{6} \right) \\ \end{array} \right) . \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ekosso, M.C., Fotue, A.J., Fotsin, H. et al. Information processing and thermodynamic properties of microtubules. Pramana - J Phys 95, 26 (2021). https://doi.org/10.1007/s12043-020-02044-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-020-02044-2

Keywords

PACS Nos

Search

Navigation