Quality Factor of Inhomogeneous Plane Waves

Abstract

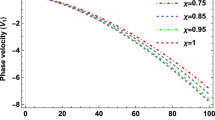
We first compare two apparently dissimilar expressions for the quality factor Q of inhomogeneous plane waves in isotropic viscoelastic media, where Q is defined as the result of an energy-balance relation. In this case, it is the ratio of twice the strain energy to the dissipated energy. Both expressions give the same Q for P-waves and Q for S-waves is independent of the inhomogeneity angle γ (isotropic media). Then, we consider the more general balance equation, which holds for anisotropic viscoelastic media, where anomalous behaviors are observed when γ exceeds some critical value (forbidden directions of propagation). This problem has already been solved analytically for SH-waves. Here, we consider the qP–qS case, which requires a numerical solution of the dispersion equation to obtain the wavenumber and attenuation factor, i.e., the real and imaginary parts of the wave vector, respectively. The forbidden directions appear when the phase velocity approaches a zero value. Generally, the phase velocity of homogeneous waves (γ = 0) exceeds that of inhomogeneous waves, while the latter show stronger attenuation (lower quality factor). In the vicinity of the forbidden directions, the opposite behavior may occur.

Appendices

APPENDIX A

1.1 Quality Factor for qP–qS Waves in Anisotropic Viscoelastic Media

We report an expression of the quality factor for anisotropic and viscoelastic media based on the energy balance obtained by Carcione and Cavallini [9]. We assume wave propagation in the (x, z)-symmetry plane of an orthorhombic medium, with the positive z-axis pointing downwards. The medium complex and frequency-dependent stiffness components are p_IJ, I, J = 1, …, 6 and the mass density is ρ. We consider the general plane-wave solution (1), where the wave vector is k = (k₁, k₃) = ω(s₁, s₃), where s_i are slowness components. The k₃-component in terms of the horizontal wavenumber k₁ is

$${{k}_{3}} = \pm \frac{\omega }{{\sqrt 2 }}\sqrt {{{K}_{1}} \mp pv\sqrt {K_{1}^{2} - 4{{K}_{2}}{{K}_{3}}} } ,$$

(A.1)

where

$${{K}_{1}} = \rho \left( {\frac{1}{{{{p}_{{55}}}}} + \frac{1}{{{{p}_{{33}}}}}} \right) + \frac{1}{{{{p}_{{55}}}}}\left[ {\frac{{{{p}_{{13}}}}}{{{{p}_{{33}}}}}\left( {{{p}_{{13}}} + 2{{p}_{{55}}}} \right) - {{p}_{{11}}}} \right]s_{1}^{2},$$

$${{K}_{2}} = \frac{1}{{{{p}_{{33}}}}}\left( {{{p}_{{11}}}s_{1}^{2} - \rho } \right),\,\,\,\,{{K}_{3}} = s_{1}^{2} - \frac{\rho }{{{{p}_{{55}}}}}.$$

The signs in k₃ correspond to (+, −): downward propagating qP wave; (+, +): downward propagating qS wave; (−, −): upward propagating qP wave; and (−, +): upward propagating qS wave. The plane-wave eigenvectors (polarizations) are

$${\mathbf{V}} = {{V}_{0}}\left( \begin{gathered} \beta \hfill \\ \xi \hfill \\ \end{gathered} \right),$$

(A.2)

where V₀ is the plane-wave amplitude and

$$\beta = pv\sqrt {\frac{{{{p}_{{55}}}k_{1}^{2} + {{p}_{{33}}}k_{3}^{2} - \rho {{\omega }^{2}}}}{{{{p}_{{11}}}k_{1}^{2} + {{p}_{{33}}}k_{3}^{2} + {{p}_{{55}}}\left( {k_{1}^{2} + k_{3}^{2}} \right) - 2\rho {{\omega }^{2}}}}} ,$$

(A.3)

and

$$\xi = \pm pv\sqrt {\frac{{{{p}_{{11}}}k_{1}^{2} + {{p}_{{55}}}k_{3}^{2} - \rho {{\omega }^{2}}}}{{{{p}_{{11}}}k_{1}^{2} + {{p}_{{33}}}k_{3}^{2} + {{p}_{{55}}}\left( {k_{1}^{2} + k_{3}^{2}} \right) - 2\rho {{\omega }^{2}}}}} .$$

(A.4)

In general, the + and − signs correspond to the qP- and qS-waves, respectively. However one must choose the signs such that ξ varies smoothly with the propagation angle.

Then, the quality factor for anisotropic media is given by equation (11), where

$$\begin{gathered} \omega {\kern 1pt} W = {{p}_{{55}}}\left( {\xi {{k}_{1}} + \beta {{k}_{3}}} \right),\,\,\,\,\omega {\kern 1pt} X = \beta {{p}_{{11}}}{{k}_{1}} + \xi {{p}_{{13}}}{{k}_{3}}, \\ \omega Z = \beta {{p}_{{13}}}{{k}_{1}} + \xi {{p}_{{33}}}{{k}_{3}}. \\ \end{gathered} $$

(A.5)

In the isotropic case the above components k₁ and k₃ are equivalent to equation (12). In the anisotropic case, a numerical solution is required to obtain k₁ and k₃, i.e., the calculation of κ and α, but in this case, equation (A.1) is the analytical solution for homogeneous waves.

APPENDIX B

1.1 Quality Factor of S-waves for Inhomogeneous Waves

For S-waves (isotropic media),

$$\frac{{\rho {{\omega }^{2}}}}{\mu } = \frac{{{{k}^{2}}}}{{{{\omega }^{2}}}} = \frac{{\operatorname{Re} \left( {{{k}^{2}}} \right) + i\operatorname{Im} \left( {{{k}^{2}}} \right)}}{{{{\omega }^{2}}}}.$$

(B.1)

Since µ = µ_R + iµ_I and taking real and imaginary parts, we obtain

$$\begin{gathered} \rho {{\omega }^{2}} = \mu {}_{R}\operatorname{Re} \left( {{{k}^{2}}} \right) - {{\mu }_{I}}\operatorname{Im} \left( {{{k}^{2}}} \right), \\ 0 = \mu {}_{R}\operatorname{Im} \left( {{{k}^{2}}} \right) - {{\mu }_{I}}\operatorname{Re} \left( {{{k}^{2}}} \right). \\ \end{gathered} $$

(B.2)

Substituting equations (B.2) into equation (10), we obtain

$$Q = \frac{{2\left\langle V \right\rangle }}{{\left\langle D \right\rangle }} = - \frac{{\operatorname{Re} \left( {{{k}^{2}}} \right)}}{{\operatorname{Im} \left( {{{k}^{2}}} \right)}}.$$

(B.3)

which is the S-wave Q factor of homogeneous plane waves, independent of the inhomogeneity angle γ (see Eqs. (3.32) in Carcione [8]). This result is also valid for SH-waves.