Introduction

Continuous-variable quantum key distribution (CV-QKD) enables information-theoretically secure key exchange between two parties using the continuous-variable properties of the quantised electromagnetic light field1,2,3,4,5. The quantum information used for generating the secret key can be imprinted onto coherent states in the amplitude and phase quadratures of laser light using electro-optical modulators at the transmitter. These quantum states are transmitted through an insecure channel – typically assumed to be fully controlled by an adversary – and measured by some form of coherent detection, e.g. radio-frequency heterodyne or phase-diverse homodyne detection at the reciever. The use of technology quite similar to that employed in classical coherent telecommunications6 is an attractive feature of CV-QKD with respect to integrability in existing telecom networks.

A CV-QKD coherent receiver uses a local oscillator (LO) to measure the quantum information carrying signal.

Modern CV-QKD implementations generate the LO from a laser at the receiver, which is independent of the transmitter laser. This simplifies the CV-QKD implementation and increases security, however, at the cost of requiring to recover the frequency and phase of the quantum signal. This process, commonly known as carrier recovery in telecommunication7, is of utmost importance for the performance of CV-QKD implementations as an impairment cannot be distinguished from excess noise generated by an eavesdropper.

The quantum signal operates in a significantly lower power regime than a typical optical telecommunications signal and correspondingly it is detected at a much lower signal-to-noise ratio (SNR). This regime is one in which traditional telecommunication algorithms for carrier recovery7 function quite poorly, if at all. Additionally, CV-QKD systems typically use a Gaussian modulation format that does not contain features present in traditional telecommunication formats, e.g. phase shift keying (PSK), which enable such algorithms to work. Therefore pilot-aided techniques in which a reference signal is transmitted together with the quantum signal have been developed and studied for CV-QKD systems8,9,10,11.

The ‘classical’ reference and the quantum signal are usually time8,9,10 or frequency multiplexed12,13 and phase noise estimation is carried out on this reference, henceforth called the ‘pilot tone’. It is advantageous to have a pilot tone with as low power as possible to minimise interference with the quantum signal. Besides undesirable scattering effects in the fibre, a high power pilot tone has a negative effect on the signal to noise and distortion ratio of the digital-to-analogue converter in the transmitter as well the analogue-to-digital conversion in the receiver, thus decreasing the effective number of bits. To avoid some of these side effects the pilot tone and the quantum signal could be multiplexed in polarisation, however, at the expense of (at least) doubling implementation complexity14.

Here, we present a machine learning framework based on Bayesian inference, implementing an unscented Kalman filter (UKF)15 to estimate the phase of a pilot tone. The UKF is an adaptive estimation algorithm capable of adjusting itself according to the differences between the estimated model and the measured system. The UKF’s performance is investigated experimentally in a Gaussian-modulated CV-QKD protocol2 operating over a 20 km fibre link using first nominally <100 Hz linewidth lasers and then substituting a standard telecommunications laser (≈10 kHz) at the transmitter. The UKF achieves exceptional performance compared to a standard reference method and the extended Kalman filter with excess noise figures below 1% of the shot noise variance for a wide range of pilot tone SNRs. For instance, with the low linewidth laser, the UKF performs consistently well down to 3.5 dB pilot tone SNR (SNRpilot), which considerably relaxes the constraints on the filtering bandwidth. The UKF therefore not only enables higher secret key rates but also promises a more robust CV-QKD system with regards to environmental factors that may deteriorate SNRpilot. Moreover, it enables secret key generation using systems that would otherwise be unable to do so using the reference method.

Phase tracking in CV-QKD systems using Bayesian inference based on an extended Kalman filter or extended Kalman smoother has recently been studied on a CV-QKD system with a discrete modulation format using 8 coherent states16. The UKF should have a performance advantage over the EKF in exchange for additional complexity, one of the motivations for this work. Gaussian modulation in comparison to discrete modulation has more mature security proofs17 but is more susceptible to phase noise (see Methods) because the optimum mean photon number of the transmitted quantum states is an order of magnitude higher. The UKF removes this as a significant limiting factor. Bayesian inference based methods have also been used for the measurement and characterisation of laser phase noise, outperforming traditional methods in particular in the low laser power regime18,19.

Results

Experimental investigation

We investigated the proposed algorithm’s performance in a CV-QKD experiment, (see Methods section for further details). The transmitter and receiver used commercially available telecom equipment and were connected by a 20-km SMF-28 fibre channel. The transmitter prepared a 50 MBaud quantum signal and a frequency-multiplexed pilot tone, both inscribed into single sidebands of the electromagnetic field by an electro-optic in-phase and quadrature modulator. After suitable attenuation, the optical signal was sent to the receiver, either directly or through the 20-km channel. Details about the modulation format at the transmitter and the coherent heterodyne detection at the receiver are described in the Methods section. After acquiring the detection signal with an oscilloscope we performed several digital-signal-processing (DSP) steps (see Methods section for further details), one of which is the proposed machine learning based carrier recovery algorithm, to recover the transmitted symbols.

Using the transmitted and recovered symbols, we performed channel parameter estimation to obtain e, the excess noise mean photon number and η, the combined optical efficiency of the transmission channel and the receiver’s measurement device. We also estimated N, the mean photon number of the transmitted thermal state, with the transmitter and receiver connected directly. In Methods section we describe in further detail how to estimate these parameters and calculate the achievable secret key rate.

In the experiment we implemented two different transmitter lasers, nominally 100 Hz linewidth fibre lasers and a standard telecoms external cavity diode laser with 10 kHz linewidth. The receiver’s LO laser was always an identical model to the fibre laser. The lasers were free running, i.e. they were neither locked in frequency nor phase. Figure 4b shows an example time trace of estimated phases. While for the fibre laser the phase varied only slightly over the course of 125k symbols (2.5 ms), the 10-kHz linewidth laser’s phase drifted over a significantly larger range, requiring a larger standard deviation of the approximating Gaussian distribution.

Figure 1a, c show the excess noise mean photon number e versus SNRpilot obtained from experimental measurements using the 100-Hz and the 10-kHz laser, respectively. Since the contribution to the excess noise caused by the electronic noise of the detector is assumed to be trusted, it was removed from the final result. The measurement set was divided into 1000 frames with 100k symbols per frame and channel parameter estimation was performed individually on each frame. The pilot tone SNR was varied by changing the filter bandwidth (from 1 MHz to 50 MHz) centred around the pilot tone frequency. This method was chosen in lieu of changing the pilot power at the transmitter to ensure a constant N across different measurements and to isolate potential effects such as receiver saturation, optical non-linearity and bleeding of pilot power into the quantum signal that could have happened from adjusting the pilot power along a wide range.

Fig. 1: Experimental results demonstrating the UKF’s performance with respect to excess noise and asymptotic secret key rate compared to other methods.
figure 1

a Excess noise mean photon number e obtained using three phase compensation methods and b respective estimated secret key rates. The thermal state at the transmitter’s output had a mean photon number N = 2.73, the detector’s electronic noise mean photon number t ≈ 0.022 was trusted and subtracted from e. We used the average value of e and assumed an error reconciliation efficiency β = 0.95 in the key rate calculations. The detector’s optical efficiency of 0.84 was treated as trusted loss, i.e., not accessible to the eavesdropper. Error bars were calculated over 1000 frames for one standard deviation. c Excess noise mean photon number for both phase compensation methods for N = 3.41 and d respective estimated secret key rates, when we used a 10-kHz laser in lieu of the 100-Hz laser in the transmitter. The error bars represent one standard deviation.

Full size image

From the plots the superiority of the UKF is clear compared to the reference method and to a lesser extent the EKF. The inset in Fig. 1a shows that the UKF has no significant performance degradation using a 100-Hz linewidth laser at SNRpilot as low as 4 dB, with e reaching 2 × 10−3 at high SNRpilot. On the other hand, the reference method performs much worse than the UKF at low SNRpilot and is still outperformed at the highest SNRpilot. The EKF performs very similarly to the UKF at high SNR but begins to deteriorate for SNRpilot < 9dB. Substituting in the 10-kHz linewidth laser gives overall worse results with the UKF deteriorating quickly at <7 dB SNRpilot, though it still achieves e < 0.01 in the best case. Both the reference method and EKF perform worse than the UKF with the EKF visibly diverging at 20 dB SNRpilot. We note that widespread deployment of CV-QKD systems using standard telecoms lasers is more realistic than using ultra low linewidth lasers.

This is further put into perspective by the graphs in Fig. 1b, d that display the secret key rate calculated in the asymptotic regime using these phase compensation methods. Using the UKF it is always possible to extract a secret key using either transmitter laser, while even at a SNRpilot = 26 dB, the reference method could achieve at best e = 0.015, which is still too high for key generation with the 100-Hz laser. Increasing the pilot tone power to quantum signal power ratio from the 3.2 used in this work to >20 (ref. 20) is expected to allow for key rate generation. The EKF yielded a faint increase in key rate over the UKF at >7.5 dB SNRpilot but significantly worse below 7.5 dB. For the 10-kHz linewidth laser, the reference method achieved e ≈ 0.06 as the best result. The EKF was consistently worse than the UKF though it managed to achieve key generation at >21.5 dB SNRpilot. The overall performance degradation may be due to the fast changing beat mode frequency of the lasers rendering the Gaussian approximation less accurate, however this requires further investigation.

Higher SNRs are limited by the pilot power in this experiment but theoretically the difference between the UKF and reference method should become negligible at sufficiently high SNR. In fact, the reference method has been used for successful key generation12,13,14 albeit this was for discrete modulations formats and/or different experimental settings.

Discussion

This work shows the performance increase achieved by employing a machine learning Bayesian inference framework implementing an unscented Kalman filter for the compensation of laser phase noise in a Gaussian modulation CV-QKD setup operating over a distance of 20 km. Using a relatively low pilot power the machine learning approach enabled secret key generation in our system for two very low linewidth lasers (100 Hz) as well as for a system using one comparatively larger linewidth laser (10 kHz). The demonstrated performance is consistent over SNRpilot range exceeding 10 dB. Future CV-QKD systems operating in telecom networks that use fibres with varying attenuation and noise, e.g., stemming from wavelength division multiplexed data transmission, would experience a degradation of the available SNRpilot. In such environments, the UKF may be the only method that guarantees key generation without having to adapt the pilot power. Finally, given the moderate symbol rates employed in CV-QKD, real-time implementations of the UKF should be feasible, thus making it a substantial element in all CV-QKD systems that implement the LO using an independent laser.

Methods

Machine learning aided phase tracking algorithm for carrier recovery

The phase noise associated with a time-varying pilot signal y(t) acquired by a radio-frequency heterodyne receiver at discrete time instants t = tk can be corrected by evaluating

$${\theta }_{k}\equiv \theta ({t}_{k})={\tan }^{-1}\left(\frac{{\mathcal{H}}(y(k))}{y(k)}\right)\,,$$
(1)

where \({\mathcal{H}}\) denotes the Hilbert transform. The linear trend in θk is removed to compensate for the frequency offset of the pilot tone leaving the phase noise. This method is standard for extracting the phase from a pilot signal and is equivalent to calculating the frequency offset, frequency shifting the pilot to baseband and then taking its argument, see Fig. 2a. In coherent detection systems the additive noise caused by the beating of the LO laser with vacuum fluctuations within the measurement bandwidth limit the efficacy of this method21, in addition to electronic noise. In principle, this can be solved by increasing the pilot signal power, however, as previously mentioned, this may be undesirable in a practical CV-QKD system.

Fig. 2: Two phase estimation algorithms.
figure 2

a Reference method and b machine learning approach.

Full size image

To overcome this pilot power limitation, we investigated a machine learning framework based on Bayesian inference. This approach allows inference of the phase from the noisy measurements yk ≔ y(k). In theory such an approach is statistically optimal with respect to the mean square error when estimating the phase15. To implement this method, a state space model that describes the evolution of the system in time is required in addition to a model that describes the measured values yk. For the state space model, the phase of the quantum signal evolves with discrete Markovian dynamics and can be represented as

$${X}_{k}:= {\theta }_{k}={\theta }_{k-1}+{q}_{k-1}\,,$$
(2)

where Xk is the system state at symbol k, θk is the phase at the same symbol and q is the unknown (phase) process noise. We note that the model in Eq. (2) is the typically used Wiener phase noise laser model which itself is an approximation of the behaviour of a real laser. The measurement model of the pilot signal in a heterodyne detection system is given by a noisy measurement outcome yk,

$${y}_{k}=A\sin ({{\Delta }}\omega k{T}_{s}+{\theta }_{k})+{n}_{k}\,,$$
(3)

where A is the amplitude of the pilot signal, Δω is the frequency offset between the LO laser and the pilot tone, Ts is the sampling time granularity and nk is the shot noise corrupting the measurement. For each symbol k Bayesian inference aims to obtain a filtering distribution

$$p({\theta }_{k}| {y}_{1:k})\,,$$
(4)

approximating q. The filtering distribution is the marginal distribution of the current θk given current and previous measurements y1:k = [y1, . . . yk]. The mean of this distribution is the statistically optimal estimated phase.

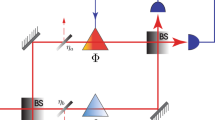
A direct implementation of the problem can be intractable, and hence there are implementations of Bayesian inference which are less optimal but tractable. The UKF handles the non-linear system (Eq. (3)) by taking a Gaussian approximation of the process noise. As shown in Fig. 2b, it does this by calculating some sigma points using the mean and standard deviation of the the approximating Gaussian distribution. These points are propagated through the measurement model which then are used to calculate the predicted mean and covariance. Similarly the mean and covariance of the measured noisy measurement are calculated to estimate the error between the predicted state and the measured pilot. The Gaussian approximation is then updated using a Metropolis-Hastings algorithm and used to estimate the symbol phase. The updated distribution is then fed into the next symbol’s estimation. This adaptive estimation allows for the algorithm to learn the system parameters using the measured pilot tone signal without knowing the system. This is especially important given that Eq. (2) is an approximation of the lasers. Should the given system parameters be significantly wrong, the major impact would be that convergence time to the optimum posterior distribution would be longer.

Figure 3 shows the number of samples for UKF convergence when the initial process noise parameter (described by the laser linewidth) is varied for a simulated 2 kHz combined linewidth system. Underestimating the laser linewidth increases the convergence time of the UKF since underestimating limits the size of the steps the UKF can take towards the actual phase. This may restrict the UKF’s ability to track the phase. Overestimating the linewidth can cause the UKF to overshoot as (barely) seen for the 100-kHz input but then settles to the system phase. The colour tints on the figure show the standard deviation of the approximating Gaussian used by the UKF.

Fig. 3: UKF convergence performance with respect to (incorrect) laser linewidth input.
figure 3

The simulated phase noise stems from a 2-kHz linewidth laser. The tints around the traces indicate the standard deviation of the approximating Gaussian distributions used by the UKF. This simulation was performed at 40 dB SNR for illustrative purposes.

Full size image

Experimental setup

The experimental setup used to perform CV-QKD is shown in Fig. 4. The transmitted symbols were drawn from independently seeded pseudo random Gaussian distributions with variance of 1 and zero mean at a rate of 50 MBaud. These digital symbols were upsampled to the 500 MSamples/s sampling rate of the arbitrary waveform generator (AWG) after which they were frequency shifted to ωq/2π = 60 MHz, i.e. multiplied with \(\exp (j{\omega }_{q}t)\), for single sideband modulation. A reference pilot tone at a frequency of ωp = 130 MHz was also multiplexed with the quantum signal for the purpose of phase noise compensation and frequency offset estimation. The pilot tone is ~5 dB higher power than the quantum signal. This radio frequency signal and a π/2-phase shifted version thereof drove the two arms of an I-Q electro-optical modulator to simultaneously modulate the quantum signal in both quadratures onto the output of laser centred at 1550.13 nm. The optical signal was then attenuated such that the mean photon number from only the quantum signal (i.e. excluding the pilot tone) was ≈2.73 at the quantum channel input. At the channel output, the transmitted optical signal was detected using a balanced heterodyne coherent receiver with a free-running LO generated by laser separate from the transmitter with an offset frequency ≈200 MHz. The LO power was 9 dBm, giving the combined shot and electronic noise clearance of ≈ 3 dB over the electronic noise. The output of the balanced receiver passed through a 200-MHz low-pass filter and was then digitised by a 10 bit digital storage oscilloscope (DSO) whose clock synchronised to that of the AWG to avoid additional penalties from clock recovery algorithm. The optical efficiency of the balanced detector (due to the non-unity quantum efficiency of the photodiodes and optical loss from connectors) was measured to be ≈0.84.

Fig. 4: CV-QKD experimental setup.
figure 4

a An ensemble of coherent states at 1550 nm was encoded into continuous-wave laser light by electro-optic in-phase/quadrature single sideband modulation driven by an arbitrary waveform generator (AWG). A reference pilot tone was digitally frequency multiplexed with these coherent states, which after suitable attenuation became the ‘quantum signal’. This pilot tone is ~3.2 times the power of the quantum signal. The polarisation of the combined quantum signal and pilot tone, transmitted through a 20-km SMF-28 fibre, was corrected with a manual polarisation controller to match the polarisation of an independent local oscillator (LO). The output of the radio-frequency heterodyne detector was sampled by a digital storage oscilloscope (DSO) at 1 GSamples/s before undergoing various digital-signal-processing (DSP) methods, including the unscented Kalman filter (UKF) assisted phase tracking. b Sample phase profiles extracted by UKF at high SNRpilot for 100 Hz and 10 kHz linewidth transmitter lasers. The receiver used the same ≈100 Hz linewidth laser as the LO for both setups.

Full size image

The measurement time was divided into frames, each consisting of 100k complex values, or the ‘quantum symbols’. A 10k symbol long CAZAC sequence22, appended to the quantum symbol sequence, aided in timing recovery, synchronisation and bulk phase offset compensation.

Digital-signal-processing

Additional DSP is performed to facilitate QKD system operation. The transmitted quantum symbols are shaped with a root raised cosine filter with roll-off of 0.4 and matched filtering is performed at the receiver. The pilot signal is filtered using a wide bandpass filter centred on its approximate location, calculated through the power spectrum of the received signal. The frequency offset is estimated through a Hilbert transform of the pilot and a linear fit of the extracted phase profile. This is re-estimated once more using the desired bandwidth filter which then shifts the pilot to baseband using the frequency offset estimate. The time-varying phase is left when taking the argument of the pilot tone. Note that this baseband pilot is the input to the UKF after downsampling to symbol rate. We generate a whitening filter based on the power spectrum of the measured vacuum noise i.e. when the LO is connected and switched on but not the quantum signal. This filter is applied to the received quantum signal and receiver calibration measurements for electronic and shot noise.

Excess noise and secret key rate calculations

To quantify the performance we use the secret key rate achievable in the asymptotic limit as well as the excess noise mean photon number at the channel output following an entangling cloner attack model as depicted in Fig. 5. The prepare-and-measure covariance matrix between the symbols chosen from a Gaussian probability distribution at the transmitter and measurement outcomes from a heterodyne (or phase diverse) receiver is

$$\gamma =\left(\begin{array}{cccc}2N & 0 & N\sqrt{2\eta } & 0\\ 0 & 2N & 0 & N\sqrt{2\eta }\\ N\sqrt{2\eta } & 0 & N\eta +e+1 & 0\\ 0 & N\sqrt{2\eta }& 0 & N\eta +e+1\end{array}\right)\,,$$
(5)

where N is the mean photon number of the transmitted thermal state, e is the excess noise mean photon number at the transmission channel output, η is the combined optical efficiency of the transmission channel and the receiver’s measurement device4. In a practical CV-QKD implementation the covariance matrix is estimated from the symbols as follows.

$$\hat{\gamma }=\left(\begin{array}{cccc}2N & 0 & \hat{z} & 0\\ 0 & 2N & 0 & \hat{z}\\ \hat{z} & 0 & \hat{y} & 0\\ 0 & \hat{z} & 0 & \hat{y}\end{array}\right)\,.$$
(6)

It is assumed that the transmitted thermal state has been previously characterised, i.e. N is known. The parameters η and e, inferred from the estimated covariance matrix as

$$\hat{\eta }=\frac{{\hat{z}}^{2}}{2{N}^{2}}\,,$$
(7)
$$\hat{e}=\hat{y}-\frac{{\hat{z}}^{2}}{2N}-1\,,$$
(8)

give the asymptotic secret key rate,

$$K=\beta I(A:B)-S(B:E)\,.$$
(9)

Here, A, B, E denote the modes of the transmitter, receiver, and eavesdropper, respectively, I is the mutual information, S is the Holevo information and β is the information reconciliation efficiency. For the sake of simplicity, we ignore finite-size effects here but more details can be found in Leverrier17.

Fig. 5: Channel model based on the entangling cloner attack.
figure 5

An eavesdropper injects one mode of an entangled state with mean photon number w into the open port of a beam splitter with transmittance η describing the optical channel loss. The excess noise mean photon number at the channel output is e = w(1 − η).

Full size image

Phase noise stemming from imperfect phase tracking effectively reduces the covariance term \(\hat{z}\) by a factor \(\kappa =\exp (-{\sigma }_{\,\text{pn}\,}^{2}/2)\), assuming Gaussian-distributed phase noise with σpn as the standard deviation. If the phase noise is untrusted, i.e. κ is unknown and unaccounted for, we obtain (via the entangling cloner model) a reduction of the actual physical transmittance of the channel to a virtual one, \({\eta }^{\prime}={\kappa }^{2}\eta\). Simultaneously, the increased excess noise is given by \({e}^{\prime}=e+(1-{\kappa }^{2})N\eta\). Thus, the larger the mean photon number of the ensemble of coherent states, the larger the effect of the phase noise.