Abstract
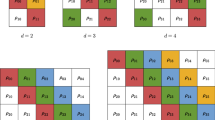
State of a \(d\)-dimensional quantum system can only be inferred by performing an informationally complete measurement with \(m\geqslant d^{2}\) outcomes. However, an experimentally accessible measurement can be informationally incomplete. Here we show that a single informationally incomplete measuring apparatus is still able to provide all the information about the quantum system if applied several times in a row. We derive a necessary and sufficient condition for such a measuring apparatus and give illustrative examples for qubits, qutrits, general \(d\)-level systems, and composite systems of \(n\) qubits, where such a measuring apparatus exists. We show that projective measurements and Lüders measurements with 2 outcomes are useless in the considered scenario.


Similar content being viewed by others
REFERENCES
A. S. Holevo, Statistical Structure of Quantum Theory (Springer, Berlin, 2001).
T. Heinosaari and M. Ziman, The Mathematical Language of Quantum Theory (Cambridge Univ. Press, Cambridge, 2012).
E. B. Davies and J. T. Lewis, ‘‘An operational approach to quantum probability,’’ Comm. Math. Phys. 17, 239–260 (1970).
A. S. Holevo, Quantum Systems, Channels, Information. A Mathematical Introduction (de Gruyter, Berlin, Boston, 2012).
C. Carmeli, T. Heinosaari, and A. Toigo, ‘‘Sequential measurements of conjugate observables,’’ J. Phys. A: Math. Theor. 44, 285304 (2011).
C. Carmeli, T. Heinosaari, and A. Toigo, ‘‘Informationally complete joint measurements on finite quantum systems,’’ Phys. Rev. A 85, 012109 (2012).
A. Kalev, J. Shang, and B.-G. Englert, ‘‘Symmetric minimal quantum tomography by successive measurements,’’ Phys. Rev. A 85, 052116 (2012).
A. Di Lorenzo, ‘‘Sequential measurement of conjugate variables as an alternative quantum state tomography,’’ Phys. Rev. Lett. 110, 010404 (2013).
J. S. Lundeen and C. Bamber, ‘‘Procedure for direct measurement of general quantum states using weak measurement,’’ Phys. Rev. Lett. 108, 070402 (2012).
G. S. Thekkadath, L. Giner, Y. Chalich, M. J. Horton, J. Banker, and J. S. Lundeen, ‘‘Direct measurement of the density matrix of a quantum system,’’ Phys. Rev. Lett. 117, 120401 (2016).
L. Calderaro, G. Foletto, D. Dequal, P. Villoresi, and G. Vallone, ‘‘Direct reconstruction of the quantum density matrix by strong measurements,’’ Phys. Rev. Lett. 121, 230501 (2018).
E. Haapasalo, T. Heinosaari, and Y. Kuramochi, ‘‘Saturation of repeated quantum measurements,’’ J. Phys. A: Math. Theor. 49, 33LT01 (2016).
I. A. Luchnikov and S. N. Filippov, ‘‘Quantum evolution in the stroboscopic limit of repeated measurements,’’ Phys. Rev. A 95, 022113 (2017).
Yu. I. Bogdanov, G. Brida, M. Genovese, S. P. Kulik, E. V. Moreva, and A. P. Shurupov, ‘‘Statistical estimation of the efficiency of quantum state tomography protocols,’’ Phys. Rev. Lett. 105, 010404 (2010).
S. N. Filippov and V. I. Man’ko, ‘‘Unitary and non-unitary matrices as a source of different bases of operators acting on Hilbert spaces,’’ J. Russ. Laser Res. 32, 56–67 (2011).
S. N. Filippov, S. Gudder, T. Heinosaari, and L. Leppäjärvi, ‘‘Operational restrictions in general probabilistic theories,’’ Found. Phys. 50, 850–876 (2020).
S. N. Filippov, T. Heinosaari, and L. Leppäjärvi, ‘‘Simulability of observables in general probabilistic theories,’’ Phys. Rev. A 97, 062102 (2018).
S. N. Filippov, ‘‘Quantum mappings and characterization of entangled quantum states,’’ J. Math. Sci. 241, 210–236 (2019).
M. Ozawa, ‘‘Quantum measuring processes of continuous observables,’’ J. Math. Phys. 25, 79–87 (1984).
M. Ozawa, ‘‘Conditional probability and a posteriori states in quantum mechanics,’’ Publ. Res. Inst. Math. Sci., Kyoto Univ. 21, 279–295 (1985).
J. Eisert, M. P. Müller, and C. Gogolin, ‘‘Quantum measurement occurrence is undecidable,’’ Phys. Rev. Lett. 108, 260501 (2012).
M. Hayashi, Quantum Information (Springer, Berlin, 2006).
P. Busch and P. J. Lahti, ‘‘The determination of the past and the future of a physical system in quantum mechanics,’’ Found. Phys. 19, 633–678 (1989).
S. N. Filippov and V. I. Man’ko, ‘‘Inverse spin-s portrait and representation of qudit states by single probability vectors,’’ J. Russ. Laser Res. 31, 32–54 (2010).
Yu. I. Bogdanov, S. P. Kulik, E. V. Moreva, I. V. Tikhonov, A. K. Gavrichenko, ‘‘Optimization of a quantum tomography protocol for polarization qubits,’’ JETP Lett. 91, 686–692 (2010).
J. M. Renes, R. Blume-Kohout, A. J. Scott, and C. M. Caves, ‘‘Symmetric informationally complete quantum measurements,’’ J. Math. Phys. 45, 2171 (2004).
S. N. Filippov and V. I. Man’ko, ‘‘Symmetric informationally complete positive operator valued measure and probability representation of quantum mechanics,’’ J. Russ. Laser Res. 31, 211–231 (2010).
W. K. Wootters and B. D. Fields, ‘‘Optimal state-determination by mutually unbiased measurements,’’ Ann. Phys. 191, 363–381 (1989).
A. Komisarski and A. Paszkiewicz, ‘‘On a system of measurements which is complete in a statistical sense,’’ Infinite Dimens. Anal., Quantum Prob. Rel. Top. 16, 1350026 (2013).
S. Brierley, S. Weigert, and I. Bengtsson, ‘‘All mutually unbiased bases in dimensions two to five,’’ Quantum Inform. Comput. 10, 803–820 (2010).
I. A. Luchnikov, S. V. Vintskevich, D. A. Grigoriev, and S. N. Filippov, ‘‘Machine learning non-Markovian quantum dynamics,’’ Phys. Rev. Lett. 124, 140502 (2020).
Author information
Authors and Affiliations
Corresponding authors
Additional information
(Submitted by A. S. Holevo)
Rights and permissions
About this article
Cite this article
Zhuravlev, V.A., Filippov, S.N. Quantum State Tomography Via Sequential Uses of the Same Informationally Incomplete Measuring Apparatus. Lobachevskii J Math 41, 2405–2414 (2020). https://doi.org/10.1134/S1995080220120434
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1995080220120434