Skip to main content
SpringerLink
Log in

Analytical Solution of Axisymmetric Contact Problem for a Poroelastic Layer

  • Published:
Mechanics of Solids Aims and scope Submit manuscript

Abstract—

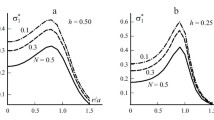
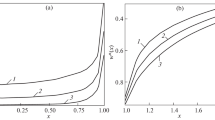
In this article, we analyze axisymmetric contact problems on the interaction of a rigid stamp with a poroelastic layer using the equations of the Cowin–Nunziato theory of poroelastic bodies. It is assumed that the stamp base has a flat or parabolic shape and there is no friction in the contact zone. The posed problems are reduced to integral equations, the main kernel part of which is the delta function, by means of special function via which the contact stresses are expressed. Using a special approximation of the integral equation kernel transform, its asymptotic solution is constructed for the case of relatively large layer thicknesses. This approach to solving integral equations of contact problems was proposed by I.I. Vorovich and was further developed by his students. Expressions for the contact stresses and the contact area in the case of a parabolic stamp are obtained in a simple analytical form. Also, a relation between the force acting on the stamp and its displacement that is one of the main characteristics in determining the mechanical parameters of a material by the indentation method is found in terms of elementary expressions. A comparative analysis of the investigated quantities for various values ​​of the parameters of porosity and layer thickness is carried out.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. G. W. Nunziato and S. C. Cowin, “A nonlinear theory of elastic materials with voids,” Arch. Ration. Mech. Anal. 72, 175–201 (1979).

    Article  MathSciNet  Google Scholar 

  2. S. C. Cowin and G. W. Nunziato, “Linear theory of elastic materials with voids,” J. Elasticity 13, 125–147 (1983).

    Article  Google Scholar 

  3. D. Iesan, “A theory of thermoelastic materials with voids,” Acta Mech. 60, 67–89 (1986).

    Article  Google Scholar 

  4. D. S. Chandrasekharaiah, “Effects of surface stresses and voids on Rayleigh waves in an elastic solid,” Int. J. Eng. Sci. 25, 205–211 (1987).

    Article  MathSciNet  Google Scholar 

  5. A. Scalia and M. A. Sumbatyan, “Contact problem for porous elastic half-plane,” J. Elasticity 60, 91–102 (2000).

    Article  Google Scholar 

  6. A. Scalia, “Contact problem for porous elastic strip,” Int. J. Eng. Sci. 40, 401–410 (2002).

    Article  Google Scholar 

  7. G.Iovane and A. V. Nasedkin, “Modal analysis of piezoelectric bodies with voids. I. Mathematical approaches,” Appl. Math. Model. 34, 60–71 (2010).

    Article  MathSciNet  Google Scholar 

  8. G.Iovane and A. V. Nasedkin, “Finite element dynamic analysis of anisotropic elastic solids with voids,” Comput. Struct. 87, 981–989 (2009).

    Article  Google Scholar 

  9. G.Iovane and A. V. Nasedkin, “Finite element analysis of static problems for elastic media with voids,” Comput. Struct. 84, 19–24 (2005).

    Article  Google Scholar 

  10. A. B. Kudimova, D. K. Nadolin, A. V. Nasedkin, et al., “Models of porous piezocomposites with 3–3 connectivity type in ACELAN finite element package,” Mater. Phys. Mech. 37 (1), 16–24 (2018).

    Google Scholar 

  11. A. V. Nasedkin, A. A. Nasedkina, and A. N. Rybyanets, “Numerical analysis of effective properties of heterogeneously polarized porous piezoceramic materials with local alloying pore surfaces,” Mater. Phys. Mech. 40 (1), 12–21 (2018).

    Google Scholar 

  12. I. I. Vorovich, V. M. Aleksandrov, and V. A. Babeshko, Non-Classical Mixed Problems on Theory of Elasticity (Nauka, Moscow, 1974) [in Russian].

    Google Scholar 

  13. V. M. Aleksandrov and M. I. Chebakov, Introduction to the Contact Mechanics (OOO TsVVR, Rostov-on-Don, 2007) [in Russian].

  14. M.I. Chebakov, “On further development of the “method of large λ” in the theory of mixed problems,” J. Appl. Math. Mech. 40 (3), 512–518 (1976).

    Article  Google Scholar 

  15. V. M. Aleksandrov and M. I. Chebakov, Analytical Methods for Contact Problems on Theory of Elasticity (Fizmatlit, Moscow, 2004) [in Russian].

    MATH  Google Scholar 

  16. V. M. Aleksandrov and M. I. Chebakov, “Mixed problems of the mechanics of continuous media associated with Hankel and Mehler–Fock integral transforms,” J. Appl. Math. Mech. 36 (3), 465–474 (1972).

    Article  Google Scholar 

  17. V. M. Aleksandrov and M. I. Chebakov, “On a method of solving dual integral equations,” J. Appl. Math. Mech. 37 (6),1031–1041 (1973).

    Article  MathSciNet  Google Scholar 

Download references

Funding

Research was financially supported by Southern Federal University, grant no. VnGr/2020-04-IM (Ministry of Science and Higher Education of the Russian Federation).

Author information

Authors and Affiliations

  1. Institute for Mathematics, Mechanics, and Computer Science named after I.I. Vorovich, Southern Federal University, 344058, Rostov-on-Don, Russia

    E. M. Kolosova & M. I. Chebakov

Authors
  1. E. M. Kolosova
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. I. Chebakov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to E. M. Kolosova or M. I. Chebakov.

Additional information

Translated by A. A. Borimova

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kolosova, E.M., Chebakov, M.I. Analytical Solution of Axisymmetric Contact Problem for a Poroelastic Layer. Mech. Solids 55, 857–864 (2020). https://doi.org/10.3103/S0025654420050118

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0025654420050118

Keywords:

Search

Navigation