1 Introduction

Many mechanical structures are used in environments with high-temperature differences. It causes significant temperature changes, stresses, and deformations. Applying heat load in some systems is inevitable, and in others, it is accidental. Some structures are subjected to thermal loads frequently during the working period. The effect of heat on the construction and performance of structures such as spacecraft, nuclear reactors, and heat exchangers are examples of this type of heat loading.

On the other hand, a thermal load may be accidentally applied to a structure. An example of this is the fire in urban and industrial buildings and facilities. Regardless of the effects of heat load, the structure’s design will not be complete and safe. An important group of constructions among the applicable structures is the beam, which forms a large part of a composite structure system. In cases where the mechanical design is composed of lean elements, e.g., beams, one of the major problems caused by rising temperature is thermal buckling [1]. The thermal effects play an important role in structural mechanics, see, e.g., [2,3,4,5,6].

As solid phase supports, magnetic microparticles (MMP) promise many significant advances in experimental works. New technology emerged by which magnetic separation can occur during magnetism. Different molecules can be isolated or absorbed by these particles in many applications such as magnetic cell separation, ribonucleic acid (RNA) purification, see, e.g., [7,8,9] and reference therein. One of the biotic and useful applications of MMPs is targeting cancer cells qua these particles can separate cells from human blood. However, timeless usages are waiting to be found.

Today, due to the widespread advances in engineering sciences, the need for optimizations resulting from small-scale technology is felt more and more. Microsensors are highly improved, high-performance materials that are just one example of applications in the micro-industry. Devices display properties such as temperature, pressure, traction, or current output the desired parameter. On the other hand, magnetic microsensors detect changes or disturbances in the magnetic field and then, based on that, extract the required information such as direction, presence, rotation angle, or potential [10,11,12,13,14,15].

Apart from the piezomagneticity, magnetic microsensors and generally magnetic particles can have another physical property, which is flexomagneticity. The difference is that flexomagnetic is a pervasive effect on all materials with any symmetry, the discovery of which dates back to the current decade. Flexomagneticity is the coupling between the polarization and the strain gradient, but piezomagneticity is the coupling between the polarization and the strain itself [16,17,18,19,20,21,22,23]. The small-scale theme is the main debate in MMPs technology, which shows the more effective role of flexomagneticity. In light of the new progress and developments which emerge these years, particularly at a small scale, the flexomagneticity debate is increasing quickly.

Based on the research background performed on the mechanics of piezomagnetic-flexomagnetic structures, theoretical research can be found. These studies were preliminarily begun by Sidhardh and Ray [24] and Zhang et al. [25]. In these introductory works, they showed studies on piezomagnetic-flexomagnetic nanostructures by investigating bending properties. The deformations were assumed as the small, and linear analysis was taken into consideration. Both published research employed the Euler–Bernoulli displacement kinematic field to model the structure as a thin beam. Magnetization influences were regarding both reverse and direct impacts. The acted static loading was vertically and uniformly imposed throughout the length of the beam. The first research examined cantilever beams. However, the second one demonstrated a premier study by evaluating several end conditions. The shortcoming of both works is a lack of considering size-dependent effects. Though they simply inspected only surface effect, nonlocal or microstructural influences were not figured out. Newly, Malikan and Eremeyev [26] carried out piezomagnetic-flexomagnetic Euler–Bernoulli small-scale beams exposed in a vibrational mode. The linear frequency analysis was done while the size-dependent impacts were explored according to the stress-driven nonlocal elasticity approach. Based on their results, it was affirmed that the flexomagnetic feature is size-dependent.

Another research on piezomagnetic-flexomagnetic small size structures has been performed by Malikan and Eremeyev [27] in which they studied the nonlinear model of natural frequencies of the structure. They fulfilled size-dependent influences based on the nonlocal strain gradient elasticity model. In addition to these, Malikan and Eremeyev [28] studied large deflections of piezo-flexomagnetic nano-size beams using two-step analytical-numerical solution techniques. They discovered that analysis of a nonlinear model of bending of a piezo-flexomagnetic nanobeam is seriously required to design nano-electro-mechanical systems (NEMS) based on piezomagnetic-flexomagnetic properties. They demonstrated many new results, of which we can refer to reducing the deflections as a result of the flexomagnetic effect. Malikan et al. [29] continued the studies on magnetic nanoparticles involving both piezomagnetic and flexomagnetic features. The new study investigated the post-buckling response of the structures, which led to some new results and achievements in the field of smart nanosensors. More recently, Malikan et al. [30] investigated the porous states in the structure of a piezomagnetic-flexomagnetic beam considering size influences. It was found that porosity affects the flexomagnetic response of the materials.

This research attempts to estimate temperature impacts on magnetic structures to extend the accomplished works on piezomagnetic-flexomagnetic properties. In doing so, this article investigates a microscale piezomagnetic-flexomagnetic beam-shaped sensor and peruses the size-dependent influences according to a strain gradient model. The elastic strains are supposed to be linear, and the kinematic displacement components are due to Euler–Bernoulli thin beam. Two presented boundary conditions are mathematically imposed, namely clamped and simple supports. The assessments are then continued with changes in associated factors, which effectively design the magnetic sensor, and the results are exhibited graphically by several figures.

2 Theoretical modeling

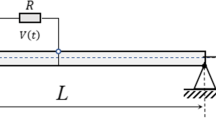
Let us discuss the applied model in more detail. Figures 1 and 2 show that the microscale beams are installed into clamped-clamped and simple-simple supports, respectively. The cross section of the beams is geometrically square. The beam is placed in a magnetic field, which acts vertically. The thermal environment is also taken into account and affects the beam in direction with the thickness only.

Fig. 1
figure 1

A square microbeam containing PM and FM embedded in fully fixed ends

Full size image
Fig. 2
figure 2

A square microbeam containing PM and FM embedded in pivot ends

Full size image

The beam is considered to act as the Euler–Bernoulli beam hypothesis as [31,32,33,34]

$$\begin{aligned}&u_{1} \left( {x,z} \right) =u\left( x \right) -z\frac{\hbox {d}w\left( x \right) }{\hbox {d}x} \end{aligned}$$
(1)
$$\begin{aligned}&u_{3} \left( {x,z} \right) =w\left( x \right) \end{aligned}$$
(2)

where we introduced axial displacement \(u\left( x \right) \) and deflection \(w\left( x \right) \) as functions of x coordinate, see Figs. 1 and 2.

The compatible components of strain–displacement relations have the following form [24,25,26,27,28,29,30,31,32,33,34,35]

$$\begin{aligned}&\varepsilon _{xx} =\frac{\hbox {d}u}{\hbox {d}x}-z\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}} \end{aligned}$$
(3)
$$\begin{aligned}&\eta _{xxz} =\frac{\hbox {d}\varepsilon _{xx} }{{\hbox {d}z}}=-\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}} \end{aligned}$$
(4)

The nonzero stress \(\sigma _{xx}\) and hyper stress \(\xi _{xxz}\) components alongside magnetic induction can be expanded as [24, 25]

$$\begin{aligned}&\sigma _{xx} =C_{11} \varepsilon _{xx} -\alpha C_{11} \Delta T-q_{31} H_{z} \end{aligned}$$
(5)
$$\begin{aligned}&\xi _{xxz} =g_{31} \eta _{xxz} -f_{31} H_{z} \end{aligned}$$
(6)
$$\begin{aligned}&B_{z} =a_{33} H_{z} +q_{31} \varepsilon _{xx} +f_{31} \eta _{xxz} \end{aligned}$$
(7)

where \(C_{11}\) is an elastic modulus, \(\alpha \) is a coefficient of thermal expansion, \(\Delta T\) is the temperature change across the cross section of the beam, \(H_{z}\) is the vertical component of the magnetic field, \(q_{31}\) is a piezomagnetic modulus, \(g_{31}\) is a higher-order elastic modulus, \(f_{31}\) is a flexomagnetic modulus responsible for coupling between magnetic flux \(B_{z}\) and strain gradient \(\eta _{xxz}\), and \(a_{33}\) is a magnetic permeability.

The characteristics equation can be derived based on a virtual displacement in the system according to the first variation in total energy relationship as below [36]

$$\begin{aligned} \delta U-\delta W=0 \end{aligned}$$
(8)

where \(\delta U\) is the first variation of the energy functional and \(\delta W\) is the work of external actions.

To establish the strain energy in the global form, one can write

$$\begin{aligned} \delta U=\int \limits _V {\left( {\sigma _{xx} \delta \varepsilon _{xx} +\xi _{xxz} \delta \eta _{xxz} -B_{z} \delta H_{z} } \right) } \hbox {d}V \end{aligned}$$
(9)

Thus, based on Eqs. (5–7), Eq. (9) can be calculated by integrating part by part as follows

$$\begin{aligned} \delta U=\delta \Pi _{U_{1} }^\mathrm{Mech} +\delta \Pi _{U_{1} }^\mathrm{Mag} +\delta \Pi _{U_{2} }^\mathrm{Mech} +\delta \Pi _{U_{2} }^\mathrm{Mag} \end{aligned}$$
(10)

where

$$\begin{aligned} \delta \Pi _{U_{1} }^\mathrm{Mech}= & {} -\int \limits _0^L {\left[ {\frac{\hbox {d}N_{x} }{\hbox {d}x}\delta u+\left( {\frac{\hbox {d}^{2}M_{x} }{\hbox {d}x^{2}}+\frac{\hbox {d}^{2}T_{xxz} }{\hbox {d}x^{2}}} \right) \delta w} \right] \hbox {d}x} \end{aligned}$$
(11)
$$\begin{aligned} \delta \Pi _{U_{1} }^\mathrm{Mag}= & {} -\int \limits _0^L {\int \limits _{{-h} /2}^{h /2} {\frac{\hbox {d}B_{z} }{{\hbox {d}z}}\delta \varPsi {\hbox {d}z}} \hbox {d}x} \end{aligned}$$
(12)
$$\begin{aligned} \delta \Pi _{U_{2} }^\mathrm{Mech}= & {} \left. {\left( {N_{x} \delta u-M_{x} \frac{\hbox {d}\delta w}{\hbox {d}x}-T_{xxz} \frac{\hbox {d}\delta w}{\hbox {d}x}+\frac{\hbox {d}M_{x} }{\hbox {d}x}\delta w+\frac{\hbox {d}T_{xxz} }{\hbox {d}x}\delta w} \right) } \right| _{0}^{L} \end{aligned}$$
(13)
$$\begin{aligned} \delta \Pi _{U_{2} }^\mathrm{Mag}= & {} \left. {\int \limits _0^L {\left( {B_{z} \delta \varPsi } \right) } } \right| _{-h/2}^{h/2} \hbox {d}x \end{aligned}$$
(14)

where the associated parameters would be

$$\begin{aligned} N_{x}= & {} \int \limits _{-h/2}^{h/2} {\sigma _{xx} {\hbox {d}z}} \end{aligned}$$
(15)
$$\begin{aligned} M_{x}= & {} \int \limits _{-h/2}^{h/2} {\sigma _{xx} z{\hbox {d}z}} \end{aligned}$$
(16)
$$\begin{aligned} T_{xxz}= & {} \int \limits _{-h/2}^{h/2} {\xi _{xxz} {\hbox {d}z}} \end{aligned}$$
(17)

which are axial, moment, and hyper stress resultants on beam elements.

The virtual work as results of an axial magnetic field and thermal environment can be expressed as [37, 38]

$$\begin{aligned} W= & {} -\frac{1}{2}\int \limits _0^L {N_{x}^{0} \left( {\frac{\hbox {d}w}{\hbox {d}x}} \right) ^{2}} \hbox {d}x \end{aligned}$$
(18)
$$\begin{aligned} \delta W= & {} -\int \limits _0^L {N_{x}^{0} \left( {\frac{\hbox {d}\delta w}{\hbox {d}x}\frac{\hbox {d}w}{\hbox {d}x}} \right) } \hbox {d}x \end{aligned}$$
(19)

We are allowed to write the relationship between magnetic potential and the magnetic component as

$$\begin{aligned} H_{z} =-\frac{\hbox {d}\varPsi }{{\hbox {d}z}} \end{aligned}$$
(20)

Let us assume the magnetic field varies linearly in direction with thickness, hence

$$\begin{aligned} \varPsi \left( {+\frac{h}{2}} \right) =\psi , \quad \varPsi \left( {-\frac{h}{2}} \right) =0 \end{aligned}$$
(21)

where the closed-circuit beside the reverse effect of the field is investigated. Plugging Eqs. (7), (12), (20) and (21) and some simplifications give [24, 25]

$$\begin{aligned} \varPsi= & {} -\frac{q_{31} }{2a_{33} }\left( {z^{2}-\frac{h^{2}}{4}} \right) \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+\frac{\psi }{h}\left( {z+\frac{h}{2}} \right) \end{aligned}$$
(22)
$$\begin{aligned} H_{z}= & {} z\frac{q_{31} }{a_{33} }\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-\frac{\psi }{h} \end{aligned}$$
(23)

To appear Eqs. (5–7) in detail, we can take the help of Eqs. (3), (4), (22), and (23), thus

$$\begin{aligned} \sigma _{xx}= & {} -z\left( {C_{11} +\frac{q_{31}^{2} }{a_{33} }} \right) \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+\frac{q_{31} \psi }{h}-\sigma ^{T} \end{aligned}$$
(24)
$$\begin{aligned} \xi _{xxz}= & {} -\left( {g_{31} +\frac{q_{31} f_{31} z}{a_{33} }} \right) \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+\frac{f_{31} \psi }{h} \end{aligned}$$
(25)
$$\begin{aligned} B_{z}= & {} -f_{31} \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-\frac{a_{33} \psi }{h} \end{aligned}$$
(26)

We now express the stress and hyper stress resultants as

$$\begin{aligned} N_{x}= & {} C_{11} A\frac{\hbox {d}u}{\hbox {d}x}+N^\mathrm{Mag} -N^{T} \end{aligned}$$
(27)
$$\begin{aligned} M_{x}= & {} -I_{z} \left( {C_{11} +\frac{q_{31}^{2} }{a_{33} }} \right) \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-M^{T} \end{aligned}$$
(28)
$$\begin{aligned} T_{xxz}= & {} -g_{31} h\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+f_{31} \psi \end{aligned}$$
(29)

From the mathematical point of view, stress- and stress-gradient models of continua are based on the nonlocal constitutive equations, i.e., the equations which relate stresses and strains using differential and/or integral operators. These relate to long-range interactions between material particles. For example, considering a crystalline lattice, they usually assume short-range interactions, i.e., interactions between closest neighbors only. On the other hand, this is an assumption, and the analysis of interactions between other particles of the lattice could bring a better description of such phenomena as strain localization. As another example, it is worth to mention that composites and metamaterials with high contrast in material properties. For example, homogenization of beam-lattice materials may lead to strain gradient continua. In a certain sense, such effective media inherit properties of beams that resist bending. Finally, dependence on the gradient of strains is the key property of such electromechanical couplings as flexoelectricity and flexomagneticity, where these phenomena related to multipole interactions.

The second strain gradient of Mindlin will be implemented to attach the microstructural property into a problem model [39,40,41,42,43]. It is crucial to note that the couple stress models [44,45,46,47,48,49,50] cannot be embedded into the energy formulation while the problem is flexoelectric or flexomagnetic ones. This problem occurs because both magnetic and couple stress terms in the energy formulation mathematically act similarly, and the couple stress term would be pointless. Therefore, the second strain gradient is employed, which is not directly placed in energy formulation. The second strain gradient relationship can be expressed as below

$$\begin{aligned} \sigma _{ij} ={C}_{{ijkl}} \left( {1\pm l^{2}\frac{\hbox {d}^{2}}{\hbox {d}x^{2}}} \right) \varepsilon _{kl} \end{aligned}$$
(30)

The model shown by Eq. (30) can be utilized in two parts, a model with a negative sign and another one with a positive sign. The positive sign makes the model destabilizing [50, 51], but the negative sign produces a stable model.

There are two models for strain gradient approach introduced by Mindlin [39, 40]. A model is named as the first and another one as the second theory of strain gradient. It should be remembered that another form of the first strain gradient theory can be couple stress models [45, 46]. Furthermore, these theories relate to the strain and its gradient.

Materials and structures with micro/sub-micro size subject to mechanical loads respond differently as macro-materials. This is called the size-dependent response. This size dependency has been evaluated according to the additional physical parameters famed as small-scale or length scale ones. The strain gradient theory also includes a length scale parameter that its numerical values are still unknown for most of the structures. Physically, the values of this parameter correlate with inner structures of materials. The advantage of using this determinative factor is avoiding to use experiments that necessity to high costs. What is more, it can help forecast the physical response of micro/nano-sized structures. Until now, a few scientists harvested approximate values for small-scale parameters existed in the microstructural analysis [52,53,54,55]. Usually, to identify the numerical values for these extra parameters, there have been requiring laboratory works. Then, it is enough to compare the experimental outcomes with the numerical results and match both analyses outputs by determining the values of small-scale parameters. However, some researchers confirmed that these additional parameters cannot be a material constant which means nobody can claim that material has its value for these parameters and the values are linked with several environmental and boundary conditions [44]. The way suggested by a lot of published works showed that the cost-effective path to study micro/nanostructures based on these length scale parameters is implementing a logical amplitude for numerical amounts of the small-scale parameters. This rational amplitude can be defined between zero to a value by which the results have no great or unreasonable difference when the parameter value is zero compared to when it is chosen as a nonzero amount.

The stress resultants in the form of a second strain gradient model can be written as follows

$$\begin{aligned} N_{x}= & {} \left( {1-l^{2}\frac{\hbox {d}^{2}}{\hbox {d}x^{2}}} \right) \left\{ {C_{11} A\frac{\hbox {d}u}{\hbox {d}x}} \right\} -N^\mathrm{Mag} -N^{T} \end{aligned}$$
(31)
$$\begin{aligned} M_{x}= & {} \left( {1-l^{2}\frac{\hbox {d}^{2}}{\hbox {d}x^{2}}} \right) \left\{ {-I_{z} \left( {C_{11} +\frac{q_{31}^{2} }{a_{33} }} \right) \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}} \right\} -M^{T} \end{aligned}$$
(32)
$$\begin{aligned} T_{xxz}= & {} \left( {1-l^{2}\frac{\hbox {d}^{2}}{\hbox {d}x^{2}}} \right) \left\{ {-g_{31} h\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+f_{31} \psi } \right\} \end{aligned}$$
(33)

As stated by the Lorentz’ law, the transverse magnetic field can generate a longitudinal mechanical force. Therefore,

$$\begin{aligned} N^\mathrm{Mag} =q_{31} \psi \end{aligned}$$
(34)

Assuming the variations of temperature in line with the thickness of the beam, the below relation can be presented [46,47,48,49,50,51,52,53,54,55,56,57]

$$\begin{aligned} \Delta T\left( z \right) =\left( {\frac{z+h / 2}{h}} \right) ^{\varphi }T,\quad {-h} /2\le z\le h /2,\quad 0\le \varphi \le \infty \end{aligned}$$
(35)

in which T is the temperature variation as

$$\begin{aligned} T=T_{f} -T_{0} \end{aligned}$$
(36)

The temperature variation along the thickness has here three forms (Fig. 3) defined in the following

$$\begin{aligned} \varphi \left\{ {{\begin{array}{*{20}c} {=0:Uniform} \\ {=1:Linear} \\ {>1:Parabolic} \\ \end{array} }} \right. \end{aligned}$$
(37)
Fig. 3
figure 3

Thermal loading across the thickness

Full size image

The temperature can cause a thermal load axially applied on the beam as below

$$\begin{aligned} N^{T}= & {} \frac{\alpha C_{11} }{1-\nu }\int \limits _{{-h} / 2}^{h /2} {\Delta T\left( z \right) {\hbox {d}z}} \end{aligned}$$
(38)
$$\begin{aligned} M^{T}= & {} \frac{\alpha C_{11} }{1-\nu }\int \limits _{{-h} / 2}^{h / 2} {\Delta T\left( z \right) z{\hbox {d}z}} \end{aligned}$$
(39)

Afterward, the total longitudinal and moment forces performed on the system can be briefly shown as

$$\begin{aligned} N_{x}^{0}= & {} N^\mathrm{Mag}+N^{T} \end{aligned}$$
(40)
$$\begin{aligned} M_{x}= & {} M^\mathrm{Mech} +M^{T} \end{aligned}$$
(41)

in which the axial resultant is divided into magnetic and thermal parts. Moreover, the moment stress resultant is sectioned into two parts, that is, mechanical and thermal ones.

Taking into account Eqs. (11), (13) and (19) and embedding all in Eq. (8) result in the local governing equations as follows

$$\begin{aligned}&\frac{\hbox {d}N_{x} }{\hbox {d}x}=0 \end{aligned}$$
(42)
$$\begin{aligned}&\frac{\hbox {d}^{2}M_{x} }{\hbox {d}x^{2}}+\frac{\hbox {d}^{2}T_{xxz} }{\hbox {d}x^{2}}+N_{x}^{0} \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}=0 \end{aligned}$$
(43)

Writing Eqs. (42) and (43) based on Eqs. (31–33), (40) and (41) leads to two independent equations which in order to solve the values of critical temperature, the second equation is required and sufficient as

$$\begin{aligned}&C_{11} A\left( {1-l^{2}\frac{\hbox {d}^{2}}{\hbox {d}x^{2}}} \right) \frac{\hbox {d}^{2}u}{\hbox {d}x^{2}}=0 \end{aligned}$$
(44a)
$$\begin{aligned}&D\left( {l^{2}\frac{\hbox {d}^{6}w}{\hbox {d}x^{6}}-\frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}} \right) +\left( {N^\mathrm{Mag}+\beta T} \right) \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}=0 \end{aligned}$$
(44b)

in which

$$\begin{aligned} D= & {} \left[ {I_{z} \left( {C_{11} +\frac{q_{31}^{2} }{a_{33} }} \right) +g_{31} h} \right] ,\\ \beta= & {} \frac{\alpha C_{11} h}{\left( {1-\nu } \right) \left( {1+\varphi } \right) } \end{aligned}$$

As it is obvious, Eq. (44a) is only based upon u and Eq. (44b) is in accordance with w only.

3 Solution approach

This section develops analytical solution methods for the present problem investigating two boundary conditions. Clamped and simply-supported end conditions are satisfied here based on the two different admissible functions describing these supports’ physical conditions mathematically. An analytical process is demonstrated [58, 59]. Hence,

$$\begin{aligned} w\left( x \right) =W\cdot X\left( x \right) \end{aligned}$$
(45)

The admissible function indices in Eq. (45) needed in the process are given [58, 60].

$$\begin{aligned}&\hbox {SS}: X\left( x \right) =\sin \left( {\frac{\pi }{L}x} \right) \end{aligned}$$
(46)
$$\begin{aligned}&\hbox {CC}: X\left( x \right) =\sin ^{2}\left( {\frac{\pi }{L}x} \right) \end{aligned}$$
(47)

The associated notations denote, respectively, for simply-supported (S) and clamped (C) boundary conditions. It is interesting to note that the end conditions can also be derived in a strain gradient phase as shown by Tables 1 and 2.

Table 1 Constitutive end conditions for CC
Full size table
Table 2 Constitutive end conditions for SS
Full size table

Substituting Eq. (45) into Eq. (44) and integrating over the longitudinal domain will lead to

$$\begin{aligned} \left( {K_{1} +TK_{2} } \right) X=0 \end{aligned}$$
(48)

Some manipulating and arranging give the linear algebraic equation in which there can be critical temperature as the unknown parameter required to be determined. The coefficients in Eq. (48) can be expressed as follows

$$\begin{aligned}&K_{1} =\int \limits _0^L {\left[ {\lambda _{1} \left( x \right) \cdot Y\left( x \right) } \right] \hbox {d}x} \end{aligned}$$
(49)
$$\begin{aligned}&K_{2} =\int \limits _0^L {\left[ {\lambda _{2} \left( x \right) \cdot Y\left( x \right) } \right] \hbox {d}x} \end{aligned}$$
(50)

in which

$$\begin{aligned}&\lambda _{1} =D\left( {l^{2}\frac{\hbox {d}^{6}w}{\hbox {d}x^{6}}-\frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}} \right) +N^\mathrm{Mag}\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}},\\&\quad \lambda _{2} =\beta \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}} \end{aligned}$$

Consequently, let us manipulate and simplify the equation based on the critical temperature load and admissible functions as

$$\begin{aligned} T=\frac{D\left( {l^{2}\int \limits _0^L {\left( {\frac{\hbox {d}^{6}X\left( x \right) }{\hbox {d}x^{6}}\cdot Y\left( x \right) } \right) \hbox {d}x} -\int \limits _0^L {\left( {\frac{\hbox {d}^{4}X\left( x \right) }{\hbox {d}x^{4}}\cdot Y\left( x \right) } \right) \hbox {d}x} } \right) +N^\mathrm{Mag}\int \limits _0^L {\left( {\frac{\hbox {d}^{2}X\left( x \right) }{\hbox {d}x^{2}}\cdot Y\left( x \right) } \right) \hbox {d}x} }{\beta \int \limits _0^L {\left( {\frac{\hbox {d}^{2}X\left( x \right) }{\hbox {d}x^{2}}\cdot Y\left( x \right) } \right) \hbox {d}x} } \end{aligned}$$
(51)

One can write the thermal analytical buckling formula for CC as:

$$\begin{aligned} T=\frac{N^\mathrm{Mag}L^{4}+4DL^{2}\pi ^{2}m^{2}+16Dl^{2}\pi ^{4}m^{4}}{\beta L^{4}} \end{aligned}$$
(52)

And also for SS as:

$$\begin{aligned} T=\frac{N^\mathrm{Mag}L^{4}+DL^{2}\pi ^{2}m^{2}+Dl^{2}\pi ^{4}m^{4}}{\beta L^{4}} \end{aligned}$$
(53)

All the numerical results will be calculated regarding \(m=\)1.

4 Solution validity

Results’ discussion shall be begun with a validation example in order to find the solution process accuracy. To do this, [61, 62] are utilized, leading to tabulated results in Tables 3 and 4. It should be noted that this comparison section is prepared for mechanical elastic buckling of a square macroscale Euler–Bernoulli beam for which the elastic properties \(E=\)1 TPa, \(\upsilon =\) 0.19 are put. It is also worthy to note that [61] applied an exact solution method and [62] exerted the numerical differential transformed technique. We try to validate both end conditions used in this article. Accordingly, we can observe a very good agreement and accordance among the tabulated results.

Table 3 For a SS beam
Full size table
Table 4 For a CC beam
Full size table

5 Discussion and results

The preparatory validation confirmed that the present analytical procedure could be transferred into further problems. Thereupon, we are here focusing on the temperature by which the piezomagnetic-flexomagnetic microscale beam buckles. At first, the structural specifications involving elasticity and magnetic features shall be identified to solve the main problem. Such the properties can be seen in Table 5, which were picked up from [63,64,65]

Table 5 Magneto-mechanical features of a microscale ferromagnetic sensor
Full size table

6 Microstructural effect

It was shown by literature and experimental works that when a particle size diminishes, the stiffness of the material can be strongly affected, in which this influence causes in enhancing the stiffness [66]. In order to consider this effect here, Fig. 4a, b is drawn for simple and clamp supports, respectively. It is worth noting that the notations P, L, and U are dedicated to parabolic, linear, and uniform thermal loading distribution (TD) along the thickness. Furthermore, in this paper, all the results of parabolic temperature distribution are extracted for second-order nonlinearity expression. As expected, when the beam goes in micro-size, the stiffness value becomes up, leading to further resistance and stability of the MMP against temperature. Depending on the type of thermal loading, the intensity of this additive trend is different. For the parabolic variation of temperature, it can be observed that the increasing slope is steeper. However, this case for uniform variation is smoother. It should be pointed out that the microscale parameter has affected the thermal loading so that the increase in the parameter increments the difference in the results of three cases. Thus, it can be concluded that the type of thermal loading for a microscale beam is more significant than a macroscale one. The beam has the highest stability against the parabolic case of temperature variation and the lowest stability to the uniform temperature variation. Comparing the results of both ends supports brings us to this conclusion that the type of thermal loading at less flexible end conditions is further important. This is obtained due to the more difference between the three cases results at CC. Moreover, it is apparent that the clamped end support is more resistant than the simple one, and further thermal stability is seen for CC. It should be remembered that all results in this paper are presented for the first mode number.

Fig. 4
figure 4

a Microscale parameter versus critical temperature for different cases of TD (\(\varPsi =0.1\)A, \(L/h=20\), SS). b Microscale parameter versus critical temperature for different cases of TD (\(\varPsi =0.1\)A, \(L/h=20\), CC)

Full size image

7 Magnetic field effect

There are various reports on the effect of the magnetic field on micro- and nanoscale smart materials. For the first time, this study will investigate a microbeam in a magnetic field considering both the effects of piezomagnetic and flexomagnetic by the aid of Fig. 5a, b. To examine the magnetic potential, we inspect the reverse effect of the magnetic field, from the external potential of zero to the potential value of one Ampere. In this section, similar to the previous section, two figures are presented for the boundary condition of simple and clamped, respectively, based on the three thermal loading modes. By looking at both figures, we can see that the magnetic potential has a significant impact on the critical buckling temperature results, and this effect leads to an increase in the amount of stability of the material against thermal load when the potential is high. Interestingly, this incremental effect is not with the same slope in the three thermal loading items for both boundary conditions, and for the parabolic thermal loading distribution, the results increase with a steeper slope.

Fig. 5
figure 5

a Magnetic parameter versus critical temperature for different cases of TD (\(l=0.1\,\upmu \hbox {m}\), \(L/h=20\), SS). b Magnetic parameter versus critical temperature for different cases of TD (\(l=0.1\,\upmu \hbox {m}\), \(L/h=20\), CC)

Full size image

8 Slenderness ratio effect

One of the necessary and influential parameters for designing beams and columns in mechanical engineering is the slenderness ratio of the beam. As a rule, this coefficient can also play an essential role in the designing of beam-shaped microsensors. Therefore, in this section, we will underestimate this coefficient in the current problem by presenting numerical results based on Fig. 6a, b. The figures are for simple and clamped boundary conditions, respectively. All three cases of thermal loading are also considered in these two figures. It should be noted that the range of slenderness ratio variations is considered between 10 and 25, which is the range of a relatively thick to a thin beam. As can be seen, the greater the ratio of length to thickness of the beam, the lower the thermal stability of the microsensor. This decrease in stability occurs in clamped boundary conditions with a steeper slope, which indicates that the beam with this boundary condition is more sensitive to the value of the slenderness coefficient. It can also be seen from the two figures that the larger the slenderness ratio, the less important the type of thermal loading. This result is obtained due to reducing the difference between the results of the three thermal loading states by increasing the slenderness coefficient.

Fig. 6
figure 6

a Slenderness ratio versus critical temperature for different cases of TD (\(\varPsi =0.1\)A, \( l=0.1\) \(\upmu \hbox {m}\), SS). b Slenderness ratio versus critical temperature for different cases of TD (\(\varPsi =0.1\)A, \( l=0.1\) \(\upmu \hbox {m}\), CC)

Full size image

9 Piezomagnetic-flexomagnetic effects

Comparing the mechanical behavior of a piezomagnetic-flexomagnetic microbeam (PFM) with an ordinary and normal microbeam (MB) can be interesting. In order to address this issue, this section was prepared, based on which four figures are presented. Figure 7a, b is prepared with micro-parameter changes in the horizontal axis for the two boundary conditions of simple and clamp, respectively. However, Fig. 8a, b is drawn by considering the magnetic potential changes in the horizontal axis and the two boundary conditions of simple and clamp, respectively. The results for all three thermal loading cases were prepared separately for both smart and ordinary microbeams. From Fig. 7a, b, it is quite clear that the biggest difference between the results of a smart beam with a normal beam is when the thermal loading is nonlinear in the direction of thickness, and the smallest difference is related to the uniform thermal loading. This difference is more evident in the results of the two beams for the simple boundary condition. The examination of Fig. 8a, b also proves this. From these two figures, it can be concluded that the higher the amount of external magnetic potential, the more important the smart beam will be, which can be understood from the increase in the difference between the results of the two beams with increasing the magnetic potential.

Fig. 7
figure 7

a Microscale parameter versus critical temperature for PFM effect (\(\varPsi =0.1\)A, \(L/h=20\), SS). b Microscale parameter versus critical temperature for PFM effect (\(\varPsi =0.1\)A, \(L/h=20\), CC)

Full size image
Fig. 8
figure 8

a Magnetic parameter versus critical temperature for PFM effect (\(l=0.1\,\upmu \hbox {m}\), \(L/h=20\), SS). b Magnetic parameter versus critical temperature for PFM effect (\(l=0.1\,\upmu \hbox {m}\), \(L/h=20\), CC)

Full size image

10 Conclusions

Herein we reported a distinct investigation on piezomagnetic-flexomagnetic micro-size beam-shaped sensors based on thin beam theory. Concerning the strain gradient theory, the microstructural effect was studied. The microbeam physical structure was defined based on magnetic microparticles. The constitutive equation, which is dominant on the problem, was obtained by linear Lagrangian strain, and the critical temperature was computed for clamped and simple end supports. The distribution of thermal loading in line with thickness was in linear, uniform, and parabolic states. Influences of essential parameters were probed, and some vital points were concluded and organized here as:

  • The microbeam’s topmost thermal stability is in the parabolic case of thermal loading distribution and the lowermost for the uniform one.

  • The higher the magnetic potential, the greater the critical temperature of buckling.

  • The type of thermal loading distribution at CC boundary conditions is further significant than the SS one.

  • For lengthy beam-shaped microsensors, the effect of the type of thermal loading distribution is insignificant.

  • The importance of piezomagnetic-flexomagnetic properties is further while the thermal loading distribution is parabolic.