Abstract
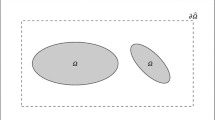
We consider a shape optimization problem for the first mixed Steklov–Dirichlet eigenvalues of domains bounded by two balls in two-point homogeneous space. We give a geometric proof which is motivated by Newton’s shell theorem.









Similar content being viewed by others
References
Agranovich, M.S.: On a mixed Poincaré–Steklov type spectral problem in a Lipschitz domain. Russ. J. Math. Phys. 13, 239–244 (2006)
Aithal, A.R., Santhanam, G.: Sharp upper bound for the first non-zero Neumann eigenvalue for bounded domains in rank-\(1\) symmetric spaces. Trans. Am. Math. Soc. 348(10), 3955–3965 (1996)
Ashbaugh, M.S., Benguria, R.D.: Sharp upper bound to the first nonzero Neumann eigenvalue for bounded domains in spaces of constant curvature. J. Lond. Math. Soc. (2) 52(2), 402–416 (1995)
Bérard-Bergery, L., Bourguignon, J.-P.: Laplacians and Riemannian submersions with totally geodesic fibres. Ill. J. Math. 26, 181–200 (1982)
Binoy, Santhanam, G.: Sharp upper bound and a comparison theorem for the first nonzero Steklov eigenvalue. J. Raman. Math. Soc. 29, 133–154 (2014)
Brehm, U.: The shape invariant of triangles and trigonometry in two-point homogeneous spaces. Geom. Dedic. 33, 59–76 (1990)
Brock, F.: An isoperimetric inequality for eigenvalues of the Stekloff problem. ZAMM Z. Angew. Math. Mech. 81, 69–71 (2001)
Bucur, D., Ferone, V., Nitsch, C., Trombetti, C.: Weinstock inequality in higher dimensions. arXiv:1710.04587
Castillon, P., Ruffini, B.: A spectral characterization of geodesic balls in non-compact rank one symmetric spaces. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 19(4), 1359–1388 (2019)
Chavel, I.: Lowest-eigenvalue inequalities, Geometry of the Laplace operator (Proc. Sympos. Pure Math., Univ. Hawaii, Honolulu, Hawaii, 1979). In: Proc. Sympos. Pure Math., vol. XXXVI, pp. 79–89. American Mathematical Society, Providence (1980)
Escobar, J.F.: An isoperimetric inequality and the first Steklov eigenvalue. J. Funct. Anal. 165, 101–116 (1999)
Fraser, A., Schoen, R.: Shape optimization for the Steklov problem in higher dimensions. Adv. Math. 348, 146–162 (2019)
Ftouhi, I.: Where to place a spherical obstacle so as to maximize the first Steklov eigenvalue. ffhal-02334941 (2019)
Hartman, P.: Ordinary differential equations, In: Classics in Applied Mathematics, vol. 38. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2002). Corrected reprint of the second (1982) edition [Birkhäuser, Boston, MA; MR0658490 (83e:34002)], With a foreword by Peter Bates
Hersch, J., Payne, L.E.: Extremal principles and isoperimetric inequalities for some mixed problems of Stekloff’s type. Z. Angew. Math. Phys. 19, 802–817 (1968)
Hsiang, W.-Y.: On the laws of trigonometries of two-point homogeneous spaces. Ann. Glob. Anal. Geom. 7, 29–45 (1989)
Izmestiev, I., Tabachnikov, S.: Ivory’s theorem revisited. J. Integr. Syst. 2(xyx006), 36 (2017)
Karcher, H.: Riemannian comparison constructions, Global differential geometry. In: Chern, S.S. (ed.) MAA Stud. Math., vol. 7, pp. 170–222. Mathematical Association of America, Washington (1989)
Kozlov, V.V.: Newton and Ivory attraction theorems in spaces of constant curvature. Vestnik Moskov. Univ. Ser. I Mat. Mekh. 68, 43–47 (2000)
Newton, I.: Philosophiae Naturalis Principia Mathematica, vol. I. Harvard University Press, Cambridge. Reprinting of the third edition (1726) with variant readings. Assembled and edited by Alexandre Koyré and I, Bernard Cohen with the assistance of Anne Whitman (1972)
Petersen, P.: Riemannian geometry, 2nd edn. In: Graduate Texts in Mathematics, vol. 171. Springer, New York (2006)
Santhanam, G., Verma, S.: On eigenvalue problems related to the Laplacian in a class of doubly connected domains. arXiv:1803.05750
Simon, L.: Lectures on geometric measure theory. In: Proceedings of the Centre for Mathematical Analysis, vol. 3. Australian National University, Centre for Mathematical Analysis, Canberra (1983)
Stekloff, W.: Sur les problèmes fondamentaux de la physique mathématique (suite et fin). Ann. Sci. École Norm. Sup. (3) 19, 455–490 (1902)
Todhunter, I.: Spherical Trigonometry, for the Use of Colleges and Schools: With Numerous Examples. CreateSpace Independent Publishing Platform (1802), Scotts Valley (2014)
Weinstock, R.: Inequalities for a classical eigenvalue problem. J. Ration. Mech. Anal. 3, 745–753 (1954)
Wolf, J.A.: Spaces of Constant Curvature, 5th edn. Publish or Perish Inc., Houston (1984)
Acknowledgements
The author wishes to express his gratitude to Jaigyoung Choe for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was partially supported by NRF-2018R1A2B6004262 and NRF-2020R1A4A3079066.
Rights and permissions
About this article
Cite this article
Seo, DH. A shape optimization problem for the first mixed Steklov–Dirichlet eigenvalue. Ann Glob Anal Geom 59, 345–365 (2021). https://doi.org/10.1007/s10455-021-09756-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10455-021-09756-7