Introduction

Specific nonlinear dynamic system behavior is complex anomalies that can induce qualitative changes in the system's steady-state trajectory such as chaos, bifurcations, co-existing attractors, and fractal basin boundaries [1,2,3,4,5,6,7]. The research field of chaotic system analysis and control has seen rapid development in recent years. The chaos appears in many mechanical and electrical systems such as lasers, nonlinear optical systems, optimization techniques, biological systems, chemical reactions, cancer treatments, fluids flow, moreover, many other applications [8,9,10,11,12,13,14,15,16]. Practically, the chaos and bifurcation are harmful to these systems as they can lead them to be unstable or make undesirable behavior, so control techniques and methodologies are required to reduce or eliminate the harmful chaotic effect. Consequently, studying chaos behavior and suppressing it has been the major target of researchers for practical nonlinear systems. Consequently, there are numerous methods to control chaotic systems, such as the (Ott, Grebogi and Yorke) OGY method [31], feed-back linearization method [32,33,34], a real-time cycle to cycle variable slope compensation method [35], time-delay feedback control [36], developing Floquet theory [26, 30, 37,38,39], fuzzy control [41, 43, 45, 46].

The stability boundary of the chaotic system relies on invariant sets like equilibrium points, periodic, quasi-periodic, and chaotic orbits are representative. In this work, the periodic and chaotic orbits are investigated to study the stability behavior of the dynamic systems. Periodic orbits are powerful tools in studying and analyzing the dynamic systems as they provide a periodic solution which shows a closed orbit in phase-space. While the chaotic orbits have an unlimited number of points in the phase portrait and its trajectory is a random-like but bounded behavior and does not intersect with each other.

The popular methods used for analyzing chaos are the Floquet theory and the Lyapunov exponent method which depends on the Poincaré map. Poincaré map creates a complex structure with a discrete state-space which is a smaller dimension than the original continuous dynamic scheme. The stability of the Poincaré map depends on the map’s Jacobian matrix, but the calculation process of the Jacobian matrix may be complex. This interpretation of the Poincaré map is seldom used as it requires developing information for a limited cycle location [24, 25]. While, the Floquet theory depends on the State Transition Matrix (STM) for the full cycle [34, 35, 37,38,39]. Both methods give the same results; however, the Floquet theory fits well with mechanical switching systems and simpler to be implemented as compared to the Lyapunov exponent method [25,26,27,28,29,30].

Chaotic systems are deterministic, nonlinear, and very sensitive to the initial condition. Accordingly, long-term prediction of chaotic systems becomes impossible, on the other hand, they are controllable systems [17,18,19]. While, the change in specific behavior of the system is known as a bifurcation [19, 20]. The bifurcation phenomenon describes the fundamental alteration in the dynamics of nonlinear systems under parameter variation. As the theory of bifurcation is a tool to help to understand equilibrium loss and its consequences for complex behavior. There are many types of periodic orbit local bifurcation such as period-doubling bifurcation, and Hopf bifurcation [20,21,22,23].

DC (direct current) motor is used in many applications and nearly most mechanical movement that can be observed around us. As it is found in several domestic appliances such as HD cameras, smart toys, mixing machines, and in advanced orthopedic bone drilling [47,48,49,50,51]. Recently, the analysis of the non-linear characteristic of an electric DC motor has become an emerging research topic. The drive system consists of a converter and a controller which produce pulse width modulation (PWM) to adjust the voltage value of the DC motor. PWM’s switching action makes the entire drive system to be time-varying and nonlinear, because the operation of the system during the ON state differs from its operation in the OFF state. The nominal steady state of the PMDC drive is the period-1 orbit, but altering some drive parameters will lead to a new attracting orbit that is periodic, quasi-periodic, or chaotic [39].

Zadeh [40] introduced the fundamental of the fuzzy logic controller (FLC) in 1965, many researchers dedicated themselves to this topic to find innovative strategies for improving the performance of the FLC system and ensuring its reliability. So, FLC can eliminate the non-linearity effects of a DC motor simply and comfortably. Designing FLC also does not need a systematic procedure or a mathematical model of a system. Besides, it improves performance and provides superior outcomes than other techniques. Hence, FLC gives better results with position control and DC/DC converters [42] and [44], stabilizes the induction motor [45], removes chaos in converters [41], and controls complicated, undefined chaotic systems Parameters [43, 46].

Most researchers deal with the impact of changing the input voltage of PMDC motors or the controller gains on the chaos behavior [20, 30, 35, 41]. Another research gap is that most control techniques deal with eliminating chaos and bifurcation without taking into consideration the performance of the system [32, 33, 37,38,39]. Therefore, the contribution of this work is to investigate another important factor in the PMDC motor which is the impact of changing the load torque on chaos behavior with taking into consideration the performance of the system. Through this work, the nominal state for the PMDC motor was explored while changing load torque, which results in losing stability and changing the trajectory from period-1 to period-2 orbit. Also, changing the load torque causes chaos. So, two techniques were used to overcome these problems. The first technique is developing Floquet theory, where the result shows that the system is still in period-1 (nominal state) orbit with changing the load torque and the system suffers from overshoot and oscillations. The second technique is the Proportional Integral (PI) fuzzy controller, where the simulation result shows that the system also still in a nominal state without overshoot or oscillations and eliminates the steady-state error. Simulation results were performed using MATLAB / SIMULINK software.

The outline of the paper is as follows:—the mathematical model, dynamic behavior of PMDC drive, and analysis of the stability of period-1 orbit are devoted in "Preliminaries", while "The controller" introduces the control of the system using a fuzzy PI controller and the next section summarizes the conclusion of the results.

Preliminaries

PMDC drive

In this section, the chaotic behavior in the drive system will be studied. The speed of the motor can be controlled through PWM to change the applied voltage of the armature. The PMDC motor specifications which are depicted in Fig. 1, are given as \(\omega_{{{\text{ref}}}}\) is the reference speed = 100 rad/s, R is the armature resistance = 7.8 Ω, L is the armature inductance = 5mH, KT is the torque constant = 0.09 Nm/A, Ke is the back electromotive force constant = 0.0984 V.s/rad, B is the viscous damping factor = 0.000015 Nm/rad/sec, TL is the load torque = 0.087 N m, J is the moment of inertia = 4.8400e−005 Nm/rad/sec2 and T is the periodic time = 0.05 ms.

Fig. 1
figure 1

Circuit diagram of the permanent magnet DC drive

Full size image

Mathematical model of the system

When the saw-tooth signal \(V_{{{\text{ramp}}}} \left( t \right)\) is greater than the control signal \(V_{{{\text{con}}}} \left( t \right)\), the model is described by

$$ \frac{dX\left( t \right)}{{dt}} = A_{{{\text{on}}}} X\left( t \right) + V_{{{\text{on}}}} . $$
(1)

When the saw-tooth signal is smaller than the control signal, the model is described by

$$ \frac{dX\left( t \right)}{{dt}} = A_{{{\text{off}}}} X\left( t \right) + V_{{{\text{off}}}} , $$
(2)

where \({ }A_{{{\text{on}}}} = A_{{{\text{off}}}} = A = \left[ {\begin{array}{*{20}c} {\frac{ - B}{J}} & {\frac{{K_{T} }}{J}} \\ {\frac{{ - K_{e} }}{L}} & {\frac{ - R}{L}} \\ \end{array} } \right]\), \(V_{{{\text{on}}}} = \left[ {\begin{array}{*{20}c} {\frac{{ - T_{L} }}{J}} \\ {\frac{{V_{{{\text{in}}}} }}{L}} \\ \end{array} } \right]\) and \(V_{{{\text{off}}}} = \left[ {\begin{array}{*{20}c} {\frac{{ - T_{L} }}{J}} \\ 0 \\ \end{array} } \right].\)

$$ V_{{{\text{con}}}} \left( t \right) = K_{P} \left( {\omega \left( t \right) - \omega_{{{\text{ref}}}} } \right), $$
(3)

where \(K_{P}\) is the proportional controller gain, \(\omega \left( t \right)\) is the shaft speed and \(\omega_{{{\text{ref}}}}\) is the reference speed:

$$ V_{{{\text{ramp}}}} \left( t \right) = V_{L} + V_{D} \left( {\frac{t}{T} \bmod 1} \right), $$
(4)

where \(V_{L}\), \(V_{U}\) are lower and upper values of the saw-tooth signal, \(V_{D} = V_{U} - V_{L}\) and T is the PWM period:

$$ X\left( t \right) = \left[ {\omega \left( t \right) i\left( t \right)} \right]^{T} = [x_{1} \left( t \right) x_{2} \left( t \right)]^{T} . $$
(5)

Dynamic behavior of the system when changing the load torque

In this section, the time-domain waveform and phase portrait is introduced to investigate the stability and chaotic behavior of the PMDC drive. The nominal steady-state behavior of this system is period-1 for KP = 1, Vin = 24 V, and TL = 0.087 Nm.

By altering the load torque to TL = 0.1 Nm at time = 0.3 s, overshoot, undershoot, and the oscillation of the system increase. Besides, the system losses its stability, and the period-doubling bifurcation occurred which is called fast scale bifurcation. The waveforms of period-2 speed and current when changing load torque at 0.3 s is depicted in Fig. 2.

Fig. 2
figure 2

Waveforms for speed and current at KP = 1, Vin = 24 V with changing load torque

Full size image

A further variation of the load torque (TL = 0.11 Nm at 0.6 s.) increases the settling time and the period-doubling bifurcation leads to chaos, as presented in Fig. 2. Such nonlinear phenomena can lead the system to dangerous or disastrous conditions. Hence, these nonlinear phenomena should be reduced as much as possible. Also, Period-1 at TL = 0.087 Nm, period-2 at TL = 0.1Nm, period-4 at TL = 0.1045 Nm, and chaos at TL = 0.11 Nm trajectories (phase portraits) are presented in Fig. 3.

Fig. 3
figure 3

a Period-1, b period-2, c period-4 and d chaos trajectories due to changing load torque

Full size image

Analysis of the chaos

Analysis of Chaos using Floquet theory was discussed in [25,26,27,28,29,30]. Floquet Theory (Filippov’s method) is applied to analyze the stability based on Floquet multipliers ([34, 37, 38] and [39]). Monodromy matrix is shown equally:

$$ M\left( {T, \, 0} \right) = S_{2} \times \Phi \left( {T,t_{\varepsilon } } \right) \, \times S_{1} \times \Phi \left( {t_{\varepsilon } ,0} \right), $$
(6)

where S1 is the Saltation matrix when the path transfer from the cut-off region to the saturation region, S2 is the Saltation matrix when the path transfer from the saturation region to the cut-off region, and ɸ (ty, tx) is the STM from tx to ty, where Φ (ty, tx) = \(e^{{A(t_{y} - t_{x} )}}\):

$$ S = I + \frac{{\left( {f_{ + } - f_{ - } } \right)n^{T} }}{{n^{T} f_{ - } + \frac{{\partial h\left( {X\left( t \right)} \right)}}{\partial t}\left| {t = t_{\varepsilon } } \right.}}, $$
(7)

where n is the normal vector, \(f_{ - }\) and \(f_{ + }\) are vector fields previously and next switching moment, I is the unit matrix, h = Vcon – Vramp, \(\frac{\partial h}{{\partial t}}\) = \(\frac{{ - \left( {V_{U} - V_{L} } \right)}}{T}\), \(f_{ + }\) = Aon X (tε) + Von, \(f_{ - }\) = Aoff X (tε) + Voff and nT = [KP 0].

The trajectory will be stable if all modulus of the Floquet multipliers is less than 1 and unstable if one of the modulus greater than 1. The results presented in Table 1 show that the trajectory loses its stability when TL = 0.1 Nm, the same as the result obtained from waveforms.

Table 1 Modulus of the Floquet multipliers when changing load torque
Full size table

The controller

Control by developing the Floquet theory

Stabilization of the system using Floquet theory was discussed in [26, 30, 37,38,39]. This technique is used to handle the effects of bifurcation and chaos that occur as a result of changing the torque of the load by forcing the path to be in period -1 (steady-state). Keeping the modulus of Floquet multipliers less than 1 by changing \(\omega_{{{\text{ref}}}}\) to \(\omega_{{{\text{ref}}}} \left( {1 + \alpha \sin \left( {\omega t} \right)} \right)\); \( \alpha\) is a control parameter, a very small signal which leads to change the value of \(S\) by changing \(\frac{\partial h}{{\partial t}}\):

$$ \frac{\partial h}{{\partial t}} = - \omega_{ref} \times \alpha \times \omega \cos (\omega t_{\varepsilon } ) - \frac{{\left( {V_{U} - V_{L} } \right)}}{{T \times K_{P} }}. $$
(8)

The relationship between α and TL is presented in Fig. 4:

$$ \alpha \left( {T_{L} } \right) = 1.8235^{{}} T_{L}^{3} - 0.65887 \, T_{L}^{2} + 0.0761^{{}} T_{L} - 0.0018526. $$
(9)
Fig. 4
figure 4

Relationship between α and TL

Full size image

Adding the supervisory controller is presented in Fig. 5. The control signal becomes

$$ V_{con} \left( t \right) = K_{P} \left( {\omega \left( t \right) - \omega_{ref} \left( {1 + \alpha \sin \left( {\omega t} \right)} \right)} \right). $$
(10)
Fig. 5
figure 5

Block diagram of the drive system with a supervisory controller

Full size image

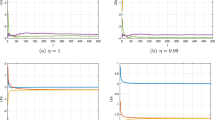
Controlling the system using the Floquet theory, the problem of bifurcation, which leads to chaos, is solved. Consequently, it makes the system in period-1 trajectory when changing the load torque. However, there is a steady-state error (ess = 0.1%), overshoot, undershoot, and oscillation when altering the load torque, as shown in Fig. 6.

Fig. 6
figure 6

Waveforms for speed and current with changing load torque by developing Floquet theory

Full size image

PI Fuzzy controller

Fuzzy logic controller (FLC) clarifies the experience and the knowledge of a human operator in linguistic variables (fuzzy rules) without any knowledge of parameter variations and dynamics of the system. Implementation of FLC depends upon the process done by human factors without the need for a mathematical model [41,42,43,44,45,46]. The fuzzy system consists of two inputs: the error and the change of error, and one output is the change of control output. The structure of the PI-fuzzy controller is shown in Fig. 7.

Fig. 7
figure 7

Structure of the PI-fuzzy controller

Full size image

The fuzzy rules make feasible changes to obtain the minimum error by deciding whether an increase or decrease Δu(k) based on (e(k) and Δ e(k)), the sets of e(k), Δ e(k) and Δ u(k) are {NB(negative big), NS(negative small), ZZ(zero), PS(positive small) and PB(positive big)}. The fuzzy rule base is presented in Table 2.

Table 2 Fuzzy rule base
Full size table

System dynamic behavior with the PI fuzzy controller when changing the load torque

The time-domain waveform and phase portrait (trajectories in the phase plane) indicate the stability of the system. Waveforms of period-1 speed and current when changing load torque are depicted in Fig. 8. At Vin = 24 V and TL = 0.087 Nm, the steady-state error is very small (ess = 0.04%) and the system is still in the stable state when changing the load torque at 0.3 s to TL = 0.1 N.m, as shown in Fig. 8. FLC improves the time response and solves the problem of period-doubling bifurcation, overshoot, and oscillation.

Fig. 8
figure 8

Waveforms for speed and current with changing load torque based on PI fuzzy controller

Full size image

A further variation of the load torque at 0.6 s to TL = 0.11 Nm, the steady-state error is still very small (ess = 0.06%), also the system still in the stable state, as shown in Fig. 8. FLC solves the problem of chaos, overshoot, and oscillation. It consequently improves the time response when changing the load torque at 0.6 s. Period-1 trajectories at TL = 0.087 Nm, TL = 0.1Nm, and TL = 0.11 Nm is presented in Fig. 9.

Fig. 9
figure 9

a Period-1 at TL = 0.087 Nm, b period-1 at TL = 0.1 Nm and c period-1 at TL = 0.11 Nm trajectories based on PI-fuzzy controller

Full size image

Conclusion

The non-linearity effect of a dynamical system is the main problem to achieve the speed control of PMDC drive. When changing the load torque of the motor, the system loses its stability and period-doubling bifurcation occurs, which leads to chaos and can damage the system. Control the system by developing the Floquet theory, solve the problem of bifurcation but there are overshoot and oscillation when changing the load torque. Adding a PI-fuzzy controller makes the speed control smoother and ensures the system’s stability when changing the load torque. The simulation results show that FLC gives a better response than that obtained when applying the other controller and tends to vanish steady-state error furthermore, removes the overshoot and the oscillation of the system. MATLAB/SIMULINK software is used to validate the model.