Testing equivalence of survival before but not after end of follow-up

Abstract

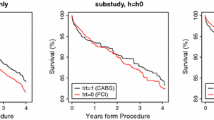
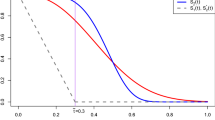
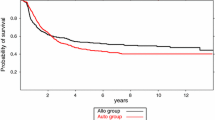
For equivalence trials with survival outcomes, a popular testing approach is the elegant test for equivalence of two survival functions suggested by Wellek (Biometrics 49: 877–881, 1993). This test evaluates whether or not the difference between the true survival curves is practically irrelevant by specifying an equivalence margin on the hazard ratio under the proportional hazards assumption. However, this approach is based on extrapolating the behavior of the survival curves to the whole time axis, whereas in practice survival times are only observed until the end of follow-up. We propose a modification of Welleks test that only addresses equivalence until end of follow-up and derive the large sample properties of this test. Another issue is the proportional hazards assumption which may not be realistic. If this assumption is violated, one may severely misjudge the actual treatment effect with a hazard ratio quantification and wrongly declare equivalence. We suggest a non-parametric test for assessing survival equivalence within the follow-up period. We derive the large sample properties of this test and provide an approximation to the limiting distribution under some mild assumptions on the functional form of the difference between the two survival curves. Both suggestions are investigated by simulation and applied to a clinical trial on survival of gastric cancer patients.

Appendices

A Proof of Proposition 1

When $\theta \ne 1$ a straightforward application of the Delta Theorem shows that

$$\begin{aligned} \sqrt{n}\cdot [\{\hat{m}_{1}(\tau ),\hat{m}_{2}(\tau )\} -\{m_{1}(\tau ),m_{2}(\tau )\}]{\mathop {\rightarrow }\limits ^{\mathcal {D}}}\mathcal {Z}, \end{aligned}$$

where $\mathcal {Z}=(\mathcal {Z}_{1},\mathcal {Z}_{2})$ is normally distributed with mean 0 and $var(\mathcal {Z}_{1})=\sigma _{1}^{2}$, $var(\mathcal {Z}_{2})=\sigma _{2}^{2}$, and

$$\begin{aligned}&cov(\mathcal {Z}_{1},\mathcal {Z}_{2})=\\&\log (\theta ^{\frac{1}{1-\theta }})\cdot \theta ^{\frac{1}{1-\theta }} \cdot [\log \{S_{0}(\tau )^{\theta }\}\cdot S_{0}(\tau )^{\theta }-\rho \cdot \{S_{0}(\tau )-\theta \cdot S_{0}(\tau )^{\theta }\}]\cdot \sigma ^{2}. \end{aligned}$$

Now define $\hat{P}$ as the indicator of $\hat{S}_{0}(\tau ) > \hat{\theta }^{\frac{1}{1-\hat{\theta }}}$, that is

$$\begin{aligned} \hat{P}=I( \hat{S}_{0}(\tau ) > \hat{\theta }^{\frac{1}{1-\hat{\theta }}}). \end{aligned}$$

Then $\hat{m}_{\tau }$ may be rewritten as:

$$\begin{aligned} \hat{m}_{\tau }=(1-\hat{P})\cdot \hat{m}_{1}(\tau ) +\hat{P}\cdot \hat{m}_{2}(\tau ). \end{aligned}$$

When $S_{0}(\tau )<\theta ^{\frac{1}{1-\theta }}$ we have that $m_{\tau }=m_{1}(\tau )$ and that $\hat{P}$ converges in probability to 0. Consequently

$$\begin{aligned} \sqrt{n}\cdot (\hat{m}_{\tau }-m_{\tau })= \sqrt{n}\cdot \{\hat{m}_{1}(\tau )-m_{1}(\tau )\}+o_{P}(1) \end{aligned}$$

and thus in this situation

$$\begin{aligned} \sqrt{n}\cdot (\hat{m}_{\tau }-m_{\tau }) {\mathop {\rightarrow }\limits ^{\mathcal {D}}}\mathcal {Z}_{1}. \end{aligned}$$

When $S_{0}(\tau )>\theta ^{\frac{1}{1-\theta }}$ we have that $m_{\tau }=m_{2}(\tau )$ and that $\hat{P}$ converges in probability to 1. Consequently

$$\begin{aligned} \sqrt{n}\cdot (\hat{m}_{\tau }-m_{\tau })= \sqrt{n}\cdot \{\hat{m}_{2}(\tau )-m_{2}(\tau )\}+o_{P}(1) \end{aligned}$$

and thus in this situation

$$\begin{aligned} \sqrt{n}\cdot (\hat{m}_{\tau }-m_{\tau }) {\mathop {\rightarrow }\limits ^{\mathcal {D}}}\mathcal {Z}_{2}. \end{aligned}$$

When $S_{0}(\tau )=\theta ^{\frac{1}{1-\theta }}$ we have that $m_{\tau }=m_{1}(\tau )=m_{2}(\tau )$. Moreover a straightforward calculation shows that $\sigma _{1}^{2}=\sigma _{2}^{2}$ and that $cor(\mathcal {Z}_{1},\mathcal {Z}_{2})=1$. Accordingly, since $\mathcal {Z}_{1}-\mathcal {Z}_{2}=0$, we may conclude by the Continuous Mapping Theorem that:

$$\begin{aligned} \hat{P}[\sqrt{n}\cdot \{\hat{m}_{2}(\tau )-m_{2} (\tau )\}-\sqrt{n}\cdot \{\hat{m}_{1}(\tau )-m_{1}(\tau )\}]=o_{P}(1). \end{aligned}$$

Consequently

$$\begin{aligned} \sqrt{n}\cdot (\hat{m}_{\tau }-m_{\tau })=&\sqrt{n}\cdot \{\hat{m}_{1}(\tau )-m_{1}(\tau )\}\\&+\hat{P}[\sqrt{n}\cdot \{\hat{m}_{2}(\tau ) -m_{2}(\tau )\}-\sqrt{n}\cdot \{\hat{m}_{1}(\tau )-m_{1}(\tau )\}]\\ =&\sqrt{n}\cdot \{\hat{m}_{1}(\tau )-m_{1}(\tau )\}+o_{P}(1) \end{aligned}$$

and thus in this situation

$$\begin{aligned} \sqrt{n}\cdot (\hat{m}_{\tau }-m_{\tau }) {\mathop {\rightarrow }\limits ^{\mathcal {D}}}\mathcal {Z}_{1}. \end{aligned}$$

This proves the first claim of Proposition 1.

To prove that $\hat{\xi }^{2}$ converges in probability to $\xi ^{2}$ note that $\hat{\sigma }_{1}^{2}$ and $\hat{\sigma }_{2}^{2}$ converge in probability to $\sigma _{1}^{2}$ and $\sigma _{2}^{2}$. Also note that

$$\begin{aligned} \hat{\xi }^{2}=(1-\hat{P})\cdot \hat{\sigma }_{1}^{2} +\hat{P}\cdot \hat{\sigma }_{2}^{2}. \end{aligned}$$

The proof now follows along the same lines as the proof of the first claim of Proposition 1.

B Proof of Proposition 2

The claim that

$$\begin{aligned} \sqrt{n}(\hat{m}_{\tau }-m_{\tau }){\mathop {\rightarrow }\limits ^{\mathcal {D}}} \max [\max _{t\in \mathcal {E^{+}}(f)}\{\mathcal {W}(t)\}, \max _{t\in \mathcal {E^{-}}(f)}\{\mathcal {-W}(t)\}] \end{aligned}$$

can be verified by copying the proof of Theorem 4.1 in Dette et al. (2018). For the special case of $\mathcal {E}^{\pm }(f)=\{t^{*}\}$ we have that

$$\begin{aligned} \max [\max _{t\in \mathcal {E^{+}}(f)}\{\mathcal {W}(t)\},\max _{t\in \mathcal {E^{-}}(f)}\{\mathcal {-W}(t)\}]=\left\{ \begin{array}{rr} \mathcal {W}(t^{\star }), &{} \mathcal {E}^{+}(f)=\{t^{\star }\} \\ -\mathcal {W}(t^{\star }), &{} \mathcal {E}^{-}(f)=\{t^{\star }\} \end{array} \right. \end{aligned}$$

From which it follows directly that

$$\begin{aligned} \sqrt{n}(\hat{m}_{\tau }-m_{\tau }){\mathop {\rightarrow }\limits ^{\mathcal {D}}} \mathcal {N}(0,\xi ^2). \end{aligned}$$

Now assume that $\mathcal {E}^{\pm }(f)=\mathcal {E}^{+}(f)=\{t^{*}\}$ and let $t^{\star }_{n}\in \mathcal {E}^{\pm }(f_{n})$. We proceed by showing that

$$\begin{aligned} P(t^{\star }_{n}\in \mathcal {E}^{+}(f_{n}))\rightarrow 1,\,\, n\rightarrow \infty . \end{aligned}$$

(7)

By the continuous mapping theorem and the weak convergence of $G_{n}$ we have that

$$\begin{aligned} \sup _{t\in [0,\tau ]}|G_{n}(t)|=O_{P}(1). \end{aligned}$$

Accordingly

$$\begin{aligned} \sup _{t\in [0,\tau ]}|f_{n}(t)-f(t)|=o_{p}(1). \end{aligned}$$

(8)

It now follows from

$$\begin{aligned}&|\sup _{t\in [0,\tau ]}f_{n}(t)-\sup _{t\in [0,\tau ]}f(t)|\le \sup _{t\in [0,\tau ]}|f_{n}(t)-f(t)|,\\&|\sup _{t\in [0,\tau ]}\{-f_{n}(t)\}-\sup _{t\in [0,\tau ]}\{-f(t)\}|\le \sup _{t\in [0,\tau ]}|f_{n}(t)-f(t)| \end{aligned}$$

that

$$\begin{aligned}&\sup _{t\in [0,\tau ]}f_{n}(t){\mathop {\rightarrow }\limits ^{\mathcal {P}}} \sup _{t\in [0,\tau ]}f(t),\\&\sup _{t\in [0,\tau ]}\{-f_{n}(t)\}{\mathop {\rightarrow }\limits ^{\mathcal {P}}} \sup _{t\in [0,\tau ]}\{-f(t)\}. \end{aligned}$$

From this we deduce that since $\mathcal {E}^{\pm }(f)=\mathcal {E}^{+}(f)=\{t^{*}\}$ and consequently $\sup _{t\in [0,\tau ]}\{-f(t)\}<\sup _{t\in [0,\tau ]}f(t)$ it holds that

$$\begin{aligned} P\big (\sup _{t\in [0,\tau ]}\{-f_{n}(t)\}<\sup _{t\in [0,\tau ]} f_{n}(t)\big )\rightarrow 1, \,\,n\rightarrow \infty . \end{aligned}$$

Since $t^{\star }_{n}\in \mathcal {E}^{+}(f_{n})$ when $\sup _{t\in [0,\tau ]}\{-f_{n}(t)\}<\sup _{t\in [0,\tau ]}f_{n}(t)$ we conclude that (7) holds.

Next we note that as a direct consequence of (8) we have

$$\begin{aligned}&f_{n}(t^{\star }_{n})-f(t^{\star }_{n}){\mathop {\rightarrow }\limits ^{\mathcal {P}}} 0,\,\,n\rightarrow \infty ,\\&f_{n}(t^{\star })-f(t^{\star }){\mathop {\rightarrow }\limits ^{\mathcal {P}}} 0, \,\,n\rightarrow \infty \end{aligned}$$

from which it follows that

$$\begin{aligned} f_{n}(t^{\star }_{n})-f_{n}(t^{\star })+f(t^{\star }) -f(t^{\star }_{n}){\mathop {\rightarrow }\limits ^{\mathcal {P}}} 0, \,\,n\rightarrow \infty . \end{aligned}$$

When $t^{\star }_{n}\in \mathcal {E}^{+}(f_{n})$ and $t^{\star }_{n}\in \mathcal {E}^{\pm }(f_{n})$ we have per definition that

$$\begin{aligned}&f_{n}(t^{\star }_{n})-f_{n}(t^{\star })\ge 0,\\&f(t^{\star })-f(t^{\star }_{n})\ge 0. \end{aligned}$$

Combining the above we conclude that

$$\begin{aligned} f(t^{\star }_{n}){\mathop {\rightarrow }\limits ^{\mathcal {P}}} f(t^{\star }),\,\,n\rightarrow \infty . \end{aligned}$$

Now note that by the definition of $t^{\star }$ we have $f(t)<f(t^{\star })$ for all $t\in [0,\tau ]$ with $t\ne t^{\star }$. Hence continuity of f and compactness of $[0,\tau ]$ implies that

$$\begin{aligned} \forall \delta>0\exists \varepsilon >0:\,\,|t-t^{\star }|\ge \delta \Rightarrow f(t^{\star })-f(t)\ge \varepsilon . \end{aligned}$$

Accordingly for any $\delta >0$ the exists a $\varepsilon >0$ so that

$$\begin{aligned} P(|t_{n}^{\star }-t^{\star }|\ge \delta )\le P(f(t^{\star })-f(t_{n}^{\star })\ge \varepsilon ). \end{aligned}$$

Since the right hand side of the above inequality converges to zero as $n\rightarrow \infty$ we conclude that:

$$\begin{aligned} t_{n}^{\star }{\mathop {\rightarrow }\limits ^{\mathcal {P}}}t^{\star }, \,\,n\rightarrow \infty . \end{aligned}$$

This claim is shown by similar arguments when $\mathcal {E}^{\pm }(f)=\mathcal {E}^{-}(f)=\{t^{*}\}$.

Finally it follows from the continuity of $\sigma _{0}^{2}(t)$ and $\sigma _{1}^{2}(t)$ combined with the uniform convergence in probability of their respective estimators that

$$\begin{aligned} \hat{\xi }^{2}{\mathop {\rightarrow }\limits ^{\mathcal {P}}}\xi ^{2}, \,\,n\rightarrow \infty . \end{aligned}$$

This concludes the proof of Proposition 2.

C Formulas for asymptotic variances

Let $T_{i}$, $C_{i}$, and $Z_{i}$ denote the failure time, censoring time, and treatment arm of the ith subject, respectively. Define the counting process and at risk process of the ith individual as:

$$\begin{aligned}&N_{i}(t)=I(T_{i}\le t,\, T_{i}\le C_{i}),\\&Y_{i}(t)=I(T_{i}\ge t, \, C_{i}\ge t). \end{aligned}$$

Then with

$$\begin{aligned}&Y^{0}(t)=\sum _{i=1}^{n}(1-Z_{i})Y_{i}(t),\\&Y^{1}(t)=\sum _{i=1}^{n}Z_{i}Y_{i}(t),\\&S_{0}(t)=Y^{0}(t)+\hat{\theta }Y^{1}(t) \end{aligned}$$

it follows directly from the derivations in Chapter VII.2.2 of Andersen et al. (1993) that consistent estimates of $\sigma ^2$, $\omega ^2$, and $\rho$ are given by:

$$\begin{aligned}&\hat{\sigma }^{2}= \left\{ n^{-1}\sum _{i=1}^{n}\int _{0}^{\tau } \frac{\hat{\theta }Y^{0}(t)Y^{1}(t)}{S_{0}(t)^{2}} dN_{i}(t)\right\} ^{-1},\\&\hat{\omega }^2=n\sum _{i=1}^{n}\int _{0}^{\tau }S_{0}(t)^{-2}dN_{i}(t),\\&\hat{\rho }=\sum _{i=1}^{n}\int _{0}^{\tau }\frac{\hat{\theta } Y^{1}(t)}{S_{0}(t)^{2}}dN_{i}(t) \end{aligned}$$

Now let

$$\begin{aligned}&n_{0}=n-\sum _{i=1}^{n}Z_{i},\\&n_{1}=n-n_{0} \end{aligned}$$

Then it follows directly from Theorem IV.3.2. in Chapter IV.3.2 of Andersen et al. (1993) that for $t\le \tau$:

$$\begin{aligned}&\hat{\sigma }_{0}^{2}(t)=n_{0}\{\hat{S}_{0}(t)\}^{2} \sum _{i=1}^{n}\int _{0}^{t}\frac{(1-Z_{i})dN_{i}(s)}{\{Y^{0}(s)\}^{2}},\\&\hat{\sigma }_{1}^{2}(t)=n_{1}\{\hat{S}_{1}(t)\}^{2} \sum _{i=1}^{n}\int _{0}^{t}\frac{Z_{i}dN_{i}(s)}{\{Y^{1}(s)\}^{2}}. \end{aligned}$$