Skip to main content
SpringerLink
Log in

Design of optimized architected structures with exact size and connectivity via an enhanced multidomain topology optimization strategy

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

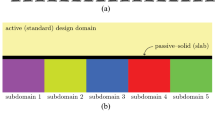
With the rapid developments of modern fabrication techniques, architected structures are increasingly used in many application areas, e.g., lightweight structures, heat exchangers, energy absorption components, aircraft engines, etc. To systematically design optimized architected structures with favorable manufacturability in terms of exact sizes and good connectivity, in the present work, an enhanced multidomain topology optimization method is developed. The design domain is divided into several subdomains and boundary layers between them first. Periodic base cells with exact sizes are distributed in each subdomain, and analyzed and optimized approximately based on the homogenization method with coarse meshes to reduce the numerical efforts. Besides, gradient boundary layers discretized by fine meshes are optimized between subdomains and boundaries to connect adjacent base cells with different patterns and address the boundary effect. Quadtree technology is used to match the meshes of different sizes. Numerical examples verify both the effectiveness and efficiency of the proposed approach for designing manufacturable optimized architected structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Schaedler TA, Carter WB (2016) Architected cellular materials. Annu Rev Mater Res 46:187–210. https://doi.org/10.1146/annurev-matsci-070115-031624

    Article  Google Scholar 

  2. Zadpoor AA (2016) Mechanical meta-materials. Mater Horiz 3:371–381. https://doi.org/10.1039/C6MH00065G

    Article  Google Scholar 

  3. Gibson LJ (2012) The hierarchical structure and mechanics of plant materials. J R Soc Interface 9:2749–2766. https://doi.org/10.1098/rsif.2012.0341

    Article  Google Scholar 

  4. Aizenberg J (2005) Skeleton of euplectella sp.: structural hierarchy from the nanoscale to the macroscale. Science 309:275–278. https://doi.org/10.1126/science.1112255

    Article  Google Scholar 

  5. Zheng XY, Lee H, Weisgraber TH et al (2014) Ultralight, ultrastiff mechanical metamaterials. Science 344:1373–1377. https://doi.org/10.1126/science.1252291

    Article  Google Scholar 

  6. Meza LR, Das S, Greer JR (2014) Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science 345:1322–1326. https://doi.org/10.1126/science.1255908

    Article  Google Scholar 

  7. Lakes R (1987) Foam structures with a negative Poisson’s ratio. Science 235:1038–1040. https://doi.org/10.1126/science.235.4792.1038

    Article  Google Scholar 

  8. Bückmann T, Kadic M, Schittny R, Wegener M (2015) Mechanical cloak design by direct lattice transformation. Proc Natl Acad Sci USA 112:4930–4934. https://doi.org/10.1073/pnas.1501240112

    Article  Google Scholar 

  9. Osanov M, Guest JK (2016) Topology optimization for architected materials design. Ann Rev Mater Res 46:211–233. https://doi.org/10.1146/annurev-matsci-070115-031826

    Article  Google Scholar 

  10. Meza LR, Zelhofer AJ, Clarke N et al (2015) Resilient 3D hierarchical architected metamaterials. Proc Natl Acad Sci USA 112:11502–11507. https://doi.org/10.1073/pnas.1509120112

    Article  Google Scholar 

  11. Bendsoe MP, Sigmund O (2013) Topology optimization: theory, methods, and applications. Springer, Berlin. https://doi.org/10.1007/978-3-662-05086-6

    Book  MATH  Google Scholar 

  12. Guo X, Cheng GD (2010) Recent development in structural design and optimization. Acta Mech Sinica 26:807–823. https://doi.org/10.1007/s10409-010-0395-7

    Article  MathSciNet  MATH  Google Scholar 

  13. Sigmund O, Maute K (2013) Topology optimization approaches. Struct Multidisc Optim 48:1031–1055. https://doi.org/10.1007/s00158-013-0978-6

    Article  Google Scholar 

  14. Sivapuram R, Dunning PD, Kim HA (2016) Simultaneous material and structural optimization by multiscale topology optimization. Struct Multidiscip Optim 54:1267–1281. https://doi.org/10.1007/s00158-016-1519-x

    Article  MathSciNet  Google Scholar 

  15. Xu L, Cheng GD (2018) Two-scale concurrent topology optimization with multiple micro materials based on principal stress orientation. Struct Multidiscip Optim 57:2093–2107. https://doi.org/10.1007/s00158-018-1916-4

    Article  MathSciNet  Google Scholar 

  16. Deng JD, Chen W (2017) Concurrent topology optimization of multiscale structures with multiple porous materials under random field loading uncertainty. Struct Multidiscip Optim 56:1–19. https://doi.org/10.1007/s00158-017-1689-1

    Article  MathSciNet  Google Scholar 

  17. Gao J, Luo Z, Li H, Gao L (2019) Topology optimization for multiscale design of porous composites with multi-domain microstructures. Comput Methods Appl Mech Eng 344:451–476. https://doi.org/10.1016/j.cma.2018.10.017

    Article  MathSciNet  MATH  Google Scholar 

  18. Bourgat JF (1979) Numerical experiments of the homogenization method. In: Glowinski R, Lions JL, Laboria I (eds) Computing methods in applied sciences and engineering, 1977, I. Springer, Berlin, pp 330–356

    Chapter  Google Scholar 

  19. Sanchez-Palencia E (1983) Homogenization method for the study of composite media. In: Verhulst F (ed) Asymptotic analysis II. Springer Berlin Heidelberg, Berlin, pp 192–214

    Chapter  Google Scholar 

  20. Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224. https://doi.org/10.1016/0045-7825(88)90086-2

    Article  MathSciNet  MATH  Google Scholar 

  21. Rodrigues H, Guedes JM, Bendsøe MP (2002) Hierarchical optimization of material and structure. Struct Multidiscip Optim 24:1–10. https://doi.org/10.1007/s00158-002-0209-z

    Article  Google Scholar 

  22. Coelho PG, Fernandes PR, Guedes JM, Rodrigues HC (2007) A hierarchical model for concurrent material and topology optimisation of three-dimensional structures. Struct Multidiscip Optim 35:107–115. https://doi.org/10.1007/s00158-007-0141-3

    Article  Google Scholar 

  23. Coelho PG, Fernandes PR, Rodrigues HC, Cardoso JB, Guedes JM (2009) Numerical modeling of bone tissue adaptation—a hierarchical approach for bone apparent density and trabecular structure. J Biomech 42:830–837. https://doi.org/10.1016/j.jbiomech.2009.01.020

    Article  Google Scholar 

  24. Liu L, Yan J, Cheng G (2008) Optimum structure with homogeneous optimum truss-like material. Comput Struct 86:1417–1425. https://doi.org/10.1016/j.compstruc.2007.04.030

    Article  Google Scholar 

  25. Niu B, Yan J, Cheng GD (2008) Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency. Struct Multidiscip Optim 39:115–132. https://doi.org/10.1007/s00158-008-0334-4

    Article  Google Scholar 

  26. Deng JD, Yan J, Cheng GD (2012) Multi-objective concurrent topology optimization of thermoelastic structures composed of homogeneous porous material. Struct Multidiscip Optim 47:583–597. https://doi.org/10.1007/s00158-012-0849-6

    Article  MathSciNet  MATH  Google Scholar 

  27. Guo X, Zhao XF, Zhang WS, Yan J, Sun GM (2015) Multiscalele robust design and optimization considering load uncertainties. Comput Methods Appl Mech Eng 283:994–1009. https://doi.org/10.1016/j.cma.2014.10.014

    Article  MATH  Google Scholar 

  28. Du ZL, Zhou XY, Picelli R, Kim HA (2018) Connecting microstructures for multiscale topology optimization with connectivity index constraints. J Mech Des. https://doi.org/10.1115/1.4041176

    Article  Google Scholar 

  29. Deng J, Pedersen CBW, Chen W (2019) Connected morphable components-based multiscale topology optimization. Front Mech Eng 14:129–140. https://doi.org/10.1007/s11465-019-0532-3

    Article  Google Scholar 

  30. Zhou XY, Du ZL, Kim HA (2019) A level set shape metamorphosis with mechanical constraints for geometrically graded microstructures. Struct Multidiscip Optim 60:1–16. https://doi.org/10.1007/s00158-019-02293-9

    Article  MathSciNet  Google Scholar 

  31. Wang Y, Chen F, Wang MY (2017) Concurrent design with connectable graded microstructures. Comput Methods Appl Mech Eng 317:84–101. https://doi.org/10.1016/j.cma.2016.12.007

    Article  MathSciNet  MATH  Google Scholar 

  32. Li H, Luo Z, Gao L, Qin Q (2018) Topology optimization for concurrent design of structures with multi-patch microstructures by level sets. Comput Methods Appl Mech Eng 331:536–561. https://doi.org/10.1016/j.cma.2017.11.033

    Article  MathSciNet  MATH  Google Scholar 

  33. Alexandersen J, Lazarov BS (2015) Topology optimisation of manufacturable microstructural details without length scale separation using a spectral coarse basis preconditioner. Comput Methods Appl Mech Eng 290:56–182. https://doi.org/10.1016/j.cma.2015.02.028

    Article  MathSciNet  MATH  Google Scholar 

  34. Fu J, Xia L, Gao L et al (2019) Topology optimization of periodic structures with substructuring. J Mech Des 141:071403. https://doi.org/10.1115/1.4042616

    Article  Google Scholar 

  35. Liu Y, Li Z, Wei P, Wang W (2018) Parameterized level-set based topology optimization method considering symmetry and pattern repetition constraints. Comput Methods Appl Mech Eng 340:1079–1101. https://doi.org/10.1016/j.cma.2018.04.034

    Article  MathSciNet  MATH  Google Scholar 

  36. Guedes J, Kikuchi N (1990) Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods. Comput Methods Appl Mech Eng 83:143–198. https://doi.org/10.1016/0045-7825(90)90148-f

    Article  MathSciNet  MATH  Google Scholar 

  37. Hassani B, Hinton E (1998) A review of homogenization and topology optimization I—homogenization theory for media with periodic structure. Comput Struct 69:707–717. https://doi.org/10.1016/s0045-7949(98)00131-x

    Article  MATH  Google Scholar 

  38. Allaire G (1992) Homogenization and two-scale convergence. SIAM J Math Anal 23:1482–1518. https://doi.org/10.1137/0523084

    Article  MathSciNet  MATH  Google Scholar 

  39. Moses E, Fuchs MB, Ryvkin M (2002) Topological design of modular structures under arbitrary loading. Struct Multidiscip Optim 24:407–417. https://doi.org/10.1007/s00158-002-0254-7

    Article  Google Scholar 

  40. Zuo ZH, Xie YM, Huang XD (2011) Optimal topological design of periodic structures for natural frequencies. J Struct Eng-ASCE 137:1229–1240. https://doi.org/10.1061/(asce)st.1943-541x.0000347

    Article  Google Scholar 

  41. Xie YM, Zuo ZH, Huang XD, Rong JH (2011) Convergence of topological patterns of optimal periodic structures under multiple scales. Struct Multidiscip Optim 46:41–50. https://doi.org/10.1007/s00158-011-0750-8

    Article  MATH  Google Scholar 

  42. Dumontet H (1985) Boundary layers stresses in elastic composites. Studies in Applied Mechanics. Elsevier 12:215–232. https://doi.org/10.1016/b978-0-444-42520-1.50014-1

    Article  MathSciNet  MATH  Google Scholar 

  43. Dumontet H (1986) Study of a boundary layer problem in elastic composite materials. Esaim-Math Model Num 20:265–286. https://doi.org/10.1051/m2an/1986200202651

    Article  MathSciNet  MATH  Google Scholar 

  44. Gupta AK (1978) A finite element for transition from a fine to a coarse grid. Int J Numer Methods Eng 12:35–45. https://doi.org/10.1002/nme.1620120104

    Article  MATH  Google Scholar 

  45. Lo SH, Wu D, Sze KY (2010) Adaptive meshing and analysis using transitional quadrilateral and hexahedral elements. Finite Elem Anal Des 46:2–16. https://doi.org/10.1016/j.finel.2009.06.010

    Article  MathSciNet  Google Scholar 

  46. Tabarraei A, Sukumar N (2005) Adaptive computations on conforming quadtree meshes. Finite Elem Anal Des 41:686–702. https://doi.org/10.1016/j.finel.2004.08.002

    Article  Google Scholar 

  47. Ball AA (1980) The interpolation function of a general serendipity rectangular element. Int J Numer Methods Eng 15:773–778. https://doi.org/10.1002/nme.1620150512

    Article  MATH  Google Scholar 

  48. Cheng GD, Cai YW, Xu L (2013) Novel implementation of homogenization method to predict effective properties of periodic materials. Acta Mech Sin 29:550–556. https://doi.org/10.1007/s10409-013-0043-0

    Article  MathSciNet  MATH  Google Scholar 

  49. Bourdin B (2001) Filters in topology optimization. Int J Numer Methods Eng 50:2143–2158. https://doi.org/10.1002/nme.116

    Article  MathSciNet  MATH  Google Scholar 

  50. Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. Int J Numer Methods Eng 24:359–373. https://doi.org/10.1002/nme.1620240207

    Article  MathSciNet  MATH  Google Scholar 

  51. Zuo ZH, Huang XD, Yang XY, Rong JH, Xie YM (2013) Comparing optimal material microstructures with optimal periodic structures. Comp Mater Sci 69:137–147. https://doi.org/10.1016/j.commatsci.2012.12.006

    Article  Google Scholar 

  52. Neves MM, Rodrigues H, Guedes JM (2000) Optimal design of periodic linear elastic microstructures. Comput Struct 76:421–429. https://doi.org/10.1016/s0045-7949(99)00172-8

    Article  Google Scholar 

  53. Guo X, Zhang W, Zhong W (2014) Doing topology optimization explicitly and geometrically—a new moving morphable components based framework. J Appl Mech 81:081009. https://doi.org/10.1115/1.4027609

    Article  Google Scholar 

  54. Liu C, Zhu Y, Sun Z et al (2018) An efficient moving morphable component (MMC)-based approach for multi-resolution topology optimization. Struct Multidisc Optim 58:2455–2479. https://doi.org/10.1007/s00158-018-2114-0

    Article  MathSciNet  Google Scholar 

  55. Wang F, Lazarov BS, Sigmund O (2011) On projection methods, convergence and robust formulations in topology optimization. Struct Multidisc Optim 43:767–784. https://doi.org/10.1007/s00158-010-0602-y

    Article  MATH  Google Scholar 

  56. Liang Y, Cheng G (2019) Topology optimization via sequential integer programming and Canonical relaxation algorithm. Comput Methods Appl Mech Eng 348:64–96. https://doi.org/10.1016/j.cma.2018.10.050

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The financial supports from the National Natural Science Foundation (11821202, 11732004, 12002077, 12002073), the National Key Research and Development Plan (2016YFB0201601), China Postdoctoral Science Foundation funded project (2020T130078, 2020M680944), Starting Grants at Dalian University of Technology (DUT20RC(3)020), Program for Changjiang Scholars, Innovative Research Team in University (PCSIRT) and 111 Project (B14013) are also gratefully acknowledged.

Author information

Authors and Affiliations

  1. State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, International Research Center for Computational Mechanics, Dalian University of Technology, Dalian, 116023, People’s Republic of China

    Chang Liu, Zongliang Du, Weisheng Zhang, Yue Mei & Xu Guo

  2. Beijing Institute of Spacecraft System Engineering, CAST, Beijing, People’s Republic of China

    Xiaoyu Zhang

  3. Ningbo Institute of Dalian University of Technology, Ningbo, 315016, People’s Republic of China

    Chang Liu, Zongliang Du, Weisheng Zhang, Yue Mei & Xu Guo

Authors
  1. Chang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zongliang Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Weisheng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaoyu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yue Mei
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Xu Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Zongliang Du or Xu Guo.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, C., Du, Z., Zhang, W. et al. Design of optimized architected structures with exact size and connectivity via an enhanced multidomain topology optimization strategy. Comput Mech 67, 743–762 (2021). https://doi.org/10.1007/s00466-020-01961-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-020-01961-8

Keywords

Search

Navigation