Unitary-coupled restricted Boltzmann machine ansatz for quantum simulations

Abstract

Neural-network quantum state (NQS) has attracted significant interests as a powerful wave-function ansatz to model quantum phenomena. In particular, a variant of NQS based on the restricted Boltzmann machine (RBM) has been adapted to model the ground state of spin lattices and the electronic structures of small molecules in quantum devices. Despite these progresses, significant challenges remain with the RBM-NQS-based quantum simulations. In this work, we present a state-preparation protocol to generate a specific set of complex-valued RBM-NQS, which we name the unitary-coupled RBM-NQS, in quantum circuits. Our proposal expands the applicability of NQS as prior works deal exclusively with real-valued RBM-NQS for quantum algorithms. With this scheme, we achieve (1) modeling complex-valued wave functions, (2) using as few as one ancilla qubit to simulate M hidden spins in an RBM architecture, and (3) avoiding post-selections to improve scalability.

Introduction

Hybrid quantum-classical (HQC) algorithms¹ offer an exciting avenue to explore the potential of a noisy intermediate-scale quantum² device without quantum error corrections. The HQC algorithms run on parametrized quantum circuits aiming to minimize an objective function, such as the average energy. The Variational Quantum Eigensolver³ (VQE) and Quantum Approximate Optimization Algorithm⁴ are two prominent examples leading the current wave of HQC algorithm developments. In particular, VQE has been experimentally demonstrated on several leading platforms of quantum computations^3,5,6,7,8. These encouraging experimental outcomes strengthen our anticipation that quantum simulations^{9,10,11,12,13} should be among the first set of applications to benefit from quantum computations. Nevertheless, it is also becoming increasingly clear that further developments^{14,15,16,17,18,19} are required to improve VQE and similar HQC algorithms if the goal is to establish an unambiguous quantum advantage for problems of realistic interests. For instance, many recent developments attempt to address the following aspects: (1) design wave-function ansatz^{5,14,20,21,22,23,24,25} with efficient usage of variational parameters and circuit depth, (2) reduce the number of required measurements^{26,27,28,29,30,31,32,33}, and (3) overcome the challenge of high-dimensional optimization^{34,35,36,37,38,39,40,41,42,43} needed for training parametrized circuits. Any of these technical challenges could potentially become a computational bottleneck for an HQC algorithm beyond the small-scale testings reported in the recent literature.

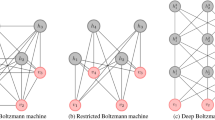
In this work, our primary focus is to investigate whether neural-network quantum states (NQS)^44,45,46 can be tailored to better fit the paradigm of HQC algorithms. We focus on a particular form of NQS based on the restricted Boltzmann Machine (RBM) architecture. Within the communities of computational many-body physics, quantum information and condensed matter physics, there is a growing trend of adopting neural networks techniques, such as the RBM architecture, for various applications. Notable examples include identification of different phases of matter^{47,48,49,50,51,52}, scalable quantum state tomography^53,54, efficient sampler to accelerate Monte Carlo simulations^55,56,57, quantum error correction codes^58,59,60,61, and variational ansatz for many-body simulations^{62,63,64,65,66,67,68,69,70,71,72}. Especially, the work by Carleo and Troyer⁶² demonstrated that a complex-valued RBM model can efficiently model many-body wave functions with fewer variational parameters than tensor-network methods for some spin-lattice models. Subsequent investigations^{73,74,75,76,77,78} have further clarified and affirmed the usefulness of variants of Boltzmann machines to model many-body quantum states of complex systems. These encouraging results and rapidly accumulated knowledge about RBM-NQS motivated us to investigate whether it is suitable to apply this family of ansatz in the context of quantum simulation algorithms. In most part of this work, we should use RBM-NQS and NQS interchangeably when there is no risk of ambiguity.

While there are already quantum simulation algorithms^79,80 using NQS as variational ansatz with encouraging results, some fundamental obstacles limit their scope of applications. For instance, the existing approaches require the preparation of an extended wave function composed of all visible and hidden spins. As each hidden spin is explicitly modeled with an ancilla qubit, these prior methods consume too many qubits, which are expensive resources for near-term quantum devices. Furthermore, there is no scalable strategy for preparing a general NQS in quantum circuits. This is because many NQS can only be obtained via non-unitary transformations on an input state. Existing NQS-based simulation algorithm⁷⁹ relies on a probabilistic post-selection to achieve the non-unitary operations. Finally, the lack of complex parameters severely limits the usefulness of the NQS for quantum simulations. For instance, (1) complex-valued wave functions allow us to simulate fermions in time reversal symmetry breaking systems such as electrons in the presence of a magnetic field. (2) To simulate quantum dynamics, it is a necessity to account for the accumulation of dynamical phase factors.

The aforementioned limitations certainly have cast doubts on whether the NQS should be used in quantum simulations; despite many of their theoretical merits as wave-function ansatz and convincing demonstrations in classical simulations cited above. To address these deficiencies, we propose a state-preparation protocol for creating complex-valued NQS in a quantum circuit. In particular, the state-preparation protocol does not use N + M qubits to model N visible spins and M hidden spins explicitly. This is because every term in a RBM Hamiltonian commutes with each other, we can explicitly arrange the order in which the unitary gates acting on the hidden spins. Hence, a single ancilla qubit (representing one hidden spin) can be recycled upon measurement and be reused to represent another hidden spin in a subsequent stage. This qubit-recyle scheme^81,82 tremendously reduces the number of physical qubits (down to just one extra ancilla at the bare minimum) needed to execute the proposed state-preparation protocol. This advantage cannot be underestimated as typical RBM-NQS might use as many as M = poly(N) hidden spins.

In order to avoid a probabilistic state preparation discussed in ref. ⁷⁹, we have done two things differently. First, we consider a further restricted subclass of RBM-NQS ansatz, dubbed the unitary-coupled RBM-NQS. For these states, the visible and hidden spins are only coupled by unitary operators, i.e. the coupling parameters for a RBM wave function are purely imaginary-valued. Owing to unitary couplings, a state preparation circuit scales as ${\mathcal{O}}(NM)$ in circuit depth. There is no obvious disadvantage to confine an ansatz selection to unitary-coupled RBM-NQS. As thoroughly analyzed in Supplementary Note 2, arbitrary RBM-NQS can be systematically converted into a unitary-coupled form without sacrificing representation accuracy. Furthermore, numerical investigations in this work demonstrate that unitary-coupled RBM can accurately model a wide range of physical systems without excessive number of hidden spins.

The second thing we have done differently is to modify a strict post-selection on hidden spins. As explained later, an NQS is properly generated when all hiddens are projected onto $\left|+\right\rangle =\left(\left|0\right\rangle +\left|1\right\rangle \right)/\sqrt{2}$. In this work, we observe that a single NQS can be decomposed into an ensemble of modified NQS, which are essentially outputted by a quantum circuit when a projective measurement on hidden spins yields a state other than $\left|+\right\rangle$. Under this ensemble scheme, expectation values for any observable of the original NQS can be estimated from these modified NQS within a Monte Carlo framework.

Finally, we modify the imaginary-time-dependent variaitonal algorithm³⁴ to better suit the specific structure of an NQS. We term this algorithm NQS-imaginary-time evolution (NQS-ITE). Due to the commutative structure of a NQS ansatz, the simulation algorithm based on the imaginary-time-dependent variational principle (ITDVP) can be drastically simplified as one just needs to perform measurement on one quantum circuit instead of working with ${\mathcal{O}}({N}_{\,\text{var}\,}^{2})$ different quantum circuits where N_var is the number of total variational parameters. For large-scale simulations, ${N}_{\text{var}}\propto {\mathcal{O}}(MN)$ could be a huge number.

In summary, the present work has both expanded the scope of application for NQS-based HQC simulations and has lowered the barrier for experimental implementations. In order to frame the significance of this work in a better perspective, we summarize and clarify the challenges we set out to address in prior works in Supplementary Note I.

Results

Preparing a complex-valued NQS in a quantum circuit

A brief introduction of NQS can be found in the “Methods” section. All NQS may be obtained from at least one bipartite Ising Hamiltonian ${\hat{H}}_{\text{RBM}}(\theta )={\sum }_{i}{b}_{i}{\hat{v}}_{i}^{z}+{\sum }_{j}{m}_{j}{\hat{h}}_{j}^{z}+{\sum }_{ij}{W}_{ij}{\hat{v}}_{i}^{z}{\hat{h}}_{j}^{z}$, where ${\hat{v}}_{i}^{z}$ or ${\hat{h}}_{j}^{z}$ is the Pauli Z operator for the visible or hidden qubit, respectively. We also denote complex-valued RBM parameters as θ = [b₁, …, b_N, m₁, …, m_M, W₁₁, …, W_NM], and use superscripts R and I to denote the real and imaginary parts, respectively. The complex-valued NQS can be created with a two-step approach. First, entangle N + M qubits (including all visible and hidden spins of an RBM architecture) according to

$$\left|{{{\Psi }}}_{\mathrm {vh}}(\theta )\right\rangle =\left[\frac{{\mathrm e}^{{\hat{H}}_{\text{RBM}}(\theta )}}{\sqrt{{\,}_{\mathrm {vh}}\left\langle ++\cdots +\right|{\mathrm e}^{2{\hat{H}}_{\text{RBM}}^{\text{R}}(\theta )}{\left|++\cdots +\right\rangle }_{{\mathrm {vh}}}}}\right]{\left|++\cdots +\right\rangle }_{{\mathrm {vh}}},$$

(1)

where $\left|+\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle )$, ${\hat{H}}_{\,\text{RBM}}^{\text{R}\,}(\theta )$ is the Hermitian part of the RBM Hamiltonian and the subscript vh denotes visible and hidden (ancilla) qubits. Equation (1) gives a conceptually simple wave function that could be generated by first applying single-qubit transformations $\exp ({b}_{i}{\hat{v}}_{i}^{z})$ and $\exp ({m}_{j}{\hat{h}}_{j}^{z})$ on individual qubits followed by $\exp ({W}_{ij}{\hat{v}}_{i}^{z}{\hat{h}}_{j}^{z})$ to couple qubits. The quantum operations are non-unitary when RBM parameters take on real parts, i.e. ${b}_{i}^{\,\text{R}\,}\,\ne \,0$, ${m}_{j}^{\,\text{R}\,}\,\ne \,0$, or ${W}_{ij}^{\,\text{R}\,}\,\ne \,0$. In general, the non-unitary two-qubit operation mediating entanglement across the visible–hidden layer are difficult to implement. One could adopt the probabilistic scheme introduced in ref. ⁷⁹ to generate the inter-layer couplings with an extra ancilla qubit. However, for complex-valued wave function, this approach in ref. ⁷⁹ is difficult to scale with the number of qubits involved. An alternative to implementing the non-unitary two-qubit operation is the quantum imaginary-time evolution algorithm proposed by ref. ⁸³; however, such algorithm requires deep circuits for systems with long correlation length.

Once the extended wave function $\left|{{{\Psi }}}_{{\mathrm {vh}}}(\theta )\right\rangle$ is generated, all ancilla qubits (i.e. hidden spins) are post-selected for ${\left|+\right\rangle }_{\mathrm h}$ and the desired NQS in Eq. (16) is reconstructed in the quantum circuit,

$$\begin{array}{lll}\left|{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle &=&\frac{{\,}_{\mathrm h}\left\langle ++\cdots +| {{{\Psi }}}_{{\mathrm {vh}}}(\theta )\right\rangle }{\sqrt{\left\langle {{{\Psi }}}_{{\mathrm {vh}}}(\theta )\right|{\hat{P}}_{+}^{(\mathrm h)}\left|{{{\Psi }}}_{{\mathrm {vh}}}(\theta )\right\rangle }}\\ &=&\frac{1}{{N}_{\mathrm v}}\mathop {\sum}\limits_{{\bf{h}}}{\mathrm e}^{{\hat{H}}_{\text{RBM}}(\theta ,{\bf{h}})}{\left|++\cdots +\right\rangle }_{\mathrm v},\end{array}$$

(2)

where ${\hat{P}}_{+}^{(\mathrm h)}={\left|++\cdots +\right\rangle }_{\mathrm h}\left\langle ++\cdots +\right|$, ${N}_{\mathrm v}=\sqrt{{\,}_{{\mathrm {vh}}}\left\langle ++\cdots +\right|{\mathrm e}^{{\hat{H}}_{\text{RBM}}(\theta )}{\hat{P}}_{+}^{(\mathrm h)}{\mathrm e}^{{\hat{H}}_{\text{RBM}}(\theta )}{\left|++\cdots +\right\rangle }_{{\mathrm {vh}}}}$ and ${\mathrm e}^{{\hat{H}}_{\text{RBM}}(\theta ,{\bf{h}})}$ is an operator acting on the visible spins only as we replace the Pauli operator ${\hat{h}}_{j}^{z}$ with a binary value (±1) of h_j ∈ h = [h₁, …, h_M]. From the second line of Eq. (2), it is clear that the hidden spins jointly mediate a specific quantum transformation, ${\sum }_{{\bf{h}}}{\mathrm e}^{{\hat{H}}_{\text{RBM}}(\theta ,{\bf{h}})}$, on the visible-spin wave function. Since this transformation invovles post-selection and non-unitary in general, the amplitude-amplification type of techniques^84,85 and other more advanced techniques such as linear combination of unitaries⁸⁶ are not convenient due to the need for extra quantum resources and longer quantum circuits are generally expected. Overall, the challenge to efficiently implement ${\sum }_{{\bf{h}}}{\mathrm e}^{{\hat{H}}_{\text{RBM}}(\theta ,{\bf{h}})}$ creates another obstacle to prepare complex-valued NQS in quantum circuits.

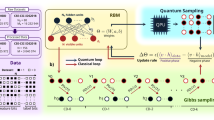
In the rest of this section, we describe a scalable state-preparation protocol that overcomes these two obstacles. In particular, we implement complex-valued NQS using as few as one ancilla qubit and entirely avoids the post-selection. To simplify presentations, we illustrate how to prepare a subset of NQS that we dub the unitary-coupled RBM-NQS, which only allow purely imaginary-valued inter-layer couplings ${W}_{ij}=i{W}_{ij}^{\,\text{I}\,}$. Generation of unitary-coupled RBM-NQS bypass the inherent challenge to mediate entanglement via non-unitary transformations. Figure 1a gives a circuit diagram of preparing a unitary-coupled RBM-NQS composed of two visible spins with inter-qubit couplings mediated by two hidden spins. The Hadarmard gates prepare the $\left|+\right\rangle$ state, and the parametrized single-qubit rotations are not fixed along the z-axis because of the non-unitary operations, $\exp \left({b}_{i}^{\,\text{R}\,}{\hat{v}}_{i}^{z}\right)$ and $\exp ({m}_{i}^{\,\text{R}\,}{\hat{h}}_{i}^{z})$. In the circuit diagram of Fig. 1a, the single-qubit rotations R_n(θ) are determined via relations of the form $\exp \left({b}_{i}^{\,\text{R}\,}{\hat{v}}_{i}^{z}\right)\left|+\right\rangle /c={R}_{n}(\theta )\left|+\right\rangle$ with the normalization factor $c=\sqrt{\left\langle +\right|\exp \left(2{b}_{i}^{\,\text{R}\,}{\hat{v}}_{i}^{z}\right)\left|+\right\rangle }$. Figure 1b gives a schematic depicting the RBM state generated by the circuit in Fig. 1a. As explained in Supplementary Note II, the unitary-coupled RBM-NQS does not necessarily suffer loss of expressive power. While we claim it is better to model quantum systems with unitary-coupled RBM-NQS for near-term applications; there is a straightforward extension of the current protocol to generate arbitrary complex-valued NQS in case it is desired. We defer the discussion of this extension to Supplementary Note VI.

Fig. 1: Quantum circuits for preparing unitary-coupled RBM states.

Unitary-coupled RBM-NQS. a Quantum circuit to directly prepare a two-qubit unitary-coupled RBM state having two hidden spins. The inter-layer coupling is mediated by unitary gates. Note ${\theta }_{ij}^{\prime}=-{\theta }_{ij}$. b Schematic of the RBM state generated by the quantum circuit in panel a. c Scalable preparation of unitary-coupled RBM state described in Eqs. (3)–(5). A sample circuit in which the hidden spins are projected onto $\left|+-\right\rangle$ is shown.

Scalable preparation of a unitary-coupled RBM-NQS in a quantum circuit

To begin, we note that Eq. (2) can be cast in an alternative form

$$\begin{array}{lll}\left|{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle &=&\frac{1}{{N}_{\mathrm v}}{\left[\left\langle +\right|\left[{\mathrm e}^{{\hat{h}}_{M}^{z}\left({m}_{M}+{\sum }_{i}i{W}_{iM}^{\text{I}}{\hat{v}}_{i}^{z}\right)}\right]\left|+\right\rangle \right]}_{M}{\left[\left\langle +\right|\left[{\mathrm e}^{{\hat{h}}_{M-1}^{z}\left({m}_{M-1}+{\sum }_{i}i{W}_{iM-1}^{\text{I}}{\hat{v}}_{i}^{z}\right)}\right]\left|+\right\rangle \right]}_{M-1}\cdots \\ &&\times {\left[\left\langle +\right|\left[{\mathrm e}^{{\hat{h}}_{1}^{z}\left({m}_{1}+{\sum }_{i}i{W}_{i1}^{\text{I}}{\hat{v}}_{i}^{z}\right)}\right]\left|+\right\rangle \right]}_{1}\ \ {\mathrm e}^{{\sum }_{i}{b}_{i}{\hat{v}}_{i}^{z}}{\left|++\cdots +\right\rangle }_{v}.\end{array}$$

(3)

Each block, ${\left[\left\langle +\right|[\cdots ]\left|+\right\rangle \right]}_{j}$, encodes jth hidden spin’s effects on all visible ones. Clearly, one can use a single ancilla qubit to implement these transformations sequentially. As shown in Eq. (3), we specifically consider ${W}_{ij}=i{W}_{ij}^{\,\text{I}\,}$ for the unitary-coupled RBM-NQS. Our proposed approach to bypass the post-selection of $\left|+\right\rangle$ on all hidden spins is inspired by the following observation,

$$\begin{array}{lll}\left\langle +\right|\left[{\mathrm e}^{{\hat{h}}_{j}^{z}\left({m}_{j}+{\sum }_{i}i{W}_{ij}^{\text{I}}{\hat{v}}_{i}^{z}\right)}\right]\left|+\right\rangle &=& \mathop {\sum}\limits_{s=\pm }\left\langle +\right|{\mathrm e}^{{m}_{j}^{\text{R}}{\hat{h}}_{j}^{z}}\left|s\right\rangle \left\langle s\right|{\mathrm e}^{\left(i{m}_{j}^{\text{I}}+{\sum }_{i}i{W}_{ij}^{\text{I}}{\hat{v}}_{i}^{z}\right){\hat{h}}_{j}^{z}}\left|+\right\rangle \\ &=& \mathop {\sum}\limits_{s=\pm }{R}_{s}({m}_{j}^{\,\text{R}\,})\left\langle s\right|{\mathrm e}^{\left(i{m}_{j}^{\text{I}}+{\sum }_{i}i{W}_{ij}^{\text{I}}{\hat{v}}_{i}^{z}\right){\hat{h}}_{j}^{z}}\left|+\right\rangle ,\end{array}$$

(4)

where a resolution of identity ${\sum }_{{s}_{j} = \pm }\left|{s}_{j}\right\rangle \left\langle {s}_{j}\right|$ for the ancilla qubit is inserted in the middle and ${R}_{s}({m}_{j}^{\,\text{R}\,})=\langle +|{\mathrm {e}}^{{m}_{j}^{\text{R}}{\hat{h}}_{j}^{z}}|s\rangle$ can be computed classically as it is the transformation matrix element associated with a single qubit. Not obtaining R_s(m_j) experimentally is the key to avoid post-selection. Note that the decomposition of $\exp ({\hat{h}}_{j}^{z}({m}_{j}+{\sum }_{i}i{W}_{ij}^{\,\text{I}\,}{\hat{v}}_{i}^{z}))$ introduced in Eq. (4) is exact as these operators commute. Using Eq. (4), we re-write Eq. (3),

$$\begin{array}{lll}\left|{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle &=& \mathop {\sum}\limits _{{s}_{M}=\pm }\cdots \mathop {\sum}\limits_{{s}_{1}=\pm }\frac{1}{{N}_{\mathrm v}}\left(\mathop{\prod }\limits_{j=1}^{M}{R}_{{s}_{j}}({m}_{j}^{\,\text{R}\,})\right)\left\langle {s}_{M}\right|\left[{\mathrm e}^{{\hat{h}}_{M}^{z}\left(i{m}_{M}^{\text{I}}+{\sum }_{i}i{W}_{iM}^{\text{I}}{\hat{v}}_{i}^{z}\right)}\right]\left|+\right\rangle \cdots \\ &&\times \left\langle {s}_{1}\right|\left[{\mathrm e}^{{\hat{h}}_{1}^{z}\left(i{m}_{1}^{\text{I}}+{\sum }_{i}i{W}_{i1}^{\text{I}}{\hat{v}}_{i}^{z}\right)}\right]\left|+\right\rangle \ \ {\mathrm e}^{{\sum }_{i}{b}_{i}{\hat{v}}_{i}^{z}}{\left|++\cdots +\right\rangle }_{v}\\ &=& \mathop {\sum}\limits _{{s}_{M}=\pm }\cdots \mathop {\sum}\limits_{{s}_{1}=\pm }\frac{{N}_{\overrightarrow{s}}}{{N}_{\mathrm v}}\left(\mathop{\prod }\limits_{j=1}^{M}{R}_{{s}_{j}}({m}_{j}^{\,\text{R}\,})\right)\left|{{{\Psi }}}_{\mathrm v}^{\overrightarrow{s}}(\theta )\right\rangle ,\end{array}$$

(5)

where $\overrightarrow{s}=[{s}_{1},\cdots \ ,{s}_{M}]$. $|{{{\Psi }}}_{\mathrm v}^{\overrightarrow{s}}(\theta )\rangle$ is a visible-spin wave function created by projecting hidden spins onto basis states ${|{s}_{1}\cdots {s}_{M}\rangle }_{\mathrm h}$ instead of enforcing the post-selection ${\left|++\cdots +\right\rangle }_{\mathrm h}$. Due to the decomposition introduced in Eq. (4), only a portion of $\exp ({\hat{H}}_{\text{RBM}})$ contributes to the generation of $|{{{\Psi }}}_{\mathrm v}^{\overrightarrow{s}}(\theta )\rangle$ and ${N}_{\overrightarrow{s}}$ is the normalization to keep $\langle {{{\Psi }}}_{\mathrm v}^{\overrightarrow{s}}| {{{\Psi }}}_{\mathrm v}^{\overrightarrow{s}}\rangle =1$. While there is no post-selection in Eq. (5), there is now a summation over all possible $\overrightarrow{s}$.

Instead of working directly with Eq. (5), we are primarily interested in the expectation value of an observable $\hat{O}$, which can be formulated as

$$\left\langle {{{\Psi }}}_{\mathrm v}(\theta )\right|\hat{O}\left|{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle =\int {\mathrm d}z| \left\langle {\bf{z}}| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle {| }^{2}\left[\int {\mathrm d}{z}^{\prime}O(z,{z}^{\prime})\frac{\left\langle {{\bf{z}}}^{\prime}| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle }{\left\langle {\bf{z}}| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle }\right].$$

(6)

The equation above can be interpreted as follows. The expectation value of an observable $\hat{O}$ can be turned into the average of the expression inside the square bracket if we can efficiently sample z according to the probability density $| \left\langle {\bf{z}}| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle {| }^{2}$, i.e. projecting the NQS in some basis. We further analyze this probability density by exposing the details of the RBM architecture,

$$\begin{array}{lll}| \left\langle {\bf{z}}| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle {| }^{2}&=&\frac{| \left\langle {\bf{z}}| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle {| }^{2}}{\left\langle {{{\Psi }}}_{\mathrm v}(\theta )| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle }\\ &=&\frac{{\sum }_{\overrightarrow{s}}\frac{{N}_{\overrightarrow{s}}^{2}}{{N}_{\mathrm v}^{2}}\left(\mathop{\prod }\nolimits_{j = 1}^{M}{R}_{{s}_{j}}^{2}({m}_{j}^{\,\text{R}\,})\right)| \left\langle {\bf{z}}| {{{\Psi }}}_{\mathrm v}^{\overrightarrow{s}}(\theta )\right\rangle {| }^{2}}{{\sum }_{\overrightarrow{s}}\frac{{N}_{\overrightarrow{s}}^{2}}{{N}_{\mathrm v}^{2}}\left(\mathop{\prod }\nolimits_{j = 1}^{M}{R}_{{s}_{j}}^{2}({m}_{j}^{\,\text{R}\,})\right)},\end{array}$$

(7)

where ${\sum }_{\overrightarrow{s}}={\sum }_{{s}_{1}}\cdots {\sum }_{{s}_{M}}$ and it is implicitly assumed that $\left\langle {{{\Psi }}}_{\mathrm v}(\theta )| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle =1$. Instead of performing the exact summation over all $\overrightarrow{s}$ in Eq. (7) (this is essentially the same summation in Eq. (5) mentioned at the end of the last paragraph), we should estimate this sum with the Monte Carlo method. We note that ${N}_{\overrightarrow{s}}^{2}$ in Eq. (7) is the probability of observing {s₁, ⋯, s_M} upon measuring those M hidden spins during the construction of the state $|{{{\Psi }}}_{\mathrm {v}}^{\overrightarrow{s}}(\theta )\rangle$. Hence, samples of $\overrightarrow{s}$ are effectively drawn from the probability density ${N}_{\overrightarrow{s}}^{2}$ during the construction of $|{{{\Psi }}}_{\mathrm {v}}^{\overrightarrow{s}}(\theta )\rangle$. In short, we replace the exact summation according to

$$\sum _{\overrightarrow{s}}{N}_{\overrightarrow{s}}^{2}f(\overrightarrow{s})\begin{array}{l}\mathop{\longrightarrow }\limits^{{\rm{Monte}}\ {\rm{Carlo}}\ {\rm{sampling}}\ {\rm{of}}\,\overrightarrow{s}}\\ \ \ \ {\rm{according}}\ {\rm{to}}\,{N}_{\overrightarrow{s}}^{2}\end{array}\frac{1}{{N}_{\exp }}\mathop{\sum }\limits_{k=1}^{{N}_{\exp }}f({\overrightarrow{s}}_{k}),$$

(8)

where $f(\overrightarrow{s})=(\prod_{j = 1}^{M}{R}_{{s}_{j}}^{2}({m}_{j}^{\,\text{R}\,}))| \langle {\bf{z}}| {{{\Psi }}}_{v}^{\overrightarrow{s}}(\theta )\rangle {| }^{2}$ or $f(\overrightarrow{s})=(\mathop{\prod }\nolimits_{j = 1}^{M}{R}_{{s}_{j}}^{2}({m}_{j}^{\,\text{R}\,}))$ for the numerator and the denominator in Eq. (7), respectively, and ${N}_{\exp }$ is the number of sampling experiments performed.

The factor $({\prod }_{j}{R}_{{s}_{j}}^{2}({m}_{j}^{\,\text{R}\,}))$ in Eq. (7) should be calculated classically. This probability $|\langle {\bf{z}}| {{{\Psi }}}_{\mathrm {v}}^{\overrightarrow{s}}(\theta )\rangle {| }^{2}$ is again sampled from projective measurements on visible spins. The only thing that is prohibitively expensive to estimate either classically or experimentally is the normalization constant N_v. This is the reason we introduce the denominator (which is really just 1) in Eq. (7) that carries another N_v to cancel the one in the numerator. By using Eqs. (6) and (7) together, the challenging post-selection is replaced with a Monte Carlo framework that needs to sample multiple $|{{{\Psi }}}_{\mathrm {v}}^{\overrightarrow{s}}(\theta )\rangle$ according to Eq. (7). It is worth noting that, by using the ensemble state preparation outlined here, only projective measurements in the computational basis are used in estimating the expectation value of an operator (e.g. the system Hamiltonian), whereas projective measurements along all three axes are typically required in the standard VQE. Additional details on the ensemble state preparation method may be found in Supplementary Note III.

Quantum simulations with NQS-ITE

Next, we discuss the ITDVP to find a ground state of a Hamiltonian $\hat{H}$. The idea is to propagate a trial wave function $\left|{{{\Psi }}}_{\mathrm v}({\theta }_{\tau })\right\rangle$ in the imaginary-time domain. If the trial wave function $\left|{{{\Psi }}}_{\mathrm v}({\theta }_{0})\right\rangle$ at time τ = 0 has a non-zero overlap with the ground state $\left|{{{\Psi }}}_{{\mathrm {gs}}}\right\rangle$, then it should converge to an ansatz closest to $\left|{{{\Psi }}}_{{\mathrm {gs}}}\right\rangle$ when τ ≫ 1. With a variational ansatz, the time-evolved $\left|{{{\Psi }}}_{\mathrm v}({\theta }_{\tau })\right\rangle$ can be prepared in a quantum circuit if θ_τ is given. In Supplementary Note IV, we summarize the standard ITDVP³⁴ for parametrized quantum circuits and explain why we need to modify the standard approach for the NQS anstaz considered in this work. In this section, we present an overview of the NQS-ITE algorithm and details of the derivation may be found in Supplementary Note V.

In short, the equations of motion for θ_τ assume the following form:

$${\dot{\theta }}_{n}=\sum _{m}{A}_{nm}^{-1}{C}_{m}.$$

(9)

The matrix A and vector C read,

$${A}_{nm}=\,{\text{Re}}\,\left({\left\langle {\hat{O}}_{n}^{\dagger }{\hat{O}}_{m}\right\rangle }_{\mathrm {v}}-{\left\langle {\hat{O}}_{n}^{\dagger }\right\rangle }_{\mathrm {v}}{\left\langle {\hat{O}}_{m}\right\rangle }_{\mathrm {v}}\right),\,{\text{and}}{C}_{m}={\text{Re}}\,\left({\left\langle {\hat{O}}_{m}^{\dagger }\hat{H}\right\rangle }_{\mathrm {v}}-{\left\langle {\hat{O}}_{m}^{\dagger }\right\rangle }_{\mathrm {v}}{\left\langle \hat{H}\right\rangle }_{\mathrm {v}}\right),$$

(10)

where ${\left\langle \cdots \right\rangle }_{\mathrm v}=\left\langle {{{\Psi }}}_{\mathrm v}(\theta )\right|\ \cdots \ \left|{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle$. The O_n operators are defined as follows,

$${\hat{O}}_{n}=\left\{\begin{array}{ll}{i}^{1-\delta }{\hat{v}}_{i}^{z},&\,\text{if}\; {\theta }_{n}={b}_{i},\\ {i}^{1-\delta }\tanh \left({m}_{j}+{\sum }_{i}i{W}_{ij}^{\,\text{I}\,}{\hat{v}}_{i}^{z}\right),&\,\text{if}\;{\theta }_{n}={m}_{j},\\ i{\hat{v}}_{i}^{z}\tanh \left({m}_{j}+{\sum }_{i}i{W}_{ij}^{\,\text{I}\,}{\hat{v}}_{i}^{z}\right),&\,\text{if}\;{\theta }_{n}={W}_{ij}^{\text{I}\,},\end{array}\right.$$

(11)

where δ = 0 if ${\theta }_{n}={b}_{i}^{\,\text{I}\,}$ or ${\theta }_{n}={m}_{j}^{\,\text{I}\,}$ and δ = 1 if ${\theta }_{n}={b}_{i}^{\,\text{R}\,}$ or ${\theta }_{n}={m}_{j}^{\,\text{R}\,}$. We note that Eqs. (9)–(11) essentially give the stochastic reconfiguration method for the variational Monte Carlo framework. In the standard ITDVP approach³⁴, every matrix element ${A}_{mn}=\left\langle {\partial }_{{\theta }_{m}}{{{\Psi }}}_{\mathrm v}(\theta )| {\partial }_{{\theta }_{n}}{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle$ requires measurements with respect to a distinct quantum circuit. Hence, it takes ${\mathcal{O}}({N}_{\,\text{var}\,}^{2})$ sets of state preparations to construct A matrix. By utilizing the commutative property of operators in the RBM Hamiltonian, only one RBM state needs to be prepared for constructing the entire A matrix. In fact, one can simultaneously estimate all ${\mathcal{O}}({N}_{\,\text{var}\,}^{2})$ matrix elements with every given sample of z according to the definition of A matrix element in Eq. (10). This could be a tremendous advantage for large-scale simulations when ${N}_{\text{var}}\propto {\mathcal{O}}(MN)$ could be a huge number.

Next, we point out an interesting observation. The standard gradient-based energy minimization, as done within the VQE approach, updates θ_n with the equation of motion ${\dot{\theta }}_{n}={C}_{n}$ where C_n being the gradient vector for the energy function ${E}_{\theta }=\left\langle {{{\Psi }}}_{\mathrm v}(\theta )| \hat{H}| {{{\Psi }}}_{\mathrm v}(\theta )\right\rangle$. The comparison of Eq. (9) to the equation of motion above reveals that the NQS-ITE introduces a preconditioner A⁻¹ to the gradient vector in order to adjust the step size to account for the intrinsically curved metric for the NQS manifold. However, the evaluations of the matrix A requires no more experimental efforts for NQS-ITE than for a standard gradient-descent-based approach as explained. As the imaginary-time method tends to give better result than the gradient descent, one should always adopt the imaginary-time propagation whenever NQS is used as the trial wave function. It is worth noting that a quantum generalization of natural gradient descent has recently been proposed for variational quantum circuits, this algorithm is also shown to be a better optimizer than the standard gradient-descent approach^87,88.

Numerical results

To demonstrate the effectiveness of RBM-NQS ansatz and NQS-ITE algorithm, we report numerical simulations on three different types of systems: molecules, spin chains, and nanostructures (triple quantum dots (TQD)). We first present results with the standard complex-valued NQS ansatz (which requires the extended state preparation protocol described in Supplementary Note VI), then we repeat the simulations for selected examples in the last subsection to demonstrate that the unitary-coupled RBM-NQS could achieve the same level of accuracy with similar number of hidden spins.

Molecular systems

We first test the NQS-ITE algorithm on common molecular benchmarks: the dissociation curves of H₂, LiH, and an H₄ chain. The molecular Hamiltonians are first projected onto a discrete set of molecular orbitals. Here, we use the conventional STO-3G basis set, which constitutes the minimum number of orbitals required to represent a given atomic shell. The resulting fermionic Hamiltonians are subsequently mapped onto qubit Hamiltonians using the Bravyi–Kitaev transformation⁸⁹. The computation of the integrals in second quantization and transformation of the Hamiltonians are done using PySCF⁹⁰ and OpenFermion⁹¹.

Modelling H₂, LiH, and linear H₄ molecules in the STO-3G basis requires 2, 4, and 8 visible spins, respectively. The ground state energies, estimated from the NQS-ITE algorithm, as a function of inter-nuclear distance are plotted in Fig. 2. Despite using a modest number of hidden spins, the NQS anstaz models the molecular wave functions very well as the NQS-ITE algorithm gives nearly exact numerical results for all cases in Fig. 2. We consider more number of hidden spins for the linear H₄ molecule in order to correctly reproduce the wave function at large bond distance. Our result on linear H₄ molecule is largely consistently with the VMC (variational Monte Carlo) result discussed in ref. ⁹², a comprehensive benchmark studies of state-of-the-art simulation methods for quantum chemistry and many-body physics. This consistency can be understood as the RBM-NQS shares many similarities with the Jastrow factor in the variational ansatz adopted for the VMC method in that benchmark test.

Fig. 2: Numerical results for molecular systems.

The ground state energy of H₂, LiH, and linear H₄ molecules as a function of inter-nuclear distances. The energies computed with the NQS-ITE algorithm and the exact diagonalization are solid red dots and solid black lines, respectively. Results for a H₂ (N = 2, M = 2), b LiH (N = 4, M = 4), and c linear H₄ (N = 8, M = 24).

Spin systems

Next, we consider the problem of finding the ground state of three prototypical spin models, i.e. the transverse-field Ising model, the antiferromagnetic Heisenberg (AFH) model and the J1–J2 model. AFH and J1–J2 models are prominent models to study frustrated systems in condensed matter physics. The spin Hamiltonians can be written as

$${H}_{\text{TFI}}=-h\sum _{i}{\hat{\sigma }}_{i}^{x}-\sum _{< ij >}{\hat{\sigma }}_{i}^{z}{\hat{\sigma }}_{j}^{z};$$

(12)

$${H}_{\text{AFH}}=-h\sum _{i}{\hat{\sigma }}_{i}^{z}+\sum _{< ij >}{\hat{\sigma }}_{i}^{x}{\hat{\sigma }}_{j}^{x}+{\hat{\sigma }}_{i}^{y}{\hat{\sigma }}_{j}^{y}+{\hat{\sigma }}_{i}^{z}{\hat{\sigma }}_{j}^{z};$$

(13)

$${H}_{\text{J1J2}}={J}_{1}\sum _{< ij >}{\hat{\sigma }}_{i}^{x}{\hat{\sigma }}_{j}^{x}+{\hat{\sigma }}_{i}^{y}{\hat{\sigma }}_{j}^{y}+{\hat{\sigma }}_{i}^{z}{\hat{\sigma }}_{j}^{z}+{J}_{2}\sum _{< < ij >>}{\hat{\sigma }}_{i}^{x}{\hat{\sigma }}_{j}^{x}+{\hat{\sigma }}_{i}^{y}{\hat{\sigma }}_{j}^{y}+{\hat{\sigma }}_{i}^{z}{\hat{\sigma }}_{j}^{z},$$

(14)

where h is the uniform field strength, <ij> denotes the nearest-neighbor couplings, and <<ij>> denotes the next nearest-neighbor couplings. Open boundary condition is assumed for these linear spin chains. In Fig. 3 we again compute the energies using the NQS-ITE algorithm. Excellent agreement between NQS-ITE and the numerically exact results are obtained as expected. M = N number of hidden spins are used in all three cases including frustrated AFH and J1–J2 chains.

Fig. 3: Numerical results for spin systems.

The ground state energy of spin chains computed with the NQS-ITE algorithm (solid red dots) and exact diagonalization (solid black lines). Results for a Heisenberg chain as a function of chain length at different values of h field, b Ising chain as a function of chain length at different values of h field, c J1–J2 chain with J1 = 1 and J2 = 0.5. In panel a, the result for h = 1 has been shifted downwards by 2 units for visibility.

Triple quantum dots (TQD)

A lateral TQD is an artificial, fully tunable molecule constructed using metallic gates localizing electrons in a semiconductor field-effect transistor. A TQD allows one to study new phenomena not present in a single or double quantum dot, e.g. topological effects^93,94. The Hamiltonian of the TQD subject to a uniform perpendicular magnetic field, ${\bf{B}}=B\hat{{\bf{z}}}$, is given by

$$H=\sum _{i,\sigma }{E}_{i\sigma }{\hat{d}}_{i\sigma }^{\dagger }{\hat{d}}_{i\sigma }+\sum _{\sigma ,i,j;\ i\ne j}{\tilde{t}}_{ij}{\hat{d}}_{i\sigma }^{\dagger }{\hat{d}}_{j\sigma }+\sum _{i}{U}_{i}{\hat{n}}_{i\downarrow }{\hat{n}}_{i\uparrow }+\frac{1}{2}\sum _{i,j;\ i\ne j}{V}_{ij}{\varrho }_{i}{\varrho }_{j},$$

(15)

where ${\hat{d}}_{i\sigma }$ (${\hat{d}}_{i\sigma }^{\dagger }$) is fermionic annihilation (creation) operator with spin σ = ±1/2 on orbital i. ${\hat{n}}_{i\sigma }={\hat{d}}_{i\sigma }^{\dagger }{\hat{d}}_{i\sigma }$ and ${\hat{\varrho }}_{i}={\hat{n}}_{i\downarrow }+{\hat{n}}_{i\uparrow }$ are the spin and charge density on orbital level i. U_i and V_ij gives the strength of on-site and off-site Coulomb repulsion, respectively. Each dot is represented by a single orbital with energy E_iσ = E_i + g^*μ_BBσ, where g^* is the effective Landé g-factor, μ_B is the Bohr magneton. The dots are connected by magnetic-field-dependent hopping matrix elements ${\tilde{t}}_{ij}={t}_{ij}{\mathrm e}^{2\pi i{\phi }_{ij}}$ where ϕ_ij = ϕ is the magnetic flux. The details of this model can be found in the “Methods” section.

The ground state energy of the TQD as a function of magnetic field is plotted in Fig. 4, we observe excellent agreement between the results from the exact diagonalization and NQS-ITE. It is worth noting that, at non-zero magnetic field, the ground state wave function of a TQD could be complex, thus a complex RBM ansatz is necessary for accurate representation of the ground state wave function. Again, RBM-NQS may model this complex system with a modest number of hiddn spins with M = N even in the non-perturbtive regime (in which Coulomb repulsioon and kinetic energy are of comparable strength) as displayed in Fig. 4b.

Fig. 4: Numerical results for triple quantum dots.

The ground state energy of a lateral TQD (N = M = 6) as a function of magnetic field obtained from the NQS-ITE algorithm (solid red dots) and the exact diagonalization (solid black lines). Panel a U_i = 50∣t∣, V_ij = 10∣t∣ and E_i = t, and b U_i = 0.5∣t∣, V_ij = 0.1∣t∣, and E_i = t.

Results with unitary-coupled RBM-NQS

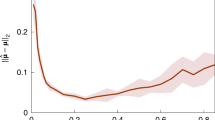
At last, we repeat calculations of a few models studied in previous sections with the unitary-coupled RBM-NQS ansatz. The key insight revealed in Figs. 5 and 6 is that, in most cases, the unitary-coupled RBM-NQS delivers comparable performance to that of the standard complex RBM-NQS. Although, it is also suggestive that the unitary-coupled RBM simulation could be improved if one either uses a smaller time-step size for the NQS-ITE algorithm or uses more number of hidden spins. The first point is well illustrated by Fig. 5c and the accompanied inset. The non-monotonic trend in the average energy (during the imaginary-time evolution) is a signature that the propagated quantum state is not well approximated by the unitary-coupled RBM ansatz when the imaginary-time-step size is large. This energy fluctuation improves consistently when the time-step size decreases as shown in the inset of Fig. 5c. Note that the NQS-ITE eventually finds the true ground state wave function even when the time-step size is not taken to be smaller.

Fig. 5: Imaginary-time evolution with RBM states.

Simulations of the ground state energy using NQS-ITE with random initialization (solid red lines), mean-field initialization (solid blue lines), and random initialization for the unitary-coupled RBM ansatz (dashed green lines). The dashed black lines show the ground state energy from exact diagonalization. Results for a H₂ at equilibrium bond length (1.05 Å), b LiH at equilibrium bond length (1.5 Å), c Heisenberg chain (N = 6, h = 0), and d Ising chain (N = 6, h = 0.5). The inset in c displays the results for the unitary-coupled RBM ansatz using different time-step sizes, δτ, where τ = steps*δτ.

The second point is illustrated by comparing the representation accuracy between a standard RBM-NQS and a unitary-coupled RBM-NQS with the same number of hidden spins. Clearly, the standard RBM ansatz achieves better accuracy. Although higher accuracy may be attained when more number of hidden spins are used for a unitary-coupled RBM ansatz. In fact, one can see that both ansatzes achieve roughly the same relative error when there are roughly same number of variational parameters for the AFH model in Fig. 6a. Note a standard RBM has almost twice the number of variational parameters (both real and imaginary coupling parameters for each visible–hidden connections).

Fig. 6: Comparison between full RBM and unitary-coupled RBM states.

Comparing relative errors between RBM-NQS and unitary-coupled RBM-NQS for a AFH model with h = 0 and M = N = 6, and b TFI model with h = 0.5 and M = N = 6. The defiintion of the relative error is ∣E_exact − E_rbm∣/∣E_exact∣ where rbm refers to either RBM-NQS or unitary-coupled RBM-NQS.

Finally, we also present another set of results (solid red lines) in Fig. 5. These results are obtained with RBM ansatz whose parameters are initialized with a mean-field solution to the original problems. As shown, a better initial guess improves the convergence rate in comparison to randomly initialized cases. Particularly, mean-field initial wave function already provides nearly exact ground state wave function for lithium hydride molecule, as it can be seen from Fig. 5b that the ground state energy from the mean-field approximation is nearly identical to the exact ground state energy. The accuracy of the mean-field approximation for LiH molecule is possibly due to the low level of electron correlations among the orbitals in minimal basis set. To test this hypothesis, we solve for the ground state of LiH using the Hartree–Fock method and found that it already provides a very accurate ground state solution. In the “Methods” section, we briefly comment how one can systematically make an intelligent guess on a good initial state under various situations.

Discussion

In conclusion, we present a practical approach to exploit a popular machine-learning model for quantum simulations on a digital quantum computer. Before fault-tolerant quantum computation becomes readily available, the HQC algorithms will prevail as a popular approach for investigating novel applications of a quantum computer. Successful experimental demonstrations of HQC algorithms have certainly attracted attentions and boosted confidence in quantum computations. Nevertheless, many obstacles still prevent a clear demonstration of unambiguous quantum advantages for these HQC algorithms. One possible path towards this goal is to investigate more powerful wave-function ansatz that can achieve a good tradeoff between expressive power and number of variational parameters. With fewer parameters, potentially, one may deal with a shorter-depth state preparation and deals with a simpler optimization problem.

From this perspective, the NQS certainly seems to be a promising option to investigate. For instance it has been shown that an RBM state could be mapped to the powerful matrix product states commonly used in condensed matter physics, but uses variational parameters more economically⁷⁷. Additionally, it is also known that a fully-connected RBM ansatz satisfies an entanglement volume scaling. Thus, it is very intriguing to further investigate whether one can exploit these properties to minimize number of variational parameters under a realistic setting. While the long-range connectivity between qubits is not necessarily easy to realize in many quantum hardwares at the moment; it is at least experimentally feasible with one of the leading hardware architectures, the ion-trap-based quantum computers^95,96 having all-to-all connectivity among qubits. Theoretically, one may also design quantum algorithms based on the deep Boltzmann machines⁹⁷ that further elevates the expressive power of Boltzmann machine architectures with only short-range couplings suitable for quantum hardware featuring local connectivity among qubits.

In this work, we set out to improve the existing NQS state-preparation protocol in the quantum circuits. As mentioned in the introduction, prior quantum algorithms using RBM ansatz suffer from several obstacles that prevents simulations for complex systems with many degrees of freedom. Our proposed state-preparation protocols have significantly expanded the scope of applications for NQS as an ansatz for quantum simulations and lowered the experimental barriers. By including complex-valued parameters into the RBM-NQS, the proposed quantum algorithm is capable of simulating some important quantum materials and quantum dynamics⁹⁸. Our numerical testings manifest encouraging signs that the NQS ansatz performs remarkably well across a variety of systems of practical and theoretical interests. Due to the qubit-recycling scheme, we reduce the number of required qubits from ${\mathcal{O}}(N+M)$ in previous works down to ${\mathcal{O}}(N)$ with sequential implementations of visible–hidden layer interactions. By imposing ${W}_{ij}=i{W}_{ij}^{\,\text{I}\,}$, we avoid the probabilistic preparation of inter-layer couplings, further improving the practicality of NQS-based simulations. The ensemble state preparation bypasses the post-selection on hidden spins.

Additionally, the circuit depth of preparing a unitary-coupled RBM state scales as ${\mathcal{O}}(NM)$ whereas the implementation for a standard RBM state either requires exponentially deep circuit or probabilitic post-selection of ancilla qubits. Finally, it has been previously shown that imaginary-time algorithm offers superior performance compared to VQE³⁴, but at the expense of more state preparations and measurements. In this work, we exploit the properties of RBM architecture and show that the number of different quantum states required in the imaginary-time algorithm could be reduced from ${\mathcal{O}}({N}_{var}^{2}) \sim {\mathcal{O}}({(NM)}^{2})$ down to just one circuit like the standard gradient descent for VQE. However, unlike standard VQE cases, the Monte Carlo approach for observable estimation allows us to perform measurement in one fixed basis for the Pauli operators. Since the variational Monte Carlo requires efficient estimation of ratios of wave function amplitudes which might not be possible for arbitrary wave-function anasatz such as the hardware efficient ones. Hence, the experimental costs for NQS-ITE is comparable to what standard VQE with UCC or hardware efficient ansatz demands if not significantly cheaper. Since Boltzmann machine is a widely used machine-learning model with many applications, we expect the HQC paradigm building on the Monte Carlo framework and the NQS ansatz in this work can be adopted for solving other important problems, such as discrete optimizations and machine learning.

Methods

RBM as trial wave function

Recently, Troyer and Carleo⁶² used the RBM neural-network architecture as wave-function ansatz to model many-body physics and attained impressive results. Since then, several other wave-function ansatz inspired by neural-network architecture have been explored. Collectively, we now refer to this set of wave-function ansatzs as the NQS. Although, in this work, we only consider RBM-NQS, which is particularly convenient to model quantum systems composed of two-level systems (TLSs) such as spin lattice commonly studied in condensed matter physics and quantum chemistry problems formulated in terms of qubits. For these systems, each TLS is directly identified with a visible spin in the corresponding RBM model. The entanglement between these TLSs (or visible spins) is mediated by the pairwise interactions between visible and hidden spins. In short, a many-body wave function in the NQS form reads

$$\left|{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle =\frac{1}{{N}_{\mathrm v}}\sum _{{\bf{v}}}\left(\sum _{{\bf{h}}}{\mathrm e}^{{E}_{\theta }({\bf{v}},{\bf{h}})}\right)\left|{\bf{v}}\right\rangle ,$$

(16)

with energy function E_θ(v, h) = ∑_ib_iv_i + ∑_jm_jh_j + ∑_ijW_ijv_ih_j, its complex conjugate ${\bar{E}}_{\theta }({\bf{v}},{\bf{h}})$, and the normalization constant ${N}_{v}=\sqrt{{\sum }_{{\bf{v}}}\left({\sum }_{{\bf{h}}}{\mathrm e}^{{\bar{E}}_{\theta }({\bf{v}},{\bf{h}})}\right)\left({\sum }_{{\bf{h}}}{\mathrm e}^{{E}_{\theta }({\bf{v}},{\bf{h}})}\right)}$. The RBM parameters are collectively denoted by θ = {b, m, W}. As shown in Eq. (16), the hidden spins are summed over in the bracket on the right-hand side of Eq. (16) to give a wave function $\left|{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle$ for the visible spins, which represent the physical system of interest. In principle, θ should possess non-vanishing imaginary components to describe complex-valued wave function.

To prepare an NQS in a quantum circuit, we should take the energy function E_θ(v, h) and promote it to an Hermitian operator by replacing the binary values of v and h with the corresponding Pauli operators. The quantum-circuit analog of Eq. (16) is decomposed into Eqs. (1) and (2): first entangle the visible and hidden spins and then post-selects the hidden spins to mediate the desire non-unitary transformation on the visible-spin wave functions.

Initial state preparation for quantum simulations

The NQS ansatz can be used in conjunction with most HQC simulation algorithms in addition to the time-dependent variational method outlined above. All these methods aim to solve highly non-trivial optimization in which the quality of solutions or the convergence rate depends crucially on the overlap of the initial state with the ground state $\left|{{{\Psi }}}_{\mathrm {gs}}\right\rangle$. The two-stage initialization protocols described here gives a systematic approach to guide the preparation of high-quality initial states. In short, the idea is to selectively optimize a subset of parameters to obtain an approximate solution that could be used as the initial state in a subsequent simulation optimizing over all parameters.

In the simplest case, one may consider a mean-field approximation, which restricts the considerations to completely factorized product-state wave function $|{{{\Psi }}}_{\mathrm {v}}^{\,\text{0}\,}(\overrightarrow{b})\rangle =|{\psi }_{{v}_{1}}({b}_{1})\rangle \otimes \cdots \otimes |{\psi }_{{\mathrm {v}}_{N}}({b}_{N})\rangle$ for all visible spins in a quantum simulation. We then subsequently use $|{{{\Psi }}}_{\mathrm {v}}^{0}(\overrightarrow{b})\rangle$ as the starting point of another simulation in which the hidden spins are introduced along with corresponding parameters {m₁, ⋯ m_M, W₁₁, ⋯ W_NM} that collectively facilitate the formation of entangled NQS, $\left|{{{\Psi }}}_{\mathrm v}(\theta )\right\rangle$. We note the mean-field approximation (single-body physics problem) can be easily done on a classical computer.

Nevertheless, for strongly correlated systems, the product states are not guaranteed to support a high overlap with $\left|{{{\Psi }}}_{\mathrm {gs}}\right\rangle$. Instead of optimizing $\overrightarrow{b}$ (the mean-field approximation) in the first run, it will be beneficial to consider an NQS with specifically designed sparse connectivity. In the second-stage calculation, the fully-connected architecture will be restored as usual, and the total number of variational parameters scale as ${\mathcal{O}}(NM)$. An obvious question is how to decide the connectivity of this sparsely connected RBM architecture for the first-stage simulation, which needs to balance the expressive power of the variational ansatz and the complexity of the optimization tasks. For lattice systems, one may consider short-range RBMs that constitute a special class of the well-established entangled-plaquette states⁷². In this case, the total number of variational parameters scale as ${\mathcal{O}}(N)$.

Simulation details for numerical studies

In all our simulations, we use a constant learning rate of 0.01. The variational parameters are initialized as Gaussian random numbers with mean zero and variance 0.01, except in cases where the initial conditions are obtained from mean-field solutions (Fig. 5, green dashed lines).

Hamiltonians of H₂, LiH and H₄

We treat the molecules in the minimal STO-3G basis and use PySCF to compute the integrals in the second quantization. The resulting fermionic Hamiltonians are subsequently mapped onto qubit Hamiltonians using Bravyi–Kitaev transformation with OpenFermion⁹¹. Due to the symmetry in H₂, the final Hamiltonian consists of 2 qubits⁹⁹, whereas the LiH and H₄ Hamiltonians contain 4 and 8 qubits, respectively.

Hamiltonian for TQD

For TQD simulations, we use the parameters from ref. ⁹⁴, i.e. t = −0.23 meV, g^* = −0.44, E_i = −∣t∣, and ϕ/B = 1.25T⁻¹. We consider two cases in Fig. 4: (a) U_i = 50∣t∣, V_ij = 10∣t∣ (strongly localized case), and (b) U_i = 0.5∣t∣, V_ij = 0.1∣t∣ (non-perturbative regime). We use Bravyi–Kitaev transformation to map the Hubbard Hamiltonian onto a qubit Hamiltonian using OpenFermion.