Keplerian trigonometry

Abstract

Taking the hint from usual parametrization of circle and hyperbola, and inspired by the pathwork initiated by Cayley and Dixon for the parametrization of the “Fermat” elliptic curve $x^3+y^3=1$, we develop an axiomatic study of what we call “Keplerian maps”, that is, functions ${{\,\mathrm{{\mathbf {m}}}\,}}(\kappa )$ mapping a real interval to a planar curve, whose variable $\kappa$ measures twice the signed area swept out by the O-ray when moving from 0 to $\kappa$. Then, given a characterization of k-curves, the images of such maps, we show how to recover the k-map of a given parametric or algebraic k-curve, by means of suitable differential problems.

1 Introduction

In recent years, there has been widespread interest in the possible generalizations of the circular functions. These generalizations are divided into two different lines of thought, depending on the possible fields of application. Some authors, like [7,8,9,10, 13,14,15,16,17, 22], taking the moves from the definition of the sine function as inverse of the arcsine function, introduced by the integral

$$\begin{aligned} J(u):=\int _0^u(1-t^2)^{-1/2} \mathrm{d}t \end{aligned}$$

(where u is precisely the arc length of the circle), define the function $\sin _p(x)$, where $p\ge 1$, as the inverse of the function

$$\begin{aligned} J_p(u):=\int _0^u(1-t^p)^{-1/p} \mathrm{d}t, \end{aligned}$$

(1)

and then define the function $\cos _p$ by placing $\cos _p:=\sin '_p$: in this manner, they get the identity $|\sin _p|^p+|\cos _p|^p=1$. This approach is motivated by some analytical properties of these functions, since, adding a second parameter q, the functions

$$\begin{aligned} J_{p,q}(u):=\int _0^u(1-t^q)^{-1/p} \mathrm{d}t, \end{aligned}$$

are related to the determination of eigenvalues of boundary value problem involving the p, q-Laplacian (see [13], eq. (3.9)), i.e. for a problem of the form

$$\begin{aligned} {\left\{ \begin{array}{ll} -\left( \left| u'\right| ^{p-2}\right) ' =\lambda \left| u\right| ^{q-2}u\\ u(a)=u(b)=0. \end{array}\right. } \end{aligned}$$

With such approach, the parameter u in equation (1) loses its geometric meaning.

On the other side, following the work initiated by Cayley and Dixon [1, 5, 6] related to Fermat’s cubic, $x^3+y^3=1$, generalized by [11] and more recently in [3, 18, 19, 21, 23, 24] to Fermat curves with arbitrary exponent, other authors define the function pair $(\cos _p,\sin _p)$ as the unique solution to the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi '=-\psi ^{p-1},\quad &{}\phi (0)=1\\ \psi '=\phi ^{p-1},\quad &{}\psi (0)=0 \,\,\,. \\ \end{array}\right. } \end{aligned}$$

(2)

Such pair of function, as it is easily seen, satisfies the identity $\sin _p^p+\cos _p^p=1.$

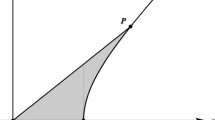
Although our approach is in line with the latter, we consider the problem from a more general point of view, that goes well beyond Fermat’s cubic and Dixon’s elliptic functions. In fact, having realized that the variable of the solution $(\cos _p,\sin _p)$ to problem (2) measures an area, as for trigonometric and hyperbolic functions, we present a general approach to what we call “Keplerian Trigonometry”, that is, the study of a wide class of planar curves admitting a (unique!) parametric representation ${{\,\mathrm{{\mathbf {m}}}\,}}_{\mathscr {C}}(\kappa ) = \cos _{\mathscr {C}}(\kappa )\,\mathbf {i}+ \sin _{\mathscr {C}}(\kappa )\,\mathbf {j}$, whose components share various properties of usual trigonometric functions, and the parameter $\kappa$ measures twice the signed area swept out by the OP-ray when the point P moves along the curve from the unit point of the X-axis.

Our work also includes a section dedicated to a combinatoric version of the problem with a combinatorics of the nonlinear differential system that takes up the particular cases of Fermat curves treated in [24].

In conclusion of the article, we apply the theoretical results to a pair of third-degree (elliptic) plane curves, linked in a similar way to that which connects trigonometric and hyperbolic functions.

2 Keplerian maps

An analytic vector function ${\mathbf {f}}(s) {:}{=}f_x(s)\,\mathbf {i}+ f_y(s)\,\mathbf {j}$¹, defined on a real interval I, will be called a planar map, or simply a map, and its image ${\mathscr {C}} {:}{=}{\mathbf {f}}(I)$ will be called a parametric curve, or p-curve. Obviously, a second map ${\mathbf {g}}$, defined on the real interval J, parametrizes the same curve $\mathscr {C}$ if, and only if, if there exists a differentiable bijective function $s(t):J \rightarrow I$ such that $s' \ne 0$ and ${\mathbf {g}}(t) = {\mathbf {f}}(s(t))$. Note that, by our definition, every p-curve consists of only one branch.

In order to focus a wide class of maps that behave like the trigonometric map

and the hyperbolic map

we observe that, in addition to mapping 0 to $\,\mathbf {i}$, for both of them, the variable is Keplerian, that is, it renders twice the signed area swept out by the OP-ray when moving from the unit point $U_x$ of the X-axis to the image of $\kappa$. Hence, it seems natural to consider the class of maps sharing that properties.

To provide a more precise wording of our aim, it is helpful to define the wedge operation $\wedge :{\mathbb {R}}^2 \times {\mathbb {R}}^2 \rightarrow {\mathbb {R}}$ by setting, for every ${\mathbf {u}}, {\mathbf {v}} \in {\mathbb {R}}^2$:

$$\begin{aligned} \mathbf {u}\wedge \mathbf {v}:= \det \begin{bmatrix} u_x &{}\quad v_x\\ u_y &{}\quad v_y \end{bmatrix}. \end{aligned}$$

The scalar $\mathbf {u}\wedge \mathbf {v}$ measures the signed area of the oriented parallelogram with sides $\mathbf {u}, \mathbf {v}$. The fact of being Keplerian the variable $\kappa$ of a map ${\mathbf {f}}$, is expressed by the identity

$$\begin{aligned} \mathop {}\!\mathrm {d}\kappa = {\mathbf {f}} (\kappa ) \wedge {\mathbf {f}} (\kappa +\mathop {}\!\mathrm {d}\kappa ), \end{aligned}$$

or better, by its equivalent²

$$\begin{aligned} {\mathbf {f}} \wedge {\mathbf {f}}' = 1. \end{aligned}$$

Here then, the maps of this new class are defined as follows.

Definition 2.1

A map ${{\,\mathrm{{\mathbf {m}}}\,}}:\!I \rightarrow {\mathbb {R}}^2$, where $0 \in I$, satisfying the following “Keplerian analytic axioms”

is called a Keplerian map (k-map for short). A k-map ${{\,\mathrm{{\mathbf {m}}}\,}}$ is called upright if the derivative of its first component vanishes at 0, that is, if $m'_x(0) = 0$.

The image of a k-map ${{\,\mathrm{{\mathbf {m}}}\,}}$ is called a Keplerian curve or k-curve. $\square$

In order to emphasise the analogy with trigonometric functions, the components of the k-map of a given k-curve ${\mathscr {C}}$ are denoted as $\cos _{{\mathscr {C}}}$ and $\sin _{{\mathscr {C}}}$, that is, we will set:

$$\begin{aligned} {{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {C}}}(\kappa ) = \cos _{{\mathscr {C}}}(\kappa )\,\,\mathbf {i}+ \sin _{\mathscr {C}}(\kappa )\,\mathbf {j}\,. \end{aligned}$$

We will refer to the component $\sin _{{\mathscr {C}}}$ as to a $\sin$-partner of $\cos _{{\mathscr {C}}}$, and symmetrically for the component $\cos _{{\mathscr {C}}}$.

Thanks to the identity $(\mathbf {f}\wedge \mathbf {f'})' =\mathbf {f}'\wedge \mathbf {f'}+\mathbf {f}\wedge \mathbf {f''} =\mathbf {f}\wedge \mathbf {f''}$, the Keplerian axioms can be restated in terms of the second derivative.

Theorem 2.2

A map ${{\,\mathrm{{\mathbf {m}}}\,}}:\!I \rightarrow {\mathbb {R}}^2$, where $0 \in I$, is a Keplerian map, whenever it satisfies the following axioms:

$\square$

Axiom (AnK 2) states that vectors ${{\,\mathrm{{\mathbf {m}}}\,}}(\kappa )$ and ${{\,\mathrm{{\mathbf {m}}}\,}}''(\kappa )$ are parallel, so there exists an analytic function $\chi (\kappa )$ such that ${{\,\mathrm{{\mathbf {m}}}\,}}''(\kappa ) = \chi (\kappa ) {{\,\mathrm{{\mathbf {m}}}\,}}(\kappa )$, where

$$\begin{aligned} \chi = \chi {{\,\mathrm{{\mathbf {m}}}\,}}\wedge {{\,\mathrm{{\mathbf {m}}}\,}}' = {{\,\mathrm{{\mathbf {m}}}\,}}'' \wedge {{\,\mathrm{{\mathbf {m}}}\,}}'. \end{aligned}$$

Actually, the preceding theorem has the following result as converse.

Theorem 2.3

Let $\chi :I \rightarrow {\mathbb {R}}$ be an analytic function such that $0\in I$; then there exists exactly one Keplerian map ${{\,\mathrm{{\mathbf {m}}}\,}}$ such that ${{\,\mathrm{{\mathbf {m}}}\,}}''(\kappa ) = \chi (\kappa ) {{\,\mathrm{{\mathbf {m}}}\,}}(\kappa )$ for every $\kappa \in I$.

Proof

The k-map ${{\,\mathrm{{\mathbf {m}}}\,}}$ is the solution of the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} {\mathbf {p}}'' = \chi \,{\mathbf {p}},\\ &{} {\mathbf {p}}(0) = \,\mathbf {i},\\ &{} {\mathbf {p}}(0)\wedge {\mathbf {p}}'(0)=1. \end{array}\right. } \end{aligned}$$

(3)

$\square$

The preceding result is the Keplerian analog of the fundamental theorem of the local theory of curves; here the function $\chi$ plays the role of the curvature: then, it seems to be consistent to call $\chi$ the Keplerian curvature of the curve ${\mathscr {C}}$.

The following result, whose proof is quite elementary, characterises the k-curves, by showing how the (unique) k-map associated to a suitable p-curve can be computed by inverting an integral.

Theorem 2.4

A parametric curve ${\mathscr {C}} = {\mathbf {f}} (I)$ is a Keplerian curve if, and only if, there exists $s_0 \in I$ such that

$$\begin{aligned} {\mathbf {f}} (s_0) = \,\mathbf {i}, \end{aligned}$$

and, for every $s \in I$:

$$\begin{aligned} {\mathbf {f}} (s) \wedge {\mathbf {f}}' (s) \ne 0. \end{aligned}$$

Moreover, the Keplerian map which parametrize ${\mathscr {C}}$ is provided by the map

$$\begin{aligned} {{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {C}}}(\kappa ) {:}{=}{\mathbf {f}}(s(\kappa )), \end{aligned}$$

where $s(\kappa )$ is the inverse of the function

$$\begin{aligned} \kappa (s) {:}{=}\int _{s_0}^s {\mathbf {f}}(u) \wedge {\mathbf {f}}'(u) \mathop {}\!\mathrm {d}u. \end{aligned}$$

$\square$

The preceding result can be restated in terms of elementary geometry, by saying that a k-curve has a unique branch, it includes the unit point $U_x$, and every its tangent line avoids the origin (Figs. 1, 2, 3 and 4).

As an application of the previous result, let us consider the unit circle involute ${\mathscr {C}}$, image of the map

$$\begin{aligned} {\mathbf {f}}(t) {:}{=}(\cos t + t \sin t)\,\mathbf {i}+(\sin t - t \cos t)\,\mathbf {j}, \,\,\, t \ge 0. \end{aligned}$$

We get    ${\mathbf {f}} \wedge {\mathbf {f}}'=t^2$,    then    $\kappa =t^3/3$,    $t = (3\kappa )^{1/3}$, and ${{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {C}}}(\kappa ) = {\mathbf {f}}(3\kappa )^{1/3}$.

Fig. 1

A keplerian curve

Fig. 2

A non keplerian curve

Fig. 3

The Keplerian parameter

Fig. 4

The unit circle involute

3 General identities

For any given k-curve ${\mathscr {C}}$, we will set $\tan _{{\mathscr {C}}}:= \sin _{{\mathscr {C}}}/\cos _{{\mathscr {C}}}$; however, we need to remark that the geometric meaning of the trigonometric tangent function is preserved only in case of upright k-curves.

As easy consequences of Keplerian axioms, we have the identities

$$\begin{aligned} \sin '_{{\mathscr {C}}}(0)&=1,\quad&\sin ''_{{\mathscr {C}}}(0)&=\sin _{{\mathscr {C}}}(0)=0,\\ \tan _{{\mathscr {C}}}'(0)&=1,\quad&\tan _{{\mathscr {C}}}''(0)&=\tan _{{\mathscr {C}}}(0)=0. \end{aligned}$$

Moreover, it is worthwhile to note that a k-curve ${\mathscr {C}}$ is a upright one if, and only if, $\cos '_{\mathscr {C}}(0)=0$. Again, from (AnK 2) we get immediately the following identities, which generalize well-known relations of circular and hyperbolic functions:

$$\begin{aligned} \tan _{{\mathscr {C}}}(\kappa )&=\frac{\sin _{{\mathscr {C}}}(\kappa )}{\cos _{{\mathscr {C}}}(\kappa )} =\frac{\sin ''_{{\mathscr {C}}}(\kappa )}{\cos ''_{{\mathscr {C}}}(\kappa )},\\ \tan '_{{\mathscr {C}}}(\kappa )&=\frac{1}{\cos ^2_{{\mathscr {C}}}(\kappa )},\\ \tan _{{\mathscr {C}}}(\kappa )&=\int _0^{\kappa }\frac{1}{\cos ^2_{{\mathscr {C}}}(u)}\mathop {}\!\mathrm {d}u ,\\ \sin _{{\mathscr {C}}}(\kappa )&=\cos _{{\mathscr {C}}}(\kappa )\int _0^{\kappa } \frac{1}{\cos ^2_{{\mathscr {C}}}(u)}\mathop {}\!\mathrm {d}u. \end{aligned}$$

By the last identity, every analytic function x(t), with $x(0)=1$, has exactly one $\sin$-partner; on the contrary, any analytic function y(t), with $y(0)=0, y'(0)=1,y''(0)=0$, admitting a $\cos$-partner x(t), has all functions $x(t)+\mu y(t)$ as additional $\cos$-partner. Obviously, “monogamy” is restored when the search of partnership is restricted to upright $\cos$-partners.

By axiom (AnK 1), any point ${\overline{P}} := {{\,\mathrm{{\mathbf {m}}}\,}}_{\mathscr {C}}(\overline{\kappa })$ of the curve ${\mathscr {C}}$ belongs to the line $\sin '_{{\mathscr {C}}}(\overline{\kappa })\,x - \cos '_{\mathscr {C}}(\overline{\kappa })\,y = 1$, which turns to be the tangent line to ${\mathscr {C}}$ at ${\overline{P}}$, intersecting the X-axis at $1/\sin '_{{\mathscr {C}}}(\overline{\kappa })$ and the Y-axis at $-1/\cos '_{{\mathscr {C}}}(\overline{\kappa })$. By this fact, we are led to define the secant and cosecant functions for the k-curve ${\mathscr {C}}$ by setting

$$\begin{aligned} \sec _{{\mathscr {C}}}(\kappa )&:= \frac{1}{\sin '_{{\mathscr {C}}}(\kappa )},\\ \csc _{{\mathscr {C}}}(\kappa )&:= -\frac{1}{\cos '_{{\mathscr {C}}}(\kappa )}. \end{aligned}$$

Remark that for the circle and the hyperbola such definitions return the usual secant and cosecant functions.

Finally, we remark that if ${\mathscr {C}}$ is a closed k-curve, its k-map is a periodic function, whose fundamental period $\Pi _{{\mathscr {C}}}$ is twice the area $\pi _{{\mathscr {C}}}$ of the region bounded by $\mathscr {C}$.

4 The arithmetic axioms—formal Keplerian maps

The analytic Keplerian axiom has a useful arithmetic counterpart.

Theorem 4.1

(The Arithmetic Keplerian Axioms) An analytic vector function $\mathbf {f}(t) {:}{=}\sum _i x_i\frac{t^i}{i!}\,\mathbf {i}+ \sum _i y_i\frac{t^i}{i!}\,\mathbf {j}$ is a Keplerian map if, and only if, the following identities hold:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\displaystyle \sum _{\begin{array}{c} i+j=h\\ h\ge 2 \end{array}}\,(j-i) \left( {\begin{array}{c}h\\ i\end{array}}\right) \, x_{i} \,y_{j}=0, \\ &{} x_{0} = y_{1} = 1,\\ &{}y_{0} = y_{2} = 0 \;. \end{array}\right. } \end{aligned}$$

(ArK)

Proof

Let ${{\,\mathrm{{\mathbf {f}}}\,}}(t)\wedge {\mathbf {f}}'(t) = \sum _i w_i\tfrac{t^i}{i!}$; then, for every $h\in {\mathbb {N}}$, we have:

$$\begin{aligned} w_h&= {{\,\mathrm{D\,}\,}}^h\bigl (x (t)y'(t) -x'(t) y(t)\bigr )\Bigl |_{t=0} = \sum _{i+j=h}\left( {\begin{array}{c}h\\ i\end{array}}\right) \Bigl ( x_i\,y_{j+1}- x_{i+1}\,y_j \Bigr ) \\&= \sum _{i+j=h}\frac{h+1-i}{h+1}\left( {\begin{array}{c}h+1\\ i\end{array}}\right) x_i\,y_{j+1} - \sum _{i+j=h}\frac{h+1-j}{h+1}\left( {\begin{array}{c}h+1\\ i\end{array}}\right) x_{i+1}\,y_j\\&= \frac{1}{h+1}\,\sum _{i+j=h+1}(j-i)\,\left( {\begin{array}{c}h+1\\ i\end{array}}\right) x_i y_j , \end{aligned}$$

and the statement follows immediately. $\square$

This new dress of the Keplerian Axioms evokes the opportunity to neglect convergence problems, by enlarging our concern to pairs of formal (exponential) series; to do that, we define a formal Keplerian map as an ordered pair

$$\begin{aligned} {{\,\mathrm{{\mathbf {f}}}\,}}(t) \,{{:}{=}}\, \left( \sum _i x_i\frac{t^i}{i!},\sum _i y_i\frac{t^i}{i!}\right) , \end{aligned}$$

satisfying the Arithmetic Keplerian Axioms.

The following statement is an immediate outcome of Theorem 4.1.

Corollary 4.2

Let ${{\,\mathrm{{\mathbf {f}}}\,}}(t) \,{{:}{=}}\, \Bigl (\sum _i x_i\frac{t^i}{i!},\sum _i y_i\frac{t^i}{i!}\Bigr )$ be a formal k-map; then, the following identities hold:

$$\begin{aligned} y_h = \frac{1}{h} \sum _{ \begin{array}{c} i+j=h \\ 0 \ne j \ne h \end{array} } (i-j)\left( {\begin{array}{c}h\\ i\end{array}}\right) \,x_i y_j, \quad \text {for every }h\ge 2, \end{aligned}$$

(4)

and, for every $h\ge 3$:

$$\begin{aligned} x_{h-1} =\frac{1}{h(h-2)} \sum _{ \begin{array}{c} i+j=h \\ 0 \ne j\ne 1 \end{array} } (j-i)\left( {\begin{array}{c}h\\ i\end{array}}\right) \,x_i y_j, \quad \text {for every }h\ge 3. \end{aligned}$$

(5)

$\square$

Identity (4) allow us to compute the unique sin-partner y(t) of any formal series x(t) with $x_0=1$; note that in any case will be $y_2=0$. Similarly, identity (5) can be employed to compute a cos-partner x(t) of any sequence y(t), with $y_0=0, y_1=1, y_2=0$, only after the choice of $x_1\in \mathbb R$.

As an application, let us compute the $\sin$-partner y(t) of the function $x(t) {:}{=}1+ a\tfrac{t^n}{n!}$; Theorem 4.1 forces the identities

$$\begin{aligned}&y_1=1,\\&y_{n+1}=(n-1)a,\\&y_i=0\quad \quad \text {whenever}\quad i{\ne } 1\!\!\!\pmod {n},\\&y_{(j+1)n+1}= - a\frac{\bigl ((j-1)n+1\bigr )}{n!} \frac{\bigl ((j+1)n\bigr )!}{(jn+1)!}\,y_{jn+1}\,. \end{aligned}$$

The series y(t) can be now redrafted as follows:

$$\begin{aligned} y(t)&= \sum _{j\ge 0} y_{jn+1}\frac{t^{jn+1}}{(jn+1)!}\\&= \sum _{j\ge 0} \frac{(-n+1)}{\bigl ((j-1)n+1\bigr )} \frac{(jn)!}{(n!)^j}(-a)^j\frac{t^{jn+1}}{(jn+1)!}\\&= t\sum _{j\ge 0} \frac{(-n+1)}{\bigl ((j-1)n+1\bigr )} \frac{j!}{(jn+1)}\frac{(-at^n/n!)^j}{j!}. \end{aligned}$$

As the ratio r(j) of two consecutive coefficients in the last series is the rational function $r(j) = {(j+\frac{1}{n}-1)(j+1)}/{(j+\frac{1}{n}+1)},$ we infer that such series is the Gauss hypergeometric function

$$\begin{aligned} y(t) = t \,_2\mathrm{F}_1 \!\! \left( \left. \genfrac{}{}{0.0pt}0{\frac{1}{n}-1,1}{\frac{1}{n}+1}\right| -a\,\frac{t^n}{n!}\right) . \end{aligned}$$

5 Finding the k-map of an algebraic curve

Our purpose is now to extend the preceding ideas to algebraic curves. Obviously, in this case, too, we must narrow our attention to Keplerian algebraic curves, that is, to algebraic curves containing the point $U_x$, whose tangent lines avoid the origin; this second condition is equivalent to claim that for every point $P{:}{=}(x,y)$ in ${\mathscr {C}}$ vectors OP and $\nabla f$ are not perpendicular, that is: $x f_x + y f_y \ne 0$.

The following theorem characterises k-algebraic curves and shows that the unique k-map of a given k-algebraic curve is the solution of a first-order differential problem.

Theorem 5.1

Let the function $f :{\mathbb {R}}^2 \rightarrow {\mathbb {R}}$ satisfy conditions $f(1,0) = 0$ and $x f_x + y f_y \ne 0$; then the algebraic curve ${\mathscr {C}} \,{{:}{=}}\, \{ (x,y)\in \mathbb {R}^2\mid \,f(x,y)=0 \}$ is Keplerian, and its k-map is the solution ${{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {C}}}$ of the differential system

$$\begin{aligned} {\left\{ \begin{array}{ll} x' =-\dfrac{f_y}{xf_x+yf_y},\quad x(0)=1, \\ y' = \dfrac{f_x}{xf_x+yf_y},\quad \quad y(0)=0 . \end{array}\right. } \end{aligned}$$

(6)

Proof

Conditions on f ensure that ${\mathscr {C}}$ is a Keplerian curve.

The solution ${\mathbf {p}}(t) = x(t)\,\mathbf {i}+ y(t)\,\mathbf {j}$ of system (6) is a k-map, as ${\mathbf {p}}(0) = \,\mathbf {i}$, and ${{\mathbf {p}} \wedge {\mathbf {p}}' =1}$.

Moreover, we have $f\bigl (x(0),y(0)\bigr )=0$ and $\tfrac{\mathop {}\!\mathrm {d}^{} f }{\mathop {}\!\mathrm {d}{t}^{}} = f_x \tfrac{\mathop {}\!\mathrm {d}^{} x }{\mathop {}\!\mathrm {d}{t}^{}} + f_y \tfrac{\mathop {}\!\mathrm {d}^{} y }{\mathop {}\!\mathrm {d}{t}^{}} = 0,$ hence, for every t in a suitable neighbourhood of 0, it is $f\bigl (x(t),y(t)\bigr )=0$, and ${\mathbf {p}} = {{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {C}}}$. $\square$

Differentiating the system (6), and after some elementary calculus, we obtain a second rule for computing the k-map of a k-algebraic curve.

Theorem 5.2

The k-map of a Keplerian algebraic curve ${\mathscr {C}} \,{{:}{=}}\, \{ (x,y)\in \mathbb {R}^2\mid \,f(x,y)=0 \}$ is the solution of the second-order problem

$$\begin{aligned} {\left\{ \begin{array}{ll} x'' = -f\!_{\vartriangle } x, \quad x(0) = 1\\ y'' = -f\!_{\vartriangle } y, \quad y(0) = 0, \quad y'(0) = 1, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} f\!_{\vartriangle }&{:}{=}\frac{f_{xx}f_y^2 -2f_{xy}f_xf_y + f_{yy}f_x^2}{(xf_x+yf_y)^3}\\&= \frac{ [{\begin{matrix} -f_{y}&f_{x} \end{matrix}}] \bigl [{\begin{matrix} f_{xx}&{}f_{xy}\\ f_{xy}&{}f_{yy} \end{matrix}}\bigr ] \bigl [{\begin{matrix} -f_{y}\\ f_{x} \end{matrix}}\bigr ] }{(x f_x+y f_y)^3}. \end{aligned}$$

$\square$

Note that the function $-f\!_{\vartriangle }$ is precisely the Keplerian curvature of ${\mathscr {C}}$ and the numerator is called offline hessian.

5.1 p-algebraic curves

When the curve ${\mathscr {C}}$ has equation $f(x,y) = 1$, where f is the irreducible homogeneous polynomial

$$\begin{aligned} f(x,y) {:}{=}\sum _{i=0}^p f_ix^{p-i}y^i \quad f_0=1 , \end{aligned}$$

we have $xf_x+yf_y=p$ , and the system (6) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = -\tfrac{1}{p} f_y \quad &{}x(0)=1, \\ y' =\tfrac{1}{p} f_x\quad &{}y(0)=0, \end{array}\right. } \end{aligned}$$

(7)

showing that the derivatives of $x=\cos _{{\mathscr {C}}}$ and $y=\sin _{\mathscr {C}}$ are the homogeneous polynomials

$$\begin{aligned} x'&= -\tfrac{1}{p}\sum _{i=1}^p if_i\,x^{p-i}y^{i-1},\\ y'&= \tfrac{1}{p}\sum _{i=0}^{p-1} (p-i)f_i\,x^{p-i-1}y^i, \end{aligned}$$

of degree $p-1$³. By repeatedly differentiating, we obtain the following theorem.

Theorem 5.3

Let the ${\mathscr {C}} {:}{=}\{ f(x,y)=1 \}$ where f is the irreducible homogeneous polynomial

$$\begin{aligned} f(x,y) {:}{=}\sum _{i=0}^p f_ix^{p-i}y^i \quad f_0=1; \end{aligned}$$

then, the nth derivatives of $x=\cos _{{\mathscr {C}}}$ and $y=\sin _{{\mathscr {C}}}$ are homogeneous polynomials of degree $n(p-2)+1$ in variables x, y. Furthermore, for every natural m, n, we will have

$$\begin{aligned} (x^m y^n)' = \tfrac{1}{p}\sum _{i=0}^p \left( n(p-i)-mi\right) f_ix^{m+p-i-1}y^{n+i-1}. \end{aligned}$$

(8)

$\square$

Let us now define the the ${\mathbb {N}} \times {\mathbb {N}}$ matrix ${\mathfrak {M}}_{\cos _{{\mathscr {C}}}}$ by setting ${\mathfrak {M}}_{\cos _{\mathscr {C}}}(0,i) {:}{=}\delta _{0,i}$ and by neatly arranging in the nth row the coefficients of the nth derivative of $\cos _{{\mathscr {C}}}$; then, the coefficients of Maclaurin series of $\cos _{{\mathscr {C}}}$ are the entries in the 0th column of ${\mathfrak {M}}_{\cos _{{\mathscr {C}}}}$, which can be recursively computed by the inverse of the law in identity (8). Analogous arguments hold for the matrix ${\mathfrak {M}}_{\sin _{{\mathscr {C}}}}$, defined by setting ${\mathfrak {M}}_{\sin _{{\mathscr {C}}}}(0,i) {:}{=}\delta _{1,i}$.

6 Some applications

6.1 A “dumpy”  cubic

As an instance of application of preceding equations, let us consider the smooth cubic ${\mathscr {D}}$ of cartesian equation

$$\begin{aligned} x^3+3xy^2-1=0. \end{aligned}$$

Such k-curve is projectively closed and symmetric with respect to the X-axis⁴: consequently, $\cos _{{\mathscr {D}}}\kappa {=}{:}\sum _i c_i\frac{\kappa ^i}{i!}$ is an even function, while $\sin _{{\mathscr {D}}}\kappa {=}{:}\sum _i s_i\frac{\kappa ^i}{i!}$ is odd (Figs. 5 and 6). The flexes of ${\mathscr {D}}$ are the points $\bigl (\tfrac{\root 3 \of {2}}{2},\pm \tfrac{\root 3 \of {2}}{2}\bigr )$ and the improper point of Y-axis; the inflectional tangent lines are $x=0$ and $x\pm y=\root 3 \of {2}$.

Fig. 5

The curve $x^3+3xy^2=1$

In our case, system (7) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} x'=-2xy, \quad x(0)=1,\\ y'=x^2+y^2, \quad y(0)=0, \end{array}\right. } \end{aligned}$$

(9)

from which we can derive that coefficients $c_i, s_i$ are integers; moreover, the building rule for both matrices $\mathfrak M_{\cos _{{\mathscr {D}}}}$ and ${\mathfrak {M}}_{\sin _{{\mathscr {D}}}}$ is

$$\begin{aligned} {\mathfrak {M}}(m,n) = (3n-2m-3) {\mathfrak {M}}(m-1,n-1) + (n+1) {\mathfrak {M}}(m-1,n+1). \end{aligned}$$

The following table shows some coefficients $c_i, s_i$ (Table 1), drawn from ${\mathfrak {M}}_{\cos _{{\mathscr {D}}}}$, ${\mathfrak {M}}_{\sin _{{\mathscr {D}}}}$, computed by means of a common spreadsheet⁵.

Table 1 First coefficients of $\cos _{{\mathscr {D}}}$ and $\sin _{{\mathscr {D}}}$

Now, let us find an analytic expression of the cosine component $\cos _{{\mathscr {D}}}$: differentiating the first equation in (9), and using the identity $x^3+3xy^2=1$, we obtain the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} x''=\dfrac{2}{3}\left( 1-4x^3\right) ,\\ x(0)=1,\quad x'(0)=0. \end{array}\right. } \end{aligned}$$

(10)

Integrating (10), we obtain the inverse cosine:

$$\begin{aligned} \kappa (x) = \frac{\sqrt{3}}{2}\int _x^1\frac{\mathop {}\!\mathrm {d}u}{\sqrt{u-u^4}}. \end{aligned}$$

(11)

Observe that condition $0 <x \le 1$ ensures that cosine is real valued. Using entry 259.50 page 134 of [4], the integral in (11) can be computed, obtaining

$$\begin{aligned} \kappa (x) = \root 4 \of {3}\,{{\,\mathrm{\mathrm {K}}\,}}(\sin \tfrac{\pi }{12}) - \frac{\root 4 \of {3}}{2} {{\,\mathrm{\mathrm {F}}\,}}\left( {{\,\mathrm{\mathrm {arcos}}\,}}\left( \tfrac{1-(\sqrt{3}+1)x}{1+(\sqrt{3}-1)x} \right) ,\sin \tfrac{\pi }{12} \right) , \end{aligned}$$

(12)

the complete and incomplete elliptic integral of first kind. Inverting, we can solve for x in (12) and obtain

$$\begin{aligned} \cos _{{\mathscr {D}}}(\kappa ) = x(\kappa ) = \frac{\sqrt{3} + 1}{\sqrt{3} + 2 - {\overline{\mathrm{cn}}}(\kappa )} \frac{1+{{\overline{\mathrm{cn}}}}(\kappa )}{2} , \end{aligned}$$

(13)

where for short we introduce:

$$\begin{aligned} {\overline{\mathrm{cn}}}(u) {:}{=}{\text {cn}}\left( \tfrac{2}{\root 4 \of {3}}\,u,\sin \tfrac{\pi }{12}\right) . \end{aligned}$$

Function $\sin _{{\mathscr {D}}}$ is obtained using the first equation in (9):

$$\begin{aligned} \sin _{{\mathscr {D}}}(\kappa )&= y(\kappa ) = -\frac{1}{2}\frac{x'(\kappa )}{x(\kappa )}\nonumber \\&= \root 4 \of {3} \,\, \frac{\sqrt{3} + 1}{\sqrt{3} + 2 - {\overline{\mathrm{cn}}}(\kappa ) } \frac{{\overline{\mathrm{sn}}}(\kappa ){\overline{\mathrm{dn}}}(\kappa )}{1+{\overline{\mathrm{cn}}}(\kappa ) } , \end{aligned}$$

(14)

where we define:

$$\begin{aligned} {\overline{\mathrm{sn}}}(u) {:}{=}{\text {sn}}\left( \tfrac{2}{\root 4 \of {3}}\,u,\sin \tfrac{\pi }{12}\right) ,\,\, {\overline{\mathrm{dn}}}(u) {:}{=}{\text {dn}}\left( \tfrac{2}{\root 4 \of {3}}\,u,\sin \tfrac{\pi }{12}\right) , \end{aligned}$$

and lastly:

$$\begin{aligned} \tan _{{\mathscr {D}}}(\kappa ) =2 \root 4 \of {3}\, \frac{{\overline{\mathrm{sn}}}(\kappa ){\overline{\mathrm{dn}}}(\kappa )}{\bigl (1+{\overline{\mathrm{cn}}}(\kappa )\bigr )^2}. \end{aligned}$$

Fig. 6

$\cos _{{\mathscr {D}}}$ and $\sin _{{\mathscr {D}}}$

Being the curve ${\mathscr {D}}$ projectively closed, its k-map ${{\,\mathrm{{\mathbf {m}}}\,}}_{\mathscr {D}}$ is periodic: with some advanced calculus it can be proven that the period is

$$\begin{aligned} \Pi _{{\mathscr {D}}} = 2\pi _{{\mathscr {D}}} = 4\int _0^1\sqrt{\frac{1-x^3}{3x}}\mathop {}\!\mathrm {d}x = \frac{1}{\root 3 \of {2}}{{\,\mathrm{\mathrm {B}}\,}}\left( \tfrac{1}{3},\tfrac{1}{3}\right) . \end{aligned}$$

On the other hand, identities (13) and (14) ensure that the period can also be given in terms of complete elliptic integral of first kind, as

$$\begin{aligned} \Pi _{{\mathscr {D}}} = 2\root 4 \of {3}\,{{\,\mathrm{\mathrm {K}}\,}}\! \left( \sin \tfrac{\pi }{12} \right) , \end{aligned}$$

in accordance with the fact that $\sin \tfrac{\pi }{12}$ is a singular modulus (see [20]).

Both the component of ${{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {D}}}$ are elliptic functions: then, their second (complex) period can be computed by starting from the classical periodicity relations for Jacobi elliptic functions (see [2] page 39):

$$\begin{aligned}&{\text {sn}}(u+2\mathrm {i}{{\,\mathrm{\mathrm {K}}\,}}') = {\text {sn}}u,\\&{\text {cn}}(u+2{{\,\mathrm{\mathrm {K}}\,}}+2\mathrm {i}{{\,\mathrm{\mathrm {K}}\,}}') ={\text {cn}}u,\\&{\text {dn}}(u+4\mathrm {i}{{\,\mathrm{\mathrm {K}}\,}}') = {\text {dn}}u, \end{aligned}$$

where, as usual, ${{\,\mathrm{\mathrm {K}}\,}}'(k)={{\,\mathrm{\mathrm {K}}\,}}(k')={{\,\mathrm{\mathrm {K}}\,}}(\sqrt{1-k^2})$. Thus, the second period is

$$\begin{aligned} \Pi _{{\mathscr {D}}}' = \root 4 \of {3}\, \left( {{\,\mathrm{\mathrm {K}}\,}}(\sin \tfrac{\pi }{12}) +\mathrm {i}{{\,\mathrm{\mathrm {K}}\,}}(\cos \tfrac{\pi }{12})\right) ; \end{aligned}$$

finally, by virtue of the singular modulus relation

$$\begin{aligned} {{\,\mathrm{\mathrm {K}}\,}}(\cos \tfrac{\pi }{12})=\sqrt{3}\,{{\,\mathrm{\mathrm {K}}\,}}(\sin \tfrac{\pi }{12}), \end{aligned}$$

we get

$$\begin{aligned} \Pi _{{\mathscr {D}}}' = \frac{1+\mathrm {i}\,\sqrt{3}}{2} \, 2\root 4 \of {3}\,{{\,\mathrm{\mathrm {K}}\,}}(\sin \tfrac{\pi }{12}) = \mathrm {e}^{\mathrm {i}\pi /3}\,\Pi _{{\mathscr {D}}}. \end{aligned}$$

In closure, the complete lattice $\Lambda _{{\mathscr {D}}}$ of periods of ${{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {D}}}$ is

$$\begin{aligned} \Lambda _{{\mathscr {D}}} = {\mathbb {Z}} \, \Pi _{{\mathscr {D}}} \oplus {\mathbb {Z}} \, \mathrm {e}^{\mathrm {i}\pi /3}\,\Pi _{{\mathscr {D}}}. \end{aligned}$$

6.2 The Humbert cubic

As a second example, let us now study the Keplerian smooth cubic ${\mathscr {H}}$ of equation

$$\begin{aligned} x^3-3xy^2-1=0. \end{aligned}$$

This cubic was studied by M.G. Humbert, in [12], Sect. 44 Eq. (7), who provided a parametrization in terms of Weierstrass $\wp$ function (Fig. 7).

The curve ${\mathscr {H}}$, also projectively closed, has symmetry axes $y=0, \,\,x=\pm \tfrac{\sqrt{3}}{3}y$; its inflexion points are improper, with $x=0, \,\, y=\pm \tfrac{\sqrt{3}}{3}x$, as inflexional lines⁶.

Fig. 7

The curve $x^3-3xy^2=1$

In this case, system (7), becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} x' = 2xy,\quad \quad x(0)=1,\\ y' = x^2 - y^2,\quad y(0)=0. \end{array}\right. } \end{aligned}$$

By implementing the same process followed in the preceding case, we can find the following analytic expression of the k-map ${{\,\mathrm{{\mathbf {m}}}\,}}_{\mathscr {H}}$

$$\begin{aligned} \cos _{{\mathscr {H}}}(\kappa )&=\frac{\sqrt{3}-1}{\sqrt{3} - 2 + {\underline{\mathrm{cn}}}(\kappa )} \,\frac{1+ {\underline{\mathrm{cn}}}(\kappa )}{2} \end{aligned}$$

(15)

$$\begin{aligned} \sin _{{\mathscr {H}}}(\kappa )&= \root 4 \of {3} \,\, \frac{\sqrt{3} - 1}{\sqrt{3} - 2 + {\underline{\mathrm{cn}}}(\kappa ) } \frac{{\underline{\mathrm{sn}}}(\kappa ){\underline{\mathrm{dn}}}(\kappa )}{1+{\underline{\mathrm{cn}}}(\kappa ) } , \end{aligned}$$

(16)

where

$$\begin{aligned} {\underline{\mathrm{cn}}}(u)&\,{{:}{=}}\, {\text {cn}}\left( \tfrac{2}{\root 4 \of {3}}\,u,\cos \tfrac{\pi }{12}\right) ,\\ {\underline{\mathrm{sn}}}(u)&\,{{:}{=}}\, {\text {sn}}\left( \tfrac{2}{\root 4 \of {3}}\,u,\cos \tfrac{\pi }{12}\right) ,\\ {\underline{\mathrm{dn}}}(u)&\,{{:}{=}}\, {\text {dn}}\left( \tfrac{2}{\root 4 \of {3}}\,u,\cos \tfrac{\pi }{12}\right) . \end{aligned}$$

Identities (15) and (16) ensure that the map ${{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {H}}}$ is periodic, with period

$$\begin{aligned} \Pi _{{\mathscr {H}}} = 2\root 4 \of {3}\,{{\,\mathrm{\mathrm {K}}\,}}\! \left( \cos \tfrac{\pi }{12} \right) = \sqrt{3}\,\Pi _{{\mathscr {D}}}. \end{aligned}$$

By considering that ${\mathscr {H}}$ is projectively closed, we can claim that the period of its k-map must equal twelve times the area of the region bounded by the curve and the lines $x=0$ and $y= \tfrac{1}{\sqrt{3}}x$; more precisely, accordingly to the fact that $\cos \tfrac{\pi }{12}$ is a singular modulus,

$$\begin{aligned} \Pi _{{\mathscr {H}}} = 12 \left( \frac{1}{2\sqrt{3}}+\int _1^\infty \biggl ( \frac{1}{\sqrt{3}}x-\sqrt{\frac{x^3-1}{3x}}\, \biggr ) \mathop {}\!\mathrm {d}x \right) = \frac{\sqrt{3}}{2}\,{{\,\mathrm{\mathrm {B}}\,}}\left( \tfrac{1}{3},\tfrac{1}{6}\right) . \end{aligned}$$

Also in this case, the components of ${{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {H}}}$ are both elliptic functions, with complex period

$$\begin{aligned} \Pi _{{\mathscr {H}}}'= & {} \frac{\sqrt{3}+\mathrm {i}}{2} \frac{2}{\root 4 \of {3}}\, {{\,\mathrm{\mathrm {K}}\,}}(\cos \tfrac{\pi }{12})\\= & {} \mathrm {e}^{\mathrm {i}\pi /6}\Pi _{{\mathscr {D}}}. \end{aligned}$$

Setting now

$$\begin{aligned} \Biggl [\begin{matrix} \Pi _{{\mathscr {H}}}''\\ \Pi _{{\mathscr {H}}}''' \end{matrix}\Biggr ] {:}{=}\Biggl [\begin{matrix} -1 &{} 2\\ -1 &{} 1 \end{matrix}\Biggr ] \Biggl [\begin{matrix} \Pi _{{\mathscr {H}}}\\ \Pi _{{\mathscr {H}}}' \end{matrix}\Biggr ] , \end{aligned}$$

we realize that $\Pi _{{\mathscr {H}}}''$ and $\Pi _{{\mathscr {H}}}'''$ generate the complete lattice $\Lambda _{{\mathscr {H}}}$ of periods of ${{\,\mathrm{{\mathbf {m}}}\,}}_{{\mathscr {H}}}$:

$$\begin{aligned} \Lambda _{{\mathscr {H}}} = {\mathbb {Z}} \, \Pi _{{\mathscr {H}}}'' \oplus {\mathbb {Z}} \, \Pi _{{\mathscr {H}}}'''. \end{aligned}$$

But, in addition, the identity

$$\begin{aligned} \Biggl [\begin{matrix} \Pi _{{\mathscr {H}}}''\\ \Pi _{{\mathscr {H}}}''' \end{matrix}\Biggr ] = \mathrm {i}\Biggl [\begin{matrix} \Pi _{{\mathscr {D}}}\\ \Pi _{{\mathscr {D}}}' \end{matrix}\Biggr ] \end{aligned}$$

proves that the lattice $\Lambda _{{\mathscr {H}}}$ is congruent to $\Lambda _{{\mathscr {D}}}$, via the rotation by $\pi /2$.

7 A final remark

All arguments outlined in these pages can apply for a wider class of parametric curves, by leaving out axiom (AnK 0). Actually, that axiom simply succeeds to exhibit the“ trigonometric” behaviour of a k-map, by displaying ${{\,\mathrm{{\mathbf {m}}}\,}}(0) = \,\mathbf {i}$: its removal must be remedied by giving the role of ${{\,\mathrm{{\mathbf {m}}}\,}}(0)$ to a point picked at will in the assigned curve.