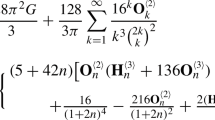Relative Growth in Hyperbolic Groups

Abstract

In this note we obtain estimates on the relative growth of normal subgroups of non-elementary hyperbolic groups, particularly those with free abelian quotient. As a corollary, we deduce that the associated relative growth series fail to be rational.

1 Introduction and Results

Let G be a non-elementary hyperbolic group equipped with a finite symmetric generating set. Write $W_n = \{ g \in G: |g| =n \}$ for the collection of elements of word length n. By a result of Coornaert [6], the growth rate of its cardinality $\# W_n$ is purely exponential, i.e. there exist constants $\lambda >1$ and $C_1,C_2 >0$ such that

$$\begin{aligned} C_1 \lambda ^n \le \#W_n \le C_2 \lambda ^n \end{aligned}$$

for all $n \ge 1$. Now suppose that N is a subgroup of G. An interesting question to ask is how $\#(W_n\cap N)$, which we call the relative growth of N, grows in comparison to $\#W_n$. A result of Gouëzel, Matheus and Maucourant [11] states that if N has infinite index in G then

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{\#(W_n \cap N)}{\#W_n} = 0. \end{aligned}$$

(1.1)

This is a subtle result that relies strongly on the hyperbolicity of G. If we suppose further that N is normal and the quotient G/N is isomorphic to ${\mathbb {Z}}^\nu$ for some $\nu \ge 1$, then we have access to more structure. With this additional information it seems reasonable to expect that we can describe the relative growth of N more precisely.

Pollicott and Sharp [22] studied this problem when G is the fundamental group of a compact orientable surface of genus at least two and N is the commutator subgroup. Sharp [23] extended this to cover hyperbolic groups G that may be realised as convex cocompact groups of isometries of real hyperbolic space whose fundamental domain can be chosen to be a finite sided polyhedron R such that $\bigcup _{g \in G} \partial R$ is a union of geodesic hyperplanes, with generators given by the side pairings. The fundamental groups of compact surfaces were shown to satisfy this condition by Bowen and Series [2]. In addition, this class includes free groups on at least two generators and certain higher dimensional examples (see Bourdon’s thesis [1]). In these cases, it was shown that there exists an integer $D \ge 1$ such that, along the subsequence Dn, the relative growth $\#(W_{Dn} \cap N)$ grows asymptotically like $\lambda ^{Dn}/(Dn)^{\nu /2}$, as $n \rightarrow \infty$. The aim of this note is to extend this result so that it applies to all non-elementary hyperbolic groups.

Before we state our main result, we recall the following standard definitions. Given two real valued sequences $a_n$ and $b_n$, we say that $a_n \sim b_n$ if $a_n/b_n \rightarrow 1$, as $n \rightarrow \infty$. Furthermore, if $b_n$ is positive, we say that $a_n = O(b_n)$ if there exists a constant $C>0$ such that $|a_n| \le Cb_n$, for all $n \ge 1$.

Theorem 1.1

Let G be a non-elementary hyperbolic group equipped with a finite symmetric generating set and let $N \triangleleft G$ be a normal subgroup with $G/N \cong {\mathbb {Z}}^\nu$ for some $\nu \ge 1$. Then

$$\begin{aligned} \# ( W_n \cap N) = O\left( \frac{\lambda ^n}{n^{\nu /2}}\right) \end{aligned}$$

as $n\rightarrow \infty$. Furthermore, there exists $D \in {\mathbb {Z}}_{\ge 0}$ and $C>0$ such that

$$\begin{aligned} \#(W_{Dn} \cap N) \sim \frac{C \lambda ^{Dn}}{(Dn)^{\nu /2}} \end{aligned}$$

as $n\rightarrow \infty$.

This theorem has the following immediate corollary.

Corollary 1.2

Let G be a non-elementary hyperbolic group equipped with a finite symmetric generating set and let $N \triangleleft G$ be a normal subgroup such that the abelianisation of G/N has rank $\nu \ge 1$. Then

$$\begin{aligned} \# ( W_n \cap N) = O\left( \frac{\lambda ^n}{n^{\nu /2}}\right) \end{aligned}$$

as $n\rightarrow \infty$.

Proof

Write the abelianisation of G/N as ${\mathbb {Z}}^\nu \times F$, where F is finite. There are then natural surjective homomorphisms $\phi : G \rightarrow G/N$ and $\psi : G/N \rightarrow {\mathbb {Z}}^\nu$. Set $\phi _0 = \psi \circ \phi$ and $N_0 = \ker \phi _0$. Then $N \subset N_0$. Furthermore, by Theorem 1.1, $\#(W_n \cap N_0) = O(\lambda ^n n^{-\nu /2})$, giving the required estimate. $\square$

Remark 1.3

The relative growth in Corollary 1.2 may occur at a slower exponential rate. Indeed, Coulon, Dal’Bo and Sambusetti recently showed that $\#(W_n \cap N) = O(\lambda _0^n)$, for some $0< \lambda _0 <\lambda$ precisely when G/N is not amenable [7]. In fact, their result does not require normality of the subgroup, in which case amenability is replaced by co-amenability of N in G, i.e. that the G-action on the coset space G/N is amenable.

To prove Theorem 1.1, we would like to employ the strategy used by the second author in [23]. However, there are significant technical obstacles which we need to overcome in order to use this method. We summarise these below.

• (i) Firstly, as mentioned above, in [23] there are strong restrictions on the hyperbolic groups and their generating sets. This makes it much easier to study the relative growth quantity $\#(W_n\cap N)$. In the current paper we need to find a new approach that works for general non-elementary hyperbolic groups, that will allow us to express $\#(W_n\cap N)$ in terms of quantities which we can analyse. To achieve this we appeal to ideas and techniques used in [5].

• (ii) Secondly, we need a good understanding of how real valued group homomorphisms on hyperbolic groups grow as we increase the word length of the input. Again, recent work of the first author [5] allows us to deduce the required properties of these homomorphisms.

We end this section with a discussion of relative growth series. We define the relative growth series for N in G (with respect to the given generators) to be the power series

$$\begin{aligned} \sum _{n=0}^\infty \#(W_n \cap N) z^n. \end{aligned}$$

When $N =G$, this is the standard growth series and, for hyperbolic groups, is well-known to be the series of a rational function [4, 10]. The requirement that a power series be rational imposes a strong constraint on the coefficients: if $\sum _{n=0}^\infty a_n z^n$ is rational then there are complex numbers $\xi _1,\ldots ,\xi _m$ and polynomials $P_1,\ldots ,P_m$ such that

$$\begin{aligned} a_n = \sum _{j=1}^m P_j(n) \xi _j^n \end{aligned}$$

(Theorem IV.9 of [8]). Comparing with the asymptotic in Theorem 1.1, we see that $\#(W_n \cap N)$ does not satisfy this constraint. Thus we obtain the following.

Corollary 1.4

Suppose G is a non-elementary hyperbolic group equipped with a finite symmetric generating set. Let $N \triangleleft G$ be a normal subgroup with $G/N \cong {\mathbb {Z}}^\nu$, for some $\nu \ge 1$. Then, the relative growth series

$$\begin{aligned} \sum _{n=1}^\infty \#(W_n \cap N) z^n \end{aligned}$$

is not the series of a rational function.

Remark 1.5

(i) The first result of this type is due to Grigorchuk, who showed that the relative growth series is not rational when G is the free group on two generators and N is the commutator subgroup (see [13]). A similar result was obtained for the fundamental groups of compact surfaces of genus $\ge 2$ in [22] and this was extended to a wider class of hyperbolic groups in [23].

(ii) We note that, Corollary 1.4 requires the asymptotic along a subsequence in Theorem 1.1 and not merely the upper bound $O(\lambda ^n/n^{\nu /2})$. Therefore, the corollary does not apply to general infinite index subgroups of hyperbolic groups and it remains an open question whether the relative growth series of such subgroups fail to be rational. In contrast, Grigorchuk showed that if N is a finite index subgroup of a free group than its relative growth series is rational [12].

2 Preliminaries

We first recall the definition of a hyperbolic group. A metric space is hyperbolic if there exist $\delta \ge 0$ for which every geodesic triangle is $\delta$-thin, i.e. given any geodesic triangle, the union of the $\delta$ neighbourhoods of any two sides of this triangle contain the third side. A finitely generated group G is said to be hyperbolic, if given any finite generating set S, the Cayley graph of G with respect to S is a hyperbolic metric space when equipped with the word metric. We say that a hyperbolic group is elementary if it contains a cyclic subgroup of finite index. We will be exclusively concerned with non-elementary hyperbolic groups.

Hyperbolic groups have nice combinatorial properties that arise due to their strongly Markov structure.

Definition 2.1

A finitely generated group G is strongly Markov if given any generating set S there exists a finite directed graph ${\mathcal {G}}$ with vertex set V, edge set E (with at most one directed edge between an ordered pair of vertices) and a labeling map $\rho : E \rightarrow S$ such that:

• (1) there exists an initial vertex $*\in V$ such that no directed edge ends at $*$;

• (2) the map taking finite paths in ${\mathcal {G}}$ starting at $*$ to G that sends a path with concurrent edges $(*,x_1), \ldots ,(x_{n-1},x_n)$ to $\rho (*,x_1)\rho (x_1,x_2) \cdots \rho (x_{n-1},x_n)$, is a bijection;

• (3) the word length of $\rho (*,x_1) \cdots \rho (x_{n-1},x_n)$ is n.

In [10] Ghys and de le Harpe extended Cannon’s work on Kleinian groups [4] and proved that hyperbolic groups are strongly Markov.

Proposition 2.2

([10], Chapitre 9, Théorème 13) Any hyperbolic group is strongly Markov.

Suppose that ${\mathcal {G}} = (E,V)$ is a directed graph associated to G satisfying the properties in Definition 2.1. We define a transition matrix A, indexed by $V \times V$, by

$$\begin{aligned} A(v_1,v_2) = \left\{ \begin{array}{@{}l@{ }l} 1 &{} \ \ \text{ if } (v_1,v_2) \in E \\ 0 &{} \ \ \text {otherwise.} \end{array} \right. \end{aligned}$$

Using A we define a space

$$\begin{aligned} \Sigma _A = \{ (x_n)_{n=0}^\infty : x_n \in V \text { and } A(x_n,x_{n+1}) = 1 \text { for all } n\in {\mathbb {Z}}_{\ge 0}\} \end{aligned}$$

and $\sigma :\Sigma _A \rightarrow \Sigma _A$ by $\sigma ((x_n)_{n=0}^\infty ) = (x_{n+1})_{n=0}^\infty$. The system $(\Sigma _A,\sigma )$ is known as a subshift of finite type.

Recall that a matrix M with zero-one entries is called irreducible if for each i, j there exists n(i, j) for which $M^{n(i,j)}(i,j) >0$. This is equivalent to the directed graph ${\mathcal {G}}$ being connected. We call M aperiodic if there exists n such that every entry of $M^n$ is strictly positive. Due to the $*$ vertex, which forms its own connected component in ${\mathcal {G}}$, A is never irreducible. However, it is possible that, after removing from A the row and column corresponding to the $*$ state, the resulting matrix is aperiodic. In fact, for the hyperbolic groups and generating sets considered by Sharp in [23], it is always possible to find a corresponding directed graph described by an aperiodic matrix (after removing $*$). It is not known whether every hyperbolic group and generating set admit a directed graph with this property and so to improve upon the results in [23], we need to exploit geometrical and combinatorial properties of hyperbolic groups to obtain additional structural information about the directed graph ${\mathcal {G}}$. Throughout the rest of this section we introduce the preliminaries that will allow us to analyse $\#(W_n\cap N)$ for general hyperbolic groups.

As mentioned above, in general, the graph ${\mathcal {G}}$ may have several connected components. By relabeling the vertex set V, we may assume that A has the form

$$\begin{aligned} A = \begin{pmatrix} A_{1,1} &{} 0 &{} \dots &{} 0 \\ A_{2,1} &{} A_{2,2} &{} \dots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ A_{m,1} &{} A_{m,2} &{} \dots &{} A_{m,m} \end{pmatrix}, \end{aligned}$$

where each $A_{j,j}$ is irreducible for $j=1,...,m$. We call the $A_{j,j}$ the irreducible components of A.

Let $\lambda >1$ denote the exponential growth rate of $W_n$. It is easy to see by Property (2) and (3) in Definition 2.1, that all of the $A_{j,j}$ must have spectral radius at most $\lambda$. Furthermore there must be at least one $A_{j,j}$ with spectral radius exactly $\lambda$. We call an irreducible component maximal if it has spectral radius $\lambda$. We label the maximal components ${\mathcal {B}}_j$ for $j=1,\ldots ,m$ and write $B_j$ for $j=1,\ldots , m$ for the matrices describing each ${\mathcal {B}}_j$. We define $\Sigma _{B_j}$, $j=1,\ldots ,m$ analogously to $\Sigma _A$. For each $\Sigma _{B_j}$ there exists $p_j \ge 1$ such that $\Sigma _{B_j}$ admits a cyclic decomposition into $p_j$ disjoint sets,

$$\begin{aligned} \Sigma _{B_j} = \bigsqcup _{k=0}^{p_j-1} \Sigma _k^j. \end{aligned}$$

We call $p_j$ the cyclic period of $\Sigma _{B_j}$. The shift map $\sigma$ sends $\Sigma _k^j$ into $\Sigma _{k+1}^j$ where $k,k+1$ are taken modulo $p_j$. Hence each $\Sigma _k^j$ is $\sigma ^{p_j}$-invariant. In fact, each system $\sigma ^{p_j} : \Sigma _k^j \rightarrow \Sigma _k^j$ is a subshift of finite type with aperiodic transition matrix.

The following key result, that relies on Coornaert’s estimates for $\#W_n$, shows that the maximal components ${\mathcal {B}}_j$ do not interact with each other. This result allows us to gain a better understanding of the structure of ${\mathcal {G}}$.

Proposition 2.3

([3], Lemma 4.10) The maximal components of A are disjoint. There does not exist a path in ${\mathcal {G}}$ that begins in one maximal component and ends in another.

Proof

For the convenience of the reader, we include a sketch of the proof. Suppose there is a path of length l between maximal components that starts at a vertex x in ${\mathcal {B}}_j$ and end at vertex y in ${\mathcal {B}}_k$. Then for large n, the number of length n paths that begin in ${\mathcal {B}}_j$, traverse $m<n-l$ edges in ${\mathcal {B}}_j$ to x, then follow our path to y in ${\mathcal {B}}_k$ and traverse $n-m-l$ edges in ${\mathcal {B}}_k$, is growing like $\lambda ^n$. Since we can vary m between 1 and $n-l$, this implies there are at least $C n \lambda ^n$ paths from ${\mathcal {B}}_j$ to ${\mathcal {B}}_k$ for some $C>0$. This would imply $\#W_n$ grows at least like $n\lambda ^n$, contradicting Coornaert’s estimates for $\#W_n$ [6]. $\square$

This fact will be useful when counting certain quantities related to relative growth. To further facilitate these counting arguments, we define the following matrices.

Definition 2.4

For each $j=1,...,m$, define a matrix $C_j$ by,

$$\begin{aligned} C_j(u,v) = \left\{ \begin{array}{@{}l@{ }l} 0&{} \ \ \text {if } u\, \hbox { or }\, v \,\hbox {belong to a maximal component that is not}\, {\mathcal {B}}_j,\\ A(u,v) &{} \ \ \text {otherwise}. \end{array} \right. \end{aligned}$$

Now suppose that $N \triangleleft G$ is a normal subgroup for which $G/N \cong {\mathbb {Z}}^\nu$ and let $\varphi : G \rightarrow G/N \cong {\mathbb {Z}}^\nu$ be the quotient homomorphism. We define a function $f: \Sigma _A \rightarrow {\mathbb {Z}}^\nu$ by

$$\begin{aligned} f( (x_n)_{n=0}^\infty ) = \varphi (\rho (x_0,x_1)), \end{aligned}$$

where $\rho$ is the labeling map from Definition 2.1. Since $f((x_n)_{n=0}^\infty )$ depends only on the first two coordinates of $(x_n)_{n=0}^\infty$, we can consider f as a map from the directed edge set of ${\mathcal {G}}$ to ${\mathbb {R}}$. We then have that $\varphi (g) = f(*,x_1)+ f(x_1,x_2) + \cdots + f(x_{|g|-1},x_{|g|})$ where $(*,x_1),...,(x_{|g|-1},x_{|g|})$ is the unique path associated to g by Property (2) of Definition 2.1. Using f, we weight the matrices $C_j$ componentwise and define, for $t \in {\mathbb {R}}^\nu$,

$$\begin{aligned} C_j(t)(u,v) = e^{2\pi i \langle t, f(u,v) \rangle } C_j(u,v). \end{aligned}$$

We define the matrices $B_j(t)$ analogously.

3 Proof of Theorem 1.1

Suppose G is a non-elementary hyperbolic group and N a normal subgroup satisfying the hypothesis of Theorem 1.1. Let $\varphi : G \rightarrow {\mathbb {Z}}^\nu$ denote the quotient homomorphism. To study the relative growth of N, we would like to express $\#(W_n \cap N)$ in terms of the matrices $C_j(t)$. Using the orthogonality identity

$$\begin{aligned} \int _{{\mathbb {R}}^\nu /{\mathbb {Z}}^\nu } e^{2\pi i \langle t, \varphi (g) \rangle } \ dt = {\left\{ \begin{array}{ll} 1 &{}\text { if } \varphi (g)=0\\ 0 &{}\text { otherwise} \end{array}\right. } \end{aligned}$$

we can write

$$\begin{aligned} \#(W_n \cap N) = \sum _{|g|=n} \int _{{\mathbb {R}}^\nu /{\mathbb {Z}}^\nu } e^{2\pi i \langle t, \varphi (g) \rangle } \ dt = \int _{{\mathbb {R}}^\nu /{\mathbb {Z}}^\nu } \sum _{|g|=n} e^{2\pi i \langle t, \varphi (g)\rangle } \ dt. \end{aligned}$$

The following result will allow us to rewrite $\#(W_n \cap N)$ in terms of the matrices $C_j$. Let $v_*$ be the vector in ${\mathbb {R}}^V$ with a one in the coordinate corresponding to the $*$ vertex and zeros elsewhere. Also, let $\mathbf{1 } \in {\mathbb {R}}^\nu$ be the vector with a 1 in each coordinate.

Lemma 3.1

There exists $\epsilon >0$ such that for all $t \in {\mathbb {R}}^\nu /{\mathbb {Z}}^\nu$

$$\begin{aligned} \sum _{|g|=n} e^{2\pi i \langle t, \varphi (g) \rangle } = \sum _{j=1}^m \langle v_*C_j^n(t) , {\mathbf{1 }} \rangle + O((\lambda -\epsilon )^n) \end{aligned}$$

as $n\rightarrow \infty$. The implied constant is independent of t.

Proof

Using the correspondence between G and $\Sigma _A$, we can write

$$\begin{aligned} \left| \sum _{|g|=n} e^{2\pi i \langle t, \varphi (g) \rangle } -\sum _{j=1}^m \langle v_*C_j^n(t), {\mathbf{1 }} \rangle \right| = (m-1) \left| \sum _{g \in M_n} e^{2 \pi i \langle t,\varphi (g) \rangle }\right| \le (m-1) \ \#M_n, \end{aligned}$$

where $M_n$ consists of the elements in G of word length n whose corresponding path in ${\mathcal {G}}$ does not enter a maximal component. It is clear that $\#M_n = O((\lambda - \epsilon )^n)$ for some $\epsilon >0$ and so the result follows. $\square$

Using this lemma, we see that

$$\begin{aligned} \#(W_n \cap N) =\sum _{j=1}^m \int _{{\mathbb {R}}^\nu /{\mathbb {Z}}^\nu } \langle v_*C_j^n(t), \mathbf{1 } \rangle \ dt + O((\lambda -\epsilon )^n). \end{aligned}$$

Hence to study the relative growth of N would like to understand the spectral behaviour of the $C_j(t)$ for $t \in {\mathbb {R}}^\nu /{\mathbb {Z}}^\nu$. From their definitions, it is clear that the matrices $C_j$ each have $p_j$ simple maximal eigenvalues of modulus $\lambda$ and the rest of the spectrum is contained in a disk of radius strictly smaller than $\lambda - \epsilon$, for some $\epsilon >0$. We shall be interested in the values of t for which the operators $C_j(t)$ have spectral radius $\lambda$. These values of t are characterised by the following lemma.

Lemma 3.2

For any $t\in {\mathbb {R}}^\nu$, the operator $C_j(t)$ has spectral radius at most $\lambda$. Furthermore, $C_j(t)$ has spectral radius exactly $\lambda$ if and only if it has $p_j$ simple maximal eigenvalues of the form $e^{2\pi i \theta } e^{2\pi i k/p_j} \lambda$ for $k=0, \ldots ,p_j-1$ and some $\theta \in {\mathbb {R}}$. This occurs if and only if $B_j(t) = e^{2\pi i \theta } M B_j M^{-1}$ where M is a diagonal matrix with modulus one diagonal entries. Furthermore, when $C_j(t)$ has $p_j$ simple maximal eigenvalues of modulus $\lambda$, the rest of the spectrum is contained in a disk of radius strictly less than $\lambda$.

Proof

When $C_j$ consists of a single component (ignoring the $*$ vertex) and so is the same as $B_j$, this is Wielandt’s Theorem [9]. When this is not the case, we can write the spectrum of $C_j(t)$ as a union of the spectra of the irreducible components making up $C_j(t)$. By definition, each $C_j$ has one component $B_j$ with spectral radius $\lambda$ and all other components have spectral radius strictly less than $\lambda$. Therefore applying Wielandt’s Theorem to each component gives the required result. $\square$

We now follow the method presented in [23]. Let $f_j = f|_{\Sigma _{B_j}}$ for $j=1,\ldots ,m$. As before, for $n \in {\mathbb {Z}}_{\ge 0},$ we will write $f_j^n$ for the nth Birkhoff sum of $f_j$, i.e. for $x \in \Sigma _{B_j}$, $f_j^n(x) = f(x) + f(\sigma (x)) + \ldots + f(\sigma ^{n-1}(x))$. If a sequence $\gamma = (x_0,x_1,...,x_n)$ is such that $B_j(x_i,x_{i+1}) =1$ for $i=0,\ldots ,n$ and $x_0 = x_n$, then we call $\gamma$ a cycle and define its length as $l(\gamma )=n$. Let ${\mathcal {C}}_j$ be the collection of all such cycles and note that the length of any cycle in ${\mathcal {C}}_j$ is a multiple of $p_j$. Given a cycle $\gamma \in {\mathcal {C}}_j$, we define its $f_j$-weight to be

$$\begin{aligned} w_{f_j}(\gamma ) = f_j(x_0,x_1) + \cdots + f_j(x_{n-1},x_n). \end{aligned}$$

Let $\Gamma _{j}$ be the subgroup of ${\mathbb {Z}}^\nu$ generated by $\{ w_{f_j}(\gamma ) : \gamma \in {\mathcal {C}}_j\}$. We define $\Delta _{j}$ to be the following subgroup of $\Gamma _{j}$,

$$\begin{aligned} \Delta _{j} = \{w_{f_j}(\gamma ) - w_{f_j}(\gamma '): \gamma , \gamma ' \in {\mathcal {C}}_j \text { and } l(\gamma )=l(\gamma ')\}. \end{aligned}$$

(This is a version of Krieger’s $\Delta$-group. This introduced in [15] as a multiplicative subgroup of ${\mathbb {R}}^+$ generated by essential values of the Radon–Nikodym cocycle and adapted to problems of classification of Markov chains [16, 20]. The higher dimensional (additive) version used here was introduced by Marcus and Tuncel [17]. For a proof that it is a group, see page 892 of [24].) We now choose two cycles $\gamma , \gamma ' \in {\mathcal {C}}_j$ such that $l(\gamma )-l(\gamma ')=p_j$ and set $c_j = w_{f_j}(\gamma ) - w_{f_j}(\gamma ')$. Applying the results of [18] to the aperiodic shift $(\Sigma _{B_j}, \sigma ^{p_j})$, we see that the group $\Gamma _{j}/\Delta _{j}$ is cyclic and is generated by the element $c_j + \Delta _j$. Our aim is to show that this group has finite order. To do so, we will use a result of Marcus and Tuncel. For each $j=1,\dots ,m$, let $E_j$ denote the directed edge set for the graph with transition matrix $B_j$. Write $V_j$ for the analogously defined vertex sets. We say that a function $g: E_j \rightarrow {\mathbb {R}}$ is cohomologous to a constant if there exists $C \in {\mathbb {R}}$ and $h: V_j \rightarrow {\mathbb {R}}$ such that $g(x,y) = C + h(y)-h(x)$ for all $(x,y) \in E_j$.

Lemma 3.3

([18]) If $\langle t,f_j^{p_j}\rangle$ is not cohomologous to a constant for any non-zero $t \in {\mathbb {R}}^\nu /{\mathbb {Z}}^\nu$, then $\Gamma _j/\Delta _j$ has finite order.

It is clear that, for $t \in {\mathbb {R}}^\nu$, $\langle t,f_j^{p_j} \rangle$ is cohomologous to a constant if and only if $\langle t, f_j \rangle$ is cohomologous to constant. Using ideas from [5], we will show that the hypothesis of the above lemma is satisfied for each $j=1,\ldots ,m$.

Lemma 3.4

For non-zero $t \in {\mathbb {R}}^\nu /{\mathbb {Z}}^\nu$ and for all $j=1,\ldots ,m$, $\langle t,f_j\rangle$ is not cohomologous to a constant.

Proof

We begin by noting that, since $\varphi$ is surjective, for any $t\in {\mathbb {R}}^\nu \backslash \{0\}$ the function $\psi _t : =\langle t,\varphi \rangle : G \rightarrow {\mathbb {R}}$ is a non-trivial group homomorphism. Theorem 1.1 and Proposition 5.1 of [5] imply that if $\langle t, f_j \rangle$ (for any $j\in \{1,\ldots ,m\}$) is cohomologous to a constant, then that constant is given by

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{\#W_n} \sum _{|g|=n} \frac{\psi _t(g)}{n}. \end{aligned}$$

Since our generating set S is symmetric, $|g|=|g^{-1}|$ for all $g\in G$ and so the above limit is 0 by symmetry. Hence we need to show that $\langle t, f_j \rangle$ is not cohomologous to 0. By Livsic’s criterion [19], $\langle t, f_j \rangle$ is cohomologous to 0 if and only if $\langle t, w_{f_j}(\gamma ) \rangle = 0$ for all loops $\gamma \in C_j$.

Suppose for contradiction that $\langle t, w_{f_j}(\gamma ) \rangle = 0$ for all loops $\gamma \in C_j$. Now, for $\gamma =(x_0,\ldots ,x_n) \in C_j$, $g_\gamma = \rho (x_0,x_1)\rho (x_1,x_2) \ldots \rho (x_{n-1},x_n)$ belongs to the kernel of $\psi _t$. Furthermore, $g_\gamma$ has word length n. Also, Property (2) from Definition 2.1 implies that for any two distinct loops $\gamma , \gamma ' \in {\mathcal {C}}_j$, we have $g_\gamma \ne g_{\gamma '}$ whenever $\gamma$ and $\gamma '$ have the same initial vertex. Since the number of loops of length $np_j$ in $C_j$ is growing like $\lambda ^{np_j}$, this implies that there exists $C>0$ such that

$$\begin{aligned} \#(W_{np_j} \cap \text {ker}(\psi _t)) \ge C\lambda ^{np_j} \end{aligned}$$

for $n\ge 1$ and hence that

$$\begin{aligned} \limsup _{n\rightarrow \infty } \frac{\#(W_n \cap \text {ker}(\psi _t))}{\#W_n} > 0. \end{aligned}$$

Since $\text {ker}(\psi _t)$ is an infinite index subgroup of G, this contradicts the result of Gouëzel, Matheus and Maucourant [11] written above as (1.1). $\square$

Remark 3.5

Since the above proof relies on the zero density result of Gouëzel, Matheus and Maucourant [11], quantifying the decay rate in (1.1) requires a priori knowledge of the convergence to zero.

Let $D'_j = \left| \Gamma _j/\Delta _j\right|$ for $j=1,\ldots ,m$. From the above discussion, we know that each $D'_j$ is finite. We also note that Lemma 3.4 shows that $\text {rank}_{{\mathbb {Z}}} ( \Gamma _j) = \nu$ and so $|{\mathbb {Z}}^\nu /\Gamma _j|$ is finite for each $j=1,\ldots ,m$. Hence $D_j = |{\mathbb {Z}}^\nu / \Delta _j|$ is finite for each $j=1,\ldots , m$. Combining this with all of the above work, allows us to state the following result that describes the spectral behaviour of the $C_j(t)$ as t varies. We use the notation $\varrho (M)$ to denote the spectral radius of a matrix M and write $\widehat{{\mathbb {Z}}^\nu }$ for the Pontryagin dual of ${\mathbb {Z}}^\nu$, i.e. the space of (continuous) homomorphisms from ${\mathbb {Z}}^\nu$ to the unit circle in ${\mathbb {C}}$.

Proposition 3.6

For $t \in {\mathbb {R}}^\nu /{\mathbb {Z}}^\nu$, define $\chi _t \in \widehat{{\mathbb {Z}}^\nu }$ by $\chi _t(x) = e^{2\pi i \langle t, x \rangle }$. Then we have that

$$\begin{aligned} \{ \chi _t: \varrho (C_j(t)) = \lambda \} = \Delta _{j}^\perp , \end{aligned}$$

where $\Delta _{j}^\perp = \{ \chi \in \widehat{{\mathbb {Z}}^\nu } : \chi (\Delta _{j}) =1\}$. Furthermore, each $\Delta _{j}^\perp$ has cardinality $D_j$ and we can label $\Delta _{j}^\perp = \{ \chi _{t^j_r} : r = 0, \ldots , D_j-1\}$ so that each $C_j(t^j_r)$ has $p_j$ simple maximal eigenvalues of the form $e^{2\pi i r/D_j} e^{2\pi i k/p_j}\lambda$ for $k=0,\ldots ,p_j-1$.

Proof

This is essentially Proposition 3 from [21] which is concerned with aperiodic matrices. However, here we need to consider the non-aperiodic matrices $C_j(t)$. To deduce this more general statement, we can apply Proposition 3 from [21] to the maximal component associated to the matrix $C_j^{p_j}(t)$. This is justified since this maximal component is aperiodic. To conclude the proof, we note that the part of the spectrum of $C_j(t)$ coming from $B_j(t)$ is invariant under the rotation $z \mapsto z e^{2\pi i/p_j}$. $\square$

Proposition 3.6 implies that there exist $D_j < \infty$ values of t for which the spectral radius of $C_j(t)$ is maximal and equal to $\lambda$. As in the above proposition we denote these values by $t=t_0^j,t_1^j\ldots ,t^j_{D_j-1}$. We now choose, for each $j=1,\ldots ,m$, a neighbourhood $U_0^j$ of zero and define $U_r^j = U_0^j + t_k^j$ for $k=0,\ldots ,D_j-1$. Results from perturbation theory guarantee that, as long as each $U_0^j$ is sufficiently small, there exists $\epsilon >0$ such that the following hold for each $j=1,\ldots ,m$.

• (1) If $t \in \bigcup _{r=0}^{D_j-1}U_r^j$, then the matrices $C_j(t)$ each have $p_j$ simple, maximal eigenvalues of the form $\lambda _j(t) e^{2\pi i k/p_j}$ for $k=0,\ldots ,p_j-1$, where $t \rightarrow \lambda _j(t)$ is analytic and independent of $k=0,\ldots ,p_j-1$.

• (2) Let $M_\nu ({\mathbb {C}})$ denote the vector space of $\nu \times \nu$ complex matrices. For each $j=1,\dots ,m$ and $k=0,\dots ,p_j-1$, there exists an analytic matrix-valued function $Q_{j,k} : \bigcup _{r=0}^{D_j-1}U_r^j \rightarrow M_\nu ({\mathbb {C}})$, where $Q_{j,k}(t)$ is the eigenprojection onto the eigenspace associated to the eigenvalue $\lambda _j(t)e^{2\pi i k/p_j}$ of the matrix $C_j(t)$.

• (3) If $t \in ({\mathbb {R}}^\nu {/}{\mathbb {Z}}^\nu ) \setminus \bigcup _{r=0}^{Dj-1}U_r^j$ then the spectral radius of each $C_j(t)$ is bounded uniformly above by $\lambda - \epsilon$.

Using this description of the spectrum, we can write

$$\begin{aligned} \#(W_n \cap N) = \sum _{j=1}^m \sum _{r=0}^{D_j -1} \sum _{k=0}^{p_j-1} \int _{U_r^j} \lambda _j(t)^n e^{2\pi i kn/p_j} \langle v_*Q_{j,k}(t) , \mathbf{1 } \rangle \, dt + O((\lambda -\epsilon )^n), \end{aligned}$$

for some $\epsilon >0$. We now observe that for $t \in U_r^j$, $\lambda _j(t) = e^{2\pi i r/D_j} \lambda _j(t-t^j_r)$. This follows from Lemma 3 of [21]. Combining this with the above expression, we deduce that there exists constants $c_{r,k}^j = \langle v_*Q_{j,k}(t_r^j),\mathbf{1 } \rangle$, for $r=0,\ldots ,D_j-1$ and $k=0,\ldots , p_j-1$, such that $\#(W_n \cap N)$ is equal to

$$\begin{aligned} \sum _{j=1}^m \left( \sum _{r=0}^{D_j-1} \sum _{k=0}^{p_j-1} e^{2\pi i n(r/D_j + k/p_j)} c_{r,k}^j \right) \int _{U_0^j} \lambda _j(t)^n \left( 1+O(\Vert t\Vert )\right) \, dt + O((\lambda -\epsilon )^n).\nonumber \\ \end{aligned}$$

(3.1)

Here we have used the fact that each projection $Q_{j,k}$ and associated remainder $R_{j,k} = I - Q_{j,k}$ satisfy $Q_{j,k}R_{j,k} = R_{j,k} Q_{j,k} = 0$ (see Theorem III.6.17 of [14]). The asymptotics of each

$$\begin{aligned} a_n^j := \int _{U_0^j} \lambda _j(t)^n \left( 1+O(\Vert t\Vert )\right) \, dt \end{aligned}$$

were studied in [21], where it was shown that, for each $j =1,\ldots ,m$, there exists $\tau _j>0$ such that

$$\begin{aligned} a_n^j \sim \frac{\tau _j \lambda ^n}{n^{\nu /2}} \end{aligned}$$

(3.2)

as $n\rightarrow \infty$. Applying this along the subsequence Dn, where D is given by the product of all the $p_1,\ldots , p_m$ and $D_1,\ldots , D_m$, we see that

$$\begin{aligned} \#(W_{Dn} \cap N) = \frac{{\widetilde{C}}\lambda ^{Dn}}{(Dn)^{\nu /2}} + o\left( \frac{\lambda ^{Dn}}{(Dn)^{\nu /2}}\right) \end{aligned}$$

(3.3)

as $n\rightarrow \infty$, where

$$\begin{aligned} {\widetilde{C}} =\sum _{j=1}^m \tau _j\left( \sum _{r=0}^{D_j-1} \sum _{k=0}^{p_j-1}c_{r,k}^j \right) . \end{aligned}$$

It is clear that ${\widetilde{C}} \in {\mathbb {R}}_{\ge 0}$. However, for (3.3) to be a useful asymptotic expression, we would like that ${\widetilde{C}}$ is strictly positive. We now show that this is always the case.

Lemma 3.7

We necessarily have that ${\widetilde{C}}>0$.

Proof

Fix $j \in \{1,\ldots , m\}$ and recall that for any loop $\gamma =(x_0,\ldots ,x_{Dn}) \in {\mathcal {C}}_j$ with $w_{f_j}(\gamma )=0$, the group element $g_\gamma = \rho (x_0,x_1)\rho (x_1,x_2) \ldots \rho (x_{Dn-1},x_{Dn})$ belongs to the kernel of $\varphi$ (or, equivalently, to N) and furthermore, $g_\gamma$ has word length Dn. Also, for any two distinct loops $\gamma , \gamma ' \in {\mathcal {C}}_j$, we have $g_\gamma \ne g_{\gamma '}$ whenever $\gamma$ and $\gamma '$ have the same initial vertex. Combining these observations and applying the pigeonhole principle gives that

$$\begin{aligned} \#(W_{Dn} \cap N ) \ge (\#V_j)^{-1} \#\{ \gamma \in {\mathcal {C}}_j : l(\gamma )=Dn, \, w_{f_j}(\gamma ) =0 \} \end{aligned}$$

for all $n \ge 1$. Pollicott and Sharp proved in [21] that

$$\begin{aligned} \#\{ \gamma \in {\mathcal {C}}_j : l(\gamma )=Dn, \, w_{f_j}(\gamma ) =0 \} \sim \frac{K \lambda ^{Dn}}{(Dn)^{\nu /2}} \end{aligned}$$

as $n\rightarrow \infty$ for some $K >0$. Hence

$$\begin{aligned} {\widetilde{C}} = \limsup _{n\rightarrow \infty } \frac{(Dn)^{\nu /2} \#(W_{Dn} \cap N)}{ \lambda ^{Dn}} \ge K(\#V_j)^{-1} >0, \end{aligned}$$

as required. $\square$

We can now conclude the proof of our main result.

Proof of Theorem 1.1

Combining (3.1) and (3.2) implies that

$$\begin{aligned} \#(W_n \cap N) = O\left( \sum _{j=1}^m \int _{U_0^j} \lambda _j(t)^n \left( 1+O(\Vert t\Vert )\right) \, dt \right) = O\left( \frac{\lambda ^n}{n^{\nu /2}}\right) \end{aligned}$$

which proves the first part of Theorem 1.1. The second part follows from (3.3) and the fact that ${\widetilde{C}} >0$. $\square$