Antiplane shear of an asymmetric sandwich plate

Abstract

An asymmetric three-layered laminate with prescribed stresses along the faces is considered. The outer layers are assumed to be much stiffer than the inner one. The focus is on long-wave low-frequency anti-plane shear. Asymptotic analysis of the original dispersion relation reveals a low-frequency harmonic supporting a slow quasi-static (or static at the limit) decay along with near cut-off wave propagation. In spite of asymmetry of the problem, the leading order shortened polynomial dispersion relation factorises into two simpler ones corresponding to the fundamental mode and the aforementioned harmonic. The associated 1D equations of motion derived in the paper are also split into two second-order operators in line with the factorisation of the shortened dispersion relation. Asymptotically justified boundary conditions are established using the Saint-Venant’s principle modified by taking into account the high-contrast properties of the laminate.

1 Introduction

Thin multi-layered structures have always been among main focuses in structural and solid mechanics. There is a substantial literature on the subject, including in particular advanced research monographs [1, 2] as well as most recent review articles [3,4,5], and insightful papers [6,7,8], to name a few. Modern industrial applications provide additional motivation to studying laminates, especially with high contrast geometric and physical properties of the layers, see for example [9,10,11,12] for photovoltaic panels and laminated glass, [13] for components of lightweight vehicles, [14] for sandwich panels in building construction. Modelling of such structures is of clear practical importance, and numerous efforts have already been made to establish various methodologies, see e.g. [15,16,17,18] and references therein, along with the citations above.

The asymptotic methods proved to be most efficient for thin elastic plates and shells, see e.g. [19,20,21,22,23,24], can also be applied to structures with high contrast properties, see [25,26,27,28,29,30]. In particular, in [28] multi-parametric nature of the problem for a symmetric sandwich plate with traction free faces was revealed with the emphasis on the effect of extra problem parameters , i.e. the ratios of thickness, densities and stiffness of the layers. In the cited paper, the conditions on these parameters are obtained ensuring the lowest shear cut-off frequency to become asymptotically small, see also [31, 32]. As a result, the range of validity for the classical plate bending theory may become rather restricted motivating derivation of two-mode approximations involving the first shear harmonic along with the fundamental bending mode.

A more explicit insight into asymptotic phenomena, observed for the plane-strain problem studied in [28], has been produced for its less technical anti-plane counterpart in [29] dealing with the antisymmetric motion with respect to the mid-surface. Such motion does not support a symmetric fundamental mode, while wave propagation occurs above the smallest cut-off frequency with its value tending to zero at the high contrast setups considered in the paper. In addition to shortened polynomial dispersion relations, the associated 1D equations of motion for long-wave low-frequency vibrations were also derived.

In this paper, we generalise the approach developed in [28, 29] for anti-plane shear of a three-layered asymmetric laminate with traction free faces. We restrict ourselves with the high contrast scenario in which outer layers are stiff, while middle one is relatively soft. The considered scalar problem is apparently the most explicit example in mechanics demonstrating a two-mode long-wave low-frequency behaviour involving the first harmonic along with the fundamental mode.

In Sect. 3, we study the exact dispersion relation presented in Sect. 2 at the long-wave low-frequency limit. It is shown that the leading order shortened polynomial equation (a rather sophisticated asymptotic behaviour of its coefficients is evaluated in “Appendix 1”) can be factorised into two ones corresponding to the fundamental mode and harmonic. In this case, the latter equation also covers a slow quasi-static (and static at zero frequency) decay below the small cut-off frequency in question, when the associated harmonic becomes evanescent. The factorisation of the asymptotic dispersion relation seems to be counter-intuitive since the coupling of two studied modes could be expected due to the asymmetry of the laminate. In fact, the assumed high contrast in problem parameters makes such coupling asymptotically negligible.

Next, in Sect. 4 we adapt a preliminary asymptotic insight coming from analysis of the dispersion relation for deriving 1D equations of motion generalising the technique established in [29], see also [20, 21]. As might be expected, the derived partial differential operator can also be factorised into two second-order operators corresponding to the fundamental mode and the lowest harmonic. As above, the operator governing the harmonic describes a slow decaying behaviour below the cut-off. In Sect. 5, following the long-term tradition in the theory for thin elastic structures, e.g. see [33], the obtained governing equations are re-written in terms of stress resultants, stress couples and also the average displacement and the angle of rotation.

In Sect. 6, we apply the Saint-Venant’s principle [34] combined with asymptotic considerations for formulating of boundary conditions extending the powerful procedure developed for homogeneous plates and shells, e.g. see [19, 35,36,37]. We start with the so-called decay conditions for a semi-infinite three-layered strip in case of its static equilibrium subject to homogeneous boundary conditions along the faces and prescribed anti-plane shear stresses at the edge, see for example [35, 38, 39]. In contrast to the conventional approach, we require a ‘strong’ decay of the boundary layer, resulting in localisation of the induced stress field over the narrow vicinity of the edge, with a typical length of the same order as the strip thickness. In this case slowly decaying solutions, characteristic of high-contrast laminates, e.g. see [40], are not counted as boundary layers.

Two decay conditions are formulated in this section. The first of them is given by an exact formula which expresses the self-equilibrium of the prescribed shear stress in agreement with the classical Saint-Venant’s principle. The second decay condition is of asymptotic nature. Fortunately, it takes an explicit form for the considered high contrast case. This condition is tested by comparison with the calculations for a symmetric sandwich using the Laplace transform technique, see “Appendix 2”.

The derived decay conditions immediately lead to the inhomogeneous boundary conditions at the edge of a finite length laminate using straightforward scheme. It consists in inserting the deviation between the given edge stress and that calculated from 1D governing equations into the decay conditions, see for greater detail [41]. It is also worth mentioning that two boundary conditions in Sect. 6 do not imply coupling of the solutions to the related second-order equations.

2 Statement of the problem

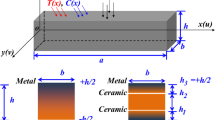
Consider a three-layered asymmetric laminate with the isotropic layers of thickness $h_1$, $h_2$ and $h_3$, see Fig. 1. The Cartesian coordinate system is chosen in such a way that the axis $x_1$ goes through the mid-plane of the core layer. In what follows two outer layers have the same material parameters.

For the antiplane shear motion, the only non-zero displacement is orthogonal to the $x_1 x_2$ plane. Hence, the equations of motion for each layer can be written as

$$\begin{aligned} \frac{\partial \sigma _{13}^q}{\partial x_1}+\frac{\partial \sigma _{23}^q}{\partial x_2}- \rho _q \dfrac{ \partial ^2 u_q}{\partial t^2}=0, \quad q=1,2,3, \end{aligned}$$

(1)

with

$$\begin{aligned} \sigma _{i3}^q= \mu _q\dfrac{\partial u_q}{\partial x_i}, \quad i=1,2, \end{aligned}$$

(2)

where $\sigma _{i3}^q$ are shear stresses, $u_q=u_q(x_1,x_2,t)$ are out of plane displacements, t is time, $\mu _q$ are Lamé parameters, and $\rho _q$ are mass densities. As we have already mentioned, $\mu _3=\mu _1$ and $\rho _3=\rho _1$.

Fig. 1

A three-layered asymmetric plate

The continuity and boundary conditions at the upper and lower faces are given by

$$\begin{aligned}&u_1 = u_2, \quad \sigma ^{1}_{23}= \sigma ^{2}_{23} \quad \text {at} \quad x_2=\frac{h_2}{2},\nonumber \\&u_2 = u_3, \quad \sigma ^{2}_{23}= \sigma ^{3}_{23} \quad \text {at} \quad x_2=-\frac{h_2}{2}, \end{aligned}$$

(3)

and

$$\begin{aligned}&\sigma ^{1}_{23}= F_1 \quad \text {at} \quad x_2=\frac{h_2}{2}+h_1,\nonumber \\&\sigma ^{3}_{23}= F_3 \quad \text {at} \quad x_2=-\frac{h_2}{2}-h_3, \end{aligned}$$

(4)

respectively. Here $F_1$ and $F_3$ are prescribed forces.

Let us seek the solution of the formulated problem (1)–(4) in the form of a travelling wave $e^{i(k x_1-\omega t)}$, where k is the wave number and $\omega$ is frequency. For a homogeneous problem $F_1=F_3=0$, this results in the dispersion relation

$$\begin{aligned}&\mu \alpha _1 \big ( \tanh (h_{12}\alpha _1)+ \tanh (h_{32} \alpha _1)\big )+\mu ^2 {\alpha _2} \tanh (\alpha _2) \nonumber \\&\quad +{\alpha _1}^2 \tanh (h_{12} \alpha _1)\tanh (h_{32} \alpha _1) \dfrac{\tanh (\alpha _2)}{\alpha _2}=0, \end{aligned}$$

(5)

where

$$\begin{aligned} \alpha _1= \sqrt{K^2 -\frac{\mu }{\rho }\varOmega ^2}, \quad \alpha _2= \sqrt{K^2 -\varOmega ^2}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&K= kh_2, \quad \varOmega = \frac{\omega h_2}{c_{22}}, \quad \mu = \frac{\mu _2}{\mu _1}, \quad \rho = \frac{\rho _2}{\rho _1}, \quad h_{12}= \frac{h_1}{h_2}, \quad h_{32}=\frac{h_3}{h_2}, \end{aligned} \end{aligned}$$

with $c_{22}=\sqrt{\mu _2/\rho _2}$.

Consider the contrast in the material parameters corresponding to stiff outer layers and a relatively soft core one, defined as

$$\begin{aligned} \mu \ll 1 , \quad \rho \sim \mu , \quad h_{12} \sim 1, \quad h_{32} \sim 1. \end{aligned}$$

(6)

This formula drastically simplifies further analysis due to the reduction of the number of the problem parameters. To certain extent, it might be adapted for laminated glass [42] and also seemingly holds for sandwich panels with several types of magnetorheological cores [2, 43].

First, setting $K = 0$ in dispersion relation (5), we have for the cut-off frequencies

$$\begin{aligned}&\sqrt{\mu \rho } \left( \tan \left( h_{12}\sqrt{\frac{\mu }{\rho }}\varOmega \right) +\tan \left( h_{32}\sqrt{\frac{\mu }{\rho }}\varOmega \right) \right) + \mu \rho \tan \left( \varOmega \right) \nonumber \\&\quad - \tan \left( h_{12}\sqrt{\frac{\mu }{\rho }}\varOmega \right) \tan \left( h_{32}\sqrt{\frac{\mu }{\rho }}\varOmega \right) \tan \left( \varOmega \right) =0. \end{aligned}$$

(7)

For this type of contrast, we have two cut-off frequencies over the low-frequency range of interest ($\varOmega \ll 1$), namely, $\varOmega =0$ and the extra small one

$$\begin{aligned} \varOmega ^2=\varOmega ^2_{sh} \approx \frac{h_{12}+h_{32}}{h_{12}h_{32}}\rho \sim \mu \ll 1. \end{aligned}$$

(8)

Next, setting $\varOmega =0$, we deduce from (5) the static equation for K

$$\begin{aligned}&K^2 \Big ( \mu \big ( \tanh (h_{12}K)+ \tanh (h_{32} K)\big )+\mu ^2 \tanh (\alpha _2) \nonumber \\&\quad + \tanh (h_{12} K)\tanh (h_{32} K) \tanh (K) \Big )=0. \end{aligned}$$

(9)

We have an obvious root $K=0$, associated with rigid body motion and another small one, given by

$$\begin{aligned} K^2 = K^2_{bl} \approx -\frac{h_{12}+h_{32}}{h_{12}h_{32}} \mu , \end{aligned}$$

(10)

The latter is associated with slowly decaying boundary layers ($|K_{bl}^2|\sim \mu \ll 1$) specific of high contrast laminates only, e.g. see [40].

Figure 2 demonstrates dispersion curves for two sets of material parameters. In particular, Fig. 2a is plotted for a laminate without contrast, while Fig. 2b corresponds to a laminate with high contrast in material properties of the layers. The values of $\varOmega _{sh}$ and $K_{bl}$ are calculated using (8) and (10), respectively, for each set of parameters. It can easily be observed that for the laminate with no contrast these values are of order 1, while for a high-contrast laminate they become small.

Fig. 2

Numerical solution of dispersion relation (5) for $h_{12} = 1.0$, $h_{32} = 1.5$ and a $\mu = 1.0$ and $\rho = 2.0$, b $\mu = 0.01$ and $\rho = 0.02$

3 Asymptotic analysis of dispersion relation

Expand all trigonometric functions in (5) in asymptotic Taylor series over the low-frequency long-wave range ($\varOmega \ll 1$ and $K \ll 1$) assuming that relations (6) hold. We arrive at a polynomial dispersion relation, which can be written as

$$\begin{aligned}&\gamma _1 K^2 + \gamma _2 \varOmega ^2 + \gamma _3 K^4 + \gamma _4 K^2 \varOmega ^2 +\gamma _5 \varOmega ^4 + \gamma _6 K^6 \nonumber \\&\quad + \gamma _7 K^4 \varOmega ^2 + \gamma _8 K^2 \varOmega ^4 + \gamma _9 \varOmega ^6+ \dots =0, \end{aligned}$$

(11)

where the coefficients $\gamma _i$ are given in “Appendix 1”.

From (68), we observe that $\gamma _1 \sim \gamma _2 \sim \mu$, and $\gamma _i \sim 1$, $i=3,\ldots ,9$. As a result, the leading order two-mode approximation takes the form

$$\begin{aligned} \gamma _1^0 K^2 + \gamma _2^0 \varOmega ^2 + \gamma _3^0 K^4 + \gamma _4^0 K^2 \varOmega ^2 +\gamma _5^0 \varOmega ^4= 0. \end{aligned}$$

It can be also factorised as

$$\begin{aligned} \left( K^2\rho _0-\varOmega ^2\right) \left\{ h_{12} h_{32}\left( K^2 \rho _0-\varOmega ^2 \right) +\mu \rho _0(h_{12}+h_{32})\right\} =0. \end{aligned}$$

(12)

Figure 2 demonstrates a good agreement between two exact dispersion curves calculated from transcendental relation (5) and polynomial approximation (12) for the chosen set of parameters. In this figure, $\varOmega _{sh}\approx 0.18$ and $|K_{bl}| \approx 0.13$, according to asymptotic formulae (8) and (10), respectively.

For the fundamental non-dispersive mode and the first harmonic, we have

$$\begin{aligned} \varOmega ^2 = \rho _0 K^2 \end{aligned}$$

(13)

and

$$\begin{aligned} \varOmega ^2=\frac{\rho _0}{h_{12}h_{32}} \left\{ \mu (h_{12}+h_{32})+h_{12}h_{32} K^2\right\} , \end{aligned}$$

(14)

respectively. It is worth mentioning that approximation (13) is valid at least over the whole range $K \sim \varOmega \ll 1$. We also note that if $K=0$ in (14) then we arrive at the expression for the cut-off frequency (8), which is of order $\sqrt{\mu }$. Alternatively, setting $\varOmega =0$ in this equation, we get (10) for K. Hence, asymptotic formula (14) is valid for both quasi-static ($\varOmega \ll \sqrt{\mu }$) and near cut-off ($\varOmega \sim K \sim \sqrt{\mu }$) behaviour. Moreover, at $\sqrt{\mu } \ll K \ll 1$ it coincides at leading order with (13).

Fig. 3

Numerical solution of dispersion relation (5) (solid line) together with asymptotic expansions (12) (dashed line) for $h_{12} = 1.0$, $h_{32} = 1.5$, $\mu = 0.01$ and $\rho = 0.02$

4 Derivation of 1D equations of motion

Introduce local dimensionless thickness variables $\xi _{2i}$, $i=1,2,3$ in such a way that they change from 0 to 1 across each layer

$$\begin{aligned}&\xi _{21}=\dfrac{1}{h_1}\left( x_2-\dfrac{h_2}{2}\right) , \quad \dfrac{h_2}{2}< x_2< \dfrac{h_2}{2} + h_1, \nonumber \\&\xi _{22}=\dfrac{1}{h_2}\left( x_2+\dfrac{h_2}{2}\right) ,\quad -\dfrac{h_2}{2}< x_2< \dfrac{h_2}{2},\nonumber \\&\xi _{23}=\dfrac{1}{h_3}\left( x_2+\dfrac{h_2}{2}+h_3 \right) ,\quad -h_3 - \dfrac{h_2}{2}< x_2 < -\dfrac{h_2}{2}. \end{aligned}$$

(15)

From (13) $\varOmega \sim K$. At the same time, (14) implies that $\varOmega \sim K \sim \sqrt{\mu }$. In the latter case, both (13) and (14) are valid. Motivated by this observation, we introduce the scaling

$$\begin{aligned} x_1=\dfrac{h_2}{\sqrt{\mu }}\xi _1, \quad t=\dfrac{h_2}{c_{22}\sqrt{\mu }}\tau . \end{aligned}$$

(16)

Then, the displacements and stresses can be normalised as

$$\begin{aligned} u_q=h_2 v^q, \quad \sigma _{13}^q=\mu _q \sqrt{\mu }S_{13}^q, \quad \sigma _{23}^q=\mu _2 S_{23}^q, \quad q=1,2,3. \end{aligned}$$

(17)

The dimensionless form of the equations in the previous section for layers 1 and 3 ($q = 1,3$) can be written as

$$\begin{aligned}&h_{q2}\dfrac{\partial S_{13}^q}{\partial \xi _1}+\dfrac{\partial S_{23}^q}{\partial \xi _{2q}}-\dfrac{h_{q2}}{\rho _0}\dfrac{\partial ^2 v^q}{\partial \tau ^2}=0, \end{aligned}$$

(18)

$$\begin{aligned}&S_{13}^q=\dfrac{\partial v^q}{\partial \xi _1}, \end{aligned}$$

(19)

$$\begin{aligned}&\mu h_{q2} S_{23}^q=\dfrac{\partial v^q}{\partial \xi _{2q}}, \end{aligned}$$

(20)

while for layer 2 we get

$$\begin{aligned}&\mu \dfrac{\partial S_{13}^2}{\partial \xi _1}+\dfrac{\partial S_{23}^2}{\partial \xi _{22}}-\mu \dfrac{\partial ^2 v^2}{\partial \tau ^2}=0, \end{aligned}$$

(21)

$$\begin{aligned}&S_{13}^2=\dfrac{\partial v^2}{\partial \xi _1}, \end{aligned}$$

(22)

$$\begin{aligned}&S_{23}^2=\dfrac{\partial v^2}{\partial \xi _{22}}. \end{aligned}$$

(23)

The continuity and boundary conditions become, respectively

$$\begin{aligned}&v^1 \big |_{\xi _{21}=0}=v^2 \big |_{\xi _{22}=1},\quad v^2 \big |_{\xi _{22}=0}=v^3 \big |_{\xi _{23}=1},\nonumber \\&S_{23}^1 \big |_{\xi _{21}=0}=S_{23}^2 \big |_{\xi _{22}=1},\quad S_{23}^2 \big |_{\xi _{22}=0}=S_{23}^3 \big |_{\xi _{23}=1}, \end{aligned}$$

(24)

and

$$\begin{aligned} S_{23}^1 \big |_{\xi _{21}=1} = \dfrac{F_1}{\mu _2} = f_1(\xi _1,\tau ), \quad S_{23}^3 \big |_{\xi _{23}=0} = \dfrac{F_3}{\mu _2} = f_3(\xi _1, \tau ). \end{aligned}$$

(25)

Now expand displacements and stresses into asymptotic series in small parameter $\mu$

$$\begin{aligned}&v^q=v_0^q+\mu v_1^q+ \cdots ,\nonumber \\&S_{j3}^q = S_{j3,0}^q + \mu S_{j3,1}^q+ \cdots , \quad q=1,2,3; \quad j=1,2. \end{aligned}$$

(26)

At leading order, we have for $q=1,3$

$$\begin{aligned}&h_{q2}\dfrac{\partial S_{13,0}^q}{\partial \xi _1}+\dfrac{\partial S_{23,0}^q}{\partial \xi _{2q}}-\dfrac{h_{q2}}{\rho _0}\dfrac{\partial ^2 v_0^q}{\partial \tau ^2}=0, \end{aligned}$$

(27)

$$\begin{aligned}&S_{13,0}^q=\dfrac{\partial v_0^q}{\partial \xi _1}, \end{aligned}$$

(28)

$$\begin{aligned}&\dfrac{\partial v_0^q}{\partial \xi _{2q}}=0, \end{aligned}$$

(29)

and for $q=2$

$$\begin{aligned} \dfrac{\partial S_{23,0}^2}{\partial \xi _{22}}=0, \quad S_{13,0}^2=\dfrac{\partial v_0^2}{\partial \xi _1}, \quad S_{23,0}^2=\dfrac{\partial v_0^2}{\partial \xi _{22}}. \end{aligned}$$

(30)

Continuity relations (24) together with boundary conditions (25) becomes

$$\begin{aligned}&v_0^1 \big |_{\xi _{21}=0}=v_0^2 \big |_{\xi _{22}=1}, \quad v_0^2 \big |_{\xi _{22}=0}=v_0^3 \big |_{\xi _{23}=1}, \end{aligned}$$

(31)

$$\begin{aligned}&S_{23,0}^1 \big |_{\xi _{21}=0}=S_{23,0}^2 \big |_{\xi _{22}=1}, \quad S_{23,0}^2 \big |_{\xi _{22}=0}=S_{23,0}^3 \big |_{\xi _{23}=1}, \end{aligned}$$

(32)

$$\begin{aligned}&S_{23,0}^1 \big |_{\xi _{21}=1} = f_1, \quad S_{23,0}^3 \big |_{\xi _{23}=0} = f_3. \end{aligned}$$

(33)

Next, we derive

$$\begin{aligned}&v_0^1 = w_1(\xi _1,\tau ),\quad v_0^3 = w_3(\xi _1, \tau ),\quad v_0^2=w_2 \xi _{22}+w_3, \end{aligned}$$

where

$$\begin{aligned} w_2=w_1-w_3, \end{aligned}$$

resulting in equations

$$\begin{aligned}&w_2 = f_1 + h_{12}\left( \dfrac{\partial ^2 w_1}{\partial \xi _1^2}-\dfrac{1}{\rho _0}\dfrac{\partial ^2 w_1}{\partial \tau ^2} \right) ,\nonumber \\&w_2 = f_3 - h_{32}\left( \dfrac{\partial ^2 w_3}{\partial \xi _1^2}-\dfrac{1}{\rho _0}\dfrac{\partial ^2 w_3}{\partial \tau ^2} \right) . \end{aligned}$$

(34)

Using above, we can derive an equation for $w_q$, $q=1,3$

$$\begin{aligned}&\left( \rho _0 \dfrac{\partial ^2 w_q}{\partial \xi _1^2} - \dfrac{\partial ^2 w_q}{\partial \tau ^2}\right) \left( \rho _0(h_{12}+h_{32})w_q \right. \nonumber \\&\quad - \left. h_{12}h_{32} \left( \rho _0 \dfrac{\partial ^2 w_q}{\partial \xi _1^2} - \dfrac{\partial ^2 w_q}{\partial \tau ^2}\right) \right) =0, \end{aligned}$$

(35)

which supports the same dispersion relation as (12) as might be expected.

In terms of stresses, we can derive equations

$$\begin{aligned}&S_{23,0}^2 = f_1 + h_{12}\left( \dfrac{\partial S_{13,0}^1}{\partial \xi _1}-\dfrac{1}{\rho _0}\dfrac{\partial ^2 w_1}{\partial \tau ^2} \right) ,\nonumber \\&S_{23,0}^2 = f_3 - h_{32}\left( \dfrac{\partial S_{13,0}^3}{\partial \xi _1}-\dfrac{1}{\rho _0}\dfrac{\partial ^2 w_3}{\partial \tau ^2} \right) , \end{aligned}$$

(36)

where

$$\begin{aligned}&S_{13,0}^q = \dfrac{\partial w_q}{\partial \xi _1}, \quad q=1,3, \end{aligned}$$

(37)

$$\begin{aligned}&S_{23,0}^2 = w_2. \end{aligned}$$

(38)

Thus,

$$\begin{aligned} \dfrac{\partial S_{13,0}^2}{\partial \xi _{22}} = S_{13,0}^1 - S_{13,0}^3. \end{aligned}$$

(39)

In what follows, we also need the equations

$$\begin{aligned}&\dfrac{\partial }{\partial \xi _1} \left( h_{12}S_{13,0}^1+h_{32}S_{13,0}^3 \right) -\dfrac{1}{\rho _0} \dfrac{\partial ^2}{\partial \tau ^2}\left( h_{12}w_1 + h_{32}w_3 \right) = f_3-f_1,\nonumber \\&\dfrac{\partial ^2 S_{13,0}^2}{\partial \xi _1 \partial \xi _{22}} - \left( \dfrac{1}{h_{12}}+\dfrac{1}{h_{32}} \right) S_{23,0}^2 -\dfrac{1}{\rho _0}\dfrac{\partial ^2 w_2}{\partial \tau ^2} =-\dfrac{f_3}{h_{32}}-\dfrac{f_1}{h_{12}}, \end{aligned}$$

(40)

obtained as a linear combination of the equations in (36). Here, the first equation corresponds to the outer stiff layers, while the second one governs the motion of the soft middle layer.

5 Equations of motion in stress resultants and stress couples

As usual for thin plates and shells [21, 33], we define, starting from (17) and (26)

$$\begin{aligned}&N = \int _{h_2/2}^{h_2/2+h_1} \sigma _{13}^1 \mathrm{d}x_2 + \int _{-h_2/2-h_3}^{-h_2/2} \sigma _{13}^3 \mathrm{d}x_2 \nonumber \\&\quad \approx \mu _1 \sqrt{\mu } \left( h_1 S_{13,0}^1+h_3 S_{13,0}^3 \right) ,\nonumber \\&T = \int _{-h_2/2}^{h_2/2} \sigma _{23}^2 \mathrm{d}x_2 \approx h_2 \mu _2 S_{23,0}^2, \nonumber \\&G = \int _{-h_2 / 2}^{h_2 / 2} \sigma _{13}^2 x_2 \mathrm{d}x_2 \approx \mu _2 \sqrt{\mu } h_2^2 \int _0^1 S_{13,0}^2 \left( \xi _{22} - \dfrac{1}{2} \right) \mathrm{d} \xi _{22}\nonumber \\&\quad = \dfrac{\mu _2 \sqrt{\mu } h_2^2}{12} \dfrac{\partial S_{13,0}^2}{\partial \xi _{22}}, \end{aligned}$$

(41)

where stress resultant N corresponds to stiff layers, while the stress resultant T and stress couple G are associated with the soft layer. Introducing the average displacement U and the angle of rotation $\phi$ as

$$\begin{aligned} U = \dfrac{h_1 u_{1}+h_3 u_{3}}{h_1+h_3} \approx \dfrac{h_2(h_1 w_{1}+h_3 w_{3})}{h_1+h_3}, \quad \phi =\dfrac{u_{1}-u_{3}}{h_2}\approx w_2, \end{aligned}$$

(42)

we can re-write above equations (40) in terms of integral quantities defined in (41) and (42)

$$\begin{aligned}&\dfrac{\partial N}{\partial x_1} - \rho _1(h_{1}+h_{3}) \dfrac{\partial ^2 U}{\partial t^2} = F_3-F_1,\nonumber \\&\dfrac{12}{h_2 \mu } \dfrac{\partial G}{\partial x_1} - \left( \dfrac{1}{h_1} +\dfrac{1}{h_{3}} \right) T -\rho _1 h_2^2 \dfrac{\partial ^2 \phi }{\partial t^2} =-h_2\left( \dfrac{F_3}{h_3} + \dfrac{F_1}{h_1} \right) . \end{aligned}$$

(43)

Forces T, N and G at leading order can be expressed in terms of U and $\phi$ as

$$\begin{aligned}&T = h_2 \mu _2 \phi ,\nonumber \\&N = \mu _1 \left( h_{1} + h_{3} \right) \dfrac{\partial U}{\partial x_1},\nonumber \\&G = \dfrac{\mu _2 h_2^3}{12} \dfrac{\partial \phi }{\partial x_1}. \end{aligned}$$

(44)

Finally, Eq. (43) can be presented as

$$\begin{aligned}&\mu _1 (h_1+h_3)\dfrac{\partial ^2 U}{\partial x_1^2} - \rho _1 (h_1+h_3) \dfrac{\partial ^2 U}{\partial t^2} = F_3 - F_1, \nonumber \\&\mu _1 h_2 \dfrac{\partial ^2 \phi }{\partial x_1^2} - \mu _2 \left( \dfrac{1}{h_{1}}+\dfrac{1}{h_{3}} \right) \phi - \rho _1 h_2 \dfrac{\partial ^2 \phi }{\partial t^2} = -\left( \dfrac{F_3}{h_3}+\dfrac{F_1}{h_1} \right) . \end{aligned}$$

(45)

6 Derivation of boundary conditions

First consider static equilibrium of a semi-infinite three-layered strip ($0\leqslant x_1<+\infty$, $-h_3-h_2/ 2 \leqslant x_2 \leqslant h_2/ 2 + h_1$) with the geometrical and mechanical properties specified in Sect. 2. Let the strip faces are traction free, while its left edge $x_1=0$ is subject to prescribed stress $p(x_2)$

$$\begin{aligned} \sigma _{13}^q \big |_{x_1=0} = p(x_2), \quad q=1,2,3. \end{aligned}$$

(46)

Our goal is to find the so-called decay conditions on the function p when

$$\begin{aligned} \sigma _{13}^q \big |_{x_1=+\infty }=0, \quad q=1,2,3. \end{aligned}$$

(47)

Moreover, we require the related boundary layer to be localised over the narrow vicinity of the edge of width h ($h \sim h_1 \sim h_2 \sim h_3$), which does not depend on the small contrast parameter $\mu$, defined above. Thus, we assume

$$\begin{aligned} \dfrac{\partial }{\partial x_1} \sim \dfrac{\partial }{\partial x_2} \sim \dfrac{1}{h}. \end{aligned}$$

(48)

Let us start from the static counterpart of the equations (1), i.e.

$$\begin{aligned} \dfrac{\partial \sigma _{13}^q}{\partial x_1} + \dfrac{\partial \sigma _{23}^q}{\partial x_2} = 0, \quad q=1,2,3, \end{aligned}$$

(49)

subject to homogeneous boundary conditions along the faces (4), setting $F_1=F_3=0$ and continuity conditions (3), together with (46) and (47). Integrating the equation of motion for the upper layer ($q=1$) over the domain $0 \leqslant x_1 < + \infty$ and $h_2 \leqslant x_2 \leqslant h_2+h_1$ and applying the aforementioned continuity and boundary conditions, we obtain

$$\begin{aligned}&\int _{0}^{+\infty } \int _{h_2 / 2}^{h_2 / 2+h_1} \left( \dfrac{\partial \sigma _{13}^1}{\partial x_1} + \dfrac{\partial \sigma _{23}^1}{\partial x_2} \right) \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad =\int _{h_2 / 2}^{h_2 / 2+h_1}\sigma _{13}^1 \Big |_{x_1=0}^{+\infty }~\mathrm{d}x_2 + \int _{0}^{+\infty }\sigma _{23}^1 \Big |_{x_2=h_2 / 2}^{h_2 / 2+h_1} ~\mathrm{d}x_1 \nonumber \\&\quad =-\int _{h_2 / 2}^{h_2 / 2+h_1} p(x_2) \mathrm{d}x_2 - \int _{0}^{+\infty } \sigma _{23}^1\Big |_{x_2=h_2 / 2} \mathrm{d}x_1=0. \end{aligned}$$

(50)

Hence,

$$\begin{aligned} \int _{0}^{+\infty } \sigma _{23}^1\Big |_{x_2=h_2 / 2} \mathrm{d}x_1 = -\int _{h_2 / 2}^{h_2 / 2+h_1} p(x_2) \mathrm{d}x_2 \end{aligned}$$

(51)

Similarly, for the bottom layer ($q=3$) we derive

$$\begin{aligned}&\int _{0}^{+\infty } \int _{-h_2 / 2-h_3}^{-h_2 / 2} \left( \dfrac{\partial \sigma _{13}^3}{\partial x_1} + \dfrac{\partial \sigma _{23}^3}{\partial x_2} \right) \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad =-\int _{-h_2 / 2-h_3}^{-h_2 / 2} p(x_2) \mathrm{d}x_2 + \int _{0}^{+\infty } \sigma _{23}^3 \Big |_{x_2=-h_2 / 2} \mathrm{d}x_1=0, \end{aligned}$$

(52)

therefore,

$$\begin{aligned} \int _{0}^{+\infty } \sigma _{23}^3 \Big |_{x_2=-h_2 / 2} \mathrm{d}x_1=\int _{-h_2 / 2-h_3}^{-h_2 / 2} p(x_2) \mathrm{d}x_2. \end{aligned}$$

(53)

For the middle layer ($q=2$), we first integrate the associated equation of motion, resulting in

$$\begin{aligned}&\int _{0}^{+\infty } \int _{-h_2 / 2}^{h_2 / 2} \left( \dfrac{\partial \sigma _{13}^2}{\partial x_1} + \dfrac{\partial \sigma _{23}^2}{\partial x_2} \right) \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad =-\int _{-h_2 / 2}^{h_2 / 2} p(x_2)\mathrm{d}x_2 + \int _0^{+\infty } \sigma _{23}^2\Big |_{x_2=h_2 / 2} \mathrm{d}x_1 - \int _0^{+\infty } \sigma _{23}^2\Big |_{x_2=-h_2 / 2} \mathrm{d}x_1=0. \end{aligned}$$

(54)

Now, we substitute (51) and (53) into the latter, taking into account the continuity conditions. As might be expected, the following exact result corresponds to the conventional decay condition, expressing the classical formulation of the Saint-Venant principle. It manifests self-equilibrium of the external load and is given by

$$\begin{aligned} \int _{-h_2 / 2-h_3}^{h_2 / 2 +h_1}p(x_2) \mathrm{d}x_2 = 0. \end{aligned}$$

(55)

Next, we multiply the equation of motion for the middle layer by $x_2$ and integrate again over its area. We obtain

$$\begin{aligned}&\int _{0}^{+\infty } \int _{-h_2 / 2}^{h_2 / 2} x_2 \left( \dfrac{\partial \sigma _{13}^2}{\partial x_1} + \dfrac{\partial \sigma _{23}^2}{\partial x_2} \right) \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad =\int _{-h_2 / 2}^{h_2 / 2}x_2\sigma _{13}^2 \Big |_{x_1=0}^{+\infty } \mathrm{d}x_2 + \int _{0}^{+\infty } \int _{-h_2 / 2}^{h_2 / 2} x_2 \dfrac{\partial \sigma _{23}^2}{\partial x_2} \mathrm{d}x_1 \mathrm{d}x_2 \nonumber \\&\quad =-\int _{-h_2 / 2}^{h_2 / 2} x_2 p(x_2)\mathrm{d}x_2 + \int _0^{+\infty }\left( x_2\sigma _{23}^2\Big |_{x_2=-h_2 / 2}^{h_2 / 2} - \int _{-h_2 / 2}^{h_2 / 2} \sigma _{23}^2 \mathrm{d}x_2 \right) \mathrm{d}x_1\nonumber \\&\quad =-\int _{-h_2 / 2}^{h_2 / 2} x_2 p(x_2)\mathrm{d}x_2 + \dfrac{h_2}{2} \int _{0}^{+\infty } \left( \sigma _{23}^2\Big |_{x_2=h_2 / 2}+\sigma _{23}^2\Big |_{x_2=-h_2 / 2} \right) \mathrm{d}x_1 \nonumber \\&\qquad -\int _0^{+\infty } \int _{-h_2 / 2}^{h_2 / 2} \sigma _{23}^2 \mathrm{d}x_2 \mathrm{d}x_1 \nonumber \\&\qquad \approx -\int _{-h_2 / 2}^{h_2 / 2} x_2 p(x_2)\mathrm{d}x_2 + \dfrac{h_2}{2} \int _{0}^{+\infty } \left( \sigma _{23}^2\Big |_{x_2=h_2 / 2}+\sigma _{23}^2\Big |_{x_2=-h_2 / 2} \right) \mathrm{d}x_1 =0, \end{aligned}$$

(56)

where we have neglected the asymptotically small $O(\mu )$ term

$$\begin{aligned} \int _0^{+\infty } \int _{-h_2 / 2}^{h_2 / 2} \sigma _{23}^2 \mathrm{d}x_2 \mathrm{d}x_1 = \mu _2 \int _0^{+\infty } u_2 \Big |_{x_2=-h_2 / 2}^{h_2 / 2}\mathrm{d}x_1 \sim \mu . \end{aligned}$$

(57)

This is due to the effect of contrast, resulting in a sort of squeezing of the softer middle layer by the stiff outer layers. In fact, we may readily deduce that in the last formula $\sigma _{23}^2 \sim p$ while $u_2(x_1, h_2 / 2) = u_1(x_1, h_2 / 2)\sim \dfrac{h \sigma _{23}^1}{\mu _1} \sim \dfrac{h p}{\mu _1}$ and $u_2(x_1, -h_2 / 2) = u_3(x_1, -h_2 / 2)\sim \dfrac{h \sigma _{23}^3}{\mu _1} \sim \dfrac{h p}{\mu _1}$. These asymptotic estimations follow from the aforementioned condition on the boundary layer given by (48). Next, substituting (51) and (53) into (54) we obtain the second decay condition on the prescribed edge load p

$$\begin{aligned} \int _{-h_2 / 2}^{h_2 / 2} x_2 p(x_2) \mathrm{d}x_2 + \dfrac{h_2}{2} \int _{h_2 / 2}^{h_2 / 2+h_1}p(x_2)\mathrm{d}x_2 - \dfrac{h_2}{2} \int _{-h_2 / 2-h_3}^{-h_2 / 2} p(x_2) \mathrm{d}x_2=0, \end{aligned}$$

(58)

which is, in contrast with the first "exact" condition (55), is of an asymptotic nature and holds only for high contrast laminates. At $h_1=h_3$ and $p(-x_2)=-p(x_2)$, the last formula reduces to decay conditions (88) derived in “Appendix 2” using Laplace transform technique.

It can be easily shown, see e.g. [39], that obtained decay conditions (55) and (58) are also valid at leading order for the low-frequency setup considered in the paper ($\partial / \partial t \ll h \sqrt{\rho _k / \mu _k}, \quad k=1,2$). Let us then adopt the latter for deriving the leading order boundary conditions at the edge $x_1=0$ of the laminate governed by formulae (1)-(4), subject to an arbitrary low-frequency loading $P(x_2,t)$, i.e.

$$\begin{aligned} \sigma _{13}^{q} \big |_{x_1=0} = P(x_2,t), \quad q=1,2,3. \end{aligned}$$

(59)

It is obvious that the function $P(x_2,t)$ is not assumed to satisfy two decay conditions above in contrast to the function $p(x_2)$.

As usual, see [19, 37, 41] for greater detail, insert the discrepancy of the prescribed edge load P and stresses $\sigma _{13}^q$, resulting from the equations of motion established in Sect. 5, into the decay conditions. Neglecting asymptotically secondary stress $\sigma _{13}^2$, see formula (17), we set in (55) and (58)

$$\begin{aligned}&p=P-\sigma _{13}^1, \quad \dfrac{h_2}{2}< x_2 < \dfrac{h_2}{2} + h_1, \end{aligned}$$

(60)

$$\begin{aligned}&p=P, \quad -\dfrac{h_2}{2}< x_2 < \dfrac{h_2}{2}, \end{aligned}$$

(61)

$$\begin{aligned}&p=P-\sigma _{13}^3, \quad -h_3 - \dfrac{h_2}{2}< x_2 < -\dfrac{h_2}{2}, \end{aligned}$$

(62)

having

$$\begin{aligned} \int _{h_2 / 2}^{h_2 / 2 + h_1} (P-\sigma _{13}^1) \mathrm{d}x_2 + \int _{-h_2 / 2}^{h_2 / 2} P \mathrm{d}x_2 + \int _{-h_3-h_2 / 2}^{-h_2 / 2 } (P-\sigma _{13}^3) \mathrm{d}x_2 =0, \end{aligned}$$

(63)

and

$$\begin{aligned} \int _{-h_2 / 2}^{h_2 / 2} x_2 P \mathrm{d}x_2 + \dfrac{h_2}{2} \int _{h_2 / 2}^{h_2 / 2+h_1}(P-\sigma _{13}^1)\mathrm{d}x_2 - \dfrac{h_2}{2} \int _{-h_2 / 2-h_3}^{-h_2 / 2} (P-\sigma _{13}^3) \mathrm{d}x_2=0, \end{aligned}$$

(64)

Finally, expressing $\sigma _{13}^1$ and $\sigma _{13}^3$ in (63) through N by formulae (41), first boundary condition becomes

$$\begin{aligned} N=\int _{-h_3 -h_2 / 2}^{h_2 / 2 + h_1} P \mathrm{d}x_2. \end{aligned}$$

(65)

Similarly, expressing second condition (64) through approximate formulae for N and G together with equation (39), we obtain

$$\begin{aligned}&\int _{-h_2 / 2}^{h_2 / 2} x_2 P \mathrm{d}x_2 + \dfrac{h_2}{2} \int _{h_2 / 2}^{h_2 / 2+h_1}Pdx_2 - \dfrac{h_2}{2} \int _{-h_2 / 2-h_3}^{-h_2 / 2} P \mathrm{d}x_2 \nonumber \\&\quad -\dfrac{h_2}{2} \left( \dfrac{h_1-h_3}{h_1+h_3} N + \dfrac{24 h_{1} h_{3}}{\mu h_2^2 (h_1+h_3)} G \right) =0. \end{aligned}$$

(66)

Finally, using (65) we arrive at the second boundary condition

$$\begin{aligned}&G= \dfrac{\mu h_2^2(h_1 + h_3)}{24 h_{1}h_{3}} \Bigg (\dfrac{2}{h_2} \int _{-h_2 / 2}^{h_2 / 2} x_2 P \mathrm{d}x_2 + \int _{h_2 / 2}^{h_2 / 2+h_1}Pdx_2 \nonumber \\&\quad - \int _{-h_2 / 2-h_3}^{-h_2 / 2} P \mathrm{d}x_2 - \dfrac{h_1-h_3}{h_1+h_3}\int _{-h_2 / 2 -h_3}^{h_2 / 2 + h_1} P \mathrm{d}x_2 \Bigg ). \end{aligned}$$

(67)

Derived boundary conditions (65) and (67) correspond to the first and second equations in (43), respectively. They can be also expressed through the average displacement U and the angle of rotation $\phi$ using (44).

7 Concluding remarks

The consideration in the paper is seemingly the optimal toy scalar problem for elucidating the effect of high contrast. In spite asymmetry of the laminate, the leading order shortened equations governing the fundamental mode and the low-frequency harmonic, (13) and (14), are not coupled. The findings in the paper facilitate asymptotic analysis of various more sophisticated formulations for strongly inhomogeneous thin structures, including vector problems for multi-layered laminates with a variety of contrast types.

It is demonstrated that the harmonic of interest describes both a static (and quasi-static) slow decay and near cut-off long wave propagation, see (14). In this case, the associated ‘weak’ boundary layer, observed earlier in statics of high-contrast laminates, e.g. see [40], can be naturally embedded into the low-dimensional theory for the interior domain, see the second 1D equation in (43).

For the first time, asymptotically justified boundary conditions (65) and (67) are established using the Saint-Venant principle adapted for a high-contrast laminate. It is remarkable that the extra approximate decay condition (58) isn’t directly related to the overall equilibrium as the conventional ‘exact’ decay condition (55).

Appendices

Appendix 1

Coefficients $\gamma _i$ in (11) are given by

$$\begin{aligned} \begin{aligned}&\gamma _1 = \mu \left( h_{12}+h_{32}+\mu \right) ,\\&\gamma _2=-\frac{\mu ^2}{\rho }\left( h_{12}+h_{32}+\rho \right) ,\\&\gamma _3=h_{12}h_{32}-\frac{\mu }{3} \left( h_{12}^3+h_{32}^3+ \mu \right) ,\\&\gamma _4=\frac{2\mu }{3\rho }\left( h_{12}^3\mu +h_{32}^3\mu -3h_{12}h_{32}+\mu \rho \right) ,\\&\gamma _5 = -\frac{\mu ^2}{3\rho ^2}\left( h_{12}^3\mu +h_{32}^3\mu -3h_{12}h_{32}+\rho ^2\right) ,\\&\gamma _6 = \frac{2\mu }{15} \left( h_{12}^5+h_{32}^5 +\mu \right) -\frac{h_{12}h_{32}}{3}\left( h_{12}^2+h_{32}^2+1\right) ,\\&\gamma _7 = -\frac{1}{15\rho }\left( 6\mu ^2\left( h_{12}^5+h_{32}^5+\rho \right) -5h_{12} h_{32}\left( 3h_{12}^2\mu +3h_{32}^2\mu +2\mu +\rho \right) \right) ,\\&\gamma _8 = \frac{\mu }{15\rho ^2}\left( 6\mu \left( h_{12}^5\mu +h_{32}^5\mu +\rho ^2 \right) - 5h_{12}h_{32}\left( 3h_{12}^2\mu +3h_{32}^2\mu +\mu +2\rho \right) \right) ,\\&\gamma _9 = -\frac{\mu ^2}{15\rho ^3} \left( 2\left( h_{12}^5\mu ^2+h_{32}^5\mu ^2+\rho ^3\right) -5h_{12}h_{32}\left( h_{12}^2\mu +h_{32}^2\mu +\rho \right) \right) . \end{aligned} \end{aligned}$$

At leading order coefficients $\gamma _i$ are given below

$$\begin{aligned}&\gamma _1^0 = \left( h_{12}+h_{32}\right) \mu ,\nonumber \\&\gamma _2^0=-\frac{h_{12}+h_{32}}{\rho _0}\mu ,\nonumber \\&\gamma _3^0=h_{12}h_{32},\nonumber \\&\gamma _4^0=-\frac{2h_{12}h_{32}}{\rho _0},\nonumber \\&\gamma _5^0 = \frac{h_{12}h_{32}}{\rho _0^2},\nonumber \\&\gamma _6^0 = -\frac{h_{12}h_{32}}{3}\left( h_{12}^2+h_{32}^2+1\right) ,\nonumber \\&\gamma _7^0 = \frac{h_{12}h_{32}}{3\rho _0}\left( 3h_{12}^2+3h_{32}^2+\rho _0+2\right) ,\nonumber \\&\gamma _8^0 = -\frac{h_{12} h_{32}}{3\rho _0^2}\left( 3h_{12}^2+3h_{32}^2+2\rho _0+1\right) ,\nonumber \\&\gamma _9^0 = \frac{h_{12}h_{32}}{3\rho _0^3}\left( h_{12}^2+h_{32}^2+\rho _0\right) , \end{aligned}$$

(68)

where $\rho _0=\rho / \mu$ .

Appendix 2

Let us find decay conditions for a symmetric three-layered plate ($h_1=h_3$) with traction free faces using Laplace transform technique. We restrict ourselves with the motion for which the displacements of the laminate are odd functions in $x_2$, i.e. $u_2(x_1,-x_2)=-u_2(x_1,x_2)$, $u_3(x_1, -x_2)=u_1(x_1,x_2)$. Let functions $U_q(s,x_2)$ denote Laplace transform of displacements $u_q$, $q=1,2,3$, i.e.

$$\begin{aligned} U_q(s,x_2)=\int _{0}^{\infty } u_q(x_1,x_2) e^{-sx_1}\mathrm{d}x_1, \end{aligned}$$

(69)

where s is Laplace transform parameter. Transforming equilibrium equations (49), we get

$$\begin{aligned} \dfrac{\partial ^2 U_q}{\partial x_2^2 } + s^2U_q = R_q, \end{aligned}$$

(70)

where $R_q(s,x_2)$ are defined through

$$\begin{aligned} R_q(s,x_2) = su_q \big |_{x_1=0} + \dfrac{\partial u_q}{\partial x_1}\bigg |_{x_1=0} = su_q \big |_{x_1=0} + \dfrac{p(x_2)}{\mu _q}. \end{aligned}$$

(71)

Solving equations (70) for odd displacements, we have

$$\begin{aligned} U_1=A_1(s) \sin sx_2 + A_2(s)\cos sx_2 + \dfrac{1}{s}\int _0^{x_2} R_1(s,x'_2)\sin s(x_2-x'_2)\mathrm{d}x'_2, \end{aligned}$$

(72)

and

$$\begin{aligned} U_2=B_1(s) \sin sx_2 + \dfrac{1}{s}\int _0^{x_2} R_2(s,x'_2)\sin s(x_2-x'_2)\mathrm{d}x'_2, \end{aligned}$$

(73)

where unknown functions $A_1$, $A_2$ and $B_1$ are determined from the transformed boundary and continuity conditions and given by

$$\begin{aligned} A_1(s)&= D^{-1}(s) \Big \{ -C_1\left( h_1+\frac{h_2}{2}\right) \left( \mu \cos ^2 \frac{sh_2}{2} + \sin ^2 \dfrac{sh_2}{2}\right) \nonumber \\&\quad + \left( S_2\left( \frac{h_2}{2}\right) -S_1\left( \frac{h_2}{2}\right) \right) \mu \sin \left( sh_1+\frac{sh_2}{2}\right) \cos \frac{sh_2}{2} \nonumber \\&\quad + \left( C_1\left( \frac{h_2}{2}\right) -\mu C_2\left( \frac{h_2}{2}\right) \right) \sin \left( sh_1+\frac{sh_2}{2}\right) \sin \frac{sh_2}{2} \Big \}, \end{aligned}$$

(74)

$$\begin{aligned} A_2(s)&= D^{-1}(s) \Big \{ C_1\left( h_1+\frac{h_2}{2}\right) (\mu -1) \sin \frac{sh_2}{2} \cos \frac{sh_2}{2} \nonumber \\&\quad + \left( S_2\left( \frac{h_2}{2}\right) -S_1\left( \frac{h_2}{2}\right) \right) \mu \cos \left( sh_1+\frac{sh_2}{2}\right) \cos \frac{sh_2}{2} \nonumber \\&\quad + \left( C_1\left( \frac{h_2}{2}\right) -\mu C_2\left( \frac{h_2}{2}\right) \right) \cos \left( sh_1+\frac{sh_2}{2}\right) \sin \frac{sh_2}{2} \Big \}, \end{aligned}$$

(75)

and

$$\begin{aligned} B_1(s)&= D^{-1}(s) \Big \{ -C_1\left( h_1+\frac{h_2}{2}\right) + \left( S_2\left( \frac{h_2}{2}\right) -S_1\left( \frac{h_2}{2}\right) \right) \sin sh_1 \nonumber \\&\quad + \left( C_1\left( \frac{h_2}{2}\right) -\mu C_2\left( \frac{h_2}{2}\right) \right) \cos sh_1 \Big \}, \end{aligned}$$

(76)

where

$$\begin{aligned} D(s) = s\left( \mu \cos s h_1 \cos \frac{sh_2}{2} - \sin s h_1 \sin \frac{sh_2}{2} \right) , \end{aligned}$$

(77)

and

$$\begin{aligned} C_{q}(s,x_2)= & {} \int _0^{x_2} R_q(x'_2)\cos s(x_2-x'_2)\mathrm{d}x'_2, \end{aligned}$$

(78)

$$\begin{aligned} S_{q}(s,x_2)= & {} \int _0^{x_2} R_q(x'_2)\sin s(x_2-x'_2)\mathrm{d}x'_2, \quad q=1,2. \end{aligned}$$

(79)

The sought for displacements is expressed through Mellin integrals as

$$\begin{aligned} u_q(x_1,x_2)=\dfrac{1}{2\pi i} \int _{\delta -i\infty }^{\delta +i\infty } U(s,x_2)e^{sx_1} \mathrm{d}s \end{aligned}$$

(80)

for $\delta > 0$. These integrals can be found using the residue theory

$$\begin{aligned} u_q(x_1,x_2) = \sum _{n=0}^{\infty } \text {Res}_{s_{n}} \{ U_q(s,x_2) e^{s x_1}\}, \end{aligned}$$

(81)

where only small poles $s_n$, corresponding to unwanted slow decay are of the concern, see also [38, 39].

At $\mu \ll 1$ and $s \ll 1$, the leading order asymptotic behaviour of denominator (77) is given by

$$\begin{aligned} D(s)= -2 s (h_1h_2 s^2-\mu ), \end{aligned}$$

(82)

resulting in two small non-zero roots

$$\begin{aligned} s^{\pm }=\pm \sqrt{\dfrac{2\mu }{h_1 h_2}}. \end{aligned}$$

(83)

The associated residues are

$$\begin{aligned}&\text {Res}_{s^{\pm }} \ \{ U_1(s,x_2) e^{s x_1}\}= \text {Res}_{s^{\pm }} \left\{ D^{-1}(s)\left( A_1(s) \sin sx_2 + A_2(s)\cos sx_2 \right) e^{s x_1} \right\} , \nonumber \\&\text {Res}_{s^{\pm }} \ \{ U_2(s,x_2) e^{s x_1}\}= \text {Res}_{s^{\pm }}\left\{ D^{-1}(s)B_1(s) \sin sx_2 e^{s x_1}\right\} , \end{aligned}$$

(84)

where D(s) is defined in (82).

Expanding now the numerators in these relations at $\mu \ll 1$ and $s \sim \sqrt{\mu }$ and using the formula

$$\begin{aligned} R_2= su_2 \big |_{x_1=0} + \dfrac{p(x_2)}{\mu \mu _1}, \end{aligned}$$

(85)

we obtain at leading order

$$\begin{aligned} \text {Res}_{s^{\pm }}= \pm \dfrac{\sqrt{2 h_2}}{4 \mu _1\sqrt{h_1} \sqrt{\mu }} \ \left( \int _{h_2/2}^{h_2/2+h_1} p(x_2)\mathrm{d}x_2+\dfrac{2}{h_2} \int _{0}^{h_2/2} p(x_2) x_2 \mathrm{d}x_2\right) , \end{aligned}$$

(86)

and

$$\begin{aligned} \text {Res}_{s^{\pm }}= \pm \dfrac{\sqrt{2} x_2}{2 \mu _1\sqrt{h_1 h_2} \sqrt{\mu }} \left( \int _{h_2/2}^{h_2/2+h_1} p(x_2)\mathrm{d}x_2+\dfrac{2}{h_2} \int _{0}^{h_2/2} p(x_2) x_2 \mathrm{d}x_2 \right) , \end{aligned}$$

(87)

for $u_1$ and $u_2$, respectively.

These residues diminish at

$$\begin{aligned} \int _{h_2/2}^{h_2/2 + h_1} p(x_2)\mathrm{d}x_2 + \dfrac{2}{h_2}\int _{0}^{h_2/2} p(x_2) x_2 \mathrm{d}x_2 = 0, \end{aligned}$$

(88)

ensuring strong decay of the boundary layer.