Abstract
In the Lagrangian approach to 2-dimensional sigma models, B-fields and D-branes contribute topological terms to the action of worldsheets of both open and closed strings. We show that these terms naturally fit into a 2-dimensional, smooth open-closed functorial field theory (FFT) in the sense of Atiyah, Segal, and Stolz–Teichner. We give a detailed construction of this smooth FFT, based on the definition of a suitable smooth bordism category. In this bordism category, all manifolds are equipped with a smooth map to a spacetime target manifold. Further, the object manifolds are allowed to have boundaries; these are the endpoints of open strings stretched between D-branes. The values of our FFT are obtained from the B-field and its D-branes via transgression. Our construction generalises work of Bunke–Turner–Willerton to include open strings. At the same time, it generalises work of Moore–Segal about open-closed TQFTs to include target spaces. We provide a number of further features of our FFT: we show that it depends functorially on the B-field and the D-branes, we show that it is thin homotopy invariant, and we show that it comes equipped with a positive reflection structure in the sense of Freed–Hopkins. Finally, we describe how our construction is related to the classification of open-closed TQFTs obtained by Lauda–Pfeiffer.
Similar content being viewed by others
1 Introduction
A topological quantum field theory (TQFT) is a symmetric monoidal functor

where \(\mathscr {B}\mathrm {ord}_d\) is a suitable category of closed oriented \((d{-}1)\)-manifolds and d-dimensional bordisms, symmetric monoidal under the disjoint union of manifolds, and where  is the category of finite-dimensional complex vector spaces, monoidal under the tensor product. The axioms of the symmetric monoidal functor \(\mathscr {Z}\) implement abstractly the sewing laws of the path integral. The idea of this formalisation goes back to Atiyah [2] and Segal [33, 34]. We refer to [3] for more information about the physical perspective. TQFTs are very rich and interesting objects. A crucial feature is that they can be classified in terms of algebraic objects: one chooses a presentation of the category \(\mathscr {B}\mathrm {ord}_d\) in terms of generators and relations and then translates these into algebraic data on the target side. In this way, for example, 2-dimensional TQFTs correspond to commutative Frobenius algebras [1, 13, 23].
is the category of finite-dimensional complex vector spaces, monoidal under the tensor product. The axioms of the symmetric monoidal functor \(\mathscr {Z}\) implement abstractly the sewing laws of the path integral. The idea of this formalisation goes back to Atiyah [2] and Segal [33, 34]. We refer to [3] for more information about the physical perspective. TQFTs are very rich and interesting objects. A crucial feature is that they can be classified in terms of algebraic objects: one chooses a presentation of the category \(\mathscr {B}\mathrm {ord}_d\) in terms of generators and relations and then translates these into algebraic data on the target side. In this way, for example, 2-dimensional TQFTs correspond to commutative Frobenius algebras [1, 13, 23].
There exist many interesting variations of the notion of a TQFT, which arise by including additional structure. In this article, we study four modifications, all at the same time, and show that the 2-dimensional sigma model with B-field and D-branes fits into this framework. Until now, only two special cases of this picture have been worked out. We shall sketch below separately the four modifications of the bordism category we study; all details are fully worked out in the main text.
(1) D-Branes We consider a set I of brane labels and form a new category \({\mathscr {OCB}\mathrm {ord}}_d^{I}\), whose objects are compact oriented \((d{-}1)\)-manifolds Y with boundary, with each boundary component equipped with a brane label \(i \in I\). Morphisms \(\Sigma :Y_0 \rightarrow Y_1\) are compact oriented d-manifolds with corners that now have an incoming boundary \(\partial _0 \Sigma \cong Y_0\), an outgoing boundary \(\partial _1 \Sigma \cong Y_1\), as well as additional brane boundary \(\partial _2 \Sigma \), whose components carry brane labels compatible with those of \(Y_0\) and \(Y_1\). Symmetric monoidal functors  are called open-closed TQFTs with D-brane labels I. In two dimensions, open-closed TQFTs have been discussed and classified by Lazaroiu [24], Moore-Segal [27], and Lauda-Pfeiffer [25]; they correspond to so-called I-coloured knowledgeable Frobenius algebras. Our motivation to include brane labels is string theory, where one needs to consider open and closed strings at the same time, and where the end-points of open strings are constrained to D-branes.
are called open-closed TQFTs with D-brane labels I. In two dimensions, open-closed TQFTs have been discussed and classified by Lazaroiu [24], Moore-Segal [27], and Lauda-Pfeiffer [25]; they correspond to so-called I-coloured knowledgeable Frobenius algebras. Our motivation to include brane labels is string theory, where one needs to consider open and closed strings at the same time, and where the end-points of open strings are constrained to D-branes.
(2) Reflection-positivity The bordism category \(\mathscr {B}\mathrm {ord}_d\) admits two canonical involutions, called dual \((..)^\vee \) and opposite \(\overline{(..)}\). The dual implements duals with respect to the symmetric monoidal structure, while the opposite is an a priori different operation that is usually not considered in the TQFT literature. The category  has similar involutions: the usual dual \(V^{\vee }\) and the complex conjugate \({\overline{V}}\) of a vector space V. While any monoidal functor sends duals to duals, demanding that a functor
has similar involutions: the usual dual \(V^{\vee }\) and the complex conjugate \({\overline{V}}\) of a vector space V. While any monoidal functor sends duals to duals, demanding that a functor  sends opposite bordisms to complex conjugate vector spaces is a constraint, and requires an additional structure called a reflection structure [15]. Basically, it consists of natural isomorphisms \(\overline{\mathscr {Z}(Y)} \cong \mathscr {Z}({\overline{Y}})\) for all objects Y of \(\mathscr {B}\mathrm {ord}_d\). It turns out that a reflection structure induces an isomorphism between \(\mathscr {Z}(Y)^\vee \) and \(\overline{\mathscr {Z}(Y)}\), and hence a non-degenerate hermitean form. A reflection structure on \(\mathscr {Z}\) is then called positive if that form is positive definite, for every object Y.
sends opposite bordisms to complex conjugate vector spaces is a constraint, and requires an additional structure called a reflection structure [15]. Basically, it consists of natural isomorphisms \(\overline{\mathscr {Z}(Y)} \cong \mathscr {Z}({\overline{Y}})\) for all objects Y of \(\mathscr {B}\mathrm {ord}_d\). It turns out that a reflection structure induces an isomorphism between \(\mathscr {Z}(Y)^\vee \) and \(\overline{\mathscr {Z}(Y)}\), and hence a non-degenerate hermitean form. A reflection structure on \(\mathscr {Z}\) is then called positive if that form is positive definite, for every object Y.
(3) Target spaces Searching for new invariants of manifolds, Turaev considered bordism categories where all manifolds are equipped with a homotopy class of maps into a fixed topological space [38]. Stolz-Teichner [35] considered an even more refined bordism category \(\mathscr {B}\mathrm {ord}_d(M)\), where all manifolds are endowed with smooth maps to a smooth manifold M, not taken up to homotopy. Symmetric monoidal functors  will be called functorial field theories (FFTs) on M. A FFT \(\mathscr {Z}\) on M may be invariant under changing the maps to M by homotopies and thus reduce to one of Turaev’s homotopy invariant FFTs. Often, however, FFTs are only invariant under thin homotopies, i.e. homotopies whose differential has at most rank d; these FFTs will be called thin homotopy invariant FFTs on M. Motivated by our construction of a FFT, we add a further property that has not been considered before: we call a FFT \(\mathscr {Z}\) superficial if it is thin homotopy invariant and, in addition, the values of \(\mathscr {Z}\) agree on two morphisms in \(\mathscr {B}\mathrm {ord}_d(M)\) with the same source and the same target whenever they have the same underlying d-manifold \(\Sigma \) and their (not necessarily homotopic) smooth maps \(\sigma , \sigma ' :\Sigma \rightarrow M\) are thin in the sense that their differential is of rank strictly less than d everywhere.
will be called functorial field theories (FFTs) on M. A FFT \(\mathscr {Z}\) on M may be invariant under changing the maps to M by homotopies and thus reduce to one of Turaev’s homotopy invariant FFTs. Often, however, FFTs are only invariant under thin homotopies, i.e. homotopies whose differential has at most rank d; these FFTs will be called thin homotopy invariant FFTs on M. Motivated by our construction of a FFT, we add a further property that has not been considered before: we call a FFT \(\mathscr {Z}\) superficial if it is thin homotopy invariant and, in addition, the values of \(\mathscr {Z}\) agree on two morphisms in \(\mathscr {B}\mathrm {ord}_d(M)\) with the same source and the same target whenever they have the same underlying d-manifold \(\Sigma \) and their (not necessarily homotopic) smooth maps \(\sigma , \sigma ' :\Sigma \rightarrow M\) are thin in the sense that their differential is of rank strictly less than d everywhere.
(4) Smoothness This becomes relevant upon including target spaces. In physical field theories, it is generally crucial not only to describe the fields themselves, but also how the fields change in space and over time. For instance, in order to derive the classical equations of motion, one analyses how the action functional changes under smooth variations of the fields. Thus, we consider smooth families of manifolds, rather than just individual ones. The formalism we use here has been invented by Stolz-Teichner [36] and is based on presheaves of categories. We define a presheaf \(\mathscr {B}\mathrm {ord}_d(M)\) of symmetric monoidal categories on a suitable category of test spaces. Then, we define a smooth FFT on M to be a morphism  of presheaves of symmetric monoidal categories, where
of presheaves of symmetric monoidal categories, where  is the presheaf that assigns to a test space its symmetric monoidal category of vector bundles. Inserting the one-point test space always brings us back to the previous (discrete) setting, but in general this looses information.
is the presheaf that assigns to a test space its symmetric monoidal category of vector bundles. Inserting the one-point test space always brings us back to the previous (discrete) setting, but in general this looses information.
Our motivation for passing from TQFTs to smooth FFTs is to think of M as the background spacetime of a classical field theory. The passage comprises a quite drastic change of perspective, since in general smooth FFTs are much richer than TQFTs: in our formalism, TQFTs turn out to be smooth FFTs on \(M=\{*\}\). In fact, this is a theorem that we prove—to our best knowledge—here for the first time (Theorem 6.9): the presheaf formalism of smooth FFTs disappears for \(M=\{*\}\) automatically and reduces the formalism indeed to the one of TQFTs. Consequently, smooth FFTs provide a common framework for classical and quantum theories. The original motivation of TQFTs to represent the sewing laws of a path integral is now enlarged to a more fundamental statement about the integrands under the path integral.
Let us briefly describe known examples of smooth FFTs on a target space M, in small dimensions d. In dimension \(d=1\), every vector bundle with connection over M defines a 1-dimensional smooth FFT, see [4, 5, 26, 37], and each of these papers proves (in different formalisms) that in fact every 1-dimensional smooth FFT arises this way. Analogously, in dimension \(d=2\), a bundle gerbe with connection over M defines a 2-dimensional smooth FFT on M. Again in a slightly different setting, this has been demonstrated by Bunke–Turner–Willerton [8]. The same smooth FFT can also be obtained by restricting the FFT we construct in this paper to the closed sector, as we show in Sect. 6.1, but our construction is functorial, rather than defined on isomorphism classes only. Each of these FFTs turns out to be superficial in our sense. For M a Lie group, many aspects of the relation between gerbes with connection and smooth FFTs have been treated earlier by Gawȩdzki [18] and Freed [16] in the process of understanding mathematical properties of Wess-Zumino-Witten models. We remark that Bunke-Turner-Willerton [8] also prove that all 2-dimensional, invertible, thin homotopy invariant, smooth FFTs on M arise from a bundle gerbe with connection over M.
Next, we describe in more detail the framework we set up in this article, which provides a unified treatment of all four modifications described above. The target space is a pair (M, Q) of a smooth manifold M and a family \(Q= \{Q_i\}_{i \in I}\) of submanifolds \(Q_i \subset M\); these submanifolds are supposed to support the D-branes, indexed by brane labels \(i \in I\). We define a presheaf \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\) of oriented open-closed d-dimensional bordisms on the target space \((M,Q)\). If an object manifold has a boundary, then each connected component of the boundary is equipped with a brane label \(i \in I\), and this component is mapped to \(Q_i \subset M\). The following is the central definition of this article, see Definition 4.5 in the main text: a smooth open-closed functorial field theory (OCFFT) on (M, Q) is a morphism

of presheaves of symmetric monoidal categories. We also describe carefully the conditions under which we call a smooth OCFFT invertible (Definition 4.6), (thin) homotopy invariant, or superficial (Definition 4.7). Moreover, we define reflection structures on smooth OCFFTs and explain positivity (Definitions 4.22 and 4.23).
The main result of this paper is the functorial construction of a 2-dimensional, invertible, reflection-positive, superficial, smooth OCFFT on a target space \((M,Q)\), taking as input a target space brane geometry on \((M,Q)\). These are pairs  consisting of a bundle gerbe
consisting of a bundle gerbe  with connection on M (in string theory called a “B-field”), and of a family
with connection on M (in string theory called a “B-field”), and of a family  of twisted vector bundles with connection over the submanifolds \(Q_i\) (the “Chan–Paton bundles”). They enter the OCFFT precisely as expected and as proposed by string theory: the bundle gerbe connection contributes a Wess–Zumino-term [17, 19, 43, 44], and the twisted vector bundles describe the coupling of the end points of open strings to the D-branes [12, 20, 22]. Our construction simultaneously generalises the FFT of Bunke–Turner–Willerton to include open strings and morphisms of target space brane geometries, and the open-closed TQFT of Lazaroiu, Moore-Segal and Lauda–Pfeiffer to include a target space and smoothness.
of twisted vector bundles with connection over the submanifolds \(Q_i\) (the “Chan–Paton bundles”). They enter the OCFFT precisely as expected and as proposed by string theory: the bundle gerbe connection contributes a Wess–Zumino-term [17, 19, 43, 44], and the twisted vector bundles describe the coupling of the end points of open strings to the D-branes [12, 20, 22]. Our construction simultaneously generalises the FFT of Bunke–Turner–Willerton to include open strings and morphisms of target space brane geometries, and the open-closed TQFT of Lazaroiu, Moore-Segal and Lauda–Pfeiffer to include a target space and smoothness.
Let us now outline some important steps in our constructions and describe how the paper is organised.
-
(a)
The complex vector spaces that our OCFFT assigns to 1-manifolds are constructed in Sect. 2. A substantial part of the construction has been performed in our previous paper [11]: the transgression of bundle gerbes and D-branes to spaces of loops and paths in M. We review the relevant parts in Sects. 2.2 and 2.4 of the present article. While in [11] it sufficed to parameterise paths and loops in M by [0, 1] and \({\mathbb {S}}^1\), respectively, for our present purposes we need to extend the formalism to oriented manifolds Y that are only diffeomorphic to either [0, 1] or \({\mathbb {S}}^1\). This is achieved using an enriched two-sided simplicial bar construction and descent theory [9]; we summarise the construction in Sect. 2.5. The vector spaces our OCFFT assigns to closed 1-manifolds are obtained from the fibres of the hermitean line bundle over the loop space of M (the transgression of the bundle gerbe) and the vector spaces assigned to open 1-manifolds are fibres of hermitean vector bundles over spaces of paths connecting two D-branes (the transgression of the twisted vector bundles). In particular, all these vector spaces are equipped with hermitean inner products, which are—as OCFFTs take values in bare vector bundles—discarded in this step.
-
(b)
The linear maps that our smooth OCFFTs assign to 2-dimensional bordisms are constructed in Sect. 3. There, we actually adopt a dual picture and construct instead the scattering amplitude associated to the bordism for given incoming and outgoing states. Our construction extends and conceptually simplifies well-known constructions of [12, 20, 22], while also providing a careful treatment of corners.
The definition of the presheaf \({\mathscr {OCB}\mathrm {ord}}_d{(M,Q)}\) of open-closed bordisms as well as the corresponding definition of smooth OCFFTs, as described above, is presented in Sect. 4. In Sect. 5 we show the following main result of this article, see Theorem 5.4, Proposition 5.7, Corollary 5.9, and Theorem 5.10.
Theorem 1
Consider a target space brane geometry  on a target space (M, Q). The constructions (a) and (b) yield a smooth OCFFT
on a target space (M, Q). The constructions (a) and (b) yield a smooth OCFFT

Moreover, this smooth OCFFT  has the following properties:
has the following properties:
-
It is invertible.
-
It is superficial, and in particular thin homotopy invariant.
-
There is a canonical positive reflection structure on
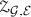 . It recovers precisely those hermitean inner products on the vector spaces in the image of
. It recovers precisely those hermitean inner products on the vector spaces in the image of 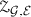 that have been discarded earlier.
that have been discarded earlier. -
The dependence on the target space brane geometry is functorial. That is, we obtain a functor

from the homotopy groupoid of target space brane geometries on (M, Q) to the groupoid of 2-dimensional, invertible, superficial, reflection-positive, smooth OCFFTs on (M, Q).
A number of further properties of the OCFFT  are investigated in Sect. 6. In Sect. 6.1 we look at closed subsectors of the theory; we relate the restriction of
are investigated in Sect. 6. In Sect. 6.1 we look at closed subsectors of the theory; we relate the restriction of  to these subsectors to previous work, in particular to that of Bunke–Turner–Willerton [8]. In Sect. 6.2 we prove the result (Theorem 6.7) that the OCFFT
to these subsectors to previous work, in particular to that of Bunke–Turner–Willerton [8]. In Sect. 6.2 we prove the result (Theorem 6.7) that the OCFFT  is homotopy invariant if and only if the connection on the bundle gerbe
is homotopy invariant if and only if the connection on the bundle gerbe  is flat. In the remaining subsections we concentrate on the reduction of our results to the case of a one-point target space \(M = \{*\}\), and explore in detail the relation to the work of Lazaroiu [24], Lauda–Pfeiffer [25] and Moore–Segal [27]. The following theorem summarises these relations.
is flat. In the remaining subsections we concentrate on the reduction of our results to the case of a one-point target space \(M = \{*\}\), and explore in detail the relation to the work of Lazaroiu [24], Lauda–Pfeiffer [25] and Moore–Segal [27]. The following theorem summarises these relations.
Theorem 2
There is a strictly commutative diagram of equivalences of categories:

The categories in the corners of this diagram are the following. \(\mathrm {TBG}(I)\) is the bicategory of target space brane geometries for the one-point target space (its only information is the index set of brane labels), and \(\mathrm {h}_1\mathrm {TBG}(I)\) is its homotopy groupoid. \(\mathrm {RP}\text {-}\mathrm {KFrob}^{I}_\mathbb {C}\) is the category of I-coloured knowledgeable Frobenius algebras whose bulk algebra is isomorphic to \(\mathbb {C}\), equipped with a version of a reflection-positive structure. The functor \(\widetilde{\mathrm {frob}}\) is described in detail in Sect. 6.3; it arises from the geometric formalism in [11]. \((\mathrm {RP}\text {-}{\mathrm {OCTQFT}}_{2}^{I})^{\times }\) is the category of 2-dimensional, invertible, reflection-positive, open-closed TQFTs, and \(\mathscr {F}\) is the functor that establishes the classification result of Lauda–Pfeiffer [25], enhanced to include reflection structures. Finally, \(\mathrm {RP}\text {-}{\mathrm {OCFFT}}_{2}(I)^{\times }\) is the category of 2-dimensional, invertible, reflection-positive, smooth OCFFTs on the one point target space. The functor \(\mathrm {ev}_{*}\) evaluates a morphism of presheaves of categories on the one-point test space. As mentioned above, it is an important statement on its own that this functor is an equivalence, which is the content of Theorem 6.9.
In upcoming work we aim to show that our functor

is an equivalence of categories, for all target spaces \((M,Q)\). This would yield a complete classification of 2-dimensional, invertible, reflection-positive, superficial, smooth OCFFTs by target space brane geometries.
2 Transgression of B-fields and D-branes
2.1 Target space brane geometry
In this section we recall the basic definitions of bundle gerbes and D-branes as well as important results on their structure on which our constructions in the later sections will be based. Bundle gerbes have been introduced in [29]. The notion of morphisms that we are going to employ originated in [28] and has been generalised in [40, 41]. For detailed proofs of the statements on the 2-category of bundle gerbes we refer the reader to the above references as well as [7, 10]; for a non-technical introduction see also [6]. The conventions used in this article are compatible with our previous article [11]. We denote by \({\mathscr {M}\mathrm {fd}}\) the category of smooth manifolds and smooth maps.
The approach to bundle gerbes we present here is the compact treatment worked out in [31]. Let  denote the category of hermitean vector bundles with connection on a manifold M. To every manifold M we assign a 2-category
denote the category of hermitean vector bundles with connection on a manifold M. To every manifold M we assign a 2-category  whose objects are 2-forms \(B \in \Omega ^2(M)\) and whose morphism categories
whose objects are 2-forms \(B \in \Omega ^2(M)\) and whose morphism categories  are the full subcategories
are the full subcategories

on those hermitean vector bundles E over M with (unitary) connection whose curvature satisfies
The composition of 1-morphisms and the horizontal composition of 2-morphisms are induced by the tensor product in  . The assignment
. The assignment  defines a presheaf of symmetric monoidal 2-categories on \({\mathscr {M}\mathrm {fd}}\).
defines a presheaf of symmetric monoidal 2-categories on \({\mathscr {M}\mathrm {fd}}\).
The sheafification of the presheaf  with respect to the Grothendieck topology of surjective submersions yields a sheaf
with respect to the Grothendieck topology of surjective submersions yields a sheaf  of symmetric monoidal 2-categories on \({\mathscr {M}\mathrm {fd}}\). Its sections are called bundle gerbes with connections. In short, a bundle gerbe
of symmetric monoidal 2-categories on \({\mathscr {M}\mathrm {fd}}\). Its sections are called bundle gerbes with connections. In short, a bundle gerbe  with connection consists of a surjective submersion \(\pi :Y \rightarrow M\), a 2-form \(B\in \Omega ^2(Y)\), a hermitian line bundle L with connection over the 2-fold fibre product \(Y^{[2]} = Y \times _M Y\), whose curvature satisfies \(\mathrm {curv}(L)=\mathrm {pr}_2^{*}B-\mathrm {pr}_1^{*}B\) (called the curving of
with connection consists of a surjective submersion \(\pi :Y \rightarrow M\), a 2-form \(B\in \Omega ^2(Y)\), a hermitian line bundle L with connection over the 2-fold fibre product \(Y^{[2]} = Y \times _M Y\), whose curvature satisfies \(\mathrm {curv}(L)=\mathrm {pr}_2^{*}B-\mathrm {pr}_1^{*}B\) (called the curving of  ), and a unitary, connection-preserving line bundle isomorphism \(\mu : \mathrm {pr}_{12}^{*}L \otimes \mathrm {pr}_{23}^{*}L \rightarrow \mathrm {pr}_{13}^{*}L\) over \(Y^{[3]}\) which satisfies an associativity condition over \(Y^{[4]}\). A morphism between bundle gerbes
), and a unitary, connection-preserving line bundle isomorphism \(\mu : \mathrm {pr}_{12}^{*}L \otimes \mathrm {pr}_{23}^{*}L \rightarrow \mathrm {pr}_{13}^{*}L\) over \(Y^{[3]}\) which satisfies an associativity condition over \(Y^{[4]}\). A morphism between bundle gerbes  and
and  with connections consists of a surjective submersion \(\zeta : Z \rightarrow Y_1 \times _M Y_2\), a hermitian vector bundle E over Z with connection whose curvature satisfies (2.1), and a unitary, connection-preserving vector bundle isomorphism
with connections consists of a surjective submersion \(\zeta : Z \rightarrow Y_1 \times _M Y_2\), a hermitian vector bundle E over Z with connection whose curvature satisfies (2.1), and a unitary, connection-preserving vector bundle isomorphism
over \(Z^{[2]}\) that is compatible with the line bundle morphisms \(\mu _1\) and \(\mu _2\). Here, all fibre products are taken over M, the maps \(\mathrm {pr}_{Y_i}\) are the canonical projections \(Y_1 \times _M Y_2 \rightarrow Y_i\), and the projections \(\mathrm {pr}_i\) are the canonical projections \(Z^{[2]} \rightarrow Z\) onto the i-th factor. In the following, for the sake of legibility we will usually not display these pullbacks explicitly unless it might cause confusion. One can show that a morphism  of bundle gerbes is invertible if and only if its vector bundle \(E \rightarrow Z\) is of rank one; see [41].
of bundle gerbes is invertible if and only if its vector bundle \(E \rightarrow Z\) is of rank one; see [41].
Example 2.1
Of crucial importance are the trivial bundle gerbes  , where \(\rho \in \Omega ^2(M)\) is any 2-form on M. These objects are exactly those in the image of the canonical inclusion
, where \(\rho \in \Omega ^2(M)\) is any 2-form on M. These objects are exactly those in the image of the canonical inclusion

Concretely, the gerbe  has as its surjective submersion the identity \(1_M :M \rightarrow M\), as its line bundle with connection the trivial line bundle \(M \times \mathbb {C}\rightarrow M\) with the trivial connection, and its structure isomorphism \(\mu \) acts as \(\mu ((x,z_1), (x,z_2)) = (x, z_1 z_2)\) for all \(x \in M\) and \(z_1, z_2 \in \mathbb {C}\). Finally, the curving of
has as its surjective submersion the identity \(1_M :M \rightarrow M\), as its line bundle with connection the trivial line bundle \(M \times \mathbb {C}\rightarrow M\) with the trivial connection, and its structure isomorphism \(\mu \) acts as \(\mu ((x,z_1), (x,z_2)) = (x, z_1 z_2)\) for all \(x \in M\) and \(z_1, z_2 \in \mathbb {C}\). Finally, the curving of  is given by the 2-form \(\rho \in \Omega ^2(M)\).
is given by the 2-form \(\rho \in \Omega ^2(M)\).
A trivialisation of a bundle gerbe  with connection on M is a 1-isomorphism
with connection on M is a 1-isomorphism  for some \(\rho \in \Omega ^2(M)\). The bundle gerbe
for some \(\rho \in \Omega ^2(M)\). The bundle gerbe  is the monoidal unit of
is the monoidal unit of  . \(\triangleleft \)
. \(\triangleleft \)
Example 2.2
Consider a 1-morphism  between two trivial bundle gerbes on M. This is a hermitean vector bundle \(E \rightarrow Z\) with connection over a surjective submersion \(\zeta :Z \rightarrow M\), and a connection-preserving isomorphism \(\alpha :\mathrm {pr}_1^*E \rightarrow \mathrm {pr}_0^*E\) over \(Z^{[2]}\), satisfying a cocycle condition over \(Z^{[3]}\). In other words,
between two trivial bundle gerbes on M. This is a hermitean vector bundle \(E \rightarrow Z\) with connection over a surjective submersion \(\zeta :Z \rightarrow M\), and a connection-preserving isomorphism \(\alpha :\mathrm {pr}_1^*E \rightarrow \mathrm {pr}_0^*E\) over \(Z^{[2]}\), satisfying a cocycle condition over \(Z^{[3]}\). In other words,  is a descent datum for a hermitean vector bundle
is a descent datum for a hermitean vector bundle  with connection on M. Descent thus induces an equivalence of categories
with connection on M. Descent thus induces an equivalence of categories

An inverse of this functor is given by the canonical inclusion

as a full subcategory. \(\triangleleft \)
We briefly recall that for any bundle gerbe with connection  and any 2-forms \(\omega _1, \omega _2 \in \Omega ^2(M)\) there exists a functor
and any 2-forms \(\omega _1, \omega _2 \in \Omega ^2(M)\) there exists a functor

which derives from the closed module category structure of the morphism categories of  over the category
over the category  [7, 10]. Explicitly, \(\Delta \) can be defined as follows, see [11]. We denote by
[7, 10]. Explicitly, \(\Delta \) can be defined as follows, see [11]. We denote by

the 2-functor that is the identity on objects, that sends a 1-morphism to the morphism defined by the dual vector bundle, and that sends a 2-morphism to the 2-morphism induced by the fibre-wise transpose of the original 2-morphism. The functor \((-)^*\) reverses the direction of 1-morphisms and 2-morphisms. Then we define \(\Delta \) to be the composition

where \(\mathsf {R}\) is the descent functor as in Example 2.2. That is, we set

If  is an isomorphism, we have
is an isomorphism, we have  ; this follows from the Definition (2.2) of the functor \(\Delta \) and the fact that
; this follows from the Definition (2.2) of the functor \(\Delta \) and the fact that  for any 1-isomorphism of bundle gerbes [40]. We further recall from [11, Remark 2.1.1] that there are canonical morphisms
for any 1-isomorphism of bundle gerbes [40]. We further recall from [11, Remark 2.1.1] that there are canonical morphisms

for all 1-morphisms  for \(a = 1,2,3\) and isomorphisms
for \(a = 1,2,3\) and isomorphisms  in
in  . Here, the first morphism is induced by composition, the second is induced by the dual in the category of hermitean vector bundles with connection, and the third is induced from the evaluation isomorphism for
. Here, the first morphism is induced by composition, the second is induced by the dual in the category of hermitean vector bundles with connection, and the third is induced from the evaluation isomorphism for  . Moreover, there exists a canonical isomorphism
. Moreover, there exists a canonical isomorphism

where \(\Gamma _{\mathrm{par}, \mathrm {uni}}\) is the functor that takes parallel unit-length global sections of a hermitean vector bundle with connection. This can be checked directly from the definition of \(\Delta \).
To conclude this section, we recall the definitions of a D-brane and of a target space brane geometry:
Definition 2.3
Let  be a bundle gerbe over M, and let \(Q \subset M\) be a submanifold. A D-brane for
be a bundle gerbe over M, and let \(Q \subset M\) be a submanifold. A D-brane for  supported on Q is a morphism
supported on Q is a morphism  of bundle gerbes over Q for some 2-form \(\omega \in \Omega ^2(Q)\).
of bundle gerbes over Q for some 2-form \(\omega \in \Omega ^2(Q)\).
We call a pair (M, Q) of a manifold M and a collection \(Q= \{Q_i\}_{i \in I}\) of submanifolds in M a target space. Given a target space (M, Q), we define a 2-groupoid \(\mathrm {TBG}(M,Q)\) of target space brane geometries on \((M,Q)\) as follows. Its objects are pairs  of a bundle gerbe with connection
of a bundle gerbe with connection  and of a family
and of a family  of D-branes
of D-branes  supported on the submanifolds \(Q_i\). A 1-morphism
supported on the submanifolds \(Q_i\). A 1-morphism

in \(\mathrm {TBG}(M,Q)\) consists of a 1-isomorphism  in
in  together with a family \(\xi =\{\xi _i\}_{i\in I}\) of 2-isomorphism
together with a family \(\xi =\{\xi _i\}_{i\in I}\) of 2-isomorphism  . Finally, a 2-isomorphism
. Finally, a 2-isomorphism  in \(\mathrm {TBG}(M,Q)\) is given by a 2-isomorphism
in \(\mathrm {TBG}(M,Q)\) is given by a 2-isomorphism  in
in  such that the diagram
such that the diagram

commutes for every D-brane label \(i \in I\). We refer to [11] for a more detailed discussion of target space brane geometry.
2.2 The transgression bundles over paths between D-branes
Let (M, Q) be a target space, and let  be a target space brane geometry. In this section we review how
be a target space brane geometry. In this section we review how  give rise to vector bundles over the spaces of paths between the submanifolds \(Q_i\) [11].
give rise to vector bundles over the spaces of paths between the submanifolds \(Q_i\) [11].
Consider two arbitrary brane labels \(i, j \in I\), and let \(P_{ij}M\) be the diffeological space of smooth paths \(\gamma :[0,1] \rightarrow M\) in M with sitting instants that start in \(Q_i\) and end in \(Q_j\). For a path \(\gamma \in P_{ij}M\) and a trivialisation  of the pullback gerbe over the interval, we set
of the pullback gerbe over the interval, we set

For later use, we point out that one can alternatively write

By construction,  is a Hilbert space of finite dimension
is a Hilbert space of finite dimension

The Hilbert space  depends on the choice of a trivialisation
depends on the choice of a trivialisation  of
of  . However, changing the trivialisation
. However, changing the trivialisation  to a trivialisation
to a trivialisation  changes the Hilbert space
changes the Hilbert space  only up to a canonical isomorphism. To see this, we note that there always exists a 2-isomorphism
only up to a canonical isomorphism. To see this, we note that there always exists a 2-isomorphism  of trivialisations of
of trivialisations of  — this follows from (2.4), for instance. Any such 2-isomorphism induces a canonical isomorphism
— this follows from (2.4), for instance. Any such 2-isomorphism induces a canonical isomorphism

where we have abbreviated \(\psi _t {{:}{=}}\Delta (1, \psi _{|t})\) for \(t \in \{0,1\}\). The following result was proved in [11, Section 4.2].
Lemma 2.4
The following statements hold true:
-
(1)
For any other isomorphism
 , we have \(r_\psi = r_{\psi '}\). We can thus denote this isomorphism by
, we have \(r_\psi = r_{\psi '}\). We can thus denote this isomorphism by  .
. -
(2)
Given a third trivialisation
 of
of  , we have
, we have 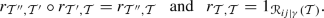
We thus define

The finite-dimensional Hilbert space \(\mathscr {R}_{ij|\gamma }\) comes with canonical isomorphisms

satisfying  for any trivialisations
for any trivialisations  of
of  . The disjoint union
. The disjoint union
comes with a canonical map \(\pi :\mathscr {R}_{ij} \rightarrow {P_{ij} M}\) which is a diffeological hermitean vector bundle of rank  over the diffeological space \(P_{ij}M\) [11, Proposition 4.2.3].
over the diffeological space \(P_{ij}M\) [11, Proposition 4.2.3].
For later use, we briefly recall the definition of the diffeology on \(\mathscr {R}_{ij}\) from [11]. Instead of using open subsets \(U \subset \mathbb {R}^n\) to define plots of diffeological spaces, we only use cartesian spaces \(U \in {\mathscr {C}\mathrm {art}}\), i.e. embedded submanifolds \(U \subset \mathbb {R}^m\) that are diffeomorphic to \(\mathbb {R}^n\) for some \(n,m \in \mathbb {N}_0\). Since any of the former test spaces can be covered by the latter, the resulting categories of diffeological spaces are equivalent. A map \({\hat{c}} :U \rightarrow \mathscr {R}_{ij}\) from an arbitrary cartesian space \(U \in {\mathscr {C}\mathrm {art}}\) to \(\mathscr {R}_{ij}\) is a plot if it has the following properties: we demand that the composition \(c {{:}{=}}\pi \circ {\hat{c}} :U \rightarrow P_{ij}M\) is a plot of \(P_{ij}M\). This means, equivalently, that the adjoint map

is a smooth map. Since \(U \cong \mathbb {R}^n\) for some \(n \in \mathbb {N}_0\), there exists a trivialisation  . Define the inclusion maps \(\iota _t :U \hookrightarrow U \times [0,1]\), \(x \mapsto (x,t)\), for any \(t \in [0,1]\). Over U we obtain the hermitean vector bundles
. Define the inclusion maps \(\iota _t :U \hookrightarrow U \times [0,1]\), \(x \mapsto (x,t)\), for any \(t \in [0,1]\). Over U we obtain the hermitean vector bundles

and we demand that there exists an open covering \(\{U_a\}_{a \in A}\) of U, together with morphisms \(\psi _a :F_{i|U_a} \rightarrow F_{j|U_a}\) over \(U_a\) for all \(a \in A\) such that

We move on to briefly recall from [11] the construction of the connection on the bundles \(\mathscr {R}_{ij} \rightarrow P_{ij}M\), which is defined via its parallel transport. Consider a smooth path \(\Gamma :[0,1] \rightarrow P_{ij}M\), and denote its adjoint map by \(\Gamma ^\dashv :[0,1]^2 \rightarrow M\). Further, we write \(\Gamma _t {{:}{=}}\Gamma ^\dashv (-,t) :[0,1] \rightarrow M\), with \(t \in \{0,1\}\), for the paths of endpoints. We let  be a trivialisation and set
be a trivialisation and set  for \(t = 0,1\). This induces hermitean vector bundles with connection
for \(t = 0,1\). This induces hermitean vector bundles with connection

over the interval [0, 1]. Observe that there is a canonical isomorphism

which is induced by the isomorphisms  from (2.8). We then define
from (2.8). We then define

where on the right-hand side, pt denotes the parallel transport in  along the interval. Here we orient the boundary of \([0,1]^2\) using an inward-pointing normal vector field to match our later conventions—this explains the different sign as compared to [11]. The following result is [11, Proposition 4.3.1]. Recall the notion of a superficial connection on a diffeological vector bundle over \(P_{ij}M\) from [11, Def. A.2.2].
along the interval. Here we orient the boundary of \([0,1]^2\) using an inward-pointing normal vector field to match our later conventions—this explains the different sign as compared to [11]. The following result is [11, Proposition 4.3.1]. Recall the notion of a superficial connection on a diffeological vector bundle over \(P_{ij}M\) from [11, Def. A.2.2].
Proposition 2.5
The morphism \(pt_{ij}\) of Eq. (2.10) defines a superficial connection on the vector bundle \(\mathscr {R}_{ij}\) over \(P_{ij}M\).
2.3 Equivariant structure on the transgression bundles
Let \(\mathrm {Diff}^+([0,1])\) denote the group of orientation-preserving diffeomorphisms of the interval. Note that such diffeomorphisms automatically fix the boundary points. The group \(\mathrm {Diff}^+([0,1])\) is a diffeological group when endowed with the usual mapping space diffeology, where a map \(f :U \rightarrow \mathrm {Diff}^+([0,1])\) is a plot if the adjoint map

is a smooth map.
Lemma 2.6
Given a target space (M, Q) and D-brane labels \(i,j \in I\), the group \(\mathrm {Diff}^+([0,1])\) acts smoothly on the space \(P_{ij}M\) via
Proof
This follows by the construction of the mapping space diffeology [21, Paragraph 1.59]. \(\square \)
Lemma 2.7
The action R lifts to a smooth action

This turns \(\mathscr {R}_{ij}\) into a \(\mathrm {Diff}^+([0,1])\)-equivariant hermitean vector bundle on \(P_{ij}M\).
Here we have used that \(\tau \) is the identity on \(\partial [0,1]\), so that the action on \(\psi \) is trivial.
Proof
We let \(f :U \rightarrow \mathrm {Diff}^+([0,1])\) be a plot, and we consider a plot \({\hat{c}} :U \rightarrow \mathscr {R}_{ij}\). In the notation of Sect. 2.2 that means that there exists a trivialisation  (where \(c {{:}{=}}\pi \circ {\hat{c}}\)), an open covering \(\{U_a\}_{a \in A}\) and morphisms \(\psi _a :F_{i|U_a} \rightarrow F_{j|U_a}\) such that
(where \(c {{:}{=}}\pi \circ {\hat{c}}\)), an open covering \(\{U_a\}_{a \in A}\) and morphisms \(\psi _a :F_{i|U_a} \rightarrow F_{j|U_a}\) such that

We need to show that \(R \circ ({\hat{c}} \times f) \circ \Delta _U\) defines a plot of \(\mathscr {R}_{ij}\), where \(\Delta _U :U \rightarrow U \times U\) denotes the diagonal map. First, observe that
which is a plot of \(P_{ij}M\) by Lemma 2.6. The plot f defines a fibre-wise diffeomorphism
Over \(U_a\), we then have

Thus, the trivialisation  and the bundle morphisms \(\psi _a\) render the composite map \(R \circ ({\hat{c}} \times f) \circ \Delta _U\) a plot of \(\mathscr {R}_{ij}\). \(\square \)
and the bundle morphisms \(\psi _a\) render the composite map \(R \circ ({\hat{c}} \times f) \circ \Delta _U\) a plot of \(\mathscr {R}_{ij}\). \(\square \)
A path \(\Gamma :[0,1] \rightarrow P_{ij}M\) is thin if the adjoint map \(\Gamma ^\dashv :[0,1]^2 \rightarrow M\) satisfies \(\mathrm {rk}(\Gamma ^\dashv _{*|t}) < 2\) for every \(t \in [0,1]^2\), where \(\Gamma _{*}^{\dashv }\) denotes the differential of \(\Gamma ^{\dashv }\). The equivariant structure R on \(\mathscr {R}_{ij}\) can be induced from the connection on \(\mathscr {R}_{ij}\) in the following way.
Proposition 2.8
Let \(F :[0,1] \rightarrow \mathrm {Diff}^+([0,1])\) be any smooth path with \(F(0) = 1_{[0,1]}\). For every \(\gamma \in P_{ij}M\) this induces a thin smooth path
from \(\gamma \) to \(\gamma \circ F(1)\). We have that
Proof
Since the expressions (2.10) and (2.11) are well-defined on equivalence classes, it suffices to prove the identity (2.12) with respect to any one representative, i.e. with respect to any one trivialisation of the pullback gerbe  over \([0,1]^2\).
over \([0,1]^2\).
First, we consider the map
which satisfies
Let  be a trivialisation. We obtain a trivialisation
be a trivialisation. We obtain a trivialisation  over \([0,1]^2\), which has the following properties:
over \([0,1]^2\), which has the following properties:
-
(1)
It has 2-form \(\rho = 0\).
-
(2)
For any \(s \in [0,1]\), we have

-
(3)
Since \(F(s)(0) = 0\) and \(F(s)(1) = 1\) for all \(s \in [0,1]\), we have that
 is the pullback of a trivialisation of a bundle gerbe over the point for \(t \in \{0,1\}\).
is the pullback of a trivialisation of a bundle gerbe over the point for \(t \in \{0,1\}\).
Combining property (3) with the fact that \(R_F \gamma (s,t) = \gamma (t)\) for all \(s \in [0,1]\) and \(t \in \{0,1\}\), we obtain that in this special case the bundles  and
and  (cf. (2.9)) are pullbacks of bundles over the point. Thus, their parallel transport is trivial. Inserting this insight and properties (1) and (2) into the definition (2.10) of the parallel transport \(pt_{ij}\) readily yields the identity (2.12). \(\square \)
(cf. (2.9)) are pullbacks of bundles over the point. Thus, their parallel transport is trivial. Inserting this insight and properties (1) and (2) into the definition (2.10) of the parallel transport \(pt_{ij}\) readily yields the identity (2.12). \(\square \)
Corollary 2.9
The lifted action R commutes with the parallel transport on the bundle \(\mathscr {R}_{ij}\). Consequently, \(\mathscr {R}_{ij}\) is \(\mathrm {Diff}^+([0,1])\)-equivariant as a hermitean diffeological vector bundle with connection.
Proof
This corollary follows from combining Proposition 2.8 with the fact that \(pt_{ij}\) is superficial (see [11, Definition A.2.2, Proposition 4.3.2]): if \(f \in \mathrm {Diff}^+([0,1])\) is any diffeomorphism, we find some smooth path in \(\mathrm {Diff}^+([0,1])\) from \(1_{[0,1]}\) to f with sitting instants. For example take \(F :[0,1] \rightarrow \mathrm {Diff}^+([0,1])\), \(F(s)(t) = (1-s)t + s\, f(t)\)—this is smooth and strictly increasing for any fixed \(s \in [0,1]\), and hence F(s) is a diffeomorphism for any s. If \(\Gamma :[0,1] \rightarrow P_{ij}M\) is any smooth path, we obtain a rank-two homotopy \(R_F \Gamma :[0,1] \rightarrow P(P_{ij}M)\) from \(\Gamma \) to \(R_f \Gamma \) (in the notation of the proof of Proposition 2.8). Since \(pt_{ij}\) is superficial, property (ii) of [11, Definition A.2.2] and Proposition 2.8 imply that
as claimed. \(\square \)
Remark 2.10
Corollary 2.9 can also be deduced directly from the explicit form (2.10) of the parallel transport on \(\mathscr {R}_{ij}\), using the fact that the induced diffeomorphism \({\hat{F}} :[0,1]^2 \rightarrow [0,1]^2\) is a fibre-wise diffeomorphism. This implies the invariance of the integral term in (2.10). \(\triangleleft \)
To conclude this section, we note that for every \(i,j \in I\), the diffeomorphism \(\mathsf {rev}:[0,1] \rightarrow [0,1]\), \(t \mapsto 1-t\) induces an isomorphism of diffeological spaces
This isomorphism lifts to a bundle isomorphism [11, Section 4.7]

Here, \(\overline{\mathscr {R}_{ij}}\) denotes the complex conjugate vector bundle, and \(\psi ^*\) is the fibre-wise hermitean adjoint of \(\psi \). Equivalently, we have a commutative square of diffeological spaces

where \(a_\mathsf {rev}\) denotes conjugation by \(\mathsf {rev}\) in \(\mathrm {Diff}^+([0,1])\). Finally, we point out that there is an isomorphism
defined implicitly by

where \(\langle -,-\rangle \) denotes the evaluation pairing. Alternatively, we can write
where \(\flat _{h_{ji}} :\overline{\mathscr {R}_{ji}} \rightarrow \mathscr {R}_{ji}^\vee \) is the musical isomorphism induced by the hermitean metric \(h_{ji}\) on \(\mathscr {R}_{ji}\).
2.4 The transgression line bundle over the loop space
Here we recall the construction of the transgression line bundle of a bundle gerbe from [42]. Let  be a bundle gerbe with connection over M. We denote by LM the diffeological free loop space of M. There exists a principal \(\mathsf {U}(1)\)-bundle
be a bundle gerbe with connection over M. We denote by LM the diffeological free loop space of M. There exists a principal \(\mathsf {U}(1)\)-bundle  over LM, whose fibre over a loop \(\gamma \) is the set of isomorphism classes of trivialisations of
over LM, whose fibre over a loop \(\gamma \) is the set of isomorphism classes of trivialisations of  . This is a \(\mathsf {U}(1)\)-torsor, since the groupoid of trivialisations of a bundle gerbe with connection is a torsor groupoid over the groupoid of hermitean line bundles with connection [41]. A line bundle
. This is a \(\mathsf {U}(1)\)-torsor, since the groupoid of trivialisations of a bundle gerbe with connection is a torsor groupoid over the groupoid of hermitean line bundles with connection [41]. A line bundle  acts on the fibre
acts on the fibre  as
as

where  is a trivialisation of
is a trivialisation of  and
and  denotes its 2-isomorphism class. It has been shown in [42] that
denotes its 2-isomorphism class. It has been shown in [42] that  is a diffeological \(\mathsf {U}(1)\)-bundle on LM. Further,
is a diffeological \(\mathsf {U}(1)\)-bundle on LM. Further,  carries a symmetrising fusion product and a superficial, fusive connection [42] (though these are not relevant here). The transgression line bundle \(\mathscr {L}\) is the associated diffeological hermitean line bundle
carries a symmetrising fusion product and a superficial, fusive connection [42] (though these are not relevant here). The transgression line bundle \(\mathscr {L}\) is the associated diffeological hermitean line bundle

Thus, the elements of the fibre \(\mathscr {L}_{|\gamma }\) over a loop \(\gamma \in LM\) are equivalence classes  , consisting of an isomorphism class of a trivialization
, consisting of an isomorphism class of a trivialization  and of a complex number \(z \in \mathbb {C}\). The equivalence relation identifies representatives
and of a complex number \(z \in \mathbb {C}\). The equivalence relation identifies representatives  if there exists a hermitean line bundle J on \({\mathbb {S}}^1\) with connection such that
if there exists a hermitean line bundle J on \({\mathbb {S}}^1\) with connection such that  and \(z = z' \cdot \mathsf {hol}(J)\).
and \(z = z' \cdot \mathsf {hol}(J)\).
Let \(\mathrm {Diff}^+({\mathbb {S}}^1)\) denote the diffeological group of orientation-preserving diffeomorphisms of \({\mathbb {S}}^1\). This acts on LM by pre-composition, i.e. via the map
The map R is smooth by arguments analogous to those in Lemma 2.6. Further, it lifts to a map

The latter map can be expressed in terms of parallel transport along paths induced by isotopies that connect \(\tau \) and \(1_{{\mathbb {S}}^1}\), in analogy with Proposition 2.8 (using the fact that \(\mathrm {Diff}^+({\mathbb {S}}^1)\) is connected). However, note that there are non-homotopic isotopies of this kind, since \({\mathbb {S}}^1\) is not simply connected. The map described above is well-defined nevertheless, due to the superficiality of the connection on \(\mathscr {L}\) (see [42, Definition 2.2.1(i), Corollary 4.3.3]). The relation between the map R from (2.17) and parallel transport was worked out in [42, Remark 4.3.7]. In particular, the map R is smooth by [42, Proposition 2.2.5].
Finally, again in analogy to Section 2.3, there is a \(\mathbb {Z}_2\)-action on LM via \(R_\mathsf {rev}:\gamma \mapsto \gamma \circ \mathsf {rev}\), with \(\mathsf {rev}:{\mathbb {S}}^1 \rightarrow {\mathbb {S}}^1\) denoting the orientation-reversing diffeomorphism \(\exp (2\pi \, \mathrm {i}\, t) \mapsto \exp (- 2\pi \, \mathrm {i}\, t)\). This descends to a \(\mathbb {Z}_2\)-action \(R_\mathsf {rev}\) on LM, which lifts to
respectively. As for \(\mathscr {R}_{ij}\), this can equivalently be cast as an isomorphism
2.5 The coherent pull-push construction
In Sect. 5 it will be crucial to not just consider the mapping spaces \(P_{ij}M\) of paths between D-branes that are parameterised over the unit interval [0, 1]. We would like to consider, for any oriented 1-manifold Y diffeomorphic to [0, 1], the spaces \(P^Y_{ij}M\) of smooth maps \(\gamma :Y \rightarrow M\) with sitting instants around the initial point \(y_0 \in Y\) and the endpoint \(y_1 \in Y\) as defined by the orientation of Y, and such that \(\gamma (y_0) \in Q_i\) and \(\gamma (y_1) \in Q_j\). The set \(P^Y_{ij}M\) of such maps is a subset of the diffeological mapping space \(M^Y\), and we endow it with the subspace diffeology. The equivariant structures on the bundles \(\mathscr {R}_{ij} \rightarrow P_{ij}M\) from Sect. 2.3 allow us to transfer the bundles \(\mathscr {R}_{ij}\) to the spaces \(P^Y_{ij}M\) in a coherent way. Analogously, we need to transfer the hermitean line bundle \(\mathscr {L}\rightarrow LM\) to the diffeological mapping space \(L^Y M\) of smooth maps \(Y \rightarrow M\) for every oriented manifold Y that is diffeomorphic to \({\mathbb {S}}^1\). In this section we make precise what we mean by this and outline a construction that achieves this transfer. The full details of this construction can be found in the separate article [9].
For \(Y_0,Y_1\) oriented manifolds (possibly with boundary), we write \(\mathrm {D}(Y_0,Y_1) {{:}{=}}\mathrm {Diff}^+(Y_0,Y_1)\) for the diffeological space of orientation-preserving diffeomorphisms from \(Y_0\) to \(Y_1\). Note that if \(Y_0 = Y_1 = Y\), the space \(\mathrm {D}(Y,Y) {{=}{:}}\mathrm {D}(Y)\) canonically has the structure of a diffeological group. For \(Y \cong [0,1]\), this group acts on the diffeological space \(P_{ij}^Y M\) by pre-composition; there is a smooth map
which is compatible with the group structure on \(\mathrm {D}(Y)\). Similarly, for \(Y_0, Y_1 \cong [0,1]\) there are smooth maps
which fit into a commutative square

in \({\mathscr {D}\mathrm {fg}}\) for any oriented manifolds \(Y_0,Y_1,Y_2 \cong [0,1]\). We also define maps
and
Note that this notation stems from the use of simplicial techniques, which are at work in the background here; for more details on this, see [9]. Let \({\mathscr {M}}_{[0,1]}\) be the groupoid of oriented manifolds Y that are isomorphic (as oriented manifolds) to [0, 1] with its standard orientation. The morphisms in \({\mathscr {M}}_{[0,1]}\) are the orientation-preserving diffeomorphisms. Note that \(Y \mapsto P^Y_{ij}M\) defines a functor \(P^{(-)}_{ij}M :{\mathscr {M}}_{[0,1]}^\mathrm {op}\rightarrow {\mathscr {D}\mathrm {fg}}\).
Definition 2.11
Let (M, Q) be a target space. A coherent hermitean vector bundle on \(P_{ij}^{(-)}M\) is a pair \((E,\mu )\) of a family \(E=\{E_{Y_0}\}_{Y_0 \in {\mathscr {M}}_{[0,1]}}\) of hermitean vector bundles \(E_{Y_0} \rightarrow P_{ij}^{Y_0} M\), together with a family \(\mu =\{\mu _{Y_1,Y_0}\}_{Y_1,Y_0 \in {\mathscr {M}}_{[0,1]}}\) of isomorphisms
of hermitian vector bundles over \(P_{ij}^{Y_0} M \times \mathrm {D}(Y_1,Y_0)\), such that
over \(P_{ij}^{Y_2} M \times \mathrm {D}(Y_2,Y_1) \times \mathrm {D}(Y_1,Y_0)\) for every \(Y_0,Y_1,Y_2 \in {\mathscr {M}}_{[0,1]}\). A morphism of coherent hermitean vector bundles on \(P_{ij}^{(-)}M\), written \(\psi :(E,\mu ) \rightarrow (F,\nu )\), consists of a family \(\psi =\{\psi _{Y_0}\}_{Y_0\in {\mathscr {M}}_{[0,1]} }\) of hermitian vector bundle morphisms \(\psi _{Y_0} :E_{Y_0} \rightarrow F_{Y_0}\) that intertwine the morphisms \(\mu \) and \(\nu \). This defines the category  of coherent hermitean vector bundles on \(P_{ij}^{(-)}M\).
of coherent hermitean vector bundles on \(P_{ij}^{(-)}M\).
We introduce the simplicial diffeological space \(\big ( P_{ij} M {//}\mathrm {D}([0,1]) \big )_\bullet \in {\mathscr {D}\mathrm {fg}}^{\Delta ^\mathrm {op}}\) by setting
i.e., it is the nerve of the action groupoid of the \(\mathrm {D}([0,1])\)-action on \(P_{ij} M\). The following definition spells out what a hermitian vector bundle over the simplicial diffeological space \((P_{ij} M {//}\mathrm {D}([0,1]) )_\bullet \) is.
Definition 2.12
An equivariant hermitean vector bundle on \(P_{ij}M\) is a pair \((E',\mu ')\) of a hermitean vector bundle \(E' \rightarrow P_{ij}M\), together with an isomorphism \(\mu ' :d_1^*E' \rightarrow d_0^*E'\) over \(P_{ij} M \times \mathrm {D}([0,1])\), such that
over \(P_{ij}M \times \mathrm {D}([0,1])^2\). A morphism of equivariant hermitean vector bundles on \(P_{ij}M\), denoted \(\psi ' :(E',\mu ') \rightarrow (F',\nu ')\), consists of a morphism \(\psi :E' \rightarrow F'\) that intertwines the morphisms \(\mu '\) and \(\nu '\). This defines the category  of equivariant hermitean vector bundles on \(P_{ij}M\).
of equivariant hermitean vector bundles on \(P_{ij}M\).
Analogously, we define the category  of equivariant hermitean vector bundles on LM and the category
of equivariant hermitean vector bundles on LM and the category  of coherent hermitean vector bundles on \(L^{(-)}M\). Now consider the diffeological space \(P_{ij}^Y M \times \mathrm {D}([0,1],Y)\). It comes with two smooth maps
of coherent hermitean vector bundles on \(L^{(-)}M\). Now consider the diffeological space \(P_{ij}^Y M \times \mathrm {D}([0,1],Y)\). It comes with two smooth maps
For any \(Y \in {\mathscr {M}}_{[0,1]}\), the map \(\Phi ^Y_0\) extends to a morphism
of simplicial diffeological spaces. Observe that the source of \(\Phi ^Y_\bullet \) is the Čech nerve of the subduction \(\Psi ^Y\). Since it is simplicial, pullback along \(\Phi ^Y_\bullet \) induces a functor

for any \(i,j \in I\), where  is the category of descent data for hermitean vector bundles with respect to the subduction \(\Psi ^Y\). We can now use the fact that
is the category of descent data for hermitean vector bundles with respect to the subduction \(\Psi ^Y\). We can now use the fact that  admits a functorial descent
admits a functorial descent  in order to obtain a hermitean vector bundle on \(P_{ij}^Y M\) from any equivariant hermitean vector bundle on \(P_{ij}M\). The above constructions and the following theorem will be discussed in more general context in [9].
in order to obtain a hermitean vector bundle on \(P_{ij}^Y M\) from any equivariant hermitean vector bundle on \(P_{ij}M\). The above constructions and the following theorem will be discussed in more general context in [9].
Theorem 2.13
Considering all \(Y \in {\mathscr {M}}_{[0,1]}\), the composition of pullback along \(\Phi ^Y_\bullet \) and descent along \(\Psi ^Y\) naturally assemble into an equivalence of categories

A completely analogous construction yields an equivalence

Let  and
and  be the equivariant hermitean vector bundles from Sects. 2.2 and 2.4, respectively. Applying the coherent pull–push of Theorem 2.13 we obtain coherent vector bundles
be the equivariant hermitean vector bundles from Sects. 2.2 and 2.4, respectively. Applying the coherent pull–push of Theorem 2.13 we obtain coherent vector bundles

We will write \(\mathscr {R}^Y_{ij} \rightarrow P^Y_{ij}M\) and \(\mathscr {L}^Y \rightarrow L^YM\) for their components over \(P^Y_{ij}M\) and over \(L^Y M\), respectively.
Remark 2.14
Since the \(\mathrm {D}([0,1])\)-equivariant structure R on the bundle \(\mathscr {R}_{ij}\) is compatible with the connection on \(\mathscr {R}_{ij}\), we could even construct the extended bundle \(\mathscr {R}^Y_{ij}\) as a coherent diffeological hermitean vector bundle with connection on \(P^{(-)}_{ij}M\) (and similarly for \(\mathscr {L}\)), but for our purposes we will only need the connection on \(\mathscr {R}_{ij}\), as given in Sect. 2.2. \(\triangleleft \)
By construction, there are canonical identifications \(\mathscr {R}^{[0,1]}_{ij} \cong \mathscr {R}_{ij}\) and \(\mathscr {L}^{{\mathbb {S}}^1} \cong \mathscr {L}\). The map \(\mathsf {rev}:[0,1] \rightarrow [0,1]\), \(t \mapsto 1-t\) induces an isomorphism
of simplicial diffeological spaces (compare also diagram (2.14)). We can thus use \(R_\mathsf {rev}\times a_\mathsf {rev}^\bullet \) to pull back the equivariant bundle \(\overline{\mathscr {R}_{ji}} \rightarrow P_{ji}M\) to an equivariant bundle \(R_\mathsf {rev}^* \overline{\mathscr {R}_{ji}} \rightarrow P_{ij}M\). Then, the morphism \(\alpha _{ij} :\mathscr {R}_{ij} \rightarrow R_\mathsf {rev}^* \overline{\mathscr {R}_{ji}}\) induces an isomorphism (which we also denote \(\alpha _{ij}\)) of \(\mathrm {D}([0,1])\)-equivariant hermitean vector bundles on \(P_{ij}M\). By the functoriality of \(\Psi _* \Phi ^*\) and the compatibility of descent of vector bundles with taking the complex conjugate vector bundle, we thus obtain an isomorphism
of coherent hermitean vector bundles on \(P^{(-)}_{ij}M\). We denote this isomorphism by \({\widehat{\alpha }}_{ij}\).
We can give yet a different perspective on this isomorphism: observe that the oriented manifold \(\overline{[0,1]}\), i.e. the unit interval with the opposite orientation, is an element of \({\mathscr {M}}_{[0,1]}\). This is established by the orientation-preserving diffeomorphism \(\mathsf {rev}:[0,1] \rightarrow \overline{[0,1]}\). Consequently, there is a commuting triangle of diffeological spaces

The morphism at the top pre-composes a path \(\gamma \) by \(\mathsf {rev}\), while still seeing \(0 \in [0,1]\) as the initial point of the new path \(\gamma \circ \mathsf {rev}\). The right-hand morphism also pre-composes by \(\mathsf {rev}\), but for the resulting path \(\gamma \circ \mathsf {rev}:[0,1] \rightarrow M\) we view \(1 \in [0,1]\) as its initial point. Finally, the left-hand map just sends a map \(\gamma \) to itself, but now views 1 as the initial point in the parameterising manifold [0, 1]. Using the coherent structure \({\widehat{R}}\) on \({\widehat{\mathscr {R}}}_{ij}\) (see Definition 2.11) and the morphism \(\alpha _{ij}\), we obtain a commutative diagram

of isomorphisms of \(\mathrm {D}([0,1])\)-equivariant hermitean vector bundles that covers diagram (2.19), where the isomorphism \({\widehat{\alpha }}^{[0,1]}_{ij}\) is defined by this diagram. Extending \({\widehat{\alpha }}^{[0,1]}_{ij}\) via \(\Psi _* \Phi ^*\) yields isomorphisms
of coherent hermitean vector bundles on \(P^{(-)}_{ij}M\) for all \(i,j \in I\).
Analogously, the map \(\mathsf {rev}:{\mathbb {S}}^1 \rightarrow {\mathbb {S}}^1\) as in Sect. 2.4 and the isomorphism \({\tilde{\lambda }}\) from the same section in diagram (2.20) yield an isomorphism
of coherent hermitean vector bundles over \(L^{(-)}M\). This also extends the isomorphisms \(\beta _{ij}\) from (2.16) and \({\tilde{\varrho }}\) from 2.18 to isomorphisms
3 Surface amplitudes
In this section we use the coherent bundles \({\widehat{\mathscr {R}}}_{ij}\) and \({\widehat{\mathscr {L}}}\) to extend the usual holonomy of bundle gerbes to amplitudes for surfaces with corners, whose boundary is partly contained in D-branes. In Sect. 5 we assemble the resulting amplitudes into a smooth functorial field theory which describes the B-field-dependent part of open-closed bosonic string amplitudes.
3.1 Scattering diagrams
First, we recall the geometric tools necessary to describe surfaces with corners. Our main reference for this interlude is [32]. An m-dimensional manifold with corners N is a topological manifold with (possibly empty) boundary, equipped with a maximal smooth atlas whose charts are continuous maps
that are homeomorphisms onto their images, with \(U \subset N\) open and \(\mathbb {R}_+\) denoting the set of non-negative real numbers. The index of a point \(x \in N\) is the number of coordinates of \(\varphi (x)\) that are zero. Compatible charts yield the same index; thus, each point \(x \in N\) has a well-defined index \(\mathrm {ind}(x) \in \{0,\ldots ,m\}\). A connected face of N is the closure of a connected component of \(\{x \in N\, |\, \mathrm {ind}(x) = 1 \}\), while a face of N is a disjoint union of connected faces. A manifold with faces is a manifold with corners such that each point \(x \in N\) belongs to \(\mathrm {ind}(x)\) different faces.
Definition 3.1
An m-dimensional \(\left\langle n \right\rangle \)-manifold is an m-dimensional manifold N with faces together with a tuple \((\partial _0 N, \ldots , \partial _{n-1} N)\) consisting of faces \(\partial _i N\) of N such that
-
(1)
\(\partial _0 N \cup \ldots \cup \partial _{n-1} N = \partial N\), where \(\partial N \subset N\) is the subset of points of non-zero index, and
-
(2)
for all \(a \ne b \in \{0,\ldots ,n\}\), the intersection \(\partial _a N \cap \partial _b N\) is either empty or a face of \(\partial _a N\) and of \(\partial _b N\).
A morphism of \(\langle n\rangle \)-manifolds \(N \rightarrow N'\) is a continuous map \(f :N \rightarrow N'\) whose representatives in all charts are smooth, and such that \(f_{|\partial _a N} :\partial _a N \rightarrow \partial _a N'\) for all \(a = 0, \ldots , {n-1}\), i.e. f is compatible with the partitions of \(\partial N\) and \(\partial N'\). A \(\langle 3\rangle ^*\)-manifold is a \(\langle 3\rangle \)-manifold N where every \(x \in N\) with \(\mathrm {ind}(x) \ge 2\) is contained in either \(\partial _0 N \cap \partial _2 N\) or \(\partial _1 N \cap \partial _2 N\). Morphisms of \(\langle 3\rangle ^*\)-manifolds are the same as those of \(\langle 3\rangle \)-manifolds.
Note that, in particular, a \(\langle 3\rangle ^*\)-manifold satisfies \(\partial _0 N \cap \partial _1 N = \emptyset \). If N is an oriented manifold with corners, all connected faces of N carry an induced orientation, which we define using an inward-pointing normal vector field. We will be concerned with compact (oriented) 2-dimensional \(\langle 3 \rangle ^*\)-manifolds N. Each connected face \(c \subset \partial N\) is a compact 1-dimensional manifold with boundary, and hence either diffeomorphic to \({\mathbb {S}}^1\) or to [0, 1]. Throughout this paper we call a 1-manifold with corners closed if it is diffeomorphic to \({\mathbb {S}}^1\) and open if it is diffeomorphic to [0, 1]. If \(c_a\) is a connected face in \(\partial _a N\) and \(c_b\) is a connected face in \(\partial _b N\) with \(a \ne b\) then \(c_a \cap c_b\) is either empty, one point, or two points.
Consider a target space (M, Q) and a target space brane geometry  . Let \(\Sigma \) be an oriented, compact, 2-dimensional \(\langle 3\rangle ^*\)-manifold and let \(\sigma :\Sigma \rightarrow M\) be a smooth map. By Definition 3.1, the boundary of \(\Sigma \) comes with a partition \(\partial \Sigma = \partial _0 \Sigma \cup \partial _1 \Sigma \cup \partial _2 \Sigma \). We then think of \(\partial _0 \Sigma \) as the incoming string boundary of \(\Sigma \), of \(\partial _1 \Sigma \) as the outgoing string boundary of \(\Sigma \), and of \(\partial _2 \Sigma \) as the brane boundary of \(\Sigma \). In order to compute a surface amplitude of
. Let \(\Sigma \) be an oriented, compact, 2-dimensional \(\langle 3\rangle ^*\)-manifold and let \(\sigma :\Sigma \rightarrow M\) be a smooth map. By Definition 3.1, the boundary of \(\Sigma \) comes with a partition \(\partial \Sigma = \partial _0 \Sigma \cup \partial _1 \Sigma \cup \partial _2 \Sigma \). We then think of \(\partial _0 \Sigma \) as the incoming string boundary of \(\Sigma \), of \(\partial _1 \Sigma \) as the outgoing string boundary of \(\Sigma \), and of \(\partial _2 \Sigma \) as the brane boundary of \(\Sigma \). In order to compute a surface amplitude of  over \(\Sigma \), we need the following decorations of \(\Sigma \).
over \(\Sigma \), we need the following decorations of \(\Sigma \).
-
(SD1)
Corners lie on D-branes: for every corner x of \(\Sigma \) (that is, a point \(x \in \Sigma \) with \(\mathrm {ind}(x)=2\)), we choose a D-brane index \(i(x) \in I\) such that \(\sigma (x) \in Q_{i(x)}\).
-
(SD2)
String endpoints move in D-branes: for each connected face \(b \subset \partial _2 \Sigma \) in the brane boundary, we choose a D-brane index \(i(b) \in I\) such that \(\sigma (b) \subset Q_{i(b)}\), and satisfying \(i(x) = i(b)\) for all corners \(x \in b \subset \partial _2 \Sigma \). Note that \(\partial b\) may be empty.
-
(SD3)
Incoming and outgoing states: per assumption on \(\Sigma \), the boundaries
$$\begin{aligned} \partial _0\Sigma = \bigsqcup _{u=1}^{n_0} c_{0,u}\ \sqcup \ \bigsqcup _{v=1}^{m_0} s_{0,v} \qquad \partial _1\Sigma = \bigsqcup _{u=1}^{n_1} c_{1,u}\ \sqcup \ \bigsqcup _{v=1}^{m_1} s_{1,v} \end{aligned}$$are disjoint unions of connected faces \(c_{0,u}, c_{1,u} \cong {\mathbb {S}}^1\) and \(s_{0,v}, s_{1,v} \cong [0,1]\). For a less cluttered notation, if \(i,j \in I\) are the brane labels assigned to the initial and end points, respectively, of the oriented edge \(s_{0,v}\), we just write \(\mathscr {R}^{s_{0,v}} {{:}{=}}\mathscr {R}^{s_{0,v}}_{ij}\) for the vector bundle constructed in Sect. 2.2; the brane labels are then understood from the data of \(s_{0,v}\). We choose an “incoming state” vector
$$\begin{aligned} \psi _0\ \in \ \bigotimes _{u=1}^{n_0} \mathscr {L}^{c_{0,u}}_{|(\sigma _{|c_{0,u}})}\ \otimes \ \bigotimes _{v=1}^{m_0} \mathscr {R}^{s_{0,v}}_{|(\sigma _{|s_{0,v}})} {{=}{:}}V_0(\Sigma ,\sigma ). \end{aligned}$$(3.1)Note that if \(\partial _0\Sigma = \emptyset \), we have \(V_0(\Sigma , \sigma ) = \mathbb {C}\). Similarly, we choose an “outgoing state” vector
$$\begin{aligned} \psi _1^\vee \ \in \ \bigotimes _{u=1}^{n_1} \mathscr {L}^{c_{1,u}}_{|(\sigma _{|c_{1,u}})}\ \otimes \ \bigotimes _{v=1}^{m_1} \mathscr {R}^{s_{1,v}}_{|(\sigma _{|s_{1,v}})} {{=}{:}}V_1(\Sigma ,\sigma )^\vee , \end{aligned}$$(3.2)Note that if \(\partial _1\Sigma = \emptyset \), we have \(V_1(\Sigma , \sigma )^\vee = \mathbb {C}\).
Remark 3.2
The reason why we use the notation \(V_1(\Sigma , \sigma )^\vee \) here will become evident in Sect. 5, where the correct vector space to assign to the outgoing boundary of \((\Sigma , \sigma )\) is the dual of the vector space considered here; the identification between \(V_1(\Sigma ,\sigma )^\vee \) and \(V_1(\Sigma , \sigma )\) will rely on the isomorphisms (2.22). \(\triangleleft \)
Definition 3.3
Let (M, Q) be a target space, and let  be a target space brane geometry.
be a target space brane geometry.
-
(1)
A quadruple \((\Sigma ,\sigma , \psi _1^\vee , \psi _0)\) of an oriented, compact, 2-dimensional \(\langle 3\rangle ^*\)-manifold \(\Sigma \) and a smooth map \(\sigma \in {\mathscr {M}\mathrm {fd}}(\Sigma ,M)\), endowed with auxiliary data as in (SD1)–(SD3) is called a scattering diagram for
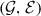 .
. -
(2)
We call two scattering diagrams \((\Sigma , \sigma , \psi _1^\vee ,\psi _0)\) and \((\Sigma ', \sigma ', \psi _1'{}^\vee ,\psi '_0)\) equivalent if there exists an orientation-preserving diffeomorphism \(t :\Sigma \rightarrow \Sigma '\) of \(\langle 3\rangle ^*\)-manifolds such that
-
t preserves maps to M, i.e. \(\sigma ' \circ t = \sigma \),
-
t preserves brane labels,
-
the states \(\psi _a\) and \(\psi '_a\) agree under the isomorphism \(V_a(\Sigma ,\sigma ) \cong V_a(\Sigma ', \sigma ')\) induced by evaluating the coherence isomorphisms \({\widehat{R}}\) of \({\widehat{\mathscr {R}}}\) and \({\widehat{\mathscr {L}}}\) on the restrictions of t to the connected components of \(\partial _a \Sigma \), for \(a = 0,1\).
We denote the equivalence class of a scattering diagram \((\Sigma , \sigma , \psi _1^\vee ,\psi _0)\) under this equivalence relation by \([\Sigma , \sigma , \psi _1^\vee ,\psi _0]\).
-
3.2 Definition of the surface amplitude
In this subsection we define the surface amplitude for scattering diagrams \((\Sigma , \sigma , \psi _1^\vee , \psi _0)\) (Definition 3.3) and then show that it depends only on the equivalence class \([(\Sigma , \sigma , \psi _1^\vee , \psi _0)]\). We first consider the case where the vectors \(\psi _0\) and \(\psi _1^\vee \) in the tensor product vector spaces (3.1) and (3.2) are pure vectors and use the following auxiliary data, on which the amplitude will not depend:
-
String boundary parameterisations: for each connected face \(s \subset \partial _0 \Sigma \) or \(s \subset \partial _1 \Sigma \) we fix an orientation-preserving diffeomorphism \(\gamma _s :{\mathbb {S}}^1 \rightarrow s\) if \(s \cong {\mathbb {S}}^1\), or \(\gamma _s :[0,1] \rightarrow s\) if \(s \cong [0,1]\).
-
Trivialisation: we fix a trivialisation
 .
.
The pure incoming state vector \(\psi _0\) is then represented (under the coherence isomorphism \({\widehat{R}}\)) by a tensor product

Here, \(n_0\) is the number of connected components \(c_{0,u}\) of \(\partial _0 \Sigma \) that are diffeomorphic to \({\mathbb {S}}^1\), and \(m_0\) is the number of connected components \(s_{0,v}\) of \(\partial _0 \Sigma \) that are diffeomorphic to [0, 1]. Further, we have used the explicit form of the bundles \(\mathscr {R}_{ij}\) and \(\mathscr {L}\) from Section 2.2 and 2.4 . Observe that once the parameterisations \(\gamma _s\) and the trivialisation  have been fixed, the tensor factors \(\psi _{0,u}\) and \(\psi _{0,v}\) each have unique representatives as in the above formula by the fact that \(({\widehat{\mathscr {R}}}_{ij}, {\widehat{R}})\) and \(({\widehat{\mathscr {L}}},{\widehat{R}})\) are coherent. An analogous statement holds true for the outgoing state vector \(\psi _1^\vee \); can be written as a linear combination of tensor products of pure states (compare (3.2))
have been fixed, the tensor factors \(\psi _{0,u}\) and \(\psi _{0,v}\) each have unique representatives as in the above formula by the fact that \(({\widehat{\mathscr {R}}}_{ij}, {\widehat{R}})\) and \(({\widehat{\mathscr {L}}},{\widehat{R}})\) are coherent. An analogous statement holds true for the outgoing state vector \(\psi _1^\vee \); can be written as a linear combination of tensor products of pure states (compare (3.2))

We now proceed to define the surface amplitude of a scattering diagram whose states \(\psi _0\) and \(\psi _1^\vee \) are pure vectors in the tensor products (3.1) and (3.2). The fully general scattering amplitude is then defined via multi-linear extension. For any \(x \in \Sigma \), let \(\iota _x :*\hookrightarrow \Sigma \) denote the inclusion of the point at x. Similarly, any connected face \(c \subset \partial \Sigma \) of \(\Sigma \) can be viewed as a submanifold of \(\Sigma \) with inclusion \(\iota _c :c \hookrightarrow \Sigma \). For each corner x of \(\Sigma \), we set  , which is a hermitean vector bundle over a point and hence a finite-dimensional Hilbert space. For each connected face \(b \subset \partial _2 \Sigma \) let
, which is a hermitean vector bundle over a point and hence a finite-dimensional Hilbert space. For each connected face \(b \subset \partial _2 \Sigma \) let  , which is a hermitean vector bundle with connection over b.
, which is a hermitean vector bundle with connection over b.
For each connected component c of \(\partial \Sigma \) we produce a number \(z_c\in \mathbb {C}\) in the following way. If c is diffeomorphic to \({\mathbb {S}}^1\), it is already a connected face in \(\partial _0 \Sigma \), \(\partial _1 \Sigma \), or \(\partial _2 \Sigma \). Otherwise, c is a union of connected faces, each of which is diffeomorphic to [0, 1]. Thus, we have to treat the following cases:
-
(SA1)
\(c \cong {\mathbb {S}}^1\) and c is some connected face \(c \subset \partial _0 \Sigma \) or \(c \subset \partial _1 \Sigma \): in this case, we have \(c = c_{\epsilon ,u}\) for some \(\epsilon \in \{0,1\}\) and \(u \in \{1, \ldots , n_\epsilon \}\) (in the notation of (3.3) and (3.4)). Further, we have chosen a parameterisation \(\gamma _{c_{\epsilon ,u}}\) of c (for \(\epsilon = 0\) or 1) and an element
 . We set $$\begin{aligned} z_c {{:}{=}}z_{c_{\epsilon ,u}}. \end{aligned}$$
. We set $$\begin{aligned} z_c {{:}{=}}z_{c_{\epsilon ,u}}. \end{aligned}$$ -
(SA2)
\(c \cong {\mathbb {S}}^1\) and \(c = b\) for some connected face \(b \subset \partial _2 \Sigma \): set
$$\begin{aligned} z_c {{:}{=}}\mathrm {tr}\big ( \mathsf {hol}(E_b) \big ) \end{aligned}$$This is well-defined because the trace of the holonomy of a vector bundle is independent of the choices of a base point and of a parameterisation.
-
(SA3)
c is a union of connected faces \(c_1,\ldots ,c_n \subset \partial \Sigma \): by definition of a \(\langle 3\rangle ^*\)-manifold we can order these faces in such a way that there are corners \(x_0,\ldots ,x_n \in c\) with \(x_n=x_0\) and \(\partial c_a = \{x_{a-1}, x_a\}\), where \(x_{a-1}\) is the initial point and \(x_a\) is the end point of \(c_a\). We define the following linear maps \(\lambda _a :E_{x_{a-1}} \rightarrow E_{x_a}\):
-
(a)
If \(c_a \subset \partial _2 \Sigma \) is brane boundary, then the hermitean vector bundle \(E_{c_a}\) over \(c_a\) comes with a connection, whose parallel transport yields an isomorphism
$$\begin{aligned} \lambda _a {{:}{=}}pt^{E_{c_a}}_{c_a} :E_{x_{a-1}} = E_{c_a|x_{a-1}} \overset{\cong }{\longrightarrow }E_{c_a|x_a} = E_{x_a}\,. \end{aligned}$$ -
(b)
If \(c_a \subset \partial _0 \Sigma \) or \(c_a \subset \partial _1 \Sigma \), then \(c_a = s_{\epsilon ,v}\) for some \(\epsilon = 0,1\) and \(v \in \{1, \ldots , m_\epsilon \}\) (in the notation of (3.3) and (3.4)). It thus comes with the element \(\psi _{s_{\epsilon ,u}}\) chosen as part of the incoming and outgoing states (compare (3.3) and (3.4)). Under the canonical isomorphism
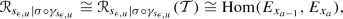
we see that \(\lambda _a {{:}{=}}\psi _{s_{\epsilon ,u}}\) defines a morphism of vector spaces \(\lambda _a :E_{x_{a-1}} \rightarrow E_{x_a}\).
We thus obtain a linear map

and we define
$$\begin{aligned} z_c {{:}{=}}\mathrm {tr}( \lambda _n \circ \ldots \circ \lambda _1). \end{aligned}$$By the cyclicity of trace, this expression is invariant under cyclic permutations of the labels \(c_1, \ldots , c_n\) of the connected faces, compatible with the orientation on \(\partial \Sigma \).
-
(a)
Definition 3.4
Let  be a target space brane geometry, and let \((\Sigma ,\sigma , \psi _1^\vee , \psi _0)\) be a scattering diagram for
be a target space brane geometry, and let \((\Sigma ,\sigma , \psi _1^\vee , \psi _0)\) be a scattering diagram for  . The surface amplitude of \((\Sigma ,\sigma , \psi _1^\vee , \psi _0)\) is defined by
. The surface amplitude of \((\Sigma ,\sigma , \psi _1^\vee , \psi _0)\) is defined by

Example 3.5
If \(\partial \Sigma = \emptyset \), the surface amplitude  recovers the surface holonomy of
recovers the surface holonomy of  over \((\Sigma ,\sigma )\) and thus the closed WZW amplitude (see e.g. [29]). In the case of only closed brane boundary it coincides with the “holonomy on D-branes” of [12]. \(\triangleleft \)
over \((\Sigma ,\sigma )\) and thus the closed WZW amplitude (see e.g. [29]). In the case of only closed brane boundary it coincides with the “holonomy on D-branes” of [12]. \(\triangleleft \)
In the following two lemmata we prove that the surface amplitude  is defined independently of the choice of auxiliary data.
is defined independently of the choice of auxiliary data.
Lemma 3.6
The surface amplitude  is independent of the trivialisation
is independent of the trivialisation  of
of  .
.
Proof
Suppose  is another trivialisation. Define a hermitean line bundle with connection
is another trivialisation. Define a hermitean line bundle with connection  over \(\Sigma \). Its curvature satisfies \(\mathrm {curv}(J) = \rho ' - \rho \). All quantities used above will be written with a prime when constructed from
over \(\Sigma \). Its curvature satisfies \(\mathrm {curv}(J) = \rho ' - \rho \). All quantities used above will be written with a prime when constructed from  instead of
instead of  . The isomorphisms (2.3) yield connection-preserving isomorphisms
. The isomorphisms (2.3) yield connection-preserving isomorphisms
for every connected face \(b \subset \partial _2 \Sigma \) and for every corner x of \(\Sigma \). Consequently, for \(c \subset \partial _2 \Sigma \) a closed 1-manifold, i.e. in case (SA2), we obtain that \(z'_c = \mathsf {hol}(J,c)^{-1} \cdot z_c\).
For the other cases, we have to represent the states \(\psi _0\) and \(\psi _1^\vee \) with respect to the new trivialisation  (cf. (SD3)). Using the parameterisations \(\gamma \), chosen as part of the auxiliary data, and the coherent structure \({\widehat{R}}\) of \({\widehat{\mathscr {R}}}\) and \({\widehat{\mathscr {L}}}\), as well as the respective formulae for changes of trivialisations of
(cf. (SD3)). Using the parameterisations \(\gamma \), chosen as part of the auxiliary data, and the coherent structure \({\widehat{R}}\) of \({\widehat{\mathscr {R}}}\) and \({\widehat{\mathscr {L}}}\), as well as the respective formulae for changes of trivialisations of  , we obtain
, we obtain

Thus, we infer that \(z'_c = \mathsf {hol}( J, c)^{-1} \cdot z_c\) for closed 1-manifolds \(c \subset \partial _0 \Sigma \) or \(c \subset \partial _1 \Sigma \). From our construction (2.6) of the isomorphisms  we obtain the following commutative diagram:
we obtain the following commutative diagram:

This holds because the 2-isomorphisms \(\psi \) used to construct  are connection-preserving. Therefore, with the above conventions for \(\lambda '_a\), we find that
are connection-preserving. Therefore, with the above conventions for \(\lambda '_a\), we find that
Putting everything together while keeping track of orientations, we obtain
as stated. The integral of \(\mathrm {curv}(J)\) comes with a positive sign because Stokes’ Theorem holds true for the orientation on the boundary induced by an outward-pointing vector field, but the holonomy is taken around the boundary with the opposite orientation. \(\square \)
Lemma 3.7
The surface amplitude is invariant under orientation-preserving reparameterisation of the string boundary components:
-
(1)
If \(s \subset \partial _0 \Sigma \) or \(s \subset \partial _1 \Sigma \) is a closed connected face and \(\tau \in \mathrm {Diff}^+({\mathbb {S}}^1)\), then the surface amplitude is invariant under changing \(\gamma _s\) to \(\gamma _s \circ \tau \).
-
(2)
If \(s \subset \partial _0 \Sigma \) or \(s \subset \partial _1 \Sigma \) is an open connected face and \(\tau \in \mathrm {Diff}^+([0,1])\), then the surface amplitude is invariant under changing \(\gamma _s\) to \(\gamma _s \circ \tau \).
Proof
In case (1), the change of parameterisation leads to a new representation of the state \(\psi _0 \in \mathscr {L}^s_{|\sigma _{|s}}\) as an element of \(\mathscr {L}\), using the coherence of \({\widehat{\mathscr {L}}}\), according to

and similarly for \(\psi _1^\vee \). Analogously, in case (2) the image of the state \(\psi _0 \in \mathscr {R}^s_{|\sigma _{|s}}\) under \({\widehat{R}}\) changes as

and accordingly for \(\psi _1^\vee \). Both claims then follow from the fact that the action of reparameterisations leaves the representing elements \(z_s\) and \(\psi _s\) unchanged—see (2.17) and (2.11). \(\square \)
It remains to prove that the surface amplitude is well-defined on equivalence classes of scattering diagrams.
Lemma 3.8
The surface amplitude is invariant under diffeomorphisms of scattering diagrams as in Definition 3.3(2).
Proof
Let \(t :\Sigma \rightarrow \Sigma '\) be a diffeomorphism as in Definition 3.3(2). Note that \(\sigma ' \circ \gamma '_{t(c)} =\sigma ' \circ t \circ \gamma _c =\sigma \circ \gamma _c\). Thus, we have
The statement then follows after choosing a trivialisation  to compute
to compute  and using the pullback
and using the pullback  to trivialise
to trivialise  and to compute
and to compute  . \(\square \)
. \(\square \)
Combining Lemmas 3.6, 3.7, and 3.8 , we obtain:
Proposition 3.9
The surface amplitude is well-defined and depends only on the equivalence class of a scattering diagram. That is, we can define

3.3 Properties of the surface amplitude
In this section we investigate further the properties of the surface amplitude of Definition 3.4. For a smooth map \(h \in {\mathscr {M}\mathrm {fd}}(N,M)\), denote its differential by \(h_* :TN \rightarrow TM\).
Definition 3.10
Let M be a manifold, N a manifold with faces, and let \(f_0, f_1 :N \rightarrow M\) be smooth maps. A thin homotopy from \(f_0\) to \(f_1\) is a smooth homotopy \(h :[0,1] \times N \rightarrow M\) between \(f_0\) and \(f_1\) such that
for all \(t \in [0,1]\) and \(x \in N\). In the case of \(f_{0|\partial N} = f_{1|\partial N}\), a (thin) homotopy rel boundary is a (thin) homotopy such that \(h(t,x) = f_0(x)\) for all \(t \in [0,1]\) and \(x \in \partial N\).
Let \((\Sigma ,\sigma _0, \psi _1^\vee , \psi _0)\) and \((\Sigma ,\sigma _1, \psi _1^\vee , \psi _0)\) be scattering diagrams for a target space brane geometry  , with the same underlying \(\langle 3\rangle ^*\)-manifold \(\Sigma \), such that \(\sigma _0\) and \(\sigma _1\) agree on \(\partial \Sigma \). A (thin) homotopy of scattering diagrams between \((\Sigma ,\sigma _0, \psi _1^\vee , \psi _0)\) and \((\Sigma ,\sigma _1, \psi _1^\vee , \psi _0)\) is a (thin) homotopy \(h :[0,1] {\times } \Sigma \rightarrow M\) rel boundary from \(\sigma _0\) to \(\sigma _1\) that preserves the brane labels picked in (SD1) and (SD2).
, with the same underlying \(\langle 3\rangle ^*\)-manifold \(\Sigma \), such that \(\sigma _0\) and \(\sigma _1\) agree on \(\partial \Sigma \). A (thin) homotopy of scattering diagrams between \((\Sigma ,\sigma _0, \psi _1^\vee , \psi _0)\) and \((\Sigma ,\sigma _1, \psi _1^\vee , \psi _0)\) is a (thin) homotopy \(h :[0,1] {\times } \Sigma \rightarrow M\) rel boundary from \(\sigma _0\) to \(\sigma _1\) that preserves the brane labels picked in (SD1) and (SD2).
Proposition 3.11
If h is a homotopy between scattering diagrams \((\Sigma ,\sigma _0, \psi _1^\vee , \psi _0)\) and \((\Sigma ,\sigma _1, \psi _1^\vee , \psi _0)\), the corresponding surface amplitudes satisfy

In particular, if h is a thin homotopy, the surface amplitudes coincide,

Proposition 3.11 will be a consequence of the following general lemma.
Lemma 3.12
Let  be a bundle gerbe with connection, defined over a surjective submersion \(\pi :Y \rightarrow M\) and with curving \(B \in \Omega ^2(Y)\).
be a bundle gerbe with connection, defined over a surjective submersion \(\pi :Y \rightarrow M\) and with curving \(B \in \Omega ^2(Y)\).
-
(1)
Consider a morphism
 , with an hermitean vector bundle E with connection over a surjective submersion \(\zeta :Z \rightarrow Y\). The 2-form \(\mathrm {curv}(E) + B \in \Omega ^2(Z, \mathrm {End}(E))\) descends to a 2-form
, with an hermitean vector bundle E with connection over a surjective submersion \(\zeta :Z \rightarrow Y\). The 2-form \(\mathrm {curv}(E) + B \in \Omega ^2(Z, \mathrm {End}(E))\) descends to a 2-form 
-
(2)
Let X be a manifold with corners, and let \(f :X \rightarrow M\) be a smooth map such that there exists a trivialisation
 for some \(\rho \in \Omega ^2(X)\). We have the identity
for some \(\rho \in \Omega ^2(X)\). We have the identity 
Proof
Ad (1): Recall that if \(B \in \Omega ^2(Y)\) is the curving 2-form of  and if \(L \rightarrow Y^{[2]}\) its defining hermitean line bundle with connection, then we have \(\mathrm {curv}(L) = d_0^*B - d_1^*B\) over \(Y^{[2]}\). We let \(\alpha \) be the vector bundle morphism over \(Z^{[2]}\) which is part of
and if \(L \rightarrow Y^{[2]}\) its defining hermitean line bundle with connection, then we have \(\mathrm {curv}(L) = d_0^*B - d_1^*B\) over \(Y^{[2]}\). We let \(\alpha \) be the vector bundle morphism over \(Z^{[2]}\) which is part of  . Since it is connection-preserving, the curvature of E and the curving 2-forms satisfy the identity
. Since it is connection-preserving, the curvature of E and the curving 2-forms satisfy the identity
as 2-forms over \(Z^{[2]} = Z \times _M Z\). Consequently, the combination \(\mathrm {curv}(E) + B\) descends to a bundle-valued 2-form

Ad (2): Let \(f :X \rightarrow M\) be a smooth map such that there exists a trivialisation  for some \(\rho \in \Omega ^2(X)\). The map f pulls back the sequence of surjective submersions \(Z \rightarrow Y \rightarrow M\) to a sequence \({\hat{f}}_Y^*Z \rightarrow f^*Y \rightarrow X\) of surjective submersions. Here \({\hat{f}}_Y :f^*Y \rightarrow Y\) is the map over f induced by the pullback of \(X \rightarrow M \leftarrow Y\). Let \({\hat{f}}_Z :f^*Z \rightarrow Z\) be the analogous induced map over \({\hat{f}}_Y\). Finally, let
for some \(\rho \in \Omega ^2(X)\). The map f pulls back the sequence of surjective submersions \(Z \rightarrow Y \rightarrow M\) to a sequence \({\hat{f}}_Y^*Z \rightarrow f^*Y \rightarrow X\) of surjective submersions. Here \({\hat{f}}_Y :f^*Y \rightarrow Y\) is the map over f induced by the pullback of \(X \rightarrow M \leftarrow Y\). Let \({\hat{f}}_Z :f^*Z \rightarrow Z\) be the analogous induced map over \({\hat{f}}_Y\). Finally, let  be the surjective submersion in the data of the trivialisation
be the surjective submersion in the data of the trivialisation  .
.
We compute the curvature of the bundle  : the morphism
: the morphism  is defined over the surjective submersion
is defined over the surjective submersion  , and if T is the bundle defining
, and if T is the bundle defining  , the bundle underlying
, the bundle underlying  is given by \({\hat{f}}_Z^*E \otimes T^\vee \). Omitting other pullbacks, we have
is given by \({\hat{f}}_Z^*E \otimes T^\vee \). Omitting other pullbacks, we have
Since the functor \(\mathsf {R}\) (see Example 2.2) is built from the descent functor for hermitean vector bundles with connection [40, 41], this yields

as claimed. \(\square \)
Proof of Proposition 3.11
First, we choose orientation-preserving parameterisations \(\gamma \) of the connected components of the string boundary of \(\Sigma \) as in Section 3.2. Consider the pullback bundle gerbe  over \([0,1] \times \Sigma \). Since \(\mathrm {H}^3([0,1] \times \Sigma , \mathbb {Z}) \cong \mathrm {H}^3(\Sigma , \mathbb {Z}) = 0\), we can choose a trivialization
over \([0,1] \times \Sigma \). Since \(\mathrm {H}^3([0,1] \times \Sigma , \mathbb {Z}) \cong \mathrm {H}^3(\Sigma , \mathbb {Z}) = 0\), we can choose a trivialization  . We have
. We have

Under the coherence isomorphism \({\widehat{R}}\), a pure vector \(\psi _0\) then corresponds to a tensor product

with
Here, x is the initial point of \(s_{0,v}\) and y is its endpoint. Further, we have set

and similarly for \(E_y\). With these choices of \(z'_{c_{0,u}}\) and \(\psi '_{s_{0,v}}\), the identity (3.7) holds true because the vectors in the second and the third lines are related by parallel transports in \(\mathscr {L}\) and \(\mathscr {R}_{ij}\) along constant paths (compare (2.10) and [11, 42]), which are identity maps.
If \(b \subset \partial _2 \Sigma \) is an open connected face, set

Its contribution to the the amplitude at \(t = 1\) is the parallel transport \(\lambda _b {{:}{=}}pt^{E_b}_{\{1\} \times b}\), which enters in the trace term (cf. (SA3)(i) and Definition 3.4). Let x and y denote the initial and endpoint of b, respectively. We have
where we have used equation (3.6) and that \(h_{|[0,1] \times b}\) has rank one. By an analogous argument, if \(b \subset \partial _2\Sigma \) is a closed connected face, its contribution to the surface amplitude at \(t=1\) differs from that at \(t=0\) by the factor \(\exp (\int _{[0,1] \times b} - \rho )\).
Inserting these findings into the expression for the surface amplitude and applying Stokes’ Theorem, we obtain the identity (3.5). \(\square \)
Proposition 3.13
Let \((\Sigma ,\sigma , \psi _1^\vee , \psi _0)\) and \((\Sigma ,\sigma ', \psi _1^\vee , \psi _0)\) be scattering diagrams for a target space brane geometry  , with the same underlying \(\langle 3\rangle ^*\)-manifold \(\Sigma \), such that \(\sigma \) and \(\sigma '\) agree on \(\partial \Sigma \). If \(\sigma , \sigma ' :\Sigma \rightarrow M\) are thin maps, i.e. \(\mathrm {rk}(\sigma _{*|x}), \mathrm {rk}(\sigma '_{*|x}) < 2\) for all \(x \in \Sigma \), then we have
, with the same underlying \(\langle 3\rangle ^*\)-manifold \(\Sigma \), such that \(\sigma \) and \(\sigma '\) agree on \(\partial \Sigma \). If \(\sigma , \sigma ' :\Sigma \rightarrow M\) are thin maps, i.e. \(\mathrm {rk}(\sigma _{*|x}), \mathrm {rk}(\sigma '_{*|x}) < 2\) for all \(x \in \Sigma \), then we have

Proof
By [11, Theorem C.1] one can find trivialisations  and
and  . In this case, the exponential terms in the surface amplitudes are trivial. Further, since \(\sigma \) and \(\sigma '\) agree on \(\partial \Sigma \) the representatives of the states agree upon changing the trivialisations on \(\partial \Sigma \), so that all remaining terms in the amplitudes agree as well. \(\square \)
. In this case, the exponential terms in the surface amplitudes are trivial. Further, since \(\sigma \) and \(\sigma '\) agree on \(\partial \Sigma \) the representatives of the states agree upon changing the trivialisations on \(\partial \Sigma \), so that all remaining terms in the amplitudes agree as well. \(\square \)
Summarising Propositions 3.11 and 3.13, the surface amplitude  has the following properties:
has the following properties:
-
(1)
 if \(\sigma _0\) and \(\sigma _1\) are thin homotopic rel boundary.
if \(\sigma _0\) and \(\sigma _1\) are thin homotopic rel boundary. -
(2)
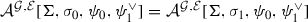 whenever \(\sigma _0\) and \(\sigma _1\) are thin maps that agree on \(\partial \Sigma \).
whenever \(\sigma _0\) and \(\sigma _1\) are thin maps that agree on \(\partial \Sigma \).
Eventually, we refer to these properties by saying that the surface amplitude  is superficial.
is superficial.
4 Smooth open-closed functorial field theories
We turn to the construction of a smooth open-closed bordism category suitable for our purposes and to the notion of smooth open-closed FFTs. Subsequently, we assemble the amplitudes defined in Sect. 3 into a smooth FFT in Sect. 5.
4.1 Smooth open-closed bordisms on a target space
Let (M, Q) be a target space. In this section, we define a smooth version of the open-closed bordism category in dimension \(d \ge 2\). Roughly speaking, its objects are smooth families of compact \((d{-}1)\)-dimensional manifolds Y, possibly with boundary, and its morphisms are smooth families of compact d-dimensional bordisms with corners. Additionally, objects and bordisms carry smooth maps to M that map brane boundaries to the submanifolds \(Q_{i}\). Our model for smooth bordism categories borrows from that in [36], modified by adding boundaries, smooth maps to a target space, and collars.
Let \({\mathscr {C}\mathrm {art}}\) denote the category of cartesian spaces, whose objects are submanifolds U of some \(\mathbb {R}^n\) that are diffeomorphic to some \(\mathbb {R}^m\), and whose morphisms are smooth maps between these submanifolds. Our goal is to assemble bordisms into a presheaf of symmetric monoidal categories on \({\mathscr {C}\mathrm {art}}\), which we will denote by \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\).
Let \(U \in {\mathscr {C}\mathrm {art}}\). If Y is a \((d{-}1)\)-manifold with boundary and if \(f :U \times Y \rightarrow M\) is a smooth map, we say that f has fibre-wise sitting instants if there exists an open neighbourhood V of \(\partial Y\) in Y and a diffeomorphism \(g :V \rightarrow \partial Y \times \mathbb {R}_{\ge 0}\) such that the following diagram commutes:

Definition 4.1
An object of the category \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) is a quintuple \((Y,f,b, {\mathsf {or}}_T,{\mathsf {or}}_\mathbb {R})\) of the following data:
-
Y is a compact \((d{-}1)\)-manifold with an orientation \({\mathsf {or}}_T\) of its stabilised tangent bundle \({\underline{\mathbb {R}}} \oplus TY\) and a map \({\mathsf {or}}_\mathbb {R}:\pi _0(Y) \rightarrow \{+,-\}\),
-
\(b :\pi _0(\partial Y) \rightarrow I\) is a map to the set I of D-brane labels,
-
\(f :U \times Y \rightarrow M\) is a smooth map with fibre-wise sitting instants and such that for each \(y \in \partial Y\) and \(x \in U\) we have \(f(x,y) \in Q_{b[y]}\), where \([y] \in \pi _0(\partial Y)\) denotes the connected component of y in \(\partial Y\).
Here we regard the symbols \(\{+,-\}\) as the two possible orientations on \(\mathbb {R}\), so that the map \({\mathsf {or}}_{{\mathbb {R}}}\) assigns to each connected component of Y an orientation on \(\mathbb {R}\) (with \(+\) amounting to the standard orientation). We induce an orientation on Y by saying that a local frame \((e_1, \ldots , e_{d-1})\) on Y at a point \(y \in Y\) is oriented if the tuple \(({\mathsf {or}}_{{\mathbb {R}}}[y], e_1, \ldots , e_{d-1})\) is oriented with respect to \({\mathsf {or}}_T\) as a local frame for the stabilised tangent bundle \({\underline{\mathbb {R}}} \oplus TY\), where \([y] \in \pi _0(Y)\) is the connected component containing y. An important difference between our bordism category and other versions is that the orientations of the manifolds Y are not part of the data of the object; the orientation of Y is determined from the orientations \({\mathsf {or}}_{{\mathbb {R}}}\) and \({\mathsf {or}}_T\). This is essential for the definition of reflection structures in Sect. 4.4.
We will generally omit the map b and the orientations \({\mathsf {or}}_T, {\mathsf {or}}_\mathbb {R}\) from the notation and abbreviate \((Y,f,b,{\mathsf {or}}_T,{\mathsf {or}}_\mathbb {R})\) by just writing (Y, f). Moreover, for (Y, f) an object in \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) with Y a connected manifold, we let \(C_\pm Y\) denote the product \(\mathbb {R}_{\pm {\mathsf {or}}_\mathbb {R}} \times Y\), where \(\mathbb {R}_+ {{:}{=}}[0, \infty )\) and \(\mathbb {R}_- {{:}{=}}(-\infty , 0]\). This is endowed with the orientation induced from \({\mathsf {or}}_T\) under the canonical identification of a frame \((r, e_1, \ldots , e_{d-1})\) of \(C_\pm Y\) at \((t,y) \in C_\pm Y\) with a frame of \(\underline{\mathbb {R}} \oplus TY\) at \(y \in Y\). Note that the datum \({\mathsf {or}}_{{\mathbb {R}}}\) does not enter in the definition of the orientation of \(C_\pm Y\); it only enters in the definition of the underlying manifold. For non-connected Y, we define \(C_\pm Y\) as the disjoint union of the component-wise construction.
Next, we define the morphisms of \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) over \(U \in {\mathscr {C}\mathrm {art}}\). To that end, we consider tuples
of the following data:
-
The pairs \((Y_a, f_a)\) are objects of \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) for \(a = 0,1\).
-
\(\Sigma \) is a compact, oriented d-dimensional \(\langle 3\rangle ^*\)-manifold with a map \(\ell :\pi _0(\partial _2 \Sigma ) \rightarrow I\) and a smooth map \(\sigma :U \times \Sigma \rightarrow M\) such that for every \(x \in U\) and \(y \in \partial _2 \Sigma \) we have that \(\sigma (x,y) \in Q_{\ell [x]}\).
-
\(W_0\) is an open neighbourhood of \(\{0\} \times Y_0\) in \(C_+ Y_0\), and \(W_1\) is an open neighbourhood of \(\{0\} \times Y_1\) in \(C_- Y_1\). We equip \(W_0\) and \(W_1\) with the orientations induced from the orientations on \(CY_0\) and \(CY_1\).
-
The \(w_a\) are smooth, orientation-preserving embeddings \(w_a :W_a \rightarrow \Sigma \). These maps must have disjoint images, satisfy that \(\partial _a \Sigma = w_a(\{0\} \times Y_a)\), for \(a = 0,1\), that \(\ell [w_a(y,t)] = b_a[y]\) for all \((t,y) \in W_a\) with \(y \in \partial Y_a\). Furthermore, they must restrict to embeddings
$$\begin{aligned} (\mathbb {R}\times \partial Y_a) \cap W_a\ \hookrightarrow \ \partial _2 \Sigma . \end{aligned}$$ -
We demand that the following diagram commutes:
 (4.2)
(4.2)One can view this diagram as a sitting instant condition on the map \(\sigma \) in a direction normal to the image of \(U \times Y_a\) in \(U \times \Sigma \).
We then define an equivalence relation on the set of tuples: consider two tuples
with the same objects \((Y_0,f_0)\) and \((Y_1,f_1)\). We say that \((\Sigma ,\sigma )\) and \((\Sigma ',\sigma ')\) are equivalent and write
if there exists a triple \((V_0, V_1, \Psi )\) consisting of a diffeomorphism \(\Psi :U \times \Sigma \rightarrow U \times \Sigma '\) that commutes with the projections to U and that preserves brane labels and the orientation on each fibre, as well as common refinements \(V_a \subset W_a \cap W'_a\) of the open neighbourhoods of \(U \times \{0\} \times Y_a\) in \(C_+Y_0\) and \(C_-Y_1\), respectively. These data have to satisfy
Definition 4.2
A morphism in \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) is an equivalence class \([\Sigma , \sigma ]\) of a tuple \((\Sigma , \sigma )\).
Composition of two morphisms \([\Sigma , \sigma ] :(Y_0,f_0) \rightarrow (Y_1,f_1)\) and \([\Sigma ', \sigma '] :(Y_1,f_1) \rightarrow (Y_2,f_2)\) in \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\) is defined by gluing the manifolds \(\Sigma \) and \(\Sigma '\) using the collars \((W_1, w_1)\) and \((W'_1, w'_1)\) of \((Y_1,f_1)\), just as in the ordinary bordism category. Note that the maps \(\sigma :\Sigma \rightarrow M\) and \(\sigma ' :\Sigma ' \rightarrow M\) glue smoothly due to the sitting instant condition (4.2). As we are using collars as part of the data of a bordism, gluing of representatives is associative up to a canonical diffeomorphism (see e.g. [23]). Moreover, this diffeomorphism induces an equivalence of tuples: the preservation of brane labels and orientations is immediate, and the compatibility with the maps to M follows from the fact that on the level of the sets underlying the bordisms, gluing amounts to forming a pushout; the universal property of the pushout then guarantees compatibility with maps out of the glued manifolds.
The identity morphism of an object \((Y,f,b,{\mathsf {or}}_T,{\mathsf {or}}_\mathbb {R}=+)\) reads as
for some \(0< \epsilon < \frac{1}{2}\). The bordism \([0,1] \times Y\) is endowed with the orientation induced from \({\mathsf {or}}_T\) under the inclusion \([0,1] \times Y \hookrightarrow \mathbb {R}\times Y\). Here we have used the canonical embeddings \(\iota _{[0,\epsilon )} :[0,\epsilon ) \hookrightarrow \mathbb {R}\) of an interval into the real line and the shift map \(sh_s :\mathbb {R}\rightarrow \mathbb {R}\), \(t \mapsto t+s\) for \(s \in \mathbb {R}\). That is, the identity bordisms are defined like in the ordinary bordism category, but multiplied by the test space U, endowed with the constant extension of f in the direction normal to \(\{0\} \times Y\). Finally, note that shrinking the collar neighbourhoods \(W_a\) of a general morphism \([\Sigma , \sigma ]\) to smaller collar neighbourhoods while restricting the collar embeddings \(w_a\) has no effect on the class \([\Sigma , \sigma ]\). Hence, our definition of the identity bordism \([\Sigma , \sigma ]\) does not depend on \(\epsilon \) and is neutral with respect to composition.
So far, we have defined a category \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\) for each cartesian space \(U\in {\mathscr {C}\mathrm {art}}\). Under the disjoint union of manifolds this becomes a symmetric monoidal category in a straightforward way. If \(g:V \rightarrow U\) is a smooth map between cartesian spaces, we define a functor \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U) \rightarrow {\mathscr {OCB}\mathrm {ord}}_d(M,Q)(V)\) by setting \(g^*(Y,f) {{:}{=}}(Y, f \circ (g \times 1_Y))\) for objects (Y, f) and
for morphisms. This turns \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\) into a presheaf of categories on \({\mathscr {C}\mathrm {art}}\), the presheaf of smooth d-dimensional, oriented open-closed bordisms on (M, Q).
Remark 4.3
We have chosen a particularly simple dependence on the test space \(U \in {\mathscr {C}\mathrm {art}}\) here, in that we only allow the maps \(\sigma \) to the target manifold M to vary over U. The full picture would be to consider bundles of \(\langle 3\rangle ^*\)-manifolds \(\Sigma \rightarrow U\) with maps \(\varsigma :\Sigma \rightarrow M\), straightforward adaptation of [36]. However, since we work over contractible test spaces, any such bundle is trivialisable, and the trivial bundles \(\Sigma = U \times \Sigma \) capture all possible smooth families in this sense. Another reason to not work with the bordism category from [36] is that we wish to make contact with earlier literature on open-closed field theories such as [24, 25, 27]. The bordism categories used in these references differ in some important features from the model of [36]; most strikingly, the identity bordisms in [36] are degenerate, and it is somewhat tedious to work out a precise relation between both versions of the bordism category. \(\triangleleft \)
Remark 4.4
The fact that we do not allow \(\Sigma \) to vary over U prohibits us from allowing its collars to vary over U: otherwise, composition of families of bordisms would yield families of bordisms that do vary over U. Thus, we keep the collars \((W_a,w_a)\) constant over U, but that requires restrictions on the smooth maps \(\sigma :U \times \Sigma \rightarrow M\): all maps \(\sigma _{|\{x\} \times \Sigma } :\Sigma \rightarrow M\), for \(x \in U\), must have sitting instants on these collars, as we impose in (4.2). However, in our setting this is not actually restrictive: consider some \(U \in {\mathscr {C}\mathrm {art}}\), some \(\langle 3\rangle ^*\)-manifold \(\Sigma \), and suppose we are given any smooth map \(\sigma :U \times \Sigma \rightarrow M\). Suppose further, we have a \((d{-}1)\)-manifold Y with a orientations \({\mathsf {or}}_T\) and \({\mathsf {or}}_\mathbb {R}\) as in the definition of an object of \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\), as well as an orientation-preserving embedding \(w_0 :W_0 \rightarrow \Sigma \), where \(W_0\) is an open neighbourhood of \(\{0\} \times Y\) in \(C_+Y\). Let us assume that Y is connected and that \({\mathsf {or}}_\mathbb {R}= +\); the following argument extends to the general case in a straightforward way. Then, we can choose a \(\delta > 0\) such that \([0, \delta ) \times Y \subset W_0\) and we can choose a smooth function \(\varepsilon :[0, \delta ) \rightarrow [0, \delta )\) that is constantly zero on \([0,\delta /3)\) and which is the identity on \((2\delta /3, \delta )\). Then, we can replace \(\sigma \) by a smooth map \(\sigma '\) such that \(\sigma ' \circ (1_U \times w_0) = \sigma \circ (1_U \times w_0) \circ (1_U \times \varepsilon \times 1_Y)\) on \([0,\delta ) \times Y\). The new map \(\sigma '\) now has sitting instants on the collar neighbourhood \([0,\delta /3) \times Y\) and for each \(x \in U\) the map \(\sigma '_{|\{x\} \times \Sigma }\) is thin homotopic to \(\sigma _{|\{x\} \times \Sigma }\). That is, up to fibre-wise thin homotopy, we still capture all families of smooth maps \(U \times \Sigma \rightarrow M\). This is analogous to the treatment of concatenation of smooth paths in [21, Paragraph 5.5]. \(\triangleleft \)
4.2 Smooth open-closed functorial field theories
Let  denote the sheaf of complex finite-dimensional vector bundles; regarded as a sheaf of symmetric monoidal categories on \({\mathscr {C}\mathrm {art}}\).
denote the sheaf of complex finite-dimensional vector bundles; regarded as a sheaf of symmetric monoidal categories on \({\mathscr {C}\mathrm {art}}\).
Definition 4.5
A smooth d-dimensional open-closed functorial field theory (OCFFT) on a target space \((M,Q)\) is a morphism

of presheaves of symmetric monoidal categories on \({\mathscr {C}\mathrm {art}}\).
The smooth OCFFTs we will construct in Sect. 5.1 have certain properties that we describe next. The first is related to the rank of the vector bundles in its image.
Definition 4.6
A smooth OCFFT \(\mathscr {Z}\) is called invertible, if for all \(U \in {\mathscr {C}\mathrm {art}}\) the following conditions are satisfied:
-
For all objects (Y, f) in \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\) with Y closed, the vector bundle \(\mathscr {Z}(Y,f)\) is of rank one.
-
For all morphisms \([\Sigma ,\sigma ]\) in \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) without brane boundary, i.e., \(\partial _2 \Sigma = \emptyset \), the vector bundle morphism \(\mathscr {Z}[\Sigma ,\sigma ]\) is an isomorphism.
We define three new equivalence relations on the set of tuples (4.1), for every test space \(U\in {\mathscr {C}\mathrm {art}}\). First, two tuples \((\Sigma ,\sigma )\) and \((\Sigma ,\sigma ')\) with the same underlying surface \(\Sigma \) are homotopy equivalent if there exists a homotopy between \(\sigma \) and \(\sigma '\) rel boundary that restricts to a constant homotopy on the images of \(W_a\) in \(\Sigma \) for \(a = 0,1\) and on \(\partial _2 \Sigma \). Secondly, the tuples \((\Sigma ,\sigma )\) and \((\Sigma ,\sigma ')\) are called thin homotopy equivalent if they are homotopy equivalent via a homotopy whose restriction to \(\{x\} \times \Sigma \) is thin for all \(x\in U\). Thirdly, the tuples \((\Sigma ,\sigma )\) and \((\Sigma ,\sigma ')\) are superficially equivalent if \(\sigma \) and \(\sigma '\) agree on \(U \times \partial \Sigma \) and if for every \(x \in U\) the maps \(\sigma \) and \(\sigma '\) restrict to thin maps on the fibre \(\{x\} \times \Sigma \).
Definition 4.7
A smooth OCFFT \(\mathscr {Z}\) on (M, Q) is called:
-
(1)
homotopy invariant if \(\mathscr {Z}[\Sigma ,\sigma ]=\mathscr {Z}[\Sigma ,\sigma ']\) whenever \((\Sigma ,\sigma )\) and \((\Sigma ',\sigma ')\) are homotopy equivalent.
-
(2)
thin homotopy invariant if \(\mathscr {Z}[\Sigma ,\sigma ]=\mathscr {Z}[\Sigma ,\sigma ']\) whenever \((\Sigma ,\sigma )\) and \((\Sigma ',\sigma ')\) are thin homotopy equivalent.
-
(3)
superficial if it is thin homotopy invariant and satisfies \(\mathscr {Z}[\Sigma ,\sigma ]=\mathscr {Z}[\Sigma ',\sigma ']\) whenever \((\Sigma ,\sigma )\) and \((\Sigma ',\sigma ')\) are superficially equivalent.
Since smooth OCFFTs are defined as morphisms in a 2-category, they come naturally organised into a category \({\mathrm {OCFFT}}_d(M,Q)\). Superficial OCFFTs, homotopy invariant OCFFTs, and thin homotopy invariant OCFFTs form, respectively, full subcategories
Invertibility will be denoted by the symbol \(()^{\times }\) in all cases, and refers again to the full subcategory on all invertible OCFFTs.
It is possible to combine the equivalence relation (4.3) and (thin) homotopy invariance on tuples into a single equivalence relation, in such a way that the composition of bordisms is well-defined on equivalence classes. This results in new presheaves \({\mathscr {OCB}\mathrm {ord}}_{d}^{h}(M,Q)\) and \({\mathscr {OCB}\mathrm {ord}}_{d}^{th}(M,Q)\) of symmetric monoidal categories, together with quotient morphisms
We have the following obvious result.
Proposition 4.8
A smooth OCFFT is (thin) homotopy invariant if and only if it factors through the quotients \({\mathscr {OCB}\mathrm {ord}}_d^{h}(M,Q)\) and \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)\), respectively.
Remark 4.9
A similar treatment of superficial OCFFTs is not easy to obtain. The reason is that two superficially equivalent bordisms may be composed separately with a fixed third bordism, whose target space map \(\sigma \) is not thin. Then, the two separate composites will in general not be superficially equivalent; superficial equivalence is not preserved under composition.
In principle, it is possible to construct a presheaf of symmetric monoidal categories \({\mathscr {OCB}\mathrm {ord}}_d^{{sf}}(M,Q)\) by starting with the free symmetric monoidal categories \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)(U)\) and imposing the relation that superficially equivalent morphisms be identified, somewhat in the spirit of Gabriel-Zisman localisation. Superficial smooth OCFFTs would then equivalently be morphisms  . However, we feel that such a construction would take us to far away from geometrical and physical intuition. Therefore, we decided to treat superficiality, and then, for the sake of consistency, also (thin) homotopy invariance as additional conditions on functors defined on \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\), rather than working with functors from \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)\), \({\mathscr {OCB}\mathrm {ord}}_d^{h}(M,Q)\), or \({\mathscr {OCB}\mathrm {ord}}_d^{{sf}}(M,Q)\). \(\triangleleft \)
. However, we feel that such a construction would take us to far away from geometrical and physical intuition. Therefore, we decided to treat superficiality, and then, for the sake of consistency, also (thin) homotopy invariance as additional conditions on functors defined on \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\), rather than working with functors from \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)\), \({\mathscr {OCB}\mathrm {ord}}_d^{h}(M,Q)\), or \({\mathscr {OCB}\mathrm {ord}}_d^{{sf}}(M,Q)\). \(\triangleleft \)
The presheaf \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)\) is interesting for another reason as well, though, namely for the study of path bordisms. Consider two objects \((Y,f_a)\in {\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\), \(a = 0,1\), with the same underlying connected manifold Y. We assume that \({\mathsf {or}}_\mathbb {R}(Y) = +\) for both objects and consider a morphism \((Y,f_0) \rightarrow (Y,f_1)\) represented by
for some smooth map \(\sigma :U \times [0,1] \times Y \rightarrow M\). As in the construction of the identity bordism (4.4), the bordism \([0,1] \times Y\) is endowed with the orientation induced from \({\mathsf {or}}_T\) under the inclusion \([0,1] \times Y \hookrightarrow \mathbb {R}\times Y\). We call such a bordism a path bordism since it represents a smooth family of paths in the diffeological mapping space \(M^Y\) with sitting instants. This is easily extended to objects with non-connected Y. The following is essentially the statement that that smooth paths in M are invertible only up to thin homotopy.
Lemma 4.10
Path bordisms are invertible in \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)\).
Proof
We can restrict ourselves to connected Y. We provide an explicit inverse path bordism in the case where \({\mathsf {or}}_\mathbb {R}= +\); in the case of \({\mathsf {or}}_\mathbb {R}= -\), the construction adapts straightforwardly. The inverse of the bordism in (4.5) is given by
where \(\mathsf {r}_s :\mathbb {R}\rightarrow \mathbb {R}\), \(t \mapsto 2s - t\) is the reflection of \(\mathbb {R}\) at \(s \in \mathbb {R}\). This is the reversal of the path in the mapping space \(M^Y\) that is defined by the bordism \([[0,1] \times Y, \sigma ]\). \(\square \)
Note that we need to employ a thin homotopy of paths in the mapping space \(M^Y\) in order to obtain the identity \([[0,1] \times Y, \sigma ]^{-1} \circ [[0,1] \times Y, \sigma ] = 1_{(Y,f)}\); that is, path bordisms are not invertible in \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\) in general, but they are always invertible in \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)\).
4.3 Duals, opposites, and hermitean structures for bordisms
In this section we work over a fixed test space \(U \in {\mathscr {C}\mathrm {art}}\), and thus with the symmetric monoidal category \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\). We note that this monoidal category has (left) duals; moreover, there is a canonical choice of duality data for every object in \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\), turning \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\) into a symmetric monoidal category with fixed duals; see Appendix 1. Indeed, if \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\) is an object, duality data \(((Y,f)^\vee , \mathrm {ev}_Y, \mathrm {coev}_Y)\) is fixed as follows:
Observe that the orientation on \({\underline{\mathbb {R}}} \oplus TY\) is unchanged, so that the orientation induced on Y is reversed, as a consequence of reversing the orientation \({\mathsf {or}}_\mathbb {R}(Y)\). The evaluation \(\mathrm {ev}_{Y}\) and coevaluation \(\mathrm {coev}_Y\) are given by the standard evaluation and coevaluation bordisms represented by the manifold \(\Sigma = [0,1] \times Y\) and its standard collars, multiplied by U and decorated with the maps \(\sigma = f \circ \mathrm {pr}_{U \times Y}\). In the following we treat this choice of fixed duals in terms of (twisted) involutions.
Definition 4.11
Let \(\mathscr {C}\) be a symmetric monoidal category. An involution on \(\mathscr {C}\) is a pair \((d, \delta )\) of a symmetric monoidal functor \(d :\mathscr {C}\rightarrow \mathscr {C}\) and a monoidal natural isomorphism \(\delta :d \circ d \rightarrow 1_\mathscr {C}\) satisfying
as natural transformations \(d \circ d \circ d \rightarrow d\). A twisted involution on \(\mathscr {C}\) is a pair \((d, \delta )\) of a symmetric monoidal functor \(d :\mathscr {C}^\mathrm {op}\rightarrow \mathscr {C}\) and a monoidal natural isomorphism \(\delta :d \circ d^\mathrm {op}\rightarrow 1_{\mathscr {C}}\) satisfying
as natural transformations \(d \circ d^\mathrm {op}\circ d \rightarrow d\). A (twisted) involution \((d, \delta )\) is called strict if \(\delta \) is the identity.
In general, in a symmetric monoidal category with fixed duals, the assignment \(x\mapsto x^{\vee }\) extends canonically to a symmetric monoidal functor \(d_{\mathscr {C}}: \mathscr {C}^{\mathrm {op}} \rightarrow \mathscr {C}\) and further to a twisted involution \((d_{\mathscr {C}},\delta _{\mathscr {C}})\), which we then call the duality involution of \(\mathscr {C}\). In the case of the symmetric monoidal category \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\) the duality involution \(d_{{\mathscr {OCB}\mathrm {ord}}}\) is in fact strict, and it is straightforward to check that its action on morphisms is explicitly given by
There is another interesting operation on \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\), given on objects and morphisms by the following definitions:
In our shorthand notation, we call \(\overline{(Y,f)}\) the opposed bordism of (Y, f). It is straightforward to check that opposition defines a strict involution
The duality involution \(d_{{\mathscr {OCB}\mathrm {ord}}}\) and the involution \(op_{{\mathscr {OCB}\mathrm {ord}}}\) are in fact related. This relation is described by a so-called hermitian structure. We first provide the relevant definitions in a more general context, following [15].
Let \(\mathscr {C}\) be a symmetric monoidal category with fixed duals, whose duality data we denote by \((x^{\vee },\mathrm {ev}_x,\mathrm {coev}_x)\), and with corresponding duality involution \((d_{\mathscr {C}},\delta )\). We suppose that \((op_{\mathscr {C}},\gamma )\) is some involution on \(\mathscr {C}\). If \(x \in \mathscr {C}\) is an object, we will also write \({\overline{x}}\) as a shorthand for \(op_{\mathscr {C}}(x)\).
Definition 4.12
A pre-hermitean structure on an object \(x \in \mathscr {C}\) is an isomorphism \(\flat _x :{\overline{x}}\rightarrow x^{\vee }\). We denote the inverse of \(\flat _x\) by \(\sharp _x {{:}{=}}\flat _x^{-1} :x^{\vee } \rightarrow {\overline{x}}\).
A pre-hermitean structure \(\flat _x\) on an object \(x \in \mathscr {C}\) defines a pre-hermitean pairing on x, by which we mean the morphism
where u is the monoidal unit in \(\mathscr {C}\). This pairing is non-degenerate in the sense that we have a pre-hermitean co-pairing
so that the usual triangle identities are satisfied.
Definition 4.13
A pre-hermitean structure \(\flat _x\) on an object \(x \in \mathscr {C}\) is called hermitean structure if its pre-hermitian pairing \(h_x\) is symmetric in the sense that the following diagram commutes

Remark 4.14
We remark that a hermitean structure relates the values of functors with different domain categories; therefore, one cannot regard it as a natural transformation. Instead, compatibility with morphisms will be treated as a condition on the morphisms, see Definition 4.15. We also remark that a property “positive-definite” cannot be defined in this general context; this will be done by hand for the category of vector bundles, see Definition 4.23. \(\triangleleft \)
Definition 4.15
Let \(f :x \rightarrow y\) be a morphism between objects with hermitian structures \(\flat _{x}\) and \(\flat _y\), respectively, and induced hermitian pairings \(h_x\) and \(h_y\), respectively. We call f is isometric if it satisfies the identity
We say that f is unitary if it is an isometric isomorphism. The adjoint of f is the composition

The name adjoint is justified by the following lemma.
Lemma 4.16
For a morphism as in Definition 4.15 we have
Proof
We compute
where we have used Lemma A.4 in the third step. \(\square \)
Proposition 4.17
Let \(f :x \rightarrow y\) be an isomorphism between objects with hermitian structures \(\flat _{x}\) and \(\flat _y\). Then, f is unitary if and only if
Proof
We need to show that f is isometric if and only if \(f^* = {\overline{f}}^{-1}\). To that end, we compute
where \(\tau ^{x}_{{{\overline{x}}},u}\) is part of the adjunction of Proposition A.3. On the other hand, using this adjunction, we may write (4.6) as \(h_x = \tau ^{x\, -1}_{{\overline{x}}, u} (\flat _x)\). Since \(\tau ^{x\, -1}_{{\overline{x}}, u}\) is bijective, we thus have that
With the definition of the adjoint morphism \(f^{*}\) this proves the assertion. \(\square \)
Example 4.18
The symmetric monoidal category  of finite-dimensional complex vector spaces has its usual fixed duals: for a vector space
of finite-dimensional complex vector spaces has its usual fixed duals: for a vector space  , we set
, we set
We consider the monoidal strict involution  sending V to the complex conjugate vector space \({\overline{V}}\). Then, a hermitean structure on
sending V to the complex conjugate vector space \({\overline{V}}\). Then, a hermitean structure on  in the sense of Definition 4.13 is the same as a hermitian metric on V (not necessarily positive definite). The notions of isometric morphisms and adjoints reproduce precisely the classical ones. Analogous statements hold for the category
in the sense of Definition 4.13 is the same as a hermitian metric on V (not necessarily positive definite). The notions of isometric morphisms and adjoints reproduce precisely the classical ones. Analogous statements hold for the category  of vector bundles over a manifold M. \(\triangleleft \)
of vector bundles over a manifold M. \(\triangleleft \)
We return to the concrete situation of the symmetric monoidal category \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) of open-closed bordisms over a test space \(U \in {\mathscr {C}\mathrm {art}}\). On each object (Y, f) of \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) we identify a canonical pre-hermitean structure
with respect to the involution \(op_{{\mathscr {OCB}\mathrm {ord}}}\). It is given by
Here we have made use of the involution \(\mathsf {r}_s :\mathbb {R}\rightarrow \mathbb {R}\), \(t \mapsto 2s - t\) that reflects the real line at an element \(s \in \mathbb {R}\). Observe that because of this reflection, the inclusion \(w_0\) in \(\flat _{(Y,f)}\) is indeed orientation-preserving if the product \([0,1] \times Y\) is endowed with the orientation induced from \({\mathsf {or}}_T\). It is straightforward to check that the pre-hermitean structure \(\flat _{(Y,f)}\) of (4.7) is hermitean.
For the following argument we consider the quotient category \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)(U)\) where thin homotopy equivalent morphisms are identified. It is easy to see that the involutions \(d_{{\mathscr {OCB}\mathrm {ord}}}\) and \(op_{{\mathscr {OCB}\mathrm {ord}}}\), as well as the hermitean structures \(\flat _{(Y,f)}\) descend to this quotient category.
Proposition 4.19
Path bordisms \(([0,1] \times Y, \sigma ) :(Y,f_0) \rightarrow (Y,f_1)\) are unitary in the symmetric monoidal category \({\mathscr {OCB}\mathrm {ord}}_2^{th}(M,Q)(U)\), with respect to the hermitean structures \(\flat _{(Y,f_0)}\) and \(\flat _{(Y,f_1)}\).
Proof
By Lemma 4.10, path bordisms are invertible in \({\mathscr {OCB}\mathrm {ord}}_d^{th}(M,Q)(U)\). Recall that the bordism \([0,1] \times Y\) in a path bordism has its orientation induced from \({\mathsf {or}}_T\). We calculate:
Here, the third identity arises from the orientation-preserving diffeomorphism
Observe that this change of orientation on \([0,1] \times Y\) is accounted for by changing the embeddings \(w_0\) and \(w_1\) accordingly. The following identity arises from another diffeomorphism and a thin homotopy to express the composition \(\sharp _{(Y,f_0)} \circ [[0,1] \times Y, \sigma ]^\vee \circ \flat _{(Y,f_1)}\) by a representative that relates directly to the standard representative of a path bordism. (The diffeomorphism in question amounts to a rescaling \([0,3] \cong [0,1]\).) Now the claim follows from Proposition 4.17. \(\square \)
Finally, we want to consider again \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\) as a presheaf over \({\mathscr {C}\mathrm {art}}\). Definition 4.11 generalizes in a straightforward way to (twisted) involutions on presheaves of symmetric monoidal categories, by requiring that the functors d and the natural isomorphism \(\delta \) are morphisms and 2-morphisms of presheaves, respectively. It is straightforward to check that in case of \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\) the duality involution \(d_{{\mathscr {OCB}\mathrm {ord}}}\) as well as the involution \(op_{{\mathscr {OCB}\mathrm {ord}}}\) are indeed morphisms of presheaves of symmetric monoidal categories over \({\mathscr {C}\mathrm {art}}\). Similarly, the duality involution  and the involution
and the involution  on the category
on the category  described in Example 4.18 become morphisms of presheaves of symmetric monoidal categories over \({\mathscr {C}\mathrm {art}}\).
described in Example 4.18 become morphisms of presheaves of symmetric monoidal categories over \({\mathscr {C}\mathrm {art}}\).
4.4 Positive reflection structures on OCFFTs
In this section we describe how a smooth OCFFT \(\mathscr {Z}\) relates the involutions \(d_{{\mathscr {OCB}\mathrm {ord}}}\) and \(op_{{\mathscr {OCB}\mathrm {ord}}}\) on the presheaf \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\) to the involutions  and
and  on the presheaf
on the presheaf  of vector bundles.
of vector bundles.
Again, we first discuss a more general setting. Let \(\mathscr {C}\) and \(\mathscr {D}\) be symmetric monoidal categories with fixed duality data and associated duality involutions \((d_{\mathscr {C}},\delta _{\mathscr {C}})\) and \((d_{\mathscr {D}},\delta _{\mathscr {D}})\). Then, for any symmetric monoidal functor \(F:\mathscr {C}\rightarrow \mathscr {D}\), there exists a unique natural isomorphism
that is compatible with evaluation and coevaluation, and which makes the diagram

commutative, see Proposition A.5. For arbitrary other (non-twisted) involutions \((op_{\mathscr {C}},\gamma _{\mathscr {C}})\) and \((op_{\mathscr {D}},\gamma _{\mathscr {D}})\), such a structure is not automatic; Proposition A.5 relies crucially on the triangle identities for duality data.
Definition 4.20
Let \(\mathscr {C}\) and \(\mathscr {D}\) be symmetric monoidal categories endowed with involutions \((op_\mathscr {C}, \gamma _\mathscr {C})\) and \((op_\mathscr {D}, \gamma _\mathscr {D})\), respectively. Let \(F :\mathscr {C}\rightarrow \mathscr {D}\) be a symmetric monoidal functor. A monoidal natural isomorphism
such that the diagram

commutes is called a homotopy fixed point structure on F.
Given a homotopy fixed point structure \(\alpha \) on a functor F and an object of x of \(\mathscr {C}\) is equipped with a (pre-)hermitean structure \(\flat _x:op_{\mathscr {C}}(x) \rightarrow d_{\mathscr {C}}(x)\), setting
defines a (pre-)hermitean structure on the image F(x). Here \(\beta \) is the canonical natural isomorphism (4.8). We have the following result.
Lemma 4.21
Suppose \(f:x \rightarrow y\) is an isometric morphism between objects with hermitean structures \(\flat _x\) and \(\flat _y\), respectively. Then, F(f) is isometric with respect to the hermitean structures \(\flat _{F,x}\) and \(\flat _{F,y}\) defined by (4.9).
Proof
For \(x,y \in \mathscr {C}\), let \(f_{x,y} :Fx \otimes Fy \rightarrow F(x \otimes y)\) denote the isomorphism that renders F a symmetric monoidal functor. For simplicity, we denote again the involutions \(op_{\mathscr {C}}\) and \(op_{\mathscr {D}}\) by \(x \mapsto {\overline{x}}\). Then, we calculate
Here we have used the naturality of \(\alpha \), the fact that (F, f) is a monoidal functor, the compatibility of \(\beta _x\) with the evaluations \(\mathrm {ev}_x\) and \(\mathrm {ev}_{Fx}\), see Proposition A.5. \(\square \)
It is again straightforward to generalise the definition of a homotopy fixed point structure to morphisms of presheaves of symmetric monoidal categories. Applying this to OCFFTs we obtain the following definition, which is an adaption of the formalism of [15] from FFTs to smooth FFTs, see [15, Def. 4.17].
Definition 4.22
A reflection structure on a smooth OCFFT  is a homotopy fixed point structure \(\alpha \) on \(\mathscr {Z}\) with respect to the involutions \(op_{\mathscr {OCB}\mathrm {ord}}\) and
is a homotopy fixed point structure \(\alpha \) on \(\mathscr {Z}\) with respect to the involutions \(op_{\mathscr {OCB}\mathrm {ord}}\) and  .
.
We recall that every object (Y, f) of \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\), for every \(U \in {\mathscr {C}\mathrm {art}}\), carries a canonical hermitean structure (4.7). Hence, by (4.9) we obtain hermitean structures \(\flat _{\mathscr {Z},(Y,f)}\) on the vector bundles \(\mathscr {Z}(Y,f)\) over U. As explained in Example 4.18, these are nothing but hermitean bundle metrics in the ordinary sense. Now the following definition makes sense:
Definition 4.23
Let  be a smooth OCFFT. A reflection structure \(\alpha \) on \(\mathscr {Z}\) is called positive if for every cartesian space \(U \in {\mathscr {C}\mathrm {art}}\) and every object \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\) the hermitean structure \(\flat _{\mathscr {Z},(Y,f)}\) on the vector bundle \(\mathscr {Z}(Y,f)\) over U is positive definite. A smooth OCFFT with a positive reflection structure will be called a reflection-positive smooth OCFFT.
be a smooth OCFFT. A reflection structure \(\alpha \) on \(\mathscr {Z}\) is called positive if for every cartesian space \(U \in {\mathscr {C}\mathrm {art}}\) and every object \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\) the hermitean structure \(\flat _{\mathscr {Z},(Y,f)}\) on the vector bundle \(\mathscr {Z}(Y,f)\) over U is positive definite. A smooth OCFFT with a positive reflection structure will be called a reflection-positive smooth OCFFT.
Reflection-positive d-dimensional smooth OCFFTs come naturally organised in a 2-category \(\mathrm {RP}\text {-}{\mathrm {OCFFT}}_{d}(M,Q)\), with full subcategories of invertible, superficial, thin homotopy invariant, and homotopy invariant smooth OCFFTs.
We close this section with the following result, obtained by combining Lemma 4.21 with Propositions 4.8 and 4.19. We plan to use this result in future work.
Proposition 4.24
Let \(\mathscr {Z}\) be a reflection-positive, thin homotopy invariant smooth OCFFT. Then, the image of any path bordism under \(\mathscr {Z}\) is a unitary vector bundle morphism.
5 Smooth OCFFTs from B-fields and D-branes
In this section, we explicitly construct a 2-dimensional smooth OCFFT over a target space (M, Q) from a target space brane geometry  as defined in Section 2.1. This construction employs the the coherent transgression vector bundles \({\widehat{\mathscr {L}}}\) and \({\widehat{\mathscr {R}}}_{ij}\) from Sect. 2 and the surface amplitude
as defined in Section 2.1. This construction employs the the coherent transgression vector bundles \({\widehat{\mathscr {L}}}\) and \({\widehat{\mathscr {R}}}_{ij}\) from Sect. 2 and the surface amplitude  from Sect. 3. We equip our smooth OCFFT with a positive reflection structure, and show that it depends functorially on the target space brane geometry.
from Sect. 3. We equip our smooth OCFFT with a positive reflection structure, and show that it depends functorially on the target space brane geometry.
5.1 From surface amplitudes to smooth OCFFTs
To begin with, we consider a cartesian space \(U \in {\mathscr {C}\mathrm {art}}\) and an object \((Y, f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\). For simplicity, let us first assume that \(Y \cong [0,1]\), with brane labels \(i,j \in I\) assigned to its initial and end point, respectively. The map \(f :U \times Y \rightarrow M\) is the adjoint of a plot \(f^{\vdash } :U \rightarrow P^Y_{ij}M\) defined by \(f^{\vdash }(x)(y) {{:}{=}}f(x,y)\) for \(x\in U\) and \(y\in Y\), i.e. \(f=(f^{\vdash })^{\dashv }\). Analogously, if \(Y \cong {\mathbb {S}}^1\), we obtain a plot \(f^{\vdash }:U \rightarrow L^Y M\). Let  be the morphism of sheaves of symmetric monoidal categories that forgets hermitean metrics and connections. We set
be the morphism of sheaves of symmetric monoidal categories that forgets hermitean metrics and connections. We set

We extend this assignment to empty Y by setting

whenever \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\) with \(Y = \emptyset \), and to non-connected Y by mapping families of disjoint unions of manifolds to tensor products of vector bundles.
We now use the amplitudes defined in Sect. 3 in order to define the field theory  on morphisms. Let \([\Sigma , \sigma ] :(Y_0,f_0) \rightarrow (Y_1,f_1)\) be a morphism in \({\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\). The two objects \((Y_a,f_a)\) define vector bundles
on morphisms. Let \([\Sigma , \sigma ] :(Y_0,f_0) \rightarrow (Y_1,f_1)\) be a morphism in \({\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\). The two objects \((Y_a,f_a)\) define vector bundles  over U, for \(a = 0,1\), via (5.1). Let
over U, for \(a = 0,1\), via (5.1). Let  and
and  be arbitrary smooth sections. We think of \(\Psi _0\) as a smoothly parameterised family of incoming states and of \(\Psi _1^\vee \) as a smoothly parameterised family of duals of outgoing states.
be arbitrary smooth sections. We think of \(\Psi _0\) as a smoothly parameterised family of incoming states and of \(\Psi _1^\vee \) as a smoothly parameterised family of duals of outgoing states.
Remark 5.1
Recall that under the canonical isomorphisms (2.16) and (2.18), and their coherent extensions (2.22), we can canonically identify the vector bundles  and
and  . We will use this identification throughout. \(\triangleleft \)
. We will use this identification throughout. \(\triangleleft \)
The following lemma is an immediate consequence of our definition of scattering diagrams (Definition 3.3) and morphisms in \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)\) (Definition 4.2).
Lemma 5.2
Let \(x\in U\).
-
If \((\Sigma ,\sigma )\) is a representative for the morphism \([\Sigma ,\sigma ]\) under the equivalence relation (4.3), then \((\Sigma , \sigma _{|\{x\} \times \Sigma }, \Psi _{1|x}^\vee , \Psi _{0|x})\) is a scattering diagram.
-
If \((\Sigma ',\sigma ')\) is another representative, then \((\Sigma ', \sigma '_{|\{x\} \times \Sigma }, \Psi _{1|x}^\vee , \Psi _{0|x})\) is an equivalent scattering diagram.
Since the surface amplitude is well-defined on equivalence classes of scattering diagrams by Proposition 3.9, we obtain a well-defined number

for every \(x\in U\). We prove first that this number depends smoothly on x.
Lemma 5.3
The function

is smooth.
Proof
Since U is diffeomorphic to \(\mathbb {R}^n\) for some \(n \in \mathbb {N}_0\) and since \(\Sigma \) is 2-dimensional, we find a trivialisation  . By the coherence of \({\widehat{\mathscr {L}}}\) and \({\widehat{\mathscr {R}}}_{ij}\), after choosing parameterisations of the connected components of \(Y_a\) (i.e. orientation-preserving diffeomorphisms to either [0, 1] or \({\mathbb {S}}^1\)), any smooth section \(\Psi _a\) of
. By the coherence of \({\widehat{\mathscr {L}}}\) and \({\widehat{\mathscr {R}}}_{ij}\), after choosing parameterisations of the connected components of \(Y_a\) (i.e. orientation-preserving diffeomorphisms to either [0, 1] or \({\mathbb {S}}^1\)), any smooth section \(\Psi _a\) of  over U can be written in a unique way as a \(C^\infty (U, \mathbb {C})\)-linear combination of tensor products of sections of the form
over U can be written in a unique way as a \(C^\infty (U, \mathbb {C})\)-linear combination of tensor products of sections of the form  for smooth functions \(z_{cl_a} :U \rightarrow \mathbb {C}\), where \(cl_a\) runs over the connected components of \(Y_a\) that are diffeomorphic to \({\mathbb {S}}^1\), and sections of the form
for smooth functions \(z_{cl_a} :U \rightarrow \mathbb {C}\), where \(cl_a\) runs over the connected components of \(Y_a\) that are diffeomorphic to \({\mathbb {S}}^1\), and sections of the form  , where
, where

Here, \(e_a\) runs over the connected components of \(Y_a\) that are diffeomorphic to [0, 1]. For the sake of legibility we have omitted pullbacks, and we have written \(e_{a,0}\) for the initial point of the oriented component of \(Y_a\) labelled by \(e_a\) and \(e_{a,1}\) for its end point. The indices \(i(e_{a,0})\) and \(i(e_{a,1}) \in I\) are the D-brane indices of the respective corners of \(\Sigma \) (see Definition 4.1). The reason that tensor products of these sections generate all smooth sections over U under \(C^\infty (U, \mathbb {C})\)-linear combinations is that, by construction of the bundles \(\mathscr {R}_{ij}\) and \(\mathscr {L}\), these sections generate each fibre of their respective pullbacks (cf. Section 2.2) that appear in  and
and  (cf. (5.1)). From the explicit construction of the surface amplitude
(cf. (5.1)). From the explicit construction of the surface amplitude  in Definition 3.4, one can now see the claimed smoothness. \(\square \)
in Definition 3.4, one can now see the claimed smoothness. \(\square \)
Now, we define a morphism

of vector bundles over U by requiring that

for all \(x \in U\) and for all smooth sections  and
and  . Since the evaluation pairing between a finite-dimensional vector space and its dual is non-degenerate, the expression (5.2) defines a bundle morphism
. Since the evaluation pairing between a finite-dimensional vector space and its dual is non-degenerate, the expression (5.2) defines a bundle morphism  which is smooth by Lemma 5.3.
which is smooth by Lemma 5.3.
Theorem 5.4
Let (M, Q) be a target space. For any target space brane geometry  , Eqs. (5.1) and (5.2) define a 2-dimensional, invertible, superficial, smooth OCFFT
, Eqs. (5.1) and (5.2) define a 2-dimensional, invertible, superficial, smooth OCFFT  on \((M, Q)\).
on \((M, Q)\).
We will decompose the proof of Theorem 5.4 into a series of smaller assertions. The compatibility with symmetric monoidal structures has been built into the definition of  on objects. On morphisms it follows from the fact that the surface amplitude
on objects. On morphisms it follows from the fact that the surface amplitude  factorises accordingly for disjoint unions of surfaces, as can readily be seen from its definition (see Sect. 3.2). The main part is now to prove that
factorises accordingly for disjoint unions of surfaces, as can readily be seen from its definition (see Sect. 3.2). The main part is now to prove that  is a morphism of presheaves of categories on \({\mathscr {C}\mathrm {art}}\). By construction, the pullbacks of objects in \({\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\) along morphisms \(V \rightarrow U\) of cartesian spaces get mapped to pullbacks of vector bundles, and the pullback of morphisms pulls back due to its fibre-wise definition (5.2). Thus, it suffices to show the functoriality of
is a morphism of presheaves of categories on \({\mathscr {C}\mathrm {art}}\). By construction, the pullbacks of objects in \({\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\) along morphisms \(V \rightarrow U\) of cartesian spaces get mapped to pullbacks of vector bundles, and the pullback of morphisms pulls back due to its fibre-wise definition (5.2). Thus, it suffices to show the functoriality of  pointwise, i.e. we only have to check that
pointwise, i.e. we only have to check that

is a functor.
Lemma 5.5
 preserves identity morphisms.
preserves identity morphisms.
Proof
Since  is respects the monoidal structure by construction, we can restrict ourselves to connected Y. Assume further that (Y, f) is an object with \({\mathsf {or}}_\mathbb {R}= +\); the case for \({\mathsf {or}}_\mathbb {R}= -\) is analogous. Recall from (4.4) that, for any object \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(*)\), we have
is respects the monoidal structure by construction, we can restrict ourselves to connected Y. Assume further that (Y, f) is an object with \({\mathsf {or}}_\mathbb {R}= +\); the case for \({\mathsf {or}}_\mathbb {R}= -\) is analogous. Recall from (4.4) that, for any object \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(*)\), we have
Let us assume that \(Y \cong [0,1]\). We choose a parameterisation \(\phi :[0,1] \rightarrow Y\) and a trivialisation  on [0, 1]. Because of the particularly simple form of the identity bordism, we can use the pullback of
on [0, 1]. Because of the particularly simple form of the identity bordism, we can use the pullback of  along the projection \([0,1]^2 \rightarrow [0,1]\) to trivialise the pullback of
along the projection \([0,1]^2 \rightarrow [0,1]\) to trivialise the pullback of  to \([0,1]^2 \cong [0,1] \times Y\). For this choice of trivialisation of the pullback of
to \([0,1]^2 \cong [0,1] \times Y\). For this choice of trivialisation of the pullback of  to \(Y \times [0,1]\), the surface integral in the amplitude
to \(Y \times [0,1]\), the surface integral in the amplitude  is trivial for any pair of incoming states \(\psi _0\) and duals of outgoing states \(\psi _1^\vee \). Further, the incoming and outgoing string boundaries of \(1_{(Y,f)}\) agree as manifolds with maps to the target space M. Consequently, the amplitude is just the evaluation pairing between the finite-dimensional vector space
is trivial for any pair of incoming states \(\psi _0\) and duals of outgoing states \(\psi _1^\vee \). Further, the incoming and outgoing string boundaries of \(1_{(Y,f)}\) agree as manifolds with maps to the target space M. Consequently, the amplitude is just the evaluation pairing between the finite-dimensional vector space  and its dual, and thus defines the identity operator
and its dual, and thus defines the identity operator

as claimed. A completely analogous argument applies for \(Y \cong {\mathbb {S}}^1\). The argument then extends to non-connected compact 1-manifolds, and thus to all objects \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(*)\), since \(\mathscr {Z}\) is symmetric monoidal. \(\square \)
Lemma 5.6
 respects the composition of bordisms.
respects the composition of bordisms.
Proof
Let \([\Sigma , \sigma ] :(Y_0, f_0) \rightarrow (Y_1, f_1)\) and \([\Sigma ', \sigma '] :(Y_1, f_1) \rightarrow (Y_2, f_2)\) be two composable bordisms in \({\mathscr {OCB}\mathrm {ord}}_2(M,Q)(*)\). Recall that their composition reads as
Here, \(\Sigma '' {{:}{=}}\Sigma \cup _{Y_1} \Sigma '\), \(\sigma '' {{:}{=}}\sigma \cup _{f_1} \sigma '\), and \({\tilde{w}}_a\) are the collar maps \(W_a \rightarrow \Sigma ''\) canonically induced by \(w_a\) for \(a = 0,2\). Choose a trivialisation  over \(\Sigma ''\). For \(a = 0,1,2\), vectors in
over \(\Sigma ''\). For \(a = 0,1,2\), vectors in  are linear combinations of tensor products of elements of \(\mathscr {L}^{Y_{a,cl_a}}\) and \(\mathscr {R}^{Y_{a,e_a}}_{e_a}\) for the respective D-branes for
are linear combinations of tensor products of elements of \(\mathscr {L}^{Y_{a,cl_a}}\) and \(\mathscr {R}^{Y_{a,e_a}}_{e_a}\) for the respective D-branes for  (cf. Sect. 3), in the notation of the proof of Lemma 5.3. Consider an arbitrary incoming state
(cf. Sect. 3), in the notation of the proof of Lemma 5.3. Consider an arbitrary incoming state  , dual outgoing state
, dual outgoing state  , and parameterisations \(\phi _a\) of the manifolds \(Y_a\) for \(a=0,1,2\). For the amplitude of the composition we then have
, and parameterisations \(\phi _a\) of the manifolds \(Y_a\) for \(a=0,1,2\). For the amplitude of the composition we then have

where \(\lambda _{c''}\) are the compositions of morphisms in  associated to \(c''\) in the construction of
associated to \(c''\) in the construction of  as in Definition 3.4. Moreover, we have used the notation \(\langle -,-\rangle _V\) for the evaluation pairing of a vector space V and its dual \(V^\vee \).
as in Definition 3.4. Moreover, we have used the notation \(\langle -,-\rangle _V\) for the evaluation pairing of a vector space V and its dual \(V^\vee \).
Every connected component \(c'' \subset \partial \Sigma ''\) which intersects the image of \(Y_1\) in \(\Sigma ''\) is naturally decomposed into two parts,
and \(c'_n\) and \(c_n\) are diffeomorphic to [0, 1] for all \(n \in \{1, \ldots , \mathsf {n}_{c''}\}\). Note that \(c''\) can only intersect the image of \(Y_1\) at points belonging to the brane boundary of \(\Sigma ''\). Similarly, every morphism \(\lambda _{c''}\) naturally decomposes as
The reason is that \(\lambda _{c''}\) is a composition of morphisms given by the morphisms \(\psi _s\) from vectors  which label open components of the open string boundary of \(c''\), and parallel transports in the bundles \(E_b\) along brane boundary components of \(c''\). The decomposition of \(\lambda _{c''}\) is then induced by decomposing the parallel transports in \(E_b\) at points where \(c''\) intersects the image of \(Y_1\). Consequently, we can rewrite the amplitude (5.3) as
which label open components of the open string boundary of \(c''\), and parallel transports in the bundles \(E_b\) along brane boundary components of \(c''\). The decomposition of \(\lambda _{c''}\) is then induced by decomposing the parallel transports in \(E_b\) at points where \(c''\) intersects the image of \(Y_1\). Consequently, we can rewrite the amplitude (5.3) as

Here we omitted labelling the identities by the vector spaces which they act on in order to avoid unnecessarily heavy notation. Let \(x \in c'' \cap Y_1\), and let \(\iota _x :*\hookrightarrow \Sigma ''\) denote its inclusion into \(\Sigma ''\). Then, the vector spaces in question are

or their duals, depending on orientations. Note that these are precisely those vector spaces which constitute  , after forgetting the inner product structure. Choosing bases \((e_{x,\mu _x})_{\mu _x = 1, \ldots , m_x}\) in each of these vector spaces \(E_x\), with dual basis elements denoted \(e^\vee _{x,\mu _x}\), we can rewrite each of the identities as
, after forgetting the inner product structure. Choosing bases \((e_{x,\mu _x})_{\mu _x = 1, \ldots , m_x}\) in each of these vector spaces \(E_x\), with dual basis elements denoted \(e^\vee _{x,\mu _x}\), we can rewrite each of the identities as
Thus, the trace is broken up into a sum over products whose factors are of the form \(\langle e_{x,\mu _x}^\vee , \lambda _{c_n} (e_{y,\mu _y})\rangle _{E_x}\), where x and y are the initial and endpoint of \(c_n\), and accordingly for paths \(c'_n\).
Now we reorder these products: we combine the factors involving the maps \(\lambda _{c_i}\), and we separately combine the factors containing the maps \(\lambda _{c'_i}\). The two ways of grouping the factors at a connected component \(s \subset Y_1\) are illustrated in the following diagram:

For \(x \in c'' \cap Y_1\), let z be the unique point in \(\partial \Sigma ''\) such that x and z are joined by a connected component of the image of \(Y_1\) in \(\Sigma ''\). Using the fact that the collection \((e_{z,\mu _z} \otimes e_{x,\mu _x}^\vee )_{\mu _x = 1,\ldots ,m_x,\, \mu _z = 1,\ldots , m_z}\) forms a basis for  , we thus arrive at
, we thus arrive at

where \((\psi _{1,k})\) is the basis for  formed by using the bases \((e_{z,\mu _z} \otimes e_{x,\mu _x}^\vee )\) in the individual tensor factors comprising
formed by using the bases \((e_{z,\mu _z} \otimes e_{x,\mu _x}^\vee )\) in the individual tensor factors comprising  . Now, by the non-degeneracy of the evaluation pairing, it follows that
. Now, by the non-degeneracy of the evaluation pairing, it follows that

for all  and
and  , which implies the claim. \(\square \)
, which implies the claim. \(\square \)
To complete the proof of Theorem 5.4 we recall that the amplitude  is superficial (Proposition 3.11 and Proposition 3.13) which readily implies that
is superficial (Proposition 3.11 and Proposition 3.13) which readily implies that  is a superficial smooth OCFFT. Finally, invertibility is immediately build in into the definition (5.1).
is a superficial smooth OCFFT. Finally, invertibility is immediately build in into the definition (5.1).
5.2 Reflection positivity
Here we show that the field theory  carries a canonical positive reflection structure in the sense of Sect. 4.4. It turns out that the hermitean metrics on the bundles
carries a canonical positive reflection structure in the sense of Sect. 4.4. It turns out that the hermitean metrics on the bundles  induced from the reflection structures are precisely the hermitean metrics on the bundles \({\widehat{\mathscr {R}}}_{ij}\) and \({\widehat{\mathscr {L}}}\) that have been forgotten in (5.1).
induced from the reflection structures are precisely the hermitean metrics on the bundles \({\widehat{\mathscr {R}}}_{ij}\) and \({\widehat{\mathscr {L}}}\) that have been forgotten in (5.1).
Consider an object \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\) over a test space \(U \in {\mathscr {C}\mathrm {art}}\). For simplicity, let us first assume that Y is connected and open, i.e. that \(Y \cong [0,1]\). We recall from (5.1) that  ; here, we omit displaying the forgetful functor \(\mathsf {U}\). Consequently, we have
; here, we omit displaying the forgetful functor \(\mathsf {U}\). Consequently, we have

On the other hand, we have

We define the vector bundle isomorphism
over U, with \(r_{ij}\) as in (2.20) and \({\widehat{\alpha }}_{ij}\) as in (2.21); see Sect. 2.5 for details. We show that this yields a natural isomorphism

Consider a morphism \([\Sigma , \sigma ]\) in \({\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\) from \((Y_0,f_0)\) to \((Y_1, f_1)\). Let  be an arbitrary smooth family of incoming states for \([\Sigma , \sigma ]\), and let
be an arbitrary smooth family of incoming states for \([\Sigma , \sigma ]\), and let  be a smooth family of outgoing dual states. We consider the evaluation
be a smooth family of outgoing dual states. We consider the evaluation

In the first step we have used nothing but the definition of the transpose of a morphism of vector bundles. The second step is seen from the explicit construction of the amplitude  in Sect. 3.2: using the coherent structure \({\widehat{R}}\) on \({\widehat{\mathscr {L}}}\) and \({\widehat{\mathscr {R}}}_{ij}\) to pass to the case where the connected components of Y are given by [0, 1] and \({\mathbb {S}}^1\) (i.e. by choosing parameterisations), the amplitude in the second line has all faces decorated with the hermitean adjoints of the linear maps that occur in the amplitude in the third line, and the integral is taken over \({\overline{\Sigma }}\). The last identity is just making use of the relation between evaluation on a complex vector space V and on its complex conjugate,
in Sect. 3.2: using the coherent structure \({\widehat{R}}\) on \({\widehat{\mathscr {L}}}\) and \({\widehat{\mathscr {R}}}_{ij}\) to pass to the case where the connected components of Y are given by [0, 1] and \({\mathbb {S}}^1\) (i.e. by choosing parameterisations), the amplitude in the second line has all faces decorated with the hermitean adjoints of the linear maps that occur in the amplitude in the third line, and the integral is taken over \({\overline{\Sigma }}\). The last identity is just making use of the relation between evaluation on a complex vector space V and on its complex conjugate,
This proves that \(\alpha \) is natural in (Y, f). Furthermore, we see that \(\alpha \) satisfies the coherence axiom from Definition 4.20 since \(op_{\mathscr {OCB}\mathrm {ord}}^2 = 1_{\mathscr {OCB}\mathrm {ord}}\) and  , and since with respect to any choice of parameterisations of Y the morphism \(\alpha \) acts on tensor factors as the morphism \(\alpha _{ij}\) from (2.13); one can readily see that \(\alpha _{ji} \circ \alpha _{ij} = 1\). This proves
, and since with respect to any choice of parameterisations of Y the morphism \(\alpha \) acts on tensor factors as the morphism \(\alpha _{ij}\) from (2.13); one can readily see that \(\alpha _{ji} \circ \alpha _{ij} = 1\). This proves
Proposition 5.7
For any target space brane geometry  , Eq. (5.5) defines a reflection structure \(\alpha \) on
, Eq. (5.5) defines a reflection structure \(\alpha \) on  .
.
We recall from Sect. 4.4 that for any test space \(U \in {\mathscr {C}\mathrm {art}}\), we have given choices of fixed duals on both \({\mathscr {OCB}\mathrm {ord}}_d(M,Q)(U)\) and on  , which are compatible with pullbacks along smooth maps \(V \rightarrow U\) of cartesian spaces. Such a choice of fixed duality data canonically defines duality functors (see Appendix 1). Further, Proposition A.5 implies that for any morphism
, which are compatible with pullbacks along smooth maps \(V \rightarrow U\) of cartesian spaces. Such a choice of fixed duality data canonically defines duality functors (see Appendix 1). Further, Proposition A.5 implies that for any morphism  the fixed duals induce a canonical monoidal natural isomorphism
the fixed duals induce a canonical monoidal natural isomorphism

For \(Y \cong [0,1]\), this is the isomorphism
defined in (2.15) and (2.16). If \(Y \cong {\mathbb {S}}^1\) instead, \(\beta _{(Y,f)}\) is given by the isomorphism \({\tilde{\varrho }}\) defined in (2.18). We extend \(\beta \) to general manifolds Y by sending disjoint unions to tensor products. Using the canonical identification of a finite-dimensional vector space with its double dual, we have

Here, the first identity is just transposing \(\beta _{(Y_0,f_0)}\). The second identity uses that \(\beta _{(Y,f)}^\vee = \beta _{(Y,f)^\vee }\) as morphisms  ; this follows right from the definition of \(\beta _{ij}\) and \({\tilde{\varrho }}\) in Sects. 2.3 and 2.4, respectively. The third identity follows from the explicit form of the amplitude
; this follows right from the definition of \(\beta _{ij}\) and \({\tilde{\varrho }}\) in Sects. 2.3 and 2.4, respectively. The third identity follows from the explicit form of the amplitude  (cf. (3.4), again using the coherence \({\widehat{R}}\) to pass to the case where the connected components of \(Y_i\) are copies of [0, 1] and of \({\mathbb {S}}^1\)): the exponential factors agree since the manifolds and maps to target space of the morphisms \([\Sigma , \sigma ]\) and \([\Sigma , \sigma ]^\vee \) agree. Moreover, the insertions of \(\beta \) and \(\beta ^{-1}\), together with the use of \(\beta \) to define \(\Psi _1^\vee \) (cf. Remark 5.1), implies that the factors \(\lambda _i\) in the amplitudes in the third and the fourth lines agree. The last two steps are transposing the morphism
(cf. (3.4), again using the coherence \({\widehat{R}}\) to pass to the case where the connected components of \(Y_i\) are copies of [0, 1] and of \({\mathbb {S}}^1\)): the exponential factors agree since the manifolds and maps to target space of the morphisms \([\Sigma , \sigma ]\) and \([\Sigma , \sigma ]^\vee \) agree. Moreover, the insertions of \(\beta \) and \(\beta ^{-1}\), together with the use of \(\beta \) to define \(\Psi _1^\vee \) (cf. Remark 5.1), implies that the factors \(\lambda _i\) in the amplitudes in the third and the fourth lines agree. The last two steps are transposing the morphism  of vector bundles and rewriting the transpose as the dual of a morphism of vector bundles.
of vector bundles and rewriting the transpose as the dual of a morphism of vector bundles.
Proposition 5.8
Let  . For any test space \(U \in {\mathscr {C}\mathrm {art}}\) and any object \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\), the hermitean structure
. For any test space \(U \in {\mathscr {C}\mathrm {art}}\) and any object \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\), the hermitean structure  on the vector bundle
on the vector bundle  over U as defined in (4.9) agrees with the hermitean structure on \(\mathscr {R}^Y_{ij}\) and \(\mathscr {L}^Y\) obtained in Sect. 2.2.
over U as defined in (4.9) agrees with the hermitean structure on \(\mathscr {R}^Y_{ij}\) and \(\mathscr {L}^Y\) obtained in Sect. 2.2.
Proof
Recall the definition of \(\flat _{(Y,f)}\) form (4.7). By (4.9) we have that

Observe that because of \(\sigma = f \circ \mathrm {pr}_Y\) we have  . Since \(U \times [0,1] \times Y\) is homotopy equivalent to Y, we have \(\mathrm {H}^2_\mathrm {dR}(U \times [0,1] \times Y) = 0\), and we may therefore choose a trivialisation
. Since \(U \times [0,1] \times Y\) is homotopy equivalent to Y, we have \(\mathrm {H}^2_\mathrm {dR}(U \times [0,1] \times Y) = 0\), and we may therefore choose a trivialisation  . We let
. We let  , for \(a = 0,1\), be smooth sections and consider the amplitude
, for \(a = 0,1\), be smooth sections and consider the amplitude

in the notation of Sect. 3.2. Note that the integral term in the surface amplitude is trivial here because of the special choice of trivialisation. For every closed component c of Y and corresponding vectors  , we obtain \(z_c = \overline{z_{c,1}}\, z_{c,0}\). For every open component c of Y and corresponding vectors
, we obtain \(z_c = \overline{z_{c,1}}\, z_{c,0}\). For every open component c of Y and corresponding vectors  we have \(z_c = \mathrm {tr}( \psi _{c,1}^*\, \psi _{c,0})\). Consequently,
we have \(z_c = \mathrm {tr}( \psi _{c,1}^*\, \psi _{c,0})\). Consequently,

where \(h_{(Y,f)}\) is the hermitean metric on the vector bundle  induced by the hermitean metrics on the transgression bundles \(\mathscr {L}^c\) and \(\mathscr {R}^c_{ij}\), for the respective connected components c of Y. On the other hand, the left-hand side of (5.6) is equal to \({\tilde{h}}_{(Y,f)}(\Psi _1, \Psi _0)\), where \({\tilde{h}}_{(Y,f)}\) is the hermitean metric on
induced by the hermitean metrics on the transgression bundles \(\mathscr {L}^c\) and \(\mathscr {R}^c_{ij}\), for the respective connected components c of Y. On the other hand, the left-hand side of (5.6) is equal to \({\tilde{h}}_{(Y,f)}(\Psi _1, \Psi _0)\), where \({\tilde{h}}_{(Y,f)}\) is the hermitean metric on  defined by the hermitean structure \(\flat _{\mathscr {Z}(Y,f)}\). \(\square \)
defined by the hermitean structure \(\flat _{\mathscr {Z}(Y,f)}\). \(\square \)
Since the hermitian metrics on \({\widehat{\mathscr {R}}}_{ij}\) and \({\widehat{\mathscr {L}}}\) are positive definite, we obtain the following.
Corollary 5.9
The reflection structure \(\alpha \) on  is positive.
is positive.
5.3 Functorial dependence on the target space brane geometry
We fix a target space (M, Q) and investigate the dependence of the functorial field theory  on the target space brane geometry
on the target space brane geometry  . For a 2-category \(\mathscr {C}\), let \(\mathrm {h}_1 \mathscr {C}\) denote its homotopy category. It has the same objects as \(\mathscr {C}\), and its morphisms are the 2-isomorphism classes of 1-morphisms in \(\mathscr {C}\).
. For a 2-category \(\mathscr {C}\), let \(\mathrm {h}_1 \mathscr {C}\) denote its homotopy category. It has the same objects as \(\mathscr {C}\), and its morphisms are the 2-isomorphism classes of 1-morphisms in \(\mathscr {C}\).
Theorem 5.10
The assignment  defined in Sects. 5.1 and 5.2 extends to a functor
defined in Sects. 5.1 and 5.2 extends to a functor
We carry out the proof of this theorem in the remainder of this section. Let us first define \(\mathscr {Z}\) on 1-morphisms  in \(\mathrm {TBG}(M,Q)\) (see Sect. 2.1 for the definition). We denote the coherent transgression bundles obtained from
in \(\mathrm {TBG}(M,Q)\) (see Sect. 2.1 for the definition). We denote the coherent transgression bundles obtained from  by \(\widehat{\mathscr {R}'}\) and \(\widehat{\mathscr {L}'}\). Consider an arbitrary test space \(U \in {\mathscr {C}\mathrm {art}}\), and let \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\). Since
by \(\widehat{\mathscr {R}'}\) and \(\widehat{\mathscr {L}'}\). Consider an arbitrary test space \(U \in {\mathscr {C}\mathrm {art}}\), and let \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_2(M,Q)(U)\). Since  is symmetric monoidal, we may restrict ourselves to connected manifolds Y.
is symmetric monoidal, we may restrict ourselves to connected manifolds Y.
We first consider the case where \(Y \cong [0,1]\). The field theory  sends the object (Y, f) to a vector bundle
sends the object (Y, f) to a vector bundle  over U. We choose a parameterisation of Y and write \({\hat{f}}\) for the composition \(U \times [0,1] \rightarrow U \times Y \rightarrow M\). Further, let \(\iota _t :U \hookrightarrow U \times [0,1]\), \(x \mapsto (x,t)\) for \(t \in [0,1]\), and write
over U. We choose a parameterisation of Y and write \({\hat{f}}\) for the composition \(U \times [0,1] \rightarrow U \times Y \rightarrow M\). Further, let \(\iota _t :U \hookrightarrow U \times [0,1]\), \(x \mapsto (x,t)\) for \(t \in [0,1]\), and write
for \(a = 0,1\). We choose a trivialisation  over \(U \times [0,1]\). Then there are canonical isomorphisms (cf. (2.5) and (5.1))
over \(U \times [0,1]\). Then there are canonical isomorphisms (cf. (2.5) and (5.1))

In this representation of the bundle  , we define isomorphisms
, we define isomorphisms

and we define  analogously. For
analogously. For  we then define smooth isomorphisms
we then define smooth isomorphisms

of vector bundles over U. For \(Y \cong {\mathbb {S}}^1\) with parameterisation \(\phi :{\mathbb {S}}^1 \rightarrow Y\) and  we set
we set

We claim that these morphisms are compatible with changes of trivialisations and with reparameterisations of Y, so that they induce a smooth bundle isomorphism

Indeed, the compatibility with reparameterisations is seen readily from the construction; acting with an orientation-preserving diffeomorphism \(g :[0,1] \rightarrow [0,1]\) sends  to
to  . Thus, if we can show the compatibility with changes of trivialisations
. Thus, if we can show the compatibility with changes of trivialisations  , then, by the functoriality of the coherent pull-push construction \(\Psi _*\Phi ^*\), this isomorphism induces an isomorphism
, then, by the functoriality of the coherent pull-push construction \(\Psi _*\Phi ^*\), this isomorphism induces an isomorphism  .
.
We check the compatibility with changes of trivialisations fibre-wise over points \(x \in U\): we set \(\jmath _x :[0,1] \rightarrow U \times [0,1]\), \(t \mapsto (x,t)\), and we set
Let  be another trivialisation and set
be another trivialisation and set

We obtain the diagram

The right-hand triangle commutes by the construction of the fibre of \(\mathscr {R}'_{ij|\gamma }\) as a colimit of the  (cf. Eq. (2.7)). The same argument applies to the left-hand triangle. We are thus left to show that the upper square in (5.9) commutes. For every \(x \in U\) there exists a 2-isomorphism
(cf. Eq. (2.7)). The same argument applies to the left-hand triangle. We are thus left to show that the upper square in (5.9) commutes. For every \(x \in U\) there exists a 2-isomorphism  , since such 2-isomorphisms are in one-to-one correspondence with parallel unit-length section of
, since such 2-isomorphisms are in one-to-one correspondence with parallel unit-length section of  . We also introduce
. We also introduce

Then we can use \(\zeta _x\) and \(\zeta '_x\) to make the canonical isomorphisms  and
and  explicit (recall (2.6)). For
explicit (recall (2.6)). For  and omitting pullbacks to \(\{x\} \times [0,1]\), we obtain the commutative diagram
and omitting pullbacks to \(\{x\} \times [0,1]\), we obtain the commutative diagram

Here we denote the horizontal inverseFootnote 1 of a (not necessarily invertible) 2-morphism \(\psi \) by \(\psi ^{(-1)}\). Observe that by (2.6) the commutativity of the outer square is the desired identity

First of all, the inner square is just the definition of  , so it commutes. The top and bottom squares are the definitions of
, so it commutes. The top and bottom squares are the definitions of  and of
and of  , respectively, whence they commute as well. Finally, the left and right squares commute as a consequence of the interchange law in a 2-category and the fact that the 2-morphisms on the vertical and horizontal arrows act on different factors in the respective compositions of 1-morphisms. Thus, the representatives
, respectively, whence they commute as well. Finally, the left and right squares commute as a consequence of the interchange law in a 2-category and the fact that the 2-morphisms on the vertical and horizontal arrows act on different factors in the respective compositions of 1-morphisms. Thus, the representatives  , which depend on choices of trivialisations, induce a well-defined isomorphism
, which depend on choices of trivialisations, induce a well-defined isomorphism

of vector bundles on U.
Lemma 5.11
Let  be a 1-isomorphism in \(\mathrm {TBG}(M,Q)\). The vector bundle isomorphisms
be a 1-isomorphism in \(\mathrm {TBG}(M,Q)\). The vector bundle isomorphisms  defined above form an isomorphism of smooth OCFFTs
defined above form an isomorphism of smooth OCFFTs

Proof
In order to see that  is natural, we consider an arbitrary smooth family of bordisms \([\Sigma , \sigma ] :(Y_0,f_0) \rightarrow (Y_1,f_1)\), parameterised over a cartesian space \(U \in {\mathscr {C}\mathrm {art}}\). Let
is natural, we consider an arbitrary smooth family of bordisms \([\Sigma , \sigma ] :(Y_0,f_0) \rightarrow (Y_1,f_1)\), parameterised over a cartesian space \(U \in {\mathscr {C}\mathrm {art}}\). Let  and
and  be smooth sections. Choose parameterisations for \(\partial _0 \Sigma \) and \(\partial _1 \Sigma \), let
be smooth sections. Choose parameterisations for \(\partial _0 \Sigma \) and \(\partial _1 \Sigma \), let  be a trivialisation, and set
be a trivialisation, and set  . The value of the scattering amplitude at a point \(x \in U\) reads as
. The value of the scattering amplitude at a point \(x \in U\) reads as

where \(\langle -,-\rangle \) is the evaluation pairing on  . We compare the amplitude (5.10) to the amplitude
. We compare the amplitude (5.10) to the amplitude

where we use the evaluation pairing on  . Observe that because the target bundle gerbes of the trivialisations
. Observe that because the target bundle gerbes of the trivialisations  and
and  agree, the exponential factors in (5.10) and (5.11) coincide. We now go through the list (SA1) to (SA3) in Section 3.2 in order determine how the factors \(z_c\) differ from the factors \(z'_c\).
agree, the exponential factors in (5.10) and (5.11) coincide. We now go through the list (SA1) to (SA3) in Section 3.2 in order determine how the factors \(z_c\) differ from the factors \(z'_c\).
Regarding (SA1), observe that since on objects (Y, f) with \(Y \cong {\mathbb {S}}^1\), the morphism  sends the element
sends the element  to
to  , we have \(z_c = z'_c\) for boundary components c of this type.
, we have \(z_c = z'_c\) for boundary components c of this type.
For (SA2), i.e. if c is a closed loop in the brane boundary \(\partial _2 \Sigma \), getting mapped to a D-brane \(Q_i\), the 2-isomorphism \(\xi _i\) induces an isomorphism of hermitean vector bundles with connection

as in (5.7). Since this isomorphism is connection-preserving, the traces of the holonomies of the source and target bundles around c are equal; hence, \(z_c = z'_c\) in this case.
Finally, for (SA3) consider an object (Y, f) with \(Y \cong [0,1]\), such that \(U \times \partial _0 Y\) gets mapped to some \(Q_i\) and such that \(U \times \partial _1 Y\) gets mapped to some \(Q_j\). From (5.8) we see that the trace in the expression for \(z_c\) in (SA3) stays unaffected; the additional terms  and
and  from the individual factors cancel each other under the trace.
from the individual factors cancel each other under the trace.
Thus, we see that the two amplitudes (5.10) and (5.11) agree factorwise, and hence that  is natural. Further, it is symmetric monoidal by construction. \(\square \)
is natural. Further, it is symmetric monoidal by construction. \(\square \)
Lemma 5.12
For every 2-isomorphism  in \(\mathrm {TBG}(M,Q)\) we have
in \(\mathrm {TBG}(M,Q)\) we have

Proof
It suffices to prove the statement for the case where \(Y_0,Y_1\) are disjoint unions of copies of [0, 1] and \({\mathbb {S}}^1\), since we have constructed  coherently with respect to parameterisations of \(Y_0\) and \(Y_1\). Using the same notation as above, we additionally define
coherently with respect to parameterisations of \(Y_0\) and \(Y_1\). Using the same notation as above, we additionally define  . First, we consider the case \(Y = [0,1]\), with initial point mapped to \(Q_i\) and end point mapped to \(Q_j\), and show that the diagram
. First, we consider the case \(Y = [0,1]\), with initial point mapped to \(Q_i\) and end point mapped to \(Q_j\), and show that the diagram

commutes. In other words, the composition  defines a morphism from
defines a morphism from  to the colimit \(\mathscr {R}'_{ij|{\hat{f}}_x}\). The commutativity is seen as follows. The connection-preserving 2-isomorphism
to the colimit \(\mathscr {R}'_{ij|{\hat{f}}_x}\). The commutativity is seen as follows. The connection-preserving 2-isomorphism  that defines the 2-isomorphism
that defines the 2-isomorphism  induces a connection-preserving isomorphism
induces a connection-preserving isomorphism

of trivialisations of  . We use this connection-preserving isomorphism in order to represent the isomorphism
. We use this connection-preserving isomorphism in order to represent the isomorphism  (cf. (2.6)). For any
(cf. (2.6)). For any

we obtain a commutative diagram

The top and bottom squares commute by definition of  and
and  , respectively, while the left and right triangles commute by definition of 2-morphisms in \(\mathrm {TBG}(M,Q)\). Consequently, we have that
, respectively, while the left and right triangles commute by definition of 2-morphisms in \(\mathrm {TBG}(M,Q)\). Consequently, we have that

for every choice of trivialisation  . The morphisms
. The morphisms  for different choices of trivialisations
for different choices of trivialisations  of
of  are compatible as we have already checked in diagram (5.9). This implies that the compositions
are compatible as we have already checked in diagram (5.9). This implies that the compositions  induce a morphism of the colimits
induce a morphism of the colimits

that only depends on the 2-isomorphism class  in \(\mathrm {TBG}(M,Q)\) of the 1-morphism
in \(\mathrm {TBG}(M,Q)\) of the 1-morphism  . \(\square \)
. \(\square \)
Proposition 5.13
For every morphism  in \(\mathrm {TBG}(M,Q)\), the morphism
in \(\mathrm {TBG}(M,Q)\), the morphism  intertwines the reflection structures on
intertwines the reflection structures on  and
and  .
.
Proof
This statement holds true because transgression maps morphisms in \(\mathrm {TBG}(M,Q)\) to bundle isomorphisms [11, Lemma 4.8.1], and by Proposition 5.8 the hermitean structure on the bundle  obtained from the reflection structure agrees with the hermitean structure obtained from transgression. \(\square \)
obtained from the reflection structure agrees with the hermitean structure obtained from transgression. \(\square \)
This completes the proof of Theorem 5.10.
Remark 5.14
We remark that by the construction of the OCFFT  , the pullback of the parallel transports on the transgression bundles over loop and path spaces agree with the images under
, the pullback of the parallel transports on the transgression bundles over loop and path spaces agree with the images under  of the associated path bordisms. That is, for example, if \(Y = [0,1]\) and \(\Gamma :U \times [0,1] \rightarrow P_{ij}M\) is a smooth family of smooth paths with sitting instants, this gives rise to a path bordism \([[0,1]^2, \Gamma ^\dashv ]\). The pullback of the parallel transport in \(\mathscr {R}_{ij}\) along \(\Gamma \) and the bundle morphism
of the associated path bordisms. That is, for example, if \(Y = [0,1]\) and \(\Gamma :U \times [0,1] \rightarrow P_{ij}M\) is a smooth family of smooth paths with sitting instants, this gives rise to a path bordism \([[0,1]^2, \Gamma ^\dashv ]\). The pullback of the parallel transport in \(\mathscr {R}_{ij}\) along \(\Gamma \) and the bundle morphism  agree as morphisms of vector bundles
agree as morphisms of vector bundles  . In fact, if we did not know the connection on the transgression bundles, this would reproduce it, and Proposition 4.19 would imply that this connection is unitary with respect to the canonically induced hermitean structures
. In fact, if we did not know the connection on the transgression bundles, this would reproduce it, and Proposition 4.19 would imply that this connection is unitary with respect to the canonically induced hermitean structures  . \(\triangleleft \)
. \(\triangleleft \)
6 Subsectors, flat gerbes, and TQFTs
In this section, we investigate several variants of the field theories  constructed in Sect. 5. We consider its closed subsectors with and without branes, and we treat the special case of flat gerbes. We conclude by showing that in the case where M is a single point our formalism is compatible with the classification of open-closed topological quantum field theories (TQFTs) in terms of coloured, knowledgeable Frobenius algebras.
constructed in Sect. 5. We consider its closed subsectors with and without branes, and we treat the special case of flat gerbes. We conclude by showing that in the case where M is a single point our formalism is compatible with the classification of open-closed topological quantum field theories (TQFTs) in terms of coloured, knowledgeable Frobenius algebras.
6.1 Closed subsectors
We consider an arbitrary target space (M, Q). We let \(\mathscr {CB}\mathrm {ord}_{d}(M,Q)\) denote the full sub-presheaf of \({\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)\) whose objects over a test space \(U \in {\mathscr {C}\mathrm {art}}\) are those objects \((Y,f) \in {\mathscr {OCB}\mathrm {ord}}_{d}(M,Q)(U)\) with \(\partial Y = \emptyset \). We emphasise that the bordisms in \(\mathscr {CB}\mathrm {ord}_d(M,Q)\) are still allowed to have non-trivial brane boundary \(\partial _2 \Sigma \ne \emptyset \), but now every connected component of \(\partial _2 \Sigma \) is necessarily diffeomorphic to \({\mathbb {S}}^1\). The involutions \(op_{{\mathscr {OCB}\mathrm {ord}}_d}\) and \(d_{{\mathscr {OCB}\mathrm {ord}}_d}\) restrict to involutions of \(\mathscr {CB}\mathrm {ord}_d(M,Q)\).
Definition 6.1
A smooth d-dimensional FFT on a target space \((M,Q)\) is a morphism

of presheaves of symmetric monoidal categories on \({\mathscr {C}\mathrm {art}}\).
Invertibility, thin homotopy invariance, superficiality, and reflection structures are defined exactly as for smooth OCFFTs. Every smooth OCFFT can be restricted to a smooth FFT, under preservation of all additional properties and reflection structures. The restriction of our OCFFT  to \(\mathscr {CB}\mathrm {ord}_d(M,Q)\) will be denoted by
to \(\mathscr {CB}\mathrm {ord}_d(M,Q)\) will be denoted by  .
.
Proposition 6.2
Let (M, Q) be a target space and  be a target space brane geometry. Then,
be a target space brane geometry. Then,

is a 2-dimensional, invertible, reflection-positive, superficial smooth FFT on (M, Q) with the following properties:
-
Its values on bordisms \((\Sigma ,\sigma )\) without boundary agree with the usual surface holonomy of the bundle gerbe
 around \(\sigma :\Sigma \rightarrow M\).
around \(\sigma :\Sigma \rightarrow M\). -
Its values on bordisms without ingoing or outgoing string boundary agree with the surface holonomy in the presence of D-branes defined in [12, 40].
In other words, our construction extends these surface holonomies to a fully fledged smooth FFT.
Proof
The statement about the values on bordisms is a straightforward comparison of our definition of Sect. 3 with the literature. \(\square \)
We define the presheaf
It has the same objects as \(\mathscr {CB}\mathrm {ord}_{d}(M,Q)\), but only those morphisms \([\Sigma ,f]\) with \(\partial _2 \Sigma = \emptyset \). For any target space (M, Q) there are canonical inclusion morphisms

The first morphism is surjective on objects and faithful over every \(U \in {\mathscr {C}\mathrm {art}}\), but in general not full, whereas the second morphism is fully faithful for every \(U \in {\mathscr {C}\mathrm {art}}\), but in general not essentially surjective. The involutions \(op_{{\mathscr {OCB}\mathrm {ord}}_d}\) and \(d_{{\mathscr {OCB}\mathrm {ord}}_d}\) restrict again to involutions of \(\mathscr {B}\mathrm {ord}_d(M)\).
Definition 6.3
A smooth d-dimensional FFT on a smooth manifold M is a morphism

of presheaves of symmetric monoidal categories on \({\mathscr {C}\mathrm {art}}\). We let \({\mathrm {FFT}}_d(M)\) denote the category of d-dimensional smooth FFTs on M with values in  .
.
Again, invertibility, thin homotopy invariance, superficiality, and reflection structures are defined exactly as for smooth FFTs on a target space (M, Q). Every smooth FFT on (M, Q) can be restricted to a smooth FFT on M. We write  for this restriction. We obtain the following.
for this restriction. We obtain the following.
Proposition 6.4
For any bundle gerbe  with connection over M,
with connection over M,

is a 2-dimensional, invertible, reflection-positive, superficial smooth FFT on M, whose values on closed bordisms coincide with the surface holonomy of  .
.
Remark 6.5
A smooth FFT on a manifold M is invertible if and only if it factors through the inclusion  , where
, where  is the sheaf of groupoids of line bundles. In particular, this holds true for the smooth FFT
is the sheaf of groupoids of line bundles. In particular, this holds true for the smooth FFT  of Proposition 6.4.
of Proposition 6.4.
We conclude this subsection with remarks on the comparison of the smooth field theories considered here and those considered in [8]. The field theories of Bunke–Turner–Willerton are symmetric monoidal functors from a thin-homotopy surface category  of M to the category
of M to the category  of complex lines. From the definitions in [8] we observe that there is an inclusion of symmetric monoidal categories
of complex lines. From the definitions in [8] we observe that there is an inclusion of symmetric monoidal categories  which is an equivalence of categories.
which is an equivalence of categories.
Proposition 6.6
Given a gerbe  with connection on M, the field theory
with connection on M, the field theory  constructed in [8] coincides with the composition
constructed in [8] coincides with the composition

where  is the component over \(* \in {\mathscr {C}\mathrm {art}}\) of our smooth FFT
is the component over \(* \in {\mathscr {C}\mathrm {art}}\) of our smooth FFT  .
.
Proof
Indeed, the value of both functors on simple objects \(({\mathbb {S}}^1,f) \in \mathscr {B}\mathrm {ord}_2^{th}(M)(*)\) is the fibre  of the transgression line bundle of
of the transgression line bundle of  at the loop \(f :{\mathbb {S}}^1 \rightarrow M\). The value on morphisms is essentially the surface holonomy of the gerbe. \(\square \)
at the loop \(f :{\mathbb {S}}^1 \rightarrow M\). The value on morphisms is essentially the surface holonomy of the gerbe. \(\square \)
Apart from the above relation between both constructions, the categories of field theories used in [8] and here are very different. However, let \(\mathrm {TIFT}(M)\) be the set of isomorphism classes of thin-invariant smooth two-dimensional field theories as defined in [8, Prop. 3.3]. We expect that there is an isomorphism of groups
between \(\mathrm {TIFT}(M)\) and the group of isomorphism classes of two-dimensional superficial, invertible smooth FFTs. Indeed, Bunke–Turner–Willerton show that \(\mathrm {TIFT}(M)\) is in bijection with isomorphism classes of gerbes with connection on M [8, Thm. 6.3], and we conjecture that our construction induces a bijection between \(\pi _0({\mathrm {FFT}}_2^{sf}(M)^\times )\) and isomorphism classes of gerbes with connection on M as well (see also the end of Sect. 1).
Let us comment on why we find that our definition of a smooth field theory is more closely aligned with direct physical intuition (see Sect. 1). In [8] a rather strict notion of smoothness is used for field theories, which requires the existence of a certain closed 3-form H on M such that for any 3-manifold V with smooth map \(v :V \rightarrow M\) the field theory  satisfies
satisfies
For any gerbe  with connection on M, the restriction
with connection on M, the restriction  of our smooth FFT satisfies this property, where
of our smooth FFT satisfies this property, where  is the curvature 3-form of
is the curvature 3-form of  . (This follows from a well-known property of the surface amplitude.)
. (This follows from a well-known property of the surface amplitude.)
This smoothness condition is powerful, but it does not encode the intuition that the values of the field theory functor should depend smoothly on the input data. Further, the smoothness property in [8] implies additional properties such as invariance under thin 3-bordism (see [8, Thm. 3.5]) which a priori are not related to the smoothness of a field theory. In our formalism, any additional properties of field theories are treated separately from smoothness and are implemented in the explicit notion of superficiality. For instance, this implies the invariance under thin three-bordism; we sketch this for the torus: given a solid torus V with a smooth rank-two map \(v :V \rightarrow M\), we can interpret these data as a thin homotopy between the bordism \([\partial V, v_{|\partial v}] :\emptyset \rightarrow \emptyset \) and a bordism \([\partial V, \sigma ] :\emptyset \rightarrow \emptyset \), where \(\sigma \) is a rank-one map. If \(\mathscr {Z}\) is a superficial smooth FFT, it now follows that \(\mathscr {Z}[\partial V, v_{|\partial v}] = \mathscr {Z}[\partial V, \sigma ]\) as complex numbers (since \(\mathscr {Z}\) is thin-homotopy invariant). By the superficiality of \(\mathscr {Z}\) (see Definition 4.7 and the preceding paragraph) it now follows that \(\mathscr {Z}[\partial V, \sigma ] = 1\).
The presheaf formalism we are using here encodes directly the smooth behaviour of the field theory on both objects and morphisms, and it fits with the modern treatment of functorial field theories [36]. Further, our formalism easily extends to field theories valued in targets other than  , whereas the implementation of smoothness in [8] makes specific use of the target category (in particular the fact that it is linear).
, whereas the implementation of smoothness in [8] makes specific use of the target category (in particular the fact that it is linear).
Finally, we work with the full category of smooth FFTs rather than with their isomorphism classes, and our construction depends functorially on the input gerbe. We further believe that this is why in [8] there was no need to consider reflection structures; we refer to an upcoming paper for details on this.
6.2 Flat gerbes and homotopy field theories
Recall the definition of a homotopy invariant smooth OCFFT from Definition 4.7.
Theorem 6.7
Let  be a target space brane geometry on a target space \((M,Q)\). The following are equivalent:
be a target space brane geometry on a target space \((M,Q)\). The following are equivalent:
-
(1)
The smooth OCFFT
 is homotopy invariant.
is homotopy invariant. -
(2)
The connection on the bundle gerbe
 is flat; that is,
is flat; that is,  .
.
Proof
If  is flat, Proposition 3.11 implies that
is flat, Proposition 3.11 implies that  is invariant under homotopies of \(\sigma \) that are constant homotopies on \(U \times \partial _2 \Sigma \) and the collar neighbourhoods of \(\partial _a \Sigma \) for \(a=0,1\).
is invariant under homotopies of \(\sigma \) that are constant homotopies on \(U \times \partial _2 \Sigma \) and the collar neighbourhoods of \(\partial _a \Sigma \) for \(a=0,1\).
In the other direction, let \(\Sigma = {\mathbb {D}}^3\) be the three-dimensional closed disc, and let \(h :{\mathbb {D}}^3 \rightarrow M\) be any smooth map. We may regard h as a smooth homotopy \(t \mapsto h_t\) of maps \(h_t :{\mathbb {S}}^2 \rightarrow M\) for \(t \in [0,1]\), with \(h_0\) a constant map. Proposition 3.11 and the homotopy invariance of  imply that
imply that

Since h was arbitrary, this implies that  . \(\square \)
. \(\square \)
Thus, field theories arising from flat gerbes are homotopy invariant FFTs, similar to those studied by Turaev [39], and for topological (rather than smooth) models of gerbes, in particular, in [30]. Our smooth OCFFTs refine these results in that they are smooth, work in the non-flat case, and include D-branes.
6.3 Open-closed TQFTs and smooth OCFFTs on the point
In [35] the paradigm has been introduced that a functorial field theory with a target space M should be viewed as a classical field theory on M, whereas a field theory over the point \((M=*)\) should be understood as a quantum field theory.
In this section we explain how our definition of a smooth OCFFT reduces to the common definition of an open-closed topological quantum field theory (OCTQFT). To this end, we consider the target space (M, Q) where M is a single point and where the collection \(Q= \{Q_i\}_{i \in I}\) is a family of copies of the point indexed by I. We write I as a shortcut for this target space. We consider the symmetric monoidal category
where \(* \in {\mathscr {C}\mathrm {art}}\) is the point, seen as a zero-dimensional cartesian space. The symmetric monoidal category \({\mathscr {OCB}\mathrm {ord}}_d^{I}\) inherits the two involutions \(d_{{\mathscr {OCB}\mathrm {ord}}}\) and \(op_{{\mathscr {OCB}\mathrm {ord}}}\). In analogy with Definitions 4.5 and 4.22 we set up the following definition.
Definition 6.8
A d-dimensional OCTQFT is a symmetric monoidal functor

An OCTQFT is called invertible if the vector spaces assigned to closed objects \(Y\cong S^1\) are 1-dimensional and all bordisms with empty brane boundary are sent to isomorphisms. Reflection structures for OCTQFTs and their positivity are defined analogously to the ones for smooth OCFFTs. Morphisms of (reflection-positive) OCTQFTs are symmetric monoidal transformations (intertwining the reflection structures). The category of d-dimensional OCTQFTs with D-brane labels I is denoted by \(\mathrm {OCTQFT}_d^I\). We use the prefix “\(\mathrm {RP}\text {-}\)” for reflection-positivity, and the notation \((..)^{\times }\) for invertibility.
The relation between smooth OCFFTs over I and OCTQFTs with D-brane labels I is the evaluation of a morphism of presheaves on \(*\in {\mathscr {C}\mathrm {art}}\), which is a functor
We remark that every smooth OCFFT over I is automatically thin homotopy invariant, superficial, and homotopy invariant, so that these properties need not to be discussed here. We describe now the surprising result hat the functor (6.1) is an equivalences of categories. This is remarkable, since it may seem that smooth FFTs on the point have vastly more structure than TQFTs, as TQFTs do not encode any smooth families of bordisms. However, functoriality in the test space, combined with our careful construction of the smooth bordism categories \({\mathscr {OCB}\mathrm {ord}}_d\), leads to the this result:
Theorem 6.9
The functor \(\mathrm {ev}_*\) is an equivalence of symmetric monoidal categories,
between the category of d-dimensional, smooth OCFFTs on I and the category of d-dimensional OCTQFTs with D-brane labels I. The functor \(\mathrm {ev}_{*}\) and this equivalence result extends to the full subcategories of reflection-positive and invertible field theories.
We remark that Theorem 6.9 holds for an empty index set \(I=\emptyset \), and hence in particular for smooth FFTs and TQFTs. For the proof of Theorem 6.9 we require the following lemma. Let \(U \in {\mathscr {C}\mathrm {art}}\) be arbitrary, and let \(c :U \rightarrow *\) be the collapse map in \({\mathscr {C}\mathrm {art}}\). Since \({\mathscr {OCB}\mathrm {ord}}_d(I)\) is a presheaf of symmetric monoidal categories on \({\mathscr {C}\mathrm {art}}\), this induces a symmetric monoidal functor
Lemma 6.10
For any \(U \in {\mathscr {C}\mathrm {art}}\), the functor \(c^*\) is bijective on objects and morphisms.
Proof
The bijectivity on objects follows directly from Definition 4.1 and the fact that \(M=*\). Let \([\Sigma ] :Y_0 \rightarrow Y_1\) be a morphism in \({\mathscr {OCB}\mathrm {ord}}_d(I)(U)\). It readily follows from Definition 4.2 that any representative \(\Sigma \) arises as the pullback of a unique representative \(\Sigma _*\) of a morphism \([\Sigma _*] :Y_{0,*} \rightarrow Y_{1,*}\) in \({\mathscr {OCB}\mathrm {ord}}_2^I\). It remains to show that \(\Sigma \) and \(\Sigma '\) are two representatives of the same bordism in \({\mathscr {OCB}\mathrm {ord}}_2(I)(U)\) if and only if \(\Sigma _*\) and \(\Sigma '_*\) represent the same bordism in \({\mathscr {OCB}\mathrm {ord}}_2^I\). To see this, let \(\Psi :U \times \Sigma \rightarrow U \times \Sigma '\) be a fibre-wise diffeomorphism that establishes the equivalence \(\Sigma \sim \Sigma '\) in \({\mathscr {OCB}\mathrm {ord}}_2(I)(U)\) (compare (4.3)). Then, restricting \(\Psi \) to the fibre over any point \(x \in U\) establishes the equivalence \(\Sigma _* \sim \Sigma '_*\) in \({\mathscr {OCB}\mathrm {ord}}_2^I\). Conversely, given any diffeomorphism \(\Psi _* :\Sigma _* \rightarrow \Sigma '_*\) that establishes \(\Sigma _* \sim \Sigma '_*\), the fibre-wise diffeomorphism \(1_U \times \Psi _* :U \times \Sigma \rightarrow U \times \Sigma '\) establishes that \(\Sigma \sim \Sigma '\). \(\square \)
Proof of Theorem 6.9
We consider the evaluation functor
that evaluates smooth field theories (and their morphisms) on the cartesian space \(* \in {\mathscr {C}\mathrm {art}}\). The functor \(\mathrm {ev}_*\) is surjective on objects: let \(Z \in {\mathrm {OCTQFT}}_d^{I}\) be arbitrary. We construct a smooth FFT \(\mathscr {Z}\in {\mathrm {OCFFT}}_d(I)\) with \(\mathrm {ev}_*(\mathscr {Z}) = Z\). First, we define \(\mathscr {Z}\) on objects. Let \(U \in {\mathscr {C}\mathrm {art}}\) be arbitrary. By Lemma 6.10, any object \(Y \in {\mathscr {OCB}\mathrm {ord}}_d(I)(U)\) is actually constant, i.e. it arises as a pullback of a unique object \(Y_* \in {\mathscr {OCB}\mathrm {ord}}_d^I\) along the collapse map \(U \rightarrow *\). We set
Also by Lemma 6.10, every morphism \([\Sigma ]\) in \({\mathscr {OCB}\mathrm {ord}}_d(I)(U)\) is the pullback of a unique morphism \([\Sigma _*] \in {\mathscr {OCB}\mathrm {ord}}_d^I\), and we set
The assignment \(\mathscr {Z}\) is functorial and symmetric monoidal since Z is so, and by construction it satisfies \(\mathrm {ev}_* \mathscr {Z}= Z\). Hence, \(\mathrm {ev}_*\) is surjective on objects.
We now show that \(\mathrm {ev}_*\) is fully faithful. To that end, let  be OCFFTs, and let \(\zeta :\mathscr {Z}\rightarrow \mathscr {Z}'\) be a natural transformation of presheaves of categories. The naturality of \(\zeta \) in \(U \in {\mathscr {C}\mathrm {art}}\) implies that we have commutative diagrams
be OCFFTs, and let \(\zeta :\mathscr {Z}\rightarrow \mathscr {Z}'\) be a natural transformation of presheaves of categories. The naturality of \(\zeta \) in \(U \in {\mathscr {C}\mathrm {art}}\) implies that we have commutative diagrams

where the horizontal vector bundle isomorphisms over U are part of the structure that makes \(\mathscr {Z}\) and \(\mathscr {Z}'\) morphisms of presheaves of categories. Combining diagram (6.2) with Lemma 6.10 now shows that any morphism \(\zeta \) is entirely determined by its value on the terminal object \(* \in {\mathscr {C}\mathrm {art}}\). The consideration of reflection structures and invertibility is straightforward. \(\square \)
Thus, in our formalism, smooth OCFFTs on the one-point target space I are equivalent to ordinary OCTQFTs with D-brane labels I.
6.4 Classification of 2-dimensional open-closed TQFTs
Two-dimensional open-closed OCTQFTs have been investigated in [24, 25, 27], for example. Our definition of the category \({\mathrm {OCTQFT}}_2^I\) coincides precisely with the one given in [25]. There, and also in [24, 27], it has been shown that 2-dimensional OCTQFTs with D-brane labels I are in equivalence to so-called I-coloured knowledgeable Frobenius algebras, as defined in [25, Section 2], see Theorem 6.12 below. We first recall the definition here for convenience.
Definition 6.11
Let I be a set. An I-coloured knowledgeable Frobenius algebra is a septuple \((\mathscr {L},\mathscr {R}, \chi , \epsilon , \theta , \iota , \iota ^*)\) of the following data:
-
(1)
\(\mathscr {L}\) is a commutative Frobenius algebra over \(\mathbb {C}\), with trace denoted by \(\vartheta \).
-
(2)
\(\mathscr {R}= \{\mathscr {R}_{ij}\}_{i,j \in I}\) is a family of finite-dimensional complex vector spaces.
-
(3)
\(\chi = \{\chi _{ijk}\}_{i,j,k \in I}\) is a collection \(\chi _{ijk} :\mathscr {R}_{jk} \otimes \mathscr {R}_{ij} \rightarrow \mathscr {R}_{ik}\) of linear maps, which satisfies an associativity condition for quadruples of elements in I.
-
(4)
\(\epsilon = \{\epsilon _i\}_{i \in I}\) is a family of elements \(\epsilon _i \in \mathscr {R}_{ii}\) that is neutral with respect to \(\chi _{iii}\). In particular, \((\mathscr {R}_{ii}, \chi _{iii}, \epsilon _i)\) is an algebra for every \(i \in I\).
-
(5)
\(\theta = \{\theta _i\}_{i \in I}\) is a collection of linear maps \(\theta _i :\mathscr {R}_{ii} \rightarrow \mathbb {C}\).
-
(6)
\(\iota = \{\iota \}_{i \in I}\) is a family of linear maps \(\iota _i :\mathscr {L}\rightarrow \mathscr {R}_{ii}\), central in the sense that
$$\begin{aligned} \chi _{iij} \big ( v \otimes \iota _i(\ell ) \big ) = \chi _{ijj} \big ( \iota _j(\ell ) \otimes v \big ) \end{aligned}$$for all \(\ell \in \mathscr {L}\) and \(v \in \mathscr {R}_{ij}\).
-
(7)
\(\iota ^* = \{\iota ^*_i\}_{i \in I}\) is a family of linear maps \(\iota ^*_i :\mathscr {R}_{ii} \rightarrow \mathscr {L}\), adjoint to \(\iota \) in the sense that
$$\begin{aligned} \vartheta \big ( \ell \cdot \iota ^*_i(c) \big ) = \theta _i \big ( \chi _{iii}(\iota _i(\ell ) \otimes v) \big ) \end{aligned}$$for all \(v \in \mathscr {R}_{ii}\) and \(\ell \in \mathscr {L}\).
For \(i,j \in I\), let \(\sigma _{ij}\) denote the pairing

The above data are subject to the following conditions:
-
\(\sigma _{ij}\) is non-degenerate; that is, it induces an isomorphism \(\Phi _{ij} :\mathscr {R}_{ij} \rightarrow \mathscr {R}_{ji}^\vee \) for every \(i,j \in I\).
-
\(\sigma = \{\sigma _{ij}\}_{i,j \in I}\) is symmetric, meaning that \(\sigma _{ij}(a \otimes b) = \sigma _{ji}(b \otimes a)\) for all \(a \in \mathscr {R}_{ji}\) and \(b \in \mathscr {R}_{ij}\).
-
If \((v_1, \ldots , v_n)\) is a basis of \(\mathscr {R}_{ij}\) with dual basis \((v^1, \ldots , v^n)\) of \(\mathscr {R}_{ji}\) under the isomorphism \(\Phi _{ij}\), then for any \(v \in \mathscr {R}_{ii}\) we have that
$$\begin{aligned} (\iota _j \circ \iota ^*_i)(v) = \sum _{k = 1}^n \chi _{jij} \big ( \chi _{iij} (v_k \otimes v) \otimes v^k \big )\,. \end{aligned}$$
A morphism
of I-coloured knowledgeable Frobenius algebras consists of a linear map \(\varphi :\mathscr {L}\rightarrow \mathscr {L}'\) and a family \(\xi = \{\xi _{ij}\}_{i,j \in I}\) of linear maps \(\xi _{ij} :\mathscr {R}_{ij} \rightarrow \mathscr {R}_{ij}'\) that respect the products, units and traces, and satisfy
for all \(i,j \in I\).
This defines a category of I-coloured knowledgeable Frobenius algebras, which we denote by \(\mathrm {KFrob}^I\). The classification result obtained in [24, 25, 27] is the following.
Theorem 6.12
There is an equivalence of categories
We briefly recall the definition of this functor. If \(\mathscr {Z}\) is a 2-dimensional OCTQFT with brane labels I, then the Frobenius algebra \(\mathscr {L}\) of \(\mathscr {F}(\mathscr {Z})\) has the underlying vector space \(\mathscr {Z}(S^1)\), the product is given by the value of \(\mathscr {Z}\) on a closed pair of pants, and the trace \(\vartheta \) is obtained from the cap bordism \(S^1 \rightarrow \emptyset \). The vector space \(\mathscr {R}_{ij}\) is \(\mathscr {Z}([0,1])\), and the linear maps \(\chi _{ijk}\) are obtained by evaluating \(\mathscr {Z}\) on an open pair of pants. The elements \(\epsilon _i\) and the linear maps \(\theta _i\) are obtained from the open cap bordisms \(\emptyset \rightarrow [0,1]\) and \([0,1] \rightarrow \emptyset \), respectively. The linear maps \(\iota _i\) and \(\iota _i^{*}\) are obtained from the unzip bordism \(S^1 \rightarrow [0,1]\) and the zip bordism \([0,1] \rightarrow S^1\), respectively.
The inclusion of reflection structures is this picture is straightforward. First we recall the definition of reflection structures on knowledgeable Frobenius algebras according to [11, Def. 3.3.3, Def. 3.3.7].
Definition 6.13
A reflection structure on an I-coloured knowledgeable Frobenius algebra \((\mathscr {L},\mathscr {R}, \chi , \epsilon , \theta , \iota , \iota ^*)\) is a pair \(({\tilde{\lambda }}, {\tilde{\alpha }})\) of an involutive algebra isomorphism \({\tilde{\lambda }} :\mathscr {L}\rightarrow {\overline{\mathscr {L}}}\) and a family \({\tilde{\alpha }} = \{{\tilde{\alpha }}_{ij}\}_{i,j \in I}\) of involutive (meaning \({\tilde{\alpha }}_{ji} \circ {\tilde{\alpha }}_{ij} = 1\) for all \(i,j \in I\)), anti-multiplicative isomorphisms \({\tilde{\alpha }}_{ij} :\mathscr {R}_{ij} \rightarrow \overline{\mathscr {R}_{ji}}\). These have to satisfy the conditions
for all \(i \in I\), \(v \in \mathscr {R}_{ii}\) and \(\ell \in \mathscr {L}\). The reflection structure \(({\tilde{\lambda }}, {\tilde{\alpha }})\) is called positive if the pairings
are positive definite for all \(i,j \in I\). An I-coloured knowledgeable Frobenius algebra with a positive reflection structure is called reflection-positive. A morphism \((\varphi , \xi )\) of I-coloured knowledgable Frobenius algebras respects reflection structures \(({\tilde{\lambda }}, {\tilde{\alpha }})\) and \(({\tilde{\lambda }}', {\tilde{\alpha }}')\) if
for all \(i,j \in I\).
Definition 6.13 gives rise to a category of reflection-positive I-coloured knowledgeable Frobenius algebras, which we denote by \(\mathrm {RP}\text {-}\mathrm {KFrob}^{I}\). The following extension of Theorem 6.12 is straightforward to deduce.
Proposition 6.14
The functor \(\mathscr {F}\) extends to an equivalence of categories
We consider the full subcategory
on those objects with \(\mathscr {L}\cong \mathbb {C}\) as Frobenius algebras, and recall the following result [11, Proposition 3.3.8].
Proposition 6.15
There is an equivalence of categories
We shall briefly recall the definition of the functor \(\widetilde{\mathrm {frob}}\). It assigns to an object  an object
an object

whose complex line \(\mathscr {L}\) is the fibre of the transgression line bundle \(\mathscr {L}\) over the loop space \(L(*) = *\). For \(i,j \in I\), the vector space \(\mathscr {R}_{ij}\) is the fibre of the transgression bundle over the path space \(P_{ij}(*) \cong *\) as constructed in Sect. 2.2. The product on the \(\mathbb {C}\)-algebra \(\mathscr {L}\) is the fusion product on the transgression line bundle \(\mathscr {L}\). In general, it can be computed from compatible trivialisations of pullbacks of  along the loops, as laid out in [11, Section 4.1], but see also [42] for more details. In the present special case of \(M = *\), with respect to a trivialisation
along the loops, as laid out in [11, Section 4.1], but see also [42] for more details. In the present special case of \(M = *\), with respect to a trivialisation  on \(M = *\), it simply reads as
on \(M = *\), it simply reads as

where \(\gamma ' {*} \gamma \) denotes concatenation. The trace on \(\mathscr {L}\) is given as

Next, we consider the morphisms \(\chi \), which stem from the concatenation of paths \(\gamma _{ij}\) and \(\gamma _{jk}\) in M for D-brane indices \(i,j,k \in I\). Let \(\gamma _{ij} :[0,1] \rightarrow *\) denote the unique smooth path in \(M = *\) from \(Q_i\) to \(Q_j\). Then,

in the notation of Sect. 2.2. We can equivalently formulate this as an evaluation: if \(\psi _{ki} \in \mathscr {R}_{ki} \cong \mathscr {R}_{ik}^\vee \), then

The unit \(\epsilon _i \in \mathscr {R}_{ii}\) is the element represented by the image of the identity 2-morphism  . In other words, with respect to the trivialisation
. In other words, with respect to the trivialisation  we have that
we have that

compare also [11, Section 4.6]. The trace \(\vartheta = h_\mathscr {L}(\mathbb {1}_\mathscr {L},-\,)\) is defined using the hermitean metric on the transgression line bundle, where \(\mathbb {1}_\mathscr {L}\) is the unit with respect to the algebra structure on the 1-dimensional vector space \(\mathscr {L}\), and analogously one defines the traces \(\theta _i\) on \(\mathscr {R}_{ii}\) as

On representatives with respect to  , the morphism \(\iota _i :\mathscr {L}\rightarrow \mathscr {R}_{ii}\) reads as
, the morphism \(\iota _i :\mathscr {L}\rightarrow \mathscr {R}_{ii}\) reads as

In the other direction, the morphism \(\iota _i^* :\mathscr {R}_{ii} \rightarrow \mathscr {L}\) acts on representatives as taking the trace. The last piece of data in [11, Def. 3.3.3, Def. 3.3.8] are the antilinear maps \({\tilde{\lambda }} :\mathscr {L}\rightarrow {\overline{\mathscr {L}}}\) and \({\tilde{\alpha }}_{ij} :\mathscr {R}_{ij} \rightarrow \overline{\mathscr {R}_{ji}}\) for every \(i,j \in I\), which define a positive reflection structure on the I-coloured knowledgeable Frobenius algebra \((\mathscr {L}, \mathscr {R}, \chi , \epsilon , \theta , \iota , \iota ^*)\). With respect to a trivialisation  , they act as
, they act as

where \(\psi ^*\) is the hermitean adjoint of \(\psi \). On morphisms, \(\widetilde{\mathrm {frob}}\) acts simply as the transgression functor.
The following is the main result of this section.
Theorem 6.16
The diagram of functors

is commutative, and all functors are equivalences of symmetric monoidal categories.
Proof
The evaluation functor on the right hand side of the diagram is an equivalence by Theorem 6.9. Propositions 6.15 and 6.14 show that \(\mathscr {F}\) and \(\widetilde{\mathrm {frob}}\) are equivalences. The two-out-of-three property of equivalences of categories implies that \(\mathscr {Z}\) is an equivalence, provided we prove that the diagram is commutative, which we do in the following.
Consider an arbitrary object  . We will spell out its image
. We will spell out its image

under the functor \(\mathscr {F}\circ \mathrm {ev}_* \circ \mathscr {Z}\) and compare it to its image

under \(\widetilde{\mathrm {frob}}\), which we described above. By construction, \(\mathscr {L}'\) is the vector space that  assigns to the unique loop in \(M = *\), and by construction of
assigns to the unique loop in \(M = *\), and by construction of  , this agrees with \(\mathscr {L}\). The vector space \(\mathscr {R}'_{ij}\), for \(i,j \in I\), is the vector space that
, this agrees with \(\mathscr {L}\). The vector space \(\mathscr {R}'_{ij}\), for \(i,j \in I\), is the vector space that  assigns to the unique path in \(M = *\) from \(Q_i = *\) to \(Q_j = *\); it is precisely the vector space \(\mathscr {R}_{ij}\). That is, we have
assigns to the unique path in \(M = *\) from \(Q_i = *\) to \(Q_j = *\); it is precisely the vector space \(\mathscr {R}_{ij}\). That is, we have
Letting \(\gamma :{\mathbb {S}}^1 \rightarrow *\) denote the unique loop in \(M = *\) and  a trivialisation of
a trivialisation of  over \(*\), the fusion product on the transgression line bundle \(\mathscr {L}\) takes the simple form
over \(*\), the fusion product on the transgression line bundle \(\mathscr {L}\) takes the simple form

On the other hand, the product \(\lambda '\) on \(\mathscr {L}'\) is obtained as the value of  on the closed pair of pants. Using the pullback of
on the closed pair of pants. Using the pullback of  to compute this amplitude and by inspection of the definitions in Sect. 3.2, we see that
to compute this amplitude and by inspection of the definitions in Sect. 3.2, we see that
The morphism \(\chi '\) is the value of  on an open (i.e. flat) pair of pants \([\Sigma , \sigma ]\) with two incoming intervals and one outgoing interval. We can compute the amplitude of this bordism decorated with the states
on an open (i.e. flat) pair of pants \([\Sigma , \sigma ]\) with two incoming intervals and one outgoing interval. We can compute the amplitude of this bordism decorated with the states  and
and  on its incoming string boundary and with the dual state
on its incoming string boundary and with the dual state  on its outgoing string boundary. The contributions of the string boundaries to that amplitude are obvious from these decorations, but for the brane boundary we need parallel transports in
on its outgoing string boundary. The contributions of the string boundaries to that amplitude are obvious from these decorations, but for the brane boundary we need parallel transports in  , where b is the restriction of \(\sigma \) to a connected component of the brane boundary of \(\Sigma \). However, since this bundle is pulled back from a bundle over the point, it is trivialisable as a vector bundle with connection, and so all the parallel transports in the amplitude are trivial. Consequently, the amplitude reads as \(\mathrm {tr}(\psi _{ki} \circ \psi _{jk} \circ \psi _{ij})\), and we conclude that
, where b is the restriction of \(\sigma \) to a connected component of the brane boundary of \(\Sigma \). However, since this bundle is pulled back from a bundle over the point, it is trivialisable as a vector bundle with connection, and so all the parallel transports in the amplitude are trivial. Consequently, the amplitude reads as \(\mathrm {tr}(\psi _{ki} \circ \psi _{jk} \circ \psi _{ij})\), and we conclude that
In the open-closed TQFT defined by  , the element \(\epsilon '_i \in \mathscr {R}'_{ii} = \mathscr {R}_{ii}\) is obtained as follows. Under
, the element \(\epsilon '_i \in \mathscr {R}'_{ii} = \mathscr {R}_{ii}\) is obtained as follows. Under  , the cap bordism \([\Sigma _{cap,i}, \sigma ] :\emptyset \rightarrow ([0,1], \gamma _{ii})\) yields a linear map \(\mathbb {C}\rightarrow \mathscr {R}_{ii}\), and \(\epsilon '_i\) is the evaluation of this linear map on \(1 \in \mathbb {C}\). From the formalism in Sect. 3.2 and the above arguments regarding the triviality of the parallel transport along the brane boundary of bordisms in the case \(M = *\) we infer that
, the cap bordism \([\Sigma _{cap,i}, \sigma ] :\emptyset \rightarrow ([0,1], \gamma _{ii})\) yields a linear map \(\mathbb {C}\rightarrow \mathscr {R}_{ii}\), and \(\epsilon '_i\) is the evaluation of this linear map on \(1 \in \mathbb {C}\). From the formalism in Sect. 3.2 and the above arguments regarding the triviality of the parallel transport along the brane boundary of bordisms in the case \(M = *\) we infer that

for every incoming state \(z \in \mathbb {C}\) and outgoing dual state \(\psi \in \mathscr {R}_{ii} \cong \mathscr {R}_{ii}^\vee \). This implies that

and thus
The trace \(\vartheta '\) on the algebra \((\mathscr {L}', \lambda ')\) is obtained as the evaluation of  on the cap bordism \({\mathbb {S}}^1 \rightarrow \emptyset \). This acts as
on the cap bordism \({\mathbb {S}}^1 \rightarrow \emptyset \). This acts as  , and thus agrees with the trace \(\vartheta \) on \(\mathscr {L}\), i.e.
, and thus agrees with the trace \(\vartheta \) on \(\mathscr {L}\), i.e.
Therefore, the rank-one, commutative Frobenius algebras \((\mathscr {L}, \lambda , \theta )\) and \((\mathscr {L}', \lambda ', \theta ')\) are equal. Recalling that the hermitean metric on \(\mathscr {R}_{ij}\) is defined on representatives as
we see from an analogous argument using the cap bordism \([0,1] \rightarrow \emptyset \) that also the traces on the algebras \(\mathscr {R}_{ii}\) and \(\mathscr {R}'_{ii}\) agree for every D-brane label, i.e.
In the field theory, \(\iota '_i\) is the morphism induced by the unzip bordism \({\mathbb {S}}^1 \rightarrow [0,1]\). Similarly to the arguments used for the cap bordisms \(\emptyset \rightarrow [0,1]\), we see that this morphism coincides with \(\iota _i\). That is,
In the other direction, we have to consider the zip bordism \([0,1] \rightarrow {\mathbb {S}}^1\), which on representatives also maps to the trace under  . This yields
. This yields
Finally, we turn to the reflection structures. On the field theory side a reflection structure \(\alpha \) on an OCTQFT naturally induces antilinear morphisms \({\tilde{\lambda }}\) and \({\tilde{\alpha }}\) on the coloured Frobenius algebra that it defines, and these antilinear morphisms behave exactly as in [11, Definition 3.3.8]. In the case of the field theory  we directly read off from (5.5) and the following paragraph that
we directly read off from (5.5) and the following paragraph that
To summarise, we have shown that

for all objects  . That is, the diagram (6.16) strictly commutes on objects.
. That is, the diagram (6.16) strictly commutes on objects.
On morphisms in \(\mathrm {TBG}(I)\), we only need to compare the induced linear maps on the vector spaces underlying the I-coloured Frobenius algebras. However, comparing the definition of the action of \(\widetilde{\mathrm {frob}}\) on morphisms in [11, Section 4.8] with the action (5.8) of \(\mathscr {Z}\) on morphisms we readily see that the induced linear maps agree. \(\square \)
We point out two consequences of Theorem 6.16. The fact that the diagonal of the diagram in Theorem 6.16 is an equivalence leads to the following result.
Corollary 6.17
The 2-dimensional, invertible, reflection-positive OCTQFTs are precisely those that can be obtained from target space brane geometry over a point, i.e., those that are restrictions of classical field theories to the point.
Secondly, we emphasise that our construction of smooth OCFFTs from target space brane geometry is an equivalence, in the special case of a one-point target space.
Corollary 6.18
The construction \(\mathscr {Z}\) of a smooth OCFFT from a target space brane geometry is an equivalence,
We mention this because we believe that the functor \(\mathscr {Z}\) is an equivalence for any target space \((M,Q)\), i.e., we conjecture that it is an equivalence
We plan to prove this equivalence in forthcoming work.
Notes
This is defined in analogy to how one defines the dual of a morphism in a monoidal category, see Appendix A, using isomorphisms \(A^{-1} \circ A \rightarrow 1\) and \(1 \rightarrow A \circ A^{-1}\) in place of the evaluation and coevaluation.
References
Abrams, L.: Two-dimensional topological quantum field theories and Frobenius algebras. J. Knot Theory Ramif. 5, 569–587 (1996)
Atiyah, M.: Topological quantum field theories. Inst. Hautes Études Sci. Publ. Math. 68, 175–186 (1988)
Baez, J.C.: Quantum quandaries: a category-theoretic perspective. In: Rickles, D.P., French, S.R.D., Saatsi, J. (eds.) Structural Foundations of Quantum Gravity. Oxford University Press (2006). arXiv:quant-ph/0404040
Barrett, J.W.: Holonomy and path structures in general relativity and Yang–Mills theory. Int. J. Theor. Phys. 30(9), 1171–1215 (1991)
Berwick-Evans, D., Pavlov, D.: Smooth one-dimensional topological field theories are vector bundles with connection (2015). arXiv:1501.00967
Bunk, S., Szabo, R.J.: Fluxes, bundle gerbes and 2-Hilbert spaces. Lett. Math. Phys. 107(10), 1877–1918 (2017). arXiv:1612.01878
Bunk, S., Sämann, C., Szabo, R.J.: The 2-Hilbert space of a prequantum bundle gerbe. Rev. Math. Phys. 30(1), 1850001, 101 (2018). arXiv:1608.08455
Bunke, U., Turner, P., Willerton, S.: Gerbes and homotopy quantum field theories. Algebraic Geom. Topol. 4, 407–437 (2004). arXiv:math/0201116
Bunk, S.: Sheaves of higher categories and presentations of smooth field theories. arXiv:2003.00592
Bunk, S.: Categorical structures on bundle gerbes and higher geometric prequantisation. PhD thesis, Heriot-Watt University, Edinburgh (2017). arXiv:1709.06174
Bunk, S., Waldorf, K.: Transgression of D-branes. arXiv:1808.04894
Carey, A.L., Johnson, S., Murray, M.K.: Holonomy on D-branes. J. Geom. Phys. 52(2), 186–216 (2002). arXiv:hep-th/0204199
Dijkgraaf, R.: A geometric approach to two dimensional conformal field theory. PhD thesis, University of Utrecht (1989)
Etingof, P., Gelaki, S., Nikshych, D., Ostrik, V.: Tensor Categories. Mathematical Surveys and Monographs, vol. 205. American Mathematical Society, Providence (2015)
Freed, D.S., Hopkins, M.J.: Reflection positivity and invertible topological phases. arXiv:1604.06527
Freed, D.S.: Classical Chern–Simons theory, part 1. Adv. Math. 113(2), 237–303 (1995). arXiv:hep-th/9206021
Gawȩdzki, K.: Topological actions in two-dimensional quantum field theories. In: ’t Hooft, G., Jaffe, A., Mack, G., Mitter, K., Stora, R. (eds.) Non-perturbative quantum field theory, pp. 101–142. Plenum Press (1988)
Gawȩdzki, K.: Wess–Zumino–Witten conformal field theory. In: Constructive Quantum Field Theory, II, NATO Adv. Sci. Inst. Ser. B Phys., vol. 234, pp. 89–120. Plenum (1990)
Gawȩdzki, K.: Abelian and non-abelian branes in WZW models and gerbes. Commun. Math. Phys. 258(1), 23–73 (2005). arXiv:hep-th/0406072
Gawedzki, K., Reis, N.: WZW branes and gerbes. Rev. Math. Phys. 14(12), 1281–1334 (2002). arXiv:hep-th/0205233
Iglesias-Zemmour, P.: Diffeology. Mathematical Surveys and Monographs, vol. 185. American Mathematical Society, Providence (2013)
Kapustin, A.: D-branes in a topologically non-trivial \(B\)-field. Adv. Theor. Math. Phys. 4, 127–154 (2000). arXiv:hep-th/9909089
Kock, J.: Frobenius Algebras and 2D Topological Quantum Field Theory. London Mathematical Society Student Texts, vol. 59. Cambridge University Press, Cambridge (2004)
Lazaroiu, C.I.: On the structure of open-closed topological field theory in two dimensions. Nucl. Phys. B 603(3), 497–530 (2001). arXiv:hep-th/0010269
Lauda, A.D., Pfeiffer, H.: Open-closed strings: two-dimensional extended TQFTs and Frobenius algebras. Topol. Appl. 155(7), 623–666 (2008). arXiv:math/0510664
Ludewig, M., Stoffel, A.: A framework for geometric field theories and their classification in dimension one. arXiv:2001.05721
Moore, G.W., Segal, G.: D-branes and K-theory in 2D topological field theory. arXiv:hep-th/0609042
Murray, M.K., Stevenson, D.: Bundle gerbes: stable isomorphism and local theory. J. Lond. Math. Soc. 62(3), 925–937 (2000). arXiv:math/9908135
Murray, M.K.: Bundle gerbes. J. Lond. Math. Soc. 54, 403–416 (1996). arXiv:dg-ga/9407015
Müller, L., Woike, L.: Parallel transport of higher flat gerbes as an extended homotopy quantum field theory. J. Homotopy Relat. Struct. 15(1), 113–142 (2020). arXiv:1802.10455
Nikolaus, T., Schweigert, C.: Equivariance in higher geometry. Adv. Math. 226(4), 3367–3408 (2011). arXiv:1004.4558
Schommer-Pries, C.J.: The classification of two-dimensional extended topological field theories. PhD thesis, University of California, Berkeley. arXiv:1112.1000
Segal, G.: The definition of conformal field theory. In: Schloß R. (ed.) Links Between Geometry and Mathematical Physics, The MPIM preprint series, vol. 58, pp. 13–17 (1987)
Segal, G.: The definition of conformal field theory, London Math. Soc. Lecture Note Ser, vol. 308, pp. 421–577. Cambridge Univ. Press, Cambridge (2004)
Stolz, S., Teichner, P.: What is an elliptic object? In: Topology, Geometry and Quantum Field Theory, London Math. Soc. Lecture Note Ser., vol. 308, pp. 247–343. Cambridge Univ. Press, Cambridge (2004). arXiv:1108.0189
Stolz, S., Teichner, P.: Supersymmetric field theories and generalized cohomology, Proc. Sympos. Pure Math., vol. 83, pp. 279–340. (2011). arXiv:1108.0189
Schreiber, U., Waldorf, K.: Parallel transport and functors. J. Homotopy Relat. Struct. 4(1), 187–244 (2009). arXiv:0705.0452
Turaev, V.: Homotopy field theory in dimension 2 and group-algebras. arXiv:math/9910010
Turaev, V.: Homotopy quantum field theory, EMS Tracts in Mathematics, vol. 10. European Mathematical Society (EMS), Zürich. Appendix 5 by Michael Müger and Appendices 6 and 7 by Alexis Virelizier (2010)
Waldorf, K.: Algebraic structures for bundle gerbes and the Wess-Zumino term in conformal field theory. PhD thesis, Universität Hamburg (2007). http://ediss.sub.uni-hamburg.de/volltexte/2008/3519/
Waldorf, K.: More morphisms between bundle gerbes. Theor. Appl. Categ. 18(9), 240–273 (2007). arXiv:math/0702652
Waldorf, K.: Transgression to loop spaces and its inverse, II: Gerbes and fusion bundles with connection. Asian J. Math. 20(1), 59–115 (2016). arXiv:1004.0031
Witten, E.: Global aspects of current algebra. Nucl. Phys. B 223(2), 422–432 (1983)
Wess, J., Zumino, B.: Consequences of anomalous Ward identities. Phys. Lett. 37B, 95–97 (1971)
Acknowledgements
We thank Ulrich Bunke, Tobias Dyckerhoff, Lukas Müller, Alexander Schenkel, Urs Schreiber, Stephan Stolz, Richard Szabo, and Peter Teichner for interesting discussions and comments. S.B. was partially supported by RTG 1670, Mathematics Inspired by String Theory and Quantum Field Theory.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Christopher Douglas.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Monoidal categories with fixed duals
Appendix 1: Monoidal categories with fixed duals
We briefly recall some basic facts about categorical duals, mostly based on [14].
Definition A.1
([14, Definition 2.10.1]) Let \(\mathscr {C}\) be a monoidal category with monoidal structure \(\otimes \) and unit object \(u \in \mathscr {C}\). Let \(x \in \mathscr {C}\) be an object. An object \(x^\vee \in \mathscr {C}\) is called a (left) dual of \(x^\vee \) if there exist morphisms \(\mathrm {ev}_x :x^\vee \otimes x \rightarrow u\) and \(\mathrm {coev}_x :u \rightarrow x \otimes x^\vee \) such that the diagrams (where we are omitting the structural isomorphisms)

commute.
The morphisms \(\mathrm {ev}_x\) and \(\mathrm {coev}_x\) are called evaluation and coevaluation, respectively. We refer to the triple \((x^\vee , \mathrm {ev}_x, \mathrm {coev}_x)\) as duality data for x. Duality data is unique in the following sense.
Proposition A.2
( [14, Proposition 2.10.5]) If an object \(x \in \mathscr {C}\) admits a dual, then any two choices of duality data \((x^{\vee },\mathrm {ev}_x,\mathrm {coev}_x)\) and \((x',\mathrm {ev}'_x,\mathrm {coev}'_x)\) for x are related by a unique isomorphism \(f:x^{\vee } \rightarrow x'\) which is compatible with the evaluation and coevaluation morphisms in the sense that
A monoidal category \(\mathscr {C}\) is said to have fixed duals, if every object is dualisable and duality data is chosen and fixed for all objects of \(\mathscr {C}\). In a monoidal category with fixed duals we have the following adjunction.
Proposition A.3
([14, Proposition 2.10.8, Remark 2.10.9]) Let \(x \in \mathscr {C}\) be an object with duality data \((x^\vee , \mathrm {ev}_x, \mathrm {coev}_x)\). Then, there is a canonical adjunction

The adjunction is established by the bijection
for objects \(y,z \in \mathscr {C}\).
We remark that the inverse of \(\tau ^{x}_{y,z}\) is given by
In a monoidal category with fixed duals, duality extends automatically to the morphisms. For a morphism \(f:x \rightarrow y\) one defines the dual morphism \(f^\vee :y^{\vee } \rightarrow x^{\vee }\) as the composition

One can show that for \(g :y \rightarrow z\) one has \((g \circ f)^\vee = f^\vee \circ g^\vee \). We note the following simple fact, of which we could not find an explicit reference.
Lemma A.4
Let \(f:x \rightarrow y\) be a morphism in a monoidal category with fixed duals; then, we have
Proof
The identity follows from the commutativity of the diagram

The left-hand triangle commutes because of the first triangle identity (A.1). The upper central rectangle is the definition of \(f^\vee \) and hence commutes. The lower central rectangle and the right-hand triangle commute by monoidality; morphisms applied to different factors of a tensor product commute in any monoidal category. \(\square \)
If \(\mathscr {C}\) is a monoidal category with fixed duals, then the assignments \(x \mapsto x^{\vee }\) and \(f \mapsto f^{\vee }\) define a functor \(d_{\mathscr {C}}:\mathscr {C}^{\mathrm {op}} \rightarrow \mathscr {C}\). Since \(x^{\vee \vee }\) and x are both dual to \(x^{\vee }\), there exists a unique isomorphism \(\delta _x: x^{\vee \vee } \rightarrow x\) by Proposition A.2. These define a monoidal natural isomorphism \(\delta _{\mathscr {C}}:d_{\mathscr {C}}\circ d_{\mathscr {C}}^{\mathrm {op}} \rightarrow 1_{\mathscr {C}}\), which additionally satisfies
as natural transformations \(d_{\mathscr {C}} \circ d_{\mathscr {C}}^{\mathrm {op}} \circ d_{\mathscr {C}} \rightarrow d_{\mathscr {C}}\). In the terminology used in Sect. 4.3, the pair \((d_{\mathscr {C}},\delta _{\mathscr {C}})\) forms a twisted involution, and is called the duality involution of the monoidal category \(\mathscr {C}\) with fixed duals.
Proposition A.5
Let \(\mathscr {C}\), \(\mathscr {D}\) be monoidal categories with fixed duals and duality involutions \((d_{\mathscr {C}},\delta _{\mathscr {C}})\) and \((d_{\mathscr {D}},\delta _{\mathscr {D}})\), respectively. Suppose \(F:\mathscr {C}\rightarrow \mathscr {D}\) is a monoidal functor, i.e. it comes with coherent natural isomorphism \(f_{x,y} :Fx \otimes Fy \rightarrow F(x \otimes y)\). Then, there is a unique monoidal natural isomorphism
that is compatible with evaluations and coevaluations in the sense that
for all \(x\in \mathscr {C}\). Moreover, it is compatible with the natural isomorphisms \(\delta _{\mathscr {C}}\) and \(\delta _{\mathscr {D}}\) in the sense that the diagram

is commutative.
Proof
Let \(x \in \mathscr {C}\) be an object with fixed left duality data \((x^\vee , \mathrm {ev}_x, \mathrm {coev}_x)\). Let \(((Fx)^\vee , \mathrm {ev}_{Fx}, \mathrm {coev}_{Fx})\) be the fixed left duality data on \(Fx \in \mathscr {D}\). Since F is monoidal, the triple
is another set of left duality data for Fx. By Proposition A.2 there exists a unique isomorphism \(\beta _x :F(x^\vee ) \rightarrow (Fx)^\vee \) compatible with the two sets of left duality data on Fx; the compatibility is expressed precisely by the two equations in (A.6). Explicitly, \(\beta _x\) is given by the composition [14, Proposition 2.10.5]

We have to show that \(\beta \) is natural. To that end, suppose \(\psi :x \rightarrow y\) is a morphism in \(\mathscr {C}\). We have to prove that the diagram

commutes. Inserting the definition of the dual morphism, we expand this diagram to

Here, the left-hand and right-hand squares commute because of the compatibility of \(\beta \) with the duality data, and the centre square commutes simply by monoidality.
To see that \(\beta \) is monoidal, first observe that for any two objects \(x,y \in \mathscr {C}\) the triple
is left duality data for \(x \otimes y\). Thus, there exists a unique isomorphism \(\delta _{x,y} :y^\vee \otimes x^\vee \rightarrow (x \otimes y)^\vee \) that is compatible with the duality data. Then consider the diagram

All of the objects in this diagram come with choices of left duality data for \(F(x \otimes y)\), and the morphisms in the diagram are each compatible with these left duality data (this uses the coherence of the natural isomorphism f and Lemma A.4). In particular, the diagram yields two possible ways of going from \(F((x \otimes y)^\vee )\) to \((Fy)^\vee \otimes (Fx)^\vee \), both of which are compatible with the left duality data on these two objects. Thus, Proposition A.2 implies that the diagram (A.3) commutes, which shows that \(\beta \) respects the tensor product.
The commutativity of the diagram (A.2) can be shown by similar methods; since it will not be used in this article we leave this as an exercise to the reader. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bunk, S., Waldorf, K. Smooth functorial field theories from B-fields and D-branes. J. Homotopy Relat. Struct. 16, 75–153 (2021). https://doi.org/10.1007/s40062-020-00272-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-020-00272-2





 . It recovers precisely those hermitean inner products on the vector spaces in the image of
. It recovers precisely those hermitean inner products on the vector spaces in the image of 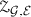 that have been discarded earlier.
that have been discarded earlier.
 , we have
, we have  .
. of
of  , we have
, we have 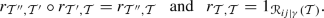

 is the pullback of a trivialisation of a bundle gerbe over the point for
is the pullback of a trivialisation of a bundle gerbe over the point for 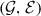 .
. .
. . We set
. We set 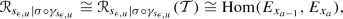

 , with an hermitean vector bundle E with connection over a surjective submersion
, with an hermitean vector bundle E with connection over a surjective submersion 
 for some
for some 
 if
if  whenever
whenever 
 around
around  is homotopy invariant.
is homotopy invariant. is flat; that is,
is flat; that is,  .
.