1 Introduction

Artificial neural network (ANN) is a nonparametric computational model based on the biological process of the human nervous system. The ANN is capable of modeling complex nonlinear processes with high accuracy and handling a large amount of data [1]. Subsequently, ANN, as a powerful tool, has been commonly used in various application domains such as classification [2], function approximation [3], pattern recognition [4], signal processing [5], computer vision [6], and so on [7, 8].

The ANN is mainly divided into three groups: feedforward neural network (FNN), recurrent neural network (RNN), and Convolutional neural network. The most common types of the FNN are single layer perceptron (SLP), multilayer perceptron (MLP), and radial basis function (RBF), while the Hopfield network and Kohonen self-organizing maps (SOM) are two examples of the RNN. Among different types of ANN, the FNN especially MLP is the most popular neural network in practical applications because of its learning and generalization capacity, nonlinearly, and robustness to noise [9,10,11]. The MLP is composed of three or more layers of different size nodes, including one input layer, one output layer, and one or more hidden layers [12].

Recently, the learning techniques have received considerable attention in machine learning such as [13, 14]. The performance of the ANN can be greatly improved based on the learning algorithm that is used for network training [9]. The training process aims to identify the best weights and biases values that minimize the cost function, known as the mean squared error (MSE) cost function. The supervised learning techniques of ANN are classified as gradient-based methods and metaheuristic-based approaches [15]. The backpropagation (BP) algorithm and its improved versions are the most widely applied gradient-based learning methods in the literature [16]. These learning methods, however, suffer from several shortcomings including slow convergence, the tendency of trapping into local optima, and heavy reliance on the initial solution. In this regard, metaheuristic algorithms (MHAs) have been proposed as reliable alternatives to the gradient-based FNNs training methods [11]. The population-based MHAs demonstrate better performance in avoiding local minima than gradient-based methods [2, 9]. Evolutionary and swarm-based algorithms, the most widely used population-based MHAs, generate a random number of solutions and update them until the best solution is obtained or convergence is reached. Such randomness provides a mechanism to move out of the local search for a global search [9].

It is worth mentioning that the population-based MHAs in a neural network can be used not only in weights and biases optimization but also in learning rule determination and neural network structure design [9, 10]. However, simultaneous optimization of network structure, weights, biases, and learning rules can drastically increase the number of parameters, which results in large-scale optimization problems [9, 15]. In this study, the MLP with a single hidden layer is optimized by concentrating on discovering the optimal set of weight and bias values.

Various MHAs have been used to solve a wide variety of complex problems such as text clustering [17,18,19,20,21,22,23], image enhancement [24], gene selection [25], task scheduling problems [26], and training neural networks. The genetic algorithm (GA) is one of the earliest and best-known optimization algorithms. It has been widely used in FNNs connection weight training [27], designing its architecture [28], and simultaneously optimizing FNNs architecture and weights [29]. A hybrid of GA and BP algorithm was presented in [30] for optimization of the neural network connection weights, while the power of GA as feature selection and component optimization of FNN was examined for breast cancer diagnosis in [31]. Two other types of evolutionary algorithm called differential evaluation (DE) [32, 33], and biogeography-based optimization (BBO) [34], have been used for training multilayer FNNs as well. A hybrid of DE with Levenberg–Marquardt (LM) PB method for optimizing FNN’s weights and biases was introduced in [35]. Swarm intelligence algorithms are another well-known population-based MHA, which are inspired by the species’ social behavior in nature. Instead of reproduction operators in evolutionary algorithms, swarm-based algorithms employ some mathematical models for updating the randomly generated solutions. In the literature for training MLP neural network and its various applications, several optimization algorithms have been studied. Some of them are artificial bee colony (ABC) [36], gray wolf optimizer (GWO) [37, 38], grasshopper optimization algorithm (GOA) [15, 39], Krill-Herd algorithm (KHA) [40], multiverse optimizer algorithm (MOA) [2, 41], whale optimization algorithm (WOA) [9], social spider optimization algorithm (SSO) [42], lightning search algorithm (LSA) [11], cuckoo search (CS) [43, 44], bat algorithm [45], artificial ant colony optimization (ACO) [46], invasive weed optimization [47], particle swarm optimization (PSO) [48], symbiotic organisms search (SOS) algorithm [10], hybrid of ABC and dragonfly algorithm (DA) [49], moth–flame optimization (MFO) [50, 51], salp swarm algorithm (SSA) [52], ant lion optimizer (ALO) [53], and group search optimizer (GSO) [54].

Despite the rapid development of the new MHAs, their success, and widespread application, the research is still open for new designs and improvements to existing ones due to duality between exploitation and exploration capabilities of optimization algorithms. There are few comparative studies in the mathematical analysis of these algorithms in terms of coverage and efficiency [55], and a global outcome is not yet available. Moreover, according to the no free lunch theorem, no optimization method is able to beat every other MHA to solve all problems [9, 15]. Besides, the problem of trapping into local optima and slow convergence remains partly unsolved in training FNN [12].

Motivated by these reasons, the black hole algorithm (BHA) and a novel enhanced version of BHA (BHACRW) are introduced to train FNN as new alternatives to existing MHAs and conventional approaches, aim to increase FNN’s accuracy. The excellent performance of the BHA in escaping local optima, high-speed convergence, its’ parameter-less-ness, and simplicity, encouraged us to use the BHA for MLP training. The BHA, proposed by Hatamlou in 2012 [56], is an efficient MHA, inspired by the real black hole behavior in space. Although the original BHA demonstrates superior results in various optimization problems, in certain datasets it lacks exploration capabilities. To address the exploration dilemma, Levy flight random walk [57] and opposition-based (complementary) learning [58] components are introduced in the original BHA’s framework result in a new optimization algorithm, called “BHACRW”. The BHA and its modified versions [59,60,61] have shown promising results in solving various optimization and engineering problem, such as pattern recognition [62], function optimization [63], electric power systems [64], management system [65], and more [61, 66, 67]. However, to the best of our knowledge, training feedforward neural networks using BHA and its improved versions is still untouched.

It is also worth noting that a hybrid of Levy flight and BHA, called LBH [61], has been considered in the literature for empowering the BHA’s global search capability to solve function and clustering problems. In LBH, levy flight is used in the updating of all-stars’ positions without any constraints, while in the BHACRW, complementary learning operator and levy flight are utilized sequentially for updating the position of half-worst solutions, if the BHA get stuck in local optima.

The main contributions of this research are: (1) BHA is proposed as a new stochastic training algorithm for FNNs. (2) For the first time, the high exploration and exploitative capability of the BHA are evaluated in determining the best values for the weight and bias parameters of FNN. (3) To boost the accuracy of FNNs, complementary learning components and Levy flight random walk are integrated into BHA to establish the new BHACRW algorithm. (3) The suggested algorithm’s performance is examined against four benchmark global optimization functions and compared with nine MHAs, including Levy firefly algorithm (LFFA) [68], gravitational search algorithm (GSA) [69], cat swarm algorithm (CSA) [70], Big Bang-Big Crunch (BB-BC) [71], ABC, PSO, GWO, BHA, and LBH. On the other hand, the classification performance of FNN using the BHACRW optimizer is evaluated against original BHA and eight well-known MHAs trainer, including GA, PSO, CS, BBO, WOA, MVO, SOS, and GSA, using mean square error (MSE) and classification accuracy metrics. The obtained results indicate that the suggested BHACRW-FNN approach produces better and, at the least, competitive results in comparison to those MHAs. (4) As a case study, BHACRW-FNN is applied to classify angiotensin-converting enzyme 2 (ACE2) gene expression for patients with asthma to identify subgroups at risk for COVID-19. The proposed classifier achieves 80% prediction accuracy on the dataset, which is the best performance compared to other conventional classifiers.

The remainder of the paper is arranged as follows: The FNN is introduced in Sect. 2. Section 3 explains the details of the suggested BHACRW method and its components including BHA, Levy flight random walk, and complementary learning approach. The FNN optimization model is explained in Sect. 4. In Sect. 5, the assessment experiments, parameter settings, and discussion have been provided. Lastly, Sect. 6 summarizes the paper’s key findings and points out potential directions for future work.

2 Feedforward Neural Network

A feedforward neural network (FNN) model is the simplest form of an ANN composed of three classes of layers: input, output, and hidden layers. Layers consist of a certain number of neurons (or nodes). Using weighted interconnections or links, each layer’s nodes have a full connection with all nodes in the adjacent layer [12].

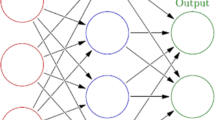
A popular class of the FNN model which is mostly used for data classification is the multilayer perceptron (MLP) [9, 10, 48]. Figure 1 shows a single hidden layer MLP network, where \( x = \left( {x_{1} , x_{2} , \ldots ,x_{n} } \right)^{\text{T}} \) represents an input vector that holds \( n \) neuron values in the input layer. \( s = \left( {s_{1} , s_{2} , \ldots ,s_{h} } \right)^{\text{T}} \) indicates \( h \) neurons output vector in the hidden layer, while \( o = \left( {o_{1} , o_{2} , \ldots ,o_{m} } \right)^{\text{T}} \) shows \( m \) neurons output vector in the output layer. \( hb \) and \( ob \) represent hidden neurons biases, and output neurons biases, respectively. When a neural network structure is designed, the number of nodes and hidden layers should be specified. A larger number of nodes and hidden layers lead to greater network complexity [9, 15]. A fixed three-layer MLP was employed in this study, where a single layer was allocated for the network’s input, hidden, and output sections.

Fig. 1
figure 1

MLP structure with a single hidden layer

Full size image

2.1 Coding Schema

In the neural network, the choice of the neurons number inside of each layer depends on the problem. The number of the features and class labels of the dataset is equal to neurons number within the input layer and output layers, respectively [40, 72]. Moreover, neurons number inside the hidden layer is estimated with the Kolmogorov theorem [9, 10], defined as:

$$ {\text{H}} = 2 * {\text{Input}} + 1 $$
(1)

Assume \( n \), \( h \), and \( m \) indicate neurons number within the input, hidden and output layers, while \( hb \) and \( ob \) show the biases number inside the hidden and output layer, respectively. To utilize the suggested methods to find the optimal weight and bias values for MLP, each solution’s dimension is computed as follows:

$$ D = \left( {n*h} \right) + \left( {h*m} \right) + hb + ob $$
(2)

A population with \( N \) solution is initialized \( P = \left( {P_{1} , P_{2} , \ldots , P_{N} } \right) \), in which each solution \( P_{i} = \left\{ {{\text{nw}}, {\text{hb}},{\text{hw}}, {\text{ob}}} \right\} \) \( \left( {i = 1, 2, \ldots , N} \right) \) provides a set of weight and bias values for MLP. In a population-based optimization algorithm, the MLP’s weight and bias values inside of search agents can be represented as a vector, matrix, or binary encoding schema. The matrix encoding approach was used in the suggested BHA-MLP and BHACRW-MLP to represent each candidate solution, which is the most suitable encoding schema for the neural network training process [48]. The following equations describe the matrix encoding strategy of the aforementioned Fig. 1:

$$ {\text{solution}} \left( {; ; i} \right) = \left[ {W_{1} , hb,W_{2}^{'} , ob} \right] $$
(3)
$$ W_{1} = \left[ {\begin{array}{*{20}c} {w_{1,1} } & \cdots & {w_{n,1} } \\ \vdots & \ddots & \vdots \\ {w_{1,h} } & \cdots & {w_{n,h} } \\ \end{array} } \right],hb = \left[ {\begin{array}{*{20}c} {hb_{1} } \\ \vdots \\ {hb_{h} } \\ \end{array} } \right],W_{2}^{'} = \left[ {\begin{array}{*{20}c} {w_{1,1} } & \cdots & {w_{h,1} } \\ \vdots & \ddots & \vdots \\ {w_{1,m} } & \cdots & {w_{h,m} } \\ \end{array} } \right],\,ob = \left[ {\begin{array}{*{20}c} {ob_{1} } \\ \vdots \\ {ob_{h} } \\ \end{array} } \right] $$
(4)

where \( W_{1} \) and \( W_{2}^{'} \) represent weight matrix and the transpose of the weight matrix of the neurons between input-hidden layers and hidden-output layers, and \( hb \) and \( ob \) denote bias matrices of neurons in hidden and output layers, respectively.

2.2 Fitness Value

Two steps are used to calculate the MLP performance value. In the first step, the weighted summation of each hidden neuron is computed using Eq. (5) as follows:

$$ s_{j} = \mathop \sum \limits_{i = 1}^{n} w_{ij} x_{i} + hb_{j} \quad j = 1,2, \ldots ,h $$
(5)

where \( w_{ij} \) describes the connection weight between the input layer’s ith node, called \( x_{i} \), and the hidden layer’s jth node. The bias of the hidden layer’s jth node is expressed by \( hb_{j} \).

An activation function is employed in the second stage to generate the hidden neuron’s output. The weighted sum of each hidden neuron (Eq. 5) is passed on to the sigmoid function, which is illustrated in the equation as follows:

$$ f\left( {s_{j} } \right) = \frac{1}{{1 + e^{{ - s_{j} }} }} $$
(6)

On MLP layers various types of activation functions can be applied. However, the sigmoid function is the most widely used activation function in previous studies [2, 5], in which optimization algorithms are utilized for training the FNN. For the sake of comparison, the same activation function has been chosen in the MLP. After determining the outputs of the hidden layer nodes, the outputs of the neurons in the output layer are computed as follows:

$$ o_{k} = \mathop \sum \limits_{j = 1}^{h} w_{jk} . f\left( {s_{j} } \right) + ob_{k} \quad k = 1,2, \ldots ,m $$
(7)
$$ o_{k} = f\left( {o_{k} } \right) = \frac{1}{{1 + e^{{ - o_{k} }} }} $$
(8)

where \( w_{jk} \) presents the connection weight between the hidden layer’s jth neuron and kth neuron of the output layer. \( ob_{k} \) shows the bias of the output layer’s kth neuron. The weight and bias matrices are passed to the MLP, and the fitness value of each solution in the suggested solution is computed using the mean squared error (MSE). The MSE is considered as the fitness function of proposed algorithms, which is expressed in Eq. (9)

$$ {\text{MSE}} = \frac{1}{n} \mathop \sum \limits_{i = 1}^{n} \left( {c - o} \right)^{2} $$
(9)

where \( n \) defines the number of training samples, \( o \) denotes predicted values of the neural network, and \( c \) symbolize the actual class labels. In addition to the MSE criterion, the classification accuracy is used to assess the classification performance of MLP on unseen data, which is determined as:

$$ {\text{Accuracy}} = \frac{{\tilde{Z}}}{Z} $$
(10)

where \( {\tilde{Z}} \) and \( z \) denote the number of samples which the classifier correctly identifies, and total sample size in the test dataset, respectively.

3 Proposed Methodology

The proposed BHACRW schema is explored in more detail in this section. It comprises three important parts which are BHA, the complementary-based learning components (C), and the Levy flight random walk (RW) learning method. The BHA’s random initialization is used at the first stage of the proposed method to generate candidate solutions for training NN. If the fitness values of the best global solution remain unchanged in three sequential iterations, new candidate solutions will be generated from the half-worst population using the complementary module. If complementary-based solutions have better fitness value than previous solutions, the old solutions will be replaced with new opposite solutions. Then, BHA will continue with the new population. However, if the new complementary-based solution has a worse fitness value than the origin, the Levy flight random walk module is preformed to reinitialize the solution without any fitness comparison, and BHA continues to find optimal solutions by using the newly generated solutions. Algorithm 1 shows the suggested BHACRW pseudo-code, and Fig. 2 illustrates the main difference between the basic BHA and the improved BHA.

Fig. 2
figure 2

The flowchart of the a basic black hole algorithm and b improved black hole algorithm

Full size image

3.1 Black Hole Algorithm

The BHA [56] belongs to the family of the physical-based optimization algorithms suggested by Hatamlou [56], which simulates the phenomenon of the black hole inside space. A mass-filled point in the space indicates a black hole (BH). All the mass around the BH falls into its center, known as the singularity. There is a strong gravitational force around the BHs singularity, called an event horizon that prevents anything from escaping [73].

Algorithm 1 Pseudocode of BHACRW

figure a

In the BH algorithm, an individual solution is called a star. The BHA begins with a random generating of the stars (population) in the search space. Then, it looks at all these stars to find the best individual solution, which is defined as a black hole (BH). Since the best location belongs to the BH in the search space, all stars begin moving toward the BH and update their positions, which are carried out through the following equation:

$$ x_{i}^{\text{new}} = x_{i}^{\text{old}} + {\text{rand}}*\left( {x_{\text{BH}} - x_{i}^{\text{old}} } \right) $$
(11)

where

  • \( x_{i}^{\text{old}} \) and \( x_{i}^{\text{new}} \) represent the \( i \) th star position (candidate solution) for iterations \( t \) and \( t + 1 \), respectively

  • \( {\text{rand}} \) describes a random value between 0 and 1.

  • \( x_{\text{BH}} \) represents the black hole’s position (best solution) in search space.

The black hole starts drawing the stars into itself. However, if a star is in a better position than the BH as it moves toward the black hole, the \( x_{\text{BH}} \) changes its current position and moves to the star’s position, and the algorithm continues [74]. Moreover, the black hole immediately swallows the stars that cross the event horizon during the process of their movement, and thus it allows the creation of new stars at random in the search space. The event horizon radius (R) is calculated using Eq. (12):

$$ R = \frac{{f_{\text{BH}} }}{{\mathop \sum \nolimits_{i = 1}^{\text{popsize}} f_{i} }} $$
(12)

where

  • \( f_{\text{BH}} \) is the black hole fitness value

  • \( f_{i} \) is the \( i \) th star’s fitness value

  • \( {\text{popsize}} \) is the total star population

The star disappears from the space solution when its distance from the black hole is smaller than the event horizon radius [56]. It is important to note that a fitness function determines the goodness of each star based on position. Optimization algorithms are essentially iterative procedures, in which some updating formulas are used to improve candidate solutions in each iteration. To learn the optimization algorithm, the iterative updating process must be integrated with a fitness function. The BHA’s learning process is conducted via Eqs. (11) and (12) in an iterative manner, in which candidate solutions (stars) move toward the optimal solution (BH). Each solution stands for a candidate for FNN’s parameters. Figure 2a illustrates the flowchart of BHA.

Because of the simple structure, flexibility, high local optima avoidance, and the BHA’s parameter-less nature, various optimization and engineering problems have been successfully solved utilizing the BHA. This inspired us to employ the BHA for training FNNs due to the difficulties of the learning process. However, the BHA fails to show its excellent performance in some datasets, so an improved version of BHA has been suggested to enhance its global search capability using the opposition-based learning components and Levy flight random walking.

3.2 The Complementary-Based Learning Components

The suggested algorithm utilizes the complementary learning components when the best global solution remains unchanged in three sequential iterations, as it is believed that better performance could be obtained using opposite positions [58]. To continue with a better population, the half-worst stars are selected, and the opposite location of each of them is computed. Then, the fitness value of the current location of the star is compared with its new opposite location. If the star’s opposite location has a higher fitness value, the star’s original position will be updated with its complementary position. The complementary positon of stars is computed using the following equation:

$$ x_{i}^{{{\text{opposite}}\left( {\text{new}} \right)}} = x_{ \hbox{max} } + x_{ \hbox{min} } - x_{i}^{\text{old}} $$
(13)

where \( \left[ {x_{ \hbox{min} } ,x_{ \hbox{max} } } \right] \) presents the initial interval of the star position.

3.3 The Levy Flight Random Walk

If the abovementioned complementary stage fails to produce better solutions, the random walk is utilized to generate new solutions. The random walk is a stochastic process describing a path with a series of random steps, in which the steps are described by the step-size following certain probability distribution. Levy flight is a type of random walk, where its step-size is based on Levy distribution. Levy flight enhances the efficiency of the BHA by improving BHA’s global search capability and avoiding local optima [61]. The stars’ new position using Levy flight random walk can be calculated by:

$$ x_{i}^{\text{new}} = x_{i}^{\text{old}} + \alpha .s $$
(14)

\( \alpha \) is an array of normally distributed random numbers, and \( s \) indicates the steps of Levy flight which is calculated as follows:

$$ s = 0.01*\left( {\frac{\mu }{{\left| \upsilon \right|^{{\frac{1}{\beta }}} }}} \right)*\left( {x_{i}^{\text{old}} - x_{\text{BH}} } \right)\quad \beta = 2/3;\;u\sim N\left( {0; \sigma_{u}^{2} } \right);\upsilon \sim N\left( {0; \sigma_{\upsilon }^{2} } \right) $$
(15)

where \( u \) and \( \upsilon \) are drawn from a normal distribution with zero mean and standard deviations \( \sigma_{u}^{2} \) and \( \sigma_{\upsilon }^{2} \). Here, \( \sigma_{\upsilon } = 1 \) and \( \sigma_{u} \) follow Levy distribution, given by:

$$ \sigma_{u} = \left\{ {\frac{{{\text{gamma}}\left( {1 + \beta } \right)*{ \sin }\left( {\frac{\pi *\beta }{2}} \right)}}{{{\text{gamma}} \left( {\left( {\frac{1 + \beta }{2}} \right)*\beta *2^{{\frac{\beta - 1}{2}}} } \right)}}} \right\}^{{\frac{1}{\beta }}} $$
(16)

Finally, the proposed algorithm generates the best candidate solution for the weight and bias of FNN. The following section describes the mechanisms for training FNNs using the BHA and BHACRW algorithms, called BHA-FNN and BHACRW-FNN.

4 Training MLP with the BHACRW

The suggested black hole-based algorithm for training a single layer MLP is described in this section. To decrease the MLP’s overall error and subsequently increase its accuracy, the BHA and BHACRW are used to train MLP by determining the best weights and biases values. In other words, we can learn the neural network, by learning its weights and biases. The equation numbers (5–8) demonstrate the FNN model, which correlates the inputs to the outputs. Candidate solutions contain a set of weight and bias values, which are initialized randomly at the first stage. The MSE is considered as the cost function expressed by Eq. (9), in which Eq. (5–8) are employed to calculate the neural network output. The minimization of the cost function in an iterative manner is referred to as neural network learning. The candidate weights and biases of MLP are updated at each iteration which leads to cost minimization.

The suggested BHACRW-MLP approach can be described in detail in the following steps:

  1. Step. 1

    A population of \( N \) solutions (stars) is randomly generated, while each solution encodes a set of MLP’s weights and biases values.

  2. Step. 2

    The goodness of each solution is assessed using MSE criteria. The MSE of MLP is calculated for each star on a given training dataset. The star with the minimum MSE is chosen as the best solution (\( x_{\text{BH}} \)).

  3. Step. 3

    Each star’s location and the best global are updated iteratively, and the event horizon is calculated to produce new solutions

  4. Step. 4

    A counter is set to count the number of iterations in which the best fitness value of the global solution stays unchanged.

  5. Step. 5

    If the counter reaches a predefined number of no improvement (here 3 times), the opposite positions for half number of the stars with the worst fitness values are calculated to establish a better population. Their fitness values are computed and compared with the stars’ previous positions. For each star, if the opposite position of the star has better fitness value, it will be inserted into the population and jump to step 7, else go to step 6.

  6. Step. 6

    For the stars whom their complementary positions are not better than their original positions, the Levy flight random walk is utilized to specify their new positions.

  7. Step. 7

    After constructing a new population, the algorithm goes to step 2, and the process is repeated until reaching the maximum number of iteration.

  8. Step. 8

    In the end, the solution with the lowest MSE is selected. The weights and biases in the best solution are assigned to MLP and its performance is assessed on the test data.

Figure 3 shows the general steps of the BHACRW-MLP procedure.

Fig. 3
figure 3

The framework of the BHACRW-MLP approach

Full size image

5 Results and Discussions

To examine the effectiveness of the suggested BHACRW approach, experiments are conducted in three parts. In the first part, the BHACRW is applied to numerical optimization problems, and its performance is compared with the result of other MHAs. The second part evaluates BHA and BHACRW performance in training MLP neural networks and a comparison of results with other well-known algorithms is provided. This part is also divided further into three subsections: experimental setup, experimental results of seven benchmark datasets, and statistical analysis. In the third part, the application of the proposed BHACRW-MLP is investigated on a real coronavirus related gene expression dataset and its performance evaluated against several conventional classification methods.

5.1 Evaluation on Numerical Function Optimization

Four standard test functions were used to assess the efficiency of BHACRW. Table 1 lists these benchmark functions with their ranges and dimensions. To properly apply BHACRW in function minimization, first, we removed the condition for testing the fixed number of iteration, second, we used regular random walk (step = 1) and used Eq. (17) instead of Eqs. (14) and (15).

$$ s = 0.01*{\text{step}}*{\text{randn }} $$
(17)

where \( {\text{randn}} \) returns a random number drawn from the standard normal distribution.

Table 1 Benchmark test functions
Full size table

All experiments were conducted on 10 separate runs, with 250 iterations per run. The population was set at 25. Under the same conditions as our experiments, the parameters setting and experimental results for other evolutionary algorithms, including ABC, PSO, LFFA, GWO, GSA, CSA, BB-BC, BHA, and LBH, were derived from Ref. [61]. The experimental results are tabulated in Table 2. Statistically speaking, for the best value and the average of 10 runs on 4 test functions, BHACRW is the best on 3 functions, LBH and GWO algorithms are the best on 1 function. Therefore, BHACRW in most function minimization outperforms all the evolutionary algorithms.

Table 2 Experimental results for test functions
Full size table

5.2 Evaluation in Training MLP Neural Network

From the University of California at Irvine (UCI) Machine Learning Repository seven standard classification datasets were employed to evaluate the efficiency of the two BHA-based trainers. The main characteristics of these datasets have been shown in Table 3, in which the size of the features, classes, and samples of the training and testing data have been reported. As can be observed, the chosen datasets contain different sizes of features and samples. It was conducted to monitor the performance of training algorithms under various conditions, which makes the process more difficult.

Table 3 Description of datasets
Full size table

5.2.1 Experimental Setup

To maintain the class distribution as much as possible, all datasets were divided into two subsets using stratified sampling, where 66% was allocated to the training set and the remaining 34% was assigned to the testing set. Besides, all datasets were standardized at the interval [− 1.1] using the min–max normalization to reduce the impact of attributes with different scales [2, 10]. The min–max normalization can be obtained by the following formula:

$$ v^{\prime} = 2*\frac{{v - { \hbox{min} }}}{{{ \hbox{max} } - { \hbox{min} }}} - 1 $$
(18)

where \( v^{\prime} \) represents the standardized value of \( v \) within the [min, max] range.

All experiments were carried out on 10 separate runs, with 500 iterations in each run [10]. The BHA and its enhanced version have not any parameters for adjustment, except the population size which is considered 200. Experimental results for other evolutionary algorithms, including GA-MLP [27], PSO-MLP [48], CS-MLP [44], BBO-MLP [75], GSA-MLP [48], MVO-MLP [2], SOS-MLP [10], and WOA-MLP [9], were derived from Ref. [9, 10] under the same conditions as our experiments. The neurons number in the hidden layer was computed by Eq. 1 [2, 9, 10, 75]. The structure of MLP for each dataset has been shown in Table 3.

5.2.2 Experimental Result

5.2.2.1 Experiment 1: Iris Dataset

Iris dataset has 4 features and 3 classes, so we used an FNN with a 4-9-3 structure to find the best optimal values for weights and biases parameters of MLP. Table 4 displays the experimental results for the proposed BHA-MLP, BHACRW-MLP, and other MHAs-based trainers on the iris dataset. The performance values of the MSE assessment criteria were reported in the table, which contains the best, worst, average, and standard deviation, and were symbolized as Best, Worst, Average, and STD in the table accordingly.

Table 4 Experimental results for the iris dataset
Full size table

Based on the results obtained, it can be seen that in most measurements the results of the BHACRW, BHA, MVO, and SOS are quite better than those of other algorithms. In Fig. 4, the average convergence trends of BHA and BHACRW and a box plot of all MSE algorithms are shown in detail. When analyzing the convergence curves (Fig. 4a), it is obvious that the BHA and BHACRW can quickly reach the minimum MSE. The comparison between the convergence curves clearly shows that at the 250th iteration the proposed algorithms can find the best values for parameters of MLP. Table 4 and Fig. 4a also show that, in neural network training, the performance of the proposed BHACRW is marginally better than simple BHA, especially in terms of best-case MSE, STD, and the worst-case MSE.

Fig. 4
figure 4

Convergence curve of BHA-MLP and BHACRW-MLP a and box plot chart b for the iris dataset

Full size image

By investigating the plot box, the proposed trainers are shown to have the smallest MSE averages after SOS and one of the most compact boxes, which shows the suggested method’s stability.

5.2.2.2 Experiment 2: Wine Dataset

The wine dataset has 13 features and 3 categories, so we used a 13-27-3 FNN model to find the best weight and bias values for MLP. Table 5 shows the results of MHAs-based MLP networks in the wine dataset. The results show that proposed algorithms could achieve the highest classification accuracy ratio of 99.16 percent. Besides, in terms of MSE measurement, they can achieve competitive results. Whereas the SOS and GSA algorithms show better results in terms of MSE compared to BHA, both of them have a high MSE variability (std) and therefore show poor stability. In this dataset, MVO shows superior performance compared to other nature-inspired algorithms.

Table 5 Experimental result for wine dataset
Full size table

The plot box shown in Fig. 5 indicates the competitive error and acceptable stability of the BHA. For the wine dataset, the results of simple BHA is better than BHACRW. The comparison of the average convergence curves reveals that the two curves are very close, which means that the algorithm can achieve an optimum MSE value at most times.

Fig. 5
figure 5

Convergence curve of BHA-MLP and BHACRW-MLP a and box plot chart b for the wine dataset

Full size image
5.2.2.3 Experiment 3: Blood Dataset Result

The blood dataset includes four features and two categories, so we employed the 4-9-3 FNN model to find the best weight and bias for MLP. Table 6 displays the blood dataset test results. In this dataset, the BHACRW has the highest accuracy and the lowest MSE compared to all nature-inspired algorithms.

Table 6 Experimental result for blood dataset
Full size table

The BHA has the third-highest accuracy with a slight difference from the SOS. As can be seen, after BHACRW, BHA and WOA achieved the lowest error in terms of MSE. The results of their evaluation were very close and competitive. According to the boxplots Fig. 6b, the BHACRW, BHA, and WOA have shown a low variability. Figure 6a also shows that the BHA-based trainer can maintain a stable balance between exploration and exploitation tendencies in terms of convergence curves, and most of the time can reach to least MSE.

Fig. 6
figure 6

Convergence curve of BHA-MLP and BHACRW-MLP a and box plot chart b for the blood dataset

Full size image
5.2.2.4 Experiment 4: Liver Disorders Dataset

The liver disorder dataset has 6 attributes and 2 classes, thus we utilized a 6-13-2 FNN model to find the best MLP weight and bias. The BHA and BHACRW techniques in competition with all other trainers could achieve better results with an MSE value of 0.1845 and 0.1808, respectively. Other competitive algorithms in terms of accuracy are SOS, MVO, and WOA; but, except for WOA, these algorithms demonstrated high variability in box plots. The box plot shows that the BHA and BHACRW-based trainers have the lowest MSE average and one of the most compact boxes indicating the consistency of the suggested methods for training. The convergence curve in Fig. 7a and the result of experiments in Table 7 confirm that the BHA and BHACRW have the fastest convergence trends as they can reach the lowest MSE before iteration 100. The result of the BHACRW is promising than BHA in terms of both MSE and accuracy.

Fig. 7
figure 7

Convergence curve of BHA-MLP and BHACRW-MLP a and box plot chart b for the Liver Disorder dataset

Full size image
Table 7 Experimental result for liver disorders dataset
Full size table
5.2.2.5 Experiment 5: Seeds Dataset

We used a 7-15-3 FNN model to figure out the best weight and bias values for MLP as the seeds dataset has 13 features and 3 categories. The findings of the evaluation of the seeds dataset are reported in Table 8. As can be seen, in terms of MSE and accuracy, BHACRW, BHA, and SOS obtained the best results. While their evaluation results have been similar and competitive, BHA has shown consistent outcomes as the standard deviation is the lowest. The box plot shows that SOS, BHACRW, and BHA have more compact boxes, but SOS has the lowest error in terms of MSE, and BHACRW has the highest accuracy. Compared to most of the MHAs’-based optimization algorithms, the MSE error of BHA and BHACRW is less than 0.03 before 100 iterations (Fig. 8a), indicating the faster convergence rate of these algorithms.

Table 8 Experimental result for seeds dataset
Full size table
Fig. 8
figure 8

Convergence curve of BHA-MLP and BHACRW-MLP a and box plot chart b for seeds dataset

Full size image
5.2.2.6 Experiment 6: Statlog (Heart) Dataset

The Statlog dataset consists of thirteen features and two categories, so we used the 13-27-2 FNN model to determine the best weight and bias for MLP. The results of the assessment for the Statlog (heart) dataset are shown in Table 9. The BHACRW shows the highest average accuracy ratio and the second-lowest MSE ratio. Although the MVO algorithm shows the lowest average MSE compared to BHACRW, it has low stability by considering the compactness of the box plot (Fig. 9b) and the standard deviation of MSE. The lowest error value (< 0.08) can be achieved by proposed BHACRW and BHA over the course of 200 iterations, which shows the faster convergence rate of our proposed algorithms compared to other algorithms.

Table 9 Experimental result for the Statlog (Heart) dataset
Full size table
Fig. 9
figure 9

Convergence curve of BHA-MLP and BHACRW-MLP a and box plot chart b for Statlog (Heart) dataset

Full size image
5.2.2.7 Experiment 7: Balance Scale dataset

The balance scale dataset is composed of four features and three categories, so the 4-9-3 FNN model is used to specify the best weight and bias for MLP. The results of identifying equilibrium scale tips for the balance scale dataset are shown in Table 10. The BHACRW has the lowest MSE and standard deviation, and it is also very competitive in terms of classification accuracy. Although the MVO algorithm displays slightly better results in terms of accuracy compared to BHACRW, it has a high MSE variability and thus indicates low stability. Figure 10a also demonstrates, in terms of convergence speed, that the BHA and BHACRW-based trainers can show a faster convergence rate compared to the other algorithms since the MSE value at the 100th iteration is less than 0.05, which is lower than the best value of all algorithms. BHACRW and BHA will maintain a good balance between exploration and exploitation and show stable performance because it has a more compact box plot.

Table 10 Experimental result for balance scale dataset
Full size table
Fig. 10
figure 10

Convergence curve of BHA-MLP and BHACRW-MLP a and box plot chart b for the balance scale dataset

Full size image

In summary, the high average accuracy and low MSE and the standard deviation obtained by both BHA and BHACRW trainers provide strong evidence that the proposed methods will consistently hamper premature convergence toward local optimization and can finding the best optimal values for MLP weights and biases.

5.2.3 Statistical Analysis

In this section, statistical analysis has been carried out to verify the significance of the results. In particular, due to the limited number of comparative approaches, the nonparametric Friedman test was used to assign average accuracy value rankings to each of the ten algorithms on seven classification datasets, which is shown in Table 11. As shown in Table 11, the proposed BHACRW-MLP has been placed in rank 1. In most comparisons, the p value suggests that the null hypothesis can be rejected. This means that the performance of the proposed approach is statistically significant vs to most of the methods. The findings obtained from the post hoc Holm test are shown in Table 12.

Table 11 Average rankings of accuracy values among 10 algorithms on seven classification datasets using Friedman test
Full size table
Table 12 Post-hoc Holm test using Stacking as a control method
Full size table

5.3 Evaluation in COVID-19 Receptor ACE2 Gene Expression Dataset

A novel virus which is known as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2 or CV2) was identified as the cause of coronavirus disease. The CV2 required ACE2 to infect the cells. ACE2 is a protein that provides the entry point for CV2 to hook into and infect human cells. In other words, ACE2 serves as a cellular gateway or a receptor for the COVID-19-causing virus. This COVID-19 infectious illness may be more severe in patients with asthma. Rhinovirus (RV) is the respiratory virus that is responsible for the majority of asthma exacerbations in children and adults. Recently, an analysis was conducted in [76] to examine the role of RV infection in ACE2 expression of asthmatic patients. It was found that RV infections in asthmatics lead to the overexpression of ACE2, and subsequently activate cytokine pathways which are associated with severe COVID-19 disease.

The experimental data of the above study is accessible through GSE149273. The GSE149273 is a sequence read archive (SRA) dataset that was downloaded from the gene expression omnibus database (GEO) and composed of 4056 common genes and three categories (RVA, RVC, Control). After downloading the count data some preprocessing steps such as (removing lowly expressed genes, converting counts to Differentially Expressed Genes (DGEList), quality control, normalization for composition bias, finding all common genes differentially expressed in (RVA, control) and (RVC, Control), extracting ACE2 gene with 90 samples) has been done. We only consider the expression of one gene, ACE2, so the 1-3-3 FNN model is used to specify the best weight and bias for MLP. For this dataset, the population size and number of iterations were considered as 50 and 100.

The performance of different classifiers including K-nearest neighbor (KNN), Naïve Bayes (NB), support vector machine (SVM), backpropagation (BP)-MLP, Bayesian neural network (BNN), decision tree (C4.5), random forest (RF), BHA-MLP, and BHACRW-MLP for the GSE149273 (ACE2 gene) dataset are shown in Table 13. Compared to all classifiers, the BHACRW-MLP achieved the highest accuracy. The BHACRW has the lowest average MSE (0.1432 ± 0.0020) and highest classification accuracy (80.00 ± 2.06) compare to BHA (0.1443 ± 0.0016, 70.00 ± 2.01). Figure 11 also demonstrates that BHACRW-based trainer has a faster convergence rate compared to BHA.

Table 13 Mean classification accuracy of proposed MLP approaches and other algorithms for GSE149273 (COVID-19) dataset
Full size table
Fig. 11
figure 11

Convergence curve of BHA-MLP and BHACRW-MLP for the COVID-19-GSE149273 dataset

Full size image

5.4 Discussion

The results of the experiments over several test functions, various benchmark classification datasets, and a real COVID-19 related gene expression dataset allow us to draw some significant conclusions.

First, adding complementary and Levy flight operators improves BHA’s efficiency and lead this enhanced BHA to show better optimization ability for various numerical test functions. Second, in neural network training, the proposed BHACRW algorithm provides high average classification accuracy and superior local avoidance in benchmark iris, wine, blood, seeds, and Statlog datasets. For dataset wine, BHA, and BHACRW’s average classification accuracy are 99.16% which means that there is only one case that cannot be properly classified in the testing dataset. It is noteworthy that while MVO has the highest accuracy in the liver disorders, and balance scale datasets, BHA exhibits comparable results. However, the accuracy demonstrated in GA is the lowest across the algorithms inquired. The low difference between the best and worst values of the classification accuracy acquired by proposed trainers provides clear evidence that these methods are reliably capable of preventing premature convergence toward local optimization and achieving the best optimum values for MLP weights and biases especially BHACRW.

Third, based on the average of MSE, BHACRW is the most successful approach among the comparable trainers in three datasets: Balance, liver disorders, and blood. While MVO and SOS acquired the minimum average MSE regarding the Statlog (heart) and seeds datasets, BHACRW was the second best method, with very close results to MVO and SOS. In the case of the remaining datasets, BHA and BHACRW demonstrate very competitive performance compared to MVO, SOS, and WOA approaches. In regard to box plot compactness and standard deviation, we have observed that the proposed approaches especially BHACRW perform well in most datasets, demonstrating their robustness and consistency as compared with other algorithms. Fourth, by considering the convergence curves and lowest error values, the proposed approaches have the fastest convergence speed for training all the given datasets and they can reach the lowest MSE in the middle of iterations. Figures 12 and 13 are graphical representations of the experimental results shown in Tables 4, 5, 6, 7, 8, 9, 10. From these figures, it is concluded that the proposed methods show well results as compared with different state-of-the-art methods for test benchmark classification datasets. It is worth discussing that the reason for the poor performance of metaheuristic algorithms is not only related to low efficiency and easily dropping into local optimal but also depends on the presence of many different tuning parameters. By contrast, BHA and BHACRW use only one population size parameter, thus removes the possibility of compromised performance due to inappropriate parameter tuning, and increases performance stability.

Fig. 12
figure 12

MSE performance graphs for each dataset using different methods

Full size image
Fig. 13
figure 13

Accuracy performance graphs for each dataset using different methods

Full size image

Lastly, the application of BHACRW-MLP on the real ACE2 gene expression dataset prove that the suggested approach is exceedingly effectual in solving real and complex classification problems.

In summary, while other papers have already shown that BHA is working well on complex combinatorial optimization problems and some real-world problems, this study shows that the BHA and proposed BHACRW are very capable of training FNN. The outcomes achieved are at the least, perceptive and competitive, at the most, superior to those got by most of the nature-inspired algorithms especially GA, PSO, CS, BBO, WOA, and GSA in all benchmark datasets.

6 Conclusion

In this study, a new modified BHA was suggested by the integration of complementary learning components and Levy flight random walk in BHA’s updating phase. The main aim of this paper is to employ both BHA and suggested BHACRW as new FNN trainers to find optimal values for weight and bias parameters. The BHA’s excellent performance in avoiding local optima, high convergence speed, and having no controlling parameter motivated us to employ the BHA for training MLPs. Furthermore, BHACRW was implemented in order to increase the efficiency and performance of the origin BHA. To benchmark the efficiency of the developed BHACRW approach, experiments were carried out in three steps. In the first stage of the experiments, the BHACRW was evaluated against 4 benchmark global optimization functions and its performance was compared with the original BHA, and eight other metaheuristic algorithms: ABC, PSO, LFFA, GWO, GSA, CSA, BB-BC, and LBH. Experimental results demonstrated BHACRW’s outstanding performance in most evaluation cases. In the second stage, seven UCI classification datasets with different characteristics were used to examine the performance of the suggested method for training MLP. The obtained result confirms the success of the proposed approach in FNN training, compared to other optimization techniques, including GA, PSO, CS, BBO, WOA, MVO, SOS, and GSA. The suggested BHACRW method performs better and in some datasets shows comparable results in the term of classification accuracy and convergence, due to its high convergence rate, and high local optima avoidance. In the third stage, the performance of the suggested BHACRW-MLP was tested on the classification of ACE2 gene expression that was overexpressed in asthmatic patients in order to recognize subgroups at risk for COVID-19. The result showed that the BHACRW-MLP classifier performed much more accurately than other conventional classification methods.

In conclusion, the present findings confirm the efficiency of the suggested approach in solving numerical functions and training FNNs for the classification of various datasets. However, there is still improvement needed in coverage speed and performance dependency of the proposed method on datasets.

For future work, the optimal structure of FNNs can be identified by BHA and BHACRW, including the number of nodes and hidden layers. Training other kinds of ANNs such as radial basis function (RBF) using the BHA and its variants is also recommended. Moreover, the suggested BHACRW approach may be applied to other applications, such as text document clustering.