Introduction

The real-world science and engineering optimization problems generally comprise a large number of decision variables and objective functions with various associated constraints [1]. The decision variable depicts characteristics of the optimization problem, while the objective function is a certain goal defined in terms of decision variable (s). The spaces where the decision variables and objective functions are defined are commonly referred to as decision space and objective space, respectively [2]. The size of the decision space and objective space increases exponentially with the increase in the number of decision variables and objective functions, respectively [3]. The selection of the number of objective functions and decision variables in any specific optimization problem generally depends on the context of optimization problems and decision-makers. It has been observed that the performance of optimization techniques is highly susceptible to the number of objective functions and decision variables involve in the optimization problems [4].

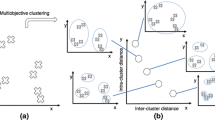
Based on the number of objective functions and decision variables, and their challenges to the MOOs metaheuristic search optimizers, the optimization problems can be categorized into six types: single-objective optimization problems (SOPs), multi-objective optimization problems (MOPs), many-objective optimization problems (MaOPs), large-scale single-objective optimization problems (L-SOPs), large-scale multi-objective optimization problems (L-MOPs), and large-scale many-objective optimization problems (L-MaOPs) [1] [5,6,7,8]. The L-SOPs, L-MOPs, and L-MaOPs are the special case SOPs, MOPs, and MaOPs, respectively. The brief description of the L-SOPs, L-MOPs, and L-MaOPs is given in Fig. 1.

Fig. 1
figure 1

Description of the L-SOPs, L-MOPs, and L-MaOPs

Full size image

To address the optimization problems of the category’s SOPs, MOPs, MaOPs, L-SOPs, and L-MOPs, a large number of related optimizers have been proposed (e.g., [7, 9, 10]). However, the development of optimization techniques addressing the challenges caused by real-world L-MaOPs gained little attention. In the real world, there can be found a large number of science and engineering optimization problems exhibiting the characteristics of L-MaOPs. For example, designing of various engineering models [11], clustering of software systems into modules [12], 13, optimization of hybrid car controller [14], calibration optimization of the automotive [15], scheduling of various industrial tasks [16, 17], software package redesigning [13] are the few examples whose problem formulation generally associated with more than three objectives and more than hundred decision variables and thus representing the class of L-MaOPs.

Even though a variety of many-objective optimizers (MaOOs) have been proposed in the past few years, most of them concentrate on MaOPs with small-scale decision variables (e.g., [18,19,20]. Similarly, on the other hand, a variety of large-scale optimizers have been proposed but most of them focus on SOPs and MOPs (e.g., [7, 21,22,23]). Recently, few studies (e.g., [3, 4, 24]) have proposed large-scale many-objective optimizers (L-MaOOs) focusing on L-MaOPs. Even there are a large number of MaOOs and some L-MaOOs have been proposed, the supremacy of most of these optimizers has not been validated over the real-world L-MaOPs. The success of MaOOs and L-MaOOs can only be justified if they perform well on the real-world optimization problems containing a large number of objectives as well as decision variables instead of just on optimization problems containing a large number of objective functions. To evaluate the success of the existing MaOOs and L-MaOOs, we have applied some of them on the software module clustering problem, a good example of an L-MaOPs.

Software module clustering is a complex optimization problem whose solution is the result of the optimization of many software modularization quality criteria (i.e., objectives) under the restriction of many software design decisions and constraints [25]. The number of decision variables and clustering objectives in software clustering problems varies depending on the size of the software projects and clustering requirements. Both characteristics i.e., a large number of objective functions and a large number of decision variables (i.e., m > 3 and n > 100, respectively) make software clustering as a large-scale many-objective software clustering problem (L-MaSCP). To find the suitability of existing MaOOs and L-MaOOs in cases of L-MaSCP concerning the varying number of objective functions and the number of decision variables, it requires an investigation of performance analysis of these optimizers.

To test the supremacy of various existing MaOOs and L-MaOOs over the L-MaSCP, an empirical investigation is conducted in this research article. As it is time-consuming to evaluate all existing MaOOs and L-MaOOs, hence we have only considered some well-known representative of MaOOs and L-MaOOs of the literature. These optimizers are S3-CMA-ES, LMOSCO, LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA. Their performance is evaluated and compared in terms of IGD, Hypervolume, and MQ through five L-MaSCPs (having 100 to 991 decision variables and 3 to 7 objective functions. This study is inspired by the work [26] where the researchers have conducted a rigorous evaluation of some existing MaOOs over the variety of L-MaOPs benchmark functions. The major limitation of their study is that they have not included real-world optimization problems in the evaluation. We have realized that to make the applicability of MaOOs and L-MaOOs to real-world L-MaOPs, an empirical study is required. To the best of our literature information, no existing works evaluated to test the performance of MaOOs and L-MaOOs on real-world L-MaOPs such as L-MaSCPs.

Relevant related work

Many-objective optimization

The formulation of various science and engineering problems as search-based optimization problems have created a big opportunity for the application of metaheuristic search optimizers. The complex and varying natures of the real-world optimization problems have felicitated deep interest in the development of new metaheuristic optimizers. The development of many-objective optimization concepts in the field of metaheuristic optimizer has made the several complex optimization problems effectively solvable. The brief information about the different categories of many-objective optimizers are as follows.

Dimensionality reduction approach

Dimensionality reduction is a simple and effective approach to addressing MaOPs. In this category, the customization is done in the optimization problem itself instead of metaheuristic optimizers. The optimization problems having a large number of objectives are reduced to an optimization problem with a small number of objectives. In this direction, a large number of dimension reduction approach have been proposed. In the literature [27,28,29,30], the authors presented many greedy-based approaches for dimensionality reduction (i.e., Greedy-k-EMOSS, Greedy-k-EMOSS-omission, Exact-δ-MOSS/k-EMOSS, Greedy-δ-MOSS, and Greedy-OAmax/avg). Some other authors [31] used the correlation-based approach to reduce the number of objective functions. In such approaches, the correlation among the objectives are computed, if there found highly correlated objectives, they are removed from the original set of objectives and formed other subset of objectives. Apart from the greedy and correlation-based objective reduction approach, there exist some other works that are based on the principal component analysis (PCA) method. The authors [32] utilized the PCA approach and further proposed two new objective reduction approach called L-PCA and NL-MVU-PCA. The L-PCA is based on the principle of maximum variance unfolding for linear while NL-MVU-PCA is based on the principle of nonlinear objective reduction.

The simplicity and effectiveness of the greedy and PCA-based dimensionality reduction approach inspired the researchers to improve the accuracy of the previous works as well as to design the new approach. Recently, many other researchers proposed various new dimensionality reduction methods to tackle MaOPs. The works [33] used the sampling and affinity propagation method to remove the redundant objective functions and named the approach as objective reduction using sampling and affinity propagation (ORSAP). The works [34] used objective subspace extraction namely OSEOR to reduce the dimensionality. In OSEOR, the conflicting information is extracted from the different objectives and based on the extracted information each objective is sorted according to their relative importance to extract the overlapped subspace. The works [35] proposed a novel approach to objective reduction using the maximal information coefficient and change rate of non-dominated population techniques. Further, they incorporated it into particle swarm optimizer (PSO) and developed the algorithm named as maximal information coefficient-based multi-objective particle swarm optimizer (MIC-MOPSO). The differential evolution using clustering-based objective reduction (DÉCOR) [36] and sequential decomposition of the objective vector and their positive correlation [37] are two effective approach for dimensionality reduction.

Relaxed dominance approach

In MaOPs, Pareto dominance-based selection pressure of the candidate solution towards the Pareto front decreases drastically, because dominance relation-based methods are unable to differentiate the non-dominated solution. To overcome the issue, many modifications in the Pareto dominance relation have been suggested. The fuzzy–Pareto dominance relation [38] and the improved fuzzy–Pareto dominance relation [39] are the two fuzzy-based selection methods have been used in designing the variety of MaOOs. The works [25] utilized the concept of fuzzy–Pareto dominance relation in designing the FP-ABC: fuzzy–Pareto dominance-driven artificial bee colony algorithm for many-objective software clustering problems. To distinguish the non-dominated solution, the works [40] presented a ϵ-domination relation. The ϵ-domination relation is used to rank the non-dominated solution in the multi-objective evolutionary algorithm. Apart from fuzzy–Pareto dominance, the concept of angle dominance is also used to differentiate the non-dominated solution. The works [41] exploited an angle dominance criterion and proposed a novel MaOOs. The α-dominance strategy [42] is found as an effective approach in differentiating the non-dominated solutions. To make the α-dominance strategy more effective for the many-objective optimization, the works [43] proposed an improved version of α-dominance strategy where they used an elliptic function to assign the rank of non-dominated solutions. The works [44] introduced a new dominance relation, referred to as θ dominance relation and further designed a θ dominance-based evolutionary algorithm (θ-DEA) to solve the MaOPs.

Diversity-based approach

In diversity-based optimization techniques, various approaches are used to overcome the difficulties encountered in the MaOPs-related to diversity. The works [45] incorporated the grid technique a most effective technique to balance the diversity and convergence of solutions during the optimization process. To this end, they used hierarchical grid-based criteria and inbuilt it into the fitness functions to assign the proper ranking of solutions. Further, the works [46] utilized the strength of grid-based approach to improving the selection process of the solution while maintaining the uniform distributions of solutions. In the approach, they designed three grid-based methods (i.e., grid crowding distance, grid ranking, and grid coordinate point distance) to determine the mutual relationship of solutions. The work [47] utilizes the potential of rotary grid technology to address the many-objective issue of MaOPs. They demonstrated that their rotary grid technology-based many-objective optimization approach is more effective compared to Pareto non-dominated sorting strategy. The work [48] introduced a novel diversity method, namely diversity ranking based evolutionary algorithm (DREA) for metaheuristic optimizers.

Aggregation-based approach

Aggregation is the simplest way of differentiating the non-dominating solutions of a MaOP. In the aggregation-based approaches, objective functions are aggregated by associating the relative weight to each objective. This approach is more suitable when the preference information regarding the relative weight is already known. Vector angle distance scaling, weighted sum, boundary intersection methods, and weighted Tchebycheff are commonly used techniques to aggregate the multi-objective optimization into the single-objective optimization functions [18, 49, 50]. The work [50] utilized the weighting coefficients to determine the relative importance of objectives. The work [49] introduced the directed line search-based approach along with the aggregation-based method in the multiple single-objective Pareto sampling (MSOPS) to address the MaOPs. The work [51] proposed a many-objective optimization technique based on the decomposition method named DBEA-Eps with systematic sampling. In work [52], the authors introduced an aggregation-based approach in the TwoArchA evolutionary algorithm to maintain the diversity and convergence of the Pareto front solutions. Further, they extended the TwoArchA and named it as TwoArchA + many-objective evolutionary algorithm.

Indicator-based approach

In the indicator-based metaheuristic optimizers, the quality indicator metrics are used to rank the non-dominated solutions of the population. To compute the indicator values of the solutions following three methods are used: R2-indicator-driven approach, distance-based indicator driven approach, and hypervolume driven approach. The work [53] utilized R2-indicator sorting, a method to generate relative ordering for the non-dominated solutions. The R2-indicator sorting is an effective method to rank as well as to perform the selection of the solutions for the next generation. The R2-indicator-based ranking method is further incorporated into a differential evolution algorithm (DEA) and genetic algorithm (GA) to tackle the MaOPs. Further, the work [54] incorporated the R2-indicator ranking method into a new multi-objective evolutionary algorithm. The work [55] defined the optimization goal in terms of indicator ranking and then used this ranking method for the selection of non-dominated solutions. After that, they proposed a multi-objective evolutionary algorithm namely, indicator-based evolutionary algorithm (IBEA).

The work [56] proposed an approximation based evolutionary multi-objective algorithm. The proposed framework allows working with various formal notions of approximations. The work [57] proposed the use of Δp indicator for ranking the non-dominated solutions and further incorporated into existing metaheuristic optimizers. They also provided the various characteristics of the Δp indicator so that it can be effectively used as the selection mechanism in the various evolutionary algorithm. The hypervolume indicator is the only ranking metric for the non-dominated solution that provides the strict monotonic relations to the Pareto dominance solutions. The work [58] proposed a new metaheuristic algorithm based on hypervolume indicator and named it as the hypervolume estimation algorithm (HypE). To compute the exact hypervolume value they used the Monte Carlo sampling approximation method. The works [59] proposed a hybrid many-objective evolutionary algorithm called reference vector-guided evolutionary algorithm based on hypervolume indicator (H-RVEA). They used the reference vectors and an adaptation strategy to decompose the optimization problem and to adjust the reference vector distribution, respectively. The work [60] presented a novel many-objective particle swarm optimization (PSO) algorithm based on the unary epsilon indicator and the direction vectors, termed as IDMOPSO.

Reference set-based approach

In reference point-based metaheuristic optimizers, a set of the reference point (i.e., best solutions) are generated and based on that points the optimization process is carried out. The reference points help in selecting the solution from the current population to generate solutions for the next generation. Recently, several many-objective optimization techniques based on the reference set method have been proposed. In these algorithms, the quality of solutions is measured corresponding to a set of reference solutions. Thus, the searching direction is controlled by the reference solution set in these algorithms. The construction of the reference set and computing the goodness of each individual of the population is the basic challenge of these approaches. The work [61] constructed the reference set by collecting the best solution of every generation into the external archive. The best solutions achieved till the time are used as a reference set to guide the further steps. Further, the authors [9] extended the work [61] by incorporating new selection and truncation strategies for the external archives. The work [19] incorporated the reference set-based approach in the original NSGA-II framework and proposed an extended version of NSGA-II.

Preference-based approach

In the preference-based approach, the preferences of the decision-makers are incorporated in the metaheuristic optimizers to guide the optimization process towards most preferred efficient points. In other words, in the preference-based many-objective optimization algorithm, instead of focusing on optimization of entire Pareto front, a subset of efficient points according to the decision-maker’s preference is considered [62, 63]. The work [62] presents a detailed survey regarding the metaheuristic algorithms where preference information of the decision-makers has been incorporated. Their study concluded that the involvement of the decision-makers preferences during the optimization process can generate more effective Pareto front in compared to the general optimization process. Moreover, the Pareto front obtained with the decision-maker’s preferences is more helpful in making the final decision. Later, many researchers have incorporated the decision-maker’s information in the optimization process to generate better and effective solutions for the many real-world optimization problems. The work [64] extended the original NSGA-II by incorporating the decision-maker’s preference during its iteration and proposed a new algorithm named as reference direction-based NSGA-II (RD-NSGA-II). In the RD-NSGA-II, a reference direction based on the decision-maker’s preferences is used to drive the optimization process towards the most effective region. To incorporate the decision-maker’s preferences in the optimization process, the work [65] utilized the polyhedron theory and proposed an interactive evolutionary algorithm (IEA).

Decomposition-based approach

In MOEA/D [18], the multi-objective optimization problem is divided into different scalar objective optimization sub-problems and each of the sub-problems is solved parallelly to obtain the final Pareto front. The MOEA/DD [66] is an advanced version of original MOEA/D where the dominance principle is also integrated along with splitting the multi-objective problem to address the many-objective optimization algorithm. Specifically, the MOEA/DD optimizer exploits both concepts i.e., dominance-based approach and scalarization of objective function approach to maintain the diversity and convergence. The dMOPSO [67] is also based on the concept of dividing the multi-objective optimization problem into a set of different single-objective optimization problem using a different set of the unique weight vector. To explore and exploit the search space of scalar single-objective optimization problem, the PSO optimizer is exploited in dMOPSO. The MPSO/DD [20] is an improved form of multi-objective particle swarm optimization where the concepts of different ideal points and decomposition strategy have been exploited to suit the different kinds of MaOPs.

Large-scale optimization

In the literature of metaheuristic search optimization, a large number of single-objective, multi-objective, and many-objective optimization optimizers have been reported. The developments of these optimizers are mostly objective function centric and had a limited consideration of the number of decision variables. It has been observed that the number of decision variables has a major influence on the performance of the single-objective, multi-objective, and many-objective optimization algorithms. The encounter of large-scale decision variables in many real-world single-objective, multi-objective, and many-objective optimization problems encouraged the researchers and academicians to design and develop large-scale single-objective, multi-objective, and many-objective optimization algorithms.

Large-scale single-objective optimization

To address the challenges caused by the large-scale decision variables in the single-objective optimization, various contributions have been made by the researchers and academicians. To scale up the existing single-objective optimization algorithms for the L-SOPs, many customized algorithms have been proposed. The [21] customized the single-objective particle swarm optimization algorithm and proposed a novel cooperative co-evolving particle swarm optimization algorithm, called (CCPSO) for the L-SOPs. To improve the performance of the CCPSO, the same authors proposed a new cooperative co-evolving particle swarm optimization algorithm, named (CCPSO2) [68]. To this contribution, they exploited the concept of random grouping and Cauchy and Gaussian distributions and incorporated into the particle swarm optimization algorithm to update the position of the particles. The [69] presented a large-scale single-objective optimization method using the concepts of oppositional-based learning (OBL) and cooperative co-evolution (CC).

The work [7] presented a competitive swarm optimizer, called CSO. The CSO was inspired by the searching mechanism of particle swarm optimization; however, it does not use the personal best position and global best position to update the particle position in search space. In place of personal best position and global best position, a pair-wise competition mechanism is exploited where the looser particle updates its position by learning from the winner particle. To increase the scalability of the particle swarm optimization algorithm in terms of decision variable, the study [70] proposed a multiple-strategy learning particle swarm optimization algorithm, named MSL-PSO. Instead of a single learning strategy, the MSL-PSO approach used different learning strategies.

Large-scale multi-objective optimization

Apart from the several contributions made towards the large-scale single-objective optimization, the large-scale multi-objective optimization also gained wide attention. The work [22] proposed a decision variable analysis based multi-objective optimization algorithm (MOEA/DVA) to address the L-MOPs. The MOEA/DVA decomposes the MOPs into the different number of simpler sub-optimization problems and further, the decision variables in each sub-optimization problem are optimized independently. To deal with the large-scale decision variables in MOPs, the work [23] utilized the concepts of cooperative co-evolutionary algorithm and fast interdependency identification algorithm. The work [10] presented a large-scale multi-objective optimization framework, named weighted optimization framework. The framework is generic and designed in such a way that it can be incorporated with a population-based metaheuristic algorithm. The framework has been tested with large-scale multi-objective optimization problem having 40–5000 variables and 2–3 objectives.

The work [71] presented a general framework for L-MOPs, named as LSMOF. The main goal of the LSMOF was to improve the computational efficiency of multi-objective metaheuristic algorithms on L-MOPs. The LSMOF used the problem reformulation and candidate solution spreading strategies to generate a set of quash-optimal solutions near the PS and uniformly distribution of approximate Pareto set. The work [72] presented a competitive swarm optimization (CSO)-based large-scale multi-objective optimization, named LMOCSO. In LMOCSO, instead of using personal best position and global best position, a competitive mechanism is utilized to update the particle's position. To solve large-scale sparse multi-objective optimization problems (e.g., structure optimization of neural network and feature selection) recently, the study [73] presented novel evolutionary algorithm where new population initialization strategy and genetic operators have been incorporated. The work [74] exploited an adaptive offspring generation in the designing of genetic algorithm based large-scale multi-objective optimization approach.

Large-scale many-objective optimization

Similar to the incorporation of strategies corresponding to large-scale characteristics in the single-objective optimization and multi-objective optimizations, recently several approaches have been developed for large-scale many-objective optimization. Last few years, there seemed sudden progress in the development of large-scale many-objective optimization algorithms, but most of the many-objective optimization approaches are focusing on addressing the particular aspects of large-scale many-objective optimization problems. Recently, some studies revealed the various issues and challenges of the large-scale many-objective optimizations triggered by the large-scale decision variables by the optimization problems and further suggested some improvement in the existing many-objective optimization algorithms.

The work [8] proposed a large-scale many-objective optimization (LMEA) to address the L-MaOP. To this contribution, the LMEA used decision variable clustering method to divide the decision variables into two groups, i.e., diversity-related variable and convergence-related variable based on their contribution in diversity and convergence, respectively. The study [24] presented several improvements in the NSGA-III [19] to address the L-MaOPs. To this contribution, they introduced an information feedback models where the historical information of the individual candidate of the previous generation is exploited to update the individuals of the current population. The work [75] utilized the concept of information feedback model into the MOEA/D and proposed a new large-scale many-objective optimization algorithm. The study [4], presented a novel large-scale many-objective optimization algorithm based on scalable small sub-populations-based covariance matrix adaptation evolution strategy (S3-CMA-ES). In the S3-CMA-ES, a series of small sub-populations instead of a whole population is used to approximate the set of Pareto-optimal solutions.

Large-scale many-objective software clustering problem

Software clustering is the process of partitioning the large and complex software structure into smaller, meaningful, and more manageable subsystems. The software clustering is widely used in redocumenting, understanding, architecture recovery or reverse engineering of software projects. In the formulation of software clustering problem as a search-based optimization problem, decision variables and objective functions are mapped in terms of the entities to be clustered and clustering goals, respectively. If the number of entities and clustering goals increases in the software clustering problem, then the number of decision variables and objective functions in the corresponding formulation of search-based optimization problem also increases in the same proportional.

Nowadays, the size and complexity of the software systems are increasing drastically due to the implementation of a large number of user and technological requirements. To perform the different software activities, generally there requires consideration of many quality criteria due to concerns of different stakeholders. So, the software clustering formulation as a search-based optimization problem for a large and complex software project comprising many clustering quality criteria makes the problem as a large-scale many-objective software clustering problem (L-MaSCPs). Similar to the L-MaOPs, the L-MaSCPs poses various challenges to the performance of metaheuristic optimizers. Hence, it becomes necessary to evaluate the performance of the various existing metaheuristic optimizers on the formulation of L-MaSCPs.

Formal definition of L-MaSCP

A more formal way to define software clustering is to partition n software entities into k (k > 1) meaningful and more manageable subsystems based on the m clustering quality criteria. If a software system containing a set of entities E = {e1, e2,..., en}, where n is the total number of entities. Then these software entities can be organized into set of subsystems K = {m1, m2,..., mk}, where k is the total number of subsystems based on the set of objective functions Q = {q1, q2,..., qm}, where m is the total number of clustering quality criteria. In case of the L-MaOPs, number of clustering criteria will always be greater than three. The mathematical definition of the L-MaOP can be defined as follows:

$$ \left\{ {\begin{array}{*{20}c} {{\text{min}} Q\left( v \right) = [q_{1} \left( v \right),q_{2} \left( v \right), \ldots ,q_{M} \left( v \right)]^{{\text{T}}} ,} & {M > 3} \\ {r_{j} \left( v \right) \ge 0} & {j = 1, \ldots P;} \\ {x_{k} \left( v \right) = 0} & {k = 1, \ldots Q;} \\ {v_{i}^{{{\text{Lower}}}} \le v_{i} \le v_{i}^{{{\text{Upper}}}} } & {i = 1, \ldots ,n} \\ \end{array} } \right., $$
(1)

where \(q_{1} \left( v \right),q_{2} \left( v \right), \ldots ,q_{M} \left( v \right)\) are the M numbers of quality criteria (i.e., objective functions). The v = {v1, v2,..., vn} is the set of decision variables. In cases of the L-MaOPs, the number of decision variable will always be greater than hundred. The \(r_{j} \left( v \right)\) and \(x_{k} \left( v \right)\) are the inequality and equality constraints, respectively. \(v_{i}^{Lower}\) and \(v_{i}^{Upper}\) are the lower and upper bound of the ith decision variable.

Objective functions

The clustering quality criteria representing the different aspects of software quality can be considered as objective functions for the software clustering problem. In search-based optimization techniques, the objective functions are considered as the main driving force that helps the optimization process proceeding towards the optimal solution. In this work, seven clustering criteria as suggested in various work [12, 76] are considered as objective functions. These objective functions are as follows: (1) number of software elements per cluster (to minimize), (2) number of the cluster in the system (to minimize), (3) number of isolated clusters (to minimize), (4) sum of inter-cluster dependencies (to minimize), (5) sum of intra-cluster dependencies (to maximize), (6) modularization quality (MQ) (to maximize), and (7) cluster cyclic dependencies (to minimize).

Decision variables

In the software clustering problem, a clustering solution is a result of the placement of each software entities into a more suitable cluster. Placement of each of the software entity can be regarded as a decision variable because it can have many possible choices to move in clusters. In large and complex software system, there can be a large number of software entities (i.e., often more than 100). Hence, the software clustering problem can be regarded as a large-scale optimization problem. If the software clustering problem contains a large number of objective functions (≥ 3) and a large number of decision variables (≥ 100), it can be regarded as a large-scale many-objective software clustering problem.

To encode the software clustering solution in terms of decision variable, we use an integer vector representation. In an integer vector encoding of the software clustering, indices of the vector are mapped with the entities of the software systems and modules in which the entities are residing is mapped with the indices values. The method of candidate solution representation for the software clustering problem is depicted in Fig. 2.

Fig. 2
figure 2

Encoding of candidate solution for the software clustering problem

Full size image

In the integer vector representation of the candidate solution for the software clustering problem, an n size of the integer vector is created, where n is the number of the decision variables (i.e., number of entities present in the software system). For example, suppose there is a hypothetical software system which contains eight entities, i.e., E =  [e1, e2, e3, e4, e5, e6, e7, e8] and let us consider these entities are clustered into three modules, i.e., M =  [m1, m2, m3] as follows: entities [e1, e2] is clustered into module [m1], entities [e4, e6, e7] is clustered into module [m2], and entities [e3, e5, e8] is clustered into module [m3]. To represent the candidate solution of this hypothetical software system, an integer vector of size eight has to be created where indices will be associated with each entity, i.e., [e1, e2, e3, e4, e5, e6, e7, e8] and their corresponding indices values will be modules [m1, m2, m3] in which that entity is residing.

Introduction to selected metaheuristic optimizers

In this study, we investigate the performance of nine metaheuristic optimizers belonging to the different categories of many-objective optimization algorithms and large-scale many-objective optimization algorithms. Seven optimizers are from the category of many-objective optimization algorithms and two optimizers are from the large-scale many-objective optimization algorithms. The main reason for selecting these metaheuristic optimizers is that they have been widely used to solve the various mathematical benchmark functions by researchers and academicians and demonstrated good performance. The summary of the algorithms is as follows:

  • Angle dominance criterion-based many-objective optimizer (ADC-MaOO) The ADC-MaOO [41] is a parameterless many-objective optimizer where an angle dominance strategy is used in place of Pareto dominance. Apart from providing sufficient pressure towards the Pareto front, the angle dominance strategy also exempts algorithm from the need for parameter tuning.

  • Diversity ranking-based evolutionary algorithm (DREA) The DREA [48] is a diversity ranking-based many-objective optimizer specially designed to address the problems of multi and many-objective optimization. The DREA uses the diversity ranking and reference vector adaptation approach to deal with the different issues of the Pareto front shapes.

  • Non-dominated sorting genetic algorithm-III (NSGA-III) The NSGA-III [19] is an enhanced version of the NSGA-II algorithm [80] which is especially customized for the optimization problems that belong to the class of MaOPs. The NSGA-III follows the same framework as defined in NSGA-II, except the selection operator. The selection method in NSGA-III is based on the reference point instead of the dominance principle.

  • Large-scale multi-objective optimization based on a competitive swarm optimizer (LMOSCO) The LMOCSO [72] is an effective metaheuristic optimizer especially designed to address the large-scale multi-objective optimization problems. The approach adopted the concept of competitive swarm mechanism to select the particles to be updated, and an effective particle updating method is designed to enhance the search capability.

  • Unary epsilon indicator and the direction vectors based many-objective particle swarm optimization (IDMOPSO) The IDMOPSO [60] is a PSO based many-objective optimizer where the concept of the unary epsilon indicator and the direction vectors have been utilized to balance the convergence and diversity of the algorithm. The IDMOPSO uses the technique of epsilon indicator strategy for selecting the personal best.

  • Large-scale many-objective optimization (LMEA) The LMEA [8] is a large-scale many-objective optimizer. It uses the concept of variable clustering where all decision variables of the optimization problem are clustered into the convergence and diversity-related variables. To evolve the convergence and diversity-related variables simultaneously, two different optimization techniques are used.

  • Reference vector-guided evolutionary algorithm based on hypervolume indicator (H-RVEA) The H-RVEA [59] is designed to address the many-objective optimization problems. In H-RVEA, the concepts of reference vector-guided evolutionary algorithm (RVEA) and hypervolume estimation algorithm (HypE) is integrated together to achieve the better approximation of the Pareto optimal.

  • Scalable small sub-populations-based covariance matrix adaptation evolution strategy (S3-CMA-ES) The S3-CMA-ES [4] divides the whole population into a series of sub-populations where each sub-population is evolved to converge towards a single solution. To optimize each sub-population, the S3-CMA-ES uses the CMA-ES algorithm as the local optimizer. In other words, the S3-CMA-ES optimizes each sub-population instead of a whole population to achieve the set of Pareto-optimal solutions.

  • Large-scale multi-objective optimization framework (LSMOF) The LSMOF [71] is a multi-objective optimization framework specially designed to accelerate the performance of the large-scale multi-objective optimization. This approach exploited the idea of problem reformulation to track the Pareto-optimal set. In this work, the LSMOF framework together with NSGA-II is used.

Experimental setup

This section presents the description of the experimentation setup prepared for the evaluation of the selected large and many-objective optimization algorithms. The experimentation setup includes: description of the test problem’s characteristics, results performance evaluation metrics, used statistical test method, and parameter settings of the different optimizers.

Test problems

Five large and complex object-oriented software projects exhibiting the large-scale many-objective optimization properties are selected in this study. These software projects are open source with varying size and complexity levels which are easily available on the web. These software projects are: written in Java programming and have different size of classes and packages. Collectively, these software projects present a variety of characteristics that reflect different difficulty levels for optimizers. Major characteristics of software projects are summarized in Table 1.

Table 1 Description of software systems
Full size table

For a software project, the clustering can be performed at the different level of source code abstraction. It can be at method level or class level or package level abstraction. In software clustering, the low-level software entities are clustered into the higher level software entities based on some clustering criteria. In this work, source code classes and packages of the selected software projects are considered as low-level and higher level software entities, respectively.

Statistical methodology

It is a well-known fact that large-scale many-objective optimization algorithms generally involve randomness in their optimization process. Hence, large-scale many-objective optimization algorithms may generate different result on the different run with the same input. In such cases, it becomes a challenging task to evaluate and compare the different randomization-based optimization algorithms. To make the effective evaluation of such optimizers, the use of statistical tests is generally suggested by the researchers and academicians. There are many statistical tests methods (i.e., parametric and non-parametric statistical tests) and their evaluation performance depends on the nature of the data. The parametric tests (e.g., t test) behave well if the distribution of data is in the normal distribution and the non-parametric tests (e.g., Wilcoxon rank-sum test) work well if the nature of the data is not in the normal distribution.

In this work, each selected optimizer is run 20 independent times and statistical test are applied on sample results to determine whether there is a significant difference between two optimizers or not. For the statistical test, we used a pair-wise Mann–Whitney–Wilcoxon rank-sum test [77] at a significance level of 5%. The difference and rank of an optimizer are defined as the same method as discussed by the authors [26]. In each pair of optimizers, if there is a significant difference is found, the optimizer having higher mean value (i.e., mean of 20 independent runs) is considered the winner and the optimizer having lower mean value is considered looser. The value of the difference metric is signifying that there is a difference between the performances of optimizers. The difference value of an optimizer provides information about the difference created between total wins and total losses of that optimizer. The superiority of the optimizer is defined using the rank which signifies that the corresponding optimizer better compared to other optimizers with that order. This ranking is determined with respect to mean difference values of the optimizers.

Parameters of algorithms

The exploration and exploitation process of the search space are generally controlled by many parameters defined in the metaheuristic optimizers. Hence, the configuration of the parameters setting has a major impact on the performance of optimization algorithms. The optimizer performing well on a particular setting of parameters values over a particular problem may not perform well on other problems with the same parameter setting. In other words, the optimized values of parameters of an optimization algorithm for a problem may not be optimized values for the other problem. Hence, to make the fair comparison of the metaheuristic optimizers over a particular problem the parameter values of the algorithms need to be optimized or tuned according to that problem. The used parameters values of each selected algorithm are provided in Table 2.

Table 2 Parameter’s values of algorithms
Full size table

In the case of our large-scale many-objective software clustering problem, we tuned the parameters of the selected large and many-objective optimization algorithms based on trial and error method. Apart from the core parameter setting, the performance of optimization algorithms also depends on the termination criterion. It has been found that some optimizers require a smaller number of function evaluations whereas some other algorithms require a larger number of function evaluations in one iteration. Hence, the termination criterion based on the number of iterations for each optimizer cannot be a fair choice. To mitigate this issue, we used the same number of function evaluations as termination criterion to each considered optimizers instead of the number of iterations as a termination criterion.

Performance indicators

To measure the success of metaheuristic optimizers, there requires quality metrics that can evaluate the effectiveness of the generated solutions. To evaluate the convergence and diversity of the obtained solutions, we used two popular quality indicators, i.e., hypervolume [78] and inverted generational distance (IGD) metric [79]. To evaluate the structural quality of the obtained solutions, we used the modularization quality (MQ) metric [12]. The MQ metric is the most widely used quality indicator for the evaluation of clustering solution.

Experimental results

This section presents the IGD, Hypervolume, and MQ results obtained through the selected metaheuristic optimizers—S3-CMA-ES, LMOSCO, LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA. The IGD, Hypervolume, and MQ results of each optimizer are presented based on the various combinations of the different number of decision variables and objective functions. The number of decision variables varies from 100 to 991 and the number of objective functions varies from 3 to 7.

The IGD, Hypervolume, and MQ results of each optimizer corresponding to the number of decision variables and objective functions are shown in Tables 3, 4, and 5, respectively. The first column of each table consists of test problems (i.e., software systems to be clustered) along with the number of decision variables. The second column presents the objective functions corresponding to each test problem. The columns 3–11 present the differences and ranks values of the selected metaheuristic optimizers computed based on the pair-wise Mann–Whitney–Wilcoxon rank-sum test. The description of differences and ranks values are as follows: the smaller the rank value denotes the better performing optimizer (e.g., rank 1 denotes that the corresponding optimizer is the best performing optimizer compared to the rest of optimizers) and the higher rank value is the indication of a worst-performing optimizer. In each table, for each pair of the software system (with the number of decision variables) and the number of objective functions, metaheuristic optimizer (s), achieved the best rank is highlighted with italics.

Table 3 Performance of algorithms in terms of the IGD using Mann–Whitney differences [ranks]
Full size table
Table 4 Performance of optimizers in terms of hypervolume using Mann–Whitney differences [ranks]
Full size table
Table 5 Performance of optimizers in terms of the MQ using Mann–Whitney differences [ranks]
Full size table

The IGD results presented in Table 3 show that the optimizers S3-CMA-ES and LMOSCO perform better compared to the LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA in most of the cases. The S3-CMA-ES and LMOSCO achieved rank 1 or 2 in most of the cases compared to the other algorithm. The S3-CMA-ES achieved Rank 1 in ten and Rank 2 in 10 out of 25 cases. Similarly, the LMOSCO achieved Rank 1 in seven and Rank 2 in 13 out of 25 cases. If we see the result, it is clear that in case of a large number of decision variables and objective functions, both optimizers i.e., S3-CMA-ES and LMOSCO are performing better to the rest of the approaches in most of the cases. For example, in the case of Xerces-J (991), where the number pf decision variable is very large the S3-CMA-ES achieves Rank 1 in three and Rank 2 in two out of five cases. The LMOSCO achieved Rank 1 in four and Rank 2 in three out of five cases. However, if we compare the results of S3-CMA-ES and LMOSCO, the overall ranks of the S3-CMA-ES are less than the overall rank of LMOSCO. Hence, the S3-CMA-ES can be considered as better optimizer to the LMOSCO optimizer.

The optimizers LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA are demonstrating nearly similar performances. The LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, and DREA achieved Rank 1 in only 1, 2, 2, 2, 1, 1, and 2 cases, respectively, out of the 25 cases. The H-RVEA could not achieve Rank 1 in any of the cases and total rank is largest among all optimizers. Theredore, H-RVEA is the worst performers. If we see the total rank-sum values of optimizers LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA, the LSMOF contains better rank-sum value among these optimizers. In case of the number of decision variables, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, and DREA have the similar response, i.e., for the small number of variables they perform better and for a large number of variables their performance starts degrading. On the other hand, the performance of H-RVEA, has less impact on the increase and decrease of the number of decision variables.

Table 4 shows the hypervolume results corresponding to the difference and ranking values of the optimizers—S3-CMA-ES, LMOSCO, LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA obtained through five L-MaSCPs with different combinations of the decisions variables and objective functions. The hypervolume results demonstrate that the optimizers S3-CMA-ES and LMOSCO outperform the optimizers LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA in most of the cases. The S3-CMA-ES and LMOSCO achieved the Rank 1 in 10 and 7 cases out of 25 cases, respectively, while the optimizers LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, and DREA achieved the Rank 1 in only 1, 1, 2, 1, 2, and 1 case out of 25 cases, respectively.

The performance of S3-CMA-ES and LMOSCO optimizers increase if the number of decision variables increases, while the performance of other optimizers, mostly decreases with the increase in the decision variables. Similar to the IGD results, the H-RVEA optimizer is performing worst compared to the all optimizers as it could not achieve Rank 1 in any of the cases. If we see the rank-sum values the optimizers S3-CMA-ES, LMOSCO, LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA achieved the total rank values are 46, 56, 118, 137, 135, 145, 146, 170, and 121, respectively. These values also validate that the S3-CMA-ES and LMOSCO are the best performers among all considered optimizers. On the other hand, the LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, and DREA are the average performer. Now if we see the results of the H-RVEA, it visible that it has the rank value in almost all cases, thus it is regarded as the worst performer among all optimizers.

The IGD and Hypervolume results presented in Tables 3 and 4 evaluated the quality of obtained Pareto front of each of the optimizers. Both metrics measure the spread and convergence simultaneously of the obtained Pareto front. Apart from the quality of spread and convergence of the obtained Pareto front for each optimizer, we have also measured the structural quality of the clustering solutions corresponding to the obtained Pareto front. To evaluate the structural quality of the clustering solutions obtained through each optimizer, we used the MQ quality measure. The MQ results of all the considered optimizers corresponding to each combination of decision variables and objective functions are shown in Table 5.

Similar to the IGD and hypervolume evaluation results presented in Tables 3 and 4, the S3-CMA-ES and LMOSCO are also able to generate better results in terms of MQ measure compared to the rest of the optimizers. If we see the ranking results of the S3-CMA-ES and LMOSCO optimizers, both optimizers have achieved the Rank 1 and Rank 2 in most of the cases. If we see the results of rest of the optimizers, i.e., LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA, the optimizers LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, and DREA are exhibiting the average performance while the H-RVEA, is having the worst performance. If we see the results of rank-sum values, the S3-CMA-ES and LMOSCO optimizers achieved the better rank-sum values compared to the rest of the optimizers. The LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, and DREA have an average rank-sum values while H-RVEA has the worst rank-sum value.

In summary, the overall results presented in terms of IGD, Hypervolume, and MQ quality metrics indicate that the S3-CMA-ES and LMOSCO optimizers are more effective for solving the L-MaSCPs compared to the LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA. Among LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA, the LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, and DREA are the average performer while H-RVEA is the worst performer. In the context of large-scale many-objective optimization problems, solvability and the effectiveness of the different metaheuristic optimizers highly depends on the number and characteristics of objective functions and decision variables. In other words, the different types of metaheuristic optimizers perform well with a particular problem optimization model. Therefore, a metaheuristic optimizer working well on a particular problem optimization model may not perform well with other problem optimization model.

To exploit the potential of the large-scale many-objective optimizers, it becomes necessary to have enough knowledge about the hidden structure of the optimization problems. The performance of the many large-scale multi/many-objective optimizers (e.g., S3-CMA-ES, LSMOF, and LMEA) depends on the characteristics of the optimization problems. The S3-CMA-ES and LMEA are based on the concept of decision variable grouping. The performance of these approaches depends on the degree of dependency or degree of separability of the decision variables or set of decision variables. The LSMOF is based on the problem transformation strategy where the optimization problems are transformed into a simpler multi-objective optimization problem with a relatively small number of decision variables. There are some other large-scale multi/many-objective optimizers (e.g., LMOSCO, NSGA-III, and DREA) do not use the concepts of decision variable grouping and problem transformation strategy. To improve the performance, these approaches incorporate various strategies into the optimization framework instead of making problem reformulation or decision variable grouping. Our study applied these approaches to solve the large-scale many-objective software module clustering problems. To test the supremacy of these approaches, we conducted a comparative study on many test problems. This study is preliminary in the direction of large-scale many-objective software module clustering and further, it requires more analysis and experimentation over a large number of problems to reveal more insights corresponding to the performance of different large-scale multi/many-objective optimizers.

Conclusion and future works

In this work, we have conducted an empirical study to investigate the effectiveness of various many-objective optimization and large-scale many-objective optimization algorithms with respect to both number of decision variables and objective functions of different types of L-MaSCPs. In this contribution, nine multi and many-objective optimization algorithms (i.e., S3-CMA-ES, LMOSCO, LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, H-RVEA, and DREA) were compared over 5 challenging L-MaSCPs containing 100–991 decision variables and 3 to 7 objective functions. Results demonstrated that the S3-CMA-ES and LMOSCO optimizers generally perform well with respect to a large number of decision variables and objective functions. These approaches were able to maintain the better value of IGD, hypervolume, and MQ despite the increased in size of the decision as well as the objective space. The LSMOF, LMEA, IDMOPSO, ADC-MaOO, NSGA-III, and DREA optimizers are overall exhibiting the average behaviour. But their performances were not satisfactory on L-MaSCPs with a large number of decision variables. They showed satisfactory responses on the L-MaSCPs with a large number of objective functions and a small number of decision variables. The H-RVEA optimizer was the worst performer algorithm compared to all optimizers. It is validated with the fact that H-RVEA could not achieve Rank 1 in any of the cases and maintained mostly higher ranks. The L-MaSCPs are the challenging problem in the software engineering and gained little attention of the application and designing of the large-scale many-objective optimization algorithms for the L-MaSCPs. Hence, our study can serve as a starting point for the designing of the large-scale many-objective optimization algorithms corresponding to the L-MaSCPs. The future work may include the investigation of the more optimizers on more real-world optimization problems which contains a large number of objectives as well as decision variables.