Multi-objective fully intuitionistic fuzzy fixed-charge solid transportation problem

Abstract

During past few decades, fuzzy decision is an important attention in the areas of science, engineering, economic system, business, etc. To solve day-to-day problem, researchers use fuzzy data in transportation problem for presenting the uncontrollable factors; and most of multi-objective transportation problems are solved using goal programming. However, when the problem contains interval-valued data, then the obtained solution was provided by goal programming may not satisfy by all decision-makers. In such condition, we consider a fixed-charge solid transportation problem in multi-objective environment where all the data are intuitionistic fuzzy numbers with membership and non-membership function. The intuitionistic fuzzy transportation problem transforms into interval-valued problem using $(\alpha ,\beta )$-cut, and thereafter, it reduces into a deterministic problem using accuracy function. Also the optimum value of alternative corresponds to the optimum value of accuracy function. A numerical example is included to illustrate the usefulness of our proposed model. Finally, conclusions and future works with the study are described.

Introduction

In the last few decades, the traditional transportation problem (TP) considers only single objective function. When a homogeneous product is transferred from a source to different destinations in competitive economic condition, there exist more than single criterion such as the transportation cost, average delivery time of product, deterioration rate of goods, fixed charge for an open route, etc. Therefore, in such a condition, the traditional TP is not sufficient to accommodate such real-life decision-making problem which contains single objective. To overcome such situation, we include TP with multi-objective functions that are contradict to each other. As a result, the single objective TP sets off into multi-objective transportation problem (MOTP).

Apart from the transportation cost, a fixed cost, sometimes called set-up cost, is taken only when solution appears with positive level and such a problem is termed as fixed-charge transportation problem (FCTP) and it is associated with 0-1 variable. For transporting some quantity, there exist landing fees at an airport, toll charges on a highway, renting cost of a vehicle, set up cost for machines in manufacturing environment, etc. which are called as fixed-charge. In the presence of such costs, the TP is called FCTP. FCTP corresponds with two types of cost, one is direct cost and another is fixed-charge where fixed-charge occurs for transportation activity in source–destination pair which is independent on transportation amount, and for direct cost, it is dependent on transportation amount for each source to each destination.

Aside from source constraints and destination constraints in classical TP, another type of constraints named as conveyance constraints are added in TP, and then, new TP is entitled as solid transportation problem (STP). Haley [10] analyzed STP formerly. Different types of conveyances, e.g., trucks, goods train, ships, cargo flights, etc. are used for transporting a homogeneous product from one source to another destination in many circumstances. Therefore, when a single type conveyance is used in a FCTP, then the TP is refereed as fixed-charge solid transportation problem (FCSTP).

For analyzing TP based on real-life situation, the transportation cost, fixed cost, supply, demand parameters, and conveyance are not always precise due to incomplete information. Therefore, uncertainty appears in various applications, such as:

• (i) Market situation fluctuates for all time, so the demand cannot be clearly determined at any stage.

• (ii) Decision-maker (DM) has some limitations in ability to tackle the related transportation cost whenever uncertainty occurs.

• (iii) Sometimes, DM cannot make up the delivery time for uncertain situation.

Fuzzy system provides only the degree of membership function of the objective function and constraints. Zadeh [29] first initiated fuzzy set (FS), and Zimmermann [30] defined fuzzy linear programming for multi-objective decision-making problem. When the existence of hesitation is occurred, then the classical fuzzy TP is not capable to tackle the situation. Therefore, to analyze this situation, we incorporate intuitionistic fuzzy (IF) environment in our proposed method. Angelov [1] first brought out the optimization abstraction in IF environment. Intuitionistic Fuzzy Set (IFS) is an extension of FS and an important fact that clearly defines the difference between the degree of acceptance function and the degree of non-acceptance function of an element in the set. Again, the total sum of acceptance value and non-acceptance value of objective function and constraints always lies between 0 and 1. To sketch the imprecise concept and to integrate hesitancy of membership function, Atanassov [2] analyzed the concept of IFS. Wan and Li [28] represented Atanassov’s intuitionistic fuzzy programming (IFP) with truth degrees for heterogeneous multi-attribute group decision-making problem. All the required abbreviations are presented in Table 1.

Table 1 Abbreviations

The major contributions of our presented approach are as follows:

• (i) In FCSTP, all the parameters and variables are considered as intuitionistic fuzzy numbers (IFNs).

• (ii) For solving the presented multi-objective fixed-charge solid transportation problem (MOFCSTP), we use linear membership and non-membership functions.

• (iii) $(\alpha ,\beta )$-cut is applied to convert the intuitionistic fuzzy transportation problem (IFTP) into an interval-valued transportation problem (IVTP).

• (iv) IVTP transforms into crisp TP by utilizing the accuracy function of the objective function.

• (v) Since different values of $\alpha$ and $\beta$ allocate different solutions, therefore, to find a better solution, DM selects the values of $\alpha$ and $\beta$, such that $\alpha +\beta \le 1$.

• (vi) For finding best Pareto-optimal solutions, we use three methods, such as fuzzy programming (FP), IFP, and goal programming (GP).

The remaining paper is depicted as follows. “Related work” interprets the related work of our proposed model. The basic preliminaries with IFS are defined in “Preliminaries”. “Mathematical model” represents the mathematical model of MOFCSTP with fully IF and thereafter interval problem and crisp problem defined in two models. Three methods, namely FP, IFP, and GP, with related models are illustrated in “Solution procedure”. A numerical example is described in “Numerical example”. “Results and discussion” provides the results and discussion. Sensitivity analysis is interpreted in “Sensitivity analysis”. “Drawbacks of existing methods and contributions with limitations of our method” specifies about the drawbacks of the existing methods and the advantages with limitations of the proposed study. “Conclusion and future research scopes” outlines the conclusions with future research scopes.

Related work

Several papers are available with inexplicit data for solving MOTP. A few of them are included with the works. TP with linear programming problem is called Hitchcock–Koopmans TP as Hitchcock [12] in his famous paper where he described transportation model. Gupta et al. [9] displayed a TP with multiple objectives that optimized by parameter estimation. They inserted gamma distribution on this stochastic capacitated problem. Maity and Roy [14] represented a TP by considering interval goal and utility function which also extended with multiple objectives. In uncertain situation, an MOTP that included cost reliability was analyzed by Maity et al. [15]. Maity and Roy [16] represented multi-choice programming on a fuzzy MOTP. Malik and Gupta [17] solved a problem of transportation system with multiple objectives which was initiated on fully interval-valued IF environment. Roy and Maity [22] solved a single objective multi-choice TP which incorporated cost and time function. In the presence of multiple objectives, multi-choice, and interval goal, a TP was interpreted by Roy et al. [23] and the solution of the problem was covered by conic scalarization approach.

The literature review provides some exact methods for solving FCTP. FCTP was first introduced by Hirsch and Dantzig [11]. Midya and Roy [18] applied interval programming to a TP with fixed-charge in the situation of interval and rough interval environment. Midya et al. [19] extended an FCTP in IF environment for green supply chain. Also, the problem was augmented by considering multiple stages and conveyance constraints. A TP with fixed-charge and multiple objectives was interpreted by Roy and Midya [25] in IF environment, and they solved the problem by comprising product blending constraints and conveyance constraints.

From literature, we see that there exist various extensions of STP. Das et al. [5] provided a green STP-location problem with multiple objectives that analyzed by fuzzy and non-fuzzy techniques for carbon emission tax, cap, and offset policy including an extra condition as dwell time in type-2 IF environment. Rani and Gulati [21] proposed STP with uncertain environment.

A good number of researchers worked in MOTP in different uncertain situations such as fuzzy environment, IF environment, etc. Atanassov and Gargov [3] represented interval-valued IFSs. Ebrahimnejad [6] represented fuzzy TP with Left and Right (LR) flat fuzzy numbers.

Ebrahimnejad and Verdegay [7] newly proposed a TP in fully IF environment. Garg [8] proposed a new ranking approach on normal intuitionistic sets that applied for the ranking of multi-attribute decision-making process and the approach completed on crisp and interval environment. Kumar and Hussian [13] briefly explained a method to solve TP with fully IF background. Niu et al. [20] developed a multiple criteria decision-making approach in IF situation by the consideration of interval-valued and double risk parameters. Roy et al. [24] analyzed an MOTP with IF uncertainty. Singh and Yadav [26] proposed a new method for finding solution of IF type-2 TP. Ulucay et al. [27] introduced IF multiple numbers on multi-criteria decision-making problems in trapezoidal fuzzy number. Some remarkable research works on MOTP are depicted in Table 2.

Table 2 Some remarkable research works of TP in tabulated form

Preliminaries

Some related definitions and basic elementary operations are introduced here. Also, these definitions and operations are all based on IFNs.

Definition 1

[2] Let X be a universal set, and then, an IFS, $\tilde{A}^I$ in X is given by: $\tilde{A}^I=\{\langle x,\mu _{\tilde{A}^I}(x),\gamma _{\tilde{A}^I}(x)\rangle : x\in X\}$, where $\mu _{\tilde{A}^I}(x),\gamma _{\tilde{A}^I}(x): X \rightarrow [0,1]$ are the degrees of membership and of non-membership that satisfy: $0\le \mu _{\tilde{A}^I}(x)+\gamma _{\tilde{A}^I}(x)\le 1$, $x\in X$. Again the degree of hesitation of an element x in the set $\tilde{A}^I$ is defined as function $\pi _{\tilde{A}^I}(x)=1-\mu _{\tilde{A}^I}(x)-\gamma _{\tilde{A}^I}(x)$. When $\pi _{\tilde{A}^I}(x)=0,~x\in X$, then the IFS transforms into an FS.

Definition 2

[2] Consider a non-empty set X and two IFSs $\tilde{A}^I$, $\tilde{B}^I$ in X which are given by $\tilde{A}^I=\{\langle x,\mu _{\tilde{A}^I}(x),\gamma _{\tilde{A}^I}(x)\rangle : x\in X\}$ and $\tilde{B}^I = \{\langle x ,\mu _{\tilde{B}^I}(x),\gamma _{\tilde{B}^I}(x)\rangle : x\in X\}$, respectively. Then, the following properties hold:

3.2.1: $\tilde{A}^I\subseteq \tilde{B}^I$ if and only if $\mu _{\tilde{A}^I}(x)\le \mu _{\tilde{B}^I}(x)$ and $\gamma _{\tilde{A}^I}(x)\ge \gamma _{\tilde{B}^I}(x)$ $\forall ~x \in X.$

3.2.2: $\tilde{A}^I\bigcap \tilde{B}^I=\{\langle x, \min (\mu _{\tilde{A}^I}(x),\mu _{\tilde{B}^I}(x)), \max (\gamma _{\tilde{A}^I}(x),\gamma _{\tilde{B}^I}(x))\rangle : x\in X\}$.

3.2.3: $\tilde{A}^I\bigcup \tilde{B}^I=\{\langle x,\max (\mu _{\tilde{A}^I}(x),\mu _{\tilde{B}^I}(x)), \min (\gamma _{\tilde{A}^I}(x),\gamma _{\tilde{B}^I}(x))\rangle : x\in X\}$.

Definition 3

[2] The Atanassov’s interval-valued intuitionistic fuzzy (IVIF) set can be defined as: ${\overline{A}}^I = \{\langle x,[\mu _{\tilde{A}^I}^l(x),\mu _{\tilde{A}^I}^u(x)],$ $[\gamma _{\tilde{A}^I}^l(x),\gamma _{\tilde{A}^I}^u(x)]\rangle : x\in X\}$, where $0\le \mu _{\tilde{A}^I}^l(x)\le \mu _{\tilde{A}^I}^u(x)\le 1$, $0\le \gamma _{\tilde{A}^I}^l(x) \le \gamma _{\tilde{A}^I}^u(x)\le 1$, $0\le \mu _{\tilde{A}^I}^l(x)+\gamma _{\tilde{A}^I}^u(x)\le 1$. $\mu _{\tilde{A}^I}^l(x), \gamma _{\tilde{A}^I}^l(x)$ are lower bounds and $\mu _{\tilde{A}^I}^u(x), \gamma _{\tilde{A}^I}^u(x)$ are upper bounds of membership and non-membership function, respectively, of the IFS $\tilde{A}^I$.

Definition 4

When the membership value and non-membership value of an IFS $\tilde{A}^I$ are equal to 1 and 0, respectively, for any point $x_0$, then the set is said to be normal. That is, for any point $x_0$, such that $\mu _{\tilde{A} ^I}(x_0)=1$ and $\gamma _{\tilde{A}^I}(x_0)=0.$

Definition 5

An IF subset $\tilde{A}^I$ of real numbers is said to be IFN $\hat{A}^I$ that satisfies the following results:

3.5.1: $\tilde{A}^I$ is normal, i.e., $\exists ~x\in X$, such that $\mu _{\tilde{A} ^I}(x)=1$.

3.5.2: $\tilde{A}^I$ is convex, i.e., for the membership function $\mu _{\tilde{A}^I}(x)$ with $\mu _{\tilde{A}^I}[\lambda x_1+(1-\lambda ) x_2]\ge \min \{\mu _{\tilde{A}^I}(x_1),\mu _{\tilde{A}^I}(x_2)\}$ for $x_1, x_2\in \mathbb {R},~\lambda \in [0,1]$.

3.5.3: $\tilde{A}^I$ is concave, i.e., for the non-membership function $\gamma _{\tilde{A}^I}(x)$ with $\gamma _{\tilde{A}^I}[\lambda x_1+(1-\lambda ) x_2]\le \max \{\gamma _{\tilde{A}^I}(x_1),\gamma _{\tilde{A}^I}(x_2)\}$ for $x_1, x_2\in \mathbb {R} ,~\lambda \in [0,1]$.

Definition 6

Consider two Atanassov’s IVIF sets $\overline{A}^I$ and $\overline{B}^I$ in the universal set X, where $\overline{A}^I$ and $\overline{B}^I$ are defined as $\overline{A}^I= \{\langle x,[\mu _{\tilde{A}^I}^l(x),\mu _{\tilde{A}^I}^u(x)], [\gamma _{\tilde{A}^I}^l(x),\gamma _{\tilde{A}^I}^u(x)]\rangle :x\in X\}$ and $\overline{B}^I= \{\langle x,[\mu _{\tilde{B}^I}^l(x),\mu _{\tilde{B}^I}^u(x)], [\gamma _{\tilde{B}^I}^l(x),\gamma _{\tilde{B}^I}^u(x)]\rangle :x\in X\}.$ The operations of IVIF sets $\overline{A}^I$ and $\overline{B}^I$ are given as:

3.6.1: $\overline{A}^I$+$\overline{B}^I$ = $\{\langle x,[\mu _{\tilde{A}^I}^l(x)+\mu _{\tilde{B}^I}^l(x)- \mu _{\tilde{A}^I}^l(x)\mu _{\tilde{B}^I}^l(x)$, $\mu _{\tilde{A}^I}^u(x)+\mu _{\tilde{B}^I}^u(x)- \mu _{\tilde{A}^I}^u(x)\mu _{\tilde{B}^I}^u(x)]$, $[\gamma _{\tilde{A}^I}^l(x)\gamma _{\tilde{B}^I}^l(x), \gamma _{\tilde{A}^I}^u(x)\gamma _{\tilde{B}^I}^u(x)]\rangle :x\in X\}$.

3.6.2: $\overline{A}^I.\overline{B}^I$ = $\{\langle x,[\mu _{\tilde{A}^I}^l(x)\mu _{\tilde{B}^I}^l(x),$ $\mu _{\tilde{A}^I}^u(x)\mu _{\tilde{B}^I}^u(x)],$ $[\gamma _{\tilde{A}^I}^l(x)+\gamma _{\tilde{B}^I}^l(x)-\gamma _{\tilde{A}^I}^l(x)\gamma _{\tilde{B}^I}^l(x),$ $\gamma _{\tilde{A}^I}^u(x)+\gamma _{\tilde{B}^I}^u(x) -\gamma _{\tilde{A}^I}^u(x)\gamma _{\tilde{B}^I}^u(x)]\rangle :x\in X\}$.

3.6.3: $r.\overline{A}^I$ = $\{\langle x,[1-(1-\mu _{\tilde{A}^I}^l(x))^r,1-(1-\mu _{\tilde{A}^I}^u(x))^r],$ $[\gamma _{\tilde{A}^I}^l(x)^r,\gamma _{\tilde{A}^I}^l(x)^r]\rangle :x\in X\},~r\ge 0$.

3.6.4: $\overline{A}^I=\overline{B}^I$ if and only if $\mu _{\tilde{A}^I}^l(x)=\mu _{\tilde{B}^I}^l(x),~ \mu _{\tilde{A}^I}^u(x)=\mu _{\tilde{B}^I}^u(x),~ \gamma _{\tilde{A}^I}^l(x)=\gamma _{\tilde{B}^I}^l(x),~ \gamma _{\tilde{A}^I}^u(x) =\gamma _{\tilde{B}^I}^u(x).$

Definition 7

If a Triangular Intuitionistic Fuzzy Number (TIFN) is of the form $\hat{A}^I=(a_1,a_2,a_3;{\overline{a}}_1,a_2,{\overline{a}}_3)$, where $({\overline{a}}_1\le a_1\le a_2\le a_3\le {\overline{a}}_3)$, then the membership and non-membership functions of $\hat{A}^I$ are defined as:

$$\begin{aligned} \mu _{\hat{A}^I}(x)= & {} \left\{ \begin{array}{ll} \frac{x-{a_1}}{{a_2}-{a_1}},&{}\text{ if } \quad {a_1}\le {x}\le {a_2},\\ \frac{{a_3}-x}{{a_3}-{a_2}},&{}\text{ if } \quad {a_2}\le {x}\le {a_3},\\ 0 ,&{} \text{ otherwise, } \end{array} \right. \\&\text{ and } \gamma _{\hat{A}^I}(x)=\left\{ \begin{array}{ll} \frac{{a_2}-x}{{a_2}-{{\overline{a}}_1}},&{}\text{ if } \quad {{\overline{a}}_1}\le {x}\le {a_2} ,\\ \frac{x-{a_2}}{{{\overline{a}}_3}-{a_2}},&{}\text{ if } \quad {a_2}\le {x}\le {{\overline{a}}_3}, \\ 1 ,&{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

The graphical presentation of membership and non-membership function of TIFN is interpreted by Fig. 1.

Fig. 1

Graphical presentation of TIFN

Arithmetic operations on TIFNs:

Let two TIFNs be $\hat{A}^I=(a_1,a_2,a_3;{\overline{a}}_1,a_2,{\overline{a}}_3)$ and $\hat{B}^I=(b_1,b_2,b_3;{\overline{b}}_1,b_2,{\overline{b}}_3)$. Then, the arithmetic operations are defined as follows:

Addition $\hat{A}^I+\hat{B}^I=(a_1+b_1,a_2+b_2,a_3+b_3;{\overline{a}}_1+{\overline{b}}_1,a_2+b_2, {\overline{a}}_3+{\overline{b}}_3)$.

Subtraction $\hat{A}^I-\hat{B}^I=(a_1-b_3,a_2-b_2,a_3-b_1;{\overline{a}}_1-{\overline{b}}_3,a_2-b_2, {\overline{a}}_3-{\overline{b}}_1).$

Multiplication $\hat{A}^I.\hat{B}^I=(\min \{a_1b_1,a_1b_3,a_3b_1,a_3b_3\}, a_2b_2, \max \{a_1b_1,a_1b_3,a_3b_1,a_3b_3\}; \min \{{\overline{a}}_1{\overline{b}}_1,{\overline{a}}_1{\overline{b}} _3,{\overline{a}}_3{\overline{b}}_1, {\overline{a}}_3{\overline{b}}_3\}, a_2b_2, \max \{{\overline{a}}_1{\overline{b}}_1,{\overline{a}}_1{\overline{b}} _3,{\overline{a}}_3{\overline{b}}_1, {\overline{a}}_3{\overline{b}}_3\})$.

Scalar multiplication Scalar multiplication for any real k is defined as $k\hat{A}^I=(ka_1,ka_2,ka_3;k{\overline{a}}_1,ka_2, k{\overline{a}}_3)$ if $k\ge 0$, and $(ka_3,ka_2,ka_1;k{\overline{a}}_3,ka_2, k{\overline{a}}_1)$ if $k< 0.$

Inequality of TIFNs $\hat{A}^I=(a_1,a_2,a_3;{\overline{a}}_1,a_2, {\overline{a}}_3)\le \hat{B}^I=(b_1,b_2,b_3;{\overline{b}}_1,b_2, {\overline{b}}_3)$ if and only if $a_1\le b_1,a_2\le b_2,a_3\le b_3,{\overline{a}}_1\le {\overline{b}}_1, {\overline{a}}_3\le {\overline{b}}_3,$ where $\hat{A}^I$ and $\hat{B}^I$ are TIFNs.

Definition 8

$(\alpha ,\beta )$-cut of a TIFN $\hat{A}^I=(a_1,a_2,a_3;{\overline{a}}_1,a_2,{\overline{a}}_3)$ is the set of all x whose degree of membership is greater than or equal to $\alpha$ and degree of non-membership is less than or equal to $\beta$. That is defined by ${\hat{A}^I}_{(\alpha ,\beta )}=\{x:\mu _{\hat{A}^I}(x)\ge \alpha$ and ${\gamma _{\hat{A}^I}(x)} \le \beta ,(\alpha +\beta )\le 1:x\in X\}$.

Now, $\mu _{\hat{A}^I}(x)\ge \alpha$, which implies that $\frac{x-a_1}{a_2-a_1}\ge \alpha ,~\frac{a_3-x}{a_3-a_2}\ge \alpha$. And $x\ge {a_1+\alpha (a_2-a_1)},~x\le {a_3-\alpha (a_3-a_2)}$. Therefore, the $\alpha$-cut of ${\hat{A}^I}$ is $[a_1+\alpha (a_2-a_1),a_3-\alpha (a_3-a_2)]$.

Again $\gamma _{\hat{A}^I}(x)\le \beta$, which implies that $\frac{a_2-x}{a_2-{\overline{a}}_1}\le \beta ,~\frac{x-a_2}{{\overline{a}}_3-a_2}\le \beta$. And $x\ge {a_2-\beta (a_2-{\overline{a}}_1)},~x\le {a_2+ \beta ({\overline{a}}_3-a_2)}$. Therefore, the $\beta$-cut of ${\hat{A}^I}$ is $[a_2-\beta (a_2-{\overline{a}}_1),a_2 +\beta ({\overline{a}}_3-a_2)]$.

Denoting $\alpha$-cut of ${\hat{A}^I}$ as $[\mu _{\hat{A}^I}^l,\mu _{\hat{A}^I}^u]= [a_1+\alpha (a_2-a_1),a_3 -\alpha (a_3-a_2)]$ and $\beta$-cut of ${\hat{A}^I}$ as $[\gamma _{\hat{A}^I}^l,\gamma _{\hat{A}^I}^u]= [a_2-\beta (a_2-{\overline{a}}_1),a_2+\beta ({\overline{a}}_3-a_2)]$. $(\alpha ,\beta )$-cut of a TIFN is explained graphically in Fig. 2.

Fig. 2

$(\alpha ,\beta )$-cut of a TIFN

Definition 9

Consider a TIFN $\hat{A}^I=(a_1,a_2,a_3;{\overline{a}}_1,a_2,{\overline{a}}_3)$. Then, the accuracy function is $M(\hat{A}^I)$: ${\overline{X}}(\hat{A}^I) \rightarrow \mathbb {R}$, where ${\overline{X}}(\hat{A}^I)$ is the collection of all IVIF sets obtained from $(\alpha , \beta )$-cut. This accuracy function is defined in terms of the IVIF set ${\overline{X}}(\hat{A}^I)$ = $\langle [\mu _{\hat{A}^I}^l,\mu _{\hat{A}^I}^u],[\gamma _{\hat{A}^I}^l, \gamma _{\hat{A}^I}^u]\rangle$ as follows: $M(\hat{A}^I)$ = $\frac{\mu _{\hat{A}^I}^l+\mu _{\hat{A}^I}^u+\gamma _{\hat{A}^I}^l+ \gamma _{\hat{A}^I}^u}{2}$.

Mathematical model

We consider an MOFCSTP (here three objective functions) where the transportation cost with fixed-charge from each source to each destination is represented by first objective function. The second objective function is the deterioration rate of goods and the third one is the transporting time of goods. Here, we assume that all the parameters are IFNs for realistic situation. The shipping cost is $\hat{c}_{ijk}^I$ per unit item for transforming a homogeneous product from ith source to jth destination using any of the kth conveyance. The optimal solutions are obtained by optimizing all the objective functions concurrently based on real situation. The fixed-charge is $\hat{f}_{ijk}^I$ for shipping product from supplier i to customer j by means of k conveyance. Each supplier $(i=1,2,\ldots ,m)$ has $\hat{a}_i^I$ units of supply, each customer $(j=1,2,\ldots ,n)$ has $\hat{b}_j^I$ units of demand, and each conveyance $(k=1,2,\ldots ,l)$ has $\hat{e}_k^I$ units of capacity. The following notations and assumptions are considered to describe our proposed mathematical model as:

Notations

•   $\hat{x}_{ijk}^I:$   IF amount of product that transported from ith source to jth destination through kth conveyance,

•   $\hat{c}_{ijk}^I:$   IF cost for unit quantity of the product that transported from ith source to jth destination through kth conveyance,

•   $\hat{f}_{ijk}^I:$   IF fixed-charge for unit quantity of the product that transported from ith source to jth destination through kth conveyance,

•   $\hat{d}_{ijk}^I:$   IF deterioration rate for unit quantity of the product that transported from ith source to jth destination through kth conveyance,

•   $\hat{t}_{ijk}^I:$   IF time of transportation for unit quantity of the product that transported from ith source to jth destination through kth conveyance,

•   ${y}_{ijk}^s:$   Binary variable taking the value“1” if the source i used and “0” otherwise, for $s=1,2,3,1',3'$,

•   ${\eta }_{ijk}^s:$   Binary variable taking the value“1” if the source i used and “0” otherwise, for $s=1,2,3,1',3'$,

•   $\hat{a}_{i}^I:$   The IF supply at ith source,

•   $\hat{b}_{j}^I:$   The IF demand at jth destination,

•   $\hat{e}_{k}^I:$   The IF capacity of kth conveyance for the TP,

•   $\hat{Z}_{r}^I:$   The IF objective function $(r=1,2,3)$,

•   $\overline{Z}_r^I:$   The interval-valued objective function $(r=1,2,3)$,

•   $Z_r:$   The objective function $(r=1,2,3)$ in crisp nature, where $Z_r=M(\hat{Z}_r^I)$.

Assumptions

• $\hat{x}_{ijk}^I=({{x}^1_{ijk},{x}^2_{ijk},{x}^3_{ijk};{x}^{1'}_{ijk},{x}^2_{ijk},{x}^{3'}_{ijk}})$, $\hat{y}_{ijk}^I=({{y}^1_{ijk},{y}^2_{ijk},{y}^3_{ijk};{y}^{1'}_{ijk},{y}^2_{ijk},{y}^{3'}_{ijk}})$,

• $\hat{\eta }_{ijk}^I=({{\eta }^1_{ijk},{\eta }^2_{ijk},{\eta }^3_{ijk};{\eta }^{1'}_{ijk},{\eta }^2_{ijk}, {\eta }^{3'}_{ijk}})$, $\hat{c}_{ijk}^I=({{c}^1_{ijk},{c}^2_{ijk},{c}^3_{ijk};{c}^{1'}_{ijk},{c}^2_{ijk},{c}^{3'}_{ijk}})$,

• $\hat{d}_{ijk}^I=({{d}^1_{ijk},{d}^2_{ijk},{d}^3_{ijk};{d}^{1'}_{ijk},{d}^2_{ijk},{d}^{3'}_{ijk}})$, $\hat{t}_{ijk}^I=({{t}^1_{ijk},{t}^2_{ijk},{t}^3_{ijk};{t}^{1'}_{ijk},{t}^2_{ijk},{t}^{3'}_{ijk}})$,

• $\hat{f}_{ijk}^I=({{f}^1_{ijk},{f}^2_{ijk},{f}^3_{ijk};{f}^{1'}_{ijk},{f}^2_{ijk},{f}^{3'}_{ijk}})$,

• ${x}^s_{ijk}\ge 0,~{y}^s_{ijk}\ge 0,{\eta }^s_{ijk}\ge 0,~{c}^s_{ijk}\ge 0,~{d}^s_{ijk}\ge 0,~{t}^s_{ijk}\ge 0,~{f}^s_{ijk}\ge 0$, $(s=1,2,3,1',3')$,

• $y^s_{ijk}=\left\{ \begin{array}{ll} 1,&{}\text{ if } \quad x^s_{ijk}>0,\\ \nonumber 0,&{} \text{ otherwise, } \\ \end{array} \right. \text{ and } \eta ^s_{ijk}=\left\{ \begin{array}{ll} 1,&{}\text{ if } \quad x^s_{ijk}>0,\\ \nonumber 0,&{} \text{ otherwise. } \\ \end{array} \right.$

The mathematical model for MOFCSTP with fully IFN is presented here as:

Model 1

$$\begin{aligned} \text{ minimize }&\hat{Z_1}^I=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l [(\hat{c}_{ijk}^I \otimes \hat{x}_{ijk}^I)\oplus (\hat{f}_{ijk}^I\otimes \hat{y}_{ijk}^I)]\nonumber \\ \end{aligned}$$

(4.1)

$$\begin{aligned} \text{ minimize }&\hat{Z_2}^I=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l(\hat{d}_{ijk}^I \otimes \hat{x}_{ijk}^I)\end{aligned}$$

(4.2)

$$\begin{aligned} \text{ minimize }&\hat{Z_3}^I=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l(\hat{t}_{ijk}^I \otimes \hat{\eta }_{ijk}^I)\end{aligned}$$

(4.3)

$$\begin{aligned} \text{ subject } \text{ to }&\sum _{j=1}^n\sum _{k=1}^l \hat{x}_{ijk}^I \le \hat{a}_{i}^I ~~(i=1,2,\ldots ,m),\end{aligned}$$

(4.4)

$$\begin{aligned}&\sum _{i=1}^m\sum _{k=1}^l \hat{x}_{ijk}^I \ge \hat{b}_j^I ~~(j=1,2,\ldots ,n),\end{aligned}$$

(4.5)

$$\begin{aligned}&\sum _{i=1}^m\sum _{j=1}^n \hat{x}_{ijk}^I \le \hat{e}_k^I ~~(k=1,2,\ldots ,l),\end{aligned}$$

(4.6)

$$\begin{aligned}&{{x}^s_{ijk}}\ge 0, \forall ~i,~j,~k ~\text{ and }~s=1,2,3,1',3' . \end{aligned}$$

(4.7)

The feasibility conditions of TP are as follows:

$$\begin{aligned} \sum _{i=1}^m \hat{a}_i^I\ge \sum _{j=1}^n \hat{b}_j^I; ~\sum _{k=1}^l \hat{e}_k^I\ge \sum _{j=1}^n\hat{b}_j^I. \end{aligned}$$

This problem is of IF nature. Therefore, transforming the above problem into interval-valued intuitionistic fuzzy transportation problem (IVIFTP) using $(\alpha , \beta )$-cut of the objective function and with the help of membership and non-membership functions. Also utilizing inequality of IFNs, we transform all the IF constraints of Model 1 into crisp constraints of Model 2. Therefore, the IVIFTP is described as:

Model 2

$$\begin{aligned} \text{ minimize }&\overline{Z}_1^I=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l \Bigg [\Bigg (\Bigg [\mu _{\hat{c}_{ijk}^I\otimes {\hat{x}_{ijk}^I}}^l,\mu _{\hat{c}_{ijk}^I\otimes {\hat{x}_{ijk}^I}}^u];\nonumber \\&\quad \Bigg [\gamma _{\hat{c}_{ijk}^I\otimes {\hat{x}_{ijk}^I}}^l,\gamma _{\hat{c}_{ijk}^I\otimes {\hat{x}_{ijk}^I}}^u\Bigg ]\Bigg ) \nonumber \\&\quad + \Bigg (\Bigg [\mu _{\hat{f}_{ijk}^I\otimes {\hat{y}_{ijk}^I}}^l,\mu _{\hat{f}_{ijk}^I\otimes {\hat{y}_{ijk}^I}}^u]; \Bigg [\gamma _{\hat{f}_{ijk}^I\otimes {\hat{y}_{ijk}^I}}^l,\gamma _{\hat{f}_{ijk}^I\otimes {\hat{y}_{ijk}^I}}^u\Bigg ]\Bigg )\Bigg ] \nonumber \\ \text{ minimize }&\overline{Z}_2^I=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l \Bigg (\Bigg [\mu _{\hat{d}_{ijk}^I\otimes {\hat{x}_{ijk}^I}}^l,\mu _{\hat{d}_{ijk}^I\otimes {\hat{x}_{ijk}^I}}^u];\nonumber \\&\quad \Bigg [\gamma _{\hat{d}_{ijk}^I\otimes {\hat{x}_{ijk}^I}}^l,\gamma _{\hat{d}_{ijk}^I\otimes {\hat{x}_{ijk}^I}}^u\Bigg ]\Bigg ) \nonumber \\ \text{ minimize }&\overline{Z}_3^I=\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l \Bigg (\Bigg [\mu _{\hat{t}_{ijk}^I\otimes {\hat{\eta }_{ijk}^I}}^l,\mu _{\hat{t}_{ijk}^I\otimes {\hat{\eta }_{ijk}^I}}^u\Bigg ];\nonumber \\&\quad \Bigg [\gamma _{\hat{t}_{ijk}^I\otimes {\hat{\eta }_{ijk}^I}}^l,\gamma _{\hat{t}_{ijk}^I\otimes {\hat{\eta }_{ijk}^I}}^u]\Bigg ) \nonumber \\ \text{ subject } \text{ to }&\sum _{j=1}^n\sum _{k=1}^l {{x}^s_{ijk}}\le {a^s_i} ~~(i=1,2,\ldots ,m),\end{aligned}$$

(4.8)

$$\begin{aligned}&\sum _{i=1}^m\sum _{k=1}^l {{x}^s_{ijk}}\ge {b^s_j} ~~(j=1,2,\ldots ,n),\end{aligned}$$

(4.9)

$$\begin{aligned}&\sum _{i=1}^m\sum _{j=1}^n {{x}^s_{ijk}}\le {e^s_k} ~~(k=1,2,\ldots ,l),\end{aligned}$$

(4.10)

$$\begin{aligned}&{{x}^{1}_{ijk}}\ge {{x}^{1'}_{ijk}},~{{x}^{2}_{ijk}}\ge {{x}^{1}_{ijk}}, ~{{x}^{3}_{ijk}}\ge {{x}^{2}_{ijk}},~{{x}^{3'}_{ijk}}\ge {{x}^{3}_{ijk}},\end{aligned}$$

(4.11)

$$\begin{aligned}&{{x}^s_{ijk}}\ge 0,\forall ~i,~j,~k ~\text{ and }~ s=1,2,3,1',3'. \end{aligned}$$

(4.12)

Here, $[\mu _{\hat{c}_{ijk}^I\otimes \hat{x}_{ijk}^I}^l,\mu _{\hat{c}_{ijk}^I\otimes \hat{x}_{ijk}^I}^u]$ and $[\gamma _{\hat{c}_{ijk}^I\otimes \hat{x}_{ijk}^I}^l,\gamma _{\hat{c}_{ijk}^I\otimes \hat{x}_{ijk}^I}^u]$ are $(\alpha ,\beta )$-cuts, respectively, of $(\hat{c}_{ijk}^I\otimes \hat{x}_{ijk}^I)$ which is defined in Def. 3.8. Hence, these are interval-valued numbers in the form of IFN $(\hat{c}_{ijk}^I\otimes \hat{x}_{ijk}^I)$. This interval-valued MOFCSTP cannot be solved in any simple way, and therefore, we transform this interval-valued problem into crisp problem by utilizing the accuracy function of the objective function using Def. 3.9. The accuracy function corresponds to each alternative which provides the minimum value. Therefore, the interval-valued problem becomes a crisp problem and the equivalent crisp problem is given in Model 3 as:

Model 3

$$\begin{aligned} \text{ minimize }\, {{Z}_1}= & {} \frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l \bigg [(1-\alpha ){{c}_{ijk}^1} {{x}_{ijk}^1}\\&+2(\alpha -\beta +1){{c}_{ijk}^2}{{x}_{ijk}^2}+(1-\alpha ){{c}_{ijk}^3}{{x}_{ijk}^3} \\&+ {\beta }{{c}_{ijk}^{1'}}{{x}_{ijk}^{1'}}+{\beta }{{c}_{ijk}^{3'}}{{x}_{ijk}^{3'}}+ (1-\alpha ){{f}_{ijk}^1}{{y}_{ijk}^1}\\&+2(\alpha -\beta +1){{f}_{ijk}^2}{{y}_{ijk}^2} \\&+ (1-\alpha ){{f}_{ijk}^3}{{y}_{ijk}^3}+{\beta }{{f}_{ijk}^{1'}}{{y}_{ijk}^{1'}}+ {\beta }{{f}_{ijk}^{3'}}{{y}_{ijk}^{3'}}\bigg ] \\ \text{ minimize }\, {{Z}_2}= & {} \frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l\bigg [(1-\alpha ){{d}_{ijk}^1} {{x}_{ijk}^1}\\&+2(\alpha -\beta +1){{d}_{ijk}^2}{{x}_{ijk}^2}+(1-\alpha ){{d}_{ijk}^3}{{x}_{ijk}^3}\\&+{\beta }{{d}_{ijk}^{1'}}{{x}_{ijk}^{1'}}+ {\beta }{{d}_{ijk}^{3'}}{{x}_{ijk}^{3'}}\bigg ]\\ \text{ minimize }\, {{Z}_3}= & {} \frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l\bigg [(1-\alpha ){{t}_{ijk}^1} {{\eta }_{ijk}^1}\\&+2(\alpha -\beta +1){{t}_{ijk}^2}{{\eta }_{ijk}^2}+(1-\alpha ){{t}_{ijk}^3}{{\eta }_{ijk}^3}\\&+{\beta }{{t}_{ijk}^{1'}}{{\eta }_{ijk}^{1'}}+{\beta }{{t}_{ijk}^{3'}}{\beta }{{\eta }_{ijk}^{3'}}\bigg ]\\ \text{ subject } \text{ to }&{ \text{ constraints }}~(4.8){-}(4.12). \end{aligned}$$

Now, we solve Model 3 by considering each objective function separately with subject to the constraints. However, there exist distinct solutions for different objective functions which are contradict to each other. To derive the best Pareto-optimal solution, we solve Model 3 with help of three methods which are FP, IFP, and GP. These methods transform the MOTP into single objective TP. Determine the upper bound as Positive Ideal Solution (PIS) and lower bound as Negative Ideal Solution (NIS) for each objective function in the pay-off matrix, displaying in Table 3. PIS and NIS are defined as PIS = ${Z_r}^* = \min ~\{{Z_r}({X_1}^*),~{Z_r}({X_2}^*),~{Z_r}({X_3}^*)\} ~(r=1,2,3)$ and NIS = ${Z_r}' = \max ~\{{Z_r}({X_1}^*),~{Z_r}({X_2}^*),~{Z_r}({X_3}^*)\} ~(r=1,2,3)$, respectively.

Table 3 Pay-off matrix

Definition 10

Pareto-optimal solution of Model 3 is a feasible solution $x^*=({x}^*_{ijk}:i=1,2,\ldots ,m;j=1,2,\ldots ,n;k=1,2,\ldots ,l)$, such that there exists no other feasible solution $x=({x}_{ijk}:i=1,2,\ldots ,m;j=1,2,\ldots ,n;k=1,2,\ldots ,l)$ with ${Z_r}(x)\le {Z_r}(x^*),~r=1,2,3$ and ${Z_r}(x)< {Z_r}(x^*)$ for at least one r.

Solution procedure

Our proposed Model 1 is in IF nature. Transforming the IFTP into crisp problem and then find Model 3. Therefore, Model 3 is equivalent to Model 1, and hence, to obtain Pareto-optimal solution, we utilize three methods as:

• FP,

• IFP and

• GP

Now, we describe the necessary steps to solve Model 3 for each method in the following subsections.

FP

Several methods are available for solving MOTP. Among these methods, FP method is a useful method that finds the Pareto-optimal solution. Therefore, to acquire the best Pareto-optimal solution, we take the advantage of FP which is used to solve intuitionistic MOFCSTP. FP was introduced by Zimmermann [30] for solving any multi-objective linear programming problem and it is very easy for solving this type of problem. Therefore, to solve the proposed Model 3 in FP, we depict the steps as:

• Step 5.1.1: Transform the IFTP into crisp problem using $(\alpha ,\beta )$-cut and then utilizing accuracy function.

• Step 5.1.2: Solve each problem independently with subject to all constraints.

• Step 5.1.3: Select the tolerance of each objective function.

• Step 5.1.4: Determine the PIS and NIS from pay-off Table 3 and formulate the membership function corresponding to each objective function defined as: find $x=(x_1,x_2, \ldots ,x_n)^\mathrm{{T}}$, such that minimize $Z_r$ and subject to ${g}_{j}(X) \le {0}, ~(j=1,2,\ldots ,m)$ and ${x}_{i} \ge {0}, ~(i=1,2,\ldots ,n),$ with tolerance $p_r, (r=1,2,3)$. The membership function is $\mu _{{r}}^I(Z_r(x))$ which is defined as:

  $$\begin{aligned} \mu _{r}^I(Z_r(x))=\left\{ \begin{array}{ll} 1,&{}\text{ if } \quad {Z_r}\le {L_r^\mathrm{{T}}},\\ 1-\frac{{Z_r}-{L_r^\mathrm{{T}}}}{{U_r^\mathrm{{T}}}-{L_r^\mathrm{{T}}}},&{}\text{ if } \quad {L_r^\mathrm {{T}}}\le {Z_r}\le {U_r^\mathrm {{T}}}, (r=1,2,3)\\ 0 ,&{} \text{ if } \quad {Z_r}\ge {U_r^\mathrm{{T}}}. \end{array} \right. \end{aligned}$$

  Here, $U_{r}^\mathrm{{T}}$ and $L_{r}^\mathrm{{T}}$ are NIS and PIS $Z_r, (r=1,2,3)$, respectively.

• Step 5.1.5: Our goal is to maximize the degree of acceptance of each objective function, and if we denote the degree of acceptance as $\alpha$, then with the help of FP, Model 3 can be formulated as:

  Model 4A

  $$\begin{aligned} \text{ maximize }&\alpha \\ \text{ subject } \text{ to }&\mu _{r}^I(Z_r(x))\ge \alpha ,(r=1,2,3),\\&\alpha \in [0,1],\\&{\text{ constraints }}~(4.8){-}(4.12). \end{aligned}$$

  Now, Model 4A is transformed into a simplified form which is noted as Model 4B: Model 4B

  $$\begin{aligned} \text{ maximize }&\alpha \\ \text{ subject } \text{ to }&{Z_r}(x)+(U_{r}^\mathrm{{T}}-L_{r}^\mathrm{{T}})\alpha \le U_{r}^\mathrm{{T}},(r=1,2,3),\\&\alpha \in [0,1],\\&{\text{ constraints }}~(4.8){-}(4.12). \end{aligned}$$

• Step 5.1.6: Solve Model 4B by mathematical programming with parameter $\alpha$ and report the solution.

Theorem 1

If $x^*=(x_{ijk}:~i=1,2,\ldots ,m; ~j=1,2,\ldots ,n; ~k=1,2,\ldots ,l)$ is an optimal solution of Model 4B, then it is also a Pareto-optimal (non-dominated) solution of Model 3.

Proof

Let $x^*$ is not a Pareto-optimal (non-dominated) solution of Model 3. Therefore, from Definition 10, we consider that there exists at least one x, such that $Z_r(x)\le Z_r(x^*)$ for $r=1,2,3$ and $Z_r(x)< Z_r(x^*)$ for at least one r. Therefore, membership function $\mu _{{r}}^I(Z_r(x))$ is strictly decreasing with respect to the corresponding objective function ${Z_r}(x)$ in [0, 1]. Hence, $\mu _{{r}}^I(Z_r(x))\ge \mu _{{r}}^I(Z_r(x^*)) ~\forall ~r$ and $\mu _{{r}}^I(Z_r(x))>\mu _{{r}}^I(Z_r(x^*))$ for at least one r. Now, $\alpha$ = $\min ~ \{\mu _{{r}}^I(Z_r(x))\}$ $\ge \min ~\{\mu _{{r}}^I(Z_r(x^*))\}$ = $\alpha ^*$ which is a contradiction that $x^*$ is an optimal solution of Model 4B. Here, $\alpha ^*$ is the value of $\alpha$ at $x^*$. This completes the proof of the theorem. $\square$

IFP

IFP is used to solve multi-objective decision-making problem and to derive Pareto-optimal solution from this problem. In our IFP, we consider three objective functions $\hat{Z}_1^I, ~\hat{Z}_2^I$ and $\hat{Z}_3^I$. These objective functions are all IF nature, and therefore, to find the crisp form of the objective function $\hat{Z}_r^I$, $(r=1,2,3)$, we use the accuracy function. For each crisp objective function ${Z_r}$, $(r=1,2,3)$, we calculate the lower bound $L_r^\mathrm{{T}}$ and the upper bound $U_r^\mathrm{{T}}$, $(r=1,2,3)$. However, there exist distinct solutions for different objective functions which are contradict to each other. To get the best Pareto-optimal solution, we solve the problem using IFP which transforms the MOTP into single objective TP. Therefore with appropriate acceptance limit, violations of the constraints, and degree of acceptance, we formulate a crisp model. The steps of this method are depicted as follows:

• Step 5.2.1: Transform the multi-objective intuitionistic fuzzy problem into interval problem using $(\alpha ,\beta )$-cut.

• Step 5.2.2: With help of accuracy functions, interval-valued problem of Step 5.2.1 becomes crisp problem.

• Step 5.2.3: Solve the crisp problem with single objective function at a time subject to the constraints with omitting the other objective functions.

• Step 5.2.4: Derive the best value and the worst value of every objective function that are PIS and NIS from Table 3.

• Step 5.2.5: Formulate membership and non-membership functions for every objective function and then establish Model 5A as:

  $$\begin{aligned}&\mu _{r}(Z_r(x))=\left\{ \begin{array}{ll} 1,&{}\text{ if } \quad {Z_r}\le {L_r^\mathrm{{T}}},\\ 1-\frac{{Z_r}-{L_r^\mathrm{{T}}}}{{U_r^\mathrm{{T}}}-{L_r^\mathrm{{T}}}},&{}\text{ if } \quad {L_r^\mathrm {{T}}}\le {Z_r}\le {U_r^\mathrm {{T}}} , (r=1,2,3)\\ 0 ,&{} \text{ if } \quad {Z_r}\ge {U_r^\mathrm{{T}}}, \end{array} \right. \\&\text{ and } \gamma _{r}(Z_r(x))=\left\{ \begin{array}{ll} 0,&{}\text{ if } \quad {Z_r}\le {L_r^F},\\ 1-\frac{{Z_r}-{L_r^F}}{{U_r^F}-{L_r^F}},&{}\text{ if } \quad {L_r^\mathrm {{F}}}\le {Z_r}\le {U_r^\mathrm {{F}}} , (r=1,2,3)\\ 1 ,&{} \text{ if } \quad {Z_r}\ge {U_r^F} . \end{array} \right. \end{aligned}$$

  Model 5A

  $$\begin{aligned} \text{ maximize }&\mu -\gamma \\ \text{ subject } \text{ to }&\mu \le \frac{{{U}_r^\mathrm{{T}}}-{{Z}_r}}{{{U}_r^\mathrm{{T}}}-{{L}_r^\mathrm{{T}}}}, (r=1,2,3),\\&\gamma \ge \frac{{{U}_r}^F-{Z_r}}{{{U}_r^F}-{{L}_r^F}}, (r=1,2,3),\\&\mu +\gamma \le 1,~ \mu \ge \gamma ,~\mu \ge 0,~\gamma \ge 0,\\&{ \text{ constraints }}~(4.8){-}(4.12). \end{aligned}$$

  Here, ${{U}_r^\mathrm{{T}}}$ = NIS for $Z_r$ and ${{L}_r^\mathrm{{T}}}$ = PIS for $Z_r$. $U_{r}^F = U_{r}^\mathrm{{T}}$, $L_{r}^F = L_{r}^\mathrm{{T}}+p_r(U_{r}^\mathrm{{T}}-L_{r}^\mathrm{{T}}),~(r=1,2,3);$ also, $\mu$ and $\gamma$ are the degrees of acceptance and rejection, respectively. $p_r,~(r=1,2,3)$ is the acceptance limit of non-membership function. The equivalent simplified model of Model 5A is as:

  Model 5B

  $$\begin{aligned} \text{ maximize }&\mu -\gamma \\ \text{ subject } \text{ to }&{Z_r}(x)+(U_{r}^\mathrm{{T}}-L_{r}^\mathrm{{T}})\mu \le U_{r}^\mathrm{{T}},\\&{Z_r}(x)-(U_{r}^F-L_{r}^F)\gamma \le U_{r}^F,\\&\mu +\gamma \le 1,~ \mu \ge \gamma ,~\mu \ge 0,~\gamma \ge 0,\\&0\le p_r\le {{U}_r^\mathrm{{T}}}-{{L}_r^\mathrm{{T}}},~r=1,2,3,\\&{ \text{ constraints }}~(4.8){-}(4.12). \end{aligned}$$

• Step 5.2.6: Solve Model 5B using LINGO iterative scheme and obtain the Pareto-optimal solution of Model 3.

Theorem 2

If $x^*=(x_{ijk}:~i=1,2,\ldots ,m; ~j=1,2,\ldots ,n; ~k=1,2,\ldots ,l)$ is an optimal solution of Model 5B, then it is also a Pareto-optimal (non-dominated) solution of Model 3.

Proof

Let $x^*$ is not a Pareto-optimal (non-dominated) solution of Model 3. Therefore, from Definition 4.1, we consider that there exists at least one x, such that $Z_r(x)\le Z_r(x^*)$ for $r=1,2,3$ and $Z_r(x)< Z_r(x^*)$ for at least one r. Therefore, membership function $\mu (Z_r(x))$ is strictly decreasing with respect to the corresponding objective function $Z_r$ in [0, 1]. Again, the non-membership function $\gamma (Z_r(x))$ strictly increases with respect to the objective function $Z_r$ in [0, 1]. Hence, $\mu (Z_r(x))\ge \mu (Z_r(x^*)) ~\forall ~r$ and $\mu (Z_r(x))>\mu (Z_r(x^*))$ for at least one r. Similarly, $\gamma (Z_r(x))\le \gamma (Z_r(x^*)) ~\forall ~r$ and $\gamma (Z_r(x))<\gamma (Z_r(x^*))$ for at least one r. Now, $(\mu -\gamma )$ = $\min ~ \{\mu (Z_r(x)),~\gamma (Z_r(x))\}$ $\ge \min ~\{\mu (Z_r(x^*)),~\gamma (Z_r(x^*))\}$ = $(\mu ^*-\gamma ^*)$ which is a contradiction that $x^*$ is an optimal solution of Model 5B. Here, $\mu ^*$ and $\gamma ^*$ are the values of $\mu$ and $\gamma$ at $x^*$, respectively. This completes the proof of the theorem. $\square$

GP

GP is generally used for solving multi-objective decision-making problems and first presented by Charnes and Cooper [4]. This method is widely used to study the conflicting objective functions mainly and minimizes the deviation among respective goals and aspiration level of all the objective functions. DMs always choose their goals. The following steps are considered to solve the proposed model by GP.

• Step 5.3.1: Solve the MOFCSTP with single objective function separately and then omitting the other objective functions at that time.

• Step 5.3.2: Find the corresponding value of every objective function and fix the goal of every objective function.

• Step 5.3.3: Formulate Model 6 using GP.

  Model 6

  $$\begin{aligned} \text{ minimize }&\sum _{r=1}^3({{d}_{r}^+}+{d}_{r}^-)\\ \text{ subject } \text{ to }&Z_r-{d_r^+}+{d_r^-}=Z_r^g,~~(r=1,2,3),\\&{ \text{ constraints }}~(4.8){-}(4.12). \end{aligned}$$

  Here, ${d_r^+}$ and ${d_r^-}~(r=1,2,3)$ are the positive and negative deviations of the objective functions, respectively, from target values. $Z_r^g$ is the corresponding goal of the objective function $Z_r, (r=1,2,3)$.

• Step 5.3.4: Solve Model 6 using LINGO iterative scheme and derive the Pareto-optimal solution of Model 3.

Now, we depict the solution methodology of the three methods in a flowchart by Fig. 3.

Fig. 3

Flowchart of optimization algorithm

Numerical example

A fruit supply company in two states S1 and S2 supply a specific type of fruits. There also exist two companies in states D1 and D2, that are received the fruits. Each state represents a supply point and a demand point. The main aim is to transporting the fruits from supply point to destination point by minimizing total transportation cost with fixed-charge, transporting time, and deterioration rate. Due to the imprecise data of market condition, transportation time, rate of deterioration, all the cost coefficients of the objective functions, supply, demand, and conveyance are TIFNs. Also whenever shipping the materials from source to destination, a fixed-charge is added in the objective function. Hence, the transportation cost in hundred dollar ($) per unit, transportation time in hour per unit, and loss of deterioration in dollar ($) are considered by three objective functions $\hat{Z}_1^I$, $\hat{Z}_2^I$, and $\hat{Z}_3^I$, respectively. The aim of this problem is to determine the unknown quantity $\hat{x}_{ijk}^I$, that are transported from ith source to jth destination with kth conveyance with IF transportation cost $\hat{c}_{ijk}^I$, fixed-charge $\hat{f}_{ijk}^I$, deterioration rate $\hat{d}_{ijk}^I$, and time $\hat{t}_{ijk}^I$ which are given in Tables 4, 5 and 6.

Table 4 IF transportation cost $\hat{c}_{ijk}^I$ and fixed-charge ${\hat{f}_{ijk}^I}$

Table 5 IF deterioration cost $\hat{d}_{ijk}^I$

Table 6 IF transportation time ${\hat{t}_{ijk}^I}$

Source $\hat{a}_i^I$ and demand $\hat{b}_j^I$ are given in each table. We choose the values of conveyances such as $\hat{e}_1^I=(200,240,260;180,240,280)$ and $\hat{e}_2^I=(200,230,250;180,230,270)$ which are not given in tabulated form. For $(\alpha , \beta )$-cut, we arbitrarily assume the values $\alpha =0.8$ and $\beta =0.1$. Now, the mathematical form of this problem which is obtained from Model 3 is as follows:

Model 7A

$$\begin{aligned} \text{ minimize }\, {{Z}_1}= & {} \frac{1}{20}\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l \bigg [{2{c}_{ijk}^1} {{x}_{ijk}^1}+{34{c}_{ijk}^2}{{x}_{ijk}^2}\\&+{2{c}_{ijk}^3}{{x}_{ijk}^3}+ {{c}_{ijk}^{1'}}{{x}_{ijk}^{1'}}+{{c}_{ijk}^{3'}}{{x}_{ijk}^{3'}}\\&+ {2{f}_{ijk}^1}{{y}_{ijk}^1}+{34{f}_{ijk}^2}{{y}_{ijk}^2}+{2{f}_{ijk}^3}{{y}_{ijk}^3}+ {{f}_{ijk}^{1'}}{{y}_{ijk}^{1'}}\\&+{{f}_{ijk}^{3'}}{{y}_{ijk}^{3'}}\bigg ]\\ \text{ minimize }\, {{Z}_2}= & {} \frac{1}{20}\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l\bigg [{2{d}_{ijk}^1} {{x}_{ijk}^1}+{34{d}_{ijk}^2}{{x}_{ijk}^2}\\&+{2{d}_{ijk}^3}{{x}_{ijk}^3}+ {{d}_{ijk}^{1'}}{{x}_{ijk}^{1'}}+{{d}_{ijk}^{3'}}{{x}_{ijk}^{3'}}\bigg ]\\ \text{ minimize }\, {{Z}_3}= & {} \frac{1}{20}\sum _{i=1}^m\sum _{j=1}^n\sum _{k=1}^l\bigg [{2{t}_{ijk}^1} {{\eta }_{ijk}^1}+{34{t}_{ijk}^2}{{\eta }_{ijk}^2}\\&+{2{t}_{ijk}^3}{{\eta }_{ijk}^3}+ {{t}_{ijk}^{1'}}{{\eta }_{ijk}^{1'}}+{{t}_{ijk}^{3'}}{{\eta }_{ijk}^{3'}}\bigg ]\\ \text{ subject } \text{ to }&{ \text{ constraints }}~(4.8){-}(4.12). \end{aligned}$$

Therefore, using all data with $m=2, n=2, l=2$, the equivalent crisp TP with the help of accuracy function is described in Model 7B as:

Model 7B

$$\begin{aligned} \text{ minimize } \,{{Z}_1}= & {} \frac{1}{20} \bigg [{204{x}_{111}^1}+{5270{x}_{111}^2}+{516{x}_{111}^3}+ {81{x}_{111}^{1'}}\\&+{279{x}_{111}^{3'}}+ {418{x}_{112}^1}+{9180{x}_{112}^2}\\&+{666{x}_{112}^3}+ {188{x}_{112}^{1'}}+{354{x}_{112}^{3'}}\\&+ {304{x}_{121}^1}+{6936{x}_{121}^2}+{510{x}_{121}^3}+ {131{x}_{121}^{1'}}\\&+{276{x}_{121}^{3'}}+{366{x}_{122}^1}+{8364{x}_{122}^2}\\&+{616{x}_{122}^3}+ {162{x}_{122}^{1'}}+{329{x}_{122}^{3'}}+ {208{x}_{211}^1}\\&+{7004{x}_{211}^2}+{518{x}_{211}^3}+ {83{x}_{211}^{1'}}+{280{x}_{211}^{3'}}\\&+ {304{x}_{212}^1}+{6936{x}_{212}^2}+{614{x}_{212}^3}\\&+{121{x}_{212}^{1'}}+{338{x}_{212}^{3'}}+{530{x}_{221}^1} +{10406{x}_{221}^2}\\&+{718{x}_{221}^3}+ {244{x}_{221}^{1'}}+{380{x}_{221}^{3'}}\\&+{206{x}_{222}^1}+{4896{x}_{222}^2}+{372{x}_{222}^3}\\&+ {72{x}_{222}^{1'}}+{217{x}_{222}^{3'}}\bigg ]\\ \text{ minimize } \,{{Z}_2}= & {} \frac{1}{200} \bigg [{14{x}_{111}^1}+{340{x}_{111}^2}+{22{x}_{111}^3}+ {6{x}_{111}^{1'}}\\&+{12{x}_{111}^{3'}}+{18{x}_{112}^1}+{340{x}_{112}^2}+{26{x}_{112}^3}\\&+ {8{x}_{112}^{1'}}+{14{x}_{112}^{3'}}+{24{x}_{121}^1}+{442{x}_{121}^2}\\&+{30{x}_{121}^3}+ {11{x}_{121}^{1'}}+{16{x}_{121}^{3'}}+{28{x}_{122}^1}\\&+{544{x}_{122}^2}+{34{x}_{122}^3}+ {13{x}_{122}^{1'}}\\&+{18{x}_{122}^{3'}}+ {6{x}_{211}^1}+{136{x}_{211}^2}+{14{x}_{211}^3}+ {2{x}_{211}^{1'}}\\&+{8{x}_{211}^{3'}}+{8{x}_{212}^1}+{170{x}_{212}^2}+{14{x}_{212}^3}\\&+ {3{x}_{212}^{1'}}+{8{x}_{212}^{3'}}+ {16{x}_{221}^1}+{340{x}_{221}^2}\\&+{26{x}_{221}^3}+{7{x}_{221}^{1'}}+{14{x}_{221}^{3'}}+ {16{x}_{222}^1}+{340{x}_{222}^2}\\&+{24{x}_{222}^3}+ {7{x}_{222}^{1'}}+{13{x}_{222}^{3'}}\bigg ]\\ \text{ minimize } \,{{Z}_3}= & {} \frac{1}{20} \bigg [{22{x}_{111}^1}+{408{x}_{111}^2}+{28{x}_{111}^3}+ {10{x}_{111}^{1'}}\\&+{15{x}_{111}^{3'}}+ {28{x}_{112}^1}+{510{x}_{112}^2}+{34{x}_{112}^3}\\&+{13{x}_{112}^{1'}}+{18{x}_{112}^{3'}}+ {12{x}_{121}^1}+{272{x}_{121}^2}\\&+{20{x}_{121}^3}+ {5{x}_{121}^{1'}}+{11{x}_{121}^{3'}}+{16{x}_{122}^1}\\&+{306{x}_{122}^2}+{22{x}_{122}^3}+ {7{x}_{122}^{1'}}+{12{x}_{122}^{3'}}\\&+ {6{x}_{211}^1}+{204{x}_{211}^2}+{16{x}_{211}^3}+ {2{x}_{211}^{1'}}\\&+{9{x}_{211}^{3'}}+{10{x}_{212}^1}+{306{x}_{212}^2}+{22{x}_{212}^3}\\&+ {4{x}_{212}^{1'}}+{12{x}_{212}^{3'}}+ {8{x}_{221}^1}+{204{x}_{221}^2}\\&+{20{x}_{221}^3}+ {3{x}_{221}^{1'}}+{11{x}_{221}^{3'}}+ {18{x}_{222}^1}\\&+{374{x}_{222}^2}+{28{x}_{222}^3}+ {8{x}_{222}^{1'}}+{15{x}_{222}^{3'}}\bigg ] \\ \text{ subject } \text{ to }&{{x}_{111}^1+{x}_{112}^1+{x}_{121}^1+{x}_{122}^1}\le 150;~ {x}_{111}^2\\&+{x}_{112}^2+{x}_{121}^2+{x}_{122}^2\le 180;\\&\quad {{x}_{111}^3+{x}_{112}^3+{x}_{121}^3+{x}_{122}^3}\le 200;~ {x}_{111}^{1'}\\&+{x}_{112}^{1'}+{x}_{121}^{1'}+{x}_{122}^{1'}\le 130;\\&\quad {{x}_{111}^{3'}+{x}_{112}^{3'}+{x}_{121}^{3'}+{x}_{122}^{3'}}\le 220;~ {x}_{211}^1\\&+{x}_{212}^1+{x}_{221}^1+{x}_{222}^1\le 250;\\&\quad {{x}_{211}^2+{x}_{212}^2+{x}_{221}^2+{x}_{222}^2}\le 290;~ {x}_{211}^3\\&+{x}_{212}^3+{x}_{221}^3+{x}_{222}^3\le 310;\\&\quad {{x}_{211}^{1'}+{x}_{212}^{1'}+{x}_{221}^{1'}+{x}_{222}^{1'}}\le 230;~ {x}_{211}^{3'}\\&+{x}_{212}^{3'}+{x}_{221}^{3'}+{x}_{222}^{3'}\le 330;\\&\quad {{x}_{111}^1+{x}_{112}^1+{x}_{211}^1+{x}_{212}^1}\ge 240;~ {x}_{111}^2\\&+{x}_{112}^2+{x}_{211}^2+{x}_{212}^2\ge 270;\\&\quad {{x}_{111}^3+{x}_{112}^3+{x}_{211}^3+{x}_{212}^3}\ge 300;~ {x}_{111}^{1'}\\&+{x}_{112}^{1'}+{x}_{211}^{1'}+{x}_{212}^{1'}\ge 220;\\&\quad {{x}_{111}^{3'}+{x}_{112}^{3'}+{x}_{211}^{3'}+{x}_{212}^{3'}}\ge 320;~ {x}_{121}^{1}\\&+{x}_{122}^{1}+{x}_{221}^{1}+{x}_{222}^{1}\ge 160;\\&\quad {{x}_{121}^2+{x}_{122}^2+{x}_{221}^2+{x}_{222}^2}\ge 200;~ {x}_{121}^3\\&+{x}_{122}^3+{x}_{221}^3+{x}_{222}^3\ge 210;~{x}_{121}^{1'}\\&+{x}_{122}^{1'}+{x}_{221}^{1'}+{x}_{222}^{1'}\ge 140;~ {{x}_{121}^{3'}+{x}_{122}^{3'}+{x}_{221}^{3'}}\\&\quad {+{x}_{222}^{3'}}\ge 230; {{x}_{111}^1+{x}_{121}^1+{x}_{211}^1+{x}_{221}^1}\le 200;~ \\&\quad {{x}_{111}^{2}+{x}_{121}^{2}}{+{x}_{211}^{2}+{x}_{221}^{2}}\le 240;\\&\quad {{x}_{111}^3+{x}_{121}^3+{x}_{211}^3+{x}_{221}^3}\le 260;~ {x}_{111}^{1'}\\&+{x}_{121}^{1'}+{x}_{211}^{1'}+{x}_{221}^{1'}\le 180;\\&\quad {{x}_{111}^{3'}+{x}_{121}^{3'}+{x}_{211}^{3'}+{x}_{221}^{3'}}\le 280;~ {x}_{112}^1\\&+{x}_{122}^1+{x}_{212}^1+{x}_{222}^1\le 200;\\&\quad {{x}_{112}^2+{x}_{122}^2+{x}_{212}^2+{x}_{222}^2}\le 230;~ {x}_{112}^3\\&+{x}_{122}^3+{x}_{212}^3+{x}_{222}^3\le 250;\\&\quad {{x}_{112}^{1'}+{x}_{122}^{1'}+{x}_{212}^{1'}+{x}_{222}^{1'}}\le 180;~ {x}_{112}^{3'}\\&+{x}_{122}^{3'}+{x}_{212}^{3'}+{x}_{222}^{3'}\le 270;\\&\qquad { \text{ constraints }}~(4.11){-}(4.12). \end{aligned}$$

Now, we solve the above multi-objective problem by considering single objective function at a time and omitting other objective functions subject to the constraints. The values of the functions are given in Table 7 which is defined as pay-off matrix. Here, we see that all the solutions are not Pareto-optimal as they contradict to each other. Therefore, to obtain Pareto-optimal solution, we are to use proposed (three) methods which are briefly described in “Solution procedure”.

Table 7 Pay-off matrix for ${Z_r},(r=1,2,3)$

Results and discussion

In “Numerical example”, we solve a numerical problem with the help of three methods such as FP, IFP, and GP, and we obtain the best Pareto-optimal solutions which are given by tabulated form in Table 8. Here, we present the obtained optimal solutions of our formulated problem using three methods as:

FP Solving Model 7B on considering each objective function separately with subject to the constraints, we find lower bound and upper bound using the accuracy function in Table 7. Since the solutions of three objective functions are different, therefore we find an optimal solution that will minimize all the objective functions. Hence, we solve Model 4B using LINGO iterative scheme; and the Pareto-optimal solution in FP method with TIFN is $\alpha =1; {\hat{x}_{111}}^I=(0,0,20;0,0,40)$, ${\hat{x}_{112}}^I=(0,30,30;0,30,30)$, ${\hat{x}_{121}}^I=(150,150,150;130,150,150)$, ${\hat{x}_{122}}^I=(0,0,0;0,0,0)$, ${\hat{x}_{211}}^I=(40,40,40;40,40,40)$, ${\hat{x}_{212}}^I=(200,200,210;180,200,210)$, ${\hat{x}_{221}}^I=(10,50,50;10,50,50)$, ${\hat{x}_{222}}^I=(0.0,10;0,0,30)$. Therefore, the crisp values of the objective functions in FP are as: $Z_1=6860.5;Z_2=789.05;Z_3=87.3$.

IFP In IFP method, we define membership and non-membership function for three objective functions. PIS and NIS are defined in Table 7. Selecting tolerance $p_r, (r=1,2,3)$ for three membership functions in appropriate way that maximizes the membership function and minimizes the non-membership function. Using Model 5B and LINGO 13 iterative scheme, we derive the Pareto-optimal solution with TIFN of Model 7B as: $\mu =0.9999$, $\gamma =0.0000895$; ${\hat{x}_{111}}^I=(0,0,10;0,0,10)$, ${\hat{x}_{112}}^I=(0,0,0;0,0,0)$, ${\hat{x}_{121}}^I=(150,180,190;130,180,210)$, ${\hat{x}_{122}}^I=(0,0,0;0,0,0)$, ${\hat{x}_{211}}^I=(47.641,57.641,57.641;47.641,57.641,57.641)$, ${\hat{x}_{212}}^I=(192.359,212.359,232.359;172.359,212.359,252.359)$, ${\hat{x}_{221}}^I=(2.359,2.359,2.359;2.359,2.359,2.359)$, ${\hat{x}_{222}}^I=(7.641,17.641,17.641;7.641,17.641,17.641)$. The crisp values of three objective functions in IFP method are as: $Z_1=6160.35;Z_2=773.42;Z_3=82.15$.

GP Solving Model 6 in GP and taking the respective goals $Z_1^g=154550.5$, $Z_2^g=772.95$, $Z_3^g=7033$, we find the Pareto-optimal solution in TIFN as $d_1=0$, $d_2=58.45$, $d_3=2870$, ${\hat{x}_{111}}^I=(150,170,190;130,170,210)$, ${\hat{x}_{112}}^I=(0,0,0;0,0,0)$, ${\hat{x}_{121}}^I=(0,10,10;0,10,10)$, ${\hat{x}_{122}}^I= (0,0,0;0,0,0)$, ${\hat{x}_{211}}^I=(50,60,60;50,60,60)$, ${\hat{x}_{212}}^I=(40,40,50;40,40,50)$, ${\hat{x}_{221}}^I=(0,0,0;0,0,0)$, ${\hat{x}_{222}}^I=(160,190,200;140,190,220)$. Now, the crisp values of the objective functions in GP are $Z_1=6173.3,Z_2=831.4,Z_3=91.$

Discussion The obtained optimal solutions of MOFCSTP are calculated from three methods and presented in Table 8.

Table 8 Comparison of result in three methods

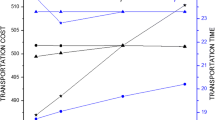
Again, a graphical presentation of the obtained solutions of three objective functions based on three programming methods is provided in Fig. 4.

Fig. 4

Achievement value of three objectives in three methods

From Table 8 and Fig. 4, a comparative study has been made among the Pareto-optimal solutions. As the problem is of minimization type, we notice that minimum value of each objective function in IFP is always less than other two methods. Therefore, we conclude that our proposed method, i.e., IFP provides more preferable result than the FP and GP.

Comparison with other state-of-art methods

To solve our proposed multi-objective model, there exist various fuzzy and non-fuzzy techniques. Fuzzy techniques are FP [21], IFP [24], Fuzzy GP [9], etc., and non-fuzzy techniques are utility function approach [14], conic scalarization approach [23], multi-choice programming [22], multi-choice GP [16], simplex algorithm [6], standard linear programming [7], etc. We select FP, IFP, and GP which have more flexibility than other state-of-art methods. Here, FP and IFP are fuzzy technique, whereas GP is non-fuzzy technique. FP is a most simplified fuzzy technique that finds Pareto-optimal solution by maximizing the membership function value. Again, IFP method is an extension of FP method that provides the solution by finding maximum membership and minimum non-membership value. When it maximizes membership function and minimizes non-membership function, then it attains most appropriate result then other fuzzy technique (such as FP) as well as non-fuzzy technique (such as GP) which were used in various articles. IFP is a better method among these methods, as this method provides not only membership value but also non-membership value. Also, there exists a facility of IFP is to choose a better solution by selecting appropriate tolerance in technically.

Sensitivity analysis

In this section, we investigate the sensitivity analysis on our proposed method, IFP, to interpret the range of the coefficients in the objective function. This is very tough to explain the range of all parameters and to find the effect of slide change by keeping the same optimal solution. Here, we initiate a simple approach [19] to analyze the sensitivity analysis of MOFCSTP with basic variables remain unchanged, though the values of the basic variables may not same. Now, the ranges of these parameters are defined by the following steps as:

• Step 1: Fixed the basic variables for the optimal solution of MOFCSTP which are obtained in IFP.

• Step 2: Varying the value of every parameter by fixing other parameters at a time and solve the Model 5B by LINGO 13.

• Step 3: Continuing Step 2, until no feasible solution appears or the basic variable changes in optimal solution.

• Step 4: Observing the range of every parameter obtained in Step 3.

  Sensitivity analysis for supply, demand, and conveyance parameters changes as:

  Let $\hat{a}_{i}^I$ turn to $\hat{a}_{i}^{I*}$ as $\hat{a}_i^{I*}=\hat{a}_i^I+\hat{\theta }_i^I, (i=1,2)$, $\hat{b}_j^I$ turn to $\hat{b}_j^{I*}$ as $\hat{b}_j^{I*}=\hat{b}_j^I+\hat{\eta }_j^{I}, (j=1,2)$ and $\hat{e}_k^{I}$ turn to $\hat{e}_k^{I*}$ as $\hat{e}_k^{I*}=\hat{e}_k^I+\hat{\tau }_k^{I}, (k=1,2)$. Here, $\hat{\theta }_i^I$, $\hat{\eta }_i^I$, and $\hat{\tau }_i^I$ are the change of initial values of parameters. Following the steps, we derive the values of $\hat{a}_i^{I*}, \hat{b}_j^{I*}$, and $\hat{e}_k^{I*}$ which are specified in Table 9.

Table 9 Ranges of supply, demand, and conveyance

Drawbacks of existing methods and contributions with limitations of our method

This section incorporates two subsections. First, subsection corresponds about the drawbacks of existing methods which are covered on TP, and second subsection focuses on the limitations of our method after defined the main advantages.

Drawbacks of existing methods

We observe from the literature review that many researchers developed several methods for solving IFTP. However, there exist some drawbacks of the methods as follows:

• Ebrahimnejad and Verdegay [7] proposed a new approach for solving fully IFTP where all the parameters are IFNs, but there exist some complexities in computation.

• Kumar and Hussain [13] presented a real-life TP with fully IF and they used ranking function which did not follow linear property. Also this method has no new concept over the existing methods in the literature and solution procedure has many complexity.

• Malik and Gupta [17] initiated fully interval-valued IF environment on MOTP and the solutions are evaluated by fuzzy GP. Hence, this problem is not included with fixed-charge, conveyance constraints. Also the solution methodology is only fuzzy technique; non-fuzzy technique is not chosen.

• Midya et al. [19] introduced an MOSTP with fixed-charge in IF environment. They considered all the parameters as IFN, but the problem is not fully IF. They solved the problem by considering two non-fuzzy techniques, but did not think about any fuzzy technique as FP, IFP, etc. Also, Roy and Midya [25] presented MOSTP with IF uncertainty, but the problem is not fully IF nature. They utilized two fuzzy techniques, which did not include any non-fuzzy technique.

• Singh and Yadav [26] represented a TP in which transportation costs are TIFNs, and supply and demand are all real numbers. They used ranking function and modified IF method for finding the basic optimal solution. Though the obtained solutions are in the form of TIFN, but this method fails whenever the demand and availability are not real numbers, such as IFNs.

Advantages and limitations of the proposed problem

The main advantages of our proposed method are given as:

• In MOFCSTP, all the parameters and variables are IFNs which accommodate more information from real-life scenario.

• Here, we use $(\alpha ,\beta )$-cut to convert the IFTP into an IVTP with a condition that DM always chooses the values $\alpha$ and $\beta$ to his/her own choice. Different values of $\alpha$ and $\beta$ provide different solutions. Since DM has a freedom to choose the values of $\alpha ,~\beta$ and, therefore, he/she selects the values of $\alpha ,~\beta$ that allocate a better solution.

• We transform the IF model into crisp model where the objective functions are in the form of interval and reducing it in crisp form with the help of accuracy function.

• To determine the Pareto-optimal solution, three methods, namely, FP, IFP, and GP, are used and then compare the obtained results of three methods.

• Our proposed method has some limitations also.

  (i) This method cannot be applied in unbalanced IFTP to obtain the IF optimal solution.

  (ii) Whenever the proposed problem is non-linear nature, our method cannot be applicable, as we use linear membership and non-membership function.

Conclusion and future research scopes

In this paper, we have considered an MOFCSTP. For realistic situations, all parameters and variables are imprecise and unpredictable. Hence, there exist some hesitations among the parameters/variables, as well as fuzzy uncertainty is not enough to tackle this situation. To analyze this situation, we have introduced IF environment with membership and non-membership function in our problem, and the problem is fully IF. Hence, the demand, availability, conveyance capacity, transportation cost, fixed-charge, deterioration rate, transportation time, and variables have been represented by TIFNs. We have used Atanassov’s IFS to express the hesitancy degree of alternative. The IF problem has been transformed into interval problem with help of $(\alpha ,\beta )$-cut, and the values of $\alpha$ and $\beta$ are chosen by the DM’s own choice. Since $\alpha$ and $\beta$ are not always fixed, therefore there exists a scope to allocate a better solution. Again, the interval problem has been reduced into crisp problem by introducing accuracy function. The formulated TP is multi-objective nature, and to extract Pareto-optimal solution, we have utilized FP, IFP, and GP. An example has been illustrated to demonstrate the applicability of our proposed method. Comparing the optimal values obtained from three methods, we have concluded that IFP provides a better result than FP and GP. In addition to that, IFP is not much complicated but more flexible and highly significant to apply in realistic balanced MOTP.

In future study, interested researchers may extend our proposed method for unbalanced TP or non-linear TP or fractional TP or neutrosophic TP, and reduce the complexity. Also, this problem can be viewed as finite time control problem or multi-item problem in uncertain environment such as type-2 fuzzy [9] or type-2 IF [5].