A generalized integro-differential theory of nonlocal elasticity of n-Helmholtz type: part I—analytical formulation and thermodynamic framework

Abstract

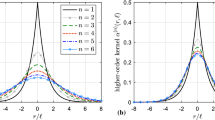
A generalized theory of nonlocal elasticity is elaborated. The proposed integral type nonlocal formulation is based on attenuation functions being assumed as the convolution product of n first order (Eringen type) kernels. The theory stems from a generalized higher-order constitutive relation between the nonlocal stress and the local strain. Inspired by the Eringen two-phase local/nonlocal integral model, this theory can also be thought of as the constitutive relation for an (n + 1)-phase material, in which one phase has local elastic behavior, and the remaining n phases comply with nonlocal elasticity of higher order. The theory is supported by a suitable thermodynamic framework. In the spirit of Eringen’s 1983 paper, the particular family of attenuation functions adopted are the Green functions associated with generalized Helmholtz type differential operators of order n —which suggests denoting this model as a generalized nonlocal elasticity theory of n-Helmholtz type. Besides the integral type nonlocal formulation, elegant and compact expressions for the differential and integro-differential counterpart are derived. For n = 1 this formulation straightforwardly leads to the Aifantis 2003 implicit gradient elasticity theory with simultaneous stress gradients and strain gradients, which was postulated to eliminate stress and strain singularities from crack tips and dislocation lines. For n = 2 an implicit gradient elasticity formulation with bi-Helmholtz type stress and strain gradients is obtained. The paper is complemented by a companion Part II on the particularization of the generalized theory of nonlocal elasticity for the one-dimensional case, along with some applications in statics and dynamics.

Appendices

Appendix 1 Expressions of the length scale parameters $\ell_{k}^{2k} (k = 1, \ldots ,n)$ for the n-Helmholtz type differential operator with multiple length scales

In this Appendix, we consider the nth order Helmholtz differential operator with multiple length scales $c_{1} \ne c_{2} \ne \ldots \ne c_{n}$. We will demonstrate Eq. (54) and we will derive the expressions of the length scale parameters $\ell_{k}^{2k} (k = 1, \ldots ,n)$ (namely $\ell_{1}^{2} ,\ell_{2}^{4} ,\ell_{3}^{6} ,\ell_{4}^{8} , \ldots$) in terms of the length scale coefficients of the n individual (factorizing) Helmholtz operators $c_{k} (k = 1,2, \ldots ,n)$ in compact form. Let us consider the definition of the nth order Helmholtz differential operator with the aid of the product operator as follows

$${\mathcal{L}}_{{\;c_{1} ,c_{2} , \ldots ,c_{n} }}^{{\;{\kern 1pt} (n)}} = {\mathcal{L}}_{H} (c_{1} ){\mathcal{L}}_{H} (c_{2} ) \cdots (n{\text{ times)}} \cdots {\mathcal{L}}_{H} (c_{n} ) = \prod\limits_{k = 1}^{n} {{\mathcal{L}}_{H} (c_{k} )}$$

(75)

in which ${\mathcal{L}}_{H} (c_{k} )[ \cdot ] = \left( {1 - c_{k}^{2} \nabla^{2} } \right)[ \cdot ]$ is the Helmholtz operator with length scale parameter $c_{k}$. For n = 2, 3 and 4 the formula (75) leads to, respectively:

• for n = 2

$${\mathcal{L}}_{{c_{1} ,c_{2} }}^{{\;{\kern 1pt} (2)}} = {\mathcal{L}}_{H} (c_{1} ){\mathcal{L}}_{H} (c_{2} ) = \left( {1 - c_{1}^{2} \nabla^{2} } \right)\left( {1 - c_{2}^{2} \nabla^{2} } \right) = 1 - \ell_{1}^{2} \nabla^{2} + \ell_{2}^{4} \nabla^{4}$$

(76)

with $\ell_{1}^{2} = c_{1}^{2} + c_{2}^{2}$ and $\ell_{2}^{4} = c_{1}^{2} c_{2}^{2}$. This result was already presented in Eq. (49) for the bi-Helmholtz differential operator ${\mathcal{L}}_{bH}$;

• for n = 3

  $${\mathcal{L}}_{{c_{1} ,c_{2} ,c_{3} }}^{{{\kern 1pt} (3)}} = {\mathcal{L}}_{H} (c_{1} ){\mathcal{L}}_{H} (c_{2} ){\mathcal{L}}_{H} (c_{3} ) = \left( {1 - c_{1}^{2} \nabla^{2} } \right)\left( {1 - c_{2}^{2} \nabla^{2} } \right)\left( {1 - c_{3}^{2} \nabla^{2} } \right) = 1 - \ell_{1}^{2} \nabla^{2} + \ell_{2}^{4} \nabla^{4} - \ell_{3}^{6} \nabla^{6}$$

  (77)

  with $\ell_{1}^{2} = c_{1}^{2} + c_{2}^{2} + c_{3}^{2}$, $\ell_{2}^{4} = c_{1}^{2} c_{2}^{2} + c_{1}^{2} c_{3}^{2} + c_{2}^{2} c_{3}^{2}$ and $\ell_{3}^{6} = c_{1}^{2} c_{2}^{2} c_{3}^{2}$;

• for n = 4

$$\begin{gathered} {\mathcal{L}}_{{c_{1} ,c_{2} ,c_{3} ,c_{4} }}^{{{\kern 1pt} (4)}} = {\mathcal{L}}_{H} (c_{1} ){\mathcal{L}}_{H} (c_{2} ){\mathcal{L}}_{H} (c_{3} ){\mathcal{L}}_{H} (c_{4} ) = \hfill \\ \left( {1 - c_{1}^{2} \nabla^{2} } \right)\left( {1 - c_{2}^{2} \nabla^{2} } \right)\left( {1 - c_{3}^{2} \nabla^{2} } \right)\left( {1 - c_{4}^{2} \nabla^{2} } \right) = 1 - \ell_{1}^{2} \nabla^{2} + \ell_{2}^{4} \nabla^{4} - \ell_{3}^{6} \nabla^{6} + \ell_{4}^{8} \nabla^{8} \hfill \\ \end{gathered}$$

(78)

with $\ell_{1}^{2} = c_{1}^{2} + c_{2}^{2} + c_{3}^{2} + c_{4}^{2}$, $\ell_{2}^{4} = c_{1}^{2} c_{2}^{2} + c_{1}^{2} c_{3}^{2} + c_{2}^{2} c_{3}^{2} + c_{1}^{2} c_{4}^{2} + c_{2}^{2} c_{4}^{2} + c_{3}^{2} c_{4}^{2}$,

$\ell_{3}^{6} = c_{1}^{2} c_{2}^{2} c_{3}^{2} + c_{1}^{2} c_{2}^{2} c_{4}^{2} + c_{1}^{2} c_{3}^{2} c_{4}^{2} + c_{2}^{2} c_{3}^{2} c_{4}^{2}$, $\ell_{4}^{8} = c_{1}^{2} c_{2}^{2} c_{3}^{2} c_{4}^{2}$.

To extend and generalize the above results up to order n, it is useful to introduce the $n \times n$ diagonal matrix collecting the squared length scale parameters $c_{j}^{2} \,(j = 1,2, \ldots ,n)$ of the individual n Helmholtz type differential operators ${\mathcal{L}}_{H} (c_{j} )$ as follows

$${\mathbf{C}} = \left[ {\begin{array}{*{20}c} {c_{1}^{2} } & 0 & \cdots & \cdots & 0 \\ 0 & {c_{2}^{2} } & 0 & \cdots & 0 \\ 0 & \ddots & {c_{j}^{2} } & \ddots & \vdots \\ \vdots & 0 & \ddots & \ddots & 0 \\ 0 & 0 & \cdots & \cdots & {c_{n}^{2} } \\ \end{array} } \right]$$

(79)

The n length scale parameters $\ell_{1} ,\ell_{2} , \ldots ,\ell_{n}$ of the resulting nth order Helmholtz differential operator can be expressed in terms of the $c_{j}$ length scales in the following compact form

$$\begin{gathered} \ell _{1}^{2} = \sum\limits_{{i = 1}}^{{m_{{n,1}} }} {[{\mathbf{C}}]_{{{\kern 1pt} i}}^{{(1)}} } \equiv {\text{tr}}\left( {\mathbf{C}} \right);\;\;\ell _{2}^{4} = \sum\limits_{{i = 1}}^{{m_{{n,2}} }} {[{\mathbf{C}}]_{{{\kern 1pt} i}}^{{(2)}} } , \ldots , \hfill \\ \ell _{k}^{{2k}} = \sum\limits_{{i = 1}}^{{m_{{n,k}} }} {[{\mathbf{C}}]_{{{\kern 1pt} i}}^{{(k)}} } ,\;\;\ell _{n}^{{2n}} = \sum\limits_{{i = 1}}^{{m_{{n,n}} }} {[{\mathbf{C}}]_{{{\kern 1pt} i}}^{{(n)}} } \equiv \det \left( {\mathbf{C}} \right) \hfill \\ \end{gathered}$$

(80)

where the symbol $[{\mathbf{C}}]_{\,i}^{(k)}$ denotes the ith minor (determinant) of order k of the square diagonal matrix ${\mathbf{C}}$, while ${\text{tr(}}{\mathbf{C}})$ and $\det \left( {\mathbf{C}} \right)$ denote the trace and determinant of the ${\mathbf{C}}$ matrix. It is well known that for a $n \times n$ diagonal matrix there are a total of $m_{n,k} = \left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)$ minors of order k [97], which represent the upper limit of the summations in (80). Thus, there are $m_{n,1} = n$ minors of order 1, whose sum gives the trace of the ${\mathbf{C}}$ matrix, and only one minor of order n ($m_{n,n} = 1$), which coincides with the determinant of the ${\mathbf{C}}$ matrix according to (80). In conclusion, the generalization of the nth order Helmholtz differential operator (75) to the general case of multiple length scale parameters $c_{k} (k = 1, \ldots ,n)$ in each individual Helmholtz operator leads to the following compact expression

$${\mathcal{L}}_{{c_{1} ,c_{2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n)}} = \prod\limits_{k = 1}^{n} {{\mathcal{L}}_{H} (c_{k} )} = \sum\limits_{k = 0}^{n} {( - 1)^{k} \ell_{k}^{2k} \,\nabla^{2k} }$$

(81)

where by $\ell_{0} = 1$ and each length scale parameter $\ell_{k}^{2k} (k = 1, \ldots ,n)$ is expressed in compact form in terms of the $c_{k}$ length scales through the relationships (80).

While the length scale parameters $\ell_{k}$ entering the nth order Helmholtz differential operator can be calibrated based on experimental data (for instance, matching the Born–von Kármán model of lattice dynamics), their physical meaning and admissibility must be checked afterwards in terms of the originating $c_{k}$ length scale coefficients that must be all real for the single Helmholtz operators. This is done by inverting the (nonlinear) relations (80) between $\ell_{k}$ and $c_{k}$ and verifying that all $c_{k}^{2}$ terms are positive. Admissibility conditions in analytical form were reported by Lazar et al. [50] for the simple case of n = 2. Numerical, rather than analytical, conditions can be derived for a generic order n.

To generalize the relationships (80) further, for the next derivations it is useful to introduce the following truncated $(n - j)^{{{\text{th}}}}$ order Helmholtz operator (with $n > j$) defined as

$${\mathcal{L}}_{{c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n - j)}} = {\mathcal{L}}_{H} (c_{j + 1} ){\mathcal{L}}_{H} (c_{j + 2} ) \cdots ((n - j){\text{ times)}} \cdots {\mathcal{L}}_{H} (c_{n} ) = \prod\limits_{k = 1}^{n - j} {{\mathcal{L}}_{H} (c_{j + k} )} \quad {\text{for }}n > j$$

(82)

which represents the product of $n - j$ Helmholtz operators. Indeed, expression (82) represents a truncated version of the nth order Helmholtz differential operator in (81) where the first j Helmholtz operators with the corresponding length scales $c_{1} , \ldots ,c_{j}$ are eliminated, while the remaining $n - j$ with length scales from $c_{j + 1}$ up to $c_{n}$ are retained. It can be demonstrated that such truncated $(n - j)^{{{\text{th}}}}$ order Helmholtz operator in (82) can be expressed in a similar format to Eq. (81) but with a slightly different definition of the length scale parameters, namely

$${\mathcal{L}}_{{c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n - j)}} = \prod\limits_{k = 1}^{n - j} {{\mathcal{L}}_{H} (c_{j + k} )} = \sum\limits_{k = 0}^{n - j} {( - 1)^{k} \ell_{j,k}^{2k} \,\nabla^{2k} }$$

(83)

where the new length scale parameters $\ell_{j,k}^{2k} (k = 1, \ldots ,n - j)$ depend not only on the order $k$ but also on the truncation order j being considered. As an example, for n = 4 Eq. (82) can be particularized in the following cases.

• for j = 1

$${\mathcal{L}}_{{c_{2} ,c_{3} ,c_{4} }}^{{{\kern 1pt} (4 - 1)}} = {\mathcal{L}}_{H} (c_{2} ){\mathcal{L}}_{H} (c_{3} ){\mathcal{L}}_{H} (c_{4} ) = \left( {1 - c_{2}^{2} \nabla^{2} } \right)\left( {1 - c_{3}^{2} \nabla^{2} } \right)\left( {1 - c_{4}^{2} \nabla^{2} } \right) = 1 - \ell_{1,1}^{2} \nabla^{2} + \ell_{1,2}^{4} \nabla^{4} - \ell_{1,3}^{6} \nabla^{6}$$

(84)

with $\ell_{1,1}^{2} = c_{2}^{2} + c_{3}^{2} + c_{4}^{2}$, $\ell_{1,2}^{4} = c_{2}^{2} c_{3}^{2} + c_{2}^{2} c_{4}^{2} + c_{3}^{2} c_{4}^{2}$, $\ell_{1,3}^{6} = c_{2}^{2} c_{3}^{2} c_{4}^{2}$;

• for j = 2

$${\mathcal{L}}_{{c_{3} ,c_{4} }}^{{{\kern 1pt} (4 - 2)}} = {\mathcal{L}}_{H} (c_{3} ){\mathcal{L}}_{H} (c_{4} ) = \left( {1 - c_{3}^{2} \nabla^{2} } \right)\left( {1 - c_{4}^{2} \nabla^{2} } \right) = 1 - \ell_{2,1}^{2} \nabla^{2} + \ell_{2,2}^{4} \nabla^{4}$$

(85)

with $\ell_{2,1}^{2} = c_{3}^{2} + c_{4}^{2}$, $\ell_{2,2}^{4} = c_{3}^{2} c_{4}^{2}$;

for j = 3

$${\mathcal{L}}_{{c_{4} }}^{{{\kern 1pt} (4 - 3)}} = {\mathcal{L}}_{H} (c_{4} ) = \left( {1 - c_{4}^{2} \nabla^{2} } \right) = 1 - \ell_{3,1}^{2} \nabla^{2}$$

(86)

with $\ell_{3,1}^{2} = c_{4}^{2}$.

To extend and generalize the above results up to order n and truncation j, it is useful to introduce the following truncated $(n - j) \times (n - j)$ diagonal matrix collecting the squared length scale parameters from $c_{j + 1}$ up to $c_{n}$ as follows

$${\mathbf{C}}^{(j)} = \left[ {\begin{array}{*{20}c} {c_{j + 1}^{2} } & 0 & \cdots & 0 \\ 0 & {c_{j + 2}^{2} } & \cdots & 0 \\ \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & \cdots & {c_{n}^{2} } \\ \end{array} } \right].$$

(87)

For the previous example of n = 4 we have

$${\mathbf{C}}^{(1)} = \left[ {\begin{array}{*{20}c} {c_{2}^{2} } & 0 & 0 \\ 0 & {c_{3}^{2} } & 0 \\ 0 & 0 & {c_{4}^{2} } \\ \end{array} } \right];\quad {\mathbf{C}}^{(2)} = \left[ {\begin{array}{*{20}c} {c_{3}^{2} } & 0 \\ 0 & {c_{4}^{2} } \\ \end{array} } \right];\quad {\mathbf{C}}^{(3)} = [c_{4}^{2} ].$$

(88)

It is worth noting that the diagonal $(n - j)$-dimensional ${\mathbf{C}}^{(j)}$ matrix in (87) is a submatrix of the previously defined ${\mathbf{C}}$ matrix in (79) by eliminating the first j rows and columns. By considering the previous results (84), (85), (86) for $j = 1,2,3$, respectively, it can easily be seen that the new length scale parameters $\ell_{j,k}^{2k} (k = 1, \ldots ,n - j)$ entering the truncated $(n - j)^{{{\text{th}}}}$ order Helmholtz operator (83) are related to the minors (determinants) of the square diagonal matrix ${\mathbf{C}}^{(j)}$ in (87) through the following relationships

$$\ell_{j,1}^{2} = \sum\limits_{i = 1}^{{m_{n - j,1} }} {[{\mathbf{C}}^{(j)} ]_{\,i}^{(1)} } \equiv {\text{tr}}\left( {{\mathbf{C}}^{(j)} } \right), \ldots ,\;\;\ell_{j,k}^{2k} = \sum\limits_{i = 1}^{{m_{n - j,k} }} {[{\mathbf{C}}^{(j)} ]_{\,i}^{(k)} } , \ldots ,\;\;\ell_{j,n - j}^{2n} = \sum\limits_{i = 1}^{{m_{n - j,n - j} }} {[{\mathbf{C}}^{(j)} ]_{\,i}^{(n - j)} } \equiv \det \left( {{\mathbf{C}}^{(j)} } \right)$$

(89)

where the symbol $[{\mathbf{C}}^{(j)} ]_{\,i}^{(k)}$ denotes the ith minor (determinant) of order k of the square diagonal matrix ${\mathbf{C}}^{(j)}$ and $m_{n - j,k} = \left( {\begin{array}{*{20}c} {n - j} \\ k \\ \end{array} } \right)$ is the number of minors of order k of the $(n - j)$-dimensional ${\mathbf{C}}^{(j)}$ matrix [97].

The general nomenclature adopted in (89) includes the previous relationships (80) as special subcase for $j = 0$: in this case, there is no truncation as the ${\mathbf{C}}^{(j)}$ matrix coincides with the entire ${\mathbf{C}}$ matrix in (79) (which can be viewed as a truncation of zero order), and the length scale coefficients in (89) $\ell_{0,k}^{2k} \equiv \ell_{k}^{2k}$ whose expressions are given above in (80).

Appendix 2 Mathematical relationships between the Helmholtz type differential operator ${\mathcal{L}}^{\;(i)}$ and the nonlocal strain tensor $\overline{\varepsilon }_{kl}^{(j)} ({\mathbf{x}})$

In this Appendix, we report some mathematical properties of the differential operator ${\mathcal{L}}^{(i)}$ in relationship to the nonlocal strain tensor $\overline{\varepsilon }_{kl}^{(j)} ({\mathbf{x}})$ for equal and different orders of differentiation and regularization i and j, respectively. As a first step, a more explicit expression for Eq. (57) is given below for a generic order n in both the differential operator and the nonlocal strain tensor ($i = j = n$), by recalling the definition of $\overline{\varepsilon }_{kl}^{(n)} ({\mathbf{x}})$ in (16) and (17) for a multiple-length-scale kernel $\alpha^{(n)} (|{\mathbf{x}} - {\mathbf{y}}|;c_{1} ,c_{2} , \ldots ,c_{n} )$, namely

$$\begin{gathered} {\mathcal{L}}_{{c_{1} ,c_{2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n)}} \overline{\varepsilon }_{kl}^{(n)} ({\mathbf{x}}) = {\mathcal{L}}_{{c_{1} ,c_{2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n)}} {\mathcal{R}}_{{{\kern 1pt} c_{1} ,c_{2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n)}} [\varepsilon_{kl} ({\mathbf{x}})] = \hfill \\ \int_{V} {\int_{V} { \cdots \int_{V} {{\mathcal{L}}_{{c_{1} }}^{{{\kern 1pt} (1)}} \alpha^{(1)} (|{\mathbf{x}} - {\mathbf{y}}_{1} |;c_{1} )\,{\mathcal{L}}_{{c_{2} }}^{{{\kern 1pt} (1)}} \alpha^{(1)} (|{\mathbf{y}}_{1} - {\mathbf{y}}_{2} |;c_{2} ) \cdots {\mathcal{L}}_{{c_{n} }}^{{{\kern 1pt} (1)}} \alpha^{(1)} (|{\mathbf{y}}_{n - 1} - {\mathbf{y}}|;c_{n} )\,\varepsilon_{kl} ({\mathbf{y}}){\text{d}}V_{{{\mathbf{y}}_{1} }} {\text{d}}V_{{{\mathbf{y}}_{2} }} \cdots {\text{d}}V_{{{\mathbf{y}}_{n - 1} }} } = } } \hfill \\ \int_{V} {\int_{V} { \cdots \int_{V} {\delta ({\mathbf{x}} - {\mathbf{y}}_{1} )\,\delta ({\mathbf{y}}_{1} - {\mathbf{y}}_{2} ) \cdots \delta ({\mathbf{y}}_{n - 1} - {\mathbf{y}})\,\varepsilon_{kl} ({\mathbf{y}}){\text{d}}V_{{{\mathbf{y}}_{1} }} {\text{d}}V_{{{\mathbf{y}}_{2} }} \cdots {\text{d}}V_{{{\mathbf{y}}_{n - 1} }} } = } } \int_{V} {\delta ({\mathbf{x}} - {\mathbf{y}})\varepsilon_{kl} ({\mathbf{y}}){\text{d}}V_{{\mathbf{y}}} } = \varepsilon_{kl} ({\mathbf{x}})\, \hfill \\ \end{gathered}$$

(90)

where account has been taken of the Green-type equality (20) and of fact that ${\mathcal{L}}$ is, by hypothesis, a differential operator with constant coefficients. The derivations and the integrands in (90) proves the fact that the nth order kernel $\alpha^{(n)}$ is the Green function of the nth order Helmholtz differential operator ${\mathcal{L}}^{\;(n)}$, as per Eq. (57).

As a second step, generic expressions for a different order in the differential operator $i = n$ and in the regularization (integral) operator j (affecting the nonlocal strain tensor), with $n > j$, are derived as follows

$$\begin{gathered} {\mathcal{L}}_{{c_{1} ,c_{2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n)}} \overline{\varepsilon }_{kl}^{(j)} ({\mathbf{x}}) = {\mathcal{L}}_{{c_{1} ,c_{2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n)}} {\mathcal{R}}_{{{\kern 1pt} c_{1} ,c_{2} , \ldots ,c_{j} }}^{{{\kern 1pt} (j)}} [\varepsilon_{kl} ({\mathbf{x}})] \hfill \\ = {\mathcal{L}}_{{c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n - j)}} \left( {{\mathcal{L}}_{{c_{1} ,c_{2} , \ldots ,c_{j} }}^{{{\kern 1pt} (j)}} {\mathcal{R}}_{{{\kern 1pt} c_{1} ,c_{2} , \ldots ,c_{j} }}^{{{\kern 1pt} (j)}} [\varepsilon_{kl} ({\mathbf{x}})]} \right) = {\mathcal{L}}_{{c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n - j)}} \varepsilon_{kl} ({\mathbf{x}}) \hfill \\ \end{gathered}$$

(91)

where account has been taken of the previous relationship (90) for equal order j for the term within round brackets. In Eq. (91) ${\mathcal{L}}_{{c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{\;{\kern 1pt} (n - j)}}$ represents the truncated $(n - j)^{{{\text{th}}}}$ order Helmholtz operator previously defined in (82), whose length scale parameters are given in (89) in terms of the $c_{k}$ length scales. As a third step, another relationship can be derived as follows

$$\begin{gathered} {\mathcal{L}}_{{c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n - j)}} \overline{\varepsilon }_{kl}^{(n)} ({\mathbf{x}}) = {\mathcal{L}}_{{c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n - j)}} {\mathcal{R}}_{{{\kern 1pt} c_{1} ,c_{2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n)}} [\varepsilon_{kl} ({\mathbf{x}})] \hfill \\ = \left( {{\mathcal{L}}_{{\,c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n - j)}} {\mathcal{R}}_{{{\kern 1pt} c_{j + 1} ,c_{j + 2} , \ldots ,c_{n} }}^{{{\kern 1pt} (n - j)}} [\varepsilon_{kl} ({\mathbf{x}})]} \right){\mathcal{R}}_{{{\kern 1pt} c_{1} ,c_{2} , \ldots ,c_{j} }}^{{{\kern 1pt} (j)}} [\varepsilon_{kl} ({\mathbf{x}})] \hfill \\ = \int_{V} { \cdots \int_{V} {\delta ({\mathbf{x}} - {\mathbf{y}}_{0} )\;\alpha^{(1)} (|{\mathbf{y}}_{0} - {\mathbf{y}}_{1} |;c_{1} ) \cdots \alpha^{(1)} (|{\mathbf{y}}_{j - 1} - {\mathbf{y}}|;c_{j} )\,\varepsilon_{kl} ({\mathbf{y}}){\text{d}}V_{{{\mathbf{y}}_{1} }} \cdots {\text{d}}V_{{{\mathbf{y}}_{j - 1} }} } } \hfill \\ = \int_{V} {\alpha^{(j)} (|{\mathbf{x}} - {\mathbf{y}}|;c_{1} , \ldots ,c_{j} )\varepsilon_{kl} ({\mathbf{y}}){\text{d}}V_{{\mathbf{y}}} } = \overline{\varepsilon }_{kl}^{(j)} ({\mathbf{x}}) \hfill \\ \end{gathered}$$

(92)

where account has been taken of the previous relationship (90) for equal order $n - j$ for the term within round brackets. These two relationships (91) and (92) are recalled in Eq. (59) of the paper and are useful for the derivation of the differential and the integro-differential form of the generalized theory of nonlocal elasticity of n-Helmholtz type.