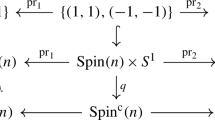Homotopy types of gauge groups of $\mathrm {PU}(p)$-bundles over spheres

Abstract

We examine the relation between the gauge groups of $\mathrm {SU}(n)$- and $\mathrm {PU}(n)$-bundles over $S^{2i}$, with $2\le i\le n$, particularly when n is a prime. As special cases, for $\mathrm {PU}(5)$-bundles over $S^4$, we show that there is a rational or p-local equivalence $\mathcal {G}_{2,k}\simeq _{(p)}\mathcal {G}_{2,l}$ for any prime p if, and only if, $(120,k)=(120,l)$, while for $\mathrm {PU}(3)$-bundles over $S^6$ there is an integral equivalence $\mathcal {G}_{3,k}\simeq \mathcal {G}_{3,l}$ if, and only if, $(120,k)=(120,l)$.

1 Introduction

Let G be a topological group and X a space. The gauge group $\mathcal {G}(P)$ of a principal G-bundle P over X is defined as the group of G-equivariant bundle automorphisms of P which cover the identity on X. A detailed introduction to gauge groups can be found in [11, 18].

The following problem is of interest: having fixed a topological group G and a space X, classify the possible homotopy types of the gauge groups $\mathcal {G}(P)$ of principal G-bundles P over X.

Crabb and Sutherland showed [5, Theorem 1.1] that if G is a compact, connected, Lie group and X is a connected, finite CW-complex, then the number of distinct homotopy types of $\mathcal {G}(P)$, as P ranges over all principal G-bundles over X, is finite. This is often in contrast with the fact that the number of isomorphisms classes of principal G-bundles over X may be infinite. However, their methods did not lead to an enumeration of the classes of gauge groups. Classification results require a different kind of analysis.

The first classification result was obtained by Kono [14] in 1991. Using the fact that principal $\mathrm {SU}(2)$-bundles over $S^4$ are classified by $k\in \mathbb {Z}\cong \pi _3(\mathrm {SU}(2))$ and denoting by $\mathcal {G}_k$ the gauge group of the principal $\mathrm {SU}(2)$-bundle $P_k\rightarrow S^4$ corresponding to the integer k, Kono showed that there is a homotopy equivalence $\mathcal {G}_k\simeq \mathcal {G}_l$ if, and only if, $(12,k)=(12,l)$, where (m, n) denotes the greatest common divisor of m and n. It thus follows that there are precisely six homotopy types of $\mathrm {SU}(2)$-gauge groups over $S^4$.

In this paper, we examine how the close relationship between the groups $\mathrm {SU}(n)$ and $\mathrm {PU}(n)$ is reflected in the homotopy properties of the gauge groups of the corresponding bundles, particularly when n is a prime. We do this by generalising certain results relating the classification of $\mathrm {PU}(n)$-gauge groups to that of $\mathrm {SU}(n)$-gauge groups from the paper [12] for the case $n=2$ (observe that $\mathrm {PU}(2)\cong {{\,\mathrm{SO}\,}}(3)$), and from [9] for the case $n=3$.

Our first main result compares certain Samelson products on $\mathrm {SU}(p)$ and $\mathrm {PU}(p)$, with $p\ge 3$ a prime. As will be illustrated in Sect. 2, the finiteness of the orders of Samelson products (in the appropriate groups of homotopy classes of maps) plays a crucial role in the homotopy classification of gauge groups. In Sect. 3, we will show the following.

Theorem 1

Let p be an odd prime and let $2\le i\le p$. Let $\epsilon _i$ and $\delta _i$ denote generators of $\pi _{2i-1}(\mathrm {PU}(p))$ and $\pi _{2i-1}(\mathrm {SU}(p))$, respectively. The orders of the Samelson products $\langle \epsilon _i,1\rangle :S^{2i-1}\wedge \mathrm {PU}(p)\rightarrow \mathrm {PU}(p)$ and $\langle \delta _i,1\rangle :S^{2i-1}\wedge \mathrm {SU}(p)\rightarrow \mathrm {SU}(p)$, where 1 denotes the appropriate identity map, coincide.

Theorem 1 is the key ingredient for the “if” direction of our classification results. The converse direction, on the other hand, will require that suitable homotopy invariants of the gauge groups be identified. In Sect. 2, we introduce the notation $\mathcal {G}_{i,k}(\mathrm {PU}(n))$, with $k\in \mathbb {Z}$, for gauge groups of $\mathrm {PU}(n)$-bundles over $S^{2i}$ in analogy with the notation used by Kono [14] and others. In Sect. 4, we give a sufficient condition for certain homotopy invariants of $\mathrm {SU}(n)$- and $\mathrm {PU}(n)$-gauge groups to coincide.

Our methods then allow us to deduce classification results for $\mathrm {PU}(p)$-gauge groups from the corresponding classification results for $\mathrm {SU}(p)$-gauge groups. As examples of applications of our results, we obtain the following complete classifications.

Theorem 2

For $\mathrm {PU}(5)$-bundles over $S^4$, it is the case that

• (a) if $\mathcal {G}_{2,k}(\mathrm {PU}(5))\simeq \mathcal {G}_{2,l}(\mathrm {PU}(5))$, then $(120,k)=(120,l)$;

• (b) if $(120,k)=(120,l)$, then $\mathcal {G}_{2,k}(\mathrm {PU}(5))\simeq \mathcal {G}_{2,l}(\mathrm {PU}(5))$ when localised rationally or at any prime.

Theorem 3

For $\mathrm {PU}(3)$-bundles over $S^6$, we have $\mathcal {G}_{3,k}(\mathrm {PU}(3))\simeq \mathcal {G}_{3,l}(\mathrm {PU}(3))$ if, and only if, $(120,k)=(120,l)$.

We should note that in [9], the $\mathrm {PU}(3)$-gauge group $\mathcal {G}_{2,k}$ is shown to be homotopy equivalent to ${\widehat{\mathcal {G}}}_{2,k}\times S^1$, where ${\widehat{\mathcal {G}}}_{2,k}$ is a space whose homotopy groups are all finite. This allows the authors of [9] to apply Lemma 2 (stated in Sect. 2.2 herein) to obtain a classification result for $\mathcal {G}_{2,k}$ that holds integrally. We expect the same result to apply more generally to gauge groups of $\mathrm {PU}(n)$-bundles over $S^{2n-2}$. However, there are currently no other cases, besides that of [9], in which such a result would be applicable.

Finally, it is worth noting that, should any further classifications of gauge groups of $\mathrm {SU}(p)$-bundles over even-dimensional spheres be obtained, our results would provide the corresponding classification results for $\mathrm {PU}(p)$-gauge groups as immediate corollaries, provided the original results were arrived at via the standard methods.

2 Homotopy types of $\mathrm {PU}(n)$-gauge groups

The projective unitary group $\mathrm {PU}(n)$ is defined as the quotient of $\mathrm {U}(n)$ by its centre

$$\begin{aligned} Z(\mathrm {U}(n))=\{\lambda I_n \mid \lambda \in \mathbb {C}\text { and }|\lambda |=1\}\cong \mathrm {U}(1). \end{aligned}$$

In marked contrast with the orthogonal case, there is a homotopy equivalence between $\mathrm {PU}(n)$ and $\mathrm {PSU}(n)$ for every n. For the purposes of this paper, one can therefore equivalently define $\mathrm {PU}(n)$ as the quotient of $\mathrm {SU}(n)$ by its centre

$$\begin{aligned} Z(\mathrm {SU}(n))=\{\lambda I_n \mid \lambda \in \mathbb {C}\text { and }\lambda ^n=1\}\cong \mathbb {Z}/n\mathbb {Z}. \end{aligned}$$

We let $q:\mathrm {SU}(n)\rightarrow \mathrm {PU}(n)$ denote the quotient map corresponding to the latter definition, which we shall use throughout. Note that q is an n-fold covering map and $\mathrm {SU}(n)$, being simply-connected, is the universal cover of $\mathrm {PU}(n)$.

2.1 Notation for $\mathrm {PU}(n)$-gauge groups

Let n and i be fixed integers such that $2\le i\le n$. As stated in the introduction, we are interested in the problem of classifying the homotopy types of the gauge groups $\mathcal {G}(P)$ as P ranges over all $\mathrm {PU}(n)$-bundles over $S^{2i}$.

If there exists a $\mathrm {PU}(n)$-equivariant bundle isomorphism $P\cong P'$, then conjugation by such an isomorphism yields a homeomorphism $\mathcal {G}(P)\cong \mathcal {G}(P')$. It therefore suffices to let P range over a set of representatives of all the isomorphism classes of $\mathrm {PU}(n)$-bundles over $S^{2i}$.

Since $S^{2i}$ is paracompact, the set of isomorphism classes of principal $\mathrm {PU}(n)$-bundles over $S^{2i}$ is in bijection with the set $[S^{2i},\mathrm {B}\mathrm {PU}(n)]_\mathrm {free}$ of free homotopy classes of maps from $S^{2i}$ to $\mathrm {B}\mathrm {PU}(n)$, the classifying space of $\mathrm {PU}(n)$. As $\mathrm {PU}(n)$ is connected, $\mathrm {B}\mathrm {PU}(n)$ is simply-connected and hence there is a bijection

$$\begin{aligned}{}[S^{2i},\mathrm {B}\mathrm {PU}(n)]_\mathrm {free}\cong [S^{2i},\mathrm {B}\mathrm {PU}(n)], \end{aligned}$$

the right-hand side denoting the set of pointed homotopy classes of maps from $S^{2i}$ to $\mathrm {B}\mathrm {PU}(n)$. Furthermore, we have bijections

$$\begin{aligned}{}[S^{2i},\mathrm {B}\mathrm {PU}(n)]\cong \pi _{2i}(\mathrm {B}\mathrm {PU}(n))\cong \pi _{2i-1}(\mathrm {PU}(n)) \cong \mathbb {Z}. \end{aligned}$$

We can therefore introduce the following labelling for the gauge groups of $\mathrm {PU}(n)$-bundles over $S^{2i}$. Let $\epsilon _i:S^{2i-1}\rightarrow \mathrm {PU}(n)$ denote a generator of $\pi _{2i-1}(\mathrm {PU}(n))$. Each isomorphism class of $\mathrm {PU}(n)$-bundles is represented by the bundle $P_k\rightarrow S^{2i}$ induced by pulling back the universal $\mathrm {PU}(n)$-bundle along the classifying map $k{\overline{\epsilon }}_i:S^{2i}\rightarrow \mathrm {B}\mathrm {PU}(n)$, where ${\overline{\epsilon }}_i$ denotes the adjoint of $\epsilon _i$ and generates $\pi _{2i}(\mathrm {B}\mathrm {PU}(n))$. We let $\mathcal {G}_{i,k}(\mathrm {PU}(n))$ (or simply $\mathcal {G}_{i,k}$ when the context is clear) denote the gauge group of $P_k\rightarrow S^{2i}$. Mutatis mutandis, the notation $\mathcal {G}_{i,k}(\mathrm {SU}(n))$ will also be used.

2.2 Classification of the homotopy types of $\mathcal {G}_{i,k}$

By [1] or [6], there is a homotopy equivalence $\mathrm {B}\mathcal {G}_{i,k}\simeq \mathrm {Map}_{k}(S^{2i},\mathrm {B}\mathrm {PU}(n))$, the latter space being the k-th component of $\mathrm {Map}(S^{2i},\mathrm {B}\mathrm {PU}(n))$, meaning the connected component containing the classifying map $k{\overline{\epsilon }}_i$.

There is an evaluation fibration

$$\begin{aligned} \mathrm {Map}^*_k(S^{2i},\mathrm {B}\mathrm {PU}(n))\longrightarrow \mathrm {Map}_k(S^{2i},\mathrm {B}\mathrm {PU}(n))\xrightarrow {\ {{\,\mathrm{ev}\,}}\ } \mathrm {B}\mathrm {PU}(n), \end{aligned}$$

where ${{\,\mathrm{ev}\,}}$ evaluates a map at the basepoint of $S^{2i}$ and the fibre is the k-th component of the pointed mapping space $\mathrm {Map}^*_k(S^{2i},\mathrm {B}\mathrm {PU}(n))$. This fibration extends to a homotopy fibration sequence

$$\begin{aligned} \mathcal {G}_{i,k}\longrightarrow \mathrm {PU}(n)\longrightarrow \mathrm {Map}^*_k(S^{2i},\mathrm {B}\mathrm {PU}(n))\longrightarrow \mathrm {B}\mathcal {G}_{i,k}\longrightarrow \mathrm {B}\mathrm {PU}(n), \end{aligned}$$

where we used the equivalences $\mathrm {B}\mathcal {G}_{i,k}\simeq \mathrm {Map}_{k}(S^{2i},\mathrm {B}\mathrm {PU}(n))$, $\varOmega \mathrm {B}\mathrm {PU}(n)\simeq \mathrm {PU}(n)$, and $\varOmega \mathrm {B}\mathcal {G}_{i,k}\simeq \mathcal {G}_{i,k}$. Furthermore, by [19] there is, for each $k\in \mathbb {Z}$, a homotopy equivalence

$$\begin{aligned} \mathrm {Map}^*_k(S^{2i},\mathrm {B}\mathrm {PU}(n))\simeq \mathrm {Map}^*_0(S^{2i},\mathrm {B}\mathrm {PU}(n)). \end{aligned}$$

The space on the right-hand side is denoted $\varOmega _0^{2i}\mathrm {B}\mathrm {PU}(n)$ and is homotopy equivalent to $\varOmega _0^{2i-1}\mathrm {PU}(n)$. We therefore have the following homotopy fibration sequence

$$\begin{aligned} \mathcal {G}_{i,k}\longrightarrow \mathrm {PU}(n)\xrightarrow {\ \partial _{i,k}\ }\varOmega _0^{2i-1}\mathrm {PU}(n)\longrightarrow \mathrm {B}\mathcal {G}_{i,k}\longrightarrow \mathrm {B}\mathrm {PU}(n), \end{aligned}$$

which exhibits the gauge group $\mathcal {G}_{i,k}$ as the homotopy fibre of the map $\partial _{i,k}$. This is a key observation, as it suggests that the homotopy theory of the gauge groups $\mathcal {G}_{i,k}$ depends on the maps $\partial _{i,k}$. In fact, more is true.

By [15, Theorem 2.6], the adjoint of $\partial _{i,k}:\mathrm {PU}(n)\rightarrow \varOmega _0^{2i-1}\mathrm {PU}(n)$ is homotopic to the Samelson product $\langle k\epsilon _i,1\rangle :S^{2i-1}\wedge \mathrm {PU}(n)\rightarrow \mathrm {PU}(n)$, where 1 denotes the identity map on $\mathrm {PU}(n)$. As the Samelson product is bilinear, $\langle k\epsilon _i,1\rangle \simeq k\langle \epsilon _i,1\rangle$, and hence, taking adjoints once more, $\partial _{i,k}\simeq k \partial _{i,1}$.

Thus, every one of the gauge groups is the homotopy fibre of the map $\partial _{i,1}$ post-composed with the appropriate power map on $\varOmega ^{2i-1}_0\mathrm {PU}(n)$. If $\partial _{i,1}$ can be determined to have finite order in $[\mathrm {PU}(n),\varOmega _0^{2i-1}\mathrm {PU}(n)]$, this will have strong implications for the homotopy types of the $\mathcal {G}_{i,k}$’s, as the following lemmas show.

Lemma 1

(Theriault [20, Lemma 3.1]) Let X be a connected CW-complex and let Y be an H-space with a homotopy inverse. Suppose that $f\in [X,Y]$ has finite order m. Then, for any integers $k,l\in \mathbb {Z}$ such that $(m,k)=(m,l)$, the homotopy fibres of kf and lf are homotopy equivalent when localised rationally or at any prime. $\square$

If, additionally, the homotopy groups of Y are all finite, as in the case of $\mathrm {PU}(n)$-bundles over $S^{2n}$, where $Y= \varOmega ^{2n-1}_0\mathrm {PU}(n)$, the following stronger lemma applies.

Lemma 2

(Hamanaka, Kono [7, Lemma 3.2]) Let X be a connected CW-complex and let Y be an H-space such that $\pi _j(Y)$ is finite for all j. Let $f\in [X,Y]$ be such that $mf\simeq *$ for some finite m and let $k,l\in \mathbb {Z}$ satisfy $(m,k)=(m,l)$. Then, there exists a homotopy equivalence $h:Y\rightarrow Y$ satisfying $hkf\simeq lf$. $\square$

Note that the order of $\partial _{i,1}$ coincides with the order of $\langle \epsilon _i,1\rangle$.

3 Samelson products on $\mathrm {PU}(p)$

Having fixed $n\ge 3$ and $2\le i\le n$, let $\delta _i:S^{2i-1}\rightarrow \mathrm {SU}(n)$ denote the generator of $\pi _{2i-1}(\mathrm {SU}(n))\cong \mathbb {Z}$ corresponding to the generator $\epsilon _i$ of $\pi _{2i-1}(\mathrm {PU}(n))$. That is, such that $q_*(\delta _i)=\epsilon _i$, where q denotes the quotient map $q:\mathrm {SU}(n)\rightarrow \mathrm {PU}(n)$ introduced in Sect. 2.

In this section, we wish to compare the orders of the Samelson products $\langle \delta _i,1\rangle$ and $\langle \epsilon _i,1\rangle$ on $\mathrm {SU}(n)$ and $\mathrm {PU}(n)$, respectively. First, observe that there is a commutative diagram

and recall the following property of the quotient map q.

Lemma 3

The quotient map $q:\mathrm {SU}(n)\rightarrow \mathrm {PU}(n)$ induces a p-local homotopy equivalence $\mathrm {SU}(n)\simeq _{(p)}\mathrm {PU}(n)$ for any prime p which does not divide n.

Proof

The quotient map q induces isomorphisms on the p-localised homotopy groups (note that $\pi _1(\mathrm {PU}(n))_{(p)}$ is trivial), and hence it is a p-local homotopy equivalence by [10, Theorem 3B(ii)]. $\square$

Lemma 4

If the prime p does not divide n, then the p-primary components of the orders of the Samelson products $\langle \delta _i,1\rangle$ and $\langle \epsilon _i,1\rangle$ coincide.

Proof

Let p be a prime which does not divide n. Then q is a p-local homotopy equivalence by Lemma 3, and hence the commutativity of (*) yields

$$\begin{aligned} \langle \delta _i,1\rangle _{(p)}=q^{-1}_{(p)}\circ \langle \epsilon _i,1\rangle _{(p)}\circ (1\wedge q_{(p)}), \end{aligned}$$

so the p-primary components of the orders of $\langle \delta _i,1\rangle$ and $\langle \epsilon _i,1\rangle$ coincide. $\square$

Hence, when n is prime, the orders of $\langle \delta _i,1\rangle$ and $\langle \epsilon _i,1\rangle$ coincide, except possibly in the number of factors of n appearing in their respective prime decompositions.

Lemma 5

For any n, the quotient map $q:\mathrm {SU}(n)\rightarrow \mathrm {PU}(n)$ induces an isomorphism

$$\begin{aligned} q_*:[S^{2i-1}\wedge \mathrm {SU}(n),\mathrm {SU}(n)]\rightarrow [S^{2i-1}\wedge \mathrm {SU}(n),\mathrm {PU}(n)]. \end{aligned}$$

Proof

Recall that $q:\mathrm {SU}(n)\rightarrow \mathrm {PU}(n)$ fits into a homotopy fibration sequence

$$\begin{aligned} \cdots \longrightarrow \mathbb {Z}/n\mathbb {Z}\longrightarrow \mathrm {SU}(n)\xrightarrow {\ q\ } \mathrm {PU}(n) \longrightarrow \mathrm {B}(\mathbb {Z}/n\mathbb {Z}). \end{aligned}$$

Since $\mathbb {Z}/n\mathbb {Z}$ is discrete, applying the functor $[S^{2i-1}\wedge \mathrm {SU}(n),-]$ yields

$$\begin{aligned} \cdots \longrightarrow 0\longrightarrow [S^{2i-1}\wedge \mathrm {SU}(n),\mathrm {SU}(n)]\xrightarrow {\ q_*\ } [S^{2i-1}\wedge \mathrm {SU}(n),\mathrm {PU}(n)] \longrightarrow 0, \end{aligned}$$

whence the statement. $\square$

Lemma 6

The order of $\langle \delta _i,1\rangle$ divides the order of $\langle \epsilon _i,1\rangle$.

Proof

Let p be a prime. If $p^k$ divides the order of $\langle \delta _i,1\rangle$ for some $k\ge 1$, then $p^k$ also divides the order of the composite $q\circ \langle \delta _i,1\rangle _{(p)}$ by Lemma 5. It then follows, by the commutativity of (*), that the order of $\langle \epsilon _i,1\rangle _{(p)}$ is at least $p^k$. $\square$

For the remainder of this section, we shall restrict to considering $\mathrm {PU}(n)$ when n is an odd prime p.

Since $\mathrm {SU}(p)$ is the universal cover of $\mathrm {PU}(p)$ and $H_*(\mathrm {SU}(p);\mathbb {Z})$ is torsion-free, by [13, Theorem 1.1] we have the following decomposition of $\mathrm {PU}(p)$.

Lemma 7

For an odd prime p, there is a p-local homotopy equivalence

$$\begin{aligned} \mathrm {PU}(p)\simeq _{(p)}L\times \prod _{j=2}^{p-1}S^{2j-1} \end{aligned}$$

where L is an H-space with $\pi _1(L)\cong \mathbb {Z}/p\mathbb {Z}$. $\square$

Let $\alpha :L_{(p)}\rightarrow \mathrm {PU}(p)_{(p)}$ be the inclusion. Then we can write the equivalence of Lemma 7 as

$$\begin{aligned} L_{(p)}\times \prod _{j=2}^{p-1} S^{2j-1}_{(p)}\xrightarrow {\ \alpha \times \prod _j {\epsilon _j}_{(p)}\ } \bigl (\mathrm {PU}(p)_{(p)}\bigr )^{p-1}\xrightarrow {\ \mu \ }\mathrm {PU}(p)_{(p)}, \end{aligned}$$

where $\mu$ is the group multiplication in $\mathrm {PU}(p)_{(p)}$. We note that this composite is equal to the product

$$\begin{aligned} (\alpha \circ \mathrm {pr}_1)\cdot \prod _{j=2}^{p-1}({\epsilon _j}_{(p)}\circ \mathrm {pr}_j) \end{aligned}$$

in the group $[L_{(p)}\times \prod _{j=2}^{p-1} S^{2j-1}_{(p)},\mathrm {PU}(p)_{(p)}]$, where $\mathrm {pr}_j$ denotes the projection onto the jth factor.

Lemma 8

With the above notation, the localised Samelson product

$$\begin{aligned} \langle \epsilon _i,1\rangle _{(p)} :S^{2i-1}_{(p)}\wedge \mathrm {PU}(p)_{(p)}\rightarrow \mathrm {PU}(p)_{(p)} \end{aligned}$$

is trivial if, and only if, each of $\langle {\epsilon _i}_{(p)},\alpha \rangle$ and $\langle \epsilon _i,\epsilon _j\rangle _{(p)}$, for $2\le j\le p-1$, are trivial.

Proof

By [9, Lemmas 3.3 and 3.4], $\langle \epsilon _i,1\rangle _{(p)}$ is trivial if, and only if, both $\langle {\epsilon _i}_{(p)},\alpha \rangle$ and $\langle \epsilon _i,\prod _j\epsilon _j\rangle _{(p)}$ are trivial. Applying the same lemmas to the second factor a further $p-3$ times gives the statement. $\square$

We therefore calculate the groups $[S^{2i-1}\wedge L,\mathrm {PU}(p)]_{(p)}$ and, for $2\le j\le p-1$, the homotopy groups $\pi _{2i+2j-2}(\mathrm {PU}(p))_{(p)}$ in order to get an upper bound on the order of $\langle \epsilon _i,1\rangle _{(p)}$.

Lemma 9

For $2\le i\le p$ and $2\le j\le p-1$, the group $\pi _{2i+2j-2}\bigl (\mathrm {PU}(p)\bigr )_{(p)}$ has exponent at most p.

Proof

Decompose $\mathrm {PU}(p)$ as in Lemma 7. Observe that, by [13, Proposition 2.2], we have $\pi _n(L)\cong \pi _n(S^{2p-1})$ for $n\ge 2$, and hence

$$\begin{aligned} \pi _{2i+2j-2}\bigl (\mathrm {PU}(p)\bigr )_{(p)}\cong \pi _{2i+2j-2}\biggl (L\times \prod _{k=2}^{p-1}S^{2k-1}\biggr )_{\!(p)}\!\!\cong \bigoplus _{k=2}^p\pi _{2i+2j-2}(S^{2k-1})_{(p)}. \end{aligned}$$

By Toda [23, Theorem 7.1], if $k\ge 2$ and $r<2p(p-1)-2$, the p-primary component of $\pi _{(2k-1)+r}(S^{2k-1})$ is either 0 or $\mathbb {Z}/p\mathbb {Z}$. Since $2i+2j-2\le 4p-4$ and

$$\begin{aligned} 4p-4<2p(p-1)-2+(2k-1) \end{aligned}$$

for all $k\ge 2$, the statement follows. $\square$

For the next part of our calculation, we will need a certain mod-p decomposition of $\varSigma ^2 L$ which will, in turn, require some cohomological information. The mod-p cohomology algebra of $\mathrm {PU}(n)$, with p any prime and n arbitrary, was determined by Baum and Browder in [2, Corollary 4.2]. In particular, we have:

Lemma 10

For p an odd prime, there is an algebra isomorphism

$$\begin{aligned} H^*(\mathrm {PU}(p);\mathbb {Z}/p\mathbb {Z})\cong \varLambda (x_1,x_3,\ldots ,x_{2p-3})\otimes \frac{\mathbb {Z}/p\mathbb {Z}[y]}{(y^p)}, \end{aligned}$$

with $|x_d|=d$, $|y|=2$, and $\beta (x_1)=y$. $\square$

For $m\ge 2$, denote by $P^{m}(p)$ the mod-p Moore space defined as the homotopy cofibre of the degree p map

$$\begin{aligned} S^{m-1}\xrightarrow {\ p \ } S^{m-1}\longrightarrow P^{m}(p) \end{aligned}$$

on the sphere $S^{m-1}$. In other words, $P^m(p)=S^{m-1}\cup _{p} e^m$. Note that, by extending the cofibre sequence to the right, we see that $\varSigma P^{m}(p)\simeq P^{m+1}(p)$.

Lemma 11

For p an odd prime, there is a p-local homotopy equivalence

$$\begin{aligned} \varSigma L \simeq _{(p)} A\vee \bigvee _{k=2}^{p-1}P^{2k+1}(p), \end{aligned}$$

with $H_*(A;\mathbb {Z}/p\mathbb {Z})$ generated by $\{u,v,w\}$, with $|u|=2$, $|v|=3$, $|w|=2p$, and subject to the relation $\beta (v)=u$.

Proof

By decomposing $\mathrm {PU}(p)$ as in Lemma 7, taking mod-p cohomology and comparing with Lemma 10, we obtain

$$\begin{aligned} H^*(L;\mathbb {Z}/p\mathbb {Z})\cong \varLambda (x_1)\otimes \frac{\mathbb {Z}/p\mathbb {Z}[y]}{(y^p)}. \end{aligned}$$

Since $H^*(L;\mathbb {Z}/p\mathbb {Z})$ is of finite type and self-dual, $H^*(L;\mathbb {Z}/p\mathbb {Z})\cong H_*(L;\mathbb {Z}/p\mathbb {Z})$ as Hopf algebras. Then, as $H_*(L;\mathbb {Z}/p\mathbb {Z})$ is primitively generated and L is a connected H-space (being a retract of $\mathrm {PU}(p)$), by [4, Theorem 4.1] there is a decomposition

$$\begin{aligned} \varSigma L \simeq _{(p)} A_1\vee A_2\vee \cdots \vee A_{p-1}, \end{aligned}$$

with each summand $A_j$ having homology $H_*(A_j;\mathbb {Z}/p\mathbb {Z})$ generated by the suspensions of monomials in $H_*(L;\mathbb {Z}/p\mathbb {Z})$ of length j (modulo $p-1$), where by length of a monomial one means the number of (not necessarily distinct) factors in that monomial.

Let ${\overline{x}}_1$ and ${\overline{y}}$ denote the duals of $x_1$ and y, and let $\sigma$ denote the suspension isomorphism for homology. Then, $H_*(A_1;\mathbb {Z}/p\mathbb {Z})$ is generated by $\sigma ({\overline{x}}_1)$, $\sigma ({\overline{y}})$, and $\sigma ({\overline{x}}_1{\overline{y}}^{p-1})$, in degrees 2, 3, and 2p, respectively. Furthermore, by the stability of the Bockstein operator $\beta$, we also have $\beta (\sigma ({\overline{y}}))=\sigma ({\overline{x}}_1)$.

On the other hand, for $j\ne 1$, the homology $H_*(A_j;\mathbb {Z}/p\mathbb {Z})$ is generated by the elements $\sigma ({\overline{x}}_1{\overline{y}}^{j-1})$ and $\sigma ({\overline{y}}^j)$, in degrees 2j and $2j+1$, respectively, subject to the relation $\beta (\sigma ({\overline{y}}^j))=\sigma ({\overline{x}}_1{\overline{y}}^{j-1})$. As the homotopy type of Moore spaces is uniquely characterised by their homology, we must have $A_j\simeq P^{2j+1}(p)$ for $j\ne 1$, yielding the decomposition in the statement. $\square$

With A as in Lemma 11, we have:

Lemma 12

There is a p-local homotopy equivalence

$$\begin{aligned} \varSigma A \simeq _{(p)} P^4(p)\vee S^{2p+1}. \end{aligned}$$

Proof

Localise at p throughout. By looking at the degrees of the generators of $H_*(A;\mathbb {Z}/p\mathbb {Z})$ in Lemma 11, we see that the 3-skeleton of A is $P^3(p)$.

Let $f:S^{2p-1}\rightarrow P^3(p)$ be the attaching map of the top cell of A, and let F be the homotopy fibre of $\rho :P^3(p)\rightarrow S^3$, the pinch map to the top cell of $P^3(p)$. As $\pi _{2p-1}(S^3)\cong 0$, the map f lifts through F via some map $\lambda :S^{2p-1}\rightarrow F$, as in the diagram:

Let $j:S^3\rightarrow P^4(p)$ be the inclusion of the bottom cell and let $S^3\{p\}$ be the homotopy fibre of the degree p map on $S^3$. As j has order p, there is a homotopy fibration diagram

which defines a map $s:S^3\{p\}\rightarrow \varOmega P^4(p)$. For connectivity reasons, the suspension map $P^3(p)\xrightarrow {\, E \,}\varOmega P^4(p)$ factors as the composite $P^3(p)\xrightarrow {\, \iota \,} S^3\{p\}\xrightarrow {\, s\,} \varOmega P^4(p)$, where $\iota$ is the inclusion of the bottom Moore space. Furthermore, there is a homotopy fibration diagram

Putting this together gives a commutative diagram

Thus $E\circ f$ factors through $\varOmega j$, implying that $\varSigma f$ factors as the composite

$$\begin{aligned} S^{2p}\xrightarrow {\ {\hat{f}}\ } S^3 \xrightarrow {\ j \ } P^4(p) \end{aligned}$$

for some map ${\hat{f}}$.

As $\pi _{2p}(S^3) \cong \mathbb {Z}/p\mathbb {Z}$, we must have ${\hat{f}}=t\alpha$, where $\alpha$ is a generator of $\pi _{2p}(S^3)$. If $\varSigma f$ were essential, then $t\ne 0$. However, the element $\alpha$ would then be detected by the Steenrod operation $\mathcal {P}^1$ in the cohomology of $\varSigma A$. This would, in turn, imply that $\mathcal {P}^1$ were non-trivial in $H^*(A;\mathbb {Z}/p\mathbb {Z})$, and hence in $H^*(\mathrm {PU}(p);\mathbb {Z}/p\mathbb {Z})$. However, $\mathcal {P}^1(H^*(\mathrm {PU}(p);\mathbb {Z}/p\mathbb {Z}))=0$, and thus we must have had $\varSigma f \simeq *$. $\square$

Lemma 13

The exponent of the group $[S^{2i-1}\wedge L,\mathrm {PU}(p)]_{(p)}$ is at most p.

Proof

By the decompositions in Lemmas 11 and 12, we have

$$\begin{aligned}{}[S^{2i-1}\wedge L,\mathrm {PU}(p)]_{(p)}&\cong \bigl [S^{2i-2}\wedge \bigl (A\vee \textstyle \bigvee _{k=2}^{p-1}P^{2k+1}(p)\bigr ),\mathrm {PU}(p)\bigr ]_{(p)}\\&\cong \bigl [S^{2i-3}\wedge \bigl (S^{2p+1}\vee \textstyle \bigvee _{k=1}^{p-1}P^{2k+2}(p)\bigr ),\mathrm {PU}(p)\bigr ]_{(p)}\\&\cong \pi _{2i+2p-2}(\mathrm {PU}(p))_{(p)}\oplus \bigoplus _{k=1}^{p-1}[P^{2k+2i-1}(p),\mathrm {PU}(p)]_{(p)}. \end{aligned}$$

Since $2i+2p-2\le 4p-2<2p(p-1)+1$ for $p\ge 3$, the group $\pi _{2i+2p-2}(\mathrm {PU}(p))_{(p)}$ consists of elements of order at most p by the same argument as in Lemma 9.

On the other hand, by [17, Theorem 7.1], the groups $[P^{2k+2i-1}(p),\mathrm {PU}(p)]$ have exponent at most p (since, for $m\ge 3$, the identity on $P^m(p)$ has order p), whence the statement. $\square$

Lemmas 8, 9, and 13 together imply:

Lemma 14

The order of the Samelson product

$$\begin{aligned} \langle \epsilon _i,1\rangle _{(p)}:S^{2i-1}_{(p)}\wedge \mathrm {PU}(p)_{(p)}\rightarrow \mathrm {PU}(p)_{(p)} \end{aligned}$$

is at most p. $\square$

We now have all the ingredients necessary to prove Theorem 1.

Proof of Theorem 1

Consider the following commutative diagram

where $\iota :\mathrm {SU}(p)\rightarrow \mathrm {U}(p)$ is the inclusion and $\eta _i:=\iota _*(\delta _i)$. By the unnumbered corollary in Bott [3, p. 250], the map $\langle \eta _i,\eta _{p-i-1}\rangle$ is non-trivial and p divides its order. Hence, the order of $\langle \delta _i,1\rangle _{(p)}$ is at least p. The result now follows from Lemmas 4, 6 and 14. $\square$

4 Homotopy invariants of $\mathrm {PU}(n)$-gauge groups

The content of Lemma 15 is a straightforward observation about how certain homotopy invariants of $\mathrm {SU}(n)$-gauge groups relate to the corresponding invariants of $\mathrm {PU}(n)$-gauge groups.

Lemma 15

Let n be arbitrary and X be a simply-connected space. Suppose further that we have $[X,\mathrm {SU}(n)]\cong 0$. Then, the quotient map $q:\mathrm {SU}(n)\rightarrow \mathrm {PU}(n)$ induces an isomorphism of groups

$$\begin{aligned}{}[X,\mathcal {G}_{i,k}(\mathrm {SU}(n))]\cong [ X,\mathcal {G}_{i,k}(\mathrm {PU}(n))] \end{aligned}$$

for any $2\le i\le n$ and any $k\in \mathbb {Z}$.

Proof

Since $[ X,\mathrm {SU}(n)]\cong 0$ and X is simply-connected, applying the functor $[X,-]$ to the homotopy fibration sequence

$$\begin{aligned} \cdots \longrightarrow \mathbb {Z}/n\mathbb {Z}\longrightarrow \mathrm {SU}(n)\xrightarrow {\ q\ } \mathrm {PU}(n) \longrightarrow \mathrm {B}(\mathbb {Z}/n\mathbb {Z}) \end{aligned}$$

shows that $[X,\mathrm {PU}(n)]\cong 0$ also.

Applying now the functor $[\varSigma X,-]$ to the homotopy fibration sequence

$$\begin{aligned} \mathrm {PU}(n)\xrightarrow {\ \partial _{i,k}\ }\varOmega _0^{2i-1}\mathrm {PU}(n)\longrightarrow \mathrm {B}\mathcal {G}_{i,k}(\mathrm {PU}(n))\longrightarrow \mathrm {B}\mathrm {PU}(n) \end{aligned}$$

described in Sect. 2, as well as to its $\mathrm {SU}(n)$ analogue, yields the following commutative diagram

where the rows are exact and the two leftmost vertical maps are isomorphisms by the same argument as in the proof of Lemma 5. The statement now follows from the five lemma. $\square$

Hamanaka and Kono showed in [7, Theorem 1.2] that, for principal $\mathrm {SU}(n)$-bundles over $S^4$, the homotopy equivalence $\mathcal {G}_{2,k}(\mathrm {SU}(n))\simeq \mathcal {G}_{2,l}(\mathrm {SU}(n))$ implies that $(n(n^2-1),k)=(n(n^2-1),l)$. As an application of Lemma 15, let us show that the analogue of this result holds for $\mathrm {PU}(n)$-gauge groups.

Corollary 1

Let $n> 3$. For principal $\mathrm {PU}(n)$-bundles over $S^4$,if

$$\begin{aligned} \mathcal {G}_{2,k}(\mathrm {PU}(n))\simeq \mathcal {G}_{2,l}(\mathrm {PU}(n)), \end{aligned}$$

then $(n(n^2-1),k)=(n(n^2-1),l)$.

Proof

First, suppose that n is even. Note that we have

$$\begin{aligned} \pi _{2n-4}(\mathrm {SU}(n))\cong \pi _{2n-2}(\mathrm {SU}(n))\cong 0. \end{aligned}$$

Hence, applying Lemma 15 with $X=S^{2n-4}$ and $X=S^{2n-2}$, we find

$$\begin{aligned} \pi _{2n-4}\bigl (\mathcal {G}_{2,k}(\mathrm {PU}(n))\bigr )\cong \pi _{2n-4}\bigl (\mathcal {G}_{2,k}(\mathrm {SU}(n))\bigr ) \end{aligned}$$

and

$$\begin{aligned} \pi _{2n-2}\bigl (\mathcal {G}_{2,k}(\mathrm {PU}(n))\bigr )\cong \pi _{2n-2}\bigl (\mathcal {G}_{2,k}(\mathrm {SU}(n))\bigr ). \end{aligned}$$

So the result follows for n even by [19, Proposition 4.2].

When n is odd, we have from [7] that $[\varSigma ^{2n-6} \mathbb {C}P^2,\mathrm {SU}(n)]\cong 0$. Hence, applying Lemma 15 with $X=\varSigma ^{2n-6}\mathbb {C}P^2$, we find

$$\begin{aligned}{}[\varSigma ^{2n-6} \mathbb {C}P^2,\mathcal {G}_{2,k}(\mathrm {PU}(n))]\cong [\varSigma ^{2n-6} \mathbb {C}P^2,\mathcal {G}_{2,k}(\mathrm {SU}(n))]. \end{aligned}$$

So the result follows for n odd by [7, Corollary 2.6]. $\square$

Following the work of [8], Mohammadi and Asadi-Golmankhaneh [16] recently showed that, for $\mathrm {SU}(n)$-bundles over $S^6$, an equivalence $\mathcal {G}_{3,k}(\mathrm {SU}(n))\simeq \mathcal {G}_{3,l}(\mathrm {SU}(n))$ implies that

$$\begin{aligned} \bigl ((n - 1)n(n + 1)(n + 2), k\bigr ) = \bigl ((n - 1)n(n + 1)(n + 2), l\bigr ). \end{aligned}$$

Hence, we also have:

Corollary 2

Let $n\ge 3$. For principal $\mathrm {PU}(n)$-bundles over $S^6$, if there is a homotopy equivalence $\mathcal {G}_{3,k}(\mathrm {PU}(n))\simeq \mathcal {G}_{3,l}(\mathrm {PU}(n))$, then

$$\begin{aligned} ((n - 1)n(n + 1)(n + 2), k) = ((n - 1)n(n + 1)(n + 2), l). \end{aligned}$$

Proof

Apply Lemma 15 with $X=\varSigma ^{2n-6}\mathbb {C}P^2$ and the result of [16]. $\square$

5 Special cases

5.1 $\mathrm {PU}(p)$-bundles over $S^4$

Theriault showed in [22] that, after localisation at an odd prime p and provided that $n<(p-1)^2+1$, the order of the Samelson product $\langle \delta _2,1\rangle :S^3\wedge \mathrm {SU}(n)\rightarrow \mathrm {SU}(n)$ is the p-primary component of the integer $n(n^2-1)$.

It then follows immediately from Theorem 1 that:

Corollary 3

After localisation at an odd prime, the order of the Samelson product $\langle \epsilon _2,1\rangle :S^3\wedge \mathrm {PU}(p)\rightarrow \mathrm {PU}(p)$ is $p(p^2-1)$. $\square$

5.2 $\mathrm {PU}(5)$-bundles over $S^4$

In [21], Theriault showed that the order of $\langle \delta _2,1\rangle :S^3\wedge \mathrm {SU}(5)\rightarrow \mathrm {SU}(5)$ is 120. Hence, by Theorem 1, the order of $\langle \epsilon _2,1\rangle :S^3\wedge \mathrm {PU}(5)\rightarrow \mathrm {PU}(5)$ is also 120.

Proof of Theorem 2

Part (i) follows from Corollary 1, while part (ii) follows from Lemma 1. $\square$

5.3 $\mathrm {PU}(3)$-bundles over $S^6$

Hamanaka and Kono showed in [8] that the order of $\langle \delta _3,1\rangle :S^5\wedge \mathrm {SU}(3)\rightarrow \mathrm {SU}(3)$ is 120. It follows from Theorem 1 that the order of $\langle \epsilon _3,1\rangle :S^5\wedge \mathrm {PU}(3)\rightarrow \mathrm {PU}(3)$ is also 120.

Proof of Theorem 3

As the homotopy groups $\pi _n(\varOmega _0^5\mathrm {PU}(3))\cong \pi _{n+5}(\mathrm {PU}(3))$ are all finite, the “if” direction follows from Lemma 2, while the “only if” direction follows from Corollary 2. $\square$