Visual high dimensional industrial process monitoring based on deep discriminant features and t-SNE

Abstract

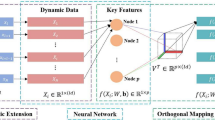
Visual process monitoring allows operators to identify and diagnose faults intuitively and quickly. The performance of visual process monitoring depends on the quality of extracted features and the performance of the visual model to visualize these features. In this study, we propose a deep model for feature extraction. First, a stacked auto-encoder is used to obtain the feature representation of the input data. Second, the feature representation is fed into a multi-layer perceptron (MLP) with the Fisher criterion as the objective function. The outputs of the MLP are the extracted discriminant features. We combine the proposed feature extraction method with the visual model consisting of t-distributed stochastic neighbor embedding (t-SNE) and a back-propagation (BP) neural network (t-SNE-BP) for visual process monitoring. In this method, an industrial data set is reorganized into a dynamic sample set containing fault trend. Subsequently, the proposed feature extraction method is used to extract discriminant features from the dynamic sample set. Finally, the t-SNE-BP model maps these discriminant features into a two-dimensional space in which the normal and fault states are represented by different regions. Visual process monitoring is performed on this two-dimensional space. The Tennessee Eastman process is used to demonstrate the performance of the proposed feature extraction and visual process monitoring methods.

Appendix

The detailed derivation of the parameter updates of MLP is as follows.

• 1. For the output data $\text{y}_{j}^{ (l )}$, $M (\text{y}_{j}^{ (l )} )$ and $N (\text{y}_{j}^{ (l )} )$ denote the average and the number of samples of the class to which $\text{y}_{j}^{l}$ belongs, respectively. For example, if $\text{y}_{j}^{ (l )}$ belongs to class $\text{Y}_{c}^{ (l )}$, then $M (\text{y}_{j}^{ (l )} ) { = }\bar{y}_{c}^{ (l )}$, and $N (\text{y}_{j}^{ (l )} ) { = }n_{c}$. ${{\partial \tilde{J} (\text{W} ,\text{b} )} \mathord{\left/ {\vphantom {{\partial \tilde{J} (\text{W} ,\text{b} )} {\partial \text{y}_{j}^{ (l )} }}} \right. \kern-0pt} {\partial \text{y}_{j}^{ (l )} }}$ is calculated as follows:

  $$ \frac{{\partial \tilde{J} (\text{W} ,\text{b} )}}{{\partial \text{y}_{j}^{ (l )} }}{ = } - \frac{{\partial \left[ {\frac{{tr (\tilde{S}_{b} )}}{{tr (\tilde{S}_{w} )}}} \right]}}{{\partial \text{y}_{j}^{ (l )} }} = - \frac{{tr (\tilde{S}_{w} )\cdot \frac{{\partial tr (\tilde{S}_{b} )}}{{\partial \text{y}_{j}^{ (l )} }} - tr (\tilde{S}_{b} )\cdot \frac{{\partial tr (\tilde{S}_{w} )}}{{\partial \text{y}_{j}^{ (l )} }}}}{{\left( {tr (\tilde{S}_{w} )} \right)^{2} }}, $$

  (12)

  where

  $$ \begin{aligned} \frac{{\partial tr (\tilde{S}_{w} )}}{{\partial \text{y}_{j}^{ (l )} }} & = \frac{\partial }{{\partial \text{y}_{j}^{ (l )} }}\frac{1}{2}\sum\limits_{i = 1}^{c} {\sum\limits_{{\text{y}^{ (l )} \in \text{Y}_{i}^{ (l )} }} {\left\| {\text{y}^{ (l )} - \bar{y}_{i}^{ (l )} } \right\|^{2} } } \\ & { = }\left( {\text{y}_{j}^{ (l )} - M (\text{y}_{j}^{ (l )} )} \right) \cdot \left( { 1- \frac{1}{{N (\text{y}_{j}^{ (l )} )}}} \right) ,\\ \end{aligned} $$

  (13)

  and

  $$ \begin{aligned} \frac{{\partial tr (\tilde{S}_{b} )}}{{\partial \text{y}_{j}^{ (l )} }} & = \frac{\partial }{{\partial \text{y}_{j}^{ (l )} }}\frac{1}{2}\sum\limits_{i = 1}^{c} {\sum\limits_{v = i + 1}^{c} {\left\| {\bar{y}_{i}^{ (l )} - \bar{y}_{v}^{ (l )} } \right\|^{2} } } \\ & { = }\sum\limits_{v = 1}^{c} {\left( {M (\text{y}_{j}^{ (l )} )- M (\text{y}_{v}^{ (l )} )} \right) \cdot \frac{1}{{N (\text{y}_{j}^{ (l )} )}}} .\\ \end{aligned} $$

  (14)

• 2. The value of $\delta^{ (l )}$ for the output layer is calculated.

  $$ \delta^{ (l )} = \frac{{\partial \tilde{J} (\text{W} ,\text{b} )}}{{\partial \text{y}_{j}^{ (l )} }} \cdot \frac{{\partial \text{y}_{j}^{ (l )} }}{{\partial \text{z}_{j}^{ (l )} }} = \frac{{\partial \tilde{J} (\text{W} ,\text{b} )}}{{\partial \text{y}_{j}^{ (l )} }} \cdot f^{\prime } \left( {\text{z}_{j}^{ (l )} } \right), $$

  (15)

  where operator $\cdot$ represents the multiplication of the corresponding position.

• 3. For layer $k = l - 1 , { }l - 2 ,\ldots , { 2}$, $\delta^{ (k )}$ is calculated as follows:

  $$ \delta^{ (k )} = \left( {\left( {\text{W}^{ (k )} } \right)^{\text{T}} \delta^{ (k + 1 )} } \right) \cdot f^{\prime } \left( {\text{z}_{j}^{ (k )} } \right). $$

  (16)

• 4. The gradients are calculated.

  $$ \begin{aligned} & \nabla_{{\text{W}^{ (k )} }} \tilde{J} (\text{W} , { }\text{b} , { }y_{j}^{ (k )} )= \delta^{ (k + 1 )} \left( {y_{j}^{ (k )} } \right)^{\text{T}} \\ & \nabla_{{b^{{^{ (k )} }} }} \tilde{J} (\text{W} , { }\text{b} , { }y_{j}^{ (k )} )= \delta^{ (k + 1 )} \\ \end{aligned} $$

  (17)

• 5. The gradients of all samples in the batch are accumulated.

  $$ \begin{aligned} & \Delta \text{W}^{ (k )} = \Delta \text{W}^{ (k )} + \nabla_{{\text{W}^{ (k )} }} \tilde{J} (\text{W} ,\text{b} ,y ) { } \\ & \Delta b^{ (k )} = \Delta b^{ (k )} + \nabla_{{b^{ (k )} }} \tilde{J} (\text{W} ,\text{b} ,y )\\ \end{aligned} $$

  (18)

• 6. The parameters are updated.

  $$ \begin{aligned} \text{W}^{ (k )} & = \text{W}^{ (k )} - \eta \left[ {\left( {\frac{1}{N}\Delta \text{W}^{ (k )} } \right) + \lambda_{1} \text{W}^{ (k )} } \right] ,\\ b^{ (k )} & = b^{ (k )} - \eta \left( {\frac{1}{N}\Delta b^{ (k )} } \right) ,\\ \end{aligned} $$

  (19)

  where $\eta$ is the learning rate, $\lambda_{1}$ penalizes the large weights to prevent overfitting, and N is the total number of samples in the batch.