Abstract
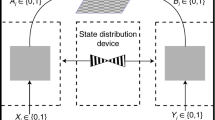
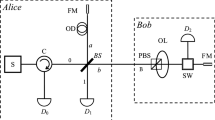
Device and semi-device-independent private quantum randomness generators are crucial for applications requiring private randomness. However, they are vulnerable to detection inefficiency attacks and this limits severely their usage for practical purposes. Here, we present a method for protecting semi-device-independent private quantum randomness generators in prepare-and-measure scenarios against detection inefficiency attacks. The key idea is the introduction of a blocking device that adds failures in the communication between the preparation and measurement devices. We prove that, for any detection efficiency, there is a blocking rate that provides protection against these attacks. We experimentally demonstrate the generation of private randomness using weak coherent states and standard avalanche photo-detectors.


Similar content being viewed by others
Notes
For example, the internal counters of P and M differ by n rounds with some probability, depending on n and the blocking rate.
References
Rarity, J.G., Owens, P.C.M., Tapster, P.R.: Quantum random-number generation and key sharing. J. Mod. Opt. 41, 2435 (1994)
National Institute of Standards and Technology. Computer Security Division. Computer Security Resource Center
Colbeck, R.: Quantum and Relativistic Protocols for Secure Multi-Party Computation. Ph.D. Thesis, Cambridge University. arXiv:0911.3814v2 (2009)
Pironio, S., Massar, S.: Security of practical private randomness generation. Phys. Rev. A 87, 012336 (2013)
Pironio, S., Acín, A., Massar, S., Boyer de la Giroday, A., Matsukevich, D.N., Maunz, P., Olmschenk, S., Hayes, D., Luo, L., Manning, T.A., Monroe, C.: Random numbers certified by Bell’s theorem. Nature 464, 1021 (2010)
Pawłowski, M., Brunner, N.: Semi-device-independent security of one-way quantum key distribution. Phys. Rev. A 84, 010302 (2011)
Li, H.-W., Pawłowski, M., Yin, Z.-Q., Guo, G.-C., Han, Z.-F.: Semi-device-independent randomness certification using \(n\rightarrow 1\) quantum random access codes. Phys. Rev. A 85, 052308 (2012)
Mironowicz, P., Tavakoli, A., Hameedi, A., Marques, B., Pawłowski, M., Bourennane, M.: Increased certification of semi-device independent random numbers using many inputs and more post-processing. New J. Phys. 18, 065004 (2016)
Lunghi, T., Brask, J.B., Lim, C.C.W., Lavigne, Q., Bowles, J., Martin, A., Zbinden, H., Brunner, N.: Self-testing quantum random number generator. Phys. Rev. Lett. 114, 150501 (2015)
Cao, Z., Zhou, H., Ma, X.: Loss-tolerant measurement-device-independent quantum random number generation. New J. Phys. 17, 125011 (2015)
Cao, Z., Zhou, H., Yuan, X., Ma, X.: Source-independent quantum random number generation. Phys. Rev. X 6, 011020 (2016)
Marangon, D.G., Vallone, G., Villoresi, P.: Source-device-independent ultrafast quantum random number generation. Phys. Rev. Lett. 118, 060503 (2017)
Brask, J.B., Martin, A., Esposito, W., Houlmann, R., Bowles, J., Zbinden, H., Brunner, N.: Megahertz-rate semi-device-independent quantum random number generators based on unambiguous state discrimination. Phys. Rev. Appl. 7, 054018 (2017)
Dall’Arno, M., Passaro, E., Gallego, R., Pawłowski, M., Acín, A.: Detection loophole attacks on semi-device-independent quantum and classical protocols. Quant. Inf. Comput. 15, 37 (2015)
Acín, A., Cavalcanti, D., Passaro, E., Pironio, S., Skrzypczyk, P.: Necessary detection efficiencies for secure quantum key distribution and bound randomness. Phys. Rev. A 93, 012319 (2016)
Hameedi, A., Marques, B., Mironowicz, P., Saha, D., Pawłowski, M., Bourennane, M.: Experimental test of nonclassicality with arbitrarily low detection efficiency. Phys. Rev. A 102, 032621 (2020)
Renner, R.: Security of Quantum Key Distribution. arXiv:quant-ph/0512258 (2005)
Koenig, R., Renner, R., Schaffner, C.: The operational meaning of min- and max-entropy. IEEE Trans. Inf. Theory 55, 4337 (2009)
Grier, D.G.: A revolution in optical manipulation. Nature 424, 810 (2003)
Lima, G., Vargas, A., Neves, L., Guzmán, R., Saavedra, C.: Manipulating spatial qudit states with programmable optical devices. Opt. Express 17, 10688 (2009)
Neves, L., Lima, G., Gómez, J.A., Monken, C.H., Saavedra, C., Pádua, S.: Generation of entangled states of qudits using twin photons. Phys. Rev. Lett. 94, 100501 (2005)
Goyeneche, D., Cañas, G., Etcheverry, S., Gómez, E.S., Xavier, G.B., Lima, G., Delgado, A.: Five measurement bases determine pure quantum states on any dimension. Phys. Rev. Lett. 115, 090401 (2015)
Cañas, G., Etcheverry, S., Gómez, E.S., Saavedra, C., Xavier, G.B., Lima, G., Cabello, A.: Experimental implementation of an eight-dimensional Kochen–Specker set and observation of its connection with the Greenberger–Horne–Zeilinger theorem. Phys. Rev. A 90, 012119 (2014)
Aguilar, E.A., Farkas, M., Martínez, D., Alvarado, M., Cariñe, J., Xavier, G.B., Barra, J.F., Cañas, G., Pawłowski, M., Lima, G.: Certifying an irreducible 1024-dimensional photonic state using refined dimension witnesses. Phys. Rev. Lett. 120, 230503 (2018)
Solís-Prosser, M.A., Fernándes, M.F., Jiménez, O., Delgado, A., Neves, L.: Experimental minimum-error quantum state discrimination in high dimensions. Phys. Rev. Lett. 118, 100501 (2017)
Marques, B., Matoso, A.A., Pimenta, W.M., Gutiérrez-Esparza, A.J., Santos, M.F., Pádua, S.: Experimental simulation of decoherence in photonics qudits. Sci. Rep. 5, 16049 (2017)
Torres-Ruiz, F.A., Lima, G., Delgado, A., Pádua, S., Saavedra, C.: Decoherence in a double-slit quantum eraser. Phys. Rev. A 81, 042104 (2010)
Lima, G., Neves, L., Guzmán, R., Gómez, E.S., Nogueira, W.A.T., Delgado, A., Vargas, A., Saavedra, C.: Experimental quantum tomography of photonic qudits via mutually unbiased basis. Opt. Express 19, 3542 (2011)
Etcheverry, S., Cañas, G., Gómez, E.S., Nogueira, W.A.T., Saavedra, C., Xavier, G.B., Lima, G.: Quantum key distribution session with 16-dimensional photonic states. Sci. Rep. 3, 2316 (2013)
Moreno, I., Velásquez, P., Fernandez-Pousa, C.R., Sánchez-López, M.M., Mateos, F.: Jones matrix method for predicting and optimizing the optical modulation properties of a liquid-crystal display. J. Appl. Phys. 94, 3697 (2003)
Liu, Y., Yuan, X., Li, M.H., Zhang, W., Zhao, Q., Zhong, J., Cao, Y., Li, Y.-H., Chen, L.-K., Li, H., Peng, T., Chen, Y.-A., Peng, C.-Z., Shi, S.-C., Wang, Z., You, L., Ma, X., Fan, J., Zhang, Q., Pan, J.-W.: High-speed device-independent quantum random number generation without a detection loophole. Phys. Rev. Lett. 120, 010503 (2018)
Eaton, J.W., Bateman, D., Hauberg, S., Wehbring, R.: GNU Octave Version 4.2.0 Manual: A High-Level Interactive Language for Numerical Computations. http://www.gnu.org/software/octave/doc/interpreter (2016)
Sturm, J.F.: Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Softw. 11, 625 (1999)
Löfberg, J.: YALMIP: a toolbox for modeling and optimization in MATLAB. In: IEEE International Symposium on Computer Aided Control Systems Design (2004). IEEE, New York, p. 284
Li, H.-W., Yin, Z.-Q., Wu, Y.-C., Zou, X.-B., Wang, S., Chen, W., Guo, G.-C., Han, Z.-F.: Semi-device-independent random-number expansion without entanglement. Phys. Rev. A 84, 034301 (2011)
Mironowicz, P., Li, H.W., Pawłowski, M.: Properties of dimension witnesses and their semi-definite programming relaxations. Phys. Rev. A 90, 022322 (2014)
Ambainis, A., Nayak, A., Ta-Shma, A., Vazirani, U.: Dense quantum coding and quantum finite automata. J. ACM 49, 496 (2002)
Ambainis, A., Leung, D., Mancinska, L., Ozols, M.: Quantum random access codes with shared randomness. arXiv:0810.2937 (2008)
Werner, R.F., Wolf, M.M.: Bell inequalities and entanglement. Quantum Info. Comput. 1, 1 (2001)
Pál, K.F., Vértesi, T.: Maximal violation of a bipartite three-setting, two-outcome Bell inequality using infinite-dimensional quantum systems. Phys. Rev. A 82, 022116 (2010)
Vandenberghe, L., Boyd, S.: Semidefinite programming. SIAM Rev. 38, 49 (1996)
Acknowledgements
This work was supported by Fondecyt 1200859, Fondecyt 1190933, Fondecyt 1190901, Fondecyt 1150101, and ANID—Millennium Science Initiative Program—ICN17_012. J.F.B. acknowledges support from Fondecyt 3170307. J.C. acknowledges support from ANID/REC/PAI77190088. A.C. acknowledges support from the Ministry of Science, Innovation and Universities (MICIU) Grant No. FIS2017-89609-P with FEDER funds, the Conserjería de Conocimiento, Investigación y Universidad, Junta de Andalucía and European Regional Development Fund (ERDF) Grant No. SOMM17/6105/UGR and the Knut and Alice Wallenberg Foundation project “Photonic Quantum Information”. G.B.X. acknowledges Ceniit Linköping University and the Swedish Research Council (VR 2017-04470) for financial support. P.M. and M.P are supported by a National Science Centre (NCN) grant 2014/14/E/ST2/00020 and FNP programme First TEAM (Grant No. First TEAM/2016-1/5), and P.M. by a DS Programs of the Faculty of Electronics, Telecommunications and Informatics, Gdańsk University of Technology. The support by the Foundation for Polish Science through IRAP project co-financed by the EU within the Smart Growth Operational Programme (Contract No. 2018/MAB/5) is acknowledged. P.M. thanks Krystyna Witalewska for help during the time of writing the manuscript. The optimizations have been performed using OCTAVE [32] with SeDuMi solver [33] and YALMIP toolbox [34].
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Guessing probability, min-entropy and randomness certification
The distribution of lengths of series of systems sent and not blocked by the blocking mechanism at a rate R is given by
where \(k \ge 1\) is the number of systems in a series.
Let us denote by \(\alpha \) the ratio between the number of systems containing synchronization signal sent by P and the total number of systems sent by P, cf. the assumption III.
In a given series of transmitted systems of length k, the average number of photons before the first synchronizing system within that series is
Using (13), we get that the probability that a particular photon received by M is not synchronized is
for \(\alpha > 0\) and \(P_\text {asyn}(R, 0) = 1\). Directly from the definition of \(\alpha \), the probability that the received system is a synchronization signal is
The probability that a received system is synchronized and not carrying a synchronization signal is
for \(\alpha > 0\) and \(P_\text {syn}(R, 0) = 0\). One can easily calculate that  . Let us define \(F_\text {syn}(R) \equiv \max _{\alpha \in [0,1]} P_\text {syn}(R, \alpha )\). Then,
. Let us define \(F_\text {syn}(R) \equiv \max _{\alpha \in [0,1]} P_\text {syn}(R, \alpha )\). Then,
If \({\mathbb {P}}\) is a mixture of distributions \({\mathbb {P}}_i\) with frequencies \(\{\omega _i\}\), \(\sum _i \omega _i = 1\), and an eavesdropper is aware which distribution i occurs, we have \(P_{guess}[{\mathbb {P}}] \equiv \sum _i \omega _i P_{guess}[{\mathbb {P}}_i]\).
Let us consider separately runs of the protocol without synchronization (abbreviated as “asyn”), runs containing synchronization signal (abbreviated as “sig”) and synchronized runs without the signal (abbreviated as “syn”).
Let \(P_{guess}^\text {asyn}(p,\eta ),P_{guess}^\text {sig}(p,\eta ),P_{guess}^\text {syn}(p,\eta )\) be functions providing upper bounds on the maximal average guessing probabilities, \(p_\text {asyn},p_\text {sig},p_\text {syn}\) be the average values of the certificate (3), and \(\eta _\text {asyn},\eta _\text {sig},\eta _\text {syn}\) be the detection efficiencies (2), in the respective runs. These values cannot be observed individually by a user, but each of them has impact on the observed values of (3) and (2).
Let \(\mathbf {p} \equiv (p_\text {asyn},p_\text {sig},p_\text {syn})\) and \(\mathbf {\eta } \equiv (\eta _\text {asyn},\eta _\text {sig},\eta _\text {syn})\). Note that \(p_\text {asyn} \le c_Q\), \(p_\text {sig} \le c_R\) and \(p_\text {syn} \le c_S(\eta _\text {syn})\). Let \({\mathscr {M}} \equiv \{\text {asyn}, \text {sig}, \text {syn}\}\), \({\bar{\eta }} \equiv \sum _{i \in {\mathscr {M}}} \eta _i P_i(R,\alpha ) \), and \(\omega _i \equiv \frac{\eta _i P_i(R,\alpha )}{{\bar{\eta }}}\) for \(i \in {\mathscr {M}}\), thus \(\sum _{i \in {\mathscr {M}}} \omega _i = 1\).
Let us also define
Using the above expression, we can give the following upper bounds on the maximal average guessing probability for the blocking parameter R, the observed value p of the certificate (3) and the observed value \(\eta \) of the detection efficiency (2):
Note that the constraints can be equivalently rewritten as \(\sum _{i \in {\mathscr {M}}} \eta _i P_{guess}(R,\alpha ) = \eta p\) and \({\bar{\eta }} = \eta \), and these forms are used in “Appendix B”.
Since (19) involves (18a) to perform maximization, we need explicit formulae for \(P_{guess}^i(p_i,\eta _i)\), \(i \in {\mathscr {M}}\). Since “sig” runs are deterministic, we have \(P_{guess}^\text {sig}(p_\text {sig},\eta _\text {sig}) \equiv 1\). \(P_{guess}^\text {asyn}(p_\text {asyn},\eta _\text {asyn})\) is a guessing probability of an eavesdropper not exploiting the detection loophole, thus it doesn’t depend on \(\eta _\text {asyn}\). We provide analysis for this function in this section below. The function \(P_{guess}^\text {syn}(p_\text {syn},\eta _\text {syn})\) has to be developed independently for different formulae for the certificate (3), as this depends on a particular form of detection loophole attack.
Let us now consider a private SDI-QRNG protocol given by some certificate of a form (3) in some fixed dimension. For some \(p \in (c_L, c_Q]\), we have the following formula for \(P_{guess}^\text {asyn}(p,\eta )\):
Without restricting the power of an eavesdropper, we may assume that
i.e., the probability of the result e does not depend on x and z. This can be obtained using proper extension of \({\mathscr {H}}_E\), or providing some additional “idle” information to an extended set E.
From (6), it follows that when \(\left\{ \rho _x \right\} \), \(\{M^b_z\}\) and \(\left\{ N^e_{x,z} \right\} \) are fixed, then for an eavesdropper having access to \({\mathscr {H}}_E\) the optimal guessing function \({\varvec{g}}: X \times Z \times E \rightarrow B\) is
i.e., a function returning a most probable result b for each x, z and e.
Using no-signaling \({\mathbb {P}}_{B|XZ}(b|x,z) = \sum _{e \in E} {\mathbb {P}}_{BE|XZ}(b,e|x,z)\) and (21), we get
Thus, we can rewrite (20) as
Obviously, \(\sum _e {\mathbb {P}}_E(e) = 1\) and the probability distribution is obtained by quantum measurements, see (9b). We can relax the latter constraint and replace \({\mathbb {P}}_E(e)\) with nonnegative coefficients \(c_e\), with \(\sum _e c_e = 1\). Then (20) can be relaxed as
where cf. (8),
Appendix B: Proof of the blocking protocol theorem
From (19), it follows that to have \(P_{guess}(R,\eta ,p) = 1\) we need
For (27a) to hold, we need \(p_\text {asyn} \le c_L\).
Now, assuming \(p_\text {asyn} \le c_L\), and using \(p_\text {sig} \le c_L\), we relax the constraints in the optimization problem (19):
Using (28) and the theorem’s assumption \(p > c_L\), we get
From (17), we know there exists \(R < 1\) such that \(P_\text {syn}(R,\alpha ) < \epsilon \). The contradiction with \(p_\text {asyn} \le c_L\) shows that (27a) cannot be satisfied for all R.
What remains for the proof is to show that also (27b) is not true. To show this considers the following relaxation of constraints in (19):
and (28b). Substituting the latter into (30), we get
Since, for some blocking rate \(R < 1\), the value of \(F_\text {syn}(R)\) is arbitrary small and \(p - c_R > 0\), we see that also (27b) is not satisfied. Therefore, there exists a blocking rate R such that \(P_{guess}(R,\eta ,p) < 1\).
Appendix C: Randomness of \(2 \rightarrow 1\) quantum random access code
A common example [6, 35, 36] of a certificate (3) is based on the so-called \(2 \rightarrow 1\) quantum random access code [37, 38] in dimension 2:
with \(X = \{00,01,10,11\}\), \(Z = \{0,1\}\), \(B = \{0,1\}\). Results of our experimental implementation of this QRAC are shown in Table 1.
To calculate the maximal average guessing probability and min-entropy in the proposed protocol, we performed optimization over the set of all probability distributions allowed by quantum mechanics using the see-saw technique [39, 40] of semi-definite programming [41] and computed \(g(p_e, e)\) from (26) with:
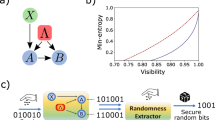
where \(\{ \rho _x \} = \{ \rho _{00},\rho _{01},\rho _{10},\rho _{11} \}\) are states, \(\{ M^b_z \} = \{ \{M^0_0,M^0_1\},\{M^1_0,M^1_1\} \}\) are measurements on a Hilbert space of dimension 2, and \({\varvec{{\tilde{g}}}}\) is a possible guessing strategy when x and z are known. We took \({\mathbb {P}}_{XZ}(x,z) = \frac{1}{ \left| X \, \right| \left| Z \, \right| } = \frac{1}{8}\). In this case, \(c_L = \frac{3}{4}\) and \(c_Q = \frac{1}{2}+\frac{\sqrt{2}}{4} \approx 0.8536\). The result of the optimization as a function of \(p_e\) is shown in Fig. 3. From (25), we conclude the following formula for G(p):
(Color online) Maximal average guessing probability for a certificate (32) based on \(2 \rightarrow 1\) quantum random access code obtained using see-saw technique with the formula (33). The function is not differentiable at points relating to changes of the optimal guessing function \({\varvec{g}}: X \times Z \rightarrow B\), which are \({\varvec{g}}_1(x_0,x_1,z) = x_0\), \({\varvec{g}}_2(x_0,x_1,z) = x_0 \cdot x_1 \vee x_1 \cdot z\) and \({\varvec{g}}_3(x_0,x_1,z) = x_z\) (reading from the left of the plot)
Now, we give the explicit formula for \(P_{guess}^\text {syn}(p_\text {syn},\eta _\text {syn})\) for the considered protocol. M is allowed not to click in \(1-\eta \) part of rounds, and using detection efficiency loophole it can mimic a higher value of the certificate (32). The method is the following.
If \(\eta \le \frac{1}{2}\), then the malevolent vendor can use the following strategy for all inputs. P is encoding one bit from the input, \(x_0\) or \(x_1\) with equal ratio. The choice which bit to encode is guided by shared randomness. If the input z matches the encoded bit, M measures the qubit and satisfies the certificate (32) with probability 1. Otherwise M outputs \(\emptyset \). An upper bound on the maximal average guessing probability is given by:
If \(\eta > \frac{1}{2}\) then in \(2(1-\eta )\) part of rounds P uses the above encoding strategy and the device attains \(W^{2 \rightarrow 1}\left[ {\mathbb {P}}\right] = 1\). In the remaining \(2\eta -1\) part of rounds, P and M use the states and measurements referring to the value of the certificate (32) equal to some \(q \in [c_L, c_Q]\). The observed average value of the certificate in such a strategy is
The detection loophole allows to achieve the value of (36) up to \(\frac{2\eta + \sqrt{2} - 1}{2 \sqrt{2} \eta } \le 1\) with \(q = c_Q\). Thus,
The value of (36) equals \(p_\text {syn} \le c_S({\eta _\text {syn}})\) if and only if \(q = \frac{\eta _\text {syn} (1+p_\text {syn}) - 1}{2\eta _\text {syn} -1}\). The maximal average guessing probability is then upper bounded by
or, equivalently,
and is lower than 1 if and only if \(p_\text {syn} > \frac{1}{2} + \frac{1}{4 \eta _\text {syn}}\) or, equivalently, \(q > \frac{3}{4}\). Using this, we get that an upper bound on the maximal average guessing probability is in this case given by
Let us now give an explicit formula for an upper bound on the maximal average guessing probability, see (19), in this scenario. Let us define, cf. (36),
We have
where \(q^\text {fun}\), cf. (18b) is given by
Let us denote
Now, use the constraint \(\eta ^\text {fun} \left( R,\alpha ,\mathbf {\eta }\right) = \eta \), or, equivalently, \( \eta _\text {sig} P_\text {sig}(R,\alpha ) = \eta - x - y\), to eliminate \(\eta _\text {sig}\). We separate further analysis in two cases.
In the case with \(\eta _\text {syn} \in [0, \frac{1}{2}]\), we have \(y \le \frac{1}{2 \eta } P_\text {syn}(R,\alpha )\). Let us denote for this case \(z^{-} \equiv x \times \left( p_\text {asyn} - \frac{3}{4}\right) \). Then, (42) transforms to
where \(A^{-}(R,\eta ,p,\alpha ) \subseteq {\mathscr {R}}^3\) is defined by the following linear constraints:
In the case with \(\eta > \frac{1}{2}\), we have \(y \ge \frac{1}{2} P_\text {syn}(R,\alpha )\). Let us now denote
As in the previous case, (42) transforms to
where \(A^{+}(R,\eta ,p,\alpha ) \subseteq {\mathscr {R}}^3\) is defined by the following linear constraints:
It is easy to see that, for fixed \(\alpha \in [0,1]\), the internal optimization in (45) and (48) is a linear program. Thus, we derive the following formula for \(P_{guess}(R,\eta ,p)\) for this scenario:
with \(P_{guess}^{\pm }(R,\eta ,p) \equiv 0\) if \(A^{\pm } = \emptyset \).
Appendix D: Direct calculations of the experimental randomness
We take the experimental value \(p = 0.8425\) and \(\eta = 0.06\) for \(R = 0.99\), as used in the setup. From our calculations of (45) and (48), it follows that the maximal average guessing probability is obtained for \(\alpha = 0.499\). In that case, \(\eta _\text {asyn} = 0.11880\), \(\eta _\text {sig} = 0\) and \(\eta _\text {syn} = 0.5\). We have \(\omega _\text {asyn} = 0.98951\), \(\omega _\text {sig} = 0\) and \(\omega _\text {syn} = 0.01049\) with \(p_\text {asyn} = 0.84083\) and \(p_\text {syn} = 1\). This gives \(G(0.84083) = 0.87155\). Direct calculation of (35) gives
and thus \(-\log _2(0.87289) \approx 0.19612\). Since only \((1-R) \times \eta = 0.0006\) emitted photons are detected, the generation ratio of min-entropy is
Analogous calculations for \(R = 0.3\), \(\eta = 0.78\), and optimal \(\alpha = 0.157\). This gives \(P_\text {asyn}(R,\alpha ) = 0.71827\), \(P_\text {sig}(R,\alpha ) = 0.157\), \(P_\text {syn} = 0.12473\) with \(\eta _\text {asyn} = 0.99912\), \(\eta _\text {sig} = 0\), \(\eta _\text {syn} = 0.5\). Here \(p_\text {asyn} = 0.82881\) and \(p_\text {syn} = 1\), giving \(G(0.82881) = 0.88854\). From this, it follows that \(\omega _\text {asyn} = 0.92004\), \(\omega _\text {sig} = 0\), and \(\omega _\text {syn} = 0.07996\). Direct calculation gives
and
Rights and permissions
About this article
Cite this article
Mironowicz, P., Cañas, G., Cariñe, J. et al. Quantum randomness protected against detection loophole attacks. Quantum Inf Process 20, 39 (2021). https://doi.org/10.1007/s11128-020-02948-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-020-02948-3