1 Introduction

The pinhole imaging system is the simplest imaging structure. Only one pinhole realizes the imaging function, but because the luminous flux is very small and the resolution is also limited, its application is greatly limited. To solve the problem, the concept of coded aperture imaging is proposed by Dick [1], which is widely used in X-ray and γ-ray imaging[2,3,4]. Since the coded aperture imaging system is not limited by the lens, the ultra-thin camera is possible. Receiving more attention in recent years, it is proposed to apply the coded aperture imaging system to the visible light [5,6,7,8,9], using URA [10]and MURA [11] as coded apertures, and other forms of coded aperture, such as diffuser [12,13,14], protective glass [15] or optical fiber [16]. The main advantages of this imaging system are the large field of view and miniaturization, but the image quality is not better than a lens. In theory, a lens-less imaging system can also achieve perfect imaging, but there is a large gap between its imaging quality and the lens imaging system. Because the reconstruction image is easily affected by noise, obtaining a good image requires a suitable reconstruction algorithm, which not only suppresses the noise, but also ensures the image resolution. Thanks to the development of computational imaging technology, many excellent algorithms are used to improve the image quality of the coded aperture imaging system, including algorithms such as ADMM [8, 12, 17] and neural networks [7, 8, 18], which can obtain better images. But at the same time, it brings new problems. To suppress the noise, the resolution of the reconstructed image will make some sacrifices. So, the SNR of the coded aperture system is a significant factor in resolution.

In this article, we have established the theoretical model and prototype of the coded aperture lens-less imaging system, analyzed the SNR of the coded aperture imaging system, and mainly considered the Poisson noise and calibration error to the SNR of the reconstructed image. The results show that the SNR is a function of the number of light-emitting points. Using LCD as the target simulator, display uniform bright squares of different sizes, and calculate the SNR of the uniform area after reconstructing the image. Simulation and experiment have relatively consistent results, more points in the scene, more noise. If the scene fills the field of view, a poor image that needs noise reduction and resolution sacrifice will be displayed. It is also mentioned in the literature [12] that the non-linear algorithm reconstructed image may cause the resolution of multiple points to decrease. We simulated the effect of increasing the number of light-emitting points on the resolution. With the increase of the number of light-emitting points, it is indeed impossible to resolve the striped target, but it can still be recognized after multi-frame superposition, indicating that for the linear algorithm, the resolution does not decrease, but is disturbed by strong noise. However, after adding constraints or using a non-linear algorithm, the SNR will be greatly improved, while the resolution is indeed reduced. To solve this problem, we analyze the properties of the SNR and proposed a segmented area imaging method to improve the quality of images.

2 The coded aperture imaging system

2.1 Optical system

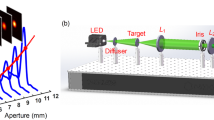
The coded aperture imaging system is a generalization of pinhole imaging. Multiple pinholes are used to replace a single pinhole. The distribution of pinholes is specially designed, so it is called a coded aperture. The system composition is shown below (Fig. 1).

Fig. 1
figure 1

Scheme of a coded aperture imaging system

Full size image

The entire imaging system consists only of a sensor and a coded aperture. The coded aperture is composed of multiple light-transmitting small holes and is parallel to the surface of the sensor. After the light emitted from a point target on the object side passes through the coded template, a pattern will be generated on the photosensitive surface of the detector, and this pattern is highly related to the coded aperture.

According to the composition of the system, the propagation of the light field is divided into three steps. First, the spherical wave emitted by the target passes through free space to reach the coded aperture, then is modulated by the coded aperture, and then diffracts to reach the sensor. The light emitted by the target is non-coherent, so the response of the light emitted by a point on the sensor, the HPSF, can be calculated first, and then the convolution of the HPSF with the scene image is used to obtain the image data recorded by the sensor. To reduce the impact of discrete sampling on simulation results, we up-sampled the simulation image and the coded aperture by ten times and used ten-time down-sampling when the sensor output data (Fig. 2).

Fig. 2
figure 2

Simulation model

Full size image

The point target \(P_0\) emits a spherical wave with a complex amplitude in the X–Y plane where the coded aperture is:

$$ U_0 \left( {x,y} \right) = \frac{A_0 }{r}e^{ikr} = \frac{A_0 }{{\sqrt {(x - x_0 )^2 + (y - y_0 )^2 + z^2 } }}e^{i\frac{2\pi }{\lambda }\sqrt {(x - x_0 )^2 + (y - y_0 )^2 + z^2 } } . $$
(1)

The light field behind the mask is:

$$ U_1 \left( {x,y} \right) = U_0 (x,y)M(x,y). $$
(2)

The distance between the coded aperture and the sensor is relatively close, which is generally smaller than the effective size of the coded aperture. Theoretically, the Fresnel diffraction conditions are not met. Rayleigh Sommerfeld diffraction [19,20,21,22] should be used, but considering that the diffraction energy of a pinhole is mainly concentrated in the Fresnel diffraction area, so it is possible to use Fresnel diffraction and Rayleigh Sommerfeld diffraction for the simulation of the diffraction from the coded aperture to the sensor. The pinhole simulation results also show that the results of the two methods are more consistent. Due to the upsampling, the calculation is relatively large in the simulation process, and the relative calculation speed of Fresnel diffraction is fast, so in this paper, we use Fresnel diffraction to simulate the diffraction process. Therefore, the complex amplitude of the light field obtained on the sensor is:

$$ U_2 (x_1 ,y_1 ) = {\text{Fresnel}}\{ U_1 (x,y)\} . $$
(3)

Based on the above analysis, we define the impulse response of the optical system as hardware PSF (HPSF),

$$ {\text{HPSF}} = U_2 (x_1 ,y_1 )U_2^* (x_1 ,y_1 ). $$
(4)

When the system captures the target X, the light intensity distribution recorded by the sensor:

$$ \tilde{Y} = t \times X \otimes {\text{HPSF}} + N, $$
(5)

where t is a coefficient related to exposure time, X is the scene, and N is noise from the sensor. The noise here represents the deviation between the measured value and the true value, including both Poisson noise and additive noise. Reconstructing X can use a deconvolution-related algorithm. For ease of analysis, we write the above formula in matrix form,

$$ \tilde{y} = t \times Hx + N, $$
(6)

H is the matrix form of the HPSF. In an ideal geometric optical model, for a coded Aperture lens-free imaging system, H consists of ‘0’ and ‘1’. But in the case of diffraction, it no longer has ‘0’ elements. Each row of H contains some or all of the elements in HPSF, and the elements arrangement order between rows is different, and x in formula (6) is the vector form of the scene, and all the elements in the scene are arranged in a certain order, which is related to the convolution operation rules. If the size of HPSF is m × n and the size of X is p × q, the size of H is [(m + p − 1)(n + q − 1)] × (p × q). For example, if X contains 10,000 pixels, H will contain more than 100 million elements, which will cause a lot of calculation. One way to reduce the complexity is to use a separable mask[5]. While this expression is mainly for the convenience of analysis, and conv2 function in MATLAB is used for calculation in the simulation experiment.

Measured value of H is expressed by \(\tilde{H}\). The reconstructed image of the target can be expressed as:

$$ \tilde{X} = \tilde{H}^{ - 1} \tilde{y}. $$
(7)

Due to the existence of noise and measurement error, there is a certain deviation(h) between \(\stackrel{\sim }{H}\) and H, so \(\stackrel{\sim }{H}\)=H–h, the above formula can be rewritten as:

$$ \begin{gathered} \tilde{x} = t\tilde{H}^{ - 1} \left( {Hx + N} \right) \\ = t \times x + t \times \tilde{H}^{ - 1} hx + \tilde{H}^{ - 1} N, \\ \end{gathered} $$
(8)

where t is the exposure time, which ensures that the detector receives enough photons, x in the first term is the ideal image of the target, and the second term is the deviation caused by the measurement error of the HPSF and is only related to the target X since h is fixed after \(\stackrel{\sim }{H}\) was measurement. The third term is the deviation caused by noise.

2.2 The SNR of the reconstructed image

To facilitate analysis, we rewrite Eq. (8) as:

$$ \left[ \begin{gathered} \tilde{x}_1 \hfill \\ \tilde{x}_2 \hfill \\ \vdots \hfill \\ \tilde{x}_{m - 1} \hfill \\ \tilde{x}_m \hfill \\ \end{gathered} \right] = t\left[ \begin{gathered} x_1 \hfill \\ x_2 \hfill \\ \vdots \hfill \\ x_{m - 1} \hfill \\ x_m \hfill \\ \end{gathered} \right] + t\left[ \begin{gathered} a_1 \hfill \\ a_2 \hfill \\ \vdots \hfill \\ a_{m - 1} \hfill \\ a_m \hfill \\ \end{gathered} \right]\left[ \begin{gathered} x_1 \hfill \\ x_2 \hfill \\ \vdots \hfill \\ x_{m - 1} \hfill \\ x_m \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} b_1 \hfill \\ b_2 \hfill \\ \vdots \hfill \\ b_{m - 1} \hfill \\ b_m \hfill \\ \end{gathered} \right]\left[ \begin{gathered} n_1 \hfill \\ n_2 \hfill \\ \vdots \hfill \\ n_{m - 1} \hfill \\ n_m \hfill \\ \end{gathered} \right], $$
(9)

where \(a_m\), \(b_m\) are all row vectors. Then we can get the value of the jth pixel,

$$ \tilde{x}_j = tx_j + t\sum_{i = 1}^m {a_j \left( i \right)} x_i + \sum_{i = 1}^m {b_j \left( i \right)} n_i . $$
(10)

Noting that \(S_1 \left( j \right) = t\sum_{i = 1}^m {a_j \left( i \right)} x_i\), which is the deviation caused by h, \(S_2 \left( j \right) = \sum_{i = 1}^m {b_j \left( i \right)} n_i\) which is the deviation caused by noise. The SNR can be defined as the ratio of the true value to the standard deviation:

$$ \begin{gathered} {\text{SNR}} = \frac{{E\left( {\tilde{x}_j } \right)}}{{\sqrt {D\left( {\tilde{x}_j } \right)} }} \\ = \frac{{td + E\left( {S_1 {| }j \in 1:p} \right) + E\left( {S_2 {| }j \in 1:p} \right)}}{{\sqrt {D\left( {x_j {| }j \in 1:p} \right) + D\left( {S_1 {| }j \in 1:p} \right) + D\left( {S_2 {| }j \in 1:p} \right)} }}, \\ \end{gathered} $$
(11)

where d and p are the brightness and the number of lighting points. E(•) is the mean function, and D(•) is the variance function. \(j \in 1:p\) means that j belongs to an integer in the closed interval [1, p], and p is the number of light points. Because \(x_j\), S1 and S2 are not related to each other, there is no covariance in the above formula, and \(x_j - E(x_j ) = 0\). When calibrating H, multiple measurements can be performed to make the elements of h as small as possible, so that its influence can be reduced as much as possible. It can be considered as the disturbance caused by h, \(D\left[ {S_1 \left( j \right){| }j \in 1:p} \right] \approx 0\), which means the variance of all \(S_1 \left( j \right)\) so

$$ {\text{SNR}} = \frac{{td + E\left[ {S_1 \left( j \right){| }j \in 1:p} \right] + E\left[ {S_2 \left( j \right){| }j \in 1:p} \right]}}{{\sqrt {D\left[ {S_1 \left( j \right){| }j \in 1:p} \right] + D\left[ {S_2 \left( j \right){| }j \in 1:p} \right]} }}. $$
(12)

Besides, \(n_i\) can be rewritten as \(n_i { = }\tilde{y}_i - y_i + n_i^g\), where \(y_i\) is the truth of the response of the detector to photons, and \(\tilde{y}_i\) is the measured value of \(y_i\), according to Poisson distribution \({\text{Possion}}\left( {y_i ,y_i } \right)\). So \(\tilde{y}_i - y_i\) is Poisson noise, and its variance is equal to \(y_i\). \(n_i^g\) is additive noise. Noting that \(S_2^p \left( j \right){ = }\sum_{i = 1}^m {b_j \left( i \right)} \tilde{y}_i\), \(S_2^g \left( j \right){ = }\sum_{i = 1}^m {b_j \left( i \right)} n_i^g\), \(S_2^r \left( j \right){ = }\sum_{i = 1}^m {b_j \left( i \right)} y_i = tx_j\). Because \(\tilde{y}_i \sim {\text{Possion}}\left( {y_i ,y_i } \right)\),

$$ S_2^p \left( j \right) \sim {\text{Skellam}}\left( {\sum_{i = 1}^m {b_j \left( i \right)} y_i ,\sum_{i = 1}^m {\left| {b_j \left( i \right)y_i } \right|} } \right), $$
(13)
$$ S_2^g \left( j \right) \sim N\left( {0,\sum_{i = 1}^m {\left[ {b_j \left( i \right)} \right]}^2 \sigma_i } \right), $$
(14)

where \(S_2^p \left( j \right)\) and \(S_2^g \left( j \right)\), respectively, conform to skellam distribution and normal distribution, \(\sigma_i\) is the variance of \(n_i^g\), and \(n_i^g\) is assumed to conform to a normal distribution. Then we can get that,

$$ E\left[ {S_2 \left( j \right){| }j \in \left( {1,p} \right)} \right] = td - td + 0 = 0, $$
(15)
$$ \begin{gathered} D\left[ {S_2 \left( j \right){| }j \in \left( {1,p} \right)} \right] = D\left[ {S_2^p \left( j \right){| }j \in \left( {1,p} \right)} \right] + D\left[ {S_2^r \left( j \right){| }j \in \left( {1,p} \right)} \right] + D\left[ {S_2^g \left( j \right){| }j \in \left( {1,p} \right)} \right] \\ { = }\sum_{i = 1}^m {\left| {b_j \left( i \right)y_i } \right|} { + }0{ + }\sum_{i = 1}^m {\left[ {b_j \left( i \right)} \right]}^2 \sigma_i . \\ \end{gathered} $$
(16)

Because the elements of H are all greater than 0, there must be \(y_i \left( {p = n} \right) \ge y_i \left( {p = n{ - }1} \right)\). If \(\sigma_i\) does not change, it is obvious that \(D\left( {S_2 {|}n = p} \right) \ge D\left( {S_2 {|}n = p - 1} \right)\).

Through the above derivation, it shows that SNR decreases as the number of luminous points increases. However, when the luminous point decreases, the SNR will not increase indefinitely. It is affected by additive noise, and there is an extreme value of SNR.

When HPSF has only one element, namely point-to-point imaging, such as lens imaging or hole imaging under ideal conditions, H is close to the identity matrix, and its SNR is no longer affected by the number of luminous points. Formula (16) also indicates that reducing the absolute value of b is beneficial to control the SNR of the reconstructed image, which provides inspiration for the design of the coding template, and can give full play to the designability of the coding template in coded aperture imaging.

3 Simulation

Formula (12) can only reveal that the SNR of each pixel decreases as the number of luminous points increases. We can infer that the SNR of each pixel becomes worse, and the SNR of the entire image will also become worse. To confirm this conjecture, the simulation experiment is carried out by using the model. The target adopts a rectangular pattern with a side length of 20 pixels to 126 pixels and applies Poisson noise to the energy distribution on the detector. Reconstructing image using wiener deconvolution with consistency parameter, the SNR of 20 × 20 pixels in the central area of the reconstructed image is counted and repeated 60 times to calculate the average value of the SNR of the reconstructed image. The result is shown in the Fig. 3.

Fig. 3
figure 3

As the target luminous point increases, the SNR of the reconstructed image using wiener deconvolution gradually decreases, sigma = 10

Full size image

The bigger the target is, the worse the SNR will be. To achieve the same SNR as the small target, R-Lucy deconvolution can be used to suppress noise. while the three-line target cannot be distinguished showing as Fig. 4(b). If the noise is not suppressed, the noise may overwhelm the signal, making it impossible to distinguish between different light-emitting points.

Fig. 4
figure 4

Reconstruction with R-Lucy algorithm shows that when the target is small, (a) has a higher resolution than when the target is large. After the target is large, R-Lucy algorithm cannot distinguish the three-line target, no matter how many cycles it has

Full size image

To improve the SNR of the reconstructed image, it can only be achieved by reducing S1 or S2. Among them, reducing S1 can make multiple measurements on HPSF, or use a modulated coded aperture to make multiple measurements and reconstruct[9] to reduce the impact of h. Reducing S2 can only be achieved by reducing the power of noise, which can be realized by reducing the luminous point number of the target.

4 Experimental settings

We built a prototype and used our method to improve image quality. The unit size of the coded aperture is 13 um, which is generated using the M sequence of 127 and extended by one cycle, as shown in the Fig. 5.

Fig. 5
figure 5

The prototype of code aperture lens-less imaging system

Full size image

The detector is B1923 CCD from Imperx, using a KAI-02170 monochrome chip. The detector has 1920 × 1080 pixels with a size of 7.4um. The angle response of the pixel drops to 50% at 18°, and the distance from the photosensitive surface to the coded aperture is 3.37 mm. Although the field of view of the coded aperture camera is very large, it is limited to the angle response of the detector, and the field of view is only about 36°. We use an LCD monitor as the target simulator. The unit size of the monitor is 0.275 mm, and the target image maintains the original resolution without zooming in and out.

Firstly, we use a point light source to illuminate, and the averaged 100 frames of data are collected as HPSF. Then to image uniform rectangular targets of different sizes, reconstruct the image, select the target area to calculate the SNR.

The results in Fig. 6 are consistent with the simulation results. Based on this result, we propose a method to improve the quality of lens-less imaging of the coded aperture. This method, we called segmented area imaging, divides a target into several regions, images them separately, and then splicing them together. Theoretically, the imaging quality is better than that of the whole region directly. Figure 7 compares the results of segmented area imaging and full-area imaging (snapshotting to get the full image), and the reconstructed images using the three algorithms all show that the image quality of the segmented area imaging is improved compared with the full-area imaging method.

Fig. 6
figure 6

The relationship between the SNR of the output image of the camera and the number of luminescence points, the exposure time, and the target brightness is constant, sigma = 10

Full size image
Fig. 7
figure 7

Experiment results. a Ground truth of Lena, b coded mask, HPSF, and recorded image, c segmented display for our method and reconstructed results as (d). e Full display for snapshot and reconstructed results as (f)

Full size image

5 Summary

In this paper, we build a simulation model of the coded aperture imaging system based on the theory of light propagation, simulate the imaging process, and analyze the SNR characteristics of the coded aperture lens-less imaging system. Both simulation experiments and prototype experiments imaged uniform targets of different sizes and reconstructed the image. The experimental results and the theoretical analysis results were more consistent. Both showed that the larger the target size, the SNR of the reconstructed image lower. Although this conclusion was the result of research on coded aperture imaging, due to its extensive mathematical model, this conclusion is also applicable to other lens-less imaging, such as scattering imaging and diffuser camera. Also, this conclusion can help researchers find better masks.

The segmented area imaging can be used to image the target in different regions to improve the image quality, but at the same time, the temporal resolution will be sacrificed, and appropriate means are needed to partition the observed target, which is more suitable for the microscopic imaging scene of static observation.