1 Introduction

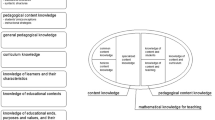
There is broad agreement that teachers play a key role in providing high-quality learning opportunities to students and fostering students’ learning (e.g., Schleicher, 2016). As a consequence, research on teacher knowledge as part of teachers’ professional competenceFootnote 1 has increased during the last decades, especially where it focuses on mathematics education (e.g., Gitomer & Zisk, 2015; Hill & Chin, 2018; Kaiser et al., 2017; Kunter et al., 2013). Following the influential work by Shulman (1987), researchers identify and distinguish three domains of teacher knowledge (Baumert et al., 2010; Grossman & Richert, 1988; Tatto & Senk, 2011): content knowledge (CK), pedagogical content knowledge (PCK), and general pedagogical knowledge (GPK).

Studies on indicators of teacher knowledge and student achievement carried out so far have focused on mathematical content knowledge and mathematics pedagogical content knowledge as the subject-specific knowledge domains, focusing on mathematics education (e.g., Baumert et al., 2010; Campbell et al., 2014; Hill & Chin, 2018; Hill, Rowan, & Ball, 2005). Although CK and PCK have been stressed as significant predictors (Shulman, 1987; Voss, Kunter, & Baumert, 2011; Voss, Kunter, Seiz, Hoehne, & Baumert, 2014), GPK has also been considered as an important resource of teacher competence (Guerriero, 2017; König, 2014). A few studies have provided evidence that indicators of teachers’ GPK predict the instructional quality provided for students (Depaepe & König, 2018; König & Pflanzl, 2016; Voss et al., 2011; Voss et al., 2014). However, according to recent reviews on GPK (König, 2014; Voss, Kunina-Habenicht, Hoehne, & Kunter, 2015), apart from one study for physics education (Lenske et al., 2016), there is no study that goes beyond and analyzes the link between this general component of teacher knowledge and students’ achievement.

In the present study, we therefore examine—focusing on mathematics education—teachers’ pedagogical competence (i.e., cognitive pedagogical facets of their professional competence), instructional quality, and student achievement using a dataset with students from 59 mathematics classrooms who completed standards-based achievement tests in mathematics during grades 7 and 8. To allow a profound operationalization of teachers’ pedagogical competence, the teacher assessment—provided online—comprises two different measures, a test originally designed in paper-and-pencil format measuring teachers’ GPK and a video-based assessment of teachers’ classroom management expertise (CME) that focuses more on aspects of educational psychology, covering situated facets of teachers’ competence (Kaiser et al., 2017). Instructional quality was captured via observational in vivo ratings in the classroom, allowing the measurement of effective classroom management, student support, and cognitive activation as the three basic dimensions of instructional quality (Praetorius, Klieme, Herbert, & Pinger, 2018).

Using a multilevel approach, we examine three research questions:

  1. 1.

    Does teachers’ pedagogical competence, indicated by GPK and CME, predict the basic dimensions of instructional quality of mathematics lessons?

  2. 2.

    Does CME, compared with GPK, serve as a stronger predictor for effective classroom management as one of the three dimensions of instructional quality from mathematics lessons?

  3. 3.

    Does teachers’ pedagogical competence, indicated by GPK and CME, predict student progress in mathematics achievement?

2 Teachers’ pedagogical competence

For the past decades, interest in research on the measurement of cognitive elements of teachers’ professional competence has been growing due to the assumption that teacher knowledge makes a significant contribution to effective teaching and student learning (Gitomer & Zisk, 2015; Hill & Chin, 2018; Kunter et al., 2013). Research on teacher expertise conducted as early as the 1980s and 1990s led to the assumption that professional teacher knowledge is a significant factor for effective teaching, thus promoting student attainment (e.g., Bromme, 2001; Hogan, Rabinowitz, & Craven, 2003). Teachers presumably need generic knowledge for successful teaching, for example, an “intellectual framework” for classroom management (Doyle, 1985, 2006; Shulman, 1987) or, more generally, knowledge of pedagogical concepts, principles, and techniques that is not necessarily bound by topic or subject matter (Wilson, Shulman, & Richert, 1987). Teachers are expected to draw on this knowledge and weave it into coherent understandings and skills when they deal with the learner and the according subject matter in the classroom (Shulman, 1987).

However, there is still the need to investigate teacher knowledge as a predictor for effective teaching and student attainment (e.g., Baumert et al., 2010). This is due, at least partly, to a lack of adequate conceptualizations and measurement instruments (König, 2014; Voss et al., 2015). Against this background, during the last decade, several research groups have started to develop test instruments measuring teacher knowledge and skills. Following the seminal classification of teacher knowledge proposed by Shulman (1987), test instruments have been developed to assess general pedagogical knowledge (GPK) of teachers (see, for an overview, König, 2014; Voss et al., 2015) complementing subject-based instruments, for example, for mathematics education (Baumert et al., 2010; Tatto & Senk, 2011).

For example, in the context of the international comparative study Teacher Education and Development Study in Mathematics 2008 (TEDS-M), a paper-and-pencil assessment was developed to survey teachers’ GPK as an outcome of initial teacher education in the USA, Germany, and Taiwan (König, Blömeke, Paine, Schmidt, & Hsieh, 2011). In TEDS-M, GPK was structured in a task-based way. That is, the test content refers to knowledge teachers need to successfully master specific tasks of their profession. This comprises the task of managing the classroom, but also to prepare, structure, and evaluate lessons, to motivate and support students, to deal with heterogeneous learning groups in the classroom, and to assess students (König et al., 2011). Thus, in TEDS-M, classroom management was not solely focused on but formed one of several dimensions to describe GPK from a broader standpoint. Besides TEDS-M, GPK was measured in other studies as well (e.g., Brühwiler, Hollenstein, Affolter, Biedermann, & Oser, 2017; Sonmark, Révai, Gottschalk, Deligiannidi, & Burns, 2017; Voss et al., 2011) with similar approaches to capturing classroom management knowledge as one of several dimensions rather than assessing it extensively. Such broadly conceptualized assessments of GPK have the advantage to proliferate our understanding on a more general level, for example, to show what we know about teachers’ GPK. However, at the same time, such assessments might fail to provide detailed insights into a particular field of instruction such as effective classroom management.

Another research issue refers to the need to create context-dependent, procedural teacher knowledge measures that go beyond the limited scope of classical paper-and-pencil assessments (Shavelson, 2010). New perspectives on the measurement of competence (Blömeke, Gustafsson, & Shavelson, 2015) emphasize the need for instruments that allow an investigation of teachers’ situational cognition, for example, to analyze the impact of individual differences in teaching experience and in-school opportunities to learn during teacher education (Kaiser et al., 2017; König et al., 2014). Although knowledge acquired during teacher education and represented as declarative knowledge is probably of great significance, especially the research on teacher expertise has worked out that both declarative and procedural knowledge contribute to the expert’s performance in the classroom (Bromme, 2001; De Jong & Ferguson-Hessler, 1996; Hogan et al., 2003; Stigler & Miller, 2018).

To account for such methodological concerns, a major current focus in the measurement of teacher knowledge and skills as part of their competence is the shift from paper-and-pencil tests to the implementation of instruments using video clips of classroom instruction as item prompts: Such studies use videos as a stimulus in the item stem, an assessment format which is frequently referred to as “video vignette” or “video-cued testing”. Video-based assessment instruments are used to address the contextual nature and the complexity of the classroom situation. They are considered to improve the measurement of teacher knowledge when compared with classical paper-and-pencil tests (Blömeke et al., 2015; Kaiser, Busse, Hoth, König, & Blömeke, 2015).

Several studies adopted this approach to provide a more ecologically valid measurement of teacher knowledge (e.g., Kersting, 2008; König et al., 2014; Seidel & Stürmer, 2014; Steffensky, Gold, Holdynski, & Möller, 2015; Voss et al., 2011). These studies thus intend to measure knowledge of a situated nature (Putnam & Borko, 2000). To expand previous research, our study uses such a methodological approach for reasons of validity as well and proposes a video-based approach for testing knowledge and skills required for successfully meeting the specific requirements involved in effective classroom management. Accordingly, we build our study on previous research as outlined in the following.

3 Instructional quality

For decades, numerous studies have analyzed the influence of teaching process characteristics on student learning outcomes over various subjects, following the process-product research paradigm and summarized in meta-analyses (Hattie, 2012; Wang, Haertel, & Walberg, 1993).

To synthesize the myriad of findings, theoretical frameworks have been developed to summarize the most relevant and reliable findings, outlining them in analysis models or heuristics (Seidel & Shavelson, 2007). As a consequence, there are different theoretical models of teaching effectiveness which refer either to generic factors (e.g., Kyriakides, Creemers, & Panayiotou, 2018; Muijs et al., 2018) or to domain-specific factors (e.g., Charalambous & Litke, 2018; Schlesinger, Jentsch, Kaiser, König, & Blömeke, 2018). As another specific model of effective teaching, which is also used in the present study, building on the current state of the art in the field, researchers have been distinguishing between three basic dimensions of teachers’ instructional quality: classroom management, student support, and cognitive activation, which are described as general dimensions holding for all school subjects (e.g., Baumert et al., 2010; Kunter et al., 2013; Praetorius et al., 2018; Schlesinger et al., 2018; Voss et al., 2014). Instructional quality in the area of classroom management is mainly related to the efficient use of allocated classroom time, the prevention of disorder in the classroom, and teachers’ expectations of student behavior (Emmer & Stough, 2001; Evertson & Weinstein, 2013). Student support as another dimension of instructional quality comprises teacher behavior that focuses on encouraging students, fostering a positive classroom climate, and providing adaptive learner support (Fauth, Decristan, Rieser, Klieme, & Büttner, 2014; Gräsel, Decristan, & König, 2017). Finally, cognitive activation in the classroom refers to whether teachers’ instructional strategies and the selected learning tasks are cognitively challenging for students (Klieme, Pauli, & Reusser, 2009; Lipowsky et al., 2009).

Various studies—mainly from mathematics education—have provided evidence that these three dimensions are empirically separable and significantly influence student progress (e.g., Baumert et al., 2010; Kunter et al., 2013; Praetorius et al., 2018). Whereas effective classroom management and cognitive activation show effects on cognitive learning outcomes, student support tends to be related to affective-motivational student variables and thus may indirectly affect cognitive learning outcomes of students. For example, in the German COACTIV study focusing on secondary mathematics teachers (Baumert et al., 2010, p. 161), student learning in lower secondary mathematics was influenced by measures of cognitive activation (β = .32, p < .05, for cognitive level of tasks; β = .17, p < .05, for curricular level of tasks) and effective classroom management (β = .30, p < .05), but not individual learning support (β = .11, n.s.). Although these three basic dimensions of instructional quality are supposed to be valid across domains, cognitive activation has particular relevance for the subject-specific aspects of instructional quality. By contrast, classroom management can be regarded as the dimension that is most similar across different subjects (Praetorius, Vieluf, Saß, Bernholt, & Klieme, 2015).

4 Pedagogical competence and instructional quality

Research in the last decades on the link between teacher competence and instructional quality used proxy measures such as teacher qualifications or the number of courses taken during teacher education (see, e.g., Boyd, Grossman, Lankford, Loeb, & Wyckoff, 2009; Darling-Hammond, 2000). Recently, researchers have started to directly assess teacher knowledge as part of teachers’ pedagogical competence and relate it to the instructional quality provided for students in the classroom (e.g., König & Pflanzl, 2016; Lenske et al., 2016; Voss et al., 2011, 2014).

König and Pflanzl (2016) used student ratings of instructional quality in a study with 246 in-service teachers. Teachers’ GPK, as measured by the TEDS-M instrument, was a significant predictor for teaching methods/teacher clarity (β = .44), effective classroom management (β = .31), and teacher student-relationships (β = .50), even when controlled for teacher education grades, teacher personality (“Big Five”), and teaching experience.

Voss et al. (2014) assessed the pedagogical-psychological knowledge (PPK) of 181 mathematics teacher candidates during the second phase of teacher education in Germany. After the study participants’ transition into early career teaching, their students were asked to rate the instructional quality with regard to the basic dimensions. Teachers’ PPK significantly predicted classroom management measures (monitoring β = .21 and disruptive student behavior β = − .20) and social support (β = .38), whereas no significant impact of PPK was found for cognitive activation (β = .10). When discussing the weak impact of PPK on cognitive activation, the authors reflected on its stronger link to subject-specific knowledge, in this case teachers’ mathematics CK and PCK, as it had been shown in the COACTIV study (Baumert et al., 2010).

Currently, there is just one study that not only linked teachers’ pedagogical competence to instructional quality but also to student achievement. Lenske et al. (2016) used video ratings of physics lessons focusing on classroom management to investigate its relevance in a mediation model between teachers’ pedagogical knowledge and student progress in physics using a pretest-posttest design. Based on a sample of 34 teachers and 993 students, Lenske et al. (2016) could provide evidence that teacher knowledge is mediated by effective classroom management as a dimension of instructional quality and thus positively affects student progress in physics.

Although these studies show that teachers’ pedagogical competence is a significant predictor for instructional quality, especially for the basic dimensions of effective classroom management and student support, they all work with classical paper-pencil tests, although they may be provided digitally. By contrast, König and Kramer (2016) used a video-based instrument testing knowledge and skills required for successfully meeting the specific requirements involved in effective classroom management (classroom management expertise test, CME, see methods section for details on the instrument). In a study, teacher candidates’ CME significantly predicted specific facets of effective classroom management as a dimension of instructional quality (Kounin’s, 1970, dimension of teachers’ with-it-ness β = .47 and clarity of rules β = .36). As these predictors are stronger than the effects reported in the previous studies, authors suggest that the situation-specific nature of the CME test might be more proximal to instructional quality than classical paper-pencil assessments.

5 The present study

Since the measurement of context-dependent, procedural teacher knowledge goes beyond the limited scope of paper-and-pencil tests measuring teacher knowledge, especially when looking at situation-specific skills such as effective classroom management, this study uses two measures of pedagogical competence (that were provided online): a general pedagogical knowledge (GPK) test originally designed as a paper-and-pencil test now provided online and a novel video-based online-assessment focusing on the classroom management expertise (CME) of (mathematics) teachers. They serve to cover important but different facets of pedagogical competence.

As described, GPK measures pedagogical concepts from a broader standpoint, whereas CME is much closer to the actual performance of the teacher in the classroom and especially more specific toward the content of classroom management.Footnote 2 CME consists of four video vignettes (see, for more technical details, the Methods section), so that test items are embedded in typical classroom situations. Test takers are required to process more complex information than when responding to GPK paper-pencil test items, and since the situations are typical, they serve as substitutes for genuine classroom situations of the individual teacher. Although some GPK test items frame a situation in general (see, e.g., the first GPK item example in Table 1), cognitive demands posed on test takers in the CME video vignettes are much more related to perceive and interpret specific details of the particular classroom management situation provided in each video clip (see item examples of the CME test in Table 1).

Table 1 Item examples from the GPK and CME tests
Full size table

Three research questions are addressed using the following hypotheses (abbreviated as H1, H2, and H3 in the following):

  1. 1.

    Does teachers’ pedagogical competence, indicated by GPK and CME, predict the basic dimensions of instructional quality?

Teachers presumably need both GPK and CME to deliver high-quality learning opportunities to their students. However, GPK and CME should be more strongly related to the challenges of classroom management and providing student learning support, whereas cognitive activation of students might be regarded as a challenge primarily dependent on subject-specific teacher knowledge. So we assume that GPK and CME are significant predictors for effective classroom management and student support as two dimensions of instructional quality (H1).

  1. 2.

    Does CME, compared with GPK, serve as a stronger predictor for effective classroom management as one of the three dimensions of instructional quality?

CME as a measure is more specific than GPK both regarding its content focus on classroom management and regarding its contextualization due to the video-based assessment approach. Following the current discussion on professional competence of teachers as a continuum (Blömeke et al., 2015), we assume that CME is a stronger predictor for effective classroom management as a dimension of instructional quality compared with GPK (H2).

  1. 3.

    Does teachers’ pedagogical competence, indicated by GPK and CME, predict students’ progress in mathematics achievement?

Research has shown that student progress in mathematics achievement can be predicted by the subject-specific knowledge of mathematics teachers (e.g., Baumert et al., 2010; Hill & Chin, 2018). Whether this holds for GPK and CME as measures of teachers’ pedagogical competence virtually remains an open question, though. As domain-specific teacher knowledge is required and following the findings from the mediation model proposed by Lenske et al. (2016), we assume that pedagogical competence is not statistically effecting domain-specific student progress directly. However, we hypothesize that pedagogical competence has an indirect statistical effect on domain-specific student progress which is mediated through dimensions of instructional quality as pointed out with the hypotheses related to our previous research questions (H3).

The investigation of the three research questions presumes that instructional quality affects students’ progress in mathematics achievement. As the correspondent analysis is not the major focus of the present study, we refrain from explicating another specific hypothesis, but refer to previous work where substantial evidence has been proliferated that at least cognitive activation and classroom management significantly predict cognitive student outcomes.

6 Method

6.1 Participants and research context

In this study, we use mathematics teacher and student data from lower secondary mathematics classrooms in the federal state of Hamburg, Germany. Mathematics teachers recruited for this study (convenience sample due to data collection constraints) either taught in the academic track (Gymnasium) or in the non-academic track (Stadtteilschule) in the federal state of Hamburg. The teachers were recruited via professional networks and promotion at the regular gatherings by the heads of the mathematics department of the schools in Hamburg and the gathering of the headships of all schools in Hamburg, differentiated by school type. Furthermore, participation was encouraged by a letter of the highly respected school inspector.

Teachers who had participated in the online survey were asked to allow observation of their mathematics classes. For each school class of the teachers, student assessment data was made available with the help of the Institute for Educational Monitoring and Quality Development (Institut für Bildungsmonitoring und Qualitätsentwicklung, IfBQ) in Hamburg.

The sample used in this study comprises 59 teachers and their classes with grade 7 and grade 8 assessment data from 1220 students.Footnote 3 In our study, each teacher was exclusively linked to one classroom; therefore, our complex sample comprises 59 teachers and 59 classrooms. On average, each classroom is represented by about 25 students (M = 24.7, SD = 2.6) with complete data for both time points. Missing student assessment data was most likely caused by the absence of a student at one or both time points, whereas an individual self-selection bias was fairly unlikely due to the non-high-stakes character of the assessment (in Hamburg, these assessments primarily serve to inform teachers on the progress and possible learning gaps of their students). During the particular time span of the two assessments, students were taught by these 59 mathematics teachers. Forty two percent of the teachers were female. On average, they were 39.2 years old (SD = 10.5) and had, by average, 10.7 years of professional experience (SD = 9.9). Their teacher education grades were, on average, fairly good (grades from graduating university: M = 1.67, SD = .52; grades from graduating induction phase (Referendariat): M = 1.96, SD = .66).Footnote 4 Thirty eight school classes were located in the academic track and 21 in the non-academic track.Footnote 5 In the present study, the track not only serves as control variable for the academic level of the learning environment but also as a proxy for the social composition of the classroom context, since, technically speaking, in the lower secondary school system in Hamburg, a very high proportion of students’ socio-economic background can be statistically explained by the school track.

6.2 Measures

6.2.1 Teachers’ pedagogical competence

Teachers’ pedagogical competence was assessed using two different tests. First, we measured teachers’ general pedagogical knowledge (GPK) with the TEDS-M test. The test comprises generic dimensions of teaching responsibilities (see Table 2). These are related to instructional models to describe effective teaching (Good & Brophy 2007; Slavin 1994). According to the theoretical framework of the test (for more details see König & Blömeke, 2010; König et al., 2011), teachers are expected to have general pedagogical knowledge allowing them to prepare, structure, and evaluate lessons (“structure”); to motivate and support student learning as well as to manage the classroom (“motivation/classroom management”); to deal with heterogeneous learning groups in the classroom (“adaptivity”); and to assess students (“assessment”). For example, teachers are required to know basic concepts of achievement motivation (e.g., motivational aspects of learning processes, Dweck, 1986). Moreover, cognitive demands make up a test design matrix (see Table 3): That means, when responding to test items, respondents are required to recall, understand/analyze, and generate GPK that is supposed to be relevant for structuring a lesson, motivating and assessing students, managing the classroom, and adapting teaching to the needs of students. Each cell is represented by a subset of items. Three item examples (see Table 1) may illustrate the test. Due to data collection constraints in the present study, we had to apply a short form of the original TEDS-M instrument with a test length reduced to 20 min. It contains 15 test items (5 multiple choice items, 10 open-response items).

Table 2 Dimensions and topics covered in the TEDS-M test of GPK (following König et al., 2011, p. 191; König & Pflanzl, 2016, p. 421)
Full size table
Table 3 TEDS-M GPK test design matrix with number of items of the short version applied (following König et al., 2011, p. 191; König & Pflanzl, 2016, p. 422)
Full size table

Second, we used the classroom management expertise (CME) measurement instrument, a novel video-based assessment developed in a previous study of our research team (König, 2015; König & Kramer, 2016; König & Lebens, 2012). It consists of four video clips of classroom instruction that refer to typical classroom management situations in which teachers are strongly challenged to manage (1) transitions between phases, (2) instructional time, (3) student behavior, and (4) instructional feedback. Whole-class interaction dominates the visible teaching situations, as in terms of effective classroom management they are more complex and thus more challenging for teachers than individual work situations during which a teacher assists a single student or a group of students (Kounin, 1970).

A variety of classroom contexts (regarding school grade, school subject, composition of the learning group, age of teacher) are represented by the video clips. Each video clip is followed by test items that the test takers are required to respond to before they watch the next clip. Items refer explicitly to the video clip. The three item examples in Table 1 relate to one video clip showing a situation of transition from working group phase to the phase of presenting results (see, for more details, König & Lebens, 2012). In total, 24 test items are used (5 multiple choice items, 19 open-response items). Items’ cognitive demands refer to accurate and holistic perception as well as interpretation. The CME total score represents a general ability of teachers focused on generic professional tasks.

For both tests, all open-response items were coded on the basis of the respective coding manuals. For the sample of 59 teachers used in the present analysis, consistency was secured based on double coding of 24 GPK questionnaires and 13 CME questionnaires. Average consistency was good for both tests (GPK: MKappa = .63, SDKappa = .30; CMEKappa: M = .79, SDKappa = .16; cf. Fleiss & Cohen, 1973).

Scaling analyses were done in a two stage process. First, IRT scaling analysis was done for each test separately using the software package Conquest (Wu, Adams, & Wilson, 1997). To increase the analytical power (Bond & Fox, 2007), the complete teacher sample (n = 118) of our research project was included. Test data were analyzed in the one-dimensional Rasch model (one parameter model).Footnote 6 Reliability was at least acceptable for both tests (GPK: WLE = .88, EAP = .90, α = .71; CME: WLE = .73, EAP = .75, α = .71).Footnote 7 Discrimination of items was, on average, good (GPK: M = .40, SD = .12; min = .12, max = .49; CME: M = .38, SD = .11, min = .15, max = .52). The weighted mean square (WMSQ; Wu et al., 1997) of items of the CME measure was in an appropriate range (.88 ≤ WMSQ ≤ 1.11) without a t value indicating significant difference, thus showing adequate fit of data to the model (Bond & Fox, 2007). Three GPK items exceeded the critical WMSQ of 1.20 (two of them with significant t value), whereas for the rest, the WMSQ was in an appropriate range as well (.82 ≤ WMSQ ≤ 1.15). Since for these three critical items the discrimination was fairly good (> .4), they were not excluded from the final scaling analysis. Another very few items with rather low discrimination (< .20) were kept for theoretical reasons. In the subsequent analyses, we used the weighted likelihood estimates (WLE, Warm, 1989) as ability parameters for teachers’ pedagogical competence. Second, to specifically examine the measurement quality of the tests within the dataset studied here, classical scaling analysis was done for each test using SPSS. Reliability was good (GPK: α = .87; CME: α = .74).

6.2.2 Instructional quality

Instructional quality was measured using a novel observation rating instrument developed by the research group (details in Schlesinger et al., 2018). In contrast to teacher and student ratings that are most frequently applied to capture instructional quality, this method accesses teachers’ instructional quality directly and prevents self-reported bias (Praetorius, Lenske, & Helmke, 2012). The observational protocol—related among others to the three basic dimensions of instructional quality—consists of 18 items that are assessed by high-inference ratings using four-point Likert scales ranging from 1 (“does not apply at all”) to 4 (“does fully apply”). Each teacher with one school class was observed for four lessons with approximately 20 min intervals resulting in 8 time points for each item, since one lesson had a regular duration of 45 min. The rating was carried out by 10 raters with at least a Bachelor’s degree in mathematics education, who had been prepared by an extensive training (30 h of theoretical and practical training) and who were randomly selected for each lesson. Interrater reliability and validity of the ratings are supported by typical examples as outlined for each item in the protocol (see Table 4). Inter-rater reliability was good (ICC > .80). Scaling analysis summarized all information using average scores. The reliability of the scales was good (.73 ≤ α ≤ .87).

Table 4 Example items and indicators of the observation protocol
Full size table

Originally, more teachers and classes were observed, which could not be included in the sample for these analyses due to missing data for students’ achievements and which led to a subject-specific enrichment of this generically defined approach (details in Jentsch et al., 2020b; a general discussion on hybrid content-specific and generic approaches to lesson observation can be found in Lindorff, Jentsch, Walkington, Kaiser, & Sammons, 2020).

6.2.3 Student achievement

Student achievement in mathematics was assessed with standardized competence tests measuring the regional educational standards in mathematics in grades 7 and 8. The assessment in grade 7 was part of the systematic evaluation of student competencies called KERMIT (Kompetenzen ermitteln) and developed in the federal state of Hamburg over a long period of time (Lücken et al., 2014) by the Hamburg Institute for Educational Monitoring and Quality Development (IfBQ). The assessment in grade 8 was part of the regular nationwide survey called VERA 8 developed by the Institute for Educational Quality Improvement (Institut zur Qualitätsentwicklung im Bildungswesen, IQB) in Berlin. Both studies are curriculum-based and have the same curricular basis, namely the national standards implemented in German schools since 2003 (KMK, 2004). In detail, the tests are referring to general competencies formulated in the national standards such as mathematical argumentation, mathematical problem solving, mathematical modeling, usage of diagrams, usage of symbolic, formal and technical elements of mathematics, and communication. Furthermore, the tests are covering fundamental mathematical ideas, namely number, measurement, space and shape, functional relations, data, and chance. Finally, the tasks cover three steps of cognitive complexity, namely reproducing, connecting, and generalizing/reflection. The Hamburg-based KERMIT assessment uses regular items from the national level in order to secure comparability (Lücken et al., 2014). These data could be matched for panel analyses. However, due to data collection constraints, no other data are available on the individual student level. This will be discussed later as a limitation of the present study.

6.3 Statistical analysis

6.3.1 Multilevel analysis

To account for the hierarchical structure of the data, two-level regression analysis (level 1: students; level 2: teachers and classes) was carried out using the software package Mplus (Muthén & Muthén, 1998-2015). All variables were used as manifest scores. Following recommendations by Bentler and Chou (1987) on the relationship between cases and number of parameters to be estimated, we refrained from specifying variables as latent due to a rather small sample on level 2 (n = 59). Student assessment data from the second time point (grade 8) were used as dependent variable. First time point data (grade 7) were used as independent variable both on level 1 (group centered) and on level 2 (class mean). The track (academic vs. non-academic) was introduced as a control variable on level 2.

We use standardized regression coefficients (β), which estimate the shared variance between two variables once variance attributable to other variables is controlled for. We use as interpretation of these coefficients the classification of Pearson’s r into associations with small (> .1), medium (> .3), or large (> .5) practical relevance (Cohen, 1992) as this provides a rough guideline, although this kind of guidelines needs to be treated with caution (Bakker et al., 2019).

6.3.2 Missing data

Only a subsample of the 59 teachers and their instructional quality could be observed resulting in 17 school classes with and 42 without observational data.Footnote 8 However, for teachers/classes with and without observation, no significant mean differences in study variables could be found, neither for the teacher knowledge scores (GPK: F(1,58) = 2.41, p = .126; CME: F(1,58) = .17, p = .679) nor for teacher background (age: F(1,58) = 1.38, p = .245; years of service: F(1,58) = .028, p = .867). Also, no significant differences in the frequency distribution of classes with and without observation related to teachers’ gender could be found (χ2 = 2.15, p (two-tailed) = .643). In a two-level model, in which student assessment data (grade 8) served as dependent variable and first time point assessment data (grade 7) were specified as independent variables (group centered on the individual level and class mean on the class level) along with the track (academic vs. non-academic) as control variable on the class level, the dichotomous predictor on the class level categorizing classes with and without observation was not statistically significant (β = .02, p = .629). Also, differences in the frequency distribution of classes with and without observation related to track (academic vs. non-academic) were not significant (χ2 = 1.52, p (two-tailed) = .218).

To deal with missing data, we applied two procedures (Schafer & Graham, 2002): We firstly conducted the analyses for the subsample with 17 teachers with non-missing data. As an alternative approach, the model-based imputation procedure using the sample of 59 teachers was applied. We then used the full information maximum likelihood option in Mplus (Muthén & Muthén, 1998-2015; Enders & Bandalos, 2001; Grund, Lüdtke, & Robitzsch, 2019). Both procedures come to nearly the same results and therefore lead to similar interpretations. The robustness of the findings is supported by similar correlative statistics of both procedures (see Table 5). In the Appendix, we provide more comprehensive information on the methodology used, including imputation. The first approach using the sub-sample with 17 teachers is outlined in the Appendix, while we present findings retrieved from the model-based imputation procedure using the full sample of 59 teachers in the following findings section.

Table 5 Descriptive statistics of study variables on the classroom level
Full size table

7 Results

7.1 Descriptive statistics

Descriptive statistics of the variables on the class level are presented in Table 5. All measures are extracted from IRT scaling analysis, thus following the logit scale metric. GPK and CME test score mean, standard deviation, and standard error are reported for our sample of 59 teachers, whereas coefficients for the three dimensions of instructional quality are based on observations in 17 classes. Correlations are provided both as inter-correlational estimates using model-based imputation in the cells below diagonal and as bivariate correlations using case deletion in the cells above diagonal. The effect size of the parameters is in all cases similar, thus showing the robustness of findings. The only difference is that there are more significant correlations due to smaller standard errors in the larger sample (cells below diagonal).

There is a positive correlation of about medium size between CME and GPK (.48/.51), showing that the video-based assessment of CME is not independent from teachers’ declarative-conceptual knowledge in the domain of general pedagogy as measured by the TEDS-M GPK test. Such a correlation shows that the two constructs have something in common but are not identical. Their covariance is about 25%, but about 75% of their variance does not change together.

Both tests are positively correlated with medium effect sizes with the dimensions of instructional quality, especially with cognitive activation (GPK: .47/.49, CME: .31/.32) and classroom management (GPK: .42/.44, CME: .25/.26), but in case of GPK also with student support (.41/.45) while the correlation of CME with student support is weak (.09/.11). CME correlations with instructional quality are generally weaker than those of GPK.

7.2 Multilevel analysis

To examine our research questions, multilevel analysis was carried out. Findings are presented in Tables 6 and 7. In Table 6, models 1 to 3 (as well as 4 to 6 and 7 to 9) contain series of the three dimensions of instructional quality predicting grade 8 student mathematics achievement. Models 3, 6, and 9, respectively, show that cognitive activation significantly predicts student progress (β ≥ .11, p < .05), in contrast to the other two dimensions (in models 1 and 7, classroom management predicts student progress only on the 10% significance level). We also included the track (academic/non-academic) which the students were enrolled in. The regression coefficient (Table 6: β ≥ .37) is significant and shows that student progress is larger in the academic track than in the non-academic track.

Table 6 Multilevel analyses predicting student mathematics achievement (grade 8) by instructional quality and pedagogical competence
Full size table
Table 7 Multilevel analyses examining direct and indirect paths of pedagogical competence on student mathematics achievement (grade 8)
Full size table

According to our research questions, measures of teachers’ pedagogical competence as additional predictors are of particular interest. We use path analysis on the class level, in which teacher competence predicts instructional quality and instructional quality predicts student achievement. In Tables 6 and 7, this is indicated by naming both the predictor and the dependent variable (e.g., “classroom management on GPK” for model 1 in Table 6). For GPK and the CME, respectively, we first examine the indirect statistical effect on student achievement through each dimension of instructional quality (GPK: models 1 to 3; CME: models 4 to 6). Then teachers’ pedagogical competence is measured using an overall variable using the sum of GPK and CME (models 7 to 9). As a second step of our analysis, for those models with significant paths from teacher knowledge to instructional quality and from instructional quality to student achievement, mediation is analyzed in Table 7. We follow the approach suggested by Baron and Kenny (1986) that requires both paths being significant before examining mediation.

Regarding our first and second research questions, findings in Table 6 show that instructional quality can be predicted by teachers’ pedagogical competence. Teachers’ GPK significantly predicts all three dimensions of instructional quality, whereas their CME only predicts cognitive activation significantly. Using pedagogical competence as a sum score, both classroom management and cognitive activation can be significantly predicted. The relevant predictors are of medium effect size (β ≥ .3). There is a good fit of each model with large proportion of variance explained.

Table 7 shows findings related to our third research question. First, in Table 7, there is a direct path from teachers’ pedagogical competence to student achievement (models 1, 3, and 5). Predictors are statistically significant but relatively low (β = .08/.10/.11). Second, examining mediation of cognitive activation leads to a reduction of the direct paths from teacher competence measures to students’ mathematics achievement. However, at the same time, the statistical effect of instructional quality on students’ mathematics achievement disappears. Therefore, against our expectation, evidence for mediation cannot be provided with the available data. Again, there is a good fit of each model with a large proportion of variance explained.

8 Discussion

This study aimed at a detailed investigation of the relation between teachers’ pedagogical competence, instructional quality, and students’ mathematics achievement. Three research questions were answered.

8.1 Teachers’ pedagogical competence predicts instructional quality

As hypothesized, teachers’ pedagogical competence as well as its facets GPK and CME predicted instructional quality. However, only GPK significantly predicted all three dimensions of instructional quality, whereas CME predicted cognitive activation only. Pedagogical competence as a sum score predicted classroom management and cognitive activation. Therefore, hypothesis H1 was only partly supported. One reason for the small CME statistical effect might be the selection bias caused by a certain selectivity of the mathematics teachers whose lessons were observed, as the teachers had to explicitly agree to classroom observations and knew the time of it in advance. As observation protocols showed, severe classroom management problems did not occur, thus leading to a limitation of instructional quality variance. Possibly this has contributed to rather low correlations of effective classroom management with both pedagogical competence and students’ mathematical progress.

8.2 The impact of situation-specific skills vs. broad general pedagogical knowledge

Against our hypothesis and also against the findings from the study by König and Kramer (2016) that worked with student ratings of instructional quality, CME did not significantly predict the instructional quality dimension of effective classroom management nor did CME turn out to be a stronger predictor than GPK. Instead, GPK or pedagogical competence as the sum score of GPK and CME predicted classroom management. We therefore do not see evidence for our second hypothesis (H2). However, as the integration of both measures, CME and GPK as indicators for pedagogical competence shows stronger statistical effects than models that only account for CME, respectively, we conclude that both kinds of teacher knowledge facets are needed to predict instructional quality and students’ progress in mathematics. This seems to be in line with theoretical assumptions for the modeling of professional competence as generally outlined by Blömeke et al. (2015) and findings from the COACTIV-R study where an integrated measure of teachers’ pedagogical-psychological knowledge with video vignettes predicted classroom management aspects of instructional quality as rated by students (Voss et al., 2014).

8.3 Direct statistical effects of pedagogical competence on student progress in mathematics

We found direct statistical effects of all three measures GPK, CME, and pedagogical competence on students’ mathematical progress. All statistical effects disappeared when cognitive activation as the only significant instructional quality dimension on students’ mathematical progress was included as a mediation variable. We therefore did not find any evidence on mediation and thus no evidence for our third hypothesis (H3). Therefore, this finding is not in line with the mediation effect as reported in the study by Lenske et al. (2016).

Although we are only partly able to support our hypotheses with the available data, one should acknowledge that nevertheless evidence is provided that teachers’ pedagogical competence is linked to teaching and learning in mathematics. Besides the study from Lenske et al. (2016) that was related to physics education, this is the first empirical evidence that in mathematics learning and teaching, non-subject specific teacher knowledge matters as well for students’ learning in mathematics. Without doubt, cognitive activation is strongly associated with subject-specific concepts of teaching and learning, but students’ mathematical progress might also be dependent on a high degree of teachers’ cognitive resources in the area of pedagogy and educational psychology. This might be due to the conceptualization of cognitive activation as a dimension of instructional quality comprising relevant concepts of the learning sciences. For example, the role of metacognitive knowledge—although involving knowledge about cognition in general—can relate to domain-specific learning tasks (Pintrich, 2002) and therefore might support students’ cognitive activation in mathematics as well. Regarding our specific study, one must emphasize that with the significant predictor of the teacher competence on cognitive activation, also the particular dimension of instructional quality was associated that shows the highest impact on student learning.

That an integration of GPK and CME into one sum score results in stronger correlative findings in our regression model related to classroom management as a dimension of instructional quality (Table 6, model 7) might show that, at least in the case of CME, it is not the single facet that is relevant. Instead, teachers need both broad content in general pedagogy and specific skills in the area of effective classroom management. This allows them to provide high-quality learning opportunities for students and to foster their learning in the particular school subject, which is mathematics in our case (Emmer & Stough, 2001; Evertson & Weinstein, 2013).

8.4 Limitations of the study

Although examination of missing data in the area of classroom observation has shown that bias seems to be fairly limited, it is difficult to precisely judge the data quality, also because only a convenience sample was available. Following Schafer and Graham (2002, p. 173), we consider our approach as a kind of “sensitivity analysis”. As a consequence, generalizability of findings, such as regarding the non-significant impact of classroom management on student progress, might be limited. In particular, the analyses based on observational data are limited in their scope due to a relatively large amount of missing data (see, for more details, the discussion in the Appendix). Another limitation might be that we were not able to control for individual student characteristics, as we only had access to student achievement data. Controlling for track is relevant but only serves as proxy for further important background variables such as socio-economic background and cannot replace other variables such as gender, migration background, or general cognitive ability. As a consequence, this also limits us in drawing conclusions toward the link between teacher competence, instructional quality, and outcomes of the individual student. Future research should focus on drawing such conclusions, since researchers currently emphasize equity (see Kelly, 2015; Kyriakides, Creemers, & Charalambous, 2019).

Regarding the concept of measuring instructional quality, one might discuss whether the use of the concept of basic dimensions of instructional quality, a specific approach of effective teaching, was adopted in the study design. It should thus be acknowledged that only one approach of effective teaching is taken into consideration, while in meta-analyses on effective teaching, other approaches as well as the impact of individual teaching factors are also considered (see, e.g., Hattie, 2012; Seidel & Shavelson, 2007; Kyriakides, Christoforou, & Charalambous, 2013). Kyriakides et al. (2013, p. 144) have a special focus on the impact of generic teaching factors on student learning, using eight teacher behavior factors that can be observed in the classroom, whereas both generic and domain-specific teaching factors are accounted for in the meta-analysis by Seidel and Shavelson (2007). Hattie (2012), by contrast, uses a very broad conceptualization for his meta-analysis comprising teacher behavior, student level, and school level factors.

Another methodological limitation is related to the CME measure. Whereas validity limitation of the CME test has already been discussed, technical issues should also be taken into considerations. One might, for example, extend the number of video vignettes in future research on instrument development, since it might not be sufficient to just use four situations of classroom management and then to generalize items related to these situations to a situation-specific skill (Kersting, 2008). Analyses using generalizability theory that have provided evidence on that issue of the CME test (Jentsch et al., 2020a) should also be applied in future studies.

Finally, one has to take into account that only linear relationships have been examined in our study. For example, a study by Lauermann and König (2016) showed that in-service teachers’ work experience had a curvilinear association with GPK. Moreover, theoretical models claim that specific teacher and school factors (including teacher knowledge) may have a curvilinear relation with student achievement (e.g., Creemers & Kyriakides, 2008; Monk, 1994). To what extent curvilinear correlations might occur between teacher competence measures and their instructional quality could be studied by future studies.

9 Conclusion

Despite certain limitations, the present study significantly contributes to our understanding of the role teachers have for student learning and the quality of instruction, at a general level and specifically in mathematics education. Taking teachers’ general pedagogical knowledge and specific classroom management expertise as relevant measures to describe their pedagogical competence, the findings generally underline the significance teacher cognitions in the area of pedagogy and educational psychology have for the professional development of teachers. The study makes visible that assessing teachers and integrating teacher assessments into the process-product research design can be a helpful approach to broaden our understanding of teaching and learning in the classroom.