$B_{(s)}$ to light tensor meson form factors via LCSR in HQEFT with applications to semileptonic decays

Abstract

In the present work, the form factors of $B_{(s)}$ to light P-wave tensor mesons ($a_2(1320)$, $K^*_2(1430)$, $f_2(1270)$, $f^\prime _2(1525)$) are calculated via the light cone sum rules (LCSR) in the framework of heavy quark effective field theory (HQEFT). Firstly, the expressions of form factors in terms of the light cone distribution amplitudes (DAs) of tensor mesons are derived via the LCSR at the leading order of heavy quark expansion. It is found that the penguin type form factors can be obtained directly from the corresponding semileptonic ones, which is similar to the case of S-wave mesons. Considering the light tensor meson DAs to twist-3, we give the numerical results of form factors systematically. As applications, we investigate the branching ratios, longitudinal polarization fractions and forward-backward asymmetries of relevant semileptonic decays induced by charged current and flavor changing neutral current (FCNC) separately. Our results may be tested by more precise experiments in the future.

1 Introduction

$B_{(s)}$ exclusive decays are of great importance in testing the standard model (SM) and probing new physics beyond it. Up to now, the decays with only S-wave mesons (including pseudoscalar and vector mesons) in the final states have been analyzed extensively both in theory and in experiment. Yet, the studies on decays containing P-wave mesons (including scalar, axial vector and tensor mesons) are relatively fewer. In the last decades, a large amount of such decays have been established experimentally [1], promoting corresponding theoretical investigations on these decays.

For the decay modes involving light tensor mesons, a large isospin violation has already been experimentally detected in $B \rightarrow \omega K^*_2 (1430)$ mode [2]. Also, $B \rightarrow \phi K^*_2 (1430)$ is mainly dominated by the longitudinal polarization [3, 4], in contrast with $B \rightarrow \phi K^*$ where the transverse polarization is comparable with the longitudinal one. In the quark model, the low-lying tensor meson with $J^{PC} = 2^{++}$ can be modeled as a constituent quark–antiquark pair with total orbital angular momentum $L=1$ and spin $S=1$. The observed tensor mesons $a_2(1320)$, $K^*_2(1430)$, $f_2(1270)$, $f^\prime _2(1525)$ form an light flavor SU(3) $1 ^3P_2$ nonet [1]. Theoretical calculations of exclusive decays require the knowledge of non-perturbative QCD, which are generally parameterized in terms of decay constants, form factors and some non-factorization contributions. The form factors of $B_{(s)}$ to tensor mesons were initially calculated in the Isgur–Scora–Grinstein–Wise (ISGW) quark model [5] and its improved version ISGW2 [6, 7]. They were also investigated via the covariant light-front quark model (LFQM) and applied to the relevant radiative decays [8, 9]. Based on the two-parton light cone distribution amplitudes (DAs) of tensor mesons given in Ref. [10], the form factors of $B_{(s)}$ to light tensor mesons were derived from light-cone sum rules (LCSR) [11] and perturbative QCD [12], respectively. In Ref. [12], the results of form factors were also used to explore the relevant semileptonic decays induced by charged current. The form factors of B to tensor mesons were also calculated using LCSR with B-meson DAs [13]. Additionally, $B_s (B)\rightarrow K^*_2 (a_2, f_2) l \nu$ and relevant form factors were investigated with the approach of three-point QCD sum rules [14].

As well known, the LCSR is a well established technique in hadron physics, which is suitable to deal with the heavy to light meson exclusive decays. The LCSR adopted in Ref. [11] is based on an expansion over $m_T/m_b$, with $m_T$ and $m_b$ denoting the mass of tensor meson and bottom quark, respectively. Therefore, the neglected higher terms in expansion may have larger contributions. In addition, this approach can not be applied to the case of $D_{(s)}$ to light tensor meson exclusive decays.

In the framework of HQEFT, the heavy quark expansion is actually based on a small parameter $\bar{\varLambda }/m_Q$, with $\bar{\varLambda }$ and $m_Q$ representing the characteristic bounding energy of heavy hadron and heavy quark mass, respectively [15, 16]. Moreover, some interesting relations between the penguin type form factors and corresponding semileptonic ones in the whole region of momentum transferred have been found in the heavy to light S-wave meson decays at the leading order of heavy quark expansion [17, 18]. Therefore, it is worthwhile to calculate the heavy to light tensor meson form factors via the LCSR in HQEFT and investigate if similar relations still hold in this case. In this paper, we intend to calculate the $B_{(s)} \rightarrow a_2(1320), K^*_2(1430), f_2(1270), f^\prime _2(1525)$ form factors systematically by using the LCSR in HQEFT and, as applications, investigate the relevant semileptonic decays.

The remaining part of this paper is organized as follows. In Sect. 2, we give the definitions of form factors and derive their expressions in terms of the DAs of tensor mesons by using the LCSR in HQEFT. Numerical analysis and results of the form factors are presented in Sect. 3. Then, based on the form factors given here, we investigate the branching ratios, longitudinal polarization fractions and forward-backward asymmetries of all the relevant semileptonic decays in Sect. 4. Section 5 is our summary.

2 Definitions of form factors and LCSR in HQEFT

2.1 Definitions of form factors

The polarization tensors of a tensor meson can be constructed in terms of the polarization vectors of a massive vector state moving along the z-axis as [10, 19]

$$\begin{aligned} \varepsilon ^{\mu \nu }_{(0)}\equiv & {} \sqrt{\frac{1}{6}} [ \varepsilon (+1)^\mu \varepsilon (-1)^\nu + \varepsilon (-1)^\mu \varepsilon (+1)^\nu ] \nonumber \\&+ \sqrt{\frac{2}{3}}\varepsilon (0)^\mu \varepsilon (0)^\nu \end{aligned}$$

(1)

$$\begin{aligned} \varepsilon ^{\mu \nu }_{(\pm 1)}\equiv & {} \sqrt{\frac{1}{2}} [ \varepsilon (\pm 1)^\mu \varepsilon (0)^\nu + \varepsilon (0)^\mu \varepsilon (\pm 1)^\nu ] \end{aligned}$$

(2)

$$\begin{aligned} \varepsilon ^{\mu \nu }_{(\pm 2)}\equiv & {} \varepsilon (\pm 1)^\mu \varepsilon (\pm 1)^\nu \end{aligned}$$

(3)

with

$$\begin{aligned} \varepsilon (0)^{\mu }= & {} ( E, 0, 0, P_3)/m_T \\ \varepsilon (\pm 1)^{ \mu }= & {} (0, \mp 1, -i, 0 )/\sqrt{2} \end{aligned}$$

The polarization tensors $\varepsilon ^{\mu \nu }_{(\lambda )}$ are symmetric and traceless, satisfying the divergence free condition $\varepsilon ^{\mu \nu }_{(\lambda )} P_\nu =0$ and the orthogonal condition $\varepsilon ^{\mu \nu }_{(\lambda )} \varepsilon ^*_{(\lambda ^\prime ) \mu \nu }= \delta _{\lambda \lambda ^\prime }$.

The form factors for $B_{(s)}$ to light tensor meson decays are defined via the corresponding hadronic matrix elements as follows [11],

$$\begin{aligned}&\langle T (P, \lambda )| \bar{q} \gamma ^\mu b | H (p_H) \rangle \nonumber \\&\quad = -i \frac{2}{m_H +m_T} \varepsilon ^{\mu \nu \alpha \beta } e^* _{(\lambda )\nu } p_{H\alpha } P_\beta V (q^2) \end{aligned}$$

(4)

$$\begin{aligned}&\langle T (P, \lambda )| \bar{q} \gamma ^\mu \gamma ^5 b | H(p_H) \rangle \nonumber \\&\quad = (m_H +m_T) \left[ e^{* \mu }_{(\lambda )} -\frac{e^*_{(\lambda )} \cdot p_H}{q^2} q^\mu \right] A_1 (q^2)\nonumber \\&\qquad - \frac{e^*_{(\lambda )} \cdot p_H}{m_H +m_T } \left[ (p_H + P)^\mu - \frac{m^2_H -m^2_T}{q^2} q^\mu \right] A_2 (q^2) \nonumber \\&\qquad +2 m_T \frac{e^*_{(\lambda )} \cdot p_H}{q^2} q^\mu A_0 (q^2) \end{aligned}$$

(5)

$$\begin{aligned}&\langle T (P, \lambda )| \bar{q} \sigma ^{\mu \nu } q_\nu b | H(p_H) \rangle \nonumber \\&\quad = 2 T_1 (q^2) \varepsilon ^{\mu \nu \alpha \beta } p_{H \nu } P_\alpha e^*_{(\lambda )\beta } \end{aligned}$$

(6)

$$\begin{aligned}&\langle T (P, \lambda )| \bar{q} \sigma ^{\mu \nu } \gamma _5 q_\nu b | H(p_H) \rangle \nonumber \\&\quad = -i T_2 (q^2) \left[ ( m^2_H - m^2_T ) e^{* \mu }_{(\lambda )} - ( e^*_{(\lambda )} \cdot p_H ) ( p_H + P )^\mu \right] \nonumber \\&\qquad - i T_3 (q^2)( e^*_{(\lambda )} \cdot p_H ) \left[ q^\mu - \frac{q^2}{ m^2_H - m^2_T} ( p_H + P )^\mu \right] \nonumber \\ \end{aligned}$$

(7)

where $q_\mu = (p_H-P)_\mu$ is the momentum transferred and $e^{* \mu }_{(\lambda )} = \varepsilon ^{* \mu \nu }_{(\lambda )} q_\nu /m_H$. H represents $B_{(s)}$. $\varepsilon ^{\mu \nu \alpha \beta }$ is the total antisymmetric Levi-Civita symbol, with $\varepsilon ^{0123}=-\,1$. $A_1$, $A_2$, $A_0$, V and $T_1$, $T_2$, $T_3$ are the semileptonic and penguin type form factors, respectively. The latter are only relevant for exclusive decays induced by FCNC.

To the leading order of heavy quark expansion, the hadronic matrix elements can be written as [15, 16]

$$\begin{aligned}&\langle T( P, \lambda )| \bar{q} \varGamma b | H ( p_H ) \rangle \nonumber \\&\quad = \sqrt{\frac{m_H}{\bar{\varLambda }_H}} [ \langle T( P, \lambda )| \bar{q} \varGamma Q^{(+)}_v | M_v \rangle + {\mathscr {O}}( 1/m_Q) ] \end{aligned}$$

(8)

where $\bar{\varLambda }_H = m_H -m_Q$. $Q^{(+)}_v$ and $|M_v \rangle$ are the effective heavy quark field and heavy meson state in HQEFT, respectively. From heavy quark spin-flavor symmetry, the leading order hadronic matrix elements

$$\begin{aligned} \langle T( P, \lambda )| \bar{q} \varGamma Q^{(+)}_v | M_v \rangle = - \mathrm{Tr} [ \varOmega (v,P) \varGamma {\mathscr {M}}_v ] \end{aligned}$$

(9)

with

$$\begin{aligned} \varOmega (v, P)= & {} L_1 (v \cdot P) e^*_{(\lambda )} \quad /\quad + L_2 ( v \cdot P) ( v \cdot e^*_{(\lambda )} ) \\&+ \left[ L_3 (v \cdot P)e^*_{(\lambda )} \quad /\quad + L_4 ( v \cdot P) ( v \cdot e^*_{(\lambda )} ) \right] \hat{P} /\\ {\mathscr {M}}_v= & {} - \sqrt{\bar{\varLambda }} \frac{1+ v \quad /}{2} \gamma ^5, \quad \hat{P}^\mu = \frac{P^\mu }{v \cdot P} \end{aligned}$$

Here, $\bar{\varLambda }=\lim _{m_Q \rightarrow \infty } \bar{\varLambda }_H$. $L_1$, $L_2$, $L_3$, $L_4$ are the leading order wave functions describing the heavy to light meson transition matrix elements in HQEFT. ${\mathscr {M}}_v$ are the heavy pseudoscalar meson wave function. According to Eqs. (4)–(9), we have

$$\begin{aligned} A_1 (q^2) \!= & {} \! \frac{2}{m_H +m_T} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} [ L_1 ( v \cdot P) \!+\! L_3 ( v \cdot P) ] \end{aligned}$$

(10)

$$\begin{aligned} A_2 (q^2)= & {} 2 ( m_H + m_T) \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \Bigg [ \frac{L_2 ( v \cdot P)}{ 2 m^2_H} \nonumber \\&+ \frac{L_3 ( v \cdot P) - L_4 ( v \cdot P)}{ 2 m_H ( v \cdot P)} \Bigg ] \end{aligned}$$

(11)

$$\begin{aligned} A_0 (q^2)= & {} \frac{1}{m_T} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \Bigg [ L_1( v \cdot P) - L_2 (v \cdot P) \nonumber \\&+ \frac{m^2_T}{ m_H v \cdot P} \left( L_3 ( v \cdot P) - L_4 ( v \cdot P) \right) \nonumber \\&+ \frac{v \cdot P}{m_H} L_2( v \cdot P) + L_4 ( v \cdot P)\Bigg ] \end{aligned}$$

(12)

$$\begin{aligned} V ( q^2)= & {} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \frac{m_H + m_T}{m_H (v \cdot P)} L_3 ( v \cdot P) \end{aligned}$$

(13)

$$\begin{aligned} T_1 ( q^2)= & {} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \left[ \frac{1}{m_H} L^\prime _1 ( v \cdot P) + \frac{1}{v \cdot P } L^\prime _3 ( v \cdot P) \right] \nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned} T_2 ( q^2)= & {} 2 \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \frac{1}{ m^2_H - m^2_T} \Bigg [ ( m_H - v \cdot P ) L^\prime _1 ( v \cdot P ) \nonumber \\&+ \frac{ m_H v \cdot P - m^2_T}{ v \cdot P } L^\prime _3 ( v \cdot P ) \Bigg ] \end{aligned}$$

(15)

$$\begin{aligned} T_3 ( q^2 )= & {} \sqrt{\frac{m_H \bar{\varLambda }}{\bar{\varLambda }_H}} \Bigg [ - \frac{1}{ m_H} L^\prime _1 ( v \cdot P ) + \frac{1}{ v \cdot P } L^\prime _3 ( v \cdot P) \nonumber \\&- \frac{ m^2_H - m^2_T}{ m^2_H v \cdot P } L^\prime _4 ( v \cdot P) \Bigg ] \end{aligned}$$

(16)

where $v \cdot P = \frac{m^2_H +m^2_T -q^2 }{2 m_H}$ is the energy of light tensor meson in the final state. $L^\prime _i (i=1, 3, 4)$ are in general different from corresponding $L_i$ as they arise from different matrix elements.

2.2 LCSR in HQEFT

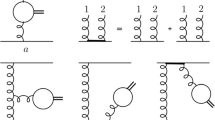
In the following, we intend to calculate the leading order wave functions describing heavy to light meson transition matrix elements in HQEFT, i.e., $L_1$, $L^\prime _1$, $L_2$, $L_3$, $L^\prime _3$, $L_4$, $L^\prime _4$ by using the LCSR. The procedure is similar to the case of $B_{(s)}$ decaying to light vector mesons [20]. Firstly, we define the following vacuum-tensor meson correlation functions,

$$\begin{aligned} C^\mu _V ( P, q)= & {} i \int d^4 x e^{i q \cdot x} \nonumber \\&\quad \times \langle T ( P , \lambda ) | {\mathscr {T}} \{ \bar{q}_1 \gamma ^\mu b(x), \bar{b} (0) i \gamma ^5 q_2 (0) \} | 0 \rangle \nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned} C^\mu _A ( P, q)= & {} i \int d^4 x e^{i q \cdot x} \nonumber \\&\quad \times \langle T ( P , \lambda ) | {\mathscr {T}} \{ \bar{q}_1 \gamma ^\mu \gamma ^5 b(x), \bar{b} (0) i \gamma ^5 q_2 (0) \} | 0 \rangle \nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned} C^\mu _T ( P, q)= & {} i \int d^4 x e^{i q \cdot x} \nonumber \\&\quad \times \langle T ( P , \lambda ) | {\mathscr {T}} \{ \bar{q}_1 \sigma ^{\mu \nu } q_\nu b(x), \bar{b} (0) i \gamma ^5 q_2 (0) \} | 0 \rangle \nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} C^{\prime \mu }_T ( P, q)= & {} i \int d^4 x e^{i q \cdot x} \nonumber \\&\quad \times \langle T ( P , \lambda ) | {\mathscr {T}} \{ \bar{q}_1 \sigma ^{\mu \nu } \gamma ^5 q_\nu b(x), \bar{b} (0) i \gamma ^5 q_2 (0) \} | 0 \rangle \nonumber \\ \end{aligned}$$

(20)

where ${\mathscr {T}}$ denotes time ordered product of operators.

On one hand, inserting a complete set of states with $B_{(s)}$ meson quantum numbers between the currents in Eqs. (17)–(20) phenomenologically, we obtain

$$\begin{aligned} C^\mu _V ( P, q)= & {} \frac{ \langle T ( P, \lambda ) | \bar{q}_1 \gamma ^\mu b | H \rangle \langle H | \bar{b} i \gamma ^5 q_2 |0 \rangle }{ m^2_H - ( P +q )^2 } \nonumber \\&+ \sum _{H^\prime } \frac{ \langle T ( P, \lambda ) | \bar{q}_1 \gamma ^\mu b | H^\prime \rangle \langle H^\prime | \bar{b} i \gamma ^5 q_2 |0 \rangle }{ m^2_{H^\prime } - ( P +q )^2 }\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned} C^\mu _A ( P, q)= & {} \frac{ \langle T ( P, \lambda ) | \bar{q}_1 \gamma ^\mu \gamma ^5 b | H \rangle \langle H | \bar{b} i \gamma ^5 q_2 |0 \rangle }{ m^2_H - ( P +q )^2 } \nonumber \\&+ \sum _{H^\prime } \frac{ \langle T ( P, \lambda ) | \bar{q}_1 \gamma ^\mu \gamma ^5 b | H^\prime \rangle \langle H^\prime | \bar{b} i \gamma ^5 q_2 |0 \rangle }{ m^2_{H^\prime } - ( P +q )^2 }\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned} C^\mu _T ( P, q)= & {} \frac{ \langle T ( P, \lambda ) | \bar{q}_1 \sigma ^{\mu \nu } q_\nu b | H \rangle \langle H | \bar{b} i \gamma ^5 q_2 |0 \rangle }{ m^2_H - ( P +q )^2 } \nonumber \\&+ \sum _{H^\prime } \frac{ \langle T ( P, \lambda ) | \bar{q}_1 \sigma ^{\mu \nu } q_\nu b | H^\prime \rangle \langle H^\prime | \bar{b} i \gamma ^5 q_2 |0 \rangle }{ m^2_{H^\prime } - ( P +q )^2 }\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned} C^{\prime \mu }_T ( P, q)= & {} \frac{ \langle T ( P, \lambda ) | \bar{q}_1 \sigma ^{\mu \nu } \gamma ^5 q_\nu b | H \rangle \langle H | \bar{b} i \gamma ^5 q_2 |0 \rangle }{ m^2_H - ( P +q )^2 } \nonumber \\&+ \sum _{H^\prime } \frac{ \langle T ( P, \lambda ) | \bar{q}_1 \sigma ^{\mu \nu } \gamma ^5 q_\nu b | H^\prime \rangle \langle H^\prime | \bar{b} i \gamma ^5 q_2 |0 \rangle }{ m^2_{H^\prime } - ( P +q )^2 }\nonumber \\ \end{aligned}$$

(24)

The effective decay constant of heavy meson in HQEFT is defined as [15, 16]

$$\begin{aligned} \langle 0 | \bar{q} \varGamma Q^{(+)}_v | {\mathscr {M}}_v \rangle = \frac{F}{2} \mathrm{Tr} \left[ \varGamma {\mathscr {M}}_v \right] \end{aligned}$$

(25)

Substituting Eqs. (8), (9), (25) into (21)–(24), we obtain

$$\begin{aligned} C^\mu _V ( P, q)= & {} \frac{-2 F}{ 2 \bar{\varLambda }_H - 2 v \cdot k } \frac{1}{ v \cdot P} L_3 ( v \cdot P ) \varepsilon ^{\mu \nu \alpha \beta } e^*_{(\lambda ) \nu } P_\alpha v_\beta \nonumber \\&+ \int ^\infty _{s_0} ds \frac{\rho _{TV} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.} \end{aligned}$$

(26)

$$\begin{aligned} C^\mu _A ( P, q)= & {} \frac{2 i F}{ 2 \bar{\varLambda }_H - 2 v \cdot k } \Bigg [ ( L_1( v \cdot P ) + L_3( v \cdot P ) ) e_{(\lambda )}^{* \mu } \nonumber \\&- L_2( v \cdot P ) v^\mu ( e_{(\lambda ) }^* \cdot v ) \nonumber \\&\quad - (L_3( v \cdot P )- L_4( v \cdot P ) ) P^\mu \frac{e_{(\lambda ) }^* \cdot v}{v \cdot P} \Bigg ] \nonumber \\&+ \int ^\infty _{s_0} ds \frac{\rho _{TA} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.} \end{aligned}$$

(27)

$$\begin{aligned} C^\mu _T ( P,q )= & {} \frac{-2i F}{ 2 \bar{\varLambda }_H - 2 v \cdot k } \Bigg [ L_1^\prime ( v \cdot P) \nonumber \\&+ \frac{m_H}{v \cdot P} L_3^\prime ( v \cdot P ) \Bigg ] \nonumber \\&\times \varepsilon ^{ \mu \nu \alpha \beta } e_{(\lambda ) \nu }^* P_\alpha v_\beta \nonumber \\&+\int ^\infty _{s_0} ds \frac{\rho _{TT} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.} \end{aligned}$$

(28)

$$\begin{aligned} C^{ \prime \mu }_T ( P,q )= & {} \frac{2 F}{ 2 \bar{\varLambda }_H - 2 v \cdot k } \Bigg [ \Bigg ( (m_H - v \cdot P) L_1^\prime ( v \cdot P) \nonumber \\&+ \frac{m_H v \cdot P - m^2_T}{ v \cdot P} L_3^\prime ( v \cdot P) \Bigg ) e_{(\lambda ) }^{* \mu } + e_{(\lambda ) }^* \cdot v \nonumber \\&\times \Bigg ( -m_H L_1^\prime ( v \cdot P) \nonumber \\&+ \frac{m^2_T - m_H v \cdot P }{ v \cdot P } L_4^\prime ( v \cdot P) \Bigg ) v^\mu \nonumber \\&+ e_{(\lambda ) }^* \cdot v \Bigg ( -\frac{m_H L_3^\prime ( v \cdot P)}{v \cdot P} + \frac{m_H - v \cdot P}{ v \cdot P} \nonumber \\&\times L_4^\prime ( v \cdot P) \Bigg ) P^\mu \Bigg ] \nonumber \\&+\int ^\infty _{s_0} ds \frac{\rho ^\prime _{TT} ( v \cdot P, s)}{ s - 2 v \cdot k } + \mathrm{subtr.} \end{aligned}$$

(29)

where $k^\mu = (P+q)^\mu - m_Q v^\mu$, denoting the residual momentum in $B_{(s)}$ meson. The integral terms represent contributions coming from the higher resonances. The subtraction terms “subtr.”are introduced to ensure the convergence of integral terms, which vanish automatically after Borel transformation and therefore do not affect the physics results.

On the other hand, we can calculate the vacuum-tensor meson correlation functions theoretically,

$$\begin{aligned}&C^\mu _V ( P, q) = \int ^\infty _0 d s \frac{\rho ^{\mathrm{th}}_{TV} ( v \cdot P, s)}{ s - 2 v \cdot k} + \mathrm{subtr.} \end{aligned}$$

(30)

$$\begin{aligned}&C^\mu _A ( P, q) = \int ^\infty _0 d s \frac{\rho ^{\mathrm{th}}_{TA} ( v \cdot P, s)}{ s - 2 v \cdot k} + \mathrm{subtr.} \end{aligned}$$

(31)

$$\begin{aligned}&C^\mu _T ( P, q) = \int ^\infty _0 d s \frac{\rho ^{\mathrm{th}}_{TT} ( v \cdot P, s)}{ s - 2 v \cdot k} + \mathrm{subtr.} \end{aligned}$$

(32)

$$\begin{aligned}&C^{\prime \mu }_T ( P, q) = \int ^\infty _0 d s \frac{\rho ^{\prime \mathrm{th}}_{TT} ( v \cdot P, s)}{ s - 2 v \cdot k} + \mathrm{subtr.} \end{aligned}$$

(33)

According to the assumption of quark hadron duality, starting from some effective threshold $s_0$, the theoretical spectral densities $\rho ^{\mathrm{th}}_{TV} ( v \cdot P, s )$, $\rho ^{\mathrm{th}}_{TA} ( v \cdot P, s )$, $\rho ^{\mathrm{th}}_{TT} ( v \cdot P, s )$, $\rho ^{\prime \mathrm{th}}_{TT} ( v \cdot P, s )$ are equal to their physical counterparts $\rho _{TV} ( v \cdot P, s )$, $\rho _{TA} ( v \cdot P, s )$, $\rho _{TT} ( v \cdot P, s )$, $\rho ^\prime _{TT} ( v \cdot P, s )$, respectively. Therefore, we have

$$\begin{aligned}&-\frac{2 F}{2 \bar{\varLambda }_H - 2 v \cdot k } \frac{1}{ v \cdot P} L_3 ( v \cdot P) \varepsilon ^{\mu \nu \alpha \beta } e^*_{(\lambda )\nu } P_\alpha v_\beta \nonumber \\&\quad = \int ^{s_0}_0 d s \frac{ \rho _{TV} ( v \cdot P, s )}{s - 2 v \cdot k} + \mathrm{subtr. } \end{aligned}$$

(34)

$$\begin{aligned}&\frac{2 i F}{2 \bar{\varLambda }_H - 2 v \cdot k } \Bigg [ \left( L_1 ( v \cdot P ) + L_3 ( v \cdot P ) \right) e_{(\lambda )}^{* \mu } \nonumber \\&\qquad - L_2 ( v \cdot P ) v^\mu e_{(\lambda )}^* \cdot v - \left( L_3 ( v \cdot P ) - L_4 ( v \cdot P ) \right) \nonumber \\&\qquad \times P^\mu \frac{e_{(\lambda )}^* \cdot v }{ v \cdot P} \Bigg ] = \int ^{s_0}_0 d s \frac{ \rho _{TA} ( v \cdot P, s )}{s - 2 v \cdot k} + \mathrm{subtr. } \end{aligned}$$

(35)

$$\begin{aligned}&\frac{-2i F}{ 2 \bar{\varLambda }_H - 2 v \cdot k } \left[ L_1^\prime ( v \cdot P) + \frac{m_H}{v \cdot P} L_3^\prime ( v \cdot P ) \right] \nonumber \\&\qquad \times \varepsilon ^{ \mu \nu \alpha \beta } e_{(\lambda ) \nu }^* P_\alpha v_\beta = \int ^{s_0}_0 d s \frac{ \rho _{TT} ( v \cdot P, s )}{s - 2 v \cdot k} + \mathrm{subtr. } \nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned}&\frac{2 F}{ 2 \bar{\varLambda }_H - 2 v \cdot k } \left[ \left( (m_H - v \cdot P) L_1^\prime ( v \cdot P) \right. \right. + \frac{m_H v \cdot P - m^2_T}{ v \cdot P} \nonumber \\&\qquad \left. \times L_3^\prime ( v \cdot P) \right) e_{(\lambda )}^{* \mu } + e_{(\lambda )}^* \cdot v \Bigg ( -m_H L_1^\prime ( v \cdot P) \nonumber \\&\qquad \left. + \frac{m^2_T - m_H v \cdot P }{ v \cdot P } L_4^\prime ( v \cdot P) \right) v^\mu + e_{(\lambda )}^* \cdot v \nonumber \\&\qquad \times \left. \left( -\frac{m_H L_3^\prime ( v \cdot P)}{v \cdot P} + \frac{m_H - v \cdot P}{ v \cdot P} L_4^\prime ( v \cdot P) \right) P^\mu \right] \nonumber \\&\quad =\int ^{s_0}_0 d s \frac{ \rho ^\prime _{TT} ( v \cdot P, s )}{s - 2 v \cdot k} + \mathrm{subtr. } \end{aligned}$$

(37)

Defining $y = v \cdot P$, $\omega = 2 v \cdot k$ and performing two sequential Borel transformation on Eqs. (30)–(33), we have

$$\begin{aligned} \rho ^{\mathrm{th}}_{TV}( y, s )= & {} \hat{B}^{-1/t}_{1/s} \hat{B}^\omega _t C^\mu _V ( y, \omega ) \end{aligned}$$

(38)

$$\begin{aligned} \rho ^{\mathrm{th}}_{TA}( y, s )= & {} \hat{B}^{-1/t}_{1/s} \hat{B}^\omega _t C^\mu _A ( y, \omega ) \end{aligned}$$

(39)

$$\begin{aligned} \rho ^{\mathrm{th}}_{TT}( y, s )= & {} \hat{B}^{-1/t}_{1/s} \hat{B}^\omega _t C^\mu _T ( y, \omega ) \end{aligned}$$

(40)

$$\begin{aligned} \rho ^{\prime \mathrm{th}}_{TT}( y, s )= & {} \hat{B}^{-1/t}_{1/s} \hat{B}^\omega _t C^{\prime \mu }_T ( y, \omega ) \end{aligned}$$

(41)

Calculating the vacuum-tensor meson correlation functions at the leading order of heavy quark expansion in HQEFT and substituting into Eqs. (38)–(41), we obtain

$$\begin{aligned}&\rho ^{\mathrm{th}}_{TV}( y, s ) = \frac{1}{2y} \left[ -f_T m^2_T \frac{1}{2 y^2} \frac{\partial }{\partial u} g_a (u) \right. \nonumber \\&\quad \left. + f^\perp _T m_T \frac{1}{y} \phi _\perp (u) \right] _{u= 1- \frac{s}{2y}} \varepsilon ^{\mu \nu \alpha \beta } v_\nu P_\alpha e^*_{(\lambda ) \beta } \end{aligned}$$

(42)

$$\begin{aligned}&\rho ^{\mathrm{th}}_{TA} ( y, s) = \frac{i}{2y} \left\{ e_{(\lambda )}^{* \mu } \left[ \frac{f_T m^2_T}{y} g_v (u) + f^\perp _T m_T \phi _\perp (u) \right. \right. \nonumber \\&\quad \left. + \frac{f^\perp _T m^3_T}{2 y^2} \left( h_3 (u) -\phi _\perp ( u ) \right) \right] - v^\mu e_{(\lambda )}^* \cdot v \left[ \frac{f_T m^4_T}{2 y^3}\right. \nonumber \\&\quad \times \left( g_3 (u) + \phi _\parallel (u) - 2 g_v (u) \right) + \frac{f^\perp _T m^3_T}{2 y^2} \frac{\partial }{\partial u} h_s (u) \nonumber \\&\quad \left. + \frac{ f^\perp _T m^3_T}{ y^2} \left( h_t (u) -\phi _\perp (u) \right) \right] - P^\mu \frac{e_{(\lambda )}^* \cdot v}{ v \cdot P} \nonumber \\&\quad \times \left[ - \frac{f_T m^2_T}{y} \left( \phi _\parallel (u) - g_v (u) \right) + f^\perp _T m_T \phi _\perp (u) \right. \nonumber \\&\quad \left. \left. - f^\perp _T \frac{m^3_T}{y^2} \left( h_t (u) - \frac{1}{2} \phi _\perp (u) - \frac{1}{2} h_3 (u) \right) \right] \right\} _{u = 1- \frac{s}{2y}} \end{aligned}$$

(43)

$$\begin{aligned}&\rho ^{\mathrm{th}}_{TT} ( y, s) = \frac{i}{2y} \left[ - \frac{m_H f^\perp _T m_T }{y} \phi _\perp (u) \right. \nonumber \\&\quad - \frac{f^\perp _T m^3_T}{2 y^2} \left( h_3 (u) - \phi _\perp (u) \right) + \frac{f_T m^2_T}{ 2 y^2 } ( m_H -y) \nonumber \\&\qquad \left. \times \frac{\partial }{ \partial u} g_a ( u) - \frac{f_T m^2_T}{y} g_v (u) \right] _{ u = 1 - \frac{s}{2y} } \end{aligned}$$

(44)

$$\begin{aligned}&\rho ^{\prime \mathrm{th}}_{TT} ( y, s) = \frac{1}{2y} \Bigg \{ e_{(\lambda )}^{* \mu } \left[ f^\perp _T m_T \left( m_H - \frac{m^2_T}{2y} - \frac{m_H m^2_T}{2 y^2} \right) \right. \nonumber \\&\quad \times \phi _\perp (u) + \frac{1}{2} f^\perp _T \frac{m^3_T}{y^2} ( m_H - y) h_3 (u) + \frac{f_T m^2_T}{y} (m_H \nonumber \\&\quad \left. -y) g_v (u) - \frac{1}{2 y^2} f_T m^2_T ( -m^2_T +y^2) \frac{\partial }{ \partial u} g_a (u) \right] \nonumber \\&\quad + e_{(\lambda )}^* \cdot v P^\mu \left[ - f^\perp _T m_T \left( \frac{m_H}{y} + (m_H -y) \frac{m^2_T}{ 2 y^3} \right) \right. \nonumber \\&\quad \times \phi _\perp (u) + f^\perp _T m^3_T \frac{1}{y^3}(m_H -y)\left( h_t (u) - \frac{1}{2} h_3 (u) \right) \nonumber \\&\quad + \frac{f_T m^2_T}{y^2} (m_H -y) \left( \phi _\parallel (u) - g_v (u) \right) + \frac{f_T m^2_T}{2y} \nonumber \\&\quad \left. \times \frac{\partial }{ \partial u} g_a (u) \right] + e_{(\lambda )}^* \cdot v v^\mu \left[ \frac{1}{2} f^\perp _T m^3_T \left( 2 \frac{m_H}{y^2} \right. \right. \nonumber \\&\quad \left. - \frac{m^2_T}{y^3} \right) \phi _\perp (u) - f^\perp _T \frac{m^5_T}{2 y^3} h_3 (u)- f^\perp _T \frac{m^3_T}{y^3} (m_H y \nonumber \\&\quad - m^2_T ) h_t (u) - f_T \frac{m^2_T}{y^2} ( m_H y - m^2_T ) \phi _\parallel (u ) \nonumber \\&\quad \left. - f_T m^4_T \frac{1}{y^2} g_v (u) - \frac{1}{2 y^2 } f_T m^4_T \frac{\partial }{\partial u} g_a (u) \right] \Bigg \} \end{aligned}$$

(45)

Here $\phi _\parallel (u)$, $\phi _\perp (u)$, $g_v (u)$, $g_a (u)$, $h_t (u)$, $h_s (u)$, $g_3 (u)$, $h_3 (u)$ are the light cone DAs of tensor mesons, which are defined as [10]

$$\begin{aligned}&\langle T (P, \lambda ) | \bar{q}_1 (x) \gamma _\mu q_2 (0) | 0 \rangle = f_T m^2_T \int _0^1 d u e^{i u P \cdot x} \nonumber \\&\quad \times \Bigg \{ P_\mu \frac{\varepsilon ^*_{(\lambda ) \alpha \beta } x^\alpha x^\beta }{ ( P \cdot x )^2} \phi _\parallel (u) + \left( \frac{\varepsilon ^*_{(\lambda ) \mu \alpha } x^\alpha }{ P \cdot x } \right. \nonumber \\&\quad \left. - P_\mu \frac{\varepsilon ^*_{(\lambda ) \alpha \beta } x^\alpha x^\beta }{ ( P \cdot x )^2} \right) g_v (u) - \frac{1}{2} x_\mu \frac{\varepsilon ^*_{(\lambda ) \alpha \beta } x^\alpha x^\beta }{ ( P \cdot x )^3} \nonumber \\&\quad \times \left( g_3 (u) + \phi _\parallel (u) - 2 g_v (u) \right) \Bigg \} \end{aligned}$$

(46)

$$\begin{aligned}&\langle T (P, \lambda ) | \bar{q}_1 (x) \gamma _\mu \gamma _5 q_2 (0) | 0 \rangle = \frac{1}{2} f_T m^2_T \int _0^1 du e^{i u P \cdot x} \nonumber \\&\quad \times \epsilon _{\mu \nu \alpha \beta } x^\nu P^\alpha \varepsilon ^{* \beta \delta }_{(\lambda )} x_\delta \frac{1}{ P \cdot x} g_a (u) \end{aligned}$$

(47)

$$\begin{aligned}&\langle T (P, \lambda ) | \bar{q}_1 (x) \sigma _{\mu \nu } q_2 (0) | 0 \rangle = -i f^\perp _T m_T \int _0^1 d u e^{i u P \cdot x} \nonumber \\&\quad \times \Bigg \{ \left[ \varepsilon ^*_{(\lambda ) \mu \alpha } x^\alpha P_\nu - \varepsilon ^*_{(\lambda ) \nu \alpha } x^\alpha P_\mu \right] \frac{1}{ P \cdot x}\phi _\perp (u) \nonumber \\&\quad + ( P_\mu x_\nu - P_\nu x_\mu ) \frac{m^2_T \varepsilon ^*_{(\lambda ) \alpha \beta } x^\alpha x^\beta }{ (P \cdot x)^3 } \left( h_t (u) - \frac{1}{2} \phi _\perp (u) \right. \nonumber \\&\quad \left. - \frac{1}{2} h_3 (u) \right) + \frac{1}{2} \left( \varepsilon ^*_{(\lambda ) \mu \alpha } x^\alpha x_\nu - \varepsilon ^*_{(\lambda ) \nu \alpha }x^\alpha x_\mu \right) \nonumber \\&\quad \times \frac{m^2_T}{ ( P \cdot x)^2} (h_3 (u) - \phi _\perp (u)) \Bigg \} \end{aligned}$$

(48)

$$\begin{aligned}&\langle T (P, \lambda ) | \bar{q}_1 (x) q_2 (0) | 0 \rangle = - \frac{i}{2} f^\perp _T m^3_T \int ^1_0 d u e^{i u P \cdot x } \nonumber \\&\quad \times \frac{\varepsilon ^*_{(\lambda ) \alpha \beta } x^\alpha x^\beta }{ P \cdot x } h_s (u) \end{aligned}$$

(49)

where {$\phi _\parallel (u)$, $\phi _\perp (u)$}, {$g_v (u)$, $g_a (u)$, $h_t (u)$, $h_s (u)$} and {$g_3 (u)$, $h_3 (u)$} are of twist-2, twist-3 and twist-4, respectively. Substituting Eqs. (42)–(45) into (34)–(37) and performing the Borel transformation $\hat{B}^\omega _t$ on both sides, we obtain the leading order wave functions describing heavy to light meson transition matrix elements in HQEFT,

$$\begin{aligned} L_1 (y)= & {} \frac{1}{4F} e^{2 \bar{\varLambda }_H/t} \int ^{s_0}_0 d s e^{-s/t} \frac{1}{y^2} \Bigg [ f_T m^2_T g_v (u) \nonumber \\&+ \frac{1}{2} f_T m^2_T \frac{\partial }{ \partial u} g_a (u) \nonumber \\&+ \frac{1}{2y} f^\perp _T m^3_T (h_3 (u) -\phi _\perp (u)) \Bigg ]_{u = 1 - \frac{s}{2y}} \end{aligned}$$

(50)

$$\begin{aligned} L_2 (y)= & {} \frac{1}{4F} e^{2 \bar{\varLambda }_H/t} \int ^{s_0}_0 d s e^{-s/t} \left[ \frac{1}{y^3} f^\perp _T m^3_T \Bigg ( -\phi _\perp (u) \right. \nonumber \\&\left. + h_t (u) + \frac{1}{2} \frac{\partial }{\partial u} h_s (u) \right) \nonumber \\&\left. + \frac{1}{2y^4} f_T m^4_T ( g_3 (u) + \phi _\parallel (u) - 2 g_v (u) ) \right] _{u= 1- \frac{s}{2y}} \end{aligned}$$

(51)

$$\begin{aligned} L_3 (y)= & {} \frac{1}{4F} e^{2 \bar{\varLambda }_H/t} \int ^{s_0}_0 d s e^{-s/t} \left[ - \frac{1}{2y^2} f_T m^2_T \frac{\partial }{\partial u} g_a (u) \right. \nonumber \\&\left. + \frac{1}{y} f^\perp _T m_T \phi _\perp (u) \right] _{u = 1- \frac{s}{2y}} \end{aligned}$$

(52)

$$\begin{aligned} L_4 (y)= & {} \frac{1}{4F} e^{2 \bar{\varLambda }_H/t} \int ^{s_0}_0 d s e^{-s/t} \frac{1}{y^2} \Bigg [ f_T m^2_T \Bigg ( \phi _\parallel (u) \nonumber \\&\left. - g_v (u) - \frac{1}{2} \frac{\partial }{\partial u} g_a (u) \right) + f^\perp _T \frac{m^3_T}{y} \left( h_t (u) \right. \nonumber \\&\left. \left. - \frac{1}{2} \phi _\perp (u) - \frac{1}{2} h_3 (u) \right) \right] _{u = 1- \frac{s}{2y}} \end{aligned}$$

(53)

It is found that the wave functions $L^\prime _1$, $L^\prime _3$ and $L^\prime _4$ are exactly the same as $L_1$, $L_2$ and $L_3$, respectively. With this consideration, from Eqs. (10) to (16), we obtain the following relations between the semileptonic and penguin type form factors,

$$\begin{aligned} T_1 (q^2)= & {} \frac{m^2_H - m^2_T +q^2}{ 2 m_H} \frac{V(q^2)}{m_H + m_T} + \frac{m_H + m_T}{2 m_H} A_1( q^2) \nonumber \\ \end{aligned}$$

(54)

$$\begin{aligned} T_2 (q^2)= & {} \frac{2}{m^2_H - m^2_T} \Bigg [ \frac{(m_H -y)(m_H + m_T)}{2} A_1 (q^2) \nonumber \\&+ \frac{m_H ( y^2- m^2_T)}{m_H + m_T} V(q^2) \Bigg ] \end{aligned}$$

(55)

$$\begin{aligned} T_3(q^2)= & {} - \frac{m_H +m_T}{2 m_H} A_1 (q^2) + \frac{m_H -m_T}{2 m_H} [ A_2 (q^2) \nonumber \\&- A_3 (q^2) ] + \frac{m^2_H +3 m^2_T -q^2}{ 2m_H ( m_H + m_T)} V(q^2) \end{aligned}$$

(56)

with

$$\begin{aligned} A_3(q^2)= & {} \frac{2 m_T(m_H+ m_T)}{q^2}\left[ \frac{m_H + m_T}{2m_T } A_1(q^2) \right. \nonumber \\&\left. - \frac{m_H - m_T}{2m_T } A_2(q^2) -A_0 (q^2) \right] \end{aligned}$$

(57)

Therefore, the penguin type form factors can be obtained directly from the corresponding semileptonic ones, which is similar to the case of S-wave mesons [15, 16].

3 Numerical analysis and results of the form factors

With Eqs. (10)–(13) and (50)–(57) given above, we are now in a position to calculate the $B_{(s)}$ $\rightarrow$ $a_2(1320)$, $K^*_2(1430)$, $f_2(1270)$, $f^\prime _2(1525)$ form factors. For this purpose, it needs to know the light cone DAs of tensor mesons, which have been studied via QCD sum rules in Ref. [10]. In the present work, we shall neglect the contributions of $g_3 (u)$ and $h_3 (u)$ and consider the light cone DAs to twist-3.

The twist-2 and twist-3 light cone DAs of tensor mesons are given by [10]

$$\begin{aligned} \phi _\parallel (u)= & {} \phi _\perp (u) = 30 u (1-u)(2u-1) \end{aligned}$$

(58)

$$\begin{aligned} g_v (u)= & {} 5 (2u-1)^2 \end{aligned}$$

(59)

$$\begin{aligned} g_a (u)= & {} 10 u (1-u) (2u-1) \end{aligned}$$

(60)

$$\begin{aligned} h_t (u)= & {} \frac{15}{2} (2u-1) (1-6u + 6 u^2 ) \end{aligned}$$

(61)

$$\begin{aligned} h_s (u)= & {} 15 u (1 -u) ( 2u-1) \end{aligned}$$

(62)

For the decay constants of light tensor mesons, we quote the values calculated via QCD sum rules [10], as shown in Table 1.

Table 1 The decay constants of light tensor mesons calculated via QCD sum rules [10]

Fig. 1

$B \rightarrow a_2(1320)$ form factors as functions of t for different $s_0$ at $q^2=0$

Fig. 2

$B \rightarrow f_2(1270)$ form factors as functions of t for different $s_0$ at $q^2=0$

Fig. 3

$B \rightarrow K^*_2(1430)$ form factors as functions of t for different $s_0$ at $q^2=0$

Other input parameters involved are as follows [1, 15, 16],

$$\begin{aligned}&m_B = 5.28 \mathrm{GeV}, \quad m_{B_s} = 5.37 \mathrm{GeV}, \quad m_b =4.75 \mathrm{GeV} \\&\bar{\varLambda } =0.53 \mathrm{GeV}, \quad F = 0.3 \mathrm{GeV}^3 \end{aligned}$$

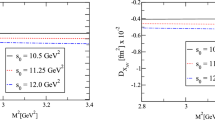
As shown in Eqs. (50)–(53), two free parameters, i.e., $s_0$, t are involved in our calculations. $s_0$ is related to the threshold energy of initial heavy meson and t is the Borel parameter. According to the requirements of LCSR, we choose the region of these two parameters so that the curves of form factors become most stable. In the evaluation, we adjust $s_0$ and t for all relevant $B \rightarrow T$ decays consistently and the same procedure is also performed for $B_s \rightarrow T$ decays. The variation of $B \rightarrow a_2 (1320), f_2(1270), K^*_2 (1430)$ form factors as functions of t for different $s_0$ at the maximally recoiling point ($q^2=0$) are shown in Figs. 1, 2 and 3, respectively.

Note that we have only shown the curves of the semileptonic type form factors here in that the penguin type form factors can be obtained directly from the corresponding semileptonic ones as mentioned above. Based on the curves given here, we can see that choosing $s_0 = 2.0 \pm 0.2 \mathrm{GeV}, t=2.0 \pm 0.5 \mathrm{GeV}$ for $B \rightarrow T$ decays is reasonable. Similarly, we can determine the region of $s_0$ and t for $B_s \rightarrow T$ decays. It is found that the region for $B_s \rightarrow T$ is the same as $B \rightarrow T$ decays.

As well known, the LCSR is expected to break down at large momentum transfer, i.e., $q^2 \sim m^2_b - 2 m_b \bar{\varLambda }$. For this reason, it is needed to extrapolate our LCSR results to the whole physical region via certain parametrization. Various parametric forms exist such as the single pole form, modified pole form and series expansion [12, 21,22,23]. Here the series expansion parametrization is adopted due to the fact that it is based on a more physical analysis. In this parametrization, the form factors are written as [21,22,23]

$$\begin{aligned} F(q^2)= \frac{1}{B_F(q^2)\varPhi _F(q^2)}\sum ^2_{k=0}\alpha ^F_k z(q^2,t_0)^k \end{aligned}$$

(63)

where

$$\begin{aligned}&B_F(q^2)= \prod _{R_F} z (q^2, m^2_{R_F}) \end{aligned}$$

(64)

$$\begin{aligned}&\varPhi _F(q^2) = \sqrt{\frac{1}{32 \pi }} \frac{q^2-t_+}{(t_+ -t_0)^{1/4}}\left[ \frac{z(q^2,0)}{-q^2}\right] ^{(n+3)/2} \nonumber \\&\quad \times \left[ \frac{z(q^2,t_0)}{t_0-q^2} \right] ^{-1/2} \left[ \frac{z(q^2,t_-)}{t_- -q^2} \right] ^{-3/4} \end{aligned}$$

(65)

$$\begin{aligned}&z(q^2,t_0)=\frac{\sqrt{t_+ -q^2}-\sqrt{t_+ -t_0}}{\sqrt{t_+ -q^2}+\sqrt{t_+ -t_0}} \end{aligned}$$

(66)

with $t_\pm = (m_H \pm m_T)^2$, $t_0= t_+ ( 1- \sqrt{1-t_-/t_+})$. A truncation has been made after the quadratic term in $z(q^2,t_0)$. $R_F$ are the resonances in the range $t_-<q^2<t_+$ with appropriate quantum numbers. The corresponding resonance masses can be found in Ref. [24], as listed in Table 2. n is the number of subtractions necessary to render the dispersion relation finite, with $n=1$ for $A_0$ and $n=2$ for $A_1, A_2, V$. Optimizing the form factor parameters by using the relation $\frac{F(0) B_F (0) \varPhi _F(0)}{\sum _{k=0}^2 \alpha _k z (0, q^2_0)^k}=1$ derived from Eq. (63), we have

$$\begin{aligned} F(q^2)= \frac{F(0) B_F(0) \varPhi _F (0) ( 1+ \sum _{k=1}^2 r_k^F z(q^2,t_0)^k)}{ B_F(q^2) \varPhi _F (q^2) ( 1+ \sum _{k=1}^2 r_k^F z(0, t_0)^k )} \end{aligned}$$

(67)

where $r_k^F = \frac{\alpha _k^F }{\alpha _0^F}$.

Table 2 Masses of resonances necessary for the series expansion parametrization of form factors [24]

Fig. 4

$B \rightarrow a_2(1320)$ form factors as functions of $q^2$

Using the LCSR predictions in low $q^2$ region (concretely, we have chosen to be $0 \le q^2 \le 6\mathrm{GeV}^2$) to fit the parameters $r_1^F, r_2^F$ in Eq. (67), we obtain the behavior of form factors in the whole physical region. The $B \rightarrow a_2(1320)$ form factors as functions of $q^2$ in the whole physical region are shown in Fig. 4. We can see that the $A_1$ decreases with $q^2$, while the behaviors of $A_2$, $A_0$, V are opposite. For other decay modes, the form factors as functions of $q^2$ have similar behaviors. Numerical results are presented in Table 3. The uncertainties of form factors come form the two free parameters $s_0$ and t. As can be seen from Table 3, the uncertainties of $B \rightarrow T$ and $B_s \rightarrow T$ form factors are about (6-8)% and (11-13)%, respectively. For the $B \rightarrow a_2(1320)$ modes, the form factors given here correspond to $a^\pm _2(1320)$. In the case of $a^0_2(1320)$ in the final states, the form factors can be obtained by multiplying $1/\sqrt{2}$ in light of the fact that the flavor content of $a^0_2(1320)$ is $1/\sqrt{2} (d\bar{d} - u\bar{u})$. The comparison of form factors at $q^2=0$ given in this work with other groups are shown in Table 4, in which the penguin type form factors are also listed for a complete analysis. From Table 4, we can find that large differences exist between the results of quark model approaches (ISGW2 [6, 7], LFQM [8, 9]) and those of sum rules (this work, LCSRT [11], LCSRB [13],QCDSR [14]) and pQCD [12]. The form factors predicted by ISGW2 all have negative signs and the magnitudes of $A_1(0), A_2(0)$ are typically larger. For the LFQM [8, 9], $A_1(0), A_2(0), T_3(0)$ are negative, while $A_0(0), V(0), T_1(0), T_2(0)$ are positive. The form factors obtained in this work are in general some larger, yet still compatible with those results of LCSRT [11], LCSRB [13], pQCD [12] and QCDSR [14] as a whole.

Table 3 The form factors of $B_{(s)} \rightarrow T$ decays, where the first, second and third results of fitting parameters correspond to the central, maximum and minimum values of form factors, respectively

Table 4 Comparison of the $B_{(s)} \rightarrow T$ form factors at $q^2=0$ given in this work with other groups. LCSRT and LCSRB denotes LCSR with tensor meson and B DAs, respectively

4 $B_{(s)}$ to light tensor meson semileptonic decays

In this section, we shall apply the form factors obtained above to investigate the corresponding semileptonic decays.

For the charged current induced semileptonic decays $B_{(s)} \rightarrow T l \bar{\nu }_l$, the differential decay width with respect to $q^2$ can be written as [12]

$$\begin{aligned} \frac{d \varGamma }{d q^2} =\frac{d \varGamma _L}{d q^2}+\frac{d \varGamma _T}{d q^2} \end{aligned}$$

(68)

where $\frac{d \varGamma _L}{d q^2}$ and $\frac{d \varGamma _T}{d q^2}$ denote the longitudinal and transverse differential decay width, respectively. Their expressions have the following forms,

$$\begin{aligned} \frac{d \varGamma _L}{d q^2}= & {} \frac{ G_F |V_{ub}|^2}{ 256 m^3_H \pi ^3 } \frac{\sqrt{\lambda _T}}{ q^2} \left( 1- \frac{m^2_l}{q^2} \right) ^2 X_L \end{aligned}$$

(69)

$$\begin{aligned} \frac{d \varGamma _T}{d q^2}= & {} \frac{ G_F |V_{ub}|^2}{ 256 m^3_H \pi ^3 } \frac{\sqrt{\lambda _T}}{ q^2} \left( 1- \frac{m^2_l}{q^2} \right) ^2 (X_+ + X_- ) \end{aligned}$$

(70)

with

$$\begin{aligned} X_L= & {} \frac{\lambda _T}{9 m^2_T m^2_H} \nonumber \\&\times \left[ ( 2 q^2 + m^2_l )h^2_0 (q^2) + 3 \lambda _T m^2_l A^2_0 (q^2) \right] \end{aligned}$$

(71)

$$\begin{aligned} X_\pm= & {} \frac{\lambda _T}{12 m^2_T m^2_H} q^2 ( 2 q^2 + m^2_l) \Bigg [ ( m_H + m_T ) A_1 (q^2) \nonumber \\&\left. \mp \frac{\sqrt{\lambda _T}}{{m_H + m_T} }V (q^2) \right] ^2 \end{aligned}$$

(72)

$$\begin{aligned} h_0 (q^2)= & {} \frac{1}{2 m_T} \Bigg [ ( m^2_H -m^2_T - q^2) ( m_H + m_T ) A_1 (q^2) \nonumber \\&\left. - \frac{\lambda _T}{m_H + m_T} A_2 (q^2) \right] \end{aligned}$$

(73)

Here $m_l$ is the mass of charged lepton and $q^2$ represents the momentum square of lepton pair.

The branching ratio can be obtained by integrating Eq. (68) over $q^2$ in the whole physical region and using the lifetimes of $B_{(s)}$ ( denoted as $\tau _H$ in the following ) as inputs,

$$\begin{aligned} Br = \frac{\tau _H}{\hbar } \varGamma = \frac{\tau _H}{\hbar } \int ^{(m_H- m_T)^2}_{m^2_l} d q^2 \frac{d \varGamma }{d q^2} \end{aligned}$$

(74)

In addition, it is also meaningful to define the longitudinal polarization fraction

$$\begin{aligned} f_L = \frac{\varGamma _L}{\varGamma } = \frac{\int ^{(m_H- m_T)^2}_{m^2_l} d q^2 \frac{d \varGamma _L}{d q^2}}{\int ^{(m_H- m_T)^2}_{m^2_l} d q^2 \frac{d \varGamma }{d q^2}} \end{aligned}$$

(75)

and forward-backward asymmetry (FBA) of lepton

$$\begin{aligned} \frac{d A_{FB}}{d q^2}= & {} \frac{\left( \int _0^1 - \int _{-1}^0 \right) d \cos \theta \frac{d^2 \varGamma }{d q^2 d \cos \theta }}{d \varGamma / d q^2} \nonumber \\= & {} \frac{1}{X_L + X_+ + X_-} \left( \frac{ 2 m^2_l \lambda _T^{3/2} }{6 m^2_T m^2_H} h_0 (q^2) A_0 (q^2) \right. \nonumber \\&\left. - \frac{\lambda _T}{8 m^2_T m^2_H} 4 q^4 \sqrt{\lambda _T} A_1 (q^2) V (q^2) \right) \end{aligned}$$

(76)

For the lifetimes of $B_{(s)}$, masses of charged leptons, CKM matrix element $|V_{ub}|$ and Fermi coupling constant $G_F$, we use the latest values given by the particle data group (PDG) [1],

$$\begin{aligned}&\tau _{\bar{B}^0} = 1.520 \times 10^{-12}s, \quad \tau _{B^-} = 1.638 \times 10^{-12}s \nonumber \\&\tau _{B_s} = 1.510 \times 10^{-12}s, \quad m_e = 0.51\times 10^{-3} GeV \nonumber \\&m_\mu = 0.106 GeV, \quad m_\tau = 1.777 GeV \nonumber \\&|V_{ub}|=(4.09 \pm 0.39) \times 10^{-3}\nonumber \\&G_F =1.166 \times 10^{-5} {\text {GeV}^{-2}} \end{aligned}$$

(77)

The FBAs of lepton as functions of $q^2$ for the decays $\bar{B}^0 \rightarrow a_2^+(1320) l^- \bar{\nu }_l(l=e, \mu , \tau )$ are shown in Fig. 5.

It is easily seen that the zero-crossing points increase significantly with the mass of charged lepton. For other charged current induced semileptonic decay modes, the behaviors of FBAs are similar. The numerical results of branching ratios (Br), longitudinal polarization fractions ($f_L$) and zero-crossing points of FBAs ($c_0$) for all $B_{(s)} \rightarrow T l \bar{\nu }_l$ decay modes are collected in Table 5.

Table 5 The Br, $f_L$ and $c_0$ for semileptonic $B_{(s)} \rightarrow T l \bar{\nu }_l$ decays, where the values of Br, $f_L$ calculated by pQCD [12] are also listed for comparison

Fig. 5

The FBAs of lepton as functions of $q^2$ for the decays $\bar{B}^0 \rightarrow a_2^+(1320) l^- \bar{\nu }_l (l=e, \mu , \tau )$

For comparison, we also list the values of Br and $f_L$ calculated via pQCD [12]. We can see that the results given in this work are compatible with the corresponding values obtained by pQCD on the whole. The Br are at the order of ${\mathscr {O}}(10^{-4})$. The results of Br and $f_L$ are almost identical for $l=e, \mu$, while those for $l=\tau$ are significantly smaller. Specially, the Br for $l=\tau$ are about one fifth of those for $l=e, \mu$. The $f_L$ are around $70\%$ for $l=e, \mu$ and $60\%$ for $l=\tau$. The first and second uncertainties of Br come from the form factors and CKM matrix element $|V_{ub}|$, respectively. The uncertainties from these two sources are at the same order of magnitude, i.e., roughly (15–20)%. In contrast, the uncertainties of $f_L$ and $c_0$ are much smaller, due to the fact that these two quantities are defined via the ratios of decay widths and therefore most of the uncertainties are canceled.

For the FCNC induced semileptonic decays $B_{(s)} \rightarrow T ll$, the differential decay width can be written as [25]

$$\begin{aligned} \frac{d \varGamma }{d q^2} = \frac{1}{4} ( 3 I^c_1 + 6 I^s_1 - I^c_2 - 2 I^s_2 ) \end{aligned}$$

(78)

with

$$\begin{aligned} I^c_1= & {} ( |A_{L0}|^2+ |A_{R0}|^2) \nonumber \\&+ 8 \frac{m_l^2}{q^2} Re[A_{L0} A^*_{R0}] + 4\frac{m_l^2}{q^2}|A_t|^2 \end{aligned}$$

(79)

$$\begin{aligned} I^s_1= & {} \frac{3}{4} [ |A_{L \perp }|^2 + |A_{L \parallel }|^2 + |A_{R \perp }|^2 + |A_{R \parallel }|^2 ] \left( 1- \frac{4m_l^2}{3 q^2} \right) \nonumber \\&+ \frac{4 m^2_l }{q^2} Re [ A_{L \perp } A^*_{R \perp } + A_{L \parallel } A^*_{R \parallel } ] \end{aligned}$$

(80)

$$\begin{aligned} I^c_2= & {} - \left( 1-\frac{4m^2_l}{q^2} \right) ( |A_{L0}|^2 + |A_{R0}|^2 ) \end{aligned}$$

(81)

$$\begin{aligned} I^s_2= & {} \frac{1}{4} \left( 1-\frac{4m^2_l}{q^2} \right) \nonumber \\&\times ( |A_{L \perp }|^2 + |A_{L \parallel }|^2 + |A_{R \perp }|^2 + |A_{R \parallel }|^2 ) \end{aligned}$$

(82)

and

$$\begin{aligned} A_{L0}= & {} N_T \frac{\sqrt{\lambda _T}}{\sqrt{6} m_H m_T}\frac{1}{2 m_T \sqrt{q^2}} \Bigg \{ ( C_9^{eff}-C_{10})\Bigg [ (m^2_H \nonumber \\&- m^2_T -q^2)(m_H + m_T)A_1(q^2) - \frac{\lambda _T}{m_H + m_T} \nonumber \\&\times A_2(q^2) \Bigg ] + 2 m_b ( C_{7L} - C_{7R}) \Bigg [ (m^2_H + 3 m^2_T \nonumber \\&-q^2)T_2 (q^2) - \frac{\lambda _T}{ m^2_H - m^2_T} T_3 (q^2) \Bigg ] \Bigg \} \end{aligned}$$

(83)

$$\begin{aligned} A_{L \perp }= & {} - \frac{\sqrt{\lambda _T}}{ 2 m_H m_T} N_T \left[ ( C_9^{eff} -C_{10} ) \frac{\sqrt{\lambda _T} }{m_H + m_T}V(q^2) \right. \nonumber \\&+ \frac{2 m_b ( C_{7L} + C_{7R} )}{q^2} \sqrt{\lambda _T} T_1(q^2) \Bigg ] \end{aligned}$$

(84)

$$\begin{aligned} A_{L \parallel }= & {} \frac{\sqrt{\lambda _T}}{ 2 m_H m_T} N_T \Bigg [ ( C_9^{eff} -C_{10} ) ( m_H + m_T) A_1 (q^2) \nonumber \\&\left. + \frac{2 m_b ( C_{7L} -C_{7R} )}{q^2} ( m^2_H - m^2_T) T_2(q^2) \right] \end{aligned}$$

(85)

$$\begin{aligned} A_t= & {} 2 N_T \frac{\sqrt{\lambda _T}}{\sqrt{6} m_H m_T} C_{10} \frac{ \sqrt{\lambda _T}}{ \sqrt{q^2}} A_0 (q^2) \end{aligned}$$

(86)

$$\begin{aligned} A_{Ri}= & {} A_{Li}|_{C_{10} \rightarrow - C_{10}}, ( i = 0, \perp , \parallel ) \end{aligned}$$

(87)

where $N_T= \sqrt{ \frac{G^2_F \alpha ^2_{em}}{3\cdot 2^{10} \pi ^5 m^3_H} |V_{tb} V^*_{tq}|^2 q^2 \lambda ^2_T \sqrt{( 1- \frac{4m^2_l}{q^2}} )}$, $(q=d, s)$. The {$A_{L0}$, $A_{R0}\}$, { $A_{L\perp }$, $A_{L\parallel }$, $A_{R \perp }$, $A_{R \parallel }$ } and $A_t$ are the longitudinal, transverse and time-like decay amplitudes, respectively. The subscripts L and R denote the chirality of corresponding amplitudes. In the SM, $C_{7L}= C_7^{eff}$, $C_{7R}= \frac{m_q}{m_b} C_7^{eff}$. We adopt the Wilson coefficients up to leading logarithmic accuracy given by Ref. [26]. At the scale $m_b$, their values are listed in Table 6.

Table 6 The values of Wilson coefficients up to leading logarithmic accuracy [26]

The effective Wilson coefficient $C_9^{eff}$ is related to $q^2$ and defined as [27]

$$\begin{aligned} C^{eff}_9 (q^2)= & {} C_9 + h(\hat{m}_c, \hat{s}) C_0 - \frac{1}{2} h(1, \hat{s}) ( 4 C_3 + 4 C_4 \nonumber \\&+ 3 C_5 + C_6) - \frac{1}{2} h( 0, \hat{s} ) ( C_3 + 3 C_4)\nonumber \\&+ \frac{2}{9} ( 3 C_3 + C_4 + 3 C_5 + C_6) \end{aligned}$$

(88)

with

$$\begin{aligned} h(z,\hat{s})= & {} - \frac{8}{9} \ln \frac{m_b}{\mu } - \frac{8}{9}\ln z + \frac{8}{27} + \frac{4}{9}x \nonumber \\&- \frac{2}{9} ( 2+x) \sqrt{| 1-x|}\nonumber \\&\times \left\{ \begin{array}{c} \ln \left| \frac{\sqrt{1-x} +1}{\sqrt{1-x}-1} \right| - i \pi \quad \mathrm{for} \quad x \equiv \frac{4 z^2}{\hat{s}} \le 1 \\ 2 \arctan \frac{1}{\sqrt{x-1}} \quad \mathrm{for} \quad x \equiv \frac{4 z^2}{\hat{s}} >1 \\ \end{array} \right. \end{aligned}$$

(89)

$$\begin{aligned} h(0, \hat{s} )= & {} - \frac{8}{9} \ln \frac{m_b}{\mu } - \frac{4}{9} \ln \hat{s} + \frac{8}{27} + \frac{4}{9} i \pi \end{aligned}$$

(90)

and $C_0= C_1+3C_2+ 3C_3 + C_4 + 3C_5 +C_6$, $\hat{s}=\frac{q^2}{m^2_b}$, $\hat{m}_c= \frac{m_c}{m_b}$.

Correspondingly, the branching ratio can be obtained by integrating Eq. (78) over $q^2$ in the whole physical region and using the lifetimes of $B_{(s)}$ as inputs,

$$\begin{aligned} Br = \frac{\tau _H}{\hbar } \varGamma = \frac{\tau _H}{\hbar } \int ^{(m_H- m_T)^2}_{4m^2_l} d q^2 \frac{d \varGamma }{d q^2} \end{aligned}$$

(91)

The longitudinal polarization fraction

$$\begin{aligned} f_L = \frac{\varGamma _L}{\varGamma } = \frac{\int ^{(m_H- m_T)^2}_{4m^2_l} d q^2 \frac{d \varGamma _L}{d q^2}}{\int ^{(m_H- m_T)^2}_{4m^2_l} d q^2 \frac{d \varGamma }{d q^2}} \end{aligned}$$

(92)

where the longitudinal differential decay width

$$\begin{aligned} \frac{d \varGamma _L}{d q^2} = \frac{1}{4} ( 3 I^c_1 - I^c_2) \end{aligned}$$

(93)

In addition, the FBA

$$\begin{aligned} \frac{d A_{FB}}{d q^2}= & {} \frac{\left( \int _0^1 - \int _{-1}^0 \right) d \cos \theta \frac{d^2 \varGamma }{d q^2 d \cos \theta }}{d \varGamma / d q^2} \nonumber \\= & {} \frac{3 I_6}{ 3 I^c_1 + 6 I^s_1 - I^c_2 - 2 I^s_2} \end{aligned}$$

(94)

with

$$\begin{aligned} I_6= 2 \sqrt{1-\frac{4 m^2_l}{q^2}} \left[ Re(A_{L \parallel } A^*_{L \perp }) - Re(A_{R \parallel } A^*_{R \perp }) \right] \end{aligned}$$

(95)

For the lifetimes of $B_{(s)}$, masses of charged leptons and Fermi coupling constant $G_F$, we use the same values as those adopted in charged current induced semileptonic decays, c.f., Eq. (77). Besides, we choose the CKM matrix elements $|V_{tb}|=1.019 \pm 0.025$, $|V_{ts}|=(39.4 \pm 2.3) \times 10^{-3}$, $|V_{td}|=(8.1 \pm 0.5) \times 10^{-3}$ and the fine-structure constant $\alpha _{em} = 1/137$ [1]. The FBAs of lepton as functions of $q^2$ for the decays $B^- \rightarrow a_2^-(1320) l^- l^+(l=e, \mu , \tau )$ are shown in Fig. 6.

Fig. 6

The FBAs of lepton as functions of $q^2$ for the decays $B^- \rightarrow a_2^-(1320) l^- l^+(l=e, \mu , \tau )$

Table 7 The Br, $f_L$ and $c_0$ for rare $B_{(s)} \rightarrow T l^- l^+$ decays, where the values calculated by LCSRB [13] and pQCD [25] are also listed for comparison

For other FCNC induced semileptonic decays, the behaviors of FBAs are similar. As can be seen from Fig. 6, the zero-crossing points of FBAs are the same for $l=e, \mu$ and do not exist for $l=\tau$, which are different from the case of charged current induced semileptonic decays (c.f., Fig. 5). The numerical results of branching ratios, longitudinal polarization fractions and zero-crossing points of FBAs for all $B_{(s)} \rightarrow T l^- l^+ ( l=e, \mu , \tau )$ decay modes are collected in Table 7, where the corresponding values for $\bar{B}^0 \rightarrow \bar{K}^{*0}_2 l^- l^+ (l = \mu , \tau )$ and $\bar{B}_s \rightarrow f^\prime _2 l^- l^+ (l=\mu , \tau )$ decays calculated by pQCD [25] are also listed for comparison. We can see that our results as a whole are compatible with the corresponding pQCD values for these decay modes. The branching ratios decrease significantly with the mass of charged lepton. For the decay modes with ee or $\mu \mu$ in the final states, the branching ratios are at the order of ${\mathscr {O}} (10^{-8}-10^{-7})$, while those for the decays with $\tau \tau$ are smaller by three orders of magnitude. As in the case of charged current induced semileptonic decays, the first and second uncertainties of branching ratios comes from the form factors and CKM matrix elements, respectively. The uncertainties from these two sources are at the same order of magnitude and roughly (15–25)%. The decay modes with $\mu \mu$ in the final states have maximum longitudinal polarization fractions, which are approximately $70\%$. In contrast, the longitudinal polarization fractions for the decays with ee and $\tau \tau$ are about $40\%$ and $50\%$, respectively. The zero-crossing points of FBAs are exactly the same for decay modes in which only the charged leptons are different. The zero-crossing points for different $B_{(s)} \rightarrow T$ rare decays are similar, with the central values ranging from 3.25 to $3.31\mathrm{GeV}^2$.

5 Summary

By using the LCSR in HQEFT, we systematically calculated the $B_{(s)} \rightarrow a_2(1320)$, $K^*_2(1430)$, $f_2(1270)$, $f^\prime _2(1525)$ form factors. We derived the expressions of form factors in terms of the light cone DAs of tensor mesons and found that the penguin type form factors can be obtained directly from the corresponding semileptonic ones at the leading order of heavy quark expansion. Considering the DAs of tensor mesons to twist-3, we give the numerical results of form factors systematically. Large differences exist between the results of quark model approaches(ISGW2 [6, 7], LFQM [8, 9]) and those of sum rules (this work, LCSRT [11], LCSRB [13],QCDSR [14]) and pQCD [12]. The form factors obtained in this work are in general some larger, yet still compatible with those results of LCSRT [11], LCSRB [13], pQCD [12] and QCDSR [14] as a whole.

With the form factors given here, we investigated the relevant charged current and FCNC induced semileptonic decays separately. For the decays induced by charged current, the zero-crossing points of FBAs increase significantly with the mass of charged lepton. The branching ratios are at the order of ${\mathscr {O}}(10^{-4})$. The results of branching ratios and longitudinal polarization fractions are almost identical for $l=e, \mu$, while those for $l=\tau$ are significantly smaller. For the FCNC induced decays, the zero-crossing points of FBAs are the same for $l=e, \mu$ and do not exist for $l=\tau$. The branching ratios decrease significantly with the mass of charged lepton. For the decay modes with ee or $\mu \mu$ in the final states, the branching ratios are at the order of ${\mathscr {O}} (10^{-8}-10^{-7})$, while those for the decays with $\tau \tau$ are smaller by three orders of magnitude. The decay modes with $\mu \mu$ in the final states have maximum longitudinal polarization fractions. For both the charged current and FCNC induced semileptonic decays, the uncertainties of branching ratios come from the form factors and CKM matrix elements, which are at the same order of magnitude, roughly (15–25)%. In contrast, the uncertainties of longitudinal polarization fractions and zero-crossing points of FBAs are much smaller, due to the fact that these two quantities are defined via the ratios of decay widths and therefore most of the uncertainties are canceled. Our results may be tested by more precise experiments in the future.