Dynamics of Entanglement and Statistical Properties in Atom-Field Interaction

Abstract

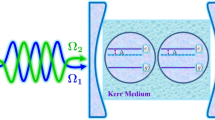
In this paper, the dynamics of entanglement between a single two-level atom interacting with one-mode cavity field is investigated with zero and large detuning parameters. The von Neumann entropy and concurrence measures are used to characterize the degree of entanglement. We find that the entanglement shows the oscillating behavior which depends on the initial amplitude of the coherent field, detuning parameter, and atom-field coupling constant. Specially, we study the generation of the robust maximally entangled state and conclude that the intensity of the coherent field and detuning parameter can be utilized as the control parameters for generating robust maximally entangled state. At the end, some important statistical features such as Wigner function, Mandel parameter, and second-order correlation function will be discussed. The comparison between the entanglement and Wigner function shows that for $\chi t=(n+\frac {1}{2})\pi$, the maximum of Wigner function has information about the entanglement between the atom and field in the Jaynes-Cummings model. Moreover, the Mandel parameter and consequently the second-order correlation function show that the radiation field has Poissonian statistics.

Appendix

The Hamiltonian of the J-C model is $\hat {H}=\hat {H_{0}}+\hat {H_{I}}$ where the interaction-free Hamiltonian is:

$$ \hat{H_{0}}= \frac{1}{2}\hbar {\omega_{0}}{\hat \sigma_{z}} + \hbar \omega {\hat a^{\dag} }\hat a, $$

and the atom-field interaction Hamiltonian with the rotating-wave approximation is:

$$ \hat{H_{I}}=\hbar \lambda (\hat{A}+\hat{A^{\dag}}), $$

where $\hat {A}=\hat {a}\hat {\sigma }_{+}$ and $\hat {A}^{\dag }=\hat {a}^{\dag }\hat {\sigma }_{-}$. The time-dependent Schrodinger-like equation in the interaction picture is [35]:

$$ i\hbar \frac{d}{{dt}}{\left| {\psi (t)} \right\rangle_{IP}} = {{\hat H}_{IP}(t)}{\left| {\psi (t)} \right\rangle_{IP}}, $$

(A.1)

with ${{\hat H}_{IP}(t)} = {e^{{i{H_{0}}t}/\hbar }}{H_{I}}{e^{- {i{H_{0}}t}/\hbar }}$. Using Baker-Hausdorf lemma, we have:

$$ {{\hat H}_{IP}(t)} = \hbar \lambda ({e^{i\varDelta t}}\hat A + {e^{- i\varDelta t}}{{\hat A}^{\dag} }). $$

(A.2)

The solution of (A.1) is given by:

$$ {\left| {\psi (t)} \right\rangle_{IP}} = \hat{\mathcal{T}}\left[ {\exp \left( - \frac{i}{\hbar }{\int\limits_{0}^{t}} {dt'{\hat{H}_{IP}}(t^{\prime})} \right)} \right]{\left| {\psi (0)} \right\rangle_{IP}}, $$

(A.3)

where $\hat {\mathcal {T}}$ is the time-ordering operator. By substituting (A.2) in (A.3) and using perturbation expansion, after some simple algebra we found that:

$$ \begin{array}{@{}rcl@{}} \hat{\mathcal{T}}\left[ {\exp \left( - \frac{i}{\hbar }{\int\limits_{0}^{t}} {dt^{\prime}{\hat{H}_{IP}}(t^{\prime})} \right)} \right]&\approx&1-\frac{\lambda}{\varDelta}\left[\hat{A}(e^{i{\varDelta} t}-1)\right.\\ &&\left.-\hat{A}^{\dag}(e^{-i{\varDelta} t}-1)\right]-\frac{i\lambda^{2}t}{\varDelta}[\hat{A},\hat{A}^{\dag}]\\ &&+\mathcal{O}\left( \frac{\lambda^{2}}{{\varDelta}^{2}}\right), \end{array} $$

clearly for △≫ λ the second and last terms are neglected and thus we have:

$$ \hat{\mathcal{T}}\left[ {\exp \left( - \frac{i}{\hbar }{\int\limits_{0}^{t}} {dt'{\hat{H}_{IP}}(t^{\prime})} \right)} \right]\approx 1-\frac{i}{\hbar}\hat{H}_{eff}t. $$

where

$$ \hat{H}_{eff}=\frac{{\hbar {\lambda^{2}}}}{\varDelta }[\hat A,{{\hat A}^{\dag} }], $$

substitution $\hat {A}$ and $\hat {A}^{\dag }$ leads to the interaction Hamiltonian for the non-resonance case with large detuning as follows:

$$ {\hat{H}_{eff}} = \hbar \chi ({\hat{\sigma}_ + }{\hat{\sigma}_ - } + {\hat{a}^{\dag} }\hat{a}{\hat{\sigma}_{z}}). $$

where $\chi =\frac {\lambda ^{2}}{\varDelta }$.