Thermodynamical phases in a PNJL model at zero temperature

Abstract

The confinement/deconfinement transition described the Polyakov–Nambu–Jona–Lasinio (PNJL) model is extended to be operative at zero temperature regime. In this study, the scalar and vector channel interaction strengths of the original PNJL model are modified by introducing a dependence on the traced Polyakov loop. In such a way the effective interactions depend on the quark phase and in turn provides a backreaction of the quarks to the gluonic sector, also at zero temperature. On general grounds from quantum chromodynamics this is an expected feature. The thermodynamics of the extended model (PNJL0) is studied in detail. It presents along with a suitable choice of the Polyakov potential, a first order confined/deconfined quark phase transition even at $T=0$. We also show that the vector channel plays an important role in order to allow $\varPhi \ne 0$ solutions for the PNJL0 model. Furthermore, the sensitivity of the combined quarkyonic and deconfinement phases to the vector interaction strength and the proposed parametrization of the Polyakov-loop potential at $T=0$ allowed to set a window for the bulk values of the relevant parameters.

1 Introduction

The physics of strongly interacting matter is described by quantum chromodynamics (QCD) [1,2,3] with quarks and gluons as the fundamental degrees of freedom, while the colorless hadrons are emergent phenomena originated from the complex nonperturbative physics of this theory. Despite being well established, nonperturbative aspects of QCD have nontrivial treatment is far from being understood, which is critical for the description of the equation of state of strongly interacting matter at finite densities and low temperatures.

The challenge is to compute hadronic observables when the strength of the QCD running coupling presents the well known strong infrared enhancement to embody spontaneous chiral symmetry breaking and at the same time quark and gluon confinement. These properties are opposite to what is know in quantum electrodynamics (QED), where the use of perturbative methods are successful and the fundamental degrees of freedom appears as asymptotic states. That is not the case for QCD where quarks and gluons are confined.

Ab-initio nonperturbative approaches are called for to solve QCD, as lattice quantum chromodynamics (LQCD) [4,5,6]. This well known method starts with the QCD action, $S_{\mathrm{QCD}}$, and evaluate the generating functional $Z=\int \mathcal {D}A\mathcal {D}\psi \mathcal {D}\bar{\psi } e^{iS_{\mathrm{QCD}}}$ by numerical simulations and finally accessing the matrix elements of the relevant operators between hadronic states. Such a procedure is performed through both, space-time discretization and Wick rotation, and changes Z to $Z'=\int \mathcal {D}A\mathcal {D}\psi \mathcal {D}\bar{\psi } e^{-S_{\mathrm{QCD}}}$, i.e., putting it in correspondence to a Statistical Mechanics formulation. The numerical calculations are performed from Monte Carlo simulations. Despite powerful, LQCD faces some intrinsic problems such as the need to extrapolation of the outcomes for lattice spacing approaching to zero, the need of powerful dedicated computational facilities, and the “fermion sign problem” [7].

Another nonperturbative continuum method to treat QCD is through Dyson–Schwinger equations (DSE) [8, 9]. They are derived from the generating functional Z and allows to obtain the equations of motion of the n-point functions, which are also known as the Euler-Lagrange equations for the QCD Green’s function. Both LQCD and the standard DSE methods have the issue of being formulated in the Euclidean space. However, the access of all observables obtained from QCD, requires its representation in the Minkowski space, that calls for a careful and not yet fully known analytical extension or other particular methods to obtain, for example, the light-front wave function of the hadronic state. A possible alternative to circumvent this problem is the use of the Nakanishi integral representation, built directly in the Minkowski space, and solve with that the DSE or even the Bethe–Salpeter equation [10,11,12]. Sum rules [13, 14], and the connection between gauge and string theories also aim to treat QCD in the infrared region. This last method was introduced by Gerard ’t Hooft [15] by suggesting the analytical calculation of amplitudes by using string theories. A clear mapping between the two theories was proposed by Juan Maldacena [16] with the famous Anti-de Sitter/Conformal Field Theory (AdS/CFT) conjecture.

Other practical possibilities to incorporate the infrared physics is the use of effective quark models, built with the aim of reproducing most of the QCD phenomenology, as for instance, their symmetries and also dynamical chiral symmetry breaking. By exploiting such approaches, many models were developed. The Nambu–Jona–Lasinio (NJL) model [17,18,19,20,21,22,23,24,25] is an example. Its improved version, namely, the Polyakov–Nambu–Jona–Lasinio (PNJL) model [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40] includes effects of confinement / deconfinement phase transition, included in the theory through an effective field of gluonic origin, namely, the Polyakov loop ($\varPhi$ and $\varPhi ^*$) [41,42,43,44]. Even that the PNJL model shows a clear improvement in comparison with the original NJL model, with respect to QCD phase structure, the Polyakov loop decouples from the baryonic fields at the zero temperature regime. This missing interaction is evident by analyzing, for instance, the pressure (P) and the energy density ($\mathcal {E}$) of PNJL models at low temperatures. The Polyakov potential, $\mathcal {U}(\varPhi ,\varPhi ^*,T)$, vanishes for $T=0$ in the most parametrizations of this quantity. Therefore, the equations of state of the NJL model are recovered at $T=0$ and, consequently, the physics of confinement implemented in $T\ne 0$ in PNJL models is simply lost.

In this work we explore the approach started with the initial study of Ref. [45] and present the thermodynamics of a PNJL model at zero temperature, named here as PNJL0 model. In the following, Sect. 2, we briefly review the basics of the original PNJL model. Its version at $T=0$, along with its main results, are discussed in Sect. 3. Finally, we present the summary and concluding remarks of our study in Sect. 4.

2 Polyakov–Nambu–Jona–Lasinio model

The PNJL model was firstly proposed in Ref. [26] as a generalization of the original NJL model due to the inclusion of confinement effects. From this point of view, the PNJL model becomes an effective model describing the QCD theory more realistically in comparison with the previous NJL version. Basically, the gluon dynamics is implemented in the NJL model by replacing the derivative $\partial ^\mu$ by $D^\mu \equiv \partial ^\mu +iA^\mu$ where $A^\mu =\delta ^\mu _0A_0$ and $A_0=gA_\alpha ^0\lambda _\alpha / 2$ (g is the gauge coupling and $\lambda _\alpha$ are the Gell-Mann matrices). The Lagrangian density of the SU(2) PNJL model is then written as

$$\begin{aligned} \mathcal {L}_{\mathrm{PNJL}}= & {} \bar{\psi }(i\gamma _\mu D^\mu - m)\psi +G_s [(\bar{\psi }\psi )^2-(\bar{\psi }\gamma _5 \tau \psi )^2 ] \nonumber \\&- G_V(\bar{\psi }\gamma _\mu \psi )^2- \mathcal {U}(\varPhi ,\varPhi ^*,T).\qquad \end{aligned}$$

(1)

with m being the current quark mass (in our case $m=m_u=m_d$). In this formulation, we also add a vector channel, regulated by the coupling constant $G_V$.

Other clear difference between PNJL and NJL models is the inclusion of the Polyakov potential $\mathcal {U}(\varPhi ,\varPhi ^*,T)$ that depends on the traced Polyakov loop and its conjugate, $\varPhi$ and $\varPhi ^*$, respectively. $\varPhi$ is defined in terms of $A_4=iA_0\equiv T\phi$ as

$$\begin{aligned} \varPhi&=\frac{1}{3}\mathrm{Tr}\left[ \,\,\mathrm{exp}\left( i\int _0^{1/T}d\tau \,A_4\right) \right] \nonumber \\&=\frac{1}{3}\mathrm{Tr} [\mathrm{exp}(i\phi ) ] =\frac{1}{3}\mathrm{Tr} \lbrace \mathrm{exp}[i(\phi _3\lambda _3+\phi _8\lambda _8)] \rbrace \nonumber \\&= \frac{1}{3} \left[ \mathrm{e}^{i(\phi _3+\phi _8/\sqrt{3})}+\mathrm{e}^{i(-\phi _3+\phi _8/\sqrt{3})} +\mathrm{e}^{-2i\phi _8/\sqrt{3}} \right] , \end{aligned}$$

(2)

in a gauge (Polyakov gauge) in which the gluon field is written in terms of the diagonal Gell-Mann matrices as $\phi =\phi _3\lambda _3+\phi _8\lambda _8$, with $\phi _3,\phi _8 \in \mathbb {R}$ (the definitions $\phi _3=A_4^3/T$ and $\phi _8=A_4^8/T$ were taken into account). Here we also use the mean-field approximation described in Refs. [32, 33, 39] that considers the mean-field configuration in which $\phi _8=0$ in Eq. (2). In this case, $\varPhi =\varPhi ^*=[2\cos (\phi _3)+1]/3$ even for nonvanishing quark chemical potentials ($\mu$).

The thermodynamics of this model is obtained through the calculation of its grand canonical potential density namely, $\varOmega _{\mathrm{PNJL}} = -T\text{ ln } (Z_{\mathrm{PNJL}})/V$, with $Z_{\mathrm{PNJL}}$ being the partition function of the model. The final expression is given by [26, 30, 31, 46, 47]

$$\begin{aligned} \varOmega _{\mathrm{PNJL}}= & {} \mathcal {U}(\varPhi ,T) + G_s\rho _s^2 - G_V\rho ^2- \frac{\gamma }{2\pi ^2}\int _0^{\varLambda }E\,k^2dk \nonumber \\&- \frac{\gamma T}{2\pi ^2N_c}\int _0^{\infty }\text{ ln } [1+3\varPhi e^{-(E - \mu )/T} \nonumber \\&+ 3\varPhi e^{-2(E - \mu )/T} + e^{-3(E - \mu )/T} ]k^2dk \nonumber \\&- \frac{\gamma T}{2\pi ^2N_c}\int _0^{\infty }\text{ ln } [1+3\varPhi e^{-(E + \mu )/T} \nonumber \\&+ 3\varPhi e^{-2(E + \mu )/T} + e^{-3(E + \mu )/T} ]k^2dk, \end{aligned}$$

(3)

with $E=(k^2+{M}^2)^{1/2}$, $\rho _s=\left<\bar{\psi }\psi \right>=\left<\bar{u}u\right> + \left<\bar{d}d\right>=2\left<\bar{u}u\right>\,$ and the degeneracy factor given by $\gamma =N_s\times N_f\times N_c=12\,$, due to the spin, flavor and color numbers, respectively ($N_s=N_f=2$ and $N_c=3$). The quantity $\varLambda$ defines the cutoff of the divergent integral. As in the NJL model, the constituent quark mass M is given in terms of the quark condensate $\rho _s$ as

$$\begin{aligned} M=m-2G_s\rho _s, \end{aligned}$$

(4)

with $\rho _s$, obtained by the condition $\partial \varOmega _{\mathrm{PNJL}}/\partial \rho _s=0$, given by

$$\begin{aligned} \rho _s= & {} \frac{\gamma }{2\pi ^2}\int _0^{\infty }\frac{M}{E(M)}k^2dk [ f(k,T,\varPhi ) + \bar{f}(k,T,\varPhi ) ] \nonumber \\&-\frac{\gamma }{2\pi ^2}\int _0^{\varLambda }\frac{M}{E(M)}k^2dk. \end{aligned}$$

(5)

The functions $f(k,T,\varPhi )$ and $\bar{f}(k,T,\varPhi )$, given as follows,

$$\begin{aligned}&f(k,T,\varPhi ) \nonumber \\&\quad =\frac{\varPhi e^{2(E-\mu )/T} + 2\varPhi e^{(E-\mu )/T}+ 1}{3\varPhi e^{2(E-\mu )/T} + 3\varPhi e^{(E-\mu )/T} + e^{3(E-\mu )/T} + 1} \end{aligned}$$

(6)

and

$$\begin{aligned}&\bar{f}(k,T,\varPhi ) \nonumber \\&\quad =\frac{ \varPhi e^{2(E+\mu )/T}+2\varPhi e^{(E+\mu )/T}+1}{ 3\varPhi e^{2(E+\mu )/T} + 3\varPhi e^{(E+\mu )/T} + e^{3(E+\mu )/T} + 1}, \end{aligned}$$

(7)

are the generalized Fermi–Dirac distributions, also used to obtain the quark density through

$$\begin{aligned} \rho= & {} -\frac{\partial \varOmega _{\mathrm{PNJL}}}{\partial \mu } \nonumber \\= & {} \frac{\gamma }{2\pi ^2}\int _0^{\infty }k^2dk[f(k,T,\varPhi ) - \bar{f}(k,T,\varPhi )].\quad \, \end{aligned}$$

(8)

Note the similarity between the grand canonical potentials of the PNJL and NJL models, where in the former there is the replacement of the usual Fermi–Dirac functions of quarks and antiquarks by the generalized functions given in Eqs. (6) and (7). Furthermore in the PNJL model, there is also the inclusion of an effective gluon potential represented by $\mathcal {U}(\varPhi ,T)$ in the grand canonical potential density.

The effective scalar field $\varPhi$ is found through the solution of $\partial \varOmega _{\mathrm{PNJL}}/\partial \varPhi =0$. This quantity is determined simultaneously to M, that is found from Eqs. (4) and (5), or equivalently, through the condition $\partial \varOmega _{\mathrm{PNJL}}/\partial \rho _s=0$. Pressure and energy density are obtained from Eq. (3) as

$$\begin{aligned}&P_{\mathrm{PNJL}}(\rho ,T) = -\varOmega _{\mathrm{PNJL}} = -\mathcal {U}(\varPhi ,T) + G_V\rho ^2 - G_s\rho _s^2 \nonumber \\&\quad + \frac{\gamma }{2\pi ^2}\int _0^{\varLambda }(k^2+M^2)^{1/2}\,k^2dk + \mathcal {E}_\mathrm{vac} \nonumber \\&\quad + \frac{\gamma }{6\pi ^2}\int _0^{\infty }\frac{k^4}{(k^2+M^2)^{1/2}}dk[f(k,T,\varPhi )+\bar{f}(k,T,\varPhi )] \end{aligned}$$

(9)

and

$$\begin{aligned}&\mathcal {E}_{\mathrm{PNJL}}(\rho ,T) = -T^2\frac{\partial (\varOmega _{\mathrm{PNJL}}/T)}{\partial T} + \mu \rho \nonumber \\&\quad = \mathcal {U}(\varPhi ,T) - T\frac{\partial \mathcal {U}}{\partial T} + G_V\rho ^2 + G_s\rho _s^2 \nonumber \\&\qquad -\frac{\gamma }{2\pi ^2}\int _0^{\varLambda }(k^2+M^2)^{1/2}\,k^2dk - \mathcal {E}_\mathrm{vac} \nonumber \\&\qquad + \frac{\gamma }{2\pi ^2}\int _0^{\infty }(k^2+M^2)^{1/2}\,k^2dk [f(k,T,\varPhi ) + \bar{f}(k,T,\varPhi )], \end{aligned}$$

(10)

respectively, with the vacuum quantity $\mathcal {E}_\mathrm{vac}$ included in the equations in order to ensure $P=\mathcal {E}=0$ at vanishing temperature and quark density. Finally, the entropy density can be obtained from $\mathcal {S}_{\mathrm{PNJL}} = -\partial \varOmega _{\mathrm{PNJL}}/\partial T$, or from $\mathcal {S}_{\mathrm{PNJL}}=(P_{\mathrm{PNJL}} + \mathcal {E}_{\mathrm{PNJL}} - \mu \rho )/T\,$. The thermodynamics of the PNJL model is quantitatively defined once the potential $\mathcal {U}(\varPhi ,T)$, and the constants $G_s$, $\varLambda$ and m are chosen. These last quantities are the same as the ones obtained in the quarks sector (NJL model), with $G_V$ being a free parameter.

3 PNJL model at zero temperature (PNJL0)

3.1 Construction of the model

It is worth notice that the limit of vanishing temperature in Eqs. (9) and (10) leads to

$$\begin{aligned} P_{\mathrm{PNJL}}&(\rho ,0) = G_V\rho ^2-G_s\rho ^2_{s} +\frac{\gamma }{2\pi ^2}\int ^{\varLambda }_{0} dk k^2(k^2+M^2)^{1/2} \nonumber \\&+ \frac{\gamma }{6\pi ^2}\int _{0}^{k_F}dk \frac{k^4}{(k^2+M^2)^{1/2}} + \mathcal {E}_\mathrm{vac} =-\varOmega _{\mathrm{PNJL}}(\rho ,0) \end{aligned}$$

(11)

and

$$\begin{aligned} \mathcal {E}_{\mathrm{PNJL}}(\rho ,0)= & {} G_V\rho ^2 + G_s\rho ^2_{s} - \mathcal {E}_\mathrm{vac} \nonumber \\&- \frac{\gamma }{2\pi ^2}\int _{k_F}^{\varLambda }dk k^2(k^2+M^2)^{1/2}, \end{aligned}$$

(12)

with $\mu = 2G_V\rho + (k_F^2+M^2)^{1/2}$, i.e., at $T=0$ one has $P_{\mathrm{PNJL}}(\rho )=P_{\mathrm{NJL}}(\rho )$ and $\mathcal {E}_{\mathrm{PNJL}}(\rho )=\mathcal {E}_{\mathrm{NJL}}(\rho )$, with $P_{\mathrm{NJL}}(\rho )$ and $\mathcal {E}_{\mathrm{NJL}}(\rho )$ being the pressure and energy density, respectively, of the original NJL model at zero temperature [17,18,19,20,21,22]. Therefore, the confinement physics from the Polyakov potential is lost at $T=0$. Such problem is due to two reasons. The first one is that the generalized Fermi–Dirac distributions, Eqs. (6)–(7), becomes the traditional step function $\theta (k_F-k)$ at $T=0$ ($k_F$ is the quark Fermi momentum). The second reason is that the gluonic contribution of the PNJL model, described by the Polyakov potential, $\mathcal {U}(\varPhi ,T)|_{T=0}$ vanishes in the most known versions.

Three most known forms of the Polyakov potential, namely, RTW05 [30], RRW06 [31, 32] and FUKU08 [27], are given respectively by $(\varPhi =\varPhi ^*)$,

$$\begin{aligned} \frac{\mathcal {U}_{\mathrm{RTW05}}}{T^4}&= -\frac{b_2(T)}{2}\varPhi ^2 - \frac{b_3}{3}\varPhi ^3 + \frac{b_4}{4}\varPhi ^4, \end{aligned}$$

(13)

$$\begin{aligned} \frac{\mathcal {U}_{\mathrm{RRW06}}}{T^4}&= -\frac{b_2(T)}{2}\varPhi ^2 + b_4(T)\text{ ln }(1 - 6\varPhi ^2 + 8\varPhi ^3 - 3\varPhi ^4), \end{aligned}$$

(14)

$$\begin{aligned} \frac{\mathcal {U}_{\mathrm{FUKU08}}}{b\,T}&= -54e^{-a/T}\varPhi ^2 + \text{ ln }(1 - 6\varPhi ^2 + 8\varPhi ^3 - 3\varPhi ^4), \end{aligned}$$

(15)

with

$$\begin{aligned} b_2(T) = a_0 + a_1\left( \frac{T_0}{T}\right) + a_2\left( \frac{T_0}{T}\right) ^2 + a_3\left( \frac{T_0}{T}\right) ^3, \end{aligned}$$

(16)

and

$$\begin{aligned} {b_4(T) = b_4\left( \frac{T_0}{T}\right) ^3.} \end{aligned}$$

(17)

These potentials are constructed to reproduce data from lattice calculations of the pure gauge sector concerning the temperature dependence of $\varPhi$ and its first order phase transition, characterized by the jump of $\varPhi$ from zero to a finite value at $T_0=270$ MeV. In Eqs. (13)–(15), a, b, $a_0$, $a_1$, $a_2$, $a_3$, $b_3$ and $b_4$ are dimensionless free parameters. Notice that for all potentials one has $\mathcal {U}=0$ at $T=0$. This phenomenology leads the thermodynamics of the PNJL model to be reduced to the NJL one at zero temperature. One exception to this result is the DS10 [48, 49] potential given by

$$\begin{aligned} \mathcal {U}_{\mathrm{DS10}}= & {} (a_0T^4 + a_1\mu ^4 + a_2T^2\mu ^2)\varPhi ^2 + \mathcal {U}_0(\varPhi ) \end{aligned}$$

(18)

with

$$\begin{aligned} \mathcal {U}_0(\varPhi )\equiv a_3T_0^4\text{ ln }(1-6\varPhi ^2+8\varPhi ^3-3\varPhi ^4). \end{aligned}$$

(19)

Our aim is to avoid the lack of confinement physics in the PNJL model at $T=0$ by taking into account the effects of the traced Polyakov loop $\varPhi$ in both the Polyakov potential and the effective interaction between the quarks, as performed in a previous initial investigation [45] where preliminary results were presented. The idea here is to introduce the traced Polyakov loop in the NJL equations of state by imposing vanishing scalar and vector couplings as the quarks become deconfined, situation predicted to occur at $\varPhi \rightarrow 1$. This phenomenology can be achieved by making the scalar and vector coupling strengths dependent on $\varPhi$ as follows,

$$\begin{aligned} G_s \longrightarrow G_s(\varPhi )= & {} G_s( 1-\varPhi ^2 ), \end{aligned}$$

(20)

and

$$\begin{aligned} G_V \longrightarrow G_V(\varPhi )= & {} G_V( 1-\varPhi ^2 ). \end{aligned}$$

(21)

In fact, such changes can be seen as a simpler version of the Entanglement PNJL (EPNJL) [50]. The implementation of Eqs. (20)–(21) in the PNJL/NJL model at $T=0$ still demands the determination of the possible $\varPhi$ values, obtained through $\partial \varOmega _{\mathrm{PNJL}}/\partial \varPhi =0$. However, the replacement of $G_s$ and $G_V$ by their $\varPhi$ dependent versions is not enough to ensure $\varPhi \ne 0$ solutions, i.e., the NJL model is recovered once more. In order to avoid this problem, besides the modifications proposed in Eqs. (20)–(21) we also add to $\varOmega _{\mathrm{PNJL}}(\rho ,0)$ the term $\mathcal {U}_0(\varPhi )$ given by Eq. (19), inspired by the $\mathcal {U}_{\mathrm{DS10}}$ Polyakov potential, with $T_0 = 190$ MeV (value very often used in the Polyakov potentials of the PNJL models [30]).

As we will discuss later on, the effect of $\mathcal {U}_0(\varPhi )$ is to ensure $\varPhi \ne 0$ solutions and also limit the traced Polyakov loop in the range of $0\leqslant \varPhi \leqslant 1$. This term was used in Refs. [48, 49] also to generate $\varPhi \ne 0$, however, for a much more sophisticated model, that takes into account hadrons and quarks degrees of freedom at the same Lagrangian density.

The quark couplings given by Eqs. (20)–(21) along with the $\mathcal {U}_0(\varPhi )$ potential added to $\varOmega _{\mathrm{PNJL}}(\rho ,0)$ lead to the following equations for the pressure and energy density, respectively,

$$\begin{aligned}&P_{\mathrm{PNJL0}}(\rho ) = -\mathcal {U}_{\mathrm{PNJL0}}(\rho ,\rho _s,\varPhi ) + G_V\rho ^2-G_s\rho ^2_{s} \nonumber \\&\quad +\frac{\gamma }{2\pi ^2}\int ^{\varLambda }_{0} dk k^2(k^2+M^2)^{1/2} + \mathcal {E}_\mathrm{vac} \nonumber \\&\quad + \frac{\gamma }{6\pi ^2}\int _{0}^{k_F}dk \frac{k^4}{(k^2+M^2)^{1/2}} = -\varOmega _{\mathrm{PNJL0}}(\rho ) \end{aligned}$$

(22)

and

$$\begin{aligned} \mathcal {E}_{\mathrm{PNJL0}}(\rho )&= \mathcal {U}_{\mathrm{PNJL0}}(\rho ,\rho _s,\varPhi ) - 2G_V\varPhi ^2\rho ^2 + G_V\rho ^2 + G_s\rho ^2_{s} \nonumber \\&\quad - \frac{\gamma }{2\pi ^2}\int _{k_F}^{\varLambda }dk k^2(k^2+M^2)^{1/2} - \mathcal {E}_\mathrm{vac}, \end{aligned}$$

(23)

in which it was possible to define a Polyakov potential as being

$$\begin{aligned} \mathcal {U}_{\mathrm{PNJL0}}(\rho _s,\rho ,\varPhi ) = G_V\varPhi ^2\rho ^2 - G_s\varPhi ^2\rho _s^2 + \mathcal {U}_0(\varPhi ) \end{aligned}$$

(24)

which includes quarks as source of $\varPhi$, as one should expect from QCD where quarks are also sources for the gluon field.

The model built above, is named as PNJL0 model, and it has constituent quark mass and quark chemical potential given by:

$$\begin{aligned} M = m - 2G_s(1-\varPhi ^2)\rho _s~, \end{aligned}$$

(25)

and

$$\begin{aligned} \mu = 2G_V(1 - \varPhi ^2) \rho + (k_F^2+M^2)^{1/2}, \end{aligned}$$

(26)

respectively. Furthermore, the quark density is written in terms of the quark Fermi momentum as $\rho =(\gamma /6\pi ^2)k_F^3$, and the quark condensate reads

$$\begin{aligned} \rho _s=-\frac{\gamma M}{2\pi ^2}\int _{k_F}^\varLambda dk\frac{k^2}{(k^2+M^2)^{1/2}}, \end{aligned}$$

(27)

which contributes to the scalar quark density.

It is worthwhile to notice that Eqs. (22) and (23) can be seen as the $T\rightarrow 0$ limit of Eqs. (9) and (10). Another important aspect in defining the Polyakov potential $\mathcal {U}_{\mathrm{PNJL0}}(\rho _s,\rho ,\varPhi )$ is the presence of the backreaction of quarks in the gluons sector, as we have already pointed out. The inverse backreaction, namely, gluons affecting the quark sector is already intrinsic in the original PNJL model, see for instance, the generalized Fermi–Dirac distribution functions in Eqs. (6) and (7). In the PNJL0 model the backreaction is complete (each sector interacts each other): the effective quark interactions vanishes at the deconfinement phase and $\mathcal {U}_0(\varPhi )$ is included in the grand canonical potential to assure confinement physics at $T=0$.

Just to be complete, we should mention that another way of including quark effects in the gluon sector was given, for example, in Refs. [51, 52], in which the authors impose a $N_f$ and $\mu$ dependence on $T_0$ in the Polyakov potentials, namely, $T_0 \rightarrow T_0(N_f,\mu )$.

3.2 $\varPhi \ne 0$ solutions for the PNJL0 model

The inclusion of $\mathcal {U}_0(\varPhi )$ in the Polyakov potential given by Eq. (24) enables the PNJL0 model to present $\varPhi \ne 0$ solutions for the condition $\partial \varOmega _{\mathrm{PNJL0}}/\partial \varPhi =0$ at zero temperature. Therefore, it becomes possible the study of the deconfinement dynamics in the $T=0$ regime, with the dimensionless constant $a_3$ in Eq. (19) regulating this effect.

We investigate how $\varOmega _{\mathrm{PNJL0}}$ behaves as a function of $\varPhi$ firstly for $G_V=0$. In Fig. 1 we display this thermodynamical potential, obtained from $\varOmega _{\mathrm{PNJL0}}=-P_{\mathrm{PNJL0}}$, Eq. (22), with the self-consistent equations (25) and (27) implemented, and without the condition $\partial \varOmega _{\mathrm{PNJL0}}/\partial \varPhi =0$ taken into account. We also use a parametrization of Ref. [19], namely, $\varLambda =587.9$ MeV, $G_s\varLambda ^2=2.44$ and $m=5.6$ MeV for this case and all the other ones. Such values produce $M_{\mathrm{vac}}=400$ MeV and $\langle \overline{u}u\rangle ^{1/3}_{\mathrm{vac}}=-240.8$ MeV for the vacuum values, $m_\pi =135$ MeV and $f_\pi =92.4$ MeV for the pion mass, and decay constant, respectively.

Fig. 1

$\varOmega _{\mathrm{PNJL0}}\times \varPhi$ for $G_V=0$ with different values of $a_3$. For each panel the quark chemical potential is given by a  $\mu =M_{\mathrm{vac}}=400$ MeV, b $\mu =415$ MeV, c $\mu =580$ MeV, and d $\mu =\varLambda =587.9$ MeV

Some features can be observed from the results depicted in Fig. 1. The first one is that the variation of $a_3$ does not produce any change in the value of $\varPhi$ concerning the minimum of $\varOmega _{\mathrm{PNJL0}}$. For all $a_3$ values one has $\partial \varOmega _{\mathrm{PNJL0}}/\partial \varPhi =0$ only at $\varPhi =0$. Notice also that positive $a_3$ values induce $\varOmega _{\mathrm{PNJL0}}$ to change its concavity, i.e, a non physical configuration. This effect is also verified for other $\mu$ values different from those shown in Fig. 1. Even for the extreme value of $\mu =\varLambda$, Fig. 1d, there is no indication that the system presents $\varPhi \ne 0$. Notice that the variation of $\mu$ for a fixed $a_3$ is also not enough to produce $\varPhi \ne 0$ solutions for $\partial \varOmega _{\mathrm{PNJL0}}/\partial \varPhi =0$. The increase in $\mu$ decreases $\varOmega _{\mathrm{PNJL0}}(\varPhi =0)$ as the only effect. This lack of $\varPhi \ne 0$ solutions means that the model can not bring confinement effects for the analyzed region of the quark chemical potential, namely, $M_{\mathrm{vac}}\leqslant \mu \leqslant \varLambda$. Therefore, for this case the PNJL0 model reduces to the NJL one as the PNJL model does. However, this picture is radically modified when $G_V\ne 0$ as one can see in Fig. 2, where $G_V=0.25G_s$ was used.

Fig. 2

The same as in Fig. 1, but for $G_V=0.25G_s$

The results displayed in Fig. 2 show that for $G_V=0.25G_s$ there is a global minima for $\varOmega _{\mathrm{PNJL0}}$ at $\varPhi \ne 0$. As an example, see that for $\mu =\varLambda =587.9$ MeV, Fig. 2d, this minimum is found at $\varPhi \approx 0.9$ for $a_3=-0.1$. For the same $a_3$ value, $\varPhi =0$ is the unique global minimum for $\mu =M_{\mathrm{vac}}=400$ MeV. This means that there is an intermediate value of $\mu$ in which there is two minima for $\varOmega _{\mathrm{PNJL0}}$, namely, one of them at $\varPhi =0$ and the other one at $\varPhi \ne 0$. Physically, this means that there exists a certain $\mu$ value, for the $a_3=-0.1$ case, in which the transition from a quark confined phase ($\varPhi =0$) to a deconfined one ($\varPhi \ne 0$) takes place. For the PNJL0 model, this $\varPhi \ne 0$ solutions are found for $G_V\ne 0$, i.e., the repulsive vector channel plays an important role for the emergence of deconfinement effects at zero temperature regime.

3.3 Confinement/deconfinement phase transition

In order to correctly identify the quark confined and deconfined thermodynamical phases in the PNJL0 model, we compute the grand canonical potential given by Eq. (22) with the self-consistent equations (25) and (27) implemented, but now along with the condition $\partial \varOmega _{\mathrm{PNJL0}}/\partial \varPhi =0$. The result of this calculation, for $G_V=0.25G_s$ and $a_3=-0.1$, is presented in Fig. 3.

Fig. 3

$\varOmega _{\mathrm{PNJL0}}$ as a function of the quark chemical potential ($\mu$) for $G_V=0.25G_s$ and $a_3=-\,0.1$

This figure displays the typical feature of systems that present first order phase transition, namely, non unique values for the thermodynamical potential that describes the system ($\varOmega _{\mathrm{PNJL0}}$) as a function of the intensive quantity ($\mu$). Thermodynamical stability [53] requires that in the range of $500 \text{ MeV }\leqslant \mu \lesssim 514 \text{ MeV }$ the dependence of the grand canonical potential with $\mu$ is the one defined by the DEF curve. The E point indicates the chemical potential value at which a first order phase transition takes place, namely, a confinement/deconfinement one, with $\varPhi$ the order parameter in this case as we will discuss later on. We name the chemical potential at this point as $\mu _{\mathrm{conf}}$ with the value of $\mu _{\mathrm{conf}} = 506.906$ MeV.

Another way to determine $\mu _{\mathrm{conf}}$ is from the analysis of $\varOmega _{\mathrm{PNJL0}}$ as a function of $\varPhi$ without imposing the condition $\partial \varOmega _{\mathrm{PNJL0}}/\partial \varPhi =0$, for each fixed value of $\mu$. The different grand potentials obtained for each $\mu$ are depicted in Fig. 4.

Fig. 4

$\varOmega _{\mathrm{PNJL0}}$ as a function of $\varPhi$ for different $\mu$ values. Curves constructed for $G_V=0.25G_s$ and $a_3=-\,0.1$

The value of $\mu _{\mathrm{conf}}$ is obtained when two minima of the thermodynamical potential appear for distinct values of $\varPhi$ with the same $\varOmega _{\mathrm{PNJL0}}$, see points $p_1$ and $p_2$ in the $\mu =\mu _{\mathrm{conf}}=506.906$ MeV curve. The $\varPhi$ values associated to these points delimit the confined quark phase (point $p_1$, $\varPhi =0$) and the deconfinement one (point $p_2$, $\varPhi \ne 0$). For curves where $\mu \ne \mu _{\mathrm{conf}}$, there is only one global minimum in $\varOmega _{\mathrm{PNJL0}}$. For such cases, the system is exclusively in one of the two thermodynamic phases concerning the quark confinement.

In Fig. 4 we also notice that the $\mu =504$ MeV curve is in a confined phase, since the minimum is attained at $\varPhi =0$, but for $\mu =510$ MeV, a $\varPhi \ne 0$ value is the possible one and identifies the system in deconfined phase. Only at $\mu =\mu _{\mathrm{conf}}$ the system undergoes a first order phase transition. Such procedure of searching for two global minima in the thermodynamical potential was also used, for instance, in the analysis of mean-field hadronic models [54], as well as for the NJL model at finite temperature [55]. Both models present the same kind of first order phase transition, but in different environments and with different order parameters. In the case of the PNJL0 model at zero temperature, $\varPhi$ is the order parameter related to the confined/deconfined phase transition. Its dependence with $\mu$, obtained through $\partial \varOmega _{\mathrm{PNJL0}}/\partial \varPhi =0$, is shown in Fig. 5.

Fig. 5

$\varPhi$ as a function of $\mu$ for the PNJL0 model with $G_V=0.25G_s$ and $a_3=-\,0.1$

The equilibrium $\varPhi$ dependence with $\mu$ is the one defined by the full line. The position of the jump in $\varPhi$ is determined by $\mu =\mu _{\mathrm{conf}}$, found by the aforementioned method of searching for two global minima in $\varOmega _{\mathrm{PNJL0}}$. The dashed line corresponds to the eliminated branches of $\varOmega _{\mathrm{PNJL0}}$ in Fig. 3.

3.4 Quarkyonic phase and effects of $a_3$ and $G_V$ on the PNJL0 model

Another thermodynamical phase structure is also observed at lower $\mu$ values, namely, $385 \text{ MeV }\leqslant \mu \leqslant 415 \text{ MeV }$, as pointed out by the inset of Fig. 3. In that region, it is verified that the correct $\varOmega _{\mathrm{PNJL0}}\times \mu$ curve must be the one described by the ABC line. The first order phase transition is given by the transition of the system from a broken chiral symmetry region to a restored one (the quark condensate is the order parameter in this case). By naming the chemical potential at the B point as $\mu _{\mathrm{chiral}}$, we obtain the value of 400.243 MeV. Notice that as $\varPhi =0$ in this region, the same thermodynamical structure is also present in the NJL model. In this case, Eqs. (22)–(26) are reduced to the NJL ones for $\varPhi =0$ (confined phase of the PNJL0 model). Strictly speaking, the PNJL0 model is exactly the NJL one until $\mu =\mu _{\mathrm{conf}}$, where nonzero $\varPhi$ values occur, i.e., in our approach the NJL thermodynamical phases can be seen as contained in the PNJL0 model.

A wider picture of the PNJL0 model, encompassing the two phase transition regions, is shown in Fig. 6. The thermodynamical stable curve in this case is the one described by the ABCDEF line.

Fig. 6

The same as in Fig. 3, but for a larger $\mu$ region

In Fig. 7, we show the $\mu$ dependence of the chiral condensate for the PNJL0 model.

Fig. 7

Chiral condensate, in units of its vacuum value, as a function of $\mu$ for the PNJL0 model with $G_V=0.25G_s$ and $a_3=-\,0.1$

For chemical potential values smaller than $\mu _{\mathrm{chiral}}=400.243$ MeV, the model behaves as the NJL one, as already discussed. Exactly at $\mu =\mu _{\mathrm{conf}}=506.906$ MeV, the discontinuity in $\varPhi$ also affects $\rho _s$ due to the backreaction mechanism presented in the PNJL0 model. We remark in the inset of the Fig. 7 the discontinuity induced in $\rho _s$ due to the one observed in $\varPhi$ (Fig. 5). The stable curve for $\rho _s$ is the one described by the full line.

Figure 7 is also useful to identify another phase of the strongly interacting matter, namely, the one defined in the region of $\mu _{\mathrm{chiral}} \leqslant \mu \leqslant \mu _{\mathrm{conf}}$. In this range, quark matter is chirally symmetric but still confined since the quark condensate is nearly vanishing and the traced Polyakov loop is zero. Only at $\mu \geqslant \mu _{\mathrm{conf}}$, the deconfined quark phase is reached, i.e, one has $\varPhi \ne 0$. This specific $\mu$ region in the range of $\mu _{\mathrm{chiral}}\leqslant \mu \leqslant \mu _{\mathrm{conf}}$ is identified as the quarkyonic phase, in the notation of Refs. [27, 56,57,58,59,60], for instance. The emergence of this phase is not possible in the usual NJL model since there is no information regarding confinement effects as there is in the PNJL0 model.

We also investigate the effects of the variation of the $a_3$ and $G_V$ parameters in the PNJL0 model. In Fig. 8 we show $\varPhi$ as a function of $\mu$ for different $a_3$ values chosen in order to produce $\mu _{\mathrm{conf}}=\mu _{\mathrm{chiral}}$ and $\mu _{\mathrm{conf}}=\varLambda$ for the chemical potentials related to the two phase transitions (broken/restored chiral symmetry phase transition and confinement/deconfinement one).

Fig. 8

$\varPhi \times \mu$ for the PNJL0 model with $G_V=0.25G_s$ and different $a_3$ values

Note that the effect of the $a_3$ increasing is to shrink the quarkyonic phase until its complete elimination, in this case for $a_3\sim -\,0.026$. For this particular value of $a_3$, $\varOmega _{\mathrm{PNJL0}}\times \mu$ present two crossing points exactly at the same $\mu$, namely, $\mu =\mu _{\mathrm{chiral}}=\mu _{\mathrm{conf}}=400.243$ MeV, as we see in Fig. 9.

Fig. 9

$\varOmega _{\mathrm{PNJL0}}$ as a function of the quark chemical potential ($\mu$) for $G_V=0.25G_s$ and $a_3=-\,0.026341$

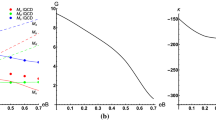
Finally, we study the impact of the $G_V$ variation in the model. In Fig. 10 it is depicted how the traced Polyakov loop is affected by the strength of the vector channel interaction.

Fig. 10

$\varPhi$ as a function of the quark chemical potential for $a_3=-\,0.1$ and different $G_V$ values. We also remark that as $G_V$ increases above $\sim G_s$, the lines begin to move significantly to the right. The reader can confer this effect in Fig. 11

It can be seen that the increase of $G_V$ also moves the entire $\varPhi$ curve to the direction of lower $\mu$ values. As a direct consequence, the quarkyonic region begins to decrease in size (as $G_V$ increases) until the situation in which $G_V\sim 1.18G_s$. In this case, the quantity defined as $\varDelta \mu =\mu _{\mathrm{conf}}-\mu _{\mathrm{chiral}}$ is vanishing. Thereafter, $\mu _{\mathrm{chiral}}$ becomes greater than $\mu _{\mathrm{conf}}$, indicating that chiral symmetry restoration takes place after deconfinement. The change of $\mu _{\mathrm{chiral}}$ as a function of $G_V$ is an effect observed also in the original NJL model [19]. Actually, the increase of $G_V$ moves the point of broken/restored chiral symmetry phase transition to higher $\mu$ values, making possible the PNJL0 model to present $\mu _{\mathrm{chiral}}>\mu _{\mathrm{conf}}$. In order to avoid this situation, we restrict $G_V$ to the maximum value that leads to $\varDelta \mu =0$, namely, $G_V\sim 1.18G_s$.¹

Studies with the aim of correctly limit the $G_V$ values were performed, for instance, in Refs. [61,62,63] where the range of $0.25G_s\leqslant G_V\leqslant 0.50G_s$ was found. In Refs. [38, 64], on the other hand, the more broad range of $0.30G_s\leqslant G_V\leqslant 3.2G_s$ was used. Here, it is possible to adopt a criterion in order to determine a range of $G_V$ based on the results shown for the PNJL0 model, namely, we define $G_V$ inside an interval of $G_V^{\mathrm{min}}\leqslant G_V\leqslant G^{\mathrm{max}}_V$, where $G^{\mathrm{min}}_V$ is the value that produces $\mu _{\mathrm{conf}}=\varLambda$, and $G_V^{\mathrm{max}}$ is the value that leads to $\mu _{\mathrm{conf}}=\mu _{\mathrm{chiral}}$ $(\varDelta \mu =0)$, according to the previous discussion. This generates a quarkyonic phase starting at $\mu =\mu _{\mathrm{chiral}}$ and extending up to a certain typical energy scale of the system as $\varLambda$, for instance. Such an approach also avoids a confinement/deconfinement phase transition taking place before the broken/restored chiral symmetry one. In the specific case of $a_3=-0.1$, this criterion leads to $G^{\mathrm{min}}_V\sim 0.069G_s$ and $G^{\mathrm{max}}_V\sim 1.18G_s$.

In Fig. 11 we also show the evolution of $\varPhi \times \mu$ curves for higher $G_V$ values. Notice that the mainly effect in these cases is to move the $\varPhi$ curve to the increasing $\mu$ direction.

Fig. 11

$\varPhi$ as a function of $\mu$ for $G_V/G_s$ = 1, 1.5, 2 and 2.5

As a last comment, we reinforce that the PNJL0 model studied in this work (zero temperature regime) produces first order phase transitions for the traced Polyakov loop, as a function of the quark chemical potential, for different values of the free parameters $G_V$ and $a_3$, as observed in Figs. 5, 8, 10, and 11. The same kind of phase transition is also found in Ref. [48, 49], where the Polyakov potential given in Eq. (18) was implemented in a hybrid SU(3) chiral model that contains both hadrons and quarks as degrees of freedom. Besides that study, in Ref. [65] another version of the PNJL model at $T=0$ was proposed. In that model, a quark density dependence is introduced in the $b_2(T)$ function of the Polyakov potential given in Eq. (14). A signal of first order phase transition is also verified in their $\varPhi \times \mu$ curves, but with the discontinuous jump of the trace Polyakov loop coinciding with the hadron-quark phase transition.

4 Summary and concluding remarks

In this work we extend a previous study performed in Ref. [45] in which a version of the Polyakov–Nambu–Jona–Lasinio model at zero temperature (PNJL0 model) was proposed. Here we explicitly show that it is possible to preserve the confinement effects of the model even at $T=0$ by imposing a $\varPhi$ dependence in the strengths of the scalar and vector interaction channels, see Eqs. (20) and (21). This modification leads to a Polyakov potential given by

$$\begin{aligned} \mathcal {U}_{\mathrm{PNJL0}}(\rho _s,\rho ,\varPhi )&= G_V\varPhi ^2\rho ^2 - G_s\varPhi ^2\rho _s^2 \nonumber \\&\quad + a_3T_0^4\text{ ln }(1-6\varPhi ^2+8\varPhi ^3-3\varPhi ^4), \end{aligned}$$

(28)

containing the backreaction of the quarks in the gluonic sector, but also the influence of the latter on the former. The last term in $\mathcal {U}_{\mathrm{PNJL0}}$ ensures nonvanishing solutions for $\varPhi$ and also limits the $\varPhi$ values to 1. We show that $\varOmega _{\mathrm{PNJL0}}\times \varPhi$ present $\varPhi \ne 0$ solutions only for $G_V\ne 0$. Therefore, the vector channel plays an important role in the PNJL0 model since it ensures the possibility of observing the confinement effects represented by nonvanishing traced Polyakov loop values. We show how these solutions generates first order phase transitions related to the confined/deconfined quark phases, since $\varPhi$ present a discontinuous jump as a function of the quark chemical potential ($\varPhi$ is the order parameter). The signature of this phase transition is identified in the $\varOmega _{\mathrm{PNJL0}}\times \mu$ curve where a crossing point is observed, see Fig. 3. Thermodynamical stability establishes that it is also possible to identify such a transition through the search of the chemical potential that produces two global minima, with the same $\varOmega _{\mathrm{PNJL0}}$ value, in the $\varOmega _{\mathrm{PNJL0}}\times \varPhi$ curve, see Fig. 4.

We also show that the first order phase transition related to the broken/restored chiral symmetry is still present in the PNJL0 at the same value of $\mu$ as in the original NJL model, as one can see in Fig. 6. The first crossing point indicates this transition, with the quark condensate being the order parameter. The region $\mu _{\mathrm{chiral}} \leqslant \mu \leqslant \mu _{\mathrm{conf}}$ is identified as the quarkyonic phase, namely, chirally symmetric ($\rho _s/\rho _{s(\hbox { vac})}\sim 0$) but still presenting confined quarks ($\varPhi =0$). The deconfined phase only takes place at $\mu \geqslant \mu _{\mathrm{conf}}$. $\mu _{\mathrm{chiral}}$ and $\mu _{\mathrm{conf}}$ are, respectively, the chemical potentials in which the broken/restored chiral symmetry and confinement/deconfinement first order phase transitions occur.

The size of the quarkyonic phase in the PNJL0 model is directly governed by the values of the $a_3$ and $G_V$ parameters. In Figs. 8 and 10 it is shown that by increasing these quantities the quarkyonic phase shrinks. In the case of the $G_V$ parameter, this situation is changed starting from a particular value of $G_V$. This feature suggested a way to define a range of possible $G_V$ values, namely, those producing $\mu _{\mathrm{conf}}=\varLambda$ (the cutoff parameter is a energy scale of the model) and $\mu _{\mathrm{conf}}=\mu _{\mathrm{chiral}}$. For the case in which $a_3=-\,0.1$, such a criteria leads to $G_V\sim 0.069G_s$ and $G_V\sim 1.18G_s$, respectively, for minimum and maximum values of the vector channel strength.

Finally, we remark the importance of the construction of QCD effective/phenomenological models at zero temperature, since a direct application is in the analysis of the hadron-quark phase transition in compact neutron stars (described at $T=0$). A recent and very important study evidences the existence of quark-matter cores in such objects [66]. The challenge of a detailed study involving relativistic hadronic models [67,68,69] and the PNJL0 model described here and in Ref. [45] is left for a future work.