Currently, metamaterials (composite structures, the properties of which differ from those of natural materials) is a rapidly developing line of research in materials science and nanotechnologies [1–3]. Among metamaterials, the most attractive objects are left-handed media, the permittivity and permeability of which are both negative [4]. The interest in left-handed media is primarily due to the possibility of implementing a negative refractive index and creating ideal lenses for subwavelength imaging below the Abbe diffraction limit. In addition, a backward wave, the phase and group velocities of which are directed oppositely, propagates in a left-handed medium.

In the first experimental studies, left-handed media were formed using periodic structures consisting of metal wires and split-ring resonators (SRRs), the repetition period of which was much smaller than the electromagnetic wave (EMW) wavelength [5, 6]. A periodic system of thin conducting wires made it possible to create a plasmonic medium with negative effective permittivity at frequencies below the plasma frequency, whereas a periodic system of SRRs was used to obtain negative effective permeability at frequencies higher than the SRR eigenfrequency. It was proposed in [7] to create a left-handed medium by combining the natural magnetic properties of a ferromagnet and artificial electrical properties of a periodic structure of ideally conducting wires. It was shown that there exists one extraordinary slow backward bulk EMW in a left-handed medium based on this gyrotropic matrix containing inclusions of metal subwave elements. This approach to creating left-handed media based on gyrotropic matrices can be extended to the case of natural electrical media (e.g., in the form of magnetoactive (anisotropic) plasma) [8]. In contrast to left-handed media based on isotropic plasma [5, 6], left-handed media based on anisotropic plasma should ensure propagation of not only ordinary, but also extraordinary, backward EMWs. In addition, left-handed medium based on magnetized plasma provide the possibility of controlling the spectrum of these waves not only by changing the SRR eigenfrequency via fitting corresponding resonator sizes, but also by changing the magnetic-induction value.

The purpose of this study was to show that it is possible to create a left-handed medium in which the spectrum of backward EMWs can be controlled by a simultaneous change in the SRR eigenfrequency and magnetic induction using a simple electrodynamic model of strip waveguide completely filled with longitudinally magnetized electron plasma containing an SRR periodic structure.

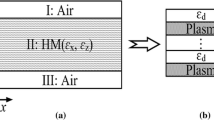
Figure 1a shows a schematic of the plasma metamaterial under consideration. It is a longitudinally magnetized plasma layer (the direction of magnetic-induction vector B0 coincides with the 0Z axis and direction of wave vector k) with a periodic SRR structure. To describe the magnetic properties of this periodic structure, the effective permeability of the medium is introduced, which is determined for ideally conducting SRRs by the following well-known expression [5]:

$${{\mu }_{{{\text{eff}}}}} = 1 - \frac{{F{{\omega }^{2}}}}{{{{\omega }^{2}} - \omega _{{0m}}^{2}}},$$
(1)

where F = π(r/T)2, r is the internal-ring radius, T is the structure period, ω0m = \(c\sqrt {3T{\text{/}}[\pi {{r}^{3}}\ln (2w{\text{/}}\delta )]} \) is the SRR resonance frequency, w is the conductor width, δ is the radial distance between the rings, and c is the speed of light in free space. Expression (1) was previously applied in the model of left-handed medium based on isotropic plasma [5, 6]. To use expression (1) in the model of left-handed medium based on anisotropic plasma, one should provide conditions under which the permittivity of anisotropic plasma will be close to that for the isotropic case. This condition can be implemented if cyclotron frequency of electrons ωce is much lower than frequency ω0m (ωce ≪ ω0m). With this approach, the proposed model can describe correctly only the EMW spectral range located either near or above frequency ω0m.

Fig. 1.
figure 1

(a) Schematic of the magnetoactive plasma metamaterial and (b) dependences of (top panel) the effective permeability of the medium μeff and (bottom panel) diagonal component ε of high-frequency permittivity tensor \(\bar {\bar {\varepsilon }}\) on normalized frequencies ω/ω0m and ω/ωce, respectively (Ωmu = ωmu/ω0m). The calculations were performed at F = 0.7, N = 1017 cm–3, and B0 = 0.1 T.

Full size image

The dispersion characteristics (DCs) of the EMWs existing in a longitudinally magnetized plasma metamaterial can be calculated using the dispersion equation for longitudinally magnetized collisionless and cold plasma [9], which can be written as follows (taking into account the effective permeability of the medium):

$$\begin{gathered} \text{[}\eta k_{z}^{2} + \varepsilon (k_{x}^{2} - {{\mu }_{{{\text{eff}}}}}k_{0}^{2}\eta )](k_{z}^{2} + k_{x}^{2} - {{\mu }_{{{\text{eff}}}}}k_{0}^{2}\varepsilon ) \\ \, + {{\mu }_{{{\text{eff}}}}}k_{0}^{2}{{g}^{2}}(k_{x}^{2} - {{\mu }_{{{\text{eff}}}}}k_{0}^{2}\eta ) = 0, \\ \end{gathered} $$
(2)

where kx and kz are the transverse and longitudinal wavenumbers, respectively; k0 = ω/c is the wavenumber in vacuum; ε = \(1 + \omega _{{pe}}^{2}{\text{/}}(\omega _{{ce}}^{2} - {{\omega }^{2}})\), g = \( - \omega _{{pe}}^{2}{{\omega }_{{ce}}}{\text{/}}[(\omega _{{ce}}^{2} - {{\omega }^{2}})\omega ]\), and η = \(1 - \omega _{{pe}}^{2}{\text{/}}{{\omega }^{2}}\) are the diagonal and off-diagonal components of tensor \(\bar {\bar {\varepsilon }}\) written for the case of a one-component (electron) plasma; ωpe = \(\sqrt {4\pi N{{e}^{2}}{\text{/}}{{m}_{e}}} \) is the plasma frequency of electrons; N is the electron concentration in plasma; e/me is the specific elementary charge; and ωce = |eB0|/(mec).

We will consider a longitudinally magnetized electron plasma layer adjacent on both sides to ideally conducting metal screens (a strip waveguide completely filled with plasma). When the Maxwell equations are solved within the quasi-static approximation (kz ≫ k0), which is valid for thin gyrotropic layers, the function of the transverse wavenumber for a strip waveguide completely filled with longitudinally magnetized gyrotropic medium is as follows:

$${{k}_{x}} = \frac{{n\pi }}{d},$$
(3)

where d is the thickness of the thin gyrotropic layer and n is the number of the thickness mode of a bulk EMW. For a thin layer of magnetoactive plasma, formula (3) is valid for a quasi-TM EMW.

Taking into account (1) and (3), dispersion equation (2) is reduced to the polynomial form with respect to circular frequency ω. The polynomial has six real positive roots, two of which correspond to high-frequency fast (ordinary and extraordinary) bulk EMWs with phase velocities exceeding the speed of light in free space (\({{{v}}_{{{\text{ph}}}}}\) > c), while the other four roots correspond to slow bulk EMWs with phase velocities much lower than the speed of light in free space (\({{{v}}_{{{\text{ph}}}}}\) ≪ c). Two of the slow EMWs are well known plasma waves: one of them corresponds to the high-frequency extraordinary slow EMW at frequency ω ~ ωpe, while the other corresponds to the low-frequency slow EMW at ω < ωce [10]. The other two slow EMWs are induced by the presence of the periodic SRR structure in the plasma layer.

Figure 1b shows the results of calculating the frequency dependences of the effective permeability and the diagonal component of tensor \(\bar {\bar {\varepsilon }}\) of high-frequency permittivity. It follows from the calculation results that μeff > 0 at ω < ω0m and ω > ωmu, and μeff < 0 at ω0m < ω < ωmu, where ωmu = \({{\omega }_{{0m}}}{\text{/}}\sqrt {1 - F} \). Diagonal component ε of tensor \(\bar {\bar {\varepsilon }}\) becomes negative at frequencies above the cyclotron frequency (ω > ωce). Note that the second diagonal component η of tensor \(\bar {\bar {\varepsilon }}\) is below zero (η < 0) at ω < ωpe. Thus, one of the two following conditions must be satisfied in order to form a left-handed medium (ε < 0, η < 0, and μeff < 0), in which slow EMWs with negative anomalous dispersion will propagate, from magnetized electron plasma:

$${{\omega }_{{ce}}} < {{\omega }_{{0m}}} < \omega < {{\omega }_{{mu}}} < {{\omega }_{{pe}}},$$
(4a)
$${{\omega }_{{ce}}} < {{\omega }_{{0m}}} < \omega < {{\omega }_{{pe}}} < {{\omega }_{{mu}}}.$$
(4b)

In Fig. 1b, the frequency range in which conditions (4a) and (4b) are satisfied is colored.

Figure 2 shows the results of calculating the DCs of slow EMWs obtained by solving dispersion equation (2) taking into account (1) and (3). The calculations were performed for the left-handed medium based on both isotropic (B0 = 0) and magnetoactive (B0 ≠ 0) plasma metamaterials. A comparison yielded that there is only one (ordinary) slow EMW with negative anomalous dispersion in the left-handed medium based on isotropic plasma metamaterial. In the case of the left-handed medium based on magnetoactive plasma metamaterial, either two (ordinary and extraordinary) slow EMWs (Fig. 2a) or one (ordinary) slow EMW (Fig. 2b) may exist. The former and latter cases are implemented under conditions (4a) and (4b), respectively. One can also see in the insets in Figs. 2a and 2b that the DC of the ordinary slow EMW contains portions of negative (anomalous) and positive (normal) dispersion. A change in the dispersion is observed in a relatively narrow frequency range, the occurrence of which is not an error due to excess machine accuracy (because it has a value of 2.220446e-016). In contrast, the extraordinary slow EMW in the frequency range where μeff < 0, ε < 0, and η < 0 has only negative anomalous dispersion (Fig. 2a). A simultaneous increase in the SRR eigenfrequency and cyclotron frequency of electrons shifts the extraordinary slow EMW to the frequency range where μeff > 0, and it becomes a wave with positive normal dispersion (Fig. 2b). It can be seen in Fig. 3 that the maximum value of the group velocity of the extraordinary slow EMW is always larger (whereas that of the ordinary slow EMW is always smaller) than the maximum value of the group velocity of the ordinary slow EMW existing in a left-handed medium based on isotropic plasma metamaterial.

Fig. 2.
figure 2

Dispersion characteristics of the (1) ordinary and (2) extraordinary slow bulk EMWs calculated for the left-handed medium based on magnetoactive plasma metamaterial at the following values of the magnetic induction and SRR eigenfrequency: (a) B0 = 1 T and  f0m = 0.2 THz and (b) B0 = 10 T and f0m = 28.3 THz. The calculations for panels (a) and (b) were performed at d = 10 μm, n = 1, N = 1019 cm–3, and F = 0.7. Dashed curves show the dispersion characteristics of the ordinary slow bulk EMW existing in the left-handed medium based on the isotropic plasma metamaterial.

Full size image
Fig. 3.
figure 3

Dependences of group velocity Vg on wavenumber k for the (1) ordinary and (2) extraordinary slow bulk EMWs existing in the left-handed medium based on the magnetoactive plasma metamaterial. The calculations were performed at d = 10 μm, n = 1, B0 = 1 T, N = 1019 cm–3,  f0m = 0.2 THz, and F = 0.7. The dashed curve shows dependence Vg(k) of the ordinary slow bulk EMW existing in the left-handed medium based on the isotropic plasma metamaterial.

Full size image

Note that the permittivities of magnetoactive plasma and isotropic plasma for the two above-considered cases differ by no more than 2% at the SRR eigenfrequency. In addition, the existence of slow EMWs in the entire frequency range  f0m < f < fmu can be achieved at F → 1. The condition T ≪ λ limits the frequency ranges of slow EMWs without DC discontinuities caused by the validity of the Bragg resonance conditions for certain wavenumbers [11].

In conclusion, it should be noted that the performed calculations of the electrodynamic characteristics of slow EMWs indicate that magnetoactive plasma can be used for creating magnetically controlled left-handed media in the THz frequency range. Not only gas-discharge media [12], but also semiconductor materials [13], can serve as plasma media (the calculations in this study were performed for the electron concentration of the latter).