Variational approximation for importance sampling

Abstract

We propose an importance sampling algorithm with proposal distribution obtained from variational approximation. This method combines the strength of both importance sampling and variational method. On one hand, this method avoids the bias from variational method. On the other hand, variational approximation provides a way to design the proposal distribution for the importance sampling algorithm. Theoretical justification of the proposed method is provided. Numerical results show that using variational approximation as the proposal can improve the performance of importance sampling and sequential importance sampling.

1 Introduction

Monte Carlo methods, such as importance sampling (IS) and Markov chain Monte Carlo (MCMC), are widely used in Bayesian inference when analytical computation based on the posterior distribution is difficult. The posterior distributions are sometimes hard to sample directly, especially for complex statistical models with both unknown parameters and latent variables. In that case, importance sampling draws samples from an easy-to-sample proposal distribution, and then corrects the bias by the importance weights. Choosing a good proposal distribution is essential to the efficiency of importance sampling algorithms. We often try to find a proposal distribution that is close to the target distribution to reduce the variance of the importance weight. For high dimensional problems, sequential importance sampling (SIS) (Liu and Chen 1998; Doucet et al. 2000) gives a way to construct the proposal distribution sequentially.

Variational Bayes (VB) (Jordan et al. 1999) tackles the problem in a different way by deriving a tractable approximation to the posterior distribution. It minimizes the Kullback-Leibler (KL) divergence (Kullback and Leibler 1951) between the posterior and the variational approximation, and uses the variational approximation to make inference. In the optimization part, VB algorithm usually uses stochastic optimization (Robbins and Monro 1951) or coordinate optimization strategy. This method is also related to the EM algorithm (Dempster et al. 1977). VB, IS and MCMC can be used for general computational problems, but in this paper we focus on the application in Bayesian settings to make the discussion more concrete.

An advantage of VB is the variational approximation can be obtained quickly, and it usually runs faster than Monte Carlo sampling algorithms such as MCMC. The variational method has been applied in many fields, such as computational biology (Sanguinetti et al. 2006), network data analysis (Hofman and Wiggins 2008; Zreik et al. 2017; O’Hagan and White 2019), natural language processing (Blei et al. 2003), and statistical inference (Armagan and Dunson 2011; Depraetere and Vandebroek 2017). However, one issue with the variation method is that the gap between the variational approximation and the true posterior distribution may lead to biased inference based on variational approximation. In many problems, the estimate based on variation approximation may not be consistent. Also the uncertainty of the VB estimate is not available.

In this paper, we consider using the variational approximation as the proposal distribution for importance sampling, and then using the importance weight to correct the bias. Since the importance sampling estimate is consistent under mild conditions, the bias issue of VB is resolved. The uncertainty of the importance sampling estimate is also relatively easy to obtain. In the meantime, since the variational approximation is close to the true posterior distribution and is usually easy to sample, it is a good choice for the importance sampling proposal distribution. So this idea combines the strength of these two methods. We will provide theoretical justification of the proposed method using the f-divergence (Ali and Silvey 1966), and implement the proposed methods on several models to demonstrate its performance in practice.

The paper is organized as follows. We first review importance sampling and variational approximation in Sect. 2, and introduce the new method in Sect. 3. Then, we provide theoretical justification in Sect. 4, and give numerical results of the new method on several examples in Sect. 5. Section 6 concludes with a discussion.

2 Literature review

2.1 Importance sampling

Suppose $\mathbf{Z}$ is a random vector with probability density function $p(\mathbf{z})$, and we want to estimate the expectation of some function $h(\mathbf{Z})$:

$$\begin{aligned} \varvec{\mu }= E_{p}(h(\mathbf{Z})) = \int h(\mathbf{z})p(\mathbf{z})d\mathbf{z}.\end{aligned}$$

If $p(\mathbf{z})$ is hard to sample directly, we may consider importance sampling (IS) to generate samples from a proposal distribution $q(\mathbf{z})$. Then the expectation $\varvec{\mu }$ can be estimated by the weighted average

$$\begin{aligned} \tilde{\varvec{\mu }}=\frac{w(\mathbf{z}^{(1)})h(\mathbf{z}^{(1)}) +\cdots + w(\mathbf{z}^{(m)})h(\mathbf{z}^{(m)})}{w(\mathbf{z}^{(1)}) + \cdots + w(\mathbf{z}^{(m)})}, \end{aligned}$$

(1)

where $w(\mathbf{z}^{(i)}) = p(\mathbf{z}^{(i)})/q(\mathbf{z}^{(i)})$ are the importance weights. The estimate $\tilde{\varvec{\mu }}$ is consistent, and it can also handle densities that are only known up to normalizing constants.

The standard error of $\tilde{\varvec{\mu }}$ can be used to measure the efficiency of the IS algorithm. Another criterion is the effective sample size (ESS) (Kong et al. 1994; Kong 1992; Martino et al. 2017):

$$\begin{aligned} \text{ ESS } = \frac{m}{1+cv^2}, \end{aligned}$$

where the coefficient of variation (cv) is defined as:

$$\begin{aligned} cv^2 = \frac{Var_q[w(\mathbf{Z})]}{E_q^2[w(\mathbf{Z})]}. \end{aligned}$$

The ESS roughly approximates the number of independent and identically distributed (i.i.d.) samples these m importance samples are equivalent to. Thus, a smaller $cv^2$ indicates that the IS algorithm is more effective in terms of the ESS. In addition, the $cv^2$ is also the $\chi ^2$ distance between the proposal distribution $q(\mathbf{z})$ and the target distribution $p(\mathbf{z})$, defined as

$$\begin{aligned} \chi ^2(p||q) = \int \frac{(p-q)^2}{q}d\mathbf{z}, \end{aligned}$$

and this will be used later in our theoretical justification.

For high dimensional problems, it is often hard to find a good proposal for IS. To overcome this difficulty, Liu and Chen (1998) and Doucet et al. (2000) provided the general framework of sequential importance sampling (SIS) to build up the proposal $q(\mathbf{z})$ sequentially. For a d-dimensional vector $\mathbf{z}=(z_1, \ldots , z_d)$, the proposal distribution can be decomposed as:

$$\begin{aligned} q(\mathbf{z}) = q_1(z_1)q_2(z_2|z_1)\cdots q_d(z_d|z_1, \ldots ,z_{d-1}).\end{aligned}$$

Each proposal distribution in the decomposition is for a low dimensional component, so it is relatively easier to design a good proposal. The target distribution $p(\mathbf{z})$ can be decomposed in a similar way by using auxiliary distributions to guide the choice of the proposal distribution (Liu and Chen 1998). The importance weight can also be computed recursively based on the decomposition. SIS has been successfully applied to many problems, including the filtering problem in hidden Markov models (or state space models).

Another variation of IS is adaptive importance sampling (AIS) (Cappé et al. 2004, 2008; Bugallo et al. 2017), which provides a scheme to find a good proposal distribution adaptively based on samples in previous steps. For multi-modal distributions, Owen (2013) suggested using mixture importance sampling as a way to carry out AIS. However, AIS does not work well for high dimensional distributions without incorporating an additional MCMC layer, and the computation time of AIS is usually much longer than importance sampling (Bugallo et al. 2017).

2.2 Variational approximation

Variational Bayesian method (Jordan et al. 1999) is a technique for approximating the intractable integrals in Bayesian inference. It is typically useful when the statistical models are relatively complex with a lot of parameters and latent variables. In Bayesian inference, suppose we have a set of n i.i.d. data $\mathbf {x}$, and all latent variables and parameters are denoted by $\mathbf {Z}$. We need to find an approximation to the posterior distribution $p(\mathbf {z}|\mathbf {x})$ that can minimize the KL divergence, i.e.,

$$\begin{aligned} q^*(\mathbf{z}) = \underset{q(\mathbf{z})\in \mathcal D}{{\text {argmin}}} \, \text {KL}(q(\mathbf{z})||p(\mathbf{z}|\mathbf{x})),\end{aligned}$$

where $\mathcal D$ is a restricted distribution family. Here $\mathcal D$ is usually a simpler family of distributions to make the optimization and inference tractable.

Xing et al. (2002) assumed the variational distribution $q(\mathbf{z})$ can be factorized over some partitions of the latent variables as follows:

$$\begin{aligned} q(\mathbf{z}) = \prod _{j=1}^M q_j(z_j),\end{aligned}$$

where M is the number of parameters and latent variables. The best distribution $q^*_j$ for each factor that solves the optimization problem can be expressed as:

$$\begin{aligned} q_j^*(z_j) = \frac{e^{E_{-j}[\log p(\mathbf{z}, \mathbf{x})]}}{\int e^{E_{-j }[\log p(\mathbf{z}, \mathbf{x})]} dz_j} \propto e^{E_{-j}[\log p(z_j, \mathbf{z}_{-j}, \mathbf{x})]}. \end{aligned}$$

(2)

Here $E_{-j}[\cdot ]$ means the expectation with respect to all $q_i(z_i)$ with $i\ne j$ and $\mathbf{z}_{-j}$ means all the elements in the vector $\mathbf{z}$ except $z_j$. However, the optimal mean-field variational approximations $q_j^*(z_j)$ cannot be computed directly because $E_{-j}[z_i]$ $(i\ne j)$ are involved in the right hand side of (2). Thus, an iterative method is often used to obtain the best solution, and such mean-field variational algorithm can only guarantee to converge to a local minimum of $\text {KL}(q(\mathbf{z})||p(\mathbf{z}|\mathbf{x}))$ (Blei et al. 2017).

Beal and Ghahramani (2003) proposed a variational Bayesian EM algorithm to estimate the marginal likelihood of probabilistic models with latent variables or incomplete data. They also compared the variational bound with a sampling-based method known as annealed importance sampling (Neal 2001). Dieng et al. (2017) proposed another variational algorithm by minimizing the $\chi$-divergence between the variational approximation and the posterior distribution.

3 VB approximation for importance sampling

Although obtaining variational approximation is faster than some sampling based methods, such as MCMC, and it learns the approximate probability density functions through optimization, the inference based on the approximation is biased due to the gap between the variational approximation and the true posterior distribution. On the other hand, IS provides a consistent estimate, but the proposal distribution is hard to design. Here we combine VB with IS by using variational approximation $q(\mathbf{z})$ as the proposal distribution for IS. It avoids the bias from VB approximation and also provides a good way to construct the proposal distribution for IS.

Suppose we have a model with prior $p(\mathbf{z})$ and likelihood function $p(\mathbf{x}|\mathbf{z})$, where $\mathbf{z}$ contains both parameters and latent variables, then the posterior distribution is

$$\begin{aligned} p(\mathbf{z}|\mathbf{x}) = \frac{p(\mathbf{z})p(\mathbf{x}|\mathbf{z})}{p(\mathbf{x})} \propto p(\mathbf{z})p(\mathbf{x}|\mathbf{z}) = p(\mathbf{x},\mathbf{z}).\end{aligned}$$

By the mean-field variational algorithm, we can obtain the variational approximation $q(\mathbf{z})$ to the posterior $p(\mathbf{z}|\mathbf{x})$. If the support of $q(\mathbf{z})$ includes the support of $p(\mathbf{z}|\mathbf{x})$, then the expectation of the function $h(\mathbf{Z})$ with respect to $p(\mathbf{z}|\mathbf{x})$ can be estimated by importance sampling as in (1), with $w(\mathbf{z}^{(i)}) = p(\mathbf{z}^{(i)}|\mathbf{x}^{(i)})/q(\mathbf{z}^{(i)})$. The variational importance sampling algorithm is summarized in Algorithm 1.

Dowling et al. (2018) used the modes of the variational distributions to initialize the location parameters of the proposal distributions in adaptive importance sampling, which is applicable when the variational approximation is in the location scale family. Our proposed method uses the variational approximation itself as the proposal distribution for importance sampling. It does not put restrictions on the proposal distribution, and it can be extended to sequential importance sampling as shown in the next section.

3.1 VB approximation for sequential importance sampling

If the dimension of the parameters and latent variables is high, or if the data arrive sequentially, SIS is often used. VB can be combined with SIS as well by constructing the proposal with VB sequentially.

Let $\mathbf{z}$ be all the hidden variables, and $\mathbf{z}_{1:t} = \{z_1,\ldots , z_t \}$ be the first t components. Let $\mathbf{x}=\{x_1,\ldots , x_T \}$ be the data which arrive sequentially. The posterior distribution of interest is $p(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})$, $t = 1,\ldots , T$. In variational approximation, we assume the approximation $q(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})$ can be factorized in the following way:

$$\begin{aligned} q(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})=\prod _{k=1}^t q(z_k| \mathbf{x}_{1:t}), \ t = 1,\ldots , T.\end{aligned}$$

We consider two different approaches for constructing the proposal distribution sequentially.

VB-SIS1. In the first method, at each time $t=1,\ldots ,T$, we minimize the KL divergence between $q(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})$ and the true posterior distribution $p(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})$, and obtain the variational distributions as follows:

$$\begin{aligned} q(\mathbf{z}_{1:1}|\mathbf{x}_{1:1})= & {} q_1(\mathbf{z}_{1:1}) \ = \ q_{11}(z_1), \\ q(\mathbf{z}_{1:2}|\mathbf{x}_{1:2})= & {} q_2(\mathbf{z}_{1:2}) \ = \ q_{21}(z_1)\,q_{22}(z_2) , \\&\vdots&\\ q(\mathbf{z}_{1:T}|\mathbf{x}_{1:T})= & {} q_T(\mathbf{z}_{1:T}) \ = \ q_{T1}(z_1)\, q_{T2}(z_2)\cdots \,q_{TT}(z_T). \end{aligned}$$

We will use $q_{tt}(z_t)$, $t=1,2,\ldots ,T$, as the proposal distributions in SIS, and we call this method VB-SIS1 with general procedure given in Algorithm 2.

VB-SIS2. Another method is to obtain the proposal distribution in the current step t by reusing the proposals in previous steps. This procedure can be represented as follows:

$$\begin{aligned} {\tilde{q}}(\mathbf{z}_{1:1}|\mathbf{x}_{1:1})= & {} {\tilde{q}}_1(\mathbf{z}_{1:1}) \ = \ {\tilde{q}}_1(z_1), \\ {\tilde{q}}(\mathbf{z}_{1:2}|\mathbf{x}_{1:2})= & {} {\tilde{q}}_2(\mathbf{z}_{1:2}) \ = \ {\tilde{q}}_1(z_1)\,{\tilde{q}}_2(z_2) , \\&\vdots&\\ {\tilde{q}}(\mathbf{z}_{1:T}|\mathbf{x}_{1:T})= & {} {\tilde{q}}_T(\mathbf{z}_{1:T}) \ = \ {\tilde{q}}_1(z_1)\, {\tilde{q}}_2(z_2)\cdots \,{\tilde{q}}_T(z_T). \end{aligned}$$

At time t, in order to obtain ${\tilde{q}}_t(\mathbf{z}_{1:t})$, we fix the proposals from previous steps ${\tilde{q}}_1(z_1),\ldots , \tilde{q}_{t-1}(z_{t-1})$, and obtain ${\tilde{q}}_t(z_t)$ by minimizing the KL divergence between ${\tilde{q}}(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})$ and the true posterior distribution $p(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})$. Since we only need to determine the variational distribution for the last latent variable at each step, the running time will be shorter than VB-SIS1. We will use ${\tilde{q}}_t(z_t)$, $t=1,\ldots ,T$, as the proposal distribution, and we call this method VB-SIS2 with general procedure given in Algorithm 3.

In some cases (such as the hidden Markov model example in Sect. 5.4), we use the following approximation to further simplify the variational approximation:

$$\begin{aligned} p(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})\approx p(\mathbf{z}_{1:t}|\mathbf{x}_{\max (1, t-\varDelta + 1):t})\end{aligned}$$

where $\varDelta$ is a tuning parameter. This approximation assumes that the observations at time $k<t-\varDelta$ almost provide no additional information to $\mathbf{z}_{1:t}$. Under this assumption, we can obtain the variational approximation at step t only based on the observations $\mathbf{x}_{\max (1, t-\varDelta + 1):t}$, that is,

$$\begin{aligned} q(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})=q(\mathbf{z}_{1:t}|\mathbf{x}_{\max (1, t-\varDelta + 1):t}).\end{aligned}$$

Naesseth et al. (2018) considered approximating the posterior distribution for the state space model by introducing variational parameters and resampling procedures. The variational SIS algorithms we proposed are different because we obtain the proposal distribution at each step by deriving variational approximation sequentially. Our variational SIS can be used for general computation based on SIS, including state space models. Adding the resampling procedure can further improve the efficiency of SIS. We will not consider it here because we would like to compare the VB proposal with the standard proposal to evaluate the efficiency gain from VB proposal. Adding resampling steps will make it hard to distinguish where the efficiency gain is coming from. In practice, users can always combine resampling with variational SIS to make it more effective in high dimensional problems.

4 Theoretical justification

To simplify the notation, we will use p and q to denote the true posterior distribution $p(\mathbf{z}|\mathbf{x})$ and the variational distribution $q(\mathbf{z})$ in this section. In variational inference, we minimize the KL divergence between q and p:

$$\begin{aligned} KL(q||p) = \int q\log \frac{q}{p} d\mathbf{z}. \end{aligned}$$

In importance sampling, the $cv^2$ is the $\chi ^2$ distance between p and q:

$$\begin{aligned} \chi ^2(p||q) = \int \frac{(p-q)^2}{q}d\mathbf{z}, \end{aligned}$$

and we hope to find a proposal distribution q with a relatively small $cv^2$.

In order to make connections between these two distances, we introduce a more general f-divergence (Ali and Silvey 1966) between p and q as:

$$\begin{aligned} D_f(p||q) = E_q\left[ f\left( \frac{p}{q}\right) \right] = \int f\left( \frac{p}{q}\right) \cdot q \, d\mathbf{z},\end{aligned}$$

where $f(\cdot )$ satisfies the following three conditions:

• (i) $f(1)=0$.

• (ii) f(x) is a convex function.

• (iii) f(x) is continuous at $x=1$.

Let $u = p/q$, $f_1(u) = -\log u$ and $f_2(u) = (u-1)^2$, then we can see that the two distances can be written as:

$$\begin{aligned} KL(q||p) = D_{f_1}(p||q)\ \ \ \ \ \text {and} \ \ \ \ \ \chi ^2(p||q) = D_{f_2}(p||q). \end{aligned}$$

Sason and Verdú (2016) showed the following f-divergence inequality:

$$\begin{aligned} 0\le KL(p||q) \le \log (1+\chi ^2(p||q)), \end{aligned}$$

and stated that there is no lower-bound on KL divergence in terms of $\chi ^2$ distance. That means the convergence in $\chi ^2$ distance implies the convergence in KL divergence, but the other way may not be true. We examine the relationship between KL divergence and $\chi ^2$ distance more closely below.

The Taylor expansion for $f_1(u)$ at $u=1$ is :

$$\begin{aligned} f_1(u) = -\log u = -\log (1+(u-1)) = -(u-1) + \frac{(u-1)^2}{2} - \frac{(u-1)^3}{3} + \cdots .\end{aligned}$$

Taking expectation on both sides with respect to q and using the fact $E_q[u] = E_q[p/q] = 1$, we obtain the following equations

$$\begin{aligned} KL(q||p) = \frac{1}{2} \chi ^2(p||q) + o((u-1)^2).\end{aligned}$$

This indicates that when u is close to 1, these two distances are equivalent, i.e.,

$$\begin{aligned} KL(q||p) \asymp \frac{1}{2}\chi ^2(p||q).\end{aligned}$$

In order to quantify the value of u, we introduce two quantities $\beta _1$ and $\beta _2$ as follows (Sason and Verdú 2016):

$$\begin{aligned} \beta _1 = \text {ess}\inf \,\frac{q}{p} = \left( \text {ess} \sup \, \frac{p}{q}\right) ^{-1}, \ \ \beta _2 = \text {ess}\inf \,\frac{p}{q}= \left( \text {ess} \sup \, \frac{q}{p}\right) ^{-1}. \end{aligned}$$

(3)

The essential infimum and the essential supremum are defined as:

$$\begin{aligned} \text {ess}\inf \,\frac{p}{q} = \sup \{b \in \mathbb R: \mu (\{x: p(x)/q(x) < b \}) = 0 \}, \\ \text {ess}\sup \,\frac{p}{q} = \inf \{a \in \mathbb R: \mu (\{x: p(x)/q(x) > a \}) = 0 \}, \end{aligned}$$

where $\mu (\cdot )$ denotes the Lebesgue measure.

Since $\int q(\mathbf{z})\,d\mathbf{z}= 1$ and $\int p(\mathbf{z}|\mathbf{x})\, d\mathbf{z}= 1$, we have $0\le \beta _1,\beta _2 \le 1$, and $\beta _1 = 1\Leftrightarrow \beta _2=1\Leftrightarrow p=q$. Suppose $0<\beta _1<1$ and $0<\beta _2<1$. We say a sequence of probability measures with densities $p_n$ converge to q if

$$\begin{aligned} \lim _{n\rightarrow \infty } \text {ess}\inf \,\frac{p_n}{q} = 1. \end{aligned}$$

(4)

Lemma 1

Suppose f is a function satisfying Conditions (i)–(iii), and a sequence of probability measures with densities $p_n$ converge to q in the sense of (4). Let

$$\begin{aligned} \beta _{1,n}^{-1} = \text {ess} \sup \,\frac{p_n}{q} , \ \ \beta _{2,n} = \text {ess}\inf \,\frac{p_n}{q}. \end{aligned}$$

Then we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \beta _{1,n}=\lim _{n\rightarrow \infty } \beta _{2,n} = 1, \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty } D_f(p_n||q) = 0.\end{aligned}$$

The proof of the lemma as well as the proof of the following theorem are in the Appendix. Define a function:

$$\begin{aligned} \kappa (t) = \frac{t\log t + (1-t)}{(t-1)-\log t},\ \ \ \ \ 0<t<1 \ \text {and} \ t>1, \end{aligned}$$

(5)

which is increasing for $t\in (0, 1)\cup (1, \infty )$. Then, from Sason and Verdú (2016), the following inequalities hold:

$$\begin{aligned} \kappa (\beta _{2,n})\le & {} \frac{KL(p_n||q)}{KL(q||p_n)} \le \kappa (\beta _{1,n}^{-1}), \end{aligned}$$

(6)

$$\begin{aligned} \frac{1}{2} \beta _{1,n}\le & {} \frac{KL(p_n||q)}{\chi ^2(p_n||q)} \le \frac{1}{2} \beta _{2,n}^{-1}, \end{aligned}$$

(7)

where $p_n$, $\beta _{1,n}$, and $\beta _{2,n}$ are defined in Lemma 1. Note that (6) and (7) do not require the convergence of $p_n$ to q. The following theorem gives the limit of the ratios in (6) and (7).

Theorem 1

Suppose a sequence of probability measures with densities $p_n$ converge to q in the sense of (4). For KL divergence and $\chi ^2$ distance, we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{KL(p_n||q)}{KL(q||p_n)} = 1 , \ \ \lim _{n\rightarrow \infty } \frac{KL(p_n||q)}{\chi ^2(p_n||q)} = \frac{1}{2} . \end{aligned}$$

From the above theorem, we immediately have the following corollary.

Corollary 1

Suppose a sequence of probability measures with densities $p_n$ converge to q in the sense of (4). For KL divergence and $\chi ^2$ distance, we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{KL(q||p_n)}{\chi ^2(p_n||q)} = \frac{1}{2}.\end{aligned}$$

The theorem and corollary show that the KL divergence and $\chi ^2$ distance are equivalent (up to a constant) when the proposal distribution and the target distribution are getting close to each other. In practice, we cannot obtain a proposal that is arbitrarily close to the target distribution, but following the insight of the theorem and corollary, we can use the KL divergence to bound the $\chi ^2$ distance . When we consider a proposal distribution q in importance sampling, we have from (6) and (7) that

$$\begin{aligned} 2\beta _2 \kappa (\beta _2) \le \frac{\chi ^2(p||q)}{KL(q||p)}\le 2\beta _1^{-1}\kappa (\beta _1^{-1}). \end{aligned}$$

(8)

Therefore the upper and lower bounds for $\chi ^2$ distance are

$$\begin{aligned} 2\beta _2 \kappa (\beta _2)KL(q||p) \le \chi ^2(p||q) \le 2\beta _1^{-1}\kappa (\beta _1^{-1}) KL(q||p). \end{aligned}$$

(9)

Our goal is to find a proposal distribution q close to the target distribution p in terms of the $\chi ^2$ distance $\chi ^2(p||q)$. The relation in (9) indicates that the distribution q that minimizes the KL divergence KL(q||p) tends to give tighter bounds for the $\chi ^2$ distance $\chi ^2(p||q)$, and under a smaller upper bound in (9), the $\chi ^2$ distance $\chi ^2(p||q)$ tends to be small as well, which is what we hope to achieve in choosing the proposal distribution for importance sampling. Therefore, it is reasonable to use the distribution q that minimizes the KL divergence KL(q||p) as the proposal distribution. This justifies the use of VB solution as the proposal distribution for importance sampling. The upper bound in (9) can give us an intuitive way to evaluate the choice of the proposal distribution since a smaller upper bound often indicates that the corresponding proposal distribution has better performance in importance sampling. This idea is illustrated in the example in Sect. 5.1 by computing $\beta _{1}$ and $\beta _{2}$ explicitly. However, the exact values of $\beta _{1}$ and $\beta _{2}$ are hard to calculate in some complex models.

5 Numerical results

All examples in this section were coded in R and run on a MacBook Pro with 2.3 GHz Intel Core i7 processor.

5.1 Univariate normal

This toy example is on Bayesian inference for a univariate normal distribution. Suppose our observed data $\mathbf{x}= \{ x_1, \ldots , x_N\}$ is a random sample from a normal distribution with mean $\mu$ and precision $\tau$. We use the normal-gamma conjugate prior for $\mu$ and $\tau$ as follows:

$$\begin{aligned} p(\mu |\tau ) = \mathcal N (\mu _0, (\lambda _0\tau )^{-1}), \ \ \ \ p(\tau ) = \text {Gamma}(a_0, b_0).\end{aligned}$$

We consider a factorized variational approximation to the posterior distribution $q(\mu , \tau ) = q_{\mu }(\mu )q_{\tau }(\tau )$. The variational approximation algorithm gives $q_{\mu }(\mu ) \sim \mathcal N(\nu , \lambda ^{-1})$ with the mean and precision:

$$\begin{aligned} \nu = \frac{\lambda _0\mu _0+N{\bar{x}}}{\lambda _0+N} \ \ \text {and} \ \ \ \lambda =(\lambda _0+N)E[\tau ] , \end{aligned}$$

and $q_{\tau }(\tau ) \sim \text {Gamma}(a, b)$ with two parameters:

$$\begin{aligned} a = a_0+ \frac{N}{2}, \ \ b = b_0 + \frac{1}{2}E_{\mu }\left[ \sum _{i=1}^N(x_n-\mu )^2+\lambda _0(\mu -\mu _0)^2\right] . \end{aligned}$$

If we follow the updating rules and compute the expectation with the parameter values from the previous step, we can obtain the variational distribution $q(\mu ,\tau )$ as in Algorithm 4.

We set the hyperparameters $\mu _0 = 1$, $\lambda _0 = 1$, $a_0 = 1$, $b_0= 1$, and generated $N = 50$ data points from N(1, 1). For this simple example, the true posterior distribution $p(\mu ,\tau |\mathbf{x})$ can be derived as

$$\begin{aligned} p(\mu |\tau , \mathbf{x})= & {} \mathcal N\left( \frac{\lambda _0\mu _0+N\bar{x}}{\lambda _0+N}, (\lambda _0+N)^{-1} \right) , \\ p(\tau |\mathbf{x})= & {} \text {Gamma}\left( a_0+\frac{N}{2}, b_0 + \frac{1}{2} \left[ \sum _{i=1}^N(x_i-{\bar{x}})^2 + \frac{\lambda _0N(\bar{x}-\mu _0)^2}{\lambda _0+N} \right] \right) . \end{aligned}$$

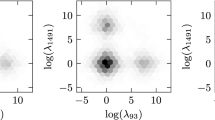
The contour plots in Fig. 1 show some resemblance between the true posterior distribution and the VB approximation.

Fig. 1

Contour plots for the true posterior and the VB approximation

We compared the performance of different methods in Table 1, including the variational Bayes method (denoted by “VB”), IS with variational distribution as the proposal (denoted by “VB as proposal”), IS with the prior as the proposal (denoted by “Prior as proposal”), and adaptive importance sampling (denoted by “AIS”) (Bugallo et al. 2017). The variational distributions are well-known standard distributions in this example, and the expectations are easy to compute. The three IS algorithms are based on $m = 100,000$ samples, and the numbers in parentheses are the standard errors. The true posterior mean is also provided (denoted by “True mean”).

Table 1 Simulation results for the univariate normal example

Table 1 shows that IS with variational distribution as proposal gives much smaller standard errors than IS with prior as the proposal and AIS. The computation time of AIS is much longer than IS with VB or prior as the proposal, since AIS needs to update the proposal distribution adaptively based on samples from previous steps, while the variational distribution and the prior are relatively easier to obtain. Using variational method directly gives a biased estimate for $\tau$ (the estimate for $\mu$ happens to be the same as the true mean), and the variability of the estimate is unknown.

Since the true posterior distribution is known in this example, we can calculate $\beta _1$ and $\beta _2$ defined in (3). The values of $\beta _1$ and $\beta _2$, which are presented in Table 2, are related to the ratio between the posterior distribution p and the proposal distribution q. They also appear in the upper and lower bounds of the $\chi ^2$ distance between p and q in (8) and (9). Since $\beta _1^{-1}$ is smaller when VB is the proposal and $\kappa (t)$ is an increasing function for $0<t<1$, that implies the upper bounds $2\beta _1^{-1}\kappa (\beta _1^{-1})$ in (8) and $2\beta _1^{-1}\kappa (\beta _1^{-1})KL(q||p)$ in (9) are smaller when VB is the proposal (note that KL(q||p) is minimized for VB proposal). Similarly, VB proposal has a larger $\beta _2$ which implies $2\beta _2 \kappa (\beta _2)$ in the lower bound in (8) and (9) is larger for the VB proposal. All these suggest that using VB as the proposal may lead to a smaller $\chi ^2$ distance and better performance.

Table 2 The values of $\beta _1^{-1}$ and $\beta _2$ for the univariate normal example

5.2 Gaussian mixture model

Suppose we have N i.i.d. observations $\mathbf{x}=\{\mathbf{x}_1, \mathbf{x}_2, \ldots , \mathbf{x}_N\}$ from a Gaussian mixture distribution, and each $\mathbf{x}_i$ is a D-dimensional vector $\mathbf{x}_i =(x_{i1}, x_{i2}, \ldots , x_{iD})^T$. Suppose there are K mixture components and $\varvec{\pi }= (\pi _1, \pi _2, \ldots , \pi _K)$ denotes the mixture proportions. The labels that indicate the membership of the observations are denoted by the latent variables $\mathbf{z}=\{\mathbf{z}_1, \mathbf{z}_2, \ldots , \mathbf{z}_N\}$, where $\mathbf{z}_i \ \sim \ \text {Multinomial}(1, \varvec{\pi })$. In other words, $\mathbf{z}_i=(z_{i1}, z_{i2}, \ldots , z_{iK})^T$ is a K-dimensional vector with one element equal to 1, which specifies the label of $\mathbf{x}_i$, and all other elements equal to 0. If the k-th element of $\mathbf{z}_i$ is 1, we write

$$\begin{aligned} \mathbf {x}_i | z _{ik} = 1 \ \sim \ \mathcal {N} (\varvec{\mu }_k, \varvec{\varLambda }^{-1}_k ), \end{aligned}$$

where $\mu _i$ and $\varvec{\varLambda }_i$ are the mean and precision matrix of each multivariate Gaussian component.

We use a symmetric Dirichlet distribution with hyperparameter $\alpha _0$ as the prior distribution for $\varvec{\pi }$:

$$\begin{aligned} p(\varvec{\pi })=\text {Dir}(\varvec{\pi }|\varvec{\alpha }_0)=C(\varvec{\alpha }_0)\prod \limits _{k=1}^K\pi _k^{\alpha _0}, \ \ \text {where} \ \varvec{\alpha }_0=(\alpha _0, \alpha _0, \ldots , \alpha _0). \end{aligned}$$

For the mean vector $\varvec{\mu }_k$ and the precision matrix $\varvec{\varLambda }_k$, we use a normal-Wishart prior distribution as the conjugate prior for these two parameters:

$$\begin{aligned}&\varvec{\varLambda }_k\sim \text {Wishart}(\varvec{W}_0, \nu _0) \ \ \Rightarrow \ \ p(\varvec{\varLambda })=\prod \limits _{k=1}^K\mathcal {W}(\varvec{\varLambda }_k|\varvec{W}_0, \nu _0),\\&\varvec{\mu }_k\sim \mathcal {N}\left( \varvec{\mu }_0,(\beta _0\varvec{\varLambda }_k)^{-1}\right) \ \ \Rightarrow \ \ p(\varvec{\mu }|\varvec{\varLambda })=\prod \limits _{k=1}^K\mathcal {N}\left( \varvec{\mu }_k|\varvec{\mu }_0,(\beta _0\varvec{\varLambda }_k)^{-1}\right) , \end{aligned}$$

where $\varvec{\varLambda }=(\varvec{\varLambda }_1,\varvec{\varLambda }_2\ldots ,\varvec{\varLambda }_K)$ and $\varvec{\mu }=(\varvec{\mu }_1,\varvec{\mu }_2,\ldots ,\varvec{\mu }_K)$. The likelihood function of the Gaussian mixture model is

$$\begin{aligned}&p(\mathbf{z}|\varvec{\pi })=\prod \limits _{i=1}^N\prod \limits _{k=1}^K\pi _k^{z_{ik}},\\&p(\mathbf {x}|\varvec{\pi }, \varvec{\mu , \varvec{\varLambda }})=\prod \limits _{i=1}^N\left( \sum \limits _{k=1}^K\pi _k \, \mathcal {N}(\mathbf {x}_i|\varvec{\mu }_k, \varvec{\varLambda }^{-1}_k )\right) .\end{aligned}$$

The posterior distribution is

$$\begin{aligned} p(\varvec{\pi }, \varvec{\mu }, \varvec{\varLambda } | \mathbf {x}) \propto p(\mathbf {x}, \varvec{\pi }, \varvec{\mu }, \varvec{\varLambda }) = p(\mathbf {x}|\varvec{\pi }, \varvec{\mu , \varvec{\varLambda }})p(\varvec{\pi })p(\varvec{\mu }|\varvec{\varLambda })p(\varvec{\varLambda }).\end{aligned}$$

For variational approximation, following Bishop (2006) we first factorize

$q(\varvec{\pi }, \varvec{\mu }, \varvec{\varLambda })$ into the following variational distribution:

$$\begin{aligned} q(\varvec{\pi }, \varvec{\mu }, \varvec{\varLambda })=q(\varvec{\pi })\prod _{k=1}^Kq(\varvec{\mu }_k, \varvec{\varLambda }_k). \end{aligned}$$

After calculating the logarithm of the optimal distribution, we get:

$$\begin{aligned}&\text {ln}\, q^*(\varvec{\pi })=(\alpha _0-1)\sum _{k=1}^K\text {ln} \, \pi _k+\sum _{i=1}^N\sum _{k=1}^Kr_{ik}\text {ln} \, \pi _k\\&\quad \Rightarrow \ \ \ \ \ q^*(\varvec{\pi })=\text {Dir}(\varvec{\pi }|\varvec{\alpha }) \ \ \ \ \ \ \ \text {where} \ \ \alpha _k=\alpha _0+N_k \ \ \text {and} \ \ N_k=\sum _{i=1}^Nr_{ik}.\end{aligned}$$

Then we further decompose the variational distribution as $q^*(\varvec{\mu }_k, \varvec{\varLambda }_k)=$

$q^*(\varvec{\mu }_k | \varvec{\varLambda }_k)q^*(\varvec{\varLambda }_k)$, and the variational joint posterior distribution of $(\varvec{\mu }_k, \varvec{\varLambda }_k)$ is also normal-Wishart distribution with different parameters from the prior distributions:

$$\begin{aligned} q^*(\varvec{\mu }_k, \varvec{\varLambda }_k)=\mathcal {N}\left( \varvec{\mu }_k|\mathbf {m}_k, (\beta _k\varvec{\varLambda }_k)^{-1}\right) \, \mathcal {W}(\varvec{\varLambda }_k|\mathbf {W}_k, \nu _k).\end{aligned}$$

If we follow the updating rules for each parameter, we can obtain the variation approximation for Gaussian mixture model as in Algorithm 5.

In the following simulation, we fix the hyperparameters $\alpha _0=1$, $\beta _0 = 5$, $\varvec{\mu }_0 = \mathbf {0}$, $\mathbf{W}_0 = \mathbf{I}_{D}$, and $\nu _0 = 5$. Tables 3, 4 and 5 show the results for different combinations of the dimension of the data D and the number of mixture components K. The variational distributions are well-known standard distributions in this example, and the expectations of all parameters are easy to compute when applying VB directly. The two IS algorithms are based on $m=10,000$ samples. The last column denotes the true parameters when we generated the observed data. The ‘True mean’ is an estimate of the true posterior mean based on 1, 000, 000 samples from importance sampling with VB approximation as the proposal.

Table 3 Simulation results for Gaussian mixture model with $D = 1$, $K = 2$, and $\alpha _0 = 1$

Table 4 Simulation results for Gaussian mixture model with $D = 1$, $K = 3$, and $\alpha _0 = 1$

Table 5 Simulation results for Gaussian mixture model with $D = 2$, $K = 2$, and $\alpha _0 = 1$

From Tables 3, 4 and 5, we can see that IS with variational distribution as proposal gives smaller standard errors than IS with prior as the proposal. In addition, using VB directly will introduce bias to the estimates.

5.3 Linear regression model

Let $\{(y_i, \mathbf {x}_i)\}_{i=1}^N$ be the observed pairs of data, where $\mathbf {x}_i \in \mathbb R ^p$. Consider the linear regression model

$$\begin{aligned} y_i=\mathbf {x}_i^T\varvec{\beta }+\epsilon _i,\end{aligned}$$

where $\varvec{\beta }\in \mathbb R^p$ and $\epsilon _i \sim N(0, \sigma ^2)$. The likelihood function is

$$\begin{aligned} \mathbf {y}|\varvec{\beta }, \sigma ^2 \sim N(\mathbf{X}\varvec{\beta }, \sigma ^2\mathbf{I}),\end{aligned}$$

where $\mathbf {y}=(y_1,y_2,\ldots ,y_N)^T$, ${\mathbf{X}}=(\mathbf {x}_1,\mathbf {x}_2,\ldots ,\mathbf {x}_N)^T$, and $\mathbf{I}$ is the identity matrix. Similar to You et al. (2014), we use inverse gamma and normal conjugate priors for $\varvec{\beta }$ and $\sigma ^2$ as follows:

$$\begin{aligned} \sigma ^2 \sim \text {Inv-Gamma}(A, B) , \ \ \varvec{\beta } \sim N(\mathbf {0}, \sigma _{\varvec{\beta }}^2\mathbf{I}),\end{aligned}$$

where $A, B, \sigma _{\varvec{\beta }}^2$ are hyperparameters.

Let $\mathbf{z}$ be all parameters of interests, i.e., $\mathbf{z}=[\varvec{\beta }^T, \sigma ^2]^T$. We consider a factorized variational approximation $q^*(\mathbf{z})=q^*_{\varvec{\beta }}(\varvec{\beta })q^*_{\sigma ^2}(\sigma ^2)$. Since we chose the conjugate priors for $\mathbf{z}$, the variational distributions can be written as:

$$\begin{aligned} q^*_{\varvec{\beta }}(\varvec{\beta }) \sim N(\varvec{\mu }_{q(\varvec{\beta })}, \varvec{\varSigma }_{q(\varvec{\beta })}), \ \ q^*_{\sigma ^2}(\sigma ^2) \sim \text {Inv-Gamma}\left( A+n/2, B_{q(\sigma ^2)}\right) . \end{aligned}$$

By solving the optimization problem iteratively, we can obtain the updating rules of all the parameters, as well as the corresponding variational algorithm in Algorithm 6.

In the simulation, we generated $N=50$ data pairs from the following true model

$$\begin{aligned} y=3+0\cdot x_1-3x_2+5x_3+\epsilon \ \ , \ \ \epsilon \sim N(0,\sigma ^2),\end{aligned}$$

where $x_1$ has no influence on the response variable y. We fix the hyperparameters $\sigma _{\varvec{\beta }} = 2$, $A = 2$, and $B = 5$. The variational distribution obtained from Algorithm 6 is used to estimate the parameters directly and also as the proposal for IS. The two IS algorithms with different proposals are both based on $m=10,000$ samples. The ‘True mean’ is an estimate of the true posterior mean based on 1, 000, 000 samples from IS with VB approximation as the proposal.

Table 6 Simulation results for linear regression model

Table 6 shows that IS with variational distribution as proposal gives smaller standard errors than IS with prior as the proposal. Using variational method directly gives a biased estimate and variability of the estimate is unknown. For example, using VB directly gives an estimate of $-0.096$ for $\beta _1$ without quantification of the uncertainty of the estimate, so it is hard to tell whether the true value of $\beta _1$ is 0. On the other hand, the $95\%$ confidence interval of the estimates based on both IS algorithms contain 0, which indicates that $\beta _1$ is not significant in the linear model.

5.4 Hidden Markov model

The hidden Markov model (HMM) consists of a Markov chain with hidden states $\mathbf{z}=\{z_0, z_1, z_2, \ldots , z_T\}$ and an observed sequence of data $\mathbf{x}=\{x_1, x_2, \ldots , x_T\}$, where $z_0$ is the initial state, and T is the length of the sequence. The hidden states evolve according to

$$\begin{aligned} Z_t|(Z_{t-1}=z_{t-1}) \sim f(z_t|z_{t-1}),\end{aligned}$$

and the dependence between the observed data and hidden state can be represented as

$$\begin{aligned} X_t|(Z_{t}=z_{t}) \sim g(x_t|z_{t}).\end{aligned}$$

Given the observed data, the posterior distribution of the hidden states can be written as:

$$\begin{aligned} p(\mathbf{z}_{0:T}|\mathbf{x}_{1:T})=\frac{p(\mathbf{z}_{0:T}, \mathbf{x}_{1:T})}{p(\mathbf{x}_{1:T})} \propto p(\mathbf{z}_{0:T}) p(\mathbf{x}_{1:T}|\mathbf{z}_{0:T}), \end{aligned}$$

where

$$\begin{aligned} p(\mathbf{z}_{0:T}) = f(z_0)\prod _{t=1}^Tf(z_t|z_{t-1})\ \ \ \text{ and }\ \ \ p(\mathbf{x}_{1:T}|\mathbf{z}_{0:T})=\prod _{t=1}^Tg(x_t|z_t).\end{aligned}$$

We consider the filtering problem, which is to infer $\mathbf{z}_{1:t}$ from the observations $\mathbf{x}_{1:t}$, $t=1,\ldots ,T$. When applying SIS to the filtering problem, the naive choice of the proposal distribution is to sample $z_t$ from $f(z_t|z_{t-1})$. However, this proposal is not very efficient because it does not take into account the information contained in the observations.

The two variational approximations in Sect. 3.1, VB-SIS1 and VB-SIS2, can be used to construct better proposals for SIS. The corresponding algorithm is the same as Algorithms 2 and 3, and the weight updating step for HMM can be written explicitly as

$$\begin{aligned} w_t(\mathbf{z}_{1:t}^{(i)})= & {} w_{t-1}(\mathbf{z}_{1:t-1}^{(i)})\frac{p(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})}{p(\mathbf{z}_{1:t-1}|\mathbf{x}_{1:t-1})q_{tt}(z_t^{(i)})} \\= & {} w_{t-1}(\mathbf{z}_{1:t-1}^{(i)})\frac{g(x_t|z_t^{(i)})f(z_t^{(i)}|z_{t-1}^{(i)})}{q_{tt}(z_t^{(i)})}, \end{aligned}$$

or

$$\begin{aligned} w_t(\mathbf{z}_{1:t}^{(i)})= & {} w_{t-1}(\mathbf{z}_{1:t-1}^{(i)})\frac{p(\mathbf{z}_{1:t}|\mathbf{x}_{1:t})}{p(\mathbf{z}_{1:t-1}|\mathbf{x}_{1:t-1})\tilde{q}_t(z_t^{(i)})} \\= & {} w_{t-1}(\mathbf{z}_{1:t-1}^{(i)})\frac{g(x_t|z_t^{(i)})f(z_t^{(i)}|z_{t-1}^{(i)})}{\tilde{q}_t(z_t^{(i)})}. \end{aligned}$$

We study two examples below, one is a discrete HMM and the other one is a continuous HMM.

5.4.1 Discrete hidden Markov model

In the discrete HMM example, assume $z_t \in \{1, \ldots ,K\}$ and $x_t\in \{1, \ldots , W\}$. Then the model can be specified by two matrices: transition matrix $\mathbf {A}_{K\times K}$ and emission matrix $\mathbf {B}_{K\times W}$, where $A_{ij}$ denotes the probability of transitioning from state i to state j and $B_{kw}$ denotes the probability of emitting observation w from state k. We propose the variational approximation similar to Wang and Blunsom (2013).

In the simulation study, we set $z_0 = 1$, $K = 3$ and $W = 4$, i.e., $z_t \in \{1,2,3\}$ and $x_t \in \{1,2,3,4\}$. The transition and emission matrices are chosen to be:

$$\begin{aligned} A = \left[ \begin{array}{ccc} 0.1&{}0.4&{}0.5 \\ 0.4 &{} 0.2 &{} 0.4 \\ 0.6&{}0.2&{}0.2 \end{array} \right] \ , \ B = \left[ \begin{array}{cccc} 0.3&{}0.3&{}0.3&{}0.1 \\ 0.4 &{} 0.1 &{} 0.2&{}0.3 \\ 0.1&{}0.6&{}0.2&{}0.1 \end{array} \right] . \end{aligned}$$

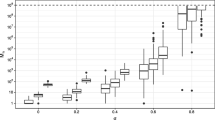
We considered different combinations of the length of the sequence T, the number of samples m, and the tuning parameter $\varDelta$. The results are presented in Tables 7 and 8 and Fig. 2.

Table 7 Simulation results for discrete HMM with $\varDelta = 7$, $T = 50$, and varying sample size m

Table 8 Simulation results for discrete HMM with $m=5000$ and varying length of sequence T

Fig. 2

$cv^2$ for variational SIS for discrete HMM with $m = 5000$, $T = 30$, and varying tuning parameter $\varDelta$

From Table 7, we can see that if we fix $\varDelta$ and the length of sequence T, the $cv^2$ for each method will not change much when we increase the number of samples m. Table 8 shows that if we fix m, then T will influence both $cv^2$ and the computation time a lot. In general, using the state evolution $f(z_t|z_{t-1})$ takes less time, but the $cv^2$ is large. VB-SIS1 gives the smallest $cv^2$, but the computation time is the longest. The performance of VB-SIS2 is somewhere between the other two methods. Note that after the data are generated, we only need to compute the variational approximation once, so this time-consuming step will not be influenced by the sample size m. Figure 2 shows how the $cv^2$ of importance sampling changes with the value of $\varDelta$. The horizontal dashed line is the $cv^2$ when the state evolution $f(z_t|z_{t-1})$ is used as the proposal, and it can serve as a benchmark.

5.4.2 Stochastic volatility model

The stochastic volatility model consists of the following state equation and observation equation:

$$\begin{aligned} Z_t = \alpha Z_{t-1} + \sigma V_t, \ \ \ X_t=\beta \exp (Z_t/2)W_t, \end{aligned}$$

where $V_t \overset{\text {i.i.d}}{\sim } \mathcal N(0, 1)$, $W_t \overset{\text {i.i.d}}{\sim } \mathcal N(0, 1)$, and both the hidden state $Z_t$ and the observation $X_t$ are continuous real-valued random variables.

In the simulation study, the initial state $Z_0 \sim \mathcal N(0, \sigma ^2/(1-\alpha ^2))$, and we set $\alpha = 0.3$, $\sigma = 5$ and $\beta = 2$. In this case, the variational distributions $\{q_t(z_t)\}_{t=1}^T$ also follow the normal distribution. We considered different combinations of the length of the sequence T, the number of samples m, and the tuning parameter $\varDelta$. The results are in Tables 9 and 10.

From Table 9, we can see that if we fix $\varDelta$ and the length of sequence T, the $cv^2$ for each method will not change much when we increase the number of samples m. Table 10 shows that if we increase the length of the observed sequence T, then the $cv^2$ increases for all proposal distributions we tested. Tables 9 and 10 indicate that using the state evolution $f(z_t|z_{t-1})$ as the proposal distribution takes less time, but the $cv^2$ is relatively large. VB-SIS1 gives the smallest $cv^2$, but the computation time is the longest. The performance of VB-SIS2 is somewhere between the other two methods. If we fix the running time, VB-SIS2 has a larger effective sample size than VB-SIS1.

Table 9 Simulation results for stochastic volatility model with $\varDelta = 7$, $T = 50$, and varying sample size m

Table 10 Simulation results for stochastic volatility model with $m=5000$ and varying length of the sequence T

5.5 Dirichlet process

The last example is a Dirichlet process (DP) mixture model widely used in Bayesian inference. Dirichlet Process can be written as $G \sim \text {DP}(\alpha , G_0)$, where $G_0$ is the base distribution of this stochastic process, and $\alpha$ is a positive scalar parameter. In addition, G and $G_0$ should have the same support, but G is a discrete distribution with countably infinite number of point masses. Given the previous $n-1$ observations, we generate the next one as follows:

$$\begin{aligned} X_n|X_1, \ldots , X_{n-1} = {\left\{ \begin{array}{ll} X_i &{} \text {w.p. } \frac{1}{n-1+\alpha } \ \ (i = 1,\ldots , n-1),\\ \text {a new draw from } G_0 &{} \text {w.p. } \frac{\alpha }{n-1+\alpha }, \end{array}\right. } \end{aligned}$$

where w.p. means “with probability”. Let K be the unique values among $\{X_1,\ldots , X_{n-1} \}$, denoted by $\{X_k^*\}_{k=1}^K$, and we can rewrite the sampling procedure as

$$\begin{aligned} X_n|X_1, \ldots , X_{n-1} = {\left\{ \begin{array}{ll} X_k^* &{} \text {w.p. } \frac{\text {num}_{n-1}(X_k^*)}{n-1+\alpha } \ \ (k = 1,\ldots , K),\\ \text {a new draw from } G_0 &{} \text {w.p. } \frac{\alpha }{n-1+\alpha }, \end{array}\right. }\end{aligned}$$

where $\text {num}_{n-1}(X_k^*)$ is the number of $X_k^*$ in the set $\{X_1,\ldots ,X_{n-1}\}$. Then, the joint density function can be written as

$$\begin{aligned} P(X_1, \ldots , X_N)= & {} P(X_1)P(X_2|X_1)\cdots P(X_N|X_1, \ldots , X_{N-1}) \\= & {} \frac{\alpha ^k\prod _{k=1}^K(\text {num}_N(X_k^*) - 1)!}{\alpha (1+\alpha )\cdots (N-1+\alpha )}\prod _{k=1}^KG_0(X_K^*), \end{aligned}$$

which does not depend on the order of variables.

Dirichlet process can also be treated as a stick breaking process. We first draw $V_1, V_2, \ldots \sim \text {Beta}(1, \alpha )$, then generate $X_1^*, X_2^*, \ldots \sim G_0$. A multinomial distribution can be derived as

$$\begin{aligned} \pi _i(\mathbf{v} )=v_i\prod \limits _{j=1}^{i-1}(1-v_j).\end{aligned}$$

The Dirichlet process G is a discrete distribution with $P(G=X_i^*)=\pi _i(\mathbf{v} )$, and it can be written as $G=\sum _{i=1}^\infty \pi _i(\mathbf{v})\delta _{X_i^*}$, where $\delta _x$ is the Dirac measure at point x. In Dirichlet process mixture model, data come from a mixture of an infinite number of distributions. If we have N observed data points $\{x_i\}_{i=1}^N$, they will be generated from at most N different components. The following is the generating procedure of DP mixture model.

• $V_1, V_2, \ldots \sim \text {Beta}(1, \alpha )$

• $\pi _i(\mathbf{v} )=v_i\prod \limits _{j=1}^{i-1}(1-v_j)$

• $y_i \sim \text {Multinomial} (\pi )$

• $\eta _k \sim G_0$

• $X_i|y_i, \varvec{\eta }\sim p(x_i|\eta _{y_i})$

Given the latent variable $z_i$, we assume the observation $x_i$ follows a distribution from an exponential family with the likelihood function $p(x_i|\eta _{y_i})$.

Following Blei and Jordan (2006) and Hughes and Sudderth (2013), let $\mathbf{Z}= \{\mathbf{V }, \varvec{\eta }, {\mathbf {Y}}\}$ be all latent variables and $\theta =\{\alpha \}$ be the hyper parameter. Since the number of different components is infinite, we introduce a truncated level T as an upper bound of the number of clusters, that is, mixture proportions $\pi _t(\mathbf{v})=0$ for $t>T$. Then we can factorize the posterior distribution and obtain the following variational decomposition:

$$\begin{aligned} q(\mathbf{v} , \varvec{\eta }, \mathbf{y}) = \prod _{t=1}^{T-1}q_{1,t}(v_t)\prod _{t=1}^{T}q_{2,t}(\eta _t)\prod _{n=1}^{N}q_{3,n}(y_n),\end{aligned}$$

where $q_{1,t}(v_t)$ are beta distributions, $q_{2,t}(\eta _t)$ are exponential family distributions, and $q_{3,n}(y_n)$ are multinomial distributions. We can use the coordinate ascent algorithm to solve the optimization problem. A general rule to choose the truncated level T is to be close to the theoretical value of the expected number of clusters, given N observations:

$$\begin{aligned} E \ [\text {number of clusters}|x_1, \ldots , x_N] = \sum _{i=1}^N\frac{\alpha }{\alpha +i-1} = \alpha (\psi (\alpha + N) - \psi (\alpha )),\end{aligned}$$

where $\psi (\cdot )$ is the digamma function.

We generated $N= 50$ observed data from DP mixture model, and implemented IS with different proposal distributions based on $m=1,000$ samples. We considered different combinations of the hyper parameters $(\alpha , T)$. Since the number of parameters is large, we only reported the $cv^2$ and the average of the ratios of the standard errors of the parameter estimates from different methods.

Table 11 Simulation results for Dirichlet process mixture models

From the results in Table 11, we can see that IS with variational distribution as proposal gives smaller $cv^2$ than IS with prior as the proposal. The average of the ratios of the standard errors is greater than 1 in all settings, which means using VB as the proposal usually gives smaller standard errors than using the naive proposal. This average ratio becomes larger when the truncated level T is close to the theoretical expectation of the number of clusters (4.49 for $\alpha =1$ and 9.11 for $\alpha =3$).

6 Discussion

In this paper, we combine variational approximation and IS to improve the performance of both methods. Using variational approximation as the proposal distribution of IS can avoid the biased estimate and the lack of uncertainty quantification of the VB estimate. It also provides a way to design a good proposal for IS. We provide theoretical justification of the proposed methods, and numerical results also show that using variational approximation as the proposal can enhance the performance of IS and SIS.

Using VB as proposal for IS tends to be computationally more expensive than some naive choice of the proposal. This is mainly due to the computational cost for finding the VB solution. Sometimes it might be worthwhile to stop the VB algorithm a little early to obtain a rough approximation and allow more time for IS to correct the bias. The tradeoff between VB-SIS1 and VB-SIS2 also illustrates this point.

There are several possible directions for future research in this area. One topic is to further improve the efficiency and performance of the algorithm, especially for models involving HMM and Dirichlet process. For example, the tuning parameter $\varDelta$ plays an important role in the proposed VB-SIS algorithm for HMM. It is of interest to develop theory or find an analytic expression for the optimal $\varDelta$. Another direction is to consider other variational approximations beyond mean-field variational approximation, which may lead to good proposals for importance sampling. Applying the proposed method in more complex models or real data examples is valuable as well.

Appendices

Appendices

Proof of Lemma 1

Proof

We have $\lim _{n\rightarrow \infty } \beta _{2,n} = 1$ immediately from the definition of convergence in (4).

Now we prove $\lim _{n\rightarrow \infty } \beta _{1,n} = 1$. For $\forall \ \epsilon > 0$ and $\delta > 0$, define $I_1^{(n)} = \{x:\frac{p_n(x)}{q(x)}< 1-\epsilon \}$, $I_2^{(n)} = \{x:1-\epsilon \le \frac{p_n(x)}{q(x)}< 1+\delta \}$, and $I_3^{(n)} = \{x:\frac{p_n(x)}{q(x)}\ge 1+\delta \}$.

From (4), we have for any given $\epsilon >0$, there exists $N\in \mathbb N$ such that for all $n>N$, we have

$$\begin{aligned} \text {ess}\inf \,\frac{p_n}{q} > 1-\epsilon .\end{aligned}$$

By the definition of essential infimum, we have

$$\begin{aligned} \sup \{b \in \mathbb R: \mu (\{x: p_n(x)/q(x) < b \}) = 0 \} > 1-\epsilon , \end{aligned}$$

which implies

$$\begin{aligned} \mu (I_1^{(n)})=\mu (\{x: p_n(x)/q(x) < 1-\epsilon \}) = 0. \end{aligned}$$

Then we have

$$\begin{aligned} \int _{I_1^{(n)}}\frac{p_n}{q}\,q\,dx = \int _{I_1^{(n)}}p_n\,dx =0 \ \ \ \text{ for } n > N.\end{aligned}$$

So

$$\begin{aligned} 1 = \int _{\mathbb {R}} p_n \,dx= & {} \int _{I_1^{(n)}}\frac{p_n}{q}\,q\,dx + \int _{I_2^{(n)}}\frac{p_n}{q}\,q\,dx + \int _{I_3^{(n)}}\frac{p_n}{q}\,q\,dx \\= & {} \int _{I_2^{(n)}}\frac{p_n}{q}\,q\,dx + \int _{I_3^{(n)}}\frac{p_n}{q}\,q\,dx \ \ \ \ \ \text{ for } n > N. \end{aligned}$$

From the definitions of $I_2^{(n)}$ and $I_3^{(n)}$, we have

$$\begin{aligned} 1= & {} \int _{I_2^{(n)}}\frac{p_n}{q}\,q\,dx + \int _{I_3^{(n)}}\frac{p_n}{q}\,q\,dx \nonumber \\\ge & {} (1-\epsilon )\int _{I_2^{(n)}}\,q\,dx + (1+\delta )\int _{I_3^{(n)}}\,q\,dx \ \ \ \ \text{ for } n > N. \end{aligned}$$

(10)

Similarly, we also have

$$\begin{aligned} 1=\int _{\mathbb {R}} q \,dx= & {} \int _{I_1^{(n)}}q\,dx + \int _{I_2^{(n)}}q\,dx + \int _{I_3^{(n)}}q\,dx \nonumber \\= & {} \int _{I_2^{(n)}}q\,dx + \int _{I_3^{(n)}}q\,dx \ \ \ \ \text{ for } n > N. \end{aligned}$$

(11)

From (10) and (11), the following inequality holds:

$$\begin{aligned} 1\ge & {} (1-\epsilon )\int _{I_2^{(n)}}\,q\,dx + (1+\delta )\left( 1-\int _{I_2^{(n)}}\,q\,dx\right) \nonumber \\= & {} (1+\delta ) - (\epsilon +\delta ) \int _{I_2^{(n)}}\,q\,dx \ \ \ \ \text{ for } n > N. \end{aligned}$$

(12)

Suppose $\limsup \limits _{n \rightarrow \infty }\int _{I_2^{(n)}}\,q\,dx = \theta (\epsilon , \delta ) \in [0,1]$, then $\liminf \limits _{n \rightarrow \infty }\int _{I_3^{(n)}}\,q\,dx = 1-\theta (\epsilon , \delta )$ based on (11). Since the definition of $I_3^{(n)}$ depends only on $\delta$, not $\epsilon$, we know that $\liminf \limits _{n \rightarrow \infty }\int _{I_3^{(n)}}\,q\,dx$ also depends only on $\delta$, not $\epsilon$. Thus $\theta (\epsilon , \delta ) = \theta (\delta )$ does not depend on $\epsilon$.

Taking limit inferior on both sides of (12), we have

$$\begin{aligned} 1\ge & {} (1+\delta ) -\limsup \limits _{n \rightarrow \infty }\left( (\epsilon +\delta ) \int _{I_2^{(n)}}\,q\,dx \right) = (1+\delta ) - (\epsilon +\delta )\theta (\delta ). \end{aligned}$$

(13)

Therefore,

$$\begin{aligned} \theta (\delta ) \ge \frac{\delta }{\delta +\epsilon }. \end{aligned}$$

(14)

Note that (14) is true for any $\epsilon > 0$ and $\delta > 0$ selected at the beginning of the proof. Since the left hand side of (14) does not depend on $\epsilon$, letting $\epsilon \rightarrow 0$ on the right hand side of (14), we have $\theta (\delta ) \ge 1$. On the other hand, $\limsup \limits _{n \rightarrow \infty }\int _{I_2^{(n)}}\,q\,dx = \theta (\delta ) \in [0,1]$. Therefore we have $\theta (\delta )=1$, which implies $\liminf \limits _{n \rightarrow \infty }\int _{I_3^{(n)}}\,q\,dx =1-\theta (\delta )= 0$ for any $\delta >0$. From the definition of $\beta _{1,n}$, we have $\lim _{n\rightarrow \infty } \beta _{1,n} = 1$.

Since $\mu (\{x: p_n(x)/q(x) < \beta _{2,n} \}) = \mu (\{x: p_n(x)/q(x) > \beta _{1,n}^{-1} \}) =0$, we have

$$\begin{aligned} D_f(p_n||q) = \int _{\{\beta _{2,n}\le \frac{p_n}{q}\le \beta _{1,n}^{-1}\}} f\left( \frac{p_n}{q}\right) \,q\,dx \le \sup _{\beta _{2,n}\le \beta \le \beta _{1,n}^{-1}}|f(\beta )|.\end{aligned}$$

Letting $n\rightarrow \infty$, due to the continuity of f at 1, we have $\lim _{n\rightarrow \infty } D_f(p_n||q) \le f(1) = 0$. $\square$

Proof of Theorem 1

Proof

From Lemma 1, we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \beta _{1,n} =\lim _{n\rightarrow \infty } \beta _{2,n}= 1. \end{aligned}$$

By L’Hospital’s rule, we have $\lim _{t \rightarrow 1}\kappa (t) = 1$, where $\kappa (t)$ is defined in (5). Therefore, take limit on the both sides of (6) and (7), we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{KL(p_n||q)}{KL(q||p_n)} = 1 \ , \ \ \lim _{n\rightarrow \infty } \frac{KL(p_n||q)}{\chi ^2(p_n||q)} = \frac{1}{2} .\end{aligned}$$

$\square$