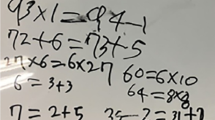Introduction

Profound knowledge in algebra is important for higher studies in mathematics (e.g. Brandell, Hemmi & Thunberg, 2008; Hemmi, Bråting, Liljekvist, Prytz, Madej, Pejlare & Palm Kaplan, 2018). This emphasizes the importance of research on mathematics education in general, and specifically on the teaching and learning of algebra. In recent years, research has shown that it is possible to teach algebra already in earlier grades by, for example, using mathematical relations and patterns to develop algebraic thinking (Kieran, Pang, Schifter, & Fong Ng, 2016). In Sweden, which is the context of this study, algebra has always been problematic for students. In international evaluations, such as the TIMSS,1 Swedish students’ results in algebra have been below average since the 1960s (Murray & Liljefors, 1983; Swedish National Agency of Education, 2008, 2012, 2016a). Even in 1995, when Swedish students performed the best ever on the TIMSS, their results in algebra remained poor (Hemmi et al. 2019). In recent decades, several efforts have been made in Sweden to improve students’ algebraic knowledge. Inspired by the early algebra movement, Sweden has revised its national curriculum and today algebra is introduced already in Grade 1 with, for example, the importance of the equal sign forming part of the core content in Grades 1–3 (Swedish National Agency of Education, 2018). Furthermore, in-service programs for teachers have been implemented and since the 1990s there has been a strong emphasis on the “Algebra for all” movement, ensuring that all students have the opportunity to study algebra (Hemmi, Bråting, & Lepik, 2020). A specific algebra textbook adapted to teacher education (Bergsten, Häggström, & Lindberg, 1997) was published in the 1990s, and has been used at several universities. The aim of the textbook was to make algebra available to all, that is, all mathematics teachers and all students (Bergsten et al., 1997). In this textbook, algebra is described by using Usiskin’s (1988) four aspects of algebra and Linchevski’s (1995) definition of pre-algebra. Hence, early algebra and algebraic thinking is part of “Algebra for all,” but it also includes traditional algebraic content like formal equation solving. Recently, a new version of the textbook was published (Häggström, Kilhamn, & Fredriksson, 2019). However, we have not yet seen any improvements to Swedish students’ algebraic skills, at least if we consider the results of the TIMSS evaluations.

Possible causes for the lack of improvements among Swedish students are studied in an ongoing research project in which Swedish school algebra is characterized, by analyzing steering documents and textbooks and by conducting focus group interviews with teachers (Bråting, Madej & Hemmi, 2018). As part of this research project, Hemmi et al. (2018) found that Swedish textbooks are rich in tasks using equalities, for example, open number sentences (e.g. 3 + 5 = _ + 2) in Grades 1–3 and equations and expressions in Grades 4–6. Knowledge about the equal sign has been emphasized as important for learning algebra by several researchers (Cai et al., 2005; Carraher & Schliemann, 2007; Kieran, 1981; Li, Ding, Capraro, & Capraro, 2008; Prediger, 2010), and it has also been shown to be a very important factor in predicting algebraic thinking skills (Matthews & Fuchs, 2020). Whether one solves an equation, uses a formula, or manipulates an algebraic expression, the meaning of the equal sign is present. Even though the equal sign can be interpreted in different ways, for example, as operational, relational, or a specification (Prediger, 2010), its mathematical definition is “a relationship between two mathematical expressions representing the same object” (Kiselman & Mouwitz, 2008). In Swedish textbooks for Grades 1–3, it is common to define the equal sign by stating that it means the same amount (e.g. Brorson, 2019). The present study deepens the results found by Hemmi et al. (2018) by looking at students’ knowledge of the equal sign in Grades 3 and 6, thereby contributing to the field of early algebra research.

It is important to note that early algebra is not about simply moving “algebra-as-most-of-us-were-taught-it in secondary school to earlier grades” (Carraher, Schliemann, & Schwartz, 2008, p. 235). Instead, it can be seen as a way to approach algebraic thinking earlier. As an example of what early algebra can entail, we call attention to the so-called Big Ideas, within which algebraic thinking can be developed early (Blanton et al., 2015). These ideas comprise EEEI (equivalence, expressions, equations, and inequalities); GA (generalized arithmetic); FT (functional thinking); VAR (variables); and PR (proportional reasoning) (Blanton et al., 2015). The present study, which focuses on how students use and describe the equal sign, is connected to two of the Big Ideas: EEEI and GA.

From the definition of the equal sign, it is clear that it describes a relation. Despite this, however, students might not acknowledge the relational structure but instead see it as a symbol for giving the answer to a problem or the result of an operation. This has been described as early as the 1930s (Renvick, 1932) and in different countries all over the world (see for example Kieran, 1981; Pang & Kim, 2018; Theis, 2005; Vermeulen & Meyer, 2017; Vincent, Bardini, Pierce, & Pearn, 2015), but we lack research on this topic in the Nordic countries. In fact, as far as we know, there are no peer-reviewed articles on this matter in the Swedish context to date. This motivates our first research question:

  • RQ1: How do Swedish students describe and use the equal sign?

Additionally, Sweden has a long tradition of a school system with high equity (Yang Hansen, Gustafsson, & Rosén, 2014), but recent studies show that the educational inequalities between Swedish schools are increasing (Kornhall & Bender, 2018; Yang Hansen & Gustafsson, 2019). Furthermore, the educational inequalities between Swedish schools are relatively high in an international perspective (UNICEF, 2018), and one factor that influences a student’s results is his or her parents’ educational level (UNICEF, 2018; Yang Hansen & Gustafsson, 2016). Furthermore, Kornhall and Bender (2018) describe that these educational inequalities between Swedish schools hold true even when looking at the teachers’ backgrounds. Teachers with less experience and lower education tend to teach at schools with students with lower socioeconomic backgrounds (Kornhall & Bender, 2018). We select our cases by choosing schools between which the educational levels of the students’ parents differ. This motivates our second research question:

  • RQ2: What differences can be seen in students’ knowledge level of the equal sign depending on which school they attend?

Finally, in our study, we will take advantage of the research from other countries. More specifically, Matthews, Rittle-Johnson, McEldoon, and Taylor (2012) developed an assessment form that can be used to classify students’ level of knowledge of the equal sign. Pang and Kim (2018) then used this assessment form in a South Korean study. Using the same form, we not only obtain results from our multiple cases but also have the opportunity to compare these results with those in the South Korean case. In doing so, we have the opportunity to compare the results in our study with those in a study from one of the countries that performs the best on the TIMSS (Mullis, Martin, Foy, & Hooper, 2016) and PISA (Schleicher, 2019). This leads us to our third and final research question:

  • RQ3: What are the similarities and/or differences between the Swedish and the South Korean case?

Theory and Relevant Research

From a historical point of view, the symbol “=” was invented by Robert Recorde in 1557 as a way to avoid writing the same words over and over again (see for example Lipscombe, 2012; Sandford, 1957; Vincent et al., 2015). In his work, Recorde uses the equal sign when solving equations and, for example, pointing out that, if one adds or removes equal amounts from expressions/quantities that are equal, then the new quantities are also equal (Recorde, 1557). This shows that already when Recorde invented the equal sign it was used to mark a relation. But as mentioned earlier, despite this strict definition, it is not uncommon for the equal sign to be perceived as a symbol for the result of an operation. Sfard (1991) describes the dual nature of mathematical conceptions using the terminology of operational and structural conceptions. An operational conception means that a process, or the product of a process, is identified with a mathematical entity, while a structural conception implies that the entity is conceived as a static structure. When looking at how students perceive the equal sign—as a mathematical entity—we benefit from this perspective. We will now compare Sfard’s (1991) terminology with that used by Blanton et al. (2015), Matthews et al. (2012), and Pang and Kim (2018), which is shown in Table 1.

Table 1 Comparing the terminology in Sfard (1991), Blanton et al. (2015), Matthews et al. (2012), and Pang and Kim (2018)
Full size table

Blanton et al. (2015) use almost the same terminology as Sfard (1991) when classifying students’ responses based on which strategy they use. According to Blanton et al. (2015), a structural strategy means using the inherent structure given by the definition of the equal sign in the equation, for example, determining equivalence without computing. For example, given 7 + 3 = _ + 4, a student realizes that if we move one from the 7 to the 3, we now have 6 and 4. Therefore, the missing number is 6. On the other hand, an operational strategy uses the equal sign as an indicator of a result (which can be viewed as an operational conception). In the previous example, the student might write 10 or 14 as the missing number, since 7 + 3 = 10 and 7 + 3 + 4 = 14. Here, the student reasons that the answer should be written after the equal sign, which implies that he or she is showing an operational conception of the equal sign. In addition to the terminology “structural and operational,” Blanton et al. (2015) also use “computational strategy.” Here, a computational strategy means that a student calculates the value on both sides of the equality/equation to compare whether the sides are equal. Hence, the student shows a structural understanding of the equal sign, even if he or she still computes the values. We can therefore argue that both a structural strategy and a computational strategy can be viewed as the student showing a structural conception of the equal sign, according to Sfard (1991).

Matthews et al. (2012) define a relational interpretation of the equal sign as an understanding that it is a symbol for sameness on both sides of it. That is, expressions or quantities on the different sides of the sign might look different, but represent the same quantity. With this interpretation, one uses the inherent structure of the equal sign. In this sense, Matthews et al.’s (2012) relational interpretation is closely connected to Sfard’s (1991) structural conception. Furthermore, Matthews et al.’s (2012) use of the term operational is consistent with how Sfard (1991) and Blanton et al. (2015) use the word. Matthews et al. (2012) have also created subcategories for both relational and operational interpretations, and use these categories when analyzing students’ level of understanding of the equal sign, with the highest knowledge level being the comparative relational level. This level is related to the structural strategy described by Blanton et al. (2015). For example, a student with this level of knowledge compares the two sides of the equal sign and uses the fact that transformations, like “moving one from the 7 to the 3” when solving 7 + 3 = _ + 4, preserve the equality. A student with knowledge on the basic relational level still recognizes the correct definition of the equal sign—i.e., that it is a relation and not an operation—but does not use this inherent structure that gives rise to the possibility to use compensatory strategies or transformations. When it comes to the two subcategories of flexible and rigid operational, they both, using the terminology of Sfard (1991), describe an operational conception of the equal sign. When it comes to the two subcategories of flexible and rigid operational, they both, using the terminology of Sfard (1991), describe an operational conception of the equal sign. The flexible operational knowledge level includes all types of equation structures compatible with an operational view of the equal sign. This includes equations with operations on the right side of the equal sign or no operations (a = a), whereas the rigid operational knowledge level can be described as that the student only is successful with equations of the type “operations-equal-answer” (Matthews et al., 2012), that is, operations on the left side of the equal sign. Note that flexible operational means that it is possible for students to maintain the pattern of “operations-equal-answer” by reading the operation backwards. Both flexible and rigid operational mean that the student uses what Blanton et al. (2015) calls an operational strategy.

In a study by Pang and Kim (2018), which builds upon Matthews et al. (2012), the authors use relational and computational thinking to describe the students’ different solutions. Here, relational thinking requires the student to use the algebraic structure of arithmetic, which includes the inherent structure of the equal sign, when presenting the solution (Pang & Kim, 2018, pp. 146–148). This is viewed as knowledge on a comparative relational level, according to Matthews et al. (2012). Furthermore, Blanton et al. (2015) would describe this kind of solution as using a structural strategy. If the student uses computations, no matter how they use the equal sign, Pang and Kim (2018) see this as computational thinking.

In our study, we will focus on the relational aspect of the equal sign. Hence, students’ operational (mis)conception of the equal sign is not our primary focus and we will therefore not do as Matthews et al. (2012) do and divide the operational interpretation of the equal sign into two knowledge levels. Instead, we use the broader term operational from Blanton et al. (2015). Since we want to look more closely at the students’ relational view of the equal sign, we follow Matthews et al. (2012) and use the terminologies comparative relational and basic relational.

In the study by Pang and Kim (2018), 695 students in Grades 2–6 solved 27 assessment items involving the equal sign, including tasks with expressions and equations. In the study, Pang and Kim found a significant difference among grades, except between the two highest grades, implying that the students’ understanding of the equal sign increases until Grade 5. For the students in their study, the most challenging task was an item requiring them to state whether or not “the equal sign means the answer to the problem” is a good definition. Depending on the grade, between 15.4% (students in Grade 6) and 27.1% (Grade 5) of the South Korean students answered correctly that this is not a good definition. Here, it is interesting that the lowest success rate was among the students in Grade 6. This can be compared with between 53.4% (Grade 2) and 97.1% (Grade 6) answering that “the equal sign means the same as” is a good definition. These results show that even though more students in higher grades know that the equal sign means “the same as.” they simultaneously view it as a marker for “the answer to the problem.”

In Sweden, ,Hemmi et al. (2018) classified the algebraic content in textbooks and in the Swedish national mathematics curriculum using the Big Ideas of algebra (Blanton et al., 2015). The study showed that the Big Idea of GA is almost non-existent in textbooks as well as in the curriculum document. On the other hand, EEEI, including the relational structure of the equal sign, is well represented in both the curriculum document and the textbooks (Hemmi et al. 2018). The relational property of the equal sign is a core aspect when it comes to representing and reasoning about equations, including solving equations. Building upon this relational structure, one can reason about the structure of the expressions involved in an equality, inequality, or equation and not only look at the expressions’ computational value. As mentioned earlier, open number sentences are dominant in Swedish textbooks for Grades 1–3 (Hemmi et al. 2018). Open number sentences such as 8 + 5 = _ + 4 can be used to reason about the structure of the expressions, but in Sweden these open number sentences become open-equation tasks since students are supposed to find the unknown number and since the structure of the equality is not mentioned (Hemmi et al. 2018). If we instead use the structure of the open number sentence 8 + 5 = _ + 4, we move one from 5 to 8 on the left side of the equal sign and get 9 + 4 = _ + 4. Hence, the equality must be true if and only if the missing number is 9. We can also generalize this example. By looking at the structure and using the general properties of numbers, for example, the associative law, we can conclude that all equalities on the form a + b = (a + x) + (b – x) hold true. This kind of reasoning, the generalization of an arithmetical situation by using the fundamental properties of numbers, is included in the second Big Idea, GA.

In another study using the Big Ideas of algebra, cross-cultural differences in the national mathematics curricula in Estonia, Finland, and Sweden were investigated and compared (see Hemmi et al., 2020). Despite the similarities in the school systems of these three neighboring countries, the results revealed several differences between them. Particularly, although all three curricula attempted to create a basis for understanding and solving equations, only the Swedish curriculum explicitly addressed the importance of understanding the meaning of the equal sign.

Methodology

The present study is a case study (cf. Bryman, 2012), with three cases comprised of students from three different schools. In this section, we first describe the cases. Then, we describe the analytic tool, the assessment form, and the procedures for the data analysis. Finally, we discuss the study’s trustworthiness and ethical aspects.

The Cases

The three schools were chosen based on the students’ parents’ average level of education according to SALSA.2 At School A, the parents have an average education level high above the Swedish average, at School B slightly above the Swedish average, and at School C below the Swedish average. All schools are in central Sweden. In total, there were 291 respondents, with 172 students in Grade 3 and 119 students in Grade 6. The numbers of participants by school and grade are shown in Table 2.

Table 2 Numbers of participants at the three schools
Full size table

The Analytic Tool and the Assessment Form

We will use the same assessment form and construct map as used by Matthews et al. (2012) as the basis for our analysis. The construct map developed by Matthews et al. (2012) consists of four levels and will be briefly presented here. For more details, we refer to Matthews et al. (2012). Levels 1 and 2 are on an operational level, with the lower level being rigid operational (Level 1). As mentioned earlier, this means that a student on this level is only successful when he or she encounters equations with operation-equals-answer, with the operation on the left side of the equal sign, i.e., a + b = c (a + b equals c). The higher of these two levels is called flexible operational (Level 2). Students on this level still have the operational view of the equal sign but can, for example, solve equations with the operation on the right side of the equal sign or successfully identify equalities with no operation, i.e., 3 = 3, as true or false. The two highest levels of the construct map are called basic relational (Level 3) and comparative relational (Level 4). On the basic relational level, the student knows that the equal sign shows a relation and can solve equations with operations on both sides, but might still not compare the two sides of the equality. In the case of the open number sentence 8 + 5 = _ + 4, this means that the student, for example, calculates 8 + 5 = 13 and, since 9 + 4 also equals 13, the missing number must be 9. On the comparative relational level, a student constantly interprets the equal sign as a relation and can, for example, compare the two sides of an equality, which includes recognizing that transformations maintain equality. In 8 + 5 = _ + 4, such a transformation can be “moving one from 5 to 8” and thereby being able to immediately read the missing number from the new open number sentence 9 + 4 = _ + 4.

Matthews et al. (2012) have also developed an assessment form, which can be used to study students’ understanding of the equal sign and mathematical equality. They also provide evidence of the reliability and validity of the assessment, making the assessment form well suited for our study. Therefore, we chose to use the assessment form, which is fully presented in Appendix A in Matthews et al. (2012). Pang and Kim (2018) have also used this assessment form, with some minor revisions in order to adapt it to the Korean context. Following Pang and Kim (2018), we used the 27 test items from Matthews et al. (2012), translating them into Swedish with revisions to two items to adapt them to a Swedish context. Since there is no Swedish correspondence to a nickel, item 11 was changed from using “5 cents” and “one nickel” to “15 minuter” (15 min) and “en kvart” (a quarter of an hour), respectively. Item 14 was adapted to the Swedish context by using Swedish kronor instead of dollars, and öre (1/100 krona) instead of cents. Finally, as the Swedish word “utsaga,” which is the correct translation of “number sentence,” is not used in primary school in Sweden, we instead used “likhet” (equality).

Data Gathering

To determine whether the assessment form was suitable in the Swedish context and whether the test items and instructions were clear to the students, we conducted a pilot study in two classes. The students were instructed to ask questions if anything was unclear to them during the test. In both classes, very few questions arose, and the ones that did arise involved what to write if they did not know how to explain their thoughts. In these cases, the students were told to write “I don’t know” as their explanation. This was added to the list of instructions given to the students in the upcoming data collection. The students in the pilot study needed up to 45 min to complete the assessment form, which was about the same time it took in the studies by Matthews et al. (2012) and Pang and Kim (2018). As nothing had to be changed after the pilot study and the instructions were the same in the pilot as in the upcoming data collection, these two classes were included in the study.

Data Analysis

Matthews et al. (2012) score the items dichotomously: 1 for correct and 0 for incorrect. For example, a student solution has to show knowledge on a comparative relational level to be categorized as a correct answer on tasks testing comparative relational knowledge of the equal sign. On the other hand, when Pang and Kim (2018) look at the students’ types of answers, they not only note whether the answer is correct or incorrect. If the test item required the students to write an explanation, each score is also divided into three subcategories: “relational thinking,” “computation,” and “incomplete or incorrect explanation” (Pang & Kim, 2018). Using our terminology, these three subcategories are “comparative relational,” “basic relational or operational,” and “incomplete or incorrect.” When coding the students’ answers, we used 0 for incorrect and 1 for correct. For selected items in which the students are required to motivate their answers and it is possible to differentiate the types of solutions, we employed the three subcategories for both correct and incorrect answers. We used a for a relational explanation, for example, by comparing the two sides, using compensatory strategies or transformations maintaining equality. This falls under the comparative relational knowledge level, according to Matthews et al. (2012). If a student uses computations or describes computations to show that the two sides are equal, we coded this with b for a basic relational or operational approach. For items testing basic or comparative relational knowledge, a correct solution of this type will indeed be basic relational since an operational approach will result in an incorrect answer. Therefore, for correct answers on these items, basic relational will coincide with Pang and Kim’s (2018) computational. Finally, the incorrect or incomplete explanations were coded with c. Hence, the code 0b, for example, is used for an answer that is incorrect and in which the student shows that he or she has used calculations to solve the task. In Matthews et al. (2012), all test items have been given a hypothesized level 1 to 4 in accordance with the four knowledge levels. The codes a, b, and c are used on all items of hypothesized level 3 or 4 (i.e. basic or comparative relational) that also require the student to write an explanation. This results in the codes being used on 14 items, which gives us a total of 4074 student answers, including blank answers. Out of these 4074 answers, only a single answer was coded with 0a. Hence, we see that this type of answer is extremely rare, which is consistent with the findings by Pang and Kim (2018). This leaves us with the incorrect answers almost always being of the type in which the student either attempts a calculation or gives an incomplete explanation (or none at all). Even though this information can be useful, it does not contribute to this study as it offers no information about whether students use a comparative relational, basic relational, or operational approach. Therefore, even though we have used these codes when coding the students’ incorrect answers, incorrect answers will not be presented using these subgroups.

To further explain our coding, here we show some examples of students’ answers to item 3 (Figs. 1, 2, and 3): “Without adding 67 + 86, can you tell whether the number sentence below is true or false? 67 + 86 = 68 + 85. How do you know?”

Fig. 1
figure 1

Example of coding “1a,” correct and comparative relational. Translation: “If you remove a 1 from 68 and put it on 85 it becomes 67+86 which was there”

Full size image
Fig. 2
figure 2

Example of coding “1b,” correct and basic relational (or operational). Translation: “Add to hundred but begin with unit digit then tenths then hundredths”

Full size image
Fig. 3
figure 3

Example of coding “1c,” incomplete or incorrect explanation. The student circles “true,” but gives an incomplete explanation. Translation: “I know it because 67+86 68+85”

Full size image

The first example shows a student changing the expression on the right side from 68 + 85 to 67 + 86, by “moving” one from 68 to 86. The student then concludes that it is the same expression as on the left side. This is an example of a comparative relational approach.

The student answers correctly that the number sentence is true. Note that the student describes a computation, but does not show the calculation explicitly. Since this type of answer is based on calculating the value of the expressions, which is used to compare the value of the two expressions, this is coded as “1b”—basic relational approach.

In the third and final example, the student has correctly circled “true,” but the explanation is incomplete. Therefore, this answer has been coded as “1c.”

Trustworthiness and Ethical Considerations

By using a case study, we limit the possibility for generalization of the study (Stake, 2005), and therefore, using statistical methods might not be useful. Instead, we aim to find interesting aspects that can be studied in more detail in the future. In our study, we used an assessment form and the construct map developed by Matthews et al. (2012). One of the strengths of Matthews et al. (2012) is that the items and the construct map are based on previous test items and the construct map from Rittle-Johnson, Matthews, Taylor, and McEldoon (2011). The items are then revised based on feedback from an expert panel and empirical evidence (Matthews et al., 2012). Rittle-Johnson et al. (2011) and Matthews et al. (2012) have tested the items and revised them when necessary, and in the process have developed a construct map for knowledge of the equal sign as an indicator of mathematical equality; that is, this construct has indeed been well defined.

Since this study includes students in Grades 3 and 6, we sent information about the study and a consent form to the students’ guardians. If a guardian did not return the consent form, that student was left out of the study. The students were also informed that they were allowed withdrawing from the study at any time until they had handed in their assessment form. As no data on the participants other than school and grade were collected, we have no way of identifying any individual students in this study.

Results

The structure of the “Results” section is as follows. First, as a partial answer to RQ1 and RQ2, we will look at students’ knowledge and definition of the equal sign. With RQ3 in mind, we will compare our results with those in the South Korean case studied by Pang and Kim (2018). Next, we will continue to answer RQ1 and RQ2 by describing the results regarding students’ ability to use the relational property of the equal sign. Again, we will look at RQ3 by comparing these results from the Swedish schools with the South Korean case. Whenever South Korea is mentioned in a table, the results come from Pang and Kim (2018).

Students’ Knowledge and Definition of the Equal Sign.

We have chosen to describe the results from three items regarding the definition of the equal sign: items 9, 12, and 13. Our results from item 12 will be compared with those from Pang and Kim (2018), and we begin by looking at this item:

Item 12 consists of three multiple-choice questions (Table 3). We can see that, in Grade 3, 39.1% of the students at School B recognize that the equal sign means “the same as.” At School C, 73.6% of the students, and at School A all but one student, answer that “the same as” is a good definition of the equal sign. In Grade 6, between 90.0 and 94.1% of the students at all three schools circle “Good” on this item. Looking at items 12b and 12c, we see the same pattern, with a higher percentage of the students at School A than at School B or C answering the items correctly in Grade 3. In Grade 6, the differences between the three schools are much smaller.

Table 3 Student responses to item 12. Frequency and percentage of correct answers
Full size table

Although most students have an understanding of the equal sign as something that means “the same as,” at the same time they believe that the equal sign means “the answer to the problem.” These results are similar to those in the South Korean case, but we note that in Grade 6 the Swedish students know that the equal sign does not mean “the answer to the problem” to a higher degree than the South Korean students do. In the next item, item 13, the students choose which of the three definitions in item 12 is the best definition of the equal sign (Table 4).

Table 4 Student responses to item 13. Frequency and percentage of answers
Full size table

Even though students choose both a and c as a good definition of the equal sign in item 12, we see here that many of them, especially those in Grade 6, choose “the same as” as the best definition. In Grade 3, we see that only 27.2% and 31.9% at Schools B and C, respectively, choose a as the best definition. This is much lower than the 79.6% of the students at School A. The third item on the same theme, item 9, requires the students to write down a definition of the equal sign in their own words (Table 5).

Table 5 Student responses to item 9
Full size table

The students’ responses on this item are in line with the results from items 12 and 13. For example, in Grade 3, more students at School A than at Schools B and C write a relational definition of the equal sign. This difference between the schools is also apparent when the students are asked to state whether or not “the same as” is a good definition of the equal sign. Note that the number of students who are able to express the definition in their own words is lower than the number of students who are able to say whether a definition is good or to choose the best definition. Furthermore, 28 students in Grade 6 across all three schools write a definition that implies an operational view of the equal sign, for example, that it “gives the answer,” but only 20 choose an operational definition as the best definition, according to Table 4. An example of this is the response of a student at School B.

This student answers the question “Can it mean something else?” on item 9 with “Nej” (No), and writes 1 + 1 = 2 as an example and explains the equal sign with “What is the answer” (Fig. 4). The same student answers 12a, 12b, and 12c correctly, and chooses a as the best definition on item 13, thereby contradicting the answer on item 9. The results on item 13 are similar to the results on item 14 (Table 6).

Fig. 4
figure 4

Example of student response to item 9

Full size image
Table 6 Student responses to item 14. Frequency and percentage of correct answers
Full size table

The only exception to the similarities with the results on item 9 (Table 5) is the results for the students in Grade 3 in School A. In School A, almost the same number of students in Grade 3 (72.2%) and Grade 6 (72.7%) writes that the equal sign means that 1 krona is the same as 100 öre. The results thus far show how the students describe the equal sign, but not whether they use the relational property of the equal sign.

Students’ Ability to Use the Relational Property of the Equal Sign.

To determine how the students use the relational property of the equal sign, we turn our attention to items 3 (Table 7 and Table 8), 8 (Table 9 and Table 10), and 24 (Table 11 and Table 12).

Table 7 Student responses to item 3 in Grade 3
Full size table
Table 8 Student responses to item 3 in Grade 6
Full size table
Table 9 Student responses to item 8 in Grade 3
Full size table
Table 10 Student responses to item 8 in Grade 6
Full size table
Table 11 Student responses to item 24 in Grade 3
Full size table
Table 12 Student responses to item 24 in Grade 6
Full size table

Table 7 and Table 8 show that there is a difference between the schools. In Grade 3, at Schools B and C, about a fifth of the students solve this item using a relational approach (see Fig. 5 for an example). On the other hand, at School A, 53.7% of the students use the relational structure of the equal sign, which is also higher than in the South Korean case. We can also see that only three more students (4.2%) at School C provide the correct answer with an incomplete explanation, which is much lower than at the other schools (Table 7). These three students write no explanation at all, which also is the most common type of incomplete explanations in all three schools.

Fig. 5
figure 5

Student solution showing a basic relational (or operational) approach. This student also draws a scale showing two equal sides and writes “= equal”

Full size image

Those differences between the schools remain in Grade 6, but have now slightly changed (Table 8). About three out of four students at School A solve this item with a comparative relational approach. None of them has shown a calculation, which would have implied a basic relational knowledge level. Seven students provide the correct answer, but do not explain how they arrived at it. Of the students at School A, 89.1% solve the item correctly. At School B, only one correct answer is not explained by the student, while six students (20%) have shown calculations like the one below. A total of 86.7% of the students at School B have given the correct answer, which is about the same as at School A (Table 8).

Schools A and B are quite similar in how many of their students in Grade 6 are able to solve this item, but at School C the percentage solving the item is lower (67.6%). Furthermore, we see that 38.2% of the students solve the item with a strategy typical of a comparative relational knowledge level, which is half of the percentage of School A (Table 8)

On item 8 (Table 9), students at School A have the highest success rate, with 57.4% of them giving the correct answer. Furthermore, the success rate is much higher at School A than at any other school, and the total success rates for Schools B and C, 6.5 and 5.6%, respectively, are slightly lower than in the South Korean case (7.9%). A third of the students at School A are able to motivate their answer that the numbers in the boxes are the same, either through calculation (22.2%) or using a comparative relational approach (11.1%). Another two students, both at School C, use a comparative relational approach.

In Grade 6, we see a higher success rate than in Grade 3 on item 8 (Table 10). In all four cases, more students use a comparative relational approach in Grade 6 than in Grade 3. However, at School A, a total of 49.1% of the students in Grade 6 answer this item correctly, which is lower than 57.4% of the students in Grade 3 at the same school. We also see that the success rate for students in Grade 6 in the South Korean study is almost 50 percentage points higher compared to the students in Grade 3. Students in Grade 6 at both Schools B and C have a higher success rate than students in Grade 3 at these two schools, but the difference is not as great as in the South Korean case. Students at both Schools A and B solve this item using a comparative relational approach to a slightly higher degree than in the South Korean case. On the other hand, many more of the students in the study by Pang and Kim (2018) than in the Swedish schools solve item 8 using calculations.

On item 24 (Table 11), in all three Swedish cases, the percentage of correct answers with incomplete explanations is higher than in the study by Pang and Kim (2018). We also see that fewer Swedish than South Korean students use a comparative relational approach. Finally, between 2.2 and 13.0% of the students in the different cases show calculations implying a basic relational knowledge level.

In Grade 6 (Table 12), the students in all four cases use a comparative relational approach to a much higher degree than in Grade 3. Students at School C show calculations or give an incomplete or non-existing explanation to a higher degree than in the other cases. When compared with the other cases, we find that less than half as many students at School C use a comparative relational approach.

Discussion

The aim of this study was to gain insight into how Swedish students describe and work with the equal sign, by looking at three research questions with different origins. The first research question, RQ1 “How do Swedish students describe and use the equal sign?,” was motivated by the high representation of EEEI in Swedish curriculum and textbooks (Hemmi et al. 2018) and the lack of research on how students in the Nordic countries use the equal sign. Therefore, we want to know how Swedish students describe and use the equal sign. The second research question, RQ2 “What differences can be seen in students’ knowledge level of the equal sign depending on which school they attend?,” originates in the reports of increased inequality in Swedish schools (Swedish National Agency of Education, 2008, 2012, 2016a). Our third and final research question, RQ3 “What are the similarities and/or differences between the Swedish cases and the South Korean case?,” compares our results with those from South Korea, one of the countries that performs the best on the TIMSS (Mullis et al., 2016) and PISA (Schleicher, 2019). The main findings we will discuss in this section are as follows:

  • Being able to describe the definition of the equal sign does not necessarily imply being able to use the relational property of the equal sign and vice versa

  • How well students perform on the assessment form depends on which school they attend, which is in line with the reported increase in school inequality in Sweden

  • In general, the students in Grade 6 in the Swedish cases know the definition of the equal sign better than the South Korean students, but for items requiring them to use the relational property of the equal sign, the results of the comparison depend on which school they attend.

We begin by discussing the results in relation to RQ1. In doing so, as it is impossible not to mention the differences between the Swedish cases, we move on to RQ2. Then, we discuss the comparison between the Swedish and the South Korean cases in regard to RQ3. Finally, we briefly comment on our method and the implications of this study.

RQ1: How do Swedish students describe and use the equal sign? Concerning RQ1, we found that most students in Grade 6 write that “the same as” is a good definition of the equal sign and that about half of the students also know that the equal sign does not mean “the answer to a problem” (see Table 3). This implies that many students hold an ambiguous view of the equal sign: it can mean both “the same as” and “the answer to a problem.” Despite this ambiguous view, most students in Grade 6 choose “the same as” as the best definition of the three alternatives in item 13 (Table 4). The same ambiguity can be seen when comparing the results on items 9 (Table 5) and 12 (Table 3). Students are less able to describe the equal sign correctly in their own words than they are able to choose “the same as” as a good definition. The fact that we found students who answer that “the same as” is a good definition and “the answer to the problem” is not good, but still write “what makes the answer” when using their own words, strengthens this result involving students having an ambiguous view of the equal sign. The student solution described in connection to Fig. 4 is another example showing that a student can hold both a relational and an operational view of the equal sign, depending on the context.

When comparing these results involving the definition of the equal sign with those from items requiring the students to use the relational property, we see something interesting in Grade 3. Very few students at School B recognize “the same as” as a good definition of the equal sign, but when it comes to determining the truth value of the number sentence 67 + 86 = 68 + 85 without adding 67 and 86, the students perform just as well as those at School C (see Table 7). The same holds true when it comes to using a comparative relational approach to finding the number that goes in the box in the equality 43 + □ = 48 + 76 (see Table 11). This indicates that being able to describe the definition of the equal sign is not the same as being able to use the relational property of the equal sign or vice versa. To be able to discuss our results further, we now have to look at the differences between the schools.

RQ2: What differences can be seen in students’ knowledge level of the equal sign depending on which school they attend? As mentioned above, we found differences between Schools B and C in Grade 3 concerning how well students know the definition and whether they use the relational property of the equal sign. When it comes to knowing that “the same as” is a good definition of the equal sign, we also see that most of the students at School A know this already in Grade 3, but that most of the students at School B and many at School C seem to learn this in Grades 4–6. This is interesting, as the importance of the equal sign is part of the core content in the Swedish mathematics curriculum document for Grades 1–3 but is not mentioned in the core content for Grades 4–6 (Swedish National Agency of Education, 2018). One explanation for this result might be that the relational property of the equal sign becomes clearer when solving equations, and equations do not appear in the Swedish curriculum until Grades 4–6 (Hemmi et al. 2018). Another aspect is that when teachers and administrators implement a specific feature, in this case the importance of the equal sign, they tend to focus on what to implement rather than how to implement it (Hiebert et al., 2005). This could lead to teachers and students only focusing on the meaning of the equal sign and not on how to use it.

Furthermore, in Grade 6, we found differences between the schools in the extent to which the students answer that “the same as” is the best definition of the equal sign (Table 4). Similar differences between the schools were also found when students write the definition of the equal sign in their own words (Table 6). These differences in Grade 6 between the schools can also be seen when students are required to use the relational property of the equal sign (see Table 10 and Table 12). In general, we found that students from School A perform better than those at School B, who in turn perform much better than students at School C on almost all test items, the sole exception being item 12a where students in School C performed slightly better than students in School B. This follows the socioeconomic differences between the schools: the education level of students’ parents is highest at School A and lowest at School C. Another interesting result is that there are much fewer differences between Schools B and C in Grade 3 than in Grade 6, where students in School C even perform equally or better than students in School B on some test items. This means that these differences between the schools increase between Grades 3 and 6. This is one example of the reported increased inequalities between Swedish schools, which includes that the inequalities are bigger in later school years than in earlier years (Swedish National Agency of Education, 2008, 2012, 2016a).

RQ3: What are the similarities and/or differences between the Swedish cases and the South Korean case? In comparing with the South Korean case, we will once more look at the results of the task “Is the number sentence 67 + 86 = 68 + 85 true or false without adding 67 + 86” (Table 7 and Table 8), and compare it with the results of the open-equation task “47 + □ = 48 + 76” (Table 11 and Table 12). We begin by looking at how the Swedish students in Grade 3 respond to the open-equation task. At both Schools A and C, the total number of correct responses to this task is slightly higher than in the study by Pang and Kim (2018). The great difference between the South Korean and the Swedish cases on this task, however, is that many South Korean students use a comparative relational approach while most of the Swedish students, at all three schools, only write the answer without explaining how they reached their conclusion. This reflects the fact that Swedish textbooks are rich in this type of open-equation items, and that the students are only required to fill in the blank without explaining how they reached their answer (Hemmi et al. 2018). Recall that Pang and Kim (2018) changed the test item slightly by replacing 43 with 47, thereby making the difference with 48 smaller. Therefore, this item might have been slightly easier for the South Korean students than for the students in our study. Another interesting aspect is that the open-equation task has a lower difficulty level than the number sentence task, according to Matthews et al. (2012). In the South Korean case, fewer students solve the number sentence task than the open-equation task using a comparative relational approach, which is consistent with the number sentence task being more difficult; but in the Swedish cases, the opposite holds true. At all three Swedish schools, more students solve the number sentence task than the open-equation task using a comparative relational approach (see Table 7, Table 8, Table 11, and Table 12). As mentioned above, one reason for this might be the richness of open-equation items of the type in item 24 in Swedish textbooks, in which students do not have to explain how they reached their answer (Hemmi et al. 2018). Therefore, open equations might lure the students into only writing the answer, as they are used to doing, even though it is stated that they should explain their thinking. The number sentence task is a similar task, but here they are not required to write a number in a box, which makes the task a bit different from what they are likely used to, and therefore, it might be clearer to them that an explanation is required. Another possible explanation for this discrepancy is that some students might not be able to maintain their focus on the test and the results might therefore be worse on task items later in the assessment form than on the earlier test items.

The most challenging test item for the South Korean students was stating whether or not “the equal sign means the answer to the problem” is a good definition (Pang & Kim, 2018), but it seems to have been quite easy for the Swedish students (Table 3). In fact, more Swedish than South Korean students have a non-operational understanding of the equal sign. As mentioned earlier, this is likely explained by the fact that the importance of the equal sign is part of the core content in the Swedish curriculum document (Swedish National Agency of Education, 2018) and therefore, its definition is emphasized in Swedish schools. In fact, in Hemmi et al.’s (2020) comparative study of the algebraic content in the national mathematics curricula in Estonia, Finland, and Sweden, the importance of the equal sign was only addressed in the Swedish curriculum document, which shows that Sweden is the odd one out even among the Nordic countries. Meanwhile, the question remains as to whether this is the right way to go. As we have seen, being able to tell what the equal sign means is not the same as being able to use it in a correct and fruitful way. Using Blanton et al.’s (2015) Big Ideas, we see that both the definition and the use of the relational property of the equal sign are parts of the Big Idea EEEI, but using the relational property belongs to a higher knowledge level than simply knowing the definition of the equal sign (Matthews et al., 2012). We can also note that IEEE is very well represented in Swedish textbooks; but using these relations and properties in a more general way, which belongs to GA, is not as well represented (Hemmi et al. 2018). Therefore, emphasizing the importance of the equal sign might not be enough to improve students’ algebraic knowledge level in general. One must also focus on what this implies for how the equal sign can be used, for example, when solving mathematical problems.

In analyzing the students’ answers, we have seen that, following Pang and Kim (2018), looking at how a student solves an item has offered us more information than merely scoring each item dichotomously like Matthews et al. (2012). For example, following Pang and Kim (2018), it shows us how many students write the answer, without an explanation, to a task requiring an explanation on the corresponding knowledge level of that test item. On the other hand, we also found that if one is not careful this extra classification at first glance can give a false result. For example, for a particular test item the percentage of total correct responses was lower in Grade 6 than in Grade 3 (see School A in Table 9 and Table 10). However, if we had followed Matthews et al. (2012) and scored each answer dichotomously, we would have only marked answers using a comparative relational approach as correct and thereby would have seen an increase in correct answers from Grade 3 to Grade 6. As described in the “Data Analysis” section, we also found that classifying incorrect answers gave no additional information. Therefore, following Matthews et al. (2012) and scoring each item dichotomously would be easier and one would not lose much information. If we do so, however, we must note that Matthews et al. (2012) hypothesized the difficulty level on the different items. While the basics of their work seem to work very well, we found that some items are easier for the students in our cases than in the study conducted in the USA by Matthews et al. (2012). Hence, to be able to take full advantage of their work, one should conduct the study on a much larger scale and calculate the difficulty level for each test item for the present population. Another possible approach to further attempting to explain the differences between Sweden and South Korea, as well as the USA, is to look at what kinds of algebraic tasks are present on the national tests in Sweden. The national tests, conducted in Grades 3, 6, and 9, are widely looked upon as a way of measuring how well a school performs compared to other Swedish schools (Nusche, Halász, Looney, Santiago, & Shewbridge, 2011). Therefore, it is unavoidable that many teachers in Sweden teach mathematics in such a way that they believe will benefit the results on the national tests. Furthermore, the national tests seem to have stronger impact on which mathematical content is taught than on how the teachers work with the content (Swedish National Agency of Education, 2016b). If the national tests emphasize the same type of task items, our study has shown that Swedish students are good at solving; this might explain some of our results. However, the kind of algebraic tasks that are present in the Swedish national tests is something that needs to be addressed in future research.

Notes

  1. 1.

    Trends in the International Mathematics and Science Study.

  2. 2.

    SALSA is an abbreviation for the Swedish National Agency of Education’s Arbetsverktyg för Lokala SambandsAnalyser, in English “tool for local correlation analysis.”