Secant Update generalized version of PSB: a new approach

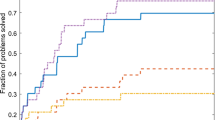
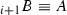Abstract

In optimization, one of the main challenges of the widely used family of Quasi-Newton methods is to find an estimate of the Hessian matrix as close as possible to the real matrix. In this paper, we develop a new update formula for the estimate of the Hessian starting from the Powell-Symetric-Broyden (PSB) formula and adding pieces of information from the previous steps of the optimization path. This lead to a multisecant version of PSB, which we call generalised PSB (gPSB), but which does not exist in general as was proven before. We provide a novel interpretation of this non-existence. In addition, we provide a formula that satisfies the multisecant condition and is as close to symmetric as possible and vice versa for a second formula. Subsequently, we add enforcement of the last secant equation and present a comparison between the different methods.

Appendices

Appendices

Preliminary lemmas

In the following proofs, we will apply the following simplifications (and their transposed version). Let $X \in \mathbb {R}^{n \times m}$, $Y \in \mathbb {R}^{n \times m}$, and $\mathbf{x}$ the last column of X (same for $\mathbf {y}$ and Y), we give here some interesting results.

Lemma A.1

$$\begin{aligned} XX^+\mathbf{x}= & {} \mathbf{x} \\ \mathbf{x} ^T(X^+)^TX^T= & {} \mathbf{x} ^T \end{aligned}$$

Proof

$XX^+\mathbf{x}$ is the last column of $XX^+X$, but $XX^+X=X$. So $XX^+\mathbf{x}$ is the last column of X which is $\mathbf{x}$. The second form is simply the transposed expression. $\square$

Lemma A.2

$$\begin{aligned} \mathbf{x} ^TXX^+= & {} \mathbf{x} ^T\\ (X^+)^TX^T\mathbf{x}= & {} \mathbf{x} \end{aligned}$$

Proof

$\mathbf{x} ^TXX^+$ is the last row of $X^TXX^+$. But $X^TXX^+=X^TX(X^T X)^{-1} X^T=X^T$. So $\mathbf{x} ^TXX^+$ is the last row of $X^T$ which is $\mathbf{x} ^T$. The second form is simply the transposed expression. $\square$

Lemma A.3

$$\begin{aligned} YX^+\mathbf{x}= & {} \mathbf {y}\\ \mathbf{x} ^T(X^+)^TY^T= & {} \mathbf {y}^T \end{aligned}$$

Proof

$YX^+\mathbf{x}$ is the last column of $YX^+X$. But $YX^+X=Y$. So $YX^+\mathbf{x}$ is the last column of Y which is $\mathbf {y}$. The second form is simply the transposed expression. $\square$

Alternating Projections applied on PSB

1.1 Closed convex sets

Here are the proofs that the sets used in Section 3.2 are closed and convex.

Lemma B.1

The set of symmetric matrices is a closed convex set.

Proof

The set of symmetric matrices is a vector subspace. So it is closed and convex. $\square$

Lemma B.2

The set of multisecant matrices is a closed convex set.

Proof

The set of multisecant matrices is the set of matrices A such that $A\mathbf {x} = \mathbf {b}$. This is an affine space. So it is closed and convex. $\square$

1.2 Projection on the set of multisecant matrices

The formula for the projection on $K_{MS}$ is (3.2):

Proof

For more readability and to avoid to handle too many subscripts, we lightly change the notation in this development. We note:

• 
• 

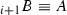
• We omit the subscript i for S and Y.

• j, k the scalar coordinates within a vector or a matrix (j-th row, k-th column).

We start with the following optimization problem:

$$\begin{aligned} \arg \min \limits _{A}&\frac{1}{2}\left\| A-B\right\| ^2_{Fr} \\ \text {such that}&AS-Y&=0 \end{aligned}$$

We take the Lagrangian of the system:

$$\begin{aligned} \mathcal {L}(A,\Lambda )= \frac{1}{2}\left\| A-B\right\| ^2_{Fr} + \sum \limits _{j,k} \Lambda _{j,k} \left( \sum \limits _l A_{j,l}S_{l,k}-Y_{j,k}\right) \end{aligned}$$

We now take the partial derivative in function of $A_{j,k}$. We first note that:

$$\begin{aligned} \frac{\partial }{\partial A_{j,k}}\sum \limits _{j,k} \Lambda _{j,k} \left( \sum \limits _l A_{j,l}S_{l,k}-Y_{j,k}\right)= & {} \frac{\partial }{\partial A_{j,k}}\sum \limits _{j,k,l} \Lambda _{j,k} A_{j,l}S_{l,k}\\= & {} \frac{\partial }{\partial A_{j,k}}\sum \limits _{j,l,k} \Lambda _{j,l} A_{j,k}S_{k,l}\\= & {} \sum \limits _l \Lambda _{j,l} S_{k,l}\\= & {} (\Lambda S^T)_{j,k} \end{aligned}$$

We find:

$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial A_{j,k}}=A_{j,k}-B_{j,k}+(\Lambda S^T)_{j,k}=0 \end{aligned}$$

The system can thus be written as:

Putting (B.1) into (B.2), we find:

Putting this back into (B.1), we have a new update formula:

$$\begin{aligned} A= & {} B+(Y-BS) (S^TS)^{-1} S^T\\ B_{i+1}= & {} B_i+(Y_i-B_iS_i)(S_i^TS_i)^{-1} S_i^T \end{aligned}$$

$\square$

1.3 Generalized PSB

Proof of Theorems 1 and 2.

Proof

As explained in Sect. 3.1, we use alternating projection. We project alternatively on the subspace of multisecant matrices ($K_{MS}$) and on the subspace of symmetric matrices ($K_{Sym}$):

• $K_{MS}$: Defined in (3.2) for the projection on the set of multisecant matrices. We call the projection $_jB$.

• $K_{Sym}$: Equation (3.1) for the projection on the set of symmetric matrices. We call the projection $_j\bar{B}$.

We recall that $(S^T S)^{-1} S^T=S^+$ (Moore-Penrose pseudoinverse). We start with and we develop:

After those two first projections, we go on:

We define:

We can easily see that, when $j=2$, corresponds to and, when $j=3$, corresponds to . We also easily check that is the projection of using equation (3.1), and that projecting with (3.2) gives .

Finally, taking the limit to infinity, we see that the sequences converge to two different formulas. On one side, we have , the symmetric formula closest to the space of matrices satisfying multiple secant equations: gPSB Sym. This proves Theorem 1.

The second formula, , gives the matrix satisfying multiple secant equations and being the closest to the symmetric matrix: gPSB MS. This proves Theroem 2. $\square$

1.4 Existence conditions of gPSB

1.4.1 Theorem 3

We give here a proof to Theorem 3, which is an alternating proof of the theorem of impossibility of existence of gPSB of Schnabel [37].

Proof

We are looking for $B \in \mathbb {R}^{n \times n}: B S=Y$ and $B=B^T$ with S and $Y \in \mathbb {R}^{n \times m}$.

Step 1: construction of $S^{\texttt {syst}}$

We will first construct a matrix that we will call $S^{\texttt {syst}}$. Therefore, using the underscript $X_{*,k}$ as the k-th column of the matrix S, we notice that $B \mathbf {s}_{*,1}=\mathbf {y}_{*,1}$ can be expressed as $S^1 \mathbf{b} =\mathbf {y}_{*,1}$ where

• $\mathbf{b} =\texttt {vec}(B)$, a column vector containing every element of B.

• $\mathbf {s}_{*,1}$ being a column vector containing the first column of S. $\mathbf {y}_{*,1}$ the first column of Y.

• $S^1$ a block diagonal $n \times n^2$ matrix containing the line vector $\mathbf {s}_{*,1}^T$ in each block of the diagonal.

We create $S^i$ and $\mathbf {y}_{*,i}$ in the same way for the following columns of S and Y.

We now express the symmetry condition in the same form: $\Sigma \mathbf{b} =\mathbf{0}$. $\Sigma$ is a $\frac{n(n-1)}{2} \times n^2$ matrix. For each couple $\{b_{ij},b_{ji}\}$ ($1 \le i \le n-1$, $i+1 \le j \le n$), we have a line containing 0 everywhere except for the place corresponding to $b_{ij}$ and $b_{ji}$ where the value is respectively 1 and $-1$.

Applying the 2 conditions $B S=Y$ and $B=B^T$ together, we have thus:

$$\begin{aligned}{}[(S^1)^T| (S^2)^T| \dots | (S^m)^T| \Sigma ]^T \mathbf{b}&=[\mathbf {y}_{*,1}^T| \mathbf {y}_{*,2}^T| \dots | \mathbf {y}_{*,m}^T| 0]^T\\ S^{\texttt {syst}} \mathbf{b}&=\mathbf {y}_i \end{aligned}$$

Here we used the symbol $[X_1|X_2]$ to indicate the concatenation of column vectors next to each other. See illustration in Example 1.

Example 1

For instance, for $n=3$ and $m=2$, we have:

$$\begin{aligned} S^{\texttt {syst}}=\left[ {\begin{array}{ccccccccc} s_{11} &{} s_{21} &{} s_{31} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} s_{11} &{} s_{21} &{} s_{31} &{} 0&{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} s_{11} &{} s_{21} &{} s_{31}\\ s_{12} &{} s_{22} &{} s_{32} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{}s_{12} &{} s_{22} &{} s_{32} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} s_{12} &{} s_{22} &{} s_{32}\\ 0 &{} 1 &{} 0 &{} -1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} -1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} -1 &{} 0 \end{array}} \right] \end{aligned}$$

Step 2: Linear dependence for $m=2$

Let’s build $S^{\texttt {syst}}$ for $m=2$. We apply then the following linear combination:

• We multiply the n first rows by the coefficients of $\mathbf {s}_{*,2}$.

• We multiply the n following rows by the coefficient of $-\mathbf {s}_{*,1}$.

• For the column corresponding to $b_{ii}$, the linear combination of the rows is then equal to zero. There are only zeroes in the rows of $\Sigma$ for these columns.

• For the columns corresponding to $b_{ij}$ with $i \ne j$, the linear combination on the 2n first rows gives a value $\delta _{ij}$. We notice that $\delta _{ij}=-\delta _{ji}$. But for these columns, there is a single row of $\Sigma$ having 1 in the column corresponding to $b_{ij}$ ($i<j)$, $-1$ in the column of $b_{ji}$ and 0 everywhere else. No other row of $\Sigma$ has a non-zero value under the column of $b_{ij}$ or $b_{ji}$. So we multiply that rows by $-\delta _{ij}$ and the linear combination gives 0 for those columns, too.

See Example 2 for an illustration.

Applying this linear combination to the matrix leads to a row containing only zeroes. So there is at least one linear dependency between the rows of $S^{\texttt {syst}}$. The rank of matrix $S^{\texttt {syst}}$ is at least one less than its number of lines.

Example 2

For our example with $n=3$, we associate the following coefficients to the successive row:

$$\begin{aligned} \left\{ s_{12}, s_{22}, s_{32}, -s_{11}, -s_{21}, -s_{31}, s_{22}s_{11}-s_{21}s_{12}, s_{32}s_{11}-s_{31}s_{12} , s_{32}s_{21}-s_{31}s_{22} \right\} \end{aligned}$$

Using this coefficient to define a linear combination of the rows, we can easily check that this combination leads to $\mathbf{0}$.

Step 3: Existence conditions for $m=2$

$\Rightarrow$ If $BS=Y$ has a solution, then $S^{\texttt {syst}} \mathbf{b} =\mathbf {y}_i$ has a solution, too. In this case, the linear combination of the lines of matrix $S^{\texttt {syst}}$ also holds for $\mathbf {y}_i$. This linear combination applied to $\mathbf {y}_i$ gives:

$$\begin{aligned} \mathbf {s}_{*,2}^T\mathbf {y}_{*,1}+(-\mathbf {s}_{*,1}^T)\mathbf {y}_{*,2}+0=0 \end{aligned}$$

$\Leftarrow$ On the other side, if $\mathbf {s}_{*,2}^T\mathbf {y}_{*,1}+(-\mathbf {s}_{*,1}^T)\mathbf {y}_{*,2}=0$, then applying the linear combination on $\mathbf {y}_i$ gives 0. The linear combination of $S^{\texttt {syst}}$ also holds for $\mathbf {y}_i$, so $S^{\texttt {syst}} \mathbf{b} =\mathbf {y}_i$ has a solution which is then also the case for $BS=Y$.

Step 4: Conditions for $m>2$

Extending to higher values of m, for each pair i, j of the columns of S and Y, we have a solution if and only if $\mathbf {s}_{*,i}^T\mathbf {y}_{*,j}=\mathbf {s}_{*,j}^T\mathbf {y}_{*,i}=\mathbf {y}_{*,i}^T\mathbf {s}_{*,j}$. For the second equality we used the fact that the transpose of a scalar is the scalar itself. This is equivalent to $\left[ S^TY\right] _{i,j}=\left[ Y^TS\right] _{i,j}$ which leads to $S^TY=Y^TS$. $\square$

1.4.2 Theorem 4

We give here the proof of Theorem 4.

Proof

Step 0: Linear dependencies for $m=2$

This has been shown above in the alternative proof of Theorem 3. By reasoning column by column, we have found one single linear combination involving all the rows.

Step 1: Linear dependencies for $m=3$

For $m=3$, we have $S^{\texttt {syst}}_3=[S_1^T| S_2^T| S_3^T| \Sigma ]^T$ (see previous demo for details about the construction of this matrix). Thanks to step 0, we know that we have 3 linear combinations (one for each couple of columns of the matrix S). However, those linear combinations can be equivalent, as one of them could be a combination of the other two. We have to prove that those combinations are different. We will proceed by contradiction: say that such a linear combination exists and prove that this is only possible if S is not full-rank. We define $S^{\texttt {syst}}_{2}=[S_1^T| S_2^T| \Sigma ]^T$.

The following facts are noted:

• (1) By hypothesis, we have $n \ge 3$.

• (2) The dimension of $S^{\texttt {syst}}_{2}$ is $\frac{n(n+3)}{2} \times n^2$. The number of rows is less or equal to the number of columns.

• (3) As we have proven that, in $S^{\texttt {syst}}_{2}$, there is only one linear combination involving every row, we can take a subset of $\frac{n(n+3)}{2}-1$ rows without losing information nor reducing the rank of the system.

• (4) There are at least $n+1$ independent rows in $S^{\texttt {syst}}_{2}$. We have indeed n independent rows in $S_1$ and at least one extra independent row in $S_2$ because S is full-rank. Therefore, the dimension of the span of its rows is at least $n+1$.

• (5) The dimension of the span of the rows of $S_3$ is at most n.

This leads us to the following conclusion: If the span of $S_3$ is included in the span of $S^{\texttt {syst}}_{2}$, then there is only one linear combination in $S^{\texttt {syst}}_3$. Otherwise, there are 3 distinct linear combinations.

For the proof by contradiction, we assume that the span of $S_3$ is included in the span of $S^{\texttt {syst}}_{2}$. Then, for each row of $S_3$, there exists a linear combination of the rows of $S^{\texttt {syst}}_{2}$ that is equal to it. Thanks to point 3 above, we know that we can remove one row of $S^{\texttt {syst}}_{2}$. We start thus by replacing the first row of $S_3$ (See Example 3).

Example 3

For the case $n=3$, we have then:

$$\begin{aligned} \left[ {\begin{array}{ccccccccc} s_{13} &{} s_{23} &{} s_{33} &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} s_{11} &{} s_{21} &{} s_{31} &{} 0&{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} s_{11} &{} s_{21} &{} s_{31}\\ s_{12} &{} s_{22} &{} s_{32} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{}s_{12} &{} s_{22} &{} s_{32} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} s_{12} &{} s_{22} &{} s_{32}\\ 0 &{} 1 &{} 0 &{} -1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} -1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} -1 &{} 0 \end{array}} \right] \end{aligned}$$

We apply then the following linear combination:

• We multiply the n first rows by the coefficients of $\mathbf {s}_{*,2}$.

• We multiply the $n+1$-th row by $-\mathbf {s}_{1,3}$.

• We multiply the $n-1$ following rows by the coefficient of $-\mathbf {s}_{*,1}$.

• For the column corresponding to $b_{ii}$, the linear combination of the rows is then equal to zero (there are only zeroes in the rows of $\Sigma$ for these columns).

• For the columns corresponding to $b_{ij}$ with $i \ne j$ and $i,j \ne 1$, the linear combination on the 2n first rows gives a value $\delta _{ij}$.

  • We notice that $\delta _{ij}=-\delta _{ji}$.

  • But for these columns, there is a single row of $\Sigma$ having 1 in the column corresponding to $b_{ij}$ ($i<j)$, $-1$ in the column of $b_{ji}$ and 0 everywhere else.

  • No other row of $\Sigma$ has a non-zero value under the column of $b_{ij}$ or $b_{ji}$.

  • So we multiply those rows by $-\delta _{ij}$ and the linear combination gives 0 for those columns, too.

• For the columns corresponding to $b_{1i}$ and $b_{i1}$ with $i \ne 1$, we should also have $\delta _{1i}=-\delta _{i1}$, but the equation is not automatically satisfied. This gives us $n-1$ equations (for $i=2,\dots ,n-1$):

  $$\begin{aligned} \mathbf {s}_{1,2}\mathbf {s}_{i,3}-\mathbf {s}_{i,2}\mathbf {s}_{1,3}=\mathbf {s}_{1,2}\mathbf {s}_{i,1}-\mathbf {s}_{i,2}\mathbf {s}_{1,1}\end{aligned}$$

  (B.3)

Applying the same reasoning but after replacing the $n+1$-th row of $S^{\texttt {syst}}_{2}$ by the first row of $S_3$ leads to another $n+1$ equations:

$$\begin{aligned} \mathbf {s}_{1,1}\mathbf {s}_{i,3}-\mathbf {s}_{i,1}\mathbf {s}_{1,3}=\mathbf {s}_{1,1}\mathbf {s}_{i,2}-\mathbf {s}_{i,1}\mathbf {s}_{1,2}\end{aligned}$$

(B.4)

Combining (B.3) and (B.4) leads to:

$$\begin{aligned} \mathbf {s}_{1,2}\mathbf {s}_{i,3}-\mathbf {s}_{i,2}\mathbf {s}_{1,3}= & {} \mathbf {s}_{i,1}\mathbf {s}_{1,3}-\mathbf {s}_{1,1}\mathbf {s}_{i,3}\\ \frac{\mathbf {s}_{1,3}}{\mathbf {s}_{i,3}}= & {} \frac{\mathbf {s}_{1,2}+\mathbf {s}_{1,1}}{\mathbf {s}_{i,2}+\mathbf {s}_{i,1}} \end{aligned}$$

We can now apply the same process but starting with successively replacing the i-th and $n+i$-th rows of $S^{\texttt {syst}}_{2}$ by the i-th row of $S_3$, for $i=2,...,n$. This leads to the general equations:

$$\begin{aligned} \frac{\mathbf {s}_{i,3}}{\mathbf {s}_{i,2}+\mathbf {s}_{i,1}}=k \quad \text {for }i=1,\dots ,n \quad \text {where }k \text { is a constant} \end{aligned}$$

The consequence is $\mathbf {s}_{*,3}=k(\mathbf {s}_{*,1}+\mathbf {s}_{*,2})$. S is then not full-rank which is in contradiction with our hypothesis. So the span of $S_3$ is not included in the span of $S^{\texttt {syst}}_{2}$ and, for $m=3$, we have 3 distinct linear combinations.

Step 2: Linear dependencies for $m>3$

The proof extends to higher values of m by applying Step 3 on every combination of 3 submatrices $S_i$. So each additional column of S adds one new linear combination with every other column. In general, for n and m given, we have a system of $m n + \frac{n^2-n}{2}$ equations with $n^2$ variables, but the rank of the matrix is only $m n + \frac{n^2-n}{2} - \frac{m^2-m}{2}$. $\square$

SUgPSB

Alternating Projections applied on SUgPSB

1.1 Closed convex sets

Here are the proofs that the sets used in Sect. 4.1 are closed and convex.

Lemma D.1

The set of symmetric matrices satisfying the last secant equation is a closed convex set.

Proof

This set is in fact a projection on the intersection of the set $K_{Sym}$ and $K_{SU}$, the latter being a special case of $K_{MS}$ (one secant equation instead of multiple secant equations).

In Lemma B.1, we have already proved that $K_{Sym}$ is closed and convex.

By application of Lemma B.2 on $K_{SU}$ where we only take one column of S and Y, we prove that $K_{SU}$ is a closed convex set.

As both sets ($K_{Sym}$ and $K_{SU}$) are closed and convex, their intersection $K_{SymSU}$ is closed and convex. $\square$

Lemma D.2

Within the set of multisecant matrices for given secant equations, the subset of matrices being the nearest to be a symmetric matrix is a closed convex set.

Proof

The set of multisecant matrices ($K_{MS}$) is an affine space. The set of symmetric matrices ($K_{Sym}$) is a vector subspace, which is a special case of an affine subspace where the origin point is null.

The end space $E_1$ as defined in [15, 21], is the set of points defined as $E_1:=\left\{ \mathbf{x} \in L_1: d(\mathbf{x} ,L_2)=d(L_1,L_2)\right\}$, where $L_1$ and $L_2$ are affine subspaces and d is the distance between a point and an affine subspace or between two affine subspaces. In Theorem 2 of [15], it is shown that $\mathbf{x} \in E_1$ solves an equation of the form $A\mathbf{x} =\mathbf{b}$, so $E_1$ is an affine space. Applying this with $K_{MS}$ as $L_1$ and $K_{Sym}$ as $L_2$, we prove that $K_{MS\triangleright Sym}$ is an affine subspace, so it is closed and convex. $\square$

1.2 PSB non symmetric start

We prove here the formula (4.1).

Theorem 9

(PSB - Direct Form from non symmetric matrix) Let $B_i \in \mathbb {R}^{n \times n}$, $\mathbf {y}_i$ and $\mathbf {s}_i \in \mathbb {R}^{n \times 1}$ and $S_i$ full-rank. Let $B_{i+1}$ such that:

• $B_{i+1}\mathbf {s}_i=\mathbf {y}_i$

• $\left\| B_{i+1}-B_i\right\| _{F}$ is minimal

Then, $B_{i+1}$ is given by:

$$\begin{aligned} B_{i+1}=\bar{B}_i + \frac{\bar{\mathbf {w}_i} \mathbf {s}_i^T}{\mathbf {s}_i^T \mathbf {s}_i}+\frac{\mathbf {s}_i \bar{\mathbf {w}_i}^T}{\mathbf {s}_i^T \mathbf {s}_i} - \frac{\bar{\mathbf {w}_i}^T \mathbf {s}_i}{(\mathbf {s}_i^T \mathbf {s}_i)^2}\mathbf {s}_i \mathbf {s}_i^T \end{aligned}$$

With

• $\bar{B}_i=\frac{B_i+B^T_i}{2}$

• $\bar{\mathbf {w}_i}=\mathbf {y}_i-\bar{B}_i\mathbf {s}_i$

Proof

We will apply the method of alternating projection with:

• $K_{Sym}$: equation (3.1) for the symmetrical projection, giving $_j\bar{B}$

• $K_{SU}$: Broyden “good” [5, 6] for the secant update projection, giving $_jB$

Let’s start with $_0B$. We first project onto the set of symmetric matrices. For more readability and as we work within one step of the Quasi-Newton process, we omit the subscripts i which refers to the step of the Quasi-Newton process. We have:

We should now project on symmetric matrices again. But is already symmetric. So the alternating projection has already converged. $\square$

1.3 SUgPSB Sym & SUgPSB MS

Proof of Theorem 5 and 6.

Proof

We project alternatively on the 2 sets: $K_{MS\triangleright Sym}$ and $K_{SymSU}$.

We find out that (D.1) is equal to (D.3). The sequence converges to a fixed point. The equations (D.1) and (D.2) respectively lead thus to the formulas of Theorems 6 (SUgPSB MS) and 5 (SUgPSB Sym). $\square$