Abstract
Ultrahot disintegrating exoplanets have been detected with tails trailing behind and/or shooting ahead of them. These tails are believed to be made of dust that are formed out of the supersonic escaping flow that emanated from the permanent day side. Conserving angular momentum, this day-side escape flux would lead the planet in orbit. In order to explain the trailing tails in observation, radiation pressure, a repulsive force pushing the escape flow away from the host star, is considered to be necessary. We here investigate whether escape could be deflected to head away from the host star by the pressure gradient force. We demonstrate in an idealized framework that escape flux from the night side can occur, and sometimes, can be even stronger than the escape from the day-side. The night-side escape infers that escape flow could trail behind the planet in orbit by virtue of angular momentum conservation even without radiation pressure. We also find analytical approximations for both day-side and night-side escape fluxes, which may be applied to study planetary evolution of disintegrating planets.
Export citation and abstract BibTeX RIS
1. Introduction
Tidally locked exoplanets, orbiting extremely close to their host stars, receive fierce radiation on the permanent day side that can melt their rocky surface to form a lava ocean there. Owing to their short orbital periods, many lava planets have been detected (Léger et al. 2011; Rouan et al. 2011; Hammond & Pierrehumbert 2017; Henning et al. 2018), and these include relatively small planets (Brogi et al. 2012; Rappaport et al. 2012, 2014; Budaj et al. 2015; Sanchis-Ojeda et al. 2015) whose radial velocity signature is below the measurement noise level (van Lieshout & Rappaport 2018).
Unexpectedly, the transit depth of these planets seem to vary from orbit to orbit, and the transit curve is asymmetric between the ingress and egress. After excluding the possibility of a binary star system, dual planet system, and others, Rappaport et al. (2012) propose that the tail is made of dust carried by the escape flow from the planet. Because of their weak gravity, these small lava planets (e.g., KIC-1255b, KOI-2700b, and K2-22b) cannot hold onto the mineral vapor evaporated from the lava ocean. The outgoing escape flow could bring aerosols from the surface, which would gradually melt under the stellar radiation, forming dusty tails that are weakening away from the planet (Rappaport et al. 2012, 2014; van Lieshout et al. 2014; Sanchis-Ojeda et al. 2015). This disintegrating process provides a unique chance to probe the chemical composition of the planet but is yet to be understood.
One interesting phenomenon that has been found is that tails associated with disintegrating exoplanets can either lead the planet in orbit or trail behind (Brogi et al. 2012; Rappaport et al. 2012, 2014). Intuitively, one would expect vaporization and atmospheric escape to occur on the day side of the planets, where the surface is directly heated by stellar radiation. Then, by conserving angular momentum, this day-side escape flow would outpace the planet in orbit and form a leading tail, rather than the trailing tails as observed around KIC-1255b and KOI-2700b (Brogi et al. 2012; Rappaport et al. 2014; Budaj et al. 2015; Sanchis-Ojeda et al. 2015), unless there is a repulsive force pushing the escape flow away from the host star relative to the planet. van Lieshout et al. (2014), Rappaport et al. (2014), and Sanchis-Ojeda et al. (2015) suggest that radiation pressure can provide such a repulsive force7 : when absorbing photons from the star, dust particles (particularly those around 1 μm van Lieshout et al. 2014) would inherit the photon's momentum and be pushed away from the star; this push forces the particles to travel in an epicycle trajectory with respect to the planet (elliptical trajectory with respect to the star) and gradually lag behind the planet.
In this work, we will investigate whether the pressure gradient force alone can deflect the flow from the day side to the night side of the planet without the help of radiation pressure, and as a consequence, the escape flow would trail behind the planet by virtue of angular momentum conservation. By doing this exercise, we expect to obtain a relationship between the escape rate and the properties (primarily, temperature and size) of the planet that is constrained by thermodynamic and dynamic laws. This is complementary to the previous studies on the trajectory and revaporization process of dust particles after leaving the planetary gravity field (van Lieshout et al. 2014; Rappaport et al. 2014; Sanchis-Ojeda et al. 2015; van Lieshout & Rappaport 2018). This relationship can help address another question: under what conditions would escape flux from the day side dominate the escape from the night side, and under what conditions would the opposite happen. Using this, we may be able to constrain the remarkable uncertainty of the planetary size through observations of its tails, assuming radiation pressure will not redistribute the partition between day-side and night-side escape.
The key to the above questions is to distinguish the day-side and night-side escape, which has been ignored in traditional 1D escape models by assuming isotropy. In our framework, atmospheric pressure gradient between the day side and night side replaces the radiation pressure in van Lieshout et al. (2014), Rappaport et al. (2014), and Sanchis-Ojeda et al. (2015), diverting the flow toward the night side (away from the star). The extremely low surface temperature on the night side drives the pressure there close to zero, making the night side as "attractive" a destination as the vacuum space. On the way toward the night side, vapor flow would turn supersonic; once that occurs, information on the air pressure, temperature, etc. cannot propagate upstream to exert impact on the upstream flow over the day side. As a result, mass would be continuously transported toward the night side at a rate that is purely determined by the conditions on the day side. Air mass from the day side accumulates near the antistellar point, making it a singular point of pressure, which in turn pumps mineral vapor upward from the night side of the planet, away from the host star.
Flow field like this has been seen in multidimensional hydrodynamic simulations for hydrogen escape (Stone & Proga 2009; Tripathi et al. 2015; Shaikhislamov et al. 2018; Debrecht et al. 2019; McCann et al. 2019). Even without radiation pressure or stellar wind, a significant proportion of atmosphere is transported toward the night side by the pressure gradient force, from where atmosphere escapes (Tripathi et al. 2015; Shaikhislamov et al. 2018; Debrecht et al. 2019). Although there are new processes (such as condensation and mass exchange between atmosphere and lava ocean) that do not exist on hot Jupiter to be considered for lava planets, we expect the general physical picture to remain qualitatively similar, except that the transport from the day side to the night side may be further enhanced by the strong pressure gradient on lava planets.8
Simulations of the aforementioned escape flow are beyond the capabilities of a traditional 1D hydrodynamic escape framework, where isotropy is assumed (Parker 1965; Watson et al. 1981; Lammer et al. 2008; Perez-Becker & Chiang 2013; Lehmer et al. 2017; Zahnle & Catling 2017; Owen 2019). Multidimensional hydrodynamic calculation has been utilized for simulating hydrogen escape on hot Jupiters (Tripathi et al. 2015; Shaikhislamov et al. 2018; Wang & Dai 2018; Debrecht et al. 2019; Khodachenko et al. 2019) but has not been applied to mineral vapor escape from small lava planets. Numerically, it could be challenging to deal with phase changes, mass exchange between mineral vapor atmosphere, and different surface types (lava ocean and solidified surface), as well as orders of magnitude of pressure variation in both the horizontal and vertical direction in a multidimensional hydrodynamic model. These motivate us to build an idealized theoretical framework that can distinguish between day-side and night-side escape.
2. Method Brief
As sketched in Figure 1, we combine three 1D models to depict the aforementioned anisotropic escape flow: (1) a day-side hydrodynamic escape model solving for the escape rate driven by the pressure gradient between the day-side surface and the vacuum space (Appendix A), (2) a horizontal transport model calculating the day-side to night-side mass transport following the surface induced by the pressure gradient force (Appendix B), and (3) a night-side hydrodynamic escape model dealing with the escape process of the mass transported from the day side (Appendix C). (2) and (3) are connected by conservation of energy and mass flux. Phase change is calculated explicitly in all three components, rather than being prescribed as in previous works, e.g., Perez-Becker & Chiang (2013). Explicit consideration of phase change is necessary, because, unlike an atmosphere that is purely composed of hydrogen or water vapor, which remains unsaturated or saturated throughout, the mineral gas could undergo multiple transitions between subsaturated and saturated states depending on its geometry and external energy sources (regions that could be saturated are denoted by the gray shading in Figure 1).
Figure 1. Model schematics. Both day-side escape and the two stages of night-side escape are considered here. We use arrows to represent the flow during each stage of escape, with corresponding section numbers marked on the side. Blue (black) arrows denote supersonic (subsonic) flow, and blue (black) dots denote the locations where a subsonic (supersonic) flow turns into a supersonic (subsonic) flow. Gray shadings denote saturation and condensation. Magenta curly arrows denote surface exchange flux. The escape cross section is illustrated by a cone in dashed lines. r is the distance from the center of the planet. θ is the tidally locked latitude counted from the substellar point, and θb denotes the latitude boundary of magma ocean.
Download figure:
Standard image High-resolution imageThe two vertical escape models are built upon Lehmer et al. (2017), and the horizontal transport model is built upon Ingersoll et al. (1985) to explicitly account for the transitions between saturation and undersaturation. Both escape and transport models solve temperature, pressure, and velocity profiles from a set of equations given by mass continuity, momentum theorem, and energy conservation, assuming steady state. The governing equations are singular around transonic points, where flow turns from subsonic to supersonic (blue dots in Figure 1). Only proper boundary conditions can avoid hydraulic jumps across these singular points. One way to solve the problem is to do a binary search for the boundary condition so that unphysical jumps and backflow are avoided (Ingersoll et al. 1985). That is what we do for the escape calculation on the night side. However, for the day side, we assume that condensed particles are re-evaporized shortly after their formation, and therefore the gaseous mass flux is conserved. This extra conservation allows us to directly calculate the escape mass flux that satisfies the boundary conditions without a binary search. We leave technical details to the appendix.
On the day side, we assume that dust, once formed, would be revaporized almost immediately by stellar radiation. This is justified for a sodium- or SiO-dominant atmosphere, because, as shown in Appendix A, even a 10 μm sodium droplet will completely vaporize in the matter of a few seconds or less, and a SiO particle will vaporize within a few minutes. As a result, condensation releases latent heating but does not cause mass loss in the mineral vapor flow. Nevertheless, for the night-side escape flow, where no stellar radiation is received, and for the transport flow, where mass exchange keeps happening between the atmosphere and the planet's surface, we instead assume dust stops interacting with the remaining vapor flow, once formed.
In principle, the model described above can be applied to any arbitrary chemical component. Here, we consider a sodium-dominant escape flow as in Mura et al. (2011), motivated by the ubiquity of the sodium tail within the solar system (a sodium tail has been observed around the Moon (Matta et al. 2009), Mercury (Potter et al. 2002), and also comet Hale-Bopp (Cremonese et al. 2002)). It is possible that sodium is also major components of escape flow in planets beyond the solar system. Actually, as long as sodium has not been exhausted from the magma ocean, its high volatility would make it, by far, the dominant component of the escape flow (Schaefer & Fegley 2009). However, because sodium only accounts for 0.29% of the total mantle mass with bulk silicate earth composition (Schaefer & Fegley 2009), sodium could be exhausted in the early stage of a planet's lifetime depending on the efficiency of the mantle–surface exchange (Kite et al. 2016). We therefore repeat the calculation assuming a SiO-dominant escape flow; the results are qualitatively similar.
In all calculations, we use planetary orbital parameters taken from KIC-1255b (Brogi et al. 2012; van Lieshout & Rappaport 2018), fix the planetary density to be the same as that of Earth, and investigate how the escape flow properties vary with substellar surface temperature T0 and planet mass Mp. The parameters used in this study are summarized in Table 1 in the Appendix.
3. Day-side and Night-side Escape on KIC-1255b as an Example
An example of the escape process is shown in Figure 2. The surface temperature is set to 2100 K and planetary mass is set to 0.03 Earth mass.
Figure 2. Properties of escape flow and transport flow for T0 = 2100 K, Mp = 0.03Mearth. (a) and (b) show the radial dependence of temperature T (red), speed w (blue), and mass flux Φ (green) for day-side escape and night-side escape, respectively. The vertical thin dashed line denotes the Roche lobe radius. Panel (a) shows the profiles for the day-side escape flow. The transonic point is marked by a blue dot on the speed curve. Wherever condensation occurs, a gray shading is overlaid on top of the mass flux curve. For the purposes of representation, we consider the whole magma ocean as one band with surface temperature set to a substellar point, rather than split it into 10 bands as we do for real escape calculations shown in Figures 4 and 5. The green cross in panel (b) marks the mass flux that can finally escape the gravity of the planet; matters that condensed before this point will fall back to the surface. (c) and (d) show the properties of the horizontal transport flow from the day side to the night side. θTL is the tidally locked latitude, the angular distance from the substellar point. Red dashed curves show the surface temperature profiles; cyan curves and magenta curves show the condensation rate D and surface exchange flux F multiplied by ap2, respectively. The rest of the curves are defined the same way as in (a) and (b).
Download figure:
Standard image High-resolution imageIn the day-side escape pathway (Figure 2(a)), the flow is initially undersaturated, due to the dilution of other chemical components. Vapor cools quickly upward, as internal energy is converted to kinetic energy and gravitational potential energy. At around 1.3 planetary radii, flow becomes saturated. Beyond the saturation level, latent heat released due to condensation becomes the main energy source, preventing further drop of temperature. However, the particles formed due to condensation almost immediately re-evaporate due to the strong stellar radiation (the lifetime of a sodium droplet is below a second; see Appendix A for details). The continuous condensation and re-evaporation ensure no loss in mass in the day-side escape flow Φ (i.e., Φ is a constant). Although mass flux is not changed, this recycling keeps energizing the flow until it escapes the gravity field of the planet. The flow turns supersonic at around 3.2 planetary radii (see blue dot in Figure 2(a)), right before the Roche lobe (the thin dashed line in Figure 2(a)).
The night-side escape pathway takes three steps: flow first gathers mass from the day side while accelerating toward the night side (Figure 2(c)); subsequently, its speed drops and pressure rises, as flow converges near the antistellar point (Figure 2(d)); finally, the high pressure and air temperature at the surface drive escape flow away the planet (Figure 2(b)).
Near the substellar point, sodium vaporizes from the magma ocean (positive surface flux F shown by the magenta curve in Figure 2(c)), because the vapor pressure is lower than that required by chemical equilibrium with the magma ocean (about 50% lower in this example). Sodium gas enters the atmosphere with the same temperature as the magma ocean beneath (atmospheric temperature (red solid curve) overlaps with the surface temperature (red dashed curve)). Away from the substellar point, the surface cools and the corresponding equilibrium pressure drops exponentially along with the surface temperature, creating a pressure gradient force accelerating the transport flow toward the night side (see the wind speed shown by the blue solid curve). In this process, the internal energy of the flow is converted to kinetic energy—as wind accelerates, the atmosphere becomes cooler than the surface. Around 33°, flow turns supersonic (marked by a blue dot). Beyond this transonic point, no information can be transported upstream to affect the mass flux and flow properties before that point. The surface temperature and the associated equilibrium pressure keep dropping toward the night side. At around 43°, the equilibrium pressure drops below the flow pressure, and sodium starts to infuse back into the magma ocean (F turns negative). At around 67°, the planet's surface solidifies and therefore can no longer provide a source of mineral vapor (sodium, in our model). That means the transported mass flux Φ would at most remain the same, if not be attenuated. While the surface is warmer than the flow above it (this is true for most of the day-side hemisphere), no infusion would occur and Φ remains unchanged.
When the flow reaches the night side (Figure 2(d)), where the surface temperature is always lower than the flow, vapor starts to infuse into the surface, as represented by a negative F. The attenuation of Φ leads to a pressure drop, which acts to accelerate and cool the flow. Along the way, supersaturation and condensation would occur (condensation is shown in a cyan curve, and the saturated regions are marked with a gray shading). Pressure drop keeps accelerating the flow until geometric convergence near the antistellar point causes mass accumulation. The mass accumulation give rise to a high surface pressure, which slows down the flow and turns it upward.9 Mass and energy are assumed to be conserved during this turning process.
The vertical escape process is shown in Figure 2(b). The flow density and pressure start high, accelerating the upward escape flow. The flow also becomes saturated soon after departing from the surface, if not already saturated at the surface, as its potential and kinetic energy increase at the expense of reducing its internal energy. Once saturated, condensation prevents further temperature drop in the escape flow (marked by gray shading in Figure 2(b)), and meanwhile, the mass flux is reduced. At the cost of losing mass flux, the rest of the flow achieves enough energy to escape from the planet's gravity field, inheriting the latent heating released by condensation. Around 200 planetary radii, flow turns supersonic, beyond which all mass has to escape. Assuming no momentum exchange between dust and the rest of gas, dust can escape the planet's gravity if and only if the total mechanical energy (kinetic energy plus potential energy) is greater than zero. In this example, this occurs around 90 planetary radii, marked by a green cross in Figure 2(b).
The same calculation assuming a SiO-dominant atmosphere yields a similar escape process (see Figure 3), except for two main differences. First, as the SiO equilibrium pressure at the surface is closer to saturation compared to sodium (due to the higher percentage of SiO in the magma), SiO-dominant atmosphere starts to condense even in the day side of the horizontal transport flow (Figure 3(c)). Second, the escape flux is two to three orders of magnitude smaller than what we obtained assuming a sodium-dominant atmosphere, which is expected because the equilibrium pressure of SiO is much lower than that of sodium (this will be discussed by the end of the next section).
Figure 3. Same as Figure 2 except for a SiO-dominant atmosphere.
Download figure:
Standard image High-resolution image4. Day-side Escape versus Night-side Escape for Generic Exoplanets
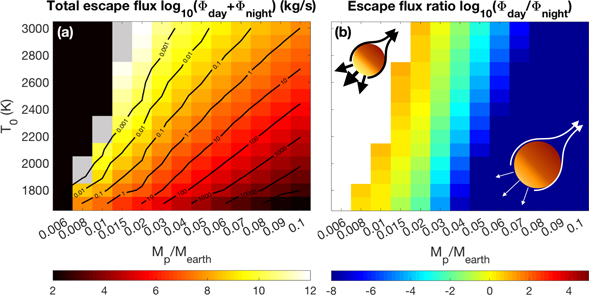
Using this idealized model, we can calculate the escape flux from the day-side and night-side pathways for generic disintegrating exoplanets. The total escape flux is shown in Figure 4(a) as a function of peak surface temperature and the planetary mass. As expected, the total escape increases with temperature and decreases with the planet's mass. Toward the limit of hot and small planets, the escape flux becomes so strong that the energy required to maintain it has the same order of magnitude as the total planetary thermal emission (gray shading). For planets in this regime, insolation has to be significantly stronger than what the planet's surface can emit in order to maintain the escape flow. Black shading marks the regime of the "runaway" escape state, as found by Lehmer et al. (2017) and Arnscheidt et al. (2019). In reality, the infinite escape flow is not achievable, because escape flux would require so much energy that the surface temperature would fall below the "runaway" threshold.
Figure 4. Summary of escape properties for various (T0, Mp) combinations. Shown from left to right are (a) the logarithm of the total escape flux in kg s−1, and (b) the logarithm of the ratio between the day-side escape and night-side escape. In panel (a), the parameter combinations where atmosphere escape would consume at least the same order of magnitude of energy as the planetary thermal emission is marked by a gray shading, and the parameter combinations leading to "runaway" escape is marked by a black shading on the upper-left corner. The e-folding time for the sodium reservoir (0.29% of total planetary mass) to be exhausted is shown by contours in units of megayears. Different flow field features are illustrated in panel (b): in the small and hot limit, escape is mostly contributed by the direct day-side escape, while the night-side escape dominates in the large and cool limit.
Download figure:
Standard image High-resolution imageAtmospheric escape would gradually exhaust the sodium reservoir on the planet; the reduced sodium concentration would in turn weaken the escape flow. The e-folding time of the sodium reservoir can be estimated as
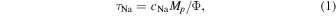
where cNa = 0.29% is the initial mass concentration of sodium for bulk silicate earth according to Schaefer et al. (2012), Mp is the mass of the planet, and Φ denotes the total escape rate. In this estimation, Φ is assumed to vary in proportion with the sodium concentration. We show τNa (units: megayears) in Figure 4(a) using black contours. The isolines of τNa are mostly aligned with those of the escape flux Φ (shading), indicating that the escape rate is the key factor in determining the "lifetime" of the sodium reservoir. According to the estimation by Perez-Becker & Chiang (2013) based on the transit depth, the escape flux should be around 107–108 kg s−1 for KIC-1255b, KOI-2700b, and K2-22b. This corresponds to an e-folding time of around 0.1–1 Myr for the sodium reservoir, according to Figure 4(a). After that, SiO and Mg, whose initial pressure contributions are one to five orders of magnitude smaller than sodium's (Schaefer & Fegley 2009; Miguel et al. 2011), would replace sodium, becoming the main component of the atmosphere (Kite et al. 2016). A similar calculation can then be carried out for the SiO-/Mg-dominant atmosphere (we repeat the calculation for SiO-dominant atmosphere in Figure 5), and so on and so forth.
Figure 5. Same as Figures 4(a) and (b) except the atmosphere is SiO instead of Na.
Download figure:
Standard image High-resolution imageAlthough both day-side and night-side escape decrease as temperature drops or planetary size increases, the day-side escape rate drops at a much faster rate, giving rise to a transition from day-side dominant escape to night-side dominant escape, as shown in Figure 4(b). Physically, this is because the day-side escape flow is driven by the difference between the pressure gradient force and gravity, while the day-to-night transport flow is driven by the pressure gradient force as a whole. The strong gravity on a relatively large planet would directly suppress the day-side escape flow but will not significantly affect the horizontal transport flow. The flow transported to the night side has to either escape from the planet or condense and fall onto the surface. Gravity will affect the percentage of mass flux that can eventually escape, but this factor is of order 1.10 As a result, the escape flow from the night side dominates that from the day side when the planet is relatively large.
FUV flux from the star could trigger additional day-side escape. With an FUV flux of 0.45 W m−2 (450 erg s−1 cm−2), the energy limit yields an escape rate of 6 × 105 kg s−1 (details are described in Appendix A), and this is a dominant contributor only in the regime marked in dark red or black in Figure 4(a).
We also repeat the same calculation for a SiO-dominant atmosphere and obtain qualitatively similar results (Figure 5). Compared to the sodium-dominant escape (Figure 4), SiO escapes at a much slower rate. At a given temperature and planetary mass, SiO escape is more difficult to be detected.
However, in reality, the atmosphere should be a mixture of volatile components (such as sodium and oxygen), less volatile components (such as SiO, Fe, and Mg), and a trace amount of refractory components (such as fayalite, pyroxene, and corundum). The dominant component is not necessarily the one that condenses, reacts, and thus provides energy. Actually, volatile species tend to take up a large portion in mass, but they are less inclined to condense. If we assume that the mixing ratio of different compositions stays fixed during the escape and transport processes,11 then the total pressure of the mixture is likely to be much greater than the pressure of a pure SiO atmosphere. This greater pressure would in turn enhance escape flow. This calculation would require one to know all the potential condensible/reactive matters in the flow and how the saturated/equilibrium pressure depends on temperature and thus is beyond the scope of our work.
Finally, we note that the time it takes to exhaust SiO/sodium is not long (far below 1 Gyr) according to the calculation. This does not mean that we would not detect disintegrating planets at all, although it does mean that only a small portion of existing planets will be detected.
5. Analytical Approximation for Escape Mass Flux
In this section, we make further simplifications to the escape model to obtain analytical approximations for the escape mass flux from the day side and the night side.
5.1. For the Day Side
Using conservation laws and transonic conditions, we have already been able to semianalytically solve for the day-side escape flux from a set of algebraic equations without integrating or iterating the 1D hydrodynamic escape model as done in Lehmer et al. (2017). Details are in Appendix A. Here, we make more simplifications to get an analytical approximation.
The first simplification we make is to ignore the surface temperature variations across the magma ocean and assume the day-side escape flow starts with the mean surface temperature 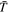 and the corresponding chemical equilibrium pressure
and the corresponding chemical equilibrium pressure 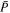 within the magma ocean,
within the magma ocean,
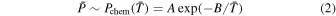
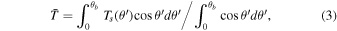
where Ts is the surface temperature set by radiative equilibrium, θb is the latitude where the surface solidifies, Ts(θb) = 1673 K, A = 109.6 Pa = 1010.6 Ba, and B = 38,000 K for sodium (Castan & Menou 2011).
The escape flow is initially unsaturated, due to the dilution of other components in the magma ocean (Henry's law), and will follow the dry adiabatic profile, TP−κ = const., where κ = R/Cp, Cp is the vapor's heat capacity at constant pressure, and R is the gas constant. Saturation would occur at Tsat. This condensation temperature can be determined by finding the intersection between the dry adiabat and the Clausius–Clapeyron relation,
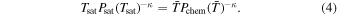
In the above equation, 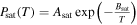 is the saturated vapor pressure at T. Asat = 109.54 Pa = 1010.54 Ba and Bsat = 12,070.4 K for sodium (Bowles & Rosenblum 1965). This saturation would occur around rsat from the center of the planet, where the gain of the gravity potential energy matches the loss of internal energy since the flow departures from the surface (we ignore the change of kinetic energy because they are small according to Figure 2(a)),
is the saturated vapor pressure at T. Asat = 109.54 Pa = 1010.54 Ba and Bsat = 12,070.4 K for sodium (Bowles & Rosenblum 1965). This saturation would occur around rsat from the center of the planet, where the gain of the gravity potential energy matches the loss of internal energy since the flow departures from the surface (we ignore the change of kinetic energy because they are small according to Figure 2(a)),
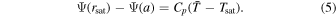
Here, Ψ(r) denotes the gravity potential at a distance r from the center of the planet toward the host star:
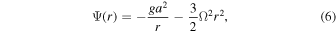
where g and a are the surface gravity and radius of the planet, and Ω is the orbital angular speed. The second term comes from the tidal force.
With Psat in such form, one can find 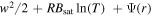 conserved as long as the flow is saturated (see Appendix A for the derivation). Here, w denotes the vertical flow speed, and T denotes the flow temperature. This conserved quantity can link the flow state at rc, the transonic point, and rsat, the point where flow just becomes saturated,
conserved as long as the flow is saturated (see Appendix A for the derivation). Here, w denotes the vertical flow speed, and T denotes the flow temperature. This conserved quantity can link the flow state at rc, the transonic point, and rsat, the point where flow just becomes saturated,
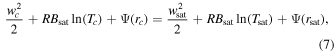
where wc and Tc denote the flow speed and temperature at rc. In the above equation, wsat is negligible compared to wc (according to Figure 4(a)). wc can be expressed with Tc using transonic conditions (Pierrehumbert 2010; Lehmer et al. 2017),
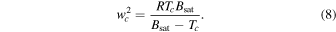
Because Tc ∼ 103 K, wc is around 500 m s−1, and thus the term 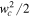 in Equation (7) is at least two to three orders of magnitude smaller than
in Equation (7) is at least two to three orders of magnitude smaller than 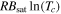 . Dropping the wc and wsat terms in Equation (7) and assuming that Ψ(rc) is close to the maximum gravity geopotential between the planet and the star, which is achieved at the Roche lobe
. Dropping the wc and wsat terms in Equation (7) and assuming that Ψ(rc) is close to the maximum gravity geopotential between the planet and the star, which is achieved at the Roche lobe 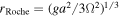 , we obtain an approximation for Tc with the help of Equation (5),
, we obtain an approximation for Tc with the help of Equation (5),
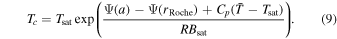
Utilizing the transonic conditions (Equation (8)) again, we get an approximation for the day-side escape flux,
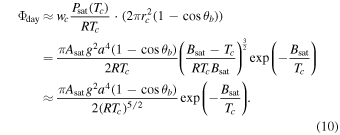
Again, θb is the latitude where the surface solidifies.
5.2. For the Night Side
The night-side escape flow is determined by how much air mass is transported from the day side to the night side and how much of this mass flux can eventually escape (demonstrated by Figures 2(c), (d), and (b)). An exact analytical solution cannot be achieved because the conservation laws are broken by condensation and by mass, momentum, and energy exchanges between transport flow and the magma ocean underneath. However, an analytical approximation is possible.
In the first stage, mineral vapor is gathered from the magma ocean and transported to the terminator. To estimate the cross-terminator mass flux, we need to know the flow speed and column mass (pressure divided by gravity acceleration g, assuming hydrostatic balance). As shown in Figure 2(c), the solidified surface on the day side almost plays no role in changing the transport flux (green curve flattens beyond the magma ocean). Within the magma ocean, the flow pressure is relaxed toward the chemical equilibrium pressure, which is set by the magma ocean surface temperature. Again, we assume the magma ocean has a uniform temperature 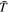 (Equation (3)), which corresponds to an equilibrium pressure of
(Equation (3)), which corresponds to an equilibrium pressure of 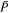 (Equation (2)).
(Equation (2)).
Flow usually turns supersonic within the magma ocean (Figure 2(c)). We here take the sonic speed at 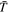 as an estimate of the flow speed,
as an estimate of the flow speed,
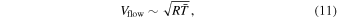
where R is the specific gas constant. Putting Equation (2) and Equation (11) together yields an estimation of the cross-terminator mass flux,
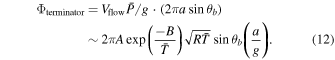
This estimation suggests that Φterminator would increase with T0, and that Φterminator is not sensitive to the planet size: the only factor directly related to planet size, a/g, is a fixed constant when the planetary density is fixed. The dependence of Φterminator on T0 is shown in Figure 6(e). Black curves are Φterminator diagnosed from the 1D transport model. Each curve corresponds to a different planet mass, and the collapse between different curves validates the insensitivity to planet size. The red dashed curve shows the analytical estimation in Equation (12). The variation of Φterminator with T0 is captured well, except for a slight overestimation.
Figure 6. Analytical estimation for the sodium escape from the day side and night side. Panels (a) and (b) show the day-side escape flux for various {T0, Mp} from the full model and from the analytical estimation (Equation (10)), respectively. Panels (c) and (d) are the same as panels (a) and (b), but for the night side. Equation (17) gives the analytical estimation for the night-side escape rate. Panel (e) shows the mass flux across the terminator as a function of substellar temperature T0. Black curves are mass flux diagnosed from the full transport model, and red dashed curves are the analytical estimation given by Equation (12). Each black curve corresponds to a different planet mass Mp. Panel (f) is similar to (e) but shows the mass flux decay on the night side as a function of Mp. Curves from top to bottom correspond to decreasing T0.
Download figure:
Standard image High-resolution imageIn the second stage, flow infuses back to the surface while passing through the cold night side. Assuming every molecule colliding with the surface gets trapped, the attenuation of mass flux Φ on the night side can be calculated,
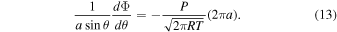
Substituting the definition 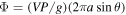 , we get
, we get
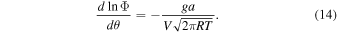
Assuming almost all internal energy has been converted to kinetic energy before flow enters the night side would allow us to substitute V with 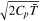 , where Cp is the vapor's heat capacity at constant pressure. Condensation is likely to occur on the night side, and then the flow temperature is fixed around 500 K by latent heating, as shown in Figure 2(d). This condensation temperature Tsat again can be determined by the subsaturation at the magma ocean surface (Equation (4)). We take Tsat as an estimation of T in Equation (14). The mass flux turning upward around the antistellar point can be approximated as
, where Cp is the vapor's heat capacity at constant pressure. Condensation is likely to occur on the night side, and then the flow temperature is fixed around 500 K by latent heating, as shown in Figure 2(d). This condensation temperature Tsat again can be determined by the subsaturation at the magma ocean surface (Equation (4)). We take Tsat as an estimation of T in Equation (14). The mass flux turning upward around the antistellar point can be approximated as
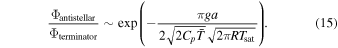
Unlike Φterminator, this factor has a stronger dependence on the planetary size than on temperature. The predicted 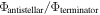 is shown by red dashed curves in Figure 6(f), in comparison with diagnosed ones (black solid).
is shown by red dashed curves in Figure 6(f), in comparison with diagnosed ones (black solid).
In the last stage, vapor transported from the day side deviates upward and escapes from the planet. In the parameter regime we explore here, internal energy alone typically is not enough for vapor to escape the gravity field (CpT < ag), meaning that part of the mass flux has to condense and give their energy to the rest-mass flux. As shown in Appendix C, the moist energy 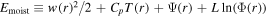 is conserved (Φ is the vertical mass flux, w is flow speed, and Ψ is the gravity potential). Equating the Emoist at the surface r = a and at infinity r = ∞ provides a constraint on the condensation ratio,
is conserved (Φ is the vertical mass flux, w is flow speed, and Ψ is the gravity potential). Equating the Emoist at the surface r = a and at infinity r = ∞ provides a constraint on the condensation ratio,
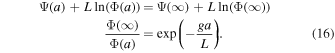
Here, we ignore the contribution from kinetic and internal energy, as they are small compared to the gravity potential in most cases we studied here. Combining Equations (12) and (15) with Equation (16) and realizing Φ(a) = Φantistellar gives the final estimation of the night-side escape flux,
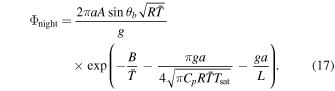
Figure 6(d) shows the above estimation for various {T0, Mp}, in comparison with the results from the full transport and escape model (Figure 6(c)). Their resemblance indicates the success of Equation (17). In fact, one more simplification can be made: the last term within the exponential (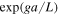 ) is always O(1), and omitting it will not introduce significant bias (not shown).
) is always O(1), and omitting it will not introduce significant bias (not shown).
The same formula can be applied to a SiO-dominant atmosphere. As shown in Figure 7, the day-side and night-side escape flux from the full escape model are reasonably predicted.
Figure 7. Same as Figure 6, except for a SiO-dominant atmosphere. Parameters used in the SiO escape calculation are summarized in Table 1.
Download figure:
Standard image High-resolution imageBy equating the day-side escape flux Φday (Equation (10)) and the night-side escape flux Φnight (Equation (17)), we can deduce the criteria dividing the regime of day-side dominant escape and the regime of night-side dominant escape,
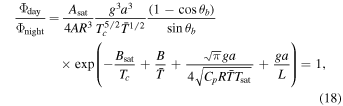
where Tc decays exponentially with ga as given by Equation (9). This first term within the exponential (second line) dwarfs all others in the above equation; therefore, night-side escape dominates day-side escape on relatively large planets. Due to the low escape rate and large mass reservoir, larger planets should have a longer lifetime and thus be more easily detected.
6. Inference for Leading and Trailing Tails
Although the day-side and night-side escape flows are assumed to follow pipes that are aligned with the planet and the star in the calculation above, by conserving angular momentum, we expect that the day-side escape flow would lead ahead of the planet in orbit and form a leading tail, and the night-side escape flow would lag behind and form a trailing tail. The lengths of the tails around disintegrating exoplanets are found to be comparable to the stellar radius (more than a hundred planetary radii!).
Tails of this length can only be explained if the dust particles in the tail are composed of refractory compositions (Rappaport et al. 2014; van Lieshout et al. 2014; Sanchis-Ojeda et al. 2015). Sublimation calculation suggests that 1 μm corundum or fayalite particles can take up to several orbital periods to vaporize, which allows them to travel over a hundred radii away from the planet under the impact of radiation pressure, before being completely vaporized (van Lieshout et al. 2014). To estimate the escape flux in this scenario, we apply the analytical solution from the previous section to a corundum (Al2O3)-dominant atmosphere. For a planet with a peak temperature of 2100 K, the maximum12 hydrodynamic escape flux that can be achieved is about 2 × 106 kg s−1 (both gas and dust included). This escape flux, however, is not enough to explain the observed transit depth (Brogi et al. 2012; Perez-Becker & Chiang 2013; Rappaport et al. 2014; Budaj et al. 2015; Sanchis-Ojeda et al. 2015), especially given that dust only accounts for a very small portion of the total mass flux. Therefore, the escape flux is likely to be mostly composed of more volatile species, and their properties would determine the escape rate—this is the scenario we try to understand in this work. With an escape flux of more than 108 kg s−1, various refractory components can be carried upward and all these components can condense as the temperature drops and become part of the dusty tail. Additionally, chemical reactions between gaseous volatile species may produce refractory compositions, and strong escape flow may be able to knock off a significant amount of refractory materials from the surface.
Besides the sublimation time of dust particles, the location of condensation may also affect the length of the tails. As shown in Figures 2(a) and (b) and 3(a) and (b), condensation occurs mostly within 10 planetary radii—this is only about a tenth of the tail length in observations (Brogi et al. 2012; Rappaport et al. 2012, 2014; Budaj et al. 2015; Sanchis-Ojeda et al. 2015). Energetically, cooling and condensation would only occur when flow is doing work against gravity or accelerating. After 10 planetary radii, the gravity of the planet would be too weak to induce any condensation, and the condensation rate converges to a relatively small constant that is controlled by the widening of the day-side and night-side pipes (the escaping flow can be accelerated by the pressure drop induced by the expansion of the cross section). A large amount of condensation beyond that distance is possible only if the escaping flow continues to do work against stellar gravity or if the escaping flow is accelerated rapidly by traveling in an elliptical orbit. Trajectory calculation considering angular momentum conservation and the potential of inertia may help answer this question quantitatively, and we have decided to leave it for future work.
In fact, radiation pressure and the pressure gradient force between the day side and night side have similar effects on the escaping flow: both turn the escaping flow from the hot day side (heading toward the star), where it emanates, toward the cold night side (heading away from the star). Radiation pressure is likely to dominate the pressure gradient force when the star is young and hot and the atmospheric pressure at the surface of the planet is low, and vice versa. The surface pressure, in turn, is controlled by the planetary temperature and the volatility of the vaporized materials. Also, the relative importance of the pressure gradient force and radiation pressure also depends on the location. Near the surface, where the pressure (and thus the gradient) is high, pressure gradient force will definitely dominate, because it needs to be greater than the planetary gravity to drive acceleration and the radiation pressure is less than 1% of the stellar gravity, which is dominated by the planetary gravity within the Hill sphere. However, the air pressure drops as the flow departs the planet, and at a far distance away from the planet, the pressure gradient force will become ignorable. The ratio of the integrated impulse induced by the pressure gradient and radiation pressure is still an open question that requires future studies.
For volatile components considered here in particular, radiation pressure may play a less important role, because dust composed of volatile species will vaporize almost "immediately" after they form. This means that the condensed-phase and the gas-phase parts of the escaping flow would travel along the same trajectory at the same speed. Then, a mass-weighted bulk radiation pressure coefficient can be defined to describe the magnitude of radiation pressure exerted on the gas and dust as a whole. Because radiation pressure seems to be strong only for particles around 0.1–1 μm (van Lieshout et al. 2014) and most of the mass stays in the gas phase, this bulk radiation pressure coefficient is likely to be small due to the dilution of large amounts gas-phase materials.13 As far as we see, there is no clear constraint determining whether the dust would be more volatile enriched or volatile depleted compared to its source (i.e., a magma ocean), because the species that have high equilibrium pressure at the surface and thus can escape faster would also sublime more easily aloft. This is something to be examined in future theoretical and observational works.
Interestingly, a lot of the parameter combinations we explored here yield a night-side escape that is even stronger than the day-side escape. Besides this, a day-side dominant escape only occurs on planets that are hot, small, and hence short lived. This further reduces the probability of observing such planets. Whether leading tail or trailing tail will be more common is a more complex question that requires consideration of the dusts' optical properties and the trajectory of the leading/trailing tails (more specifically, how elliptical the trajectory would be), and is out of the scope of current work. However, the ratio between the day-side and night-side escape flux may provide an upper bound for the ratio between the leading tail and the trailing tail, as radiation pressure can convert the day-side escape flow to the night-side one but not the reverse. The observations of tail properties may be able to put constraints on the mass and radius of these disintegrating exoplanets, which are poorly constrained because of their small sizes and thick dusty envelopes (van Lieshout & Rappaport 2018).
7. Conclusion
In this work, we attempt to understand the first-order anisotropy of the mineral escape flow from ultrahot rocky planets, a necessary step to explaining why some planets have trailing dusty tails, some have leading tails, and others have both (Brogi et al. 2012; Rappaport et al. 2014; Budaj et al. 2015; Sanchis-Ojeda et al. 2015). Instead of running a multidimensional hydrodynamic escape model, we depict the flow field using three 1D models: one for day-side escape, one for horizontal transport from the day side to the night side, and one for night-side escape. We attempt to capture, in this framework, the essential physical processes of mineral vapor escape, such as the phase changes, the exchanges in mass with the planetary surface, and the orders of magnitude pressure drop from the day side to the night side, which could be challenging for multidimensional simulations.
We demonstrate, using this first-order anisotropic model, that escape can occur not only on the ultrahot day side but also on the cold night side. This night-side escape flow is fed by mineral vapor transport from the day side and can be even stronger than the day-side escape when the planet is relatively cool and large. The night-side escape flow would naturally trail behind the planet by conserving angular momentum. In this physical picture, the pressure gradient force between the day side and night side plays a similar role to radiation pressure proposed by Rappaport et al. (2012, 2014), Sanchis-Ojeda et al. (2015), and van Lieshout et al. (2014). Planets dominated by the day-side escape tend to be hot and small, and the escape rates are high; the opposite is true for night-side-dominant escape (Figures 4(a) and (b)).
Useful inferences on planetary mass (the second question) could be obtained from the tail properties. Our results suggest that, although the total escape flux is affected by both temperature and planetary mass, the partition between day-side and night-side escape seems to be mainly controlled by the planetary mass. Therefore, with all other factors fixed, a larger and heavier planet is more likely to be followed by a trailing tail, and vice versa, in the absence of radiation pressure. Under the impact of radiation pressure, day-side escape flow could potentially be turned around and thereby trail behind the planet. A trailing tail, therefore, can be a result of radiation pressure or the pressure gradient between the day side and the night side. This degeneracy makes it hard to constrain the masses of planets with trailing tails, unless we know about the radiation pressure coefficients (this further requires knowing the composition and size of dust particles; van Lieshout et al. 2014). However, in order for a planet to have a leading tail, the day-side escape flow has to be significant and that can put an upper limit on the planetary mass. Applying this constraint to K2-22b, a disintegrating planet with a leading tail and a 2100 K substellar point temperature (Sanchis-Ojeda et al. 2015), suggests an upper bound of planetary mass around 0.03 Earth mass (based on Figures 4 and 5; the sodium and SiO calculation suggest roughly the same bound). After the chemical compositions of the escape flows are identified through spectrometry by future missions, we may be able to better constrain the planet size from the total escape flux and the partition between leading and trailing tails.
The advantage of this idealized framework is that it helps us to build up physical understandings of the escape process and offers guidance in deriving analytical approximations of the day-side and night-side escape rates, which can be used to explore a wide range of parameters such as chemical composition, planetary size, planetary gravity, and surface temperature. For FUV-driven hydrogen escape, Watson et al. (1981) derived a formula for the energy-limit escape rate. However, mineral vapor escape from rocky planets is far from this regime (Perez-Becker & Chiang 2013), preventing us from directly applying the energy-limit escape formula. For escape from the day side, we provide a new method to compute the exact escape rates semianalytically and to estimate the escape rate purely analytically, using conservation laws. This avoids doing iterations and integrations as in the original work (Lehmer et al. 2017). For the night-side escape, we obtain an analytical approximation solution. These analytical approximations accurately reproduce the escape rates from the full hydrodynamic model for both sodium- and SiO-dominant atmosphere (Figures 6 and 7) and may be applied to studies on planetary evolution and planetary spectrometry.
We thank Prof. Saul Rappaport, Prof. Andrew Ingersol, Prof. Edwin Kite, and Prof. Ming Cai for insightful discussions. F.D. is supported by NASA grants NNX16AR86G and 80NSSC18K0829, and W.K. was supported by the Lorenz/Houghton Fellowship in MIT while doing this work.
Appendix
As sketched in Figure 1, our model is composed of three parts: a day-side hydrodynamic escape model (Appendix A) and a horizontal transport model calculating the day-side to night-side mass transport induced by the pressure gradient force (Appendix B), connected to a night-side hydrodynamic escape model (Appendix C).
Phase change is considered explicitly in all these processes. This is necessary, because, unlike hydrogen or water vapor, which remain unsaturated or saturated all the way through, the mineral gas could undergo multiple transitions between the subsaturated and saturated states depending on the geometry and external energy sources. Saturated regions are demonstrated by the gray shading in Figure 1. The mineral gas starts its journey highly subsaturated when leaving the magma ocean, and then it can either escape directly from the day side or follow the surface to the night side before escaping from there. Whichever pathway it takes, the gas could become saturated through adiabatic expansion. The expansion is partially caused by the acceleration induced by the pressure gradient force (this applies to both vertical escape and horizontal transport), and partially caused by the geometric expansion along each pathway. For gas taking the day-side escape pathway, geometry always causes expansion as the escape cross section increases with the square of the distance from the planet r (demonstrated by a cone drawn in dashed lines in Figure 1). For gas taking the night-side escape pathway, geometry causes expansion before the terminator as the transport circumference increases along the path; beyond the terminator, the transport circumference starts to shrink, compressing the gas and turning it subsaturated.
Vertical escape of condensible matters have been considered in previous works. Lehmer et al. (2017) has extended the 1D vertical escape model for saturated water vapor escape by replacing the dry air state equation with the Clausius–Clapeyron relation. However, we did not directly borrow their model, because (1) we need to explicitly consider the multiple conversions between saturated and subsaturated states of the mineral gas flow, and (2) we want to account for the condensation-induced attenuation of mass flux, which, in their calculation, is considered conserved. Perez-Becker & Chiang (2013) consider the mineral gas escape from the day side as we do here. But instead of explicitly accounting for the phase transitions, they prescribe a condensation profile. They found that the escape flux could vary by orders of magnitude when different condensation ratio profiles are prescribed (Figure 4 in their paper), motivating us to explicitly discuss the condensation process.
In the rest of the appendix, we will present the details of the three components of our model.
Appendix A: 1D Hydrodynamic Escape Model for the Day Side
Since Parker's work in the 1960s (Parker 1965), the 1D hydrodynamic escape model has been used to calculate the hydrogen escape from early planetary atmospheres and hot Jupiters (e.g., Kasting & Pollack 1983; Watson et al. 1981; Yelle 2004; Tian et al. 2005; Murray-Clay et al. 2009; Zahnle & Catling 2017; Zahnle et al. 1990), and the stream vapor escape from early icy moons and exoplanets (Lehmer et al. 2017; Arnscheidt et al. 2019). These works are summarized by review papers, Owen (2019) and Lammer et al. (2008).
Our model is built upon Lehmer et al. (2017), but we will add an adiabatic escape before the flow becomes saturated. The governing equations here include a mass continuity equation, a momentum equation, and an energy conservation equation. The first two can be written as follows:
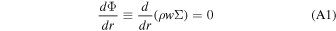
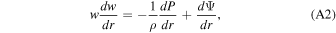
where Φ refers to the mass flux, w to vertical velocity, D to condensation, ρ to atmospheric density, r to denote the distance from the center of the planet, and g and a to denote the surface gravity and the radius of the planet. Parameters used in this study is summarized in Table 1. Σ is the cross section of the escaping flow. For the day side, we assume that the flow is radial, and thus Σ increases with the square of r. These assumptions are supported by the multidimensional hydrodynamic escape calculation done by Debrecht et al. (2019),

Ψ denotes the gravity potential,
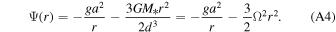
The second term in the above formula is the tidal term. M* is the mass of the host star, d is the distance between the star and the planet, and Ω is the orbital angular speed. This tidal term would turn the gravity force toward the host star beyond Roche lobe 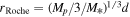 , where Mp = ga2/G is the mass of the planet. This has been shown to be able to significantly enhance the escape flux (Murray-Clay et al. 2009).
, where Mp = ga2/G is the mass of the planet. This has been shown to be able to significantly enhance the escape flux (Murray-Clay et al. 2009).
Table 1. Parameter Definitions
| Symbol | Name | Definition/Value |
|---|---|---|
| M* | mass of host star | 0.67 MSun |
| d | semimajor axis | 0.013 au |
|
FUV flux received by the planet | 0.45 W m−2 (450 erg s−1 cm−2) |
| hν0 | mean energy of FUV photon | 0.20 eV |
| TN | night-side surface temperature | 50 K |
| Tm | melting temperature of magma | 1673 K |
| α | exchange efficiency at vapor-condensed interface | 1 |
| Sodium-dominant atmosphere | ||
| μ | molecular weight | 0.023 kg mol−1 (23 g mol−1) |
| L | vaporization enthalpy | 96.96 kJ mol−1 (9.696 × 1011 erg mol−1) (Fink & Leibowitz 1995) |
| Cp | heat capacity | 903.3 J kg−1 K−1 (9.033 × 106 erg g−1 K−1) |
| Achem | parameter for chemical equilibrium pressure | 109.6 Pa (1010.6 Ba) (Castan & Menou 2011) |
| Bchem | parameter for chemical equilibrium pressure | 38000 K (Castan & Menou 2011) |
| Asat | parameter for saturated vapor pressure | 109.54 Pa (1010.54 Ba) (Bowles & Rosenblum 1965) |
| Bsat | parameter for saturated vapor pressure | 12070.4 K (Bowles & Rosenblum 1965) |
| ρdroplet | density of sodium droplet | 968 kg m−3 (0.968 g cm−3) |
| Adroplet | reflectivity of sodium droplet | 0.1 (Barnett et al. 1986) |
| cNa | sodium concentration in mantle and crust | 0.29% (Schaefer et al. 2012) |
| SiO-dominant atmosphere | ||
| μ | molecular weight | 0.044 kg mol−1 (44 g mol−1) |
| L | vaporization enthalpy | 411.5 kJ mol−1 (4.115 × 1012 erg mol−1) (Fink & Leibowitz 1995) |
| Cp | heat capacity | 661 J kg−1 K−1 (6.61 × 106 erg g−1 K−1) |
| Achem | parameter for chemical equilibrium pressure | 1014.086 Pa (1015.086 Ba) |
| Bchem | parameter for chemical equilibrium pressure | 70300 K |
| Asat | parameter for saturated vapor pressure | 1013.1 Pa (1014.1 Ba) (Bowles & Rosenblum 1965) |
| Bsat | parameter for saturated vapor pressure | 49520 K (Bowles & Rosenblum 1965) |
| Al2O3-dominant atmosphere | ||
| μ | molecular weight | 0.102 kg mol−1 (102 g mol−1) |
| L | vaporization enthalpy | 643 kJ mol−1 (6.43 × 1012 erg mol−1) (van Lieshout et al. 2014) |
| Cp | heat capacity | 755 J kg−1 K−1 (7.75 × 106 erg g−1 K−1) |
| Achem | parameter for chemical equilibrium pressure | 1012.5 Pa (1013.5 Ba) |
| Bchem | parameter for chemical equilibrium pressure | 71380 K |
| Asat | parameter for saturated vapor pressure | 1016.1 Pa (1017.1 Ba) (van Lieshout et al. 2014) |
| Bsat | parameter for saturated vapor pressure | 77365 K (van Lieshout et al. 2014) |
Download table as: ASCIITypeset image
The third equation is the equation of state. When the flow is undersaturated, the equation of state is the conservation of potential temperature Θ (or entropy equivalently),
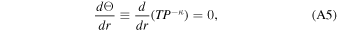
where κ = R/Cp. For sodium, κ = 2/5. When the flow becomes saturated, the equation of state is the Clausius–Clapeyron relation,
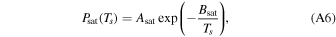
where Asat = 109.54 Pa = 1010.54 Ba, and Bsat = 12,070.4 K for sodium vapor (Bowles & Rosenblum 1965).
As Equation (A1) shows, we assume no mass loss even when condensation happens, as in Lehmer et al. (2017). This assumption is proper for sodium vapor escape on the day side, because the volatile sodium droplets would absorb the stellar radiation from the day side and quickly get re-evaporated. Actually, a sodium droplet under radiative equilibrium with the stellar radiation  would have a temperature of
would have a temperature of 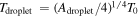 , where Adroplet = 0.1 is the reflectivity of liquid sodium (Barnett et al. 1986). This would lead to an evaporation flux of
, where Adroplet = 0.1 is the reflectivity of liquid sodium (Barnett et al. 1986). This would lead to an evaporation flux of 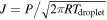 per unit surface area. A droplet of rdroplet = 10 μm would completely vaporize within
per unit surface area. A droplet of rdroplet = 10 μm would completely vaporize within 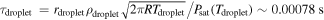 , with T0 = 2500 K and ρdroplet = 968 kg m−3. That means the droplet re-evaporates almost immediately after it reaches its equilibrium temperature. Given the high volatility of sodium, a better estimation of sodium dust's lifetime under the Sun is given by the energy budget
, with T0 = 2500 K and ρdroplet = 968 kg m−3. That means the droplet re-evaporates almost immediately after it reaches its equilibrium temperature. Given the high volatility of sodium, a better estimation of sodium dust's lifetime under the Sun is given by the energy budget 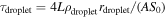 , which gives 0.75 s. Such a short sodium droplet lifetime indicates that the mass flux of vapor is indeed almost conserved. This energy source is taken into account by ignoring the mass loss in the mass continuity equation. However, as will be discussed in Appendix C, the re-evaporation of the night-side escape flow is negligible in the absence of stellar radiation.
, which gives 0.75 s. Such a short sodium droplet lifetime indicates that the mass flux of vapor is indeed almost conserved. This energy source is taken into account by ignoring the mass loss in the mass continuity equation. However, as will be discussed in Appendix C, the re-evaporation of the night-side escape flow is negligible in the absence of stellar radiation.
The property of escape flow before condensation can be solved from Equations (A1) and (A2) with Equations (A5) and (A6), given the initial condition at the surface,
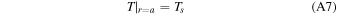
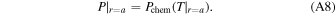
Here, we assume the surface vapor temperature T∣r=a is the same as the magma ocean and the surface vapor pressure P∣r=a is in chemical equilibrium with the ocean. In reality, the vapor pressure would be lower because vaporization requires the atmosphere to be subsaturated at the surface. We take the form of Pchem from Castan & Menou (2011),
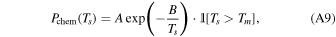
where Achem = 109.6 Pa = 1010.6 Ba and Bchem = 38,000 K. This equilibrium pressure is much lower than the saturated pressure for the same temperature, because sodium only takes a small fraction in the magma ocean, and the equilibrium pressure drops following Henry's law. 1[Ts > Tm] = 1 within the magma ocean when the surface temperature Ts is higher than the melting temperature of the magma Tm = 1673 (Kite et al. 2016) and 1[Ts > Tm] = 0 elsewhere.
As pointed out by Kasting & Pollack (1983), Watson et al. (1981), Yelle (2004), Tian et al. (2005), Murray-Clay et al. (2009), Zahnle & Catling (2017), and Zahnle et al. (1990), the above equation is singular around the transonic point, and requiring a smooth transition across the singular point puts constraints on the flow properties there. Because of the unforeseeable condensation, our situation is slightly more complicated than the dry adiabatic escape (Pierrehumbert 2010) and the pure steam escape (Lehmer et al. 2017). Therefore, we need to consider two possibilities: flow turning supersonic while it is undersaturated, versus flow turning supersonic while it is saturated.
For the first case, some manipulations of Equations (A1), (A2), and (A5) lead to
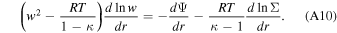
To avoid jumps in w, the left-hand side and right-hand side have to vanish simultaneously at the transonic point, which leads to the transonic condition below,
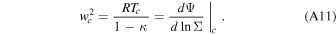
The subscript  indicates that certain variables are evaluated at the transonic point.
indicates that certain variables are evaluated at the transonic point.
For the second case (i.e., the flow becomes saturated before the transonic point), Equations (A1), (A2), and (A9) give
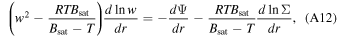
which, in turn, leads to a different transonic condition,
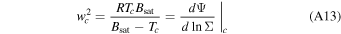
With the transonic conditions, one may make a guess of wc, solve for Tc and rc, and then integrate the momentum equation (Equation (A2)) downward to the surface to match the bottom boundary condition given by Equations (A7) and (A8), as done in Lehmer et al. (2017). We here do it in a slightly different way. Instead of making guesses and doing iterations, we take advantage of conservation laws to directly solve for the flow properties at the transonic point and thereby the escape flux, saving us from going through the iteration.
We first assume that escape flow is still undersaturated when turning supersonic. For an undersaturated flow, there are three conserved quantities, potential temperature Θ, mass flux Φ, and energy density
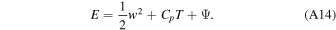
The conservation of Θ, Φ, and E before the transonic point yields
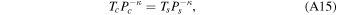
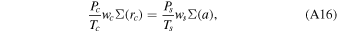
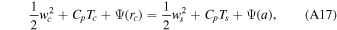
where the subscript  denotes quantities evaluated at the surface, r = a. Combining Equations (A15)–(A17) with the transonic condition (Equation (A11)), we get five equations, from which the five unknowns, rc, wc, Tc, Pc and ws, can be solved.
denotes quantities evaluated at the surface, r = a. Combining Equations (A15)–(A17) with the transonic condition (Equation (A11)), we get five equations, from which the five unknowns, rc, wc, Tc, Pc and ws, can be solved.
We then examine whether the escape flow is indeed undersaturated all the way to the supersonic point by comparing Pc with the saturated vapor pressure Psat(Tc). If the escape flow turns out to be saturated before the transonic point, we can only apply the {Θ, Φ, E} conservation laws before saturation occurs:

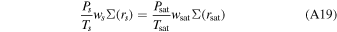
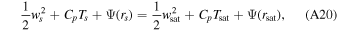
where 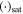 denotes quantities evaluated at the saturation level rsat. Beyond rsat, E and Θ are no longer conserved, instead we have the Clausius–Clapeyron relation (Equation (A6)) and a Bernoulli function type of conserved quantity (can be derived from Equation (A2) by replacing ρ, P with T using the Clausius–Clapeyron relation and ideal gas law) linking rsat and rc:
denotes quantities evaluated at the saturation level rsat. Beyond rsat, E and Θ are no longer conserved, instead we have the Clausius–Clapeyron relation (Equation (A6)) and a Bernoulli function type of conserved quantity (can be derived from Equation (A2) by replacing ρ, P with T using the Clausius–Clapeyron relation and ideal gas law) linking rsat and rc:
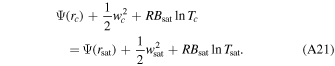
Then, with eight equations, namely, Equations (A13), (A16), (A6), and (A18)–(A21), the eight unknowns, rc, Tc, Pc, wc, ws, rsat, Psat, and Tsat, can be solved.
With the flow properties at the transonic point, we can directly calculate the escape flux,

as well as other conserved quantities. Then, flow properties at any given location r can be solved from the conservation laws, which are all algebraic equations.
Because the surface temperature decreases away from the substellar point, and the dependence of P on T is highly nonlinear (exponential), we divide the region covered by magma ocean into Nθ isothermal sectors and calculate the total escape rate by summing over the escape from each sector. Direct escape beyond the magma ocean is ignored. In most cases, we found Nθ = 5 is good enough. Too few sectors will lead to underestimation of the escape flux.
Absorption of UV flux from the star triggers ionization in the interior of the escape flow, which in turn leads to heating and stronger escape. Simulating this would require explicitly coupling ionization, radiative transfer models with the hydrodynamic escape model as done in Murray-Clay et al. (2009), and is out of our scope here. Actually, as pointed out by Perez-Becker & Chiang (2013), energy deposition by photoionization is not necessary for driving an escape flow, because most of the disintegrating terrestrial planets are small in size and hence have weak gravity. To get an order of magnitude estimate, we take the energy-limit escape given by Watson et al. (1981),
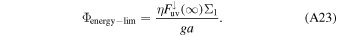
In the above equation,  is the efficiency for FUV flux with mean photon energy of hν0 = 20 eV to be converted to thermal energy in the vapor. Ionization takes energy Eionize; this part of the energy cannot be thermalized until recombination (ignored) happens. Σ1 is the cross section of the escape flow where the FUV flux is absorbed (optical depth equals one). Because we only attempt to get an estimation for orders of magnitude, we let Σ1 = πa2 for simplicity. The downward FUV flux
is the efficiency for FUV flux with mean photon energy of hν0 = 20 eV to be converted to thermal energy in the vapor. Ionization takes energy Eionize; this part of the energy cannot be thermalized until recombination (ignored) happens. Σ1 is the cross section of the escape flow where the FUV flux is absorbed (optical depth equals one). Because we only attempt to get an estimation for orders of magnitude, we let Σ1 = πa2 for simplicity. The downward FUV flux 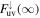 at the top of the atmosphere is set to 0.45 W m−2. This value has been used to calculate the hydrogen escape from hot Jupiter whose host star is not a T Tauri star (Murray-Clay et al. 2009). The UV-induced escape turns out to be around 106 kg s−1, negligible compared to the thermally driven escape for most cases except those marked by the dark red color in Figures 4(a) and 5(a).
at the top of the atmosphere is set to 0.45 W m−2. This value has been used to calculate the hydrogen escape from hot Jupiter whose host star is not a T Tauri star (Murray-Clay et al. 2009). The UV-induced escape turns out to be around 106 kg s−1, negligible compared to the thermally driven escape for most cases except those marked by the dark red color in Figures 4(a) and 5(a).
Appendix B: 1D Horizontal Transport Model
Our horizontal transport model is built upon that of Ingersoll et al. (1985), which was used to calculate how SO2 is transported from the day side to the night side of Io. We will not repeat the derivations; rather, we will present the equations and highlight the changes we made. Interested readers are referred to Ingersoll et al. (1985) for more details. The governing equations include the conservation of vertically integrated mass flux, momentum flux, and energy flux:
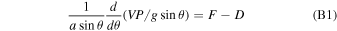
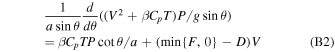
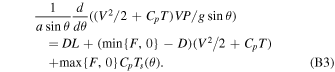
We use V for the flow speed, P for surface atmosphere pressure, T for average air temperature, Ts for surface temperature, F for the mass exchange with the surface (positive for vaporization), L for latent heat, a for the planet radius, and g for the gravity acceleration rate of the planet. Parameters used in this study are summarized in Table 1. The mass exchange F is positive (negative) when the atmosphere pressure P is lower (higher) than Pchem, the chemical equilibrium pressure with the magma ocean,
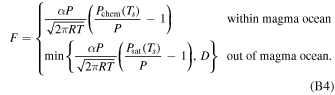
Physically, the above formula means that a proportion α of the total number of collisions per unit time per area 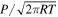 act to restore the vapor pressure toward the equilibrium pressure Pchem(Ts). With α = 1 (default), every collision counts. We ignore the fact that the exchange efficiency is usually less than 1; this becomes increasingly important when the surface temperature is relatively warm (Haynes et al. 2002). Meanwhile, we also ignore the turbulence induced exchange in the surface boundary layer, which was found to be unimportant in Ingersoll (1989) in the context of Io and Castan & Menou (2011) in the context of tidally locked super-Earth. With the turbulence drag coefficient Cd set to 0.01 as in Ingersoll et al. (1985), the characteristic speed corresponding to the turbulent exchange is only CdV ≲ 20 m s−1. This is much smaller than that corresponding to F, which is close to the sound speed.
act to restore the vapor pressure toward the equilibrium pressure Pchem(Ts). With α = 1 (default), every collision counts. We ignore the fact that the exchange efficiency is usually less than 1; this becomes increasingly important when the surface temperature is relatively warm (Haynes et al. 2002). Meanwhile, we also ignore the turbulence induced exchange in the surface boundary layer, which was found to be unimportant in Ingersoll (1989) in the context of Io and Castan & Menou (2011) in the context of tidally locked super-Earth. With the turbulence drag coefficient Cd set to 0.01 as in Ingersoll et al. (1985), the characteristic speed corresponding to the turbulent exchange is only CdV ≲ 20 m s−1. This is much smaller than that corresponding to F, which is close to the sound speed.
Within the magma ocean, the equilibrium pressure is determined by the chemical equilibrium between the gas phase and the dissolved phase (Equation (A9)). Outside of the magma ocean, the equilibrium pressure instead is given by the Clausius–Clapeyron relation (Equation (A6)). Another change is that there is no sodium reservoir at the surface outside of the magma ocean, therefore, the outward mass flux F cannot exceed the amount of local condensation D. This corresponds to the 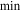 operator in Equation (B4).
operator in Equation (B4).
We assume the surface temperature is in radiative equilibrium close to the substellar point, and it gradually cools down until it reaches an arbitrary minimum night-side temperature TN = 50 K14 (Castan & Menou 2011; Kite et al. 2016):
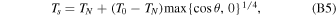
θ is the angle distance from the substellar point, and T0 is the substellar point. In reality, the surface temperature would deviate from the radiative equilibrium because of the greenhouse effect and blocking of solar radiation by dust in the escape flow (Perez-Becker & Chiang 2013).
A major change we make here is to explicitly consider the condensation due to oversaturation. The condensation D is positive when the gas pressure P is higher than the saturated vapor pressure Psat(T). D not only enters the mass equation (Equation (B1)) but also the momentum and energy equations (Equations (B2) and (B3)) because the condensed mass will take its momentum and energy with it so that the flow speed and the flow energy density will not be affected. Meanwhile, condensation will cause a latent heating release DL in the interior of the flow (Equation (B3)), preventing further temperature drop in the flow.
We integrate Equations (B1)–(B3) from the substellar point to the night-side using finite difference method. When the atmosphere is undersaturated, D equals zero. We can integrate forward the mass flux 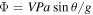 and the dry energy density of the flow E = V2/2 + CpT knowing the surface exchange flux F, which in turn can be calculated from Equation (B4) given Ts, ,T and P at the current grid point:
and the dry energy density of the flow E = V2/2 + CpT knowing the surface exchange flux F, which in turn can be calculated from Equation (B4) given Ts, ,T and P at the current grid point:
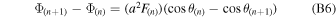
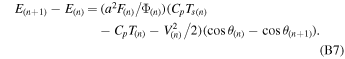
Subscripts in the above equation denote the index of the grid point. With Φ(n+1) and E(n+1) solved from the above equations, the number of unknowns reduces to one. The new grid points' T(n+1) and P(n+1) are linked with V(n+1) through
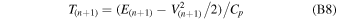
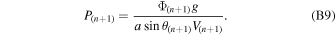
Substituting the above equations to the finite-differenced momentum equation (Equation (B2)) leads to
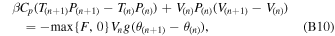
from which V(n+1) can be solved.
When the flow becomes saturated, D is no longer zero and is unknown, but the Clausius–Clapeyron relation will link P with T, keeping the total number of unknowns at three. To make the integration faster, we cancel D in Equations (B1)–(B3) to get
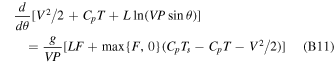
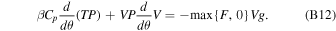
Rewriting the above equations using finite difference and combining the definition of F in Equation (B4) and the Clausius–Clapeyron relation in Equation (A6) yield an algebraic equation set, from which V, T in the next grid point can be solved knowing the current state of the flow.
The reservoir constraint in the formula for F (Equation (B4)) needs some additional care, because the upper bound for F is set by the unknown condensation rate D. For regions within the magma ocean, the reservoir constraint is not relevant. The night side (θ > 90°) is also one of the unconstrained regions because the surface temperature TN = 50 K is cold enough to prevent any re-evaporation. However, most of day-side "land" surface can be much warmer than the vapor on top of it. Thus, whatever condensed out of the atmosphere would be re-evaporated from the surface at a rate prescribed by the saturated vapor pressure at the surface, but this re-evaporation should not exceed the condensation, as the solidified surface does not continuously supply sodium.
For these regions, we first solve Equation (B11) and (B12) assuming the reservoir limit has been reached, i.e., F = D > 0. Under this limit, the mass flux Φ will not change,

With the above mass continuity equation and the Clausius–Clapeyron relation (Equation (A6)), the unknowns in Equations (B11) and (B12) reduce to T and D, and everything about the flow at the new grid point can be solved. Then, we compare the above F solution with the surface flux intended by the pressure imbalance ignoring the reservoir constraint
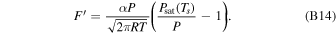
If  , then the D = F assumption is valid; otherwise, we recalculate D, T without the reservoir constraint. Solving the reservoir-constrained situation first turns out to be critical for the stability of the integration, because without reservoir constraint, the intended surface flux could be gigantic and that could lead to nonphysical solutions.
, then the D = F assumption is valid; otherwise, we recalculate D, T without the reservoir constraint. Solving the reservoir-constrained situation first turns out to be critical for the stability of the integration, because without reservoir constraint, the intended surface flux could be gigantic and that could lead to nonphysical solutions.
As mentioned by Ingersoll et al. (1985) and Castan & Menou (2011), one needs to make a guess of the pressure at the substellar point P0 to start the integration. A too large P0 (too close to the Pchem there) will make the mass gain from the magma ocean F not large enough to support the flow. In the midst of the integration, the flow will slow down and return, inconsistent with the boundary condition V = 0 at the antistellar point. A too small P0 will lead to too strong sublimation and too fast acceleration so that the solution will no longer exist beyond a certain point. We identify these two types of mistakes and avoid them by adjusting the initial guess of P0 until a smooth solution is found for the whole domain.
No mass can pass the antistellar point by definition. We stop the integration when the speed drops below one-half of the peak speed, and we expect the flow to turn upward beyond this point as sketched in Figure 1.
Appendix C: 1D Hydrodynamic Escape Model for the Night Side
The governing equations here again include the conservation of mass flux, momentum flux, and energy flux:
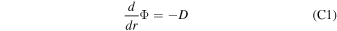
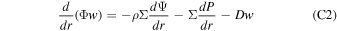
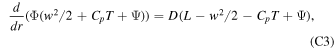
where D represents the mass loss due to condensation, and the definition of the other symbols follows that in the day-side hydrodynamic model.
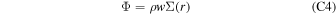
is the upward mass flux and
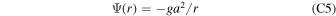
is the gravity potential. For any given r, the flow cross section is given by
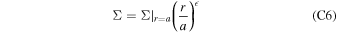
where  is a small real number. Other parameters used in this study are summarized in Table 1. As sketched in Figure 1, for the night side, we let
is a small real number. Other parameters used in this study are summarized in Table 1. As sketched in Figure 1, for the night side, we let  = 0.2, and this corresponds to a slowly expanding night-side cone away from the planet. The night-side escape flux is relatively insensitive to
= 0.2, and this corresponds to a slowly expanding night-side cone away from the planet. The night-side escape flux is relatively insensitive to  , unless
, unless  is smaller than 0.02. The insensitivity of the escape rate to
is smaller than 0.02. The insensitivity of the escape rate to  is because we fix the mass flux at the surface. As demonstrated in Section 5.2, the ratio between the mass flux that eventually escapes from the night side and the flux that we imposed at the bottom boundary of the escape model is determined by what percentage of the escape gas needs to give their latent heating up to the remaining gas (by condensing) so that the remaining gas has enough energy to escape from the planetary gravity field. However, we do notice that, with an extremely small
is because we fix the mass flux at the surface. As demonstrated in Section 5.2, the ratio between the mass flux that eventually escapes from the night side and the flux that we imposed at the bottom boundary of the escape model is determined by what percentage of the escape gas needs to give their latent heating up to the remaining gas (by condensing) so that the remaining gas has enough energy to escape from the planetary gravity field. However, we do notice that, with an extremely small  , the escape flow would be geometrically confined to a subsonic breeze, just like what happens when stellar pressure is imposed onto the day-side escape flow in Murray-Clay et al. (2009).
, the escape flow would be geometrically confined to a subsonic breeze, just like what happens when stellar pressure is imposed onto the day-side escape flow in Murray-Clay et al. (2009).
Because the escape flow on the night side does not receive direct radiation from the star, mineral vapor, once condensed, can hardly re-evaporate. Therefore, we think it is necessary to consider not only the latent heating release but also the mass loss and pressure drop due to condensation D, which is ignored in previous works, e.g., Perez-Becker & Chiang (2013), Lehmer et al. (2017), and Zahnle & Catling (2017). In our calculation, we will ignore the momentum exchange between dust and the rest vapor, and thus we would expect a different speed distribution and thus a different trajectory for the dusty and gaseous tails. As shown below, the night-side mass flux at the surface is set to be equal to the mass flux of the horizontal transport flow. Ignoring mass loss due to condensation as in previous studies is equivalent to forcing a 100% escape of whatever transported close to the antistellar point. This could be unphysical because we would expect zero escape if the planetary gravity is indefinitely strong.
This condensation-induced mass loss is represented by D in Equations (C1)–(C3). We let D > 0 whenever the atmospheric pressure P is higher than the saturated vapor pressure Psat (Equation (A6)), and re-evaporation (D < 0) happens when P < Psat.15 We stop the re-evaporation by turning the flow undersaturated, when the local upward mass flux Φ equals/exceeds that the flow begins with.
The initial state of the night-side escape model is connected with the final state of the horizontal transport model through mass flux and energy flux continuity. As mentioned in Appendix B, we stop the horizontal transport when the flow speed drops below 50% of its peak value and force the flow turn upward. At this turning point, complex physics processes such as turbulent mixing, conversions between kinetic energy and thermal energy, and phase change may occur, and fully resolving these processes would require a 3D hydrodynamic simulation that can deal with orders of magnitude pressure change in a short distance, which is beyond the scope of our work. For simplicity, we take the final energy flux and mass flux from the horizontal transport model and use it as the initial condition for the vertical escape model:
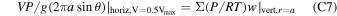
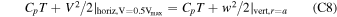
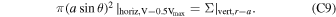
We call the above equations the connection conditions, connecting the "last moment" in horizontal transport model and the "first step" in the vertical escape model. This way, we conserve the energy and mass input from the horizontal flow while allowing the high pressure formed at the antistellar point to slow down the horizontal flow and convert the associated kinetic energy to thermal energy.
This connection condition could lead to an initial state that is supersaturated. It is particularly likely to happen when the planetary gravity is strong, as escape flow would get trapped and become dense. If the connection condition yields an initial state T, P, where P > Psat(T), we first let the vapor at the surface first undergo an initial condensation without changing its w, so that the adjusted 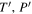 follow the Clausius–Clapeyron relation:
follow the Clausius–Clapeyron relation:
We solve the adjusted 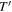 from the above equation, and then update the pressure using
from the above equation, and then update the pressure using 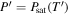 .
.
Starting from the surface, flow is usually undersaturated, except in some rare cases, where vapor starts superdense on the night side (to be discussed later). For undersaturated escape flow, three conserved quantities can be found after some term rearrangements of Equations (C1)–(C3): mass flux Φ, energy E, and potential temperature Θ:
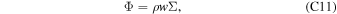
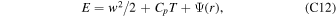
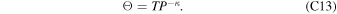
Φ, E, and Θ can be calculated given the initial condition.
Then w, T, and P can be solved from the above algebraic equations, until the flow cools down and turns saturated. The location where flow turns saturated rsat can be calculated by solving Equations (C11)–(C13) together with the Clausius–Clapeyron relation (Equation (A6)).
After the flow turns saturated, the atmosphere pressure P is linked with temperature T through the Clausius–Clapeyron relation (Equation (A6)). Besides this relation, another two conserved quantities can be derived from Equations (C1)–(C3):
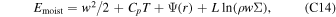
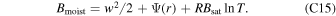
The moist energy Emoist is conserved for undersaturated flow, too. Emoist and Bmoist can be calculated before doing the integration, knowing rsat and the vapor properties there. Then, we can solve the w, P, and T profiles from Equations (C14), (C15), and (A6).
As Σ increases with r, vapor becomes thinner and colder. Eventually, vapor would either condense into dust, or it would stop behaving like fluid as the collision between molecules becomes less and less frequent. The latter becomes relevant beyond the exobase, whose definition is
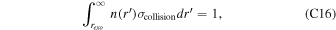
where σcollision is the collision cross section of sodium. For simplicity, we treat both cases as condensation. That means all vapor will condense by the end. Once condensation happens, we assume the dust's kinetic energy is conserved. Those with kinetic energy higher than the highest potential along its path will be able to escape, and the rest will fall back to the surface. Because the escape flow's kinetic energy always increases with r, an equivalent way to state the escape criterion is that dust can escape the planetary gravity if and only if they condense beyond rescape:
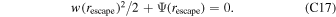
With rescape, the escape flux can be determined as
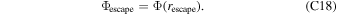
Similar to the horizontal transport model, singularity forms when flow turns supersonic. This has been noted by Kasting & Pollack (1983), Watson et al. (1981), Yelle (2004), Tian et al. (2005), and Murray-Clay et al. (2009). Actually, the connection conditions (Equation (C7))–(C9) do not fully constrain the flow properties at the surface. Instead, there is one degree of freedom left. We thus need to make a guess for the initial speed w∣r=a. A too large initial w∣r=a would lead to an unphysical large pressure drop due to the adiabatic cooling and/or condensation, which, in turn, accelerates the flow even more. Beyond a certain point, the solution will no longer exist. On the other hand, starting from too small initial w∣r=a, the flow would end up slowing down and turning backward. Only a proper initial guess allows the solution to pass the singularity smoothly. We find out this proper initial condition through a binary search.
Appendix D: Other Remarks for the Model
We here focus on a sodium-dominant atmosphere, but our method can easily be applied to other less volatile components, such as SiO, Mg, and even SiO2, Fe, Fe2SO4, MgSO3, and Al2O3 (van Lieshout et al. 2014). The orbital parameters are taken from from KIC-1255b (Brogi et al. 2012; van Lieshout & Rappaport 2018), as summarized in Table 1.
Finally, we want to highlight the assumptions we have made in our idealized model.
In the horizontal transport model, we completely ignore the rotation of the planet. Following Ingersoll et al. (1985), we assume that the transport flow is in hydrostatic balance.16 This indicates that no radial escape flow will occur and that the mass flux of the transport flow will only be changed by condensation and surface exchange. Turbulence mixing in the boundary layer is ignored, as its effects are likely to be negligible (Ingersoll 1989; Kite et al. 2016).
On the day side, we assume that sodium dust would be revaporized by the stellar radiation immediately, while on the night side, we assume that dust, once formed, will stop interacting with the rest of the gas and enter a Kepler orbit determined by their initial energy and angular momentum, leading to a drop in pressure and mass flux. Actually, the different assumptions would only affect the flow property near the surface, where most condensation occurs, while the final escape fluxes would only be subtly affected, if at all. This is because the escape fluxes are mostly determined by the continuity conditions (Equations (A10)–(A13)) around the transonic point, where most condensation has already occurred.
We set P and T at the bottom boundary in the day-side vertical escape model using the surface temperature and corresponding equilibrium pressure. However, as we found in the horizontal transport model, the surface pressure is actually below the equilibrium pressure set by the magma ocean and vaporization relies on this subsaturation. This assumption could lead to the overestimation of the escape flux. Meanwhile, we also ignore the extra pressure induced by the stellar radiation and stellar wind on the day side and that could suppress the supersonic escape flow to a breeze as shown by Murray-Clay et al. (2009).
The bottom boundary condition for the night-side escape model is set to conserve the mass and energy flux from the horizontal transport model. The assumption behind is that all energy would take the form of either internal energy or mean flow kinetic energy (very small compared to internal energy in most cases), and no energy has to be wasted on turbulence. This may be relevant here because the initial flow speed is quite slow, and possibly that will give the flow plenty of time to damp turbulence into internal energy. The cross section of the escape flow involves a large uncertainty, too. We here arbitrarily stop the horizontal flow and let them turn upward when the flow speed drops 50% from the peak value. A different choice could significantly change the results for cases with strong gravity, because, in those cases, lots of mass flux get lost due to the supersaturation in the small cross section. We also ignore the radiative cooling over time. This effect should be weak as sodium vapor around 1000 K is not hot enough to emit through its major spectrum lines.
Particle entrainment is not considered in the calculation, but we do not expect that will significantly change the results given that the initial velocity is typically small and thus the entrained particles at the surface are likely to fall back to the surface under gravity. What is also not considered is the chemical reaction, FUV-driven ionization, and heating. They could provide extra heat to the escape flow and enhance the escape flux as a result.
Footnotes
- 7
Stellar wind also contributes but is negligible compared to radiation pressure (Rappaport et al. 2014).
- 8
The pressure on the night side is not zero on hot Jupiters with a hydrogen envelope, but should be close to zero on lava planets in the absence of transport flow. This difference makes it difficult to compare our results with previous multidimensional hydrodynamic simulations.
- 9
We let the flow turn once its speed drops over 50% from the peak. Results are not sensitive to this arbitrary choice. As shown later, a reasonably good analytical estimation can be obtained without using this information.
- 10
As shown in Section 5.2, the escape percentage is
 , where Φ(a) is the gravity potential at the surface with reference set at infinity and L is the sublimation enthalpy). In the relevant parameter regime, Φ(a) is smaller or at most comparable with L; otherwise, the escape flow would be very weak.
, where Φ(a) is the gravity potential at the surface with reference set at infinity and L is the sublimation enthalpy). In the relevant parameter regime, Φ(a) is smaller or at most comparable with L; otherwise, the escape flow would be very weak. - 11
This is true for the day-side escape flow as the dust tend to be melted soon after they form under the fierce stellar radiation. Our model for the night-side escape flow assumes that the night-side flow remains in the shade of the planet, and thus, no evaporation would happen. But in reality, the night-side flow would lag behind the planet in orbit as it heads away from the star, according to angular momentum conservation. Melting would also occur after flow leaves the planetary shade.
- 12
As planetary radius decreases, the decrease of surface area would eventually dominate the increase of escape rate per area.
- 13
The portion of dust in the escaping flow should peak near the planet, where the condensation rate is high (see Figures 2(a) and (b)). But because the flow is slow there, the amount of dusts can be carried by the escaping flow is limited.
- 14
The results will not be affected by the choice of TN, as long as TN is lower than the air temperature, which is above 500 K.
- 15
Aerosols may travel at different speeds from the vapor flow, so re-evaporation may cause change to the mean upward momentum of the flow. That is ignored here.
- 16
The hydrostatic assumption is not used in the vertically escaping model, as the whole purpose is to calculate the vertical acceleration of the flow.