1 Introduction

Functionally graded materials (FGM) have attracted interest in the scientific community in the last decades due to their promising possible applications in several branches of engineering and applied sciences. Among the literature we may quote [1,2,3,4], where actual realizations of functional grading are widely illustrated, with details on the technological processes involved. Thus, many investigations have been performed also on the field of structural mechanics. Without pretending to be exhaustive, and only to give a hint, we may quote the monographs [1, 5, 6], where a lot of problems are solved with a view towards structural applications.

One benchmark study in structural mechanics is on the possible buckling of an element, since the pioneering works by Euler on the bifurcated solutions of a compressed elastic column. About buckling of FGM structural elements, we may quote the papers [7], dealing with the so-called Timoshenko beams, and [8], dealing with circular plates. There actually is a vast literature on this subject, considering various beam models (purely flexible, fully deformable, shear-deformable at higher orders with respect to the standard theories), various plate models (according to Kirchhoff and Love, Reissner and Mindlin, Von Kármán), plus interactions with elastic foundations, porosity and other physical aspects. However, this is out of our scope, since in this short note we wish to deal with a simple problem and look for possible closed-form solutions.

Indeed, it is not necessary to remark how closed-form solutions can be of interest in engineering; one may quote the monograph [9] and the paper [10], devoted to the search of such solutions for problems of technical interest. In a recent paper [11], one of the authors investigated the possibility of finding closed-form solutions for the buckling of FGM circular thin plates under uniform radial compression. The present short technical note investigates the possibility to extend the study in [11] to a more general functional grading, following the suggestions of literature, for instance in [11,12,13,14]. The novel point of this note with respect to the quoted literature is the finding of results in a nearly closed form, which makes them quite suitable for possible applications. Since this is only a short note, paving the way for a more vast and profound investigation, we do not pretend to be exhaustive. We are satisfied to show that by recent technological suggestions we are able to find closed-form solutions for buckling loads; we will not then investigate here about possible imperfections, post-buckling behaviour, sensitivity to initial imperfections, limit loads for actual equilibria.

2 Formulation of the problem

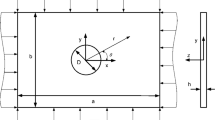
Let us consider a circular plate of radius \(R\) and uniform thickness \(h \ll R\). Under these hypotheses, the plate is considered thin and can be described by the so-called Kirchhoff–Love model: material fibres orthogonal to the middle plane in the reference shape remain orthogonal to the deflected middle surface.

Let us fix a cylindrical coordinate system with origin at the centre of the middle plane of the plate and let ρ, ϕ, z be the radial, angular and transverse coordinates of a point of the plate, respectively. The middle plane of the plate is characterized by z = 0; the kinematic and resultant action fields are defined on it.

In order to model FGM, Young’s modulus \(E\) is assumed to vary both along the radius and the thickness of the plate, i.e., \(E = E\left( {\rho ,z} \right)\). By contrast, Poisson’s ratio v is assumed uniform over the plate, which means that the shear modulus G is made to vary accordingly; however, the law of functional grading for G will not enter the field equations and we will henceforth not give any further detail on this.

Let w be the deflection of the middle plane, describing a surface of revolution for axial symmetry; let θ be the angle between the axis of revolution of the deflected surface and any normal to it. For axial symmetry, these fields depend on the radial variable ρ only. According to the Kirchhoff–Love model, θ coincides with the rotation of a material fibre originally orthogonal to the middle plane in a meridian plane, i.e. ([14,15,16,17])

$$\theta = - \frac{dw}{{d\rho }}$$
(1)

Let \(\chi_{\rho }\), \(\chi_{\phi }\) be the local radial and hoop curvatures of the middle plane, respectively. These are representative of the behaviour of the entire plate, since shear deformations are neglected, and are given by ([14,15,16,17]):

$$\chi_{\rho } = \frac{d\theta }{{d\rho }} = - \frac{{d^{2} w }}{{d\rho^{2} }},\qquad\chi_{\phi } = \frac{\theta }{\rho } = - \frac{1}{\rho }\frac{dw}{{d\rho }}$$
(2)

where, for the sake of simplicity, the dependence of the indicated fields on the radial coordinate ρ is omitted.

Let the material of the plate be linear elastic, with chemical composition varying smoothly across the plate.

The elongation of the radial fibres \(\varepsilon_{\rho }\) will depend linearly on \(z\) through the local curvature \(\chi_{\rho }\); analogously, that of the hoop fibres \(\varepsilon_{\phi }\) will depend linearly on \(z\) through the local curvature \(\chi_{\phi }\) ([14,15,16,17]):

$$\varepsilon_{\rho } \left( {\rho ,z} \right) = \chi_{\rho } z,\qquad \varepsilon_{\phi } \left( {\rho ,z} \right) = \chi_{\phi } z$$
(3)

By Hooke’s law, the normal stresses along the radial and hoop directions, \(\sigma_{\rho }\) and \(\sigma_{\phi }\), are ([14,15,16,17]):

$$\begin{gathered} \sigma_{\rho } \left( {\rho ,z} \right) = \frac{{E\left( {\rho ,z} \right)}}{{1 - \nu^{2} }}\left( {\varepsilon_{\rho } + \nu \varepsilon_{\phi } } \right) = \frac{{E\left( {\rho ,z} \right) z}}{{1 - \nu^{2} }}\left( { \chi_{\rho } + \nu \chi_{\phi } } \right), \hfill \\ \sigma_{\phi } \left( {\rho ,z} \right) = \frac{{E\left( {\rho ,z} \right)}}{{1 - \nu^{2} }}\left( {\varepsilon_{\phi } + \nu \varepsilon_{\rho } } \right) = \frac{{E\left( {\rho ,z} \right) z}}{{1 - \nu^{2} }}\left( { \chi_{\phi } + \nu \chi_{\rho } } \right) \hfill \\ \end{gathered}$$
(4)

By integrating the product of the expressions in Eq. (4) for \(\sigma_{\rho }\) and \(\sigma_{\phi }\) by the lever arm z over the thickness, we obtain the radial and hoop bending moments \(M_{\rho } , M_{\phi }\) per unit of length ([14,15,16,17]):

$$\begin{gathered} M_{\rho } \left( {\rho ,z} \right) = \mathop \int \limits_{ - h/2}^{h/2} z \sigma_{\rho } dz = \mathop \int \limits_{ - h/2}^{h/2} \frac{{E\left( {\rho ,z} \right) z^{2} }}{{1 - \nu^{2} }}\left( { \chi_{\rho } + \nu \chi_{\phi } } \right) dz, \hfill \\ M_{\phi } \left( {\rho ,z} \right) = \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} z \sigma_{\phi } dz = \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \frac{{E\left( {\rho ,z} \right)z^{2} }}{{1 - \nu^{2} }}\left( { \chi_{\phi } + \nu \chi_{\rho } } \right) dz \hfill \\ \end{gathered}$$
(5)

Remark that no shearing stress, shearing strain, and mixed resultant moment exist, due to axial symmetry ([14,15,16,17]). Moreover, in Eq. (5) the stress resultants depend on both radial and transverse coordinates due to the functional grading, which, inspired by some literature ([8, 11,12,13,14]), is assumed to be described by:

$$\nu = \nu_{0} ,\qquad E = E\left( {\rho , z} \right) = E_{0} \left( \rho \right) \left[ {1 + n \left( {\frac{2 z}{h}} \right)^{2} } \right],\ n > 0,\qquad E_{0} \left( \rho \right) = E_{1} \left[ {1 - \frac{1}{m} \left( {\frac{\rho }{R}} \right)^{2} } \right],\ m > 1$$
(6)

The uniform value \(\nu_{0}\) of Poisson’s ratio is admissible for metals and their alloys, and \(E_{1}\) is uniform across the plate. The real parameters \( n, m \) are form factors of the distribution of Young’s modulus and can be fixed, e.g., using conditions for the local composition of the plate at special places.

The functional grading in Eq. (6), suitable for our scopes of easier calculation and the seek for closed-form expressions, has solid bases in the literature, as remarked above, and is application-oriented. Indeed, it foresees a stiffer, heavier material towards the upper and lower faces of the plate, to increase its global strength, and a softer, lighter material moving from the centre to the outer edge, to keep global strength while sparing weight.

Replacing the distributions of Eq. (6) into Eq. (5) yields

$$\begin{gathered} M_{\rho } \left( \rho \right) = \left( { \chi_{\rho } + \nu \chi_{\phi } } \right) \frac{{h^{3} }}{{1 - \nu^{2} }} E_{0} \left( \rho \right) \left[ {\frac{1}{12} + \frac{n}{20}} \right] = D\left( \rho \right) \left( { \chi_{\rho } + \nu \chi_{\phi } } \right), \hfill \\ M_{\phi } \left( \rho \right) = \left( { \chi_{\phi } + \nu \chi_{\rho } } \right) \frac{{h^{3} }}{{1 - \nu^{2} }} E_{0} \left( \rho \right) \left[ {\frac{1}{12} + \frac{n}{20}} \right] = D\left( \rho \right) \left( { \chi_{\phi } + \nu \chi_{\rho } } \right) \hfill \\ \end{gathered}$$
(7)

where \(D\left( \rho \right)\) denotes the local flexural rigidity, expressed as

$$D\left( \rho \right) = a E_{0} \left( \rho \right),\qquad a = \frac{{h^{3} }}{{1 - \nu^{2} }}\left[ {\frac{1}{12} + \frac{n}{20}} \right] = {\text{uniform}}$$
(8)

while in a homogeneous plate it is uniformly given by ([14,15,16,17])

$$D = \frac{{E h^{3} }}{{12 \left( {1 - \nu^{2} } \right)}}$$
(9)

Thus, by the functional grading (6) the variation of Young’s modulus along the radius and the thickness makes the flexural rigidity depend only on \(\rho\), modulo the amplification factor \(a\) in Eq. (8–2). This is due to the symmetric distribution of Young’s modulus with respect to \(z\) and has interesting consequences.

Indeed, symmetric mechanical properties of the plate with respect to its middle plane imply that the latter necessarily coincides with the neutral surface. Further, this makes all the standard equations for plates that we find in ([14,15,16,17]) valid, since all the mechanical fields of interest may be reduced to the plane \(z=0\): consequently, bulk equations and boundary conditions are well defined on the middle plane and on its outer circumference. Hence, the usual considerations for possible buckling hold, and no special theories, nor adjusted boundary conditions, are required: we will then proceed with usual means.

Inserting Eq. (2) into Eq. (7), and denoting \(\rho\)-derivatives by primes, yields

$$M_{\rho } \left( \rho \right) = D\left( \rho \right) \left( {\theta^{\prime}\left( \rho \right) + \nu \frac{\theta \left( \rho \right)}{\rho }} \right) ;\qquad M_{\phi } \left( \rho \right) = D\left( \rho \right)\left( {\frac{\theta \left( \rho \right)}{\rho } + \nu \theta^{\prime}\left( \rho \right)} \right)$$
(10)

The local balance of moment along the radial direction is ([14,15,16,17]):

$$M_{\rho } \left( \rho \right) + \rho M_{\rho }^{^{\prime}} \left( \rho \right) - M_{\phi } \left( \rho \right) + \rho Q\left( \rho \right) = 0$$
(11)

where \(Q(\rho )\) is the transverse shearing force per unit length, which is constitutively unprescribed and can thus be determined only via the balance of transverse force.

Let the external compressive load \({N}_{\rho }\) be applied uniformly along the outer edge of the plate \((\rho =R)\), with no eccentricity with respect to the middle plane; due to the assumed symmetry of material properties, this is reasonable and represents the “perfectly loaded” structural element, similar to the centred compression of a Bernoulli–Euler beam. Moreover, we suppose that the plate remains plane until buckling, and there is no bending or deflection during the pre-buckling phase (that is, the fundamental path is trivial): this is also a standard assumption, and is reasonable since, as already remarked, by the functional grading (6) the global strength of the plate is maintained while sparing weight.

In any possible adjacent configuration in which the presence of a deflection of the middle surface is admitted, the balance of transverse force yields the value of the shearing force ([10,11,12,13,14])

$$Q\left( \rho \right) = N_{\rho } \theta \left( \rho \right) = - N_{\rho } w^{\prime}\left( \rho \right)$$
(12)

Substituting Eq. (8) and (10) into Eq. (11) and (12) yields the novel field equation for the buckled shape

$$a E_{1} \left[ {1 - \frac{1}{m} \left( {\frac{\rho }{R}} \right)^{2} } \right]\left( {\theta^{\prime\prime}\left( \rho \right) + \frac{\theta ^{\prime}\left( \rho \right)}{\rho } - \frac{\theta \left( \rho \right)}{{\rho^{2} }}} \right) - a E_{1} \left[ {\frac{2 \rho }{{m R^{2} }}} \right]\left( {\theta^{\prime}\left( \rho \right) + \nu \frac{\theta \left( \rho \right)}{\rho }} \right) + N_{\rho } \theta \left( \rho \right) = 0$$
(13)

In order to abstract from the actual values of the geometrical and physical parameters involved, let us perform a non-dimensional analysis. If we then let \(\rho =rR\), Eq. (13) assumes the dimensionless form

$$r^{2} \left( {1 - \frac{{r^{2} }}{m}} \right)\left( {\frac{{d^{2} \theta \left( r \right)}}{{dr^{2} }}} \right) + r\left( {1 - \frac{{3 r^{2} }}{m}} \right)\left( {\frac{d\theta \left( r \right)}{{dr}}} \right) + \left[ {\left( {1 - 2\nu } \right)\frac{{r^{2} }}{m} + \frac{{N_{\rho } r^{2} R^{2} }}{{aE_{1} }} - 1} \right]\theta \left( r \right) = 0$$
(14)

Equation (14) is a second-order ordinary differential equation with variable coefficients, which must be completed by two boundary conditions to look for solutions. The first derives from axial symmetry: the transverse fibre at the centre of the plate must remain vertical, i.e., \(\theta \left( {r = 0} \right) = 0\), which results in

$$\theta \left( r \right) = \frac{{i\,r\,C\ {}_{2}^{ } F_{1} \left[ {1 - \frac{1}{2}\sqrt b ,1 + \frac{1}{2}\sqrt b ;2;\frac{{r^{2} }}{m}} \right]}}{\sqrt m },\quad i = \sqrt { - 1},\quad b = 2\left( {1 - v} \right) + mp,\quad p = \frac{{N_{\rho } R^{2} }}{{aE_{1} }}$$
(15)

where \({}_{2}^{ } F_{1} \left[ {c,d;e;z} \right]\) is Gauss’ hypergeometric function ([18]) and \(C\) is an integration constant, since just one boundary condition was used; \(C\) must be imaginary in order for the rotation to assume a real value. By imposing the second boundary condition at the outer edge of the plate \(\left( {\rho = R \Rightarrow r = 1} \right)\), the latter may attain a configuration different from the fundamental, trivial, one, provided by \(C=0\). This non-triviality condition, expressed in terms of the non-dimensional compressive load ratio p, provides the value of the buckling load. As usual, the buckling mode may be found, but \(C\) remains undetermined [19].

Equation (14) may be turned in terms of the transverse displacement \(w\left( r \right)\), yielding

$$r^{2} \left( {1 - \frac{{r^{2} }}{m}} \right)\left( {\frac{{d^{3} w\left( r \right)}}{{dr^{3} }}} \right) + r\left( {1 - \frac{{3 r^{2} }}{m}} \right)\left( {\frac{{d^{2} w\left( r \right)}}{{dr^{2} }}} \right) + \left[ {\left( {1 - 2\nu } \right)\frac{{r^{2} }}{m} + \frac{{N_{\rho } r^{2} R^{2} }}{{aE_{1} }} - 1} \right]\frac{dw\left( r \right)}{{dr}} = 0$$
(16)

Equation (16) is a third-order ordinary differential equation, and maintains the same expression in non-dimensional form; again, the transverse fibre at the centre of the plate cannot rotate, i.e., \(w^{\prime}\left( {r = 0} \right) = 0\), which results in

$$w\left( r \right) = \frac{{2{\text{i}}\sqrt m A\left\{ {1 - {}_{j}^{ } F_{k} \left[ {\left\{ { - \frac{1}{2}\sqrt b ,\frac{1}{2}\sqrt b } \right\},\left\{ 1 \right\},\frac{{r^{2} }}{m}} \right]} \right\} + bB}}{b}$$
(17)

In Eq. (17) \({}_{j}{}{F}_{k}[{c}_{j};{d}_{k};z]\) is the generalized hypergeometric function ([20]) and \(A, B\) are integration constants, in general complex. By imposing the two remaining boundary conditions at the outer edge of the plate, and using the non-triviality condition, the buckling load and mode can be found.

3 Clamped plate

If the outer edge of the plate is clamped, we use Eq. (14) and (15); the relevant boundary condition is

$$\theta \left( {r = 1} \right) = \frac{{i\, C\ {}_{2}^{ } F_{1} \left[ {1 - \frac{1}{2}\sqrt b ,1 + \frac{1}{2}\sqrt b ;2;\frac{1}{m}} \right]}}{\sqrt m } = \frac{{\zeta \left( {m,p} \right)}}{\sqrt m } = 0$$
(18)

Once again, remark that, due to the symmetry of material properties with respect to the middle plane, the usual expressions for the boundary conditions may be provided – a clamp prevents the corresponding rotation of the transverse material fibres, whence Eq. (18).

Equation (18) admits non-trivial solutions for \(C\), hence buckled shapes for the plate, if the numerator \(\zeta (m,p)\) of its left-hand side vanishes. This condition can be graphically visualized by intersecting the two-dimensional surface represented by the numerator of the left-hand side of Eq. (18)

$$\zeta \left( {m,p} \right) = {}_{2}^{ } F_{1} \left[ {1 - \frac{1}{2}\sqrt b ,1 + \frac{1}{2}\sqrt b ;2;\frac{1}{m}} \right],$$
(19)

depending on the parameters m and p for a given value \(\nu = 1/3,\) with the plane \(\zeta = 0\), as shown in Fig. 1; the curve common to the two surfaces collects all the solutions of Eq. (18).

Fig. 1
figure 1

Graphical visualization of the solutions of Eq. (18)

Full size image

To provide an approximate (yet meaningful) analytical formulation of the critical values \({p}_{cr}\) of \(p\) as a function of the shape factor \(m\), at least in the range \(1.1\le m\le 5\), we tabulate the values \({p}_{cr}\) corresponding to equally spaced nodes, then approximate the data with a second-order polynomial by the least square method, yielding

$$p_{cr} \left( m \right) = - 0.5843 m^{2} + 4.7771 m + 3.5402$$
(20)

4 Simply supported plate

If the outer edge of the plate is simply supported, the additional boundary conditions for Eq. (16) and (17) are

$$w\left( {r = 1} \right) = 0,\qquad M_{\rho } \left( {r = 1} \right) = 0$$
(21)

where the usual comments on the standard expressions for the conditions provided by the support.

The first Eq. (21) provides a relationship between \(A\) and \(B\)

$$B = \frac{{2iA\sqrt m \left( {{}_{j}^{ } F_{k} \left[ {\left\{ { - \frac{1}{2}\sqrt b ,\frac{1}{2}\sqrt b } \right\},\left\{ 1 \right\},\frac{1}{m}} \right] - 1} \right)}}{b}$$
(22)

The second Eq. (21) accounts for the constraint, ineffective towards rotation about \(\phi\), thus exerting null bending couple in the same direction; due to Eq. (10), this condition equals

$$\frac{{d^{2} w\left( {r = 1} \right)}}{{dr^{2} }} + v\frac{{dw\left( {r = 1} \right)}}{dr} = 0$$
(23)

Inserting Eq. (17) and (22) into Eq. (23), in order to have non-trivial solutions one must satisfy

$$4m\left( {1 + v} \right){}_{j}^{ } F_{k} \left[ {\left\{ {1 - \frac{1}{2}\sqrt b ,1 + \frac{1}{2}\sqrt b } \right\},\left\{ 2 \right\},\frac{1}{m}} \right] + b{}_{j}^{ } F_{k} \left[ {\left\{ {2 - \frac{1}{2}\sqrt b ,2 + \frac{1}{2}\sqrt b } \right\},\left\{ 3 \right\},\frac{1}{m}} \right] = 0$$
(24)

yielding the critical multipliers of the applied load. As before, the solution of Eq. (24) is shown graphically, intersecting the surface given by its left-hand side (evaluated for \(\nu =1/3\)) with the plane \(\zeta =0\), see Fig. 2.

Fig. 2
figure 2

Graphical visualization of the solutions of Eq. (24)

Full size image

Proceeding as in the case of the clamped plate, the least square method leads to

$$p_{cr}\,\left( m \right) = - 0.0988\,m^{2} + 0.8311\,m + 2.2313$$
(25)

5 An example

In order to provide a numerical example, a composite Aluminium-Alumina plate is studied; these materials have Young’s Modulus 70 GPa and 380 GPa, respectively. It is further assumed \(h=1 mm\) and \(R=25 mm\).

The following functional material grading conditions are considered:

$$E\left(\rho =0, z=0\right)={E}_{Al}=150 \mathrm{GPa}$$

\(E\left( {\rho = 0, z = \pm h/2} \right) = E_{{Al_{2} O_{3} }} = 380 {\text{GPa}}\) (the top and bottom faces of the plate are pure Alumina at centre)

\(E\left( {\rho = R, z = 0} \right) = 70 {\text{GPa}}\) (the middle boundary circle of the plate is pure Aluminium)

These conditions are verified only if the parameters \(n\), \(m\) and \({E}_{1}\) assume the values

$$E_{1} = 150 {\text{GPa,}}\quad \quad \, n = 1.533\quad \quad m = 1.875$$

Once these values, plus \(\nu =1/3\), are fixed, the buckling load for the clamped plate is found by Eq. (15), (20)

$${N}_{\rho }=\frac{{E}_{1} {h}^{3}}{{R}^{2} (1-{\nu }^{2})} \left[\frac{1}{12}+\frac{n}{20}\right]\left[-0.5843 {m}^{2}+4.7771 m+3.5402\right]=450.022\mathrm{ kN}/\mathrm{m}$$

and that for the simply supported plate is found by Eqs. (15), (25)

$${N}_{\rho }=\frac{{E}_{1} {h}^{3}}{{R}^{2} (1-{\nu }^{2})} \left[\frac{1}{12}+\frac{n}{20}\right][-0.0988 {m}^{2}+0.8311 m+ 2.2313]=148.337\mathrm{ kN}/\mathrm{m}$$

In order to compare these results with those provided by literature for a homogeneous and isotropic material, the parameter \(n\) must be near zero, while \(m\) must be indefinitely large. Let us then pose \(n\to 0\) in Eq. (6), so that the material is uniform along the thickness of the plate and has Young’s modulus \({E}_{0}\left(\rho \right)\) that varies only along the radius. However, since the least-square approximation for the buckling load was obtained for \(1.1\le m\le 5\), it is improper to evaluate the buckling load for \(m\to \infty\), in order to have an actual uniform plate. Thus, the buckling load is compared for \(m\) providing the vertex of the parabolas in Eqs. (20) and (25) (thus, Young’s modulus \({E}_{0}\left(\rho \right)\) has a small variation with respect to \({E}_{1}\)). In the branch preceding this point, the polynomial function well fits the data: after that point the parabolas in Eqs. (20) and (25) tend to decrease while the actual buckling load continues to increase asymptotically (i.e., a different interpolating function is necessary).

For the clamped plate, the vertex of the parabola corresponds to \(m=\mathrm{4.088}\) and the buckling load is

$${N}_{\rho }\approx 13.304 \frac{{E}_{1} {h}^{3}}{12 \left(1-{\nu }^{2}\right)}\frac{1}{{ R}^{2} }\approx 1.217\frac{{E}_{1} {h}^{3}}{{ R}^{2}}$$

where, as usual, \(\nu=1/3\). This value differs from the result of literature ([10, 11, 14,15,16,17]) by 9.38%: the functional grading has a softening effect, which is physically expected. This effect, though, is rather limited with respect to the gain in stiffness only where requested (the top and bottom faces) and the sparing in weight.

For the simply supported plate, the vertex of the parabola corresponds to \(m=\mathrm{4.206}\) and the buckling load is

$${N}_{\rho }\approx \mathrm{3.979} \frac{{E}_{1} {h}^{3}}{12 \left(1-{\nu }^{2}\right)}\frac{1}{{ R}^{2} }\approx 0.357\frac{{E}_{1} {h}^{3}}{{ R}^{2}}$$

where, again, \(\nu=1/3\). This value differs from the result of literature ([10, 11, 14,15,16,17]) by 7.07%; similar comments as those for the clamped plate can be provided.

6 Final remarks

We investigated the possibility to find closed-form expressions for the buckling loads of uniformly compressed circular plates, the material of which is functionally graded following a quadratic law along both the radius and thickness, inspired by some recent literature; metals and some alloys may comply with it. The functional grading aims at grossly maintaining the strength of the plate while sparing weight; the symmetric distribution of the material properties with respect to the middle plane of the plate makes the standard bulk equations and boundary conditions valid, yet it highlights the differences with respect to the homogeneous case. Indeed, the bending stiffness varies along the radius of the middle plane and the bulk equations are without constant coefficients. The non-triviality conditions providing buckling are expressed in closed form, which is not usual in the literature. The dependence of the critical value of the load multiplier on a certain range of the characteristic parameter of the functional grading is also found in closed form by a least square method, and this is also not common in the literature. A numerical example is provided; a comparison with known results of the literature is provided, together with a mechanical interpretation. This short note paves the way for the search of other closed-form solutions of technical interest.