Elastic spherical inhomogeneity in an infinite elastic solid: an exact analysis by an engineering treatment of the problem based on the corresponding cavity solution

Abstract

In the present work, solutions are recapitulated according to the theory of elasticity for the deformations of an adhesive spherical inhomogeneity in an infinite matrix under remote uniform axial and axial-symmetrical radial tension. Stress fields in the inhomogeneity and at the interface in the matrix are provided, too. It is shown that the sphere is deformed to a spheroid under any of the loading cases considered. Due to the axial-symmetric setup of the problem, the deformation is fully described by the two displacement values at line segments on the principal axes of the spheroid. The displacements depend on the applied remote load and on two traction fields at the inhomogeneity-matrix interface. For any combination of inhomogeneity and matrix stiffness, the condition of compatibility of deformations yields a system of two linear equations with the two magnitudes of the tractions as unknowns. Thus, the problem is reduced to a formulation for solving a twofold statically indetermined structure. The system is solved and the exact solution of the general spherical inhomogeneity problem with differing stiffness in terms of Young’s moduli and Poisson’s ratios of inclusion and matrix is presented.

1 Introduction

Inhomogeneities as inclusions or discontinuities interact with the surrounding structure generating inner restraints which affect a disturbance of the stress strain field with local stress concentrations. A first step in avoiding failure of a component consists in determining the stresses by an analysis of the problem. Generally, the analysis of non-homogeneous stress–strain fields requires the continuum-mechanical solution in the frame of the theory of elasticity. Irrespective of the numerical option, such as the finite element method (FEM), the analytical treatment of mathematically accessible systems is favored as a closed form exact solution given by a adequate compact formula opens insight in the mechanical connections. Such solutions are particularly suited for the takeover in handbooks and practical applications.

A first solution of a spherical inhomogeneity in an infinite solid has been achieved by Goodier [1] using harmonic functions which satisfy the equations of equilibrium and kinematics. However, the analysis is performed only for the special cases of a cavity and a rigid inhomogeneity. Edwards [2] succeeded in the analysis of an prolate spheroidal cave and inhomogeneity considering various stiffness properties in inhomogeneity and matrix. The general equations of equilibrium and kinematics are solved by a three-function approach with harmonic functions after Papcovich–Neuber in the formulation of Sadowsky and Sternberg [3] for a total of five load cases. Edwards first time drew attention to the remarkable fact that under a uniform outer load stress field the stress and strain state within the spheroidal inhomogeneity is also uniform. In his famous work Eshelby [4] showed that for an ellipsoidal inhomogeneity subject to a constant eigenstrain the total strain field within the inhomogeneity is also constant and confirmed Edward’s result. It depends on the Eshelby-tensor of rank 4 with known components for an isotropic inclusion and matrix. The remarkable result of homogeneity of the stress and strain states within the inhomogeneity correlates with the deformation of the interface due to a homogeneous traction; in both inhomogeneity and matrix, the sphere is deformed to a spheroid. The traction is self-adjusting, so that in particular compatibility at the interface is fulfilled, as described in [5, 6] for the two-dimensional example of the circular and elliptical inhomogeneity. This correlation is also valid for spherical and ellipsoidal inhomogeneities.

All the cited solutions are derived applying complicated analytical methods which result in difficult and extended solutions. Unfortunately, their realization is commonly accompanied by a numerical evaluation, uncomfortable for application in practice. This may be the reason why inclusion and inhomogeneity problems are widely left unconsidered in handbooks of elasticity as in Roark’s Formulas [7]. Peterson’s Handbook of Stress Concentration Factors [8] and other catalogues [9,10,11] offer merely solutions for specific stiffness relations and loading situations.

The work presented here demonstrates that an exact solution of an infinite solid with a spherical inhomogeneity with mismatching elastic constants can be achieved by an engineering procedure based on the notch stresses of the corresponding cavity system and leading to a sufficiently condensed formula. Exploiting the known homogeneity of the stress–strain states within the inhomogeneity and the resulting deformation characteristics, it is concluded that there do exist contact stresses between matrix and inhomogeneity depending on the Young’s moduli and Poisson’s ratios of matrix and inhomogeneity. The task is to formulate an equation system of the unknown stress components which satisfies the condition of compatible deformations of the interface between matrix and inhomogeneity. The method already used in [5, 6] for a circular and an elliptical inhomogeneity in plates of plane stress state is here extended to the three-dimensional problem of a spherical inhomogeneity. The sought stress components in the interface follow from a superposition of the two special cases

• (a) the solid with a (pseudo-)inhomogeneity of equal stiffness $E_{i}= E_{m}$ and $\nu _{i} = \nu _{m}$ and

• (b) the solid with a fictitious inhomogeneity of vanishing stiffness $E_{i} = 0$ and $\nu _{i} = 0$

both under a uniform axial and an axial-symmetric radial loading.

For material strength aspects, the interest is focused on the stress concentrations in a component or the meso-structure, given by handy formulae or diagrams of the relevant stresses. In the case of inclusion and inhomogeneity, problems these are regularly found close to the interface between inhomogeneity and matrix. Therefore, the analysis presented here is for the most restricted to the determination of the stress components inside the inhomogeneity and at the interface of the matrix. Not before the very end of the paper an example is shown that the entire stress fields in the matrix can be specified having merely the remote homogeneous loading stresses and the stresses inside the inhomogeneity at hand, the latter calculated with the formulas provided here.

2 Infinite body with a perfectly bonded spherical inhomogeneity of equal stiffness under remote uniform axial load $S_z$ and axial-symmetrical radial load $S_\mathrm{r}$

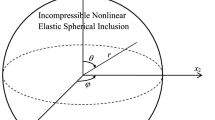
The analysis of the axial-symmetrical problem is formulated using a cylindrical coordinate system with the coordinate r for the radial and z for the axial dimension, Fig. 1.

The surface of a spherical inhomogeneity can be described by the meridians A$^{\prime }$ in Fig. 2 with the pole and by the equator .

The three-dimensional stress and strain states are determined by the stress components $\sigma _r$, $\sigma _z$, $\sigma _\varphi$, and the strain components $\varepsilon _r$, $\varepsilon _z$, $\varepsilon _\varphi$ , Fig. 3.

Fig. 1

Axissymmetrical coordinate system: a a $r-z$-plane, b the equatorial plane $z =0$

Fig. 2

Axonometric projection of a sphere with meridian A$^{\prime }$, pole A and equator B

Fig. 3

3D-element on equator B with the stress components $\sigma _r$, $\sigma _z$, $\sigma _\varphi$ and the strain components $\varepsilon _r$, $\varepsilon _z$, $\varepsilon _\varphi$

2.1 Axial loading stress $S_z$

Now consider an infinite axial-symmetrical body with a perfectly bonded spherical inhomogeneity with matching material parameters $E_\mathrm{i} = E_\mathrm{m}$ and $\nu _\mathrm{i} = \nu _\mathrm{m}$ loaded by a uniform remote stress $S_z$, Fig. 4. This trivial limit case of the general inhomogeneity problem is identical to the homogeneous structure, subsequently marked by the superscript $^O$. The load $S_z$ causes a homogeneous stress field in inhomogeneity and surrounding matrix

Fig. 4

Homogeneous body with a spherical region unloaded (a), loaded and deformed by an axial stress $S_z$ shown in a $r-z$-plane (b) and the equatorial plane $z=0$ (c)

$$\begin{aligned} \sigma _z^{\scriptscriptstyle O}= & {} S_z \end{aligned}$$

(1)

$$\begin{aligned} \sigma _r^{\scriptscriptstyle O}= & {} \sigma _\varphi ^{\scriptscriptstyle O} = \tau _{zr}^{\scriptscriptstyle O} = 0 \end{aligned}$$

(2)

connected with a homogeneous strain field

$$\begin{aligned} \varepsilon _z^{\scriptscriptstyle O}= & {} \frac{S_z}{E_\mathrm{m}} \end{aligned}$$

(3)

$$\begin{aligned} \varepsilon _r^{\scriptscriptstyle O}= & {} \varepsilon _\varphi ^{\scriptscriptstyle O} = -\nu _\mathrm{m} \frac{S_z}{E_\mathrm{m}} \end{aligned}$$

(4)

leading after integration to the displacements of the sphere surface C

$$\begin{aligned} v_{z,c}^{\scriptscriptstyle O}(S_z)= & {} \frac{z_c}{ E_\mathrm{m}} S_z \end{aligned}$$

(5)

$$\begin{aligned} v_{r,c}^{\scriptscriptstyle O}(S_z)= & {} -\frac{\nu _\mathrm{m} r_c}{ E_\mathrm{m}} S_z. \end{aligned}$$

(6)

Displacements proportional to the radial and axial coordinates as given in Eqs. (5) and (6), Fig. 5, deform the original sphere to an ellipsoid, to say a shape of geometrical affinity of the original sphere. The correspondence of uniform strain distribution and ellipsoidal deformation becomes obvious.

With respect to the ellipsoidal distortion, the displacements of the inhomogeneity surface can be defined by the displacement values at the pole and the equator

$$\begin{aligned} v_{z,A}^{\scriptscriptstyle O}(S_z)= & {} \frac{R}{ E_\mathrm{m}} S_z = v_{z,i,A}^{\scriptscriptstyle O} = v_{z,m,A}^{\scriptscriptstyle O} \end{aligned}$$

(7)

$$\begin{aligned} v_{r,B}^{\scriptscriptstyle O}(S_z)= & {} - \frac{\nu _\mathrm{m} R}{ E_\mathrm{m}} S_z = v_{r,i,B}^{\scriptscriptstyle O} = v_{r,m,B}^{\scriptscriptstyle O} \end{aligned}$$

(8)

Fig. 5

Homogeneous body with a spherical region under axial loading $S_z$—affine displacements of the interface in the $r-z$-plane

2.2 Axial-symmetrical radial loading stress $S_r$

The axial-symmetrical radial tension load $S_r$ causes stresses

$$\begin{aligned} \sigma _r^{\scriptscriptstyle O}= & {} \sigma _\varphi ^{\scriptscriptstyle O} = S_r \end{aligned}$$

(9)

$$\begin{aligned} \sigma _z^{\scriptscriptstyle O}= & {} \tau _{rz}^{\scriptscriptstyle O} = 0 \end{aligned}$$

(10)

and the homogeneous strains

$$\begin{aligned} \varepsilon _r^{\scriptscriptstyle O}= & {} \varepsilon _\varphi ^{\scriptscriptstyle O} = \frac{1-\nu _\mathrm{m}}{E_\mathrm{m}} S_r \end{aligned}$$

(11)

$$\begin{aligned} \varepsilon _z^{\scriptscriptstyle O}= & {} - \frac{2 \nu _\mathrm{m}}{E_\mathrm{m}} S_r. \end{aligned}$$

(12)

Integration of the strains generates displacements of the sphere at C, Fig. 6, as describing again ellipsoidal deformations, Fig. 7, which are adequately defined by

$$\begin{aligned} v_{z,c}^{\scriptscriptstyle O}(S_r)= & {} -\frac{ 2 \nu _\mathrm{m} z_c}{ E_\mathrm{m}} S_r \end{aligned}$$

(13)

$$\begin{aligned} v_{r,c}^{\scriptscriptstyle O}(S_r)= & {} \frac{ (1-\nu _\mathrm{m}) r_c}{ E_\mathrm{m}} S_r \end{aligned}$$

(14)

Fig. 6

Homogeneous body with a spherical region unloaded (a), loaded and deformed by an radial stress $S_r$ shown in a $r-z$-plane (b) and the equatorial plane $z=0$ (c)

$$\begin{aligned} v_{z,A}^{\scriptscriptstyle O}(S_r)= & {} -\frac{ 2 \nu _\mathrm{m} R}{ E_\mathrm{m}} S_r = v_{z,i,A}^{\scriptscriptstyle O} = v_{z,m,A}^{\scriptscriptstyle O} \end{aligned}$$

(15)

$$\begin{aligned} v_{r,B}^{\scriptscriptstyle O}(S_r)= & {} \frac{ (1-\nu _\mathrm{m}) R}{ E_\mathrm{m}} S_r = v_{r,i,B}^{\scriptscriptstyle O} = v_{r,m,B}^{\scriptscriptstyle O} \end{aligned}$$

(16)

Fig. 7

Homogeneous body with a spherical region under radial loading $S_r$ affine displacements of the interface in the $r-z$-plane

3 Infinite body with a spherical cave under remote uniform axial load $S_z$ and axial-symmetric radial load $S_r$

The body with a spherical cave can be considered here as being a second limit case of the inhomogeneity problem. This case, in the following denoted by the superscript $^I$, is characterized by a complete loss of stiffness with Young’s modulus $E_\mathrm{i}=0$, leading to a zero stress within the fictitious inhomogeneity region,

$$\begin{aligned} \sigma _{z,i}^I = \sigma _{r,i}^I = \tau _{zr,i}^I = 0. \end{aligned}$$

(17)

Although stresses have vanished in the inhomogeneity region, a strain field may be defined. The constant strain components can be obtained from the matrix strains at the cave surface, Fig. 8. At the pole compatibility demands

Fig. 8

Body with a spherical cave under axial loading $S_z$—stress states at the cave surface (a) and strain states at the cave surface and fictitious strains inside the cave (b)

$$\begin{aligned} \varepsilon _{r,i,A}^{\scriptscriptstyle I} = \varepsilon _{r,m,A}^{\scriptscriptstyle I} \end{aligned}$$

(18)

and at the equator

$$\begin{aligned} \varepsilon _{z,i,B}^{\scriptscriptstyle I}= & {} \varepsilon _{z,m,B}^{\scriptscriptstyle I} \end{aligned}$$

(19)

$$\begin{aligned} \varepsilon _{\varphi ,i,B}^{\scriptscriptstyle I}= & {} \varepsilon _{\varphi ,m,B}^{\scriptscriptstyle I} \end{aligned}$$

(20)

where $\varepsilon _{z,i,B}^{\scriptscriptstyle I}$, $\varepsilon _{\varphi ,i,B}^{\scriptscriptstyle I}$ are the fictitious strain components of the inhomogeneity and $\varepsilon _{z,m,B}^{\scriptscriptstyle I}$, $\varepsilon _{\varphi ,m,B}^{\scriptscriptstyle I}$ the strains of the matrix at and the radial components $\varepsilon _{r,i,A}^{\scriptscriptstyle I}$, $\varepsilon _{r,m,A}^{\scriptscriptstyle I}$ at all in tangential direction as shown in Fig. 8. The strain components $\varepsilon _{z,m,B}^{\scriptscriptstyle I}$, $\varepsilon _{\varphi ,m,B}^{\scriptscriptstyle I}$ and $\varepsilon _{\varphi ,m,A}^{\scriptscriptstyle I}$ are correlated with the tangential stress components by

$$\begin{aligned} \varepsilon _{z,m,B}^{\scriptscriptstyle I}= & {} \frac{ 1}{ E_\mathrm{m}} \left( \sigma _{z,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I} \right) = \varepsilon _{z,i,B}^{\scriptscriptstyle I} \end{aligned}$$

(21)

$$\begin{aligned} \varepsilon _{\varphi ,m,B}^{\scriptscriptstyle I}= & {} \frac{ 1}{ E_\mathrm{m}} \left( \sigma _{\varphi ,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{z,m,B}^{\scriptscriptstyle I} \right) = \varepsilon _{\varphi ,i,B}^{\scriptscriptstyle I} \end{aligned}$$

(22)

$$\begin{aligned} \varepsilon _{r,m,A}^{\scriptscriptstyle I}= & {} \frac{ 1}{ E_\mathrm{m}} \sigma _{r,m,A}^{\scriptscriptstyle I} \left( 1 - \nu _\mathrm{m} \right) = \varepsilon _{r,i,A}^{\scriptscriptstyle I} \end{aligned}$$

(23)

and assuming uniform strain distribution inside the inhomogeneity region

$$\begin{aligned} \varepsilon _{z,i}^{\scriptscriptstyle I}= & {} \varepsilon _{z,i,B}^{\scriptscriptstyle I} \end{aligned}$$

(24)

$$\begin{aligned} \varepsilon _{\varphi ,i}^{\scriptscriptstyle I}= & {} \varepsilon _{\varphi ,i,B}^{\scriptscriptstyle I} \end{aligned}$$

(25)

$$\begin{aligned} \varepsilon _{r,i}^{\scriptscriptstyle I}= & {} \varepsilon _{r,i,A}^{\scriptscriptstyle I} \end{aligned}$$

(26)

where $\varepsilon _{r,i}^{\scriptscriptstyle I}$ has to be identical with $\varepsilon _{\varphi ,i}^{\scriptscriptstyle I}$.

3.1 Axial loading stress $S_z$

The stress $\sigma _{z,m,B}^{\scriptscriptstyle I}$, $\sigma _{\varphi ,m,B}^{\scriptscriptstyle I}$ and $\sigma _{r,m,A}^{\scriptscriptstyle I}$ can be taken from the solution of Neuber [12] in 1937 and other publications [1, 8]. For axial loading $S_z$, the stress components at the pole read

$$\begin{aligned} \sigma _{r,m,A}^{\scriptscriptstyle I} = -\frac{ 3 (1+5 \nu _\mathrm{m})}{ 2 (7-5\nu _\mathrm{m})} S_z \end{aligned}$$

(27)

and at the equator

$$\begin{aligned} \sigma _{z,m,B}^{\scriptscriptstyle I}= & {} \frac{ 3 (9-5 \nu _\mathrm{m})}{ 2 (7-5\nu _\mathrm{m})} S_z \end{aligned}$$

(28)

$$\begin{aligned} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I}= & {} \frac{ 3 (5 \nu _\mathrm{m} -1)}{ 2 (7-5\nu _\mathrm{m})} S_z \end{aligned}$$

(29)

Introducing the composed stress factors

$$\begin{aligned} \sigma _{z,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I}= & {} \frac{3}{2} (1-\nu _\mathrm{m})\left[ \frac{9+5 \nu _\mathrm{m}}{7-5 \nu _\mathrm{m}}\right] S_z = C_p S_z \end{aligned}$$

(30)

$$\begin{aligned} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{z,m,B}^{\scriptscriptstyle I}= & {} -\frac{3}{2} (1-\nu _\mathrm{m})\left[ \frac{1+5 \nu _\mathrm{m}}{7-5 \nu _\mathrm{m}}\right] S_z = C_q S_z \end{aligned}$$

(31)

there follows from Eqs. (21) to (23) for the strain components

$$\begin{aligned} \varepsilon _{z,m,B}^{\scriptscriptstyle I}= & {} \varepsilon _{z,i,B}^{\scriptscriptstyle I} = \varepsilon _{z,i}^{\scriptscriptstyle I} \nonumber \\= & {} \frac{ 1}{ E_\mathrm{m}} \left( \sigma _{z,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I} \right) = \frac{C_p}{E} S_z \end{aligned}$$

(32)

$$\begin{aligned} \varepsilon _{\varphi ,m,B}^{\scriptscriptstyle I}= & {} \varepsilon _{\varphi ,i,B}^{\scriptscriptstyle I} = \varepsilon _{\varphi ,i}^{\scriptscriptstyle I} \nonumber \\= & {} \frac{ 1}{ E_\mathrm{m}} \left( \sigma _{\varphi ,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{z,m,B}^{\scriptscriptstyle I} \right) = \frac{C_q}{E} S_z \end{aligned}$$

(33)

$$\begin{aligned} \varepsilon _{r,m,A}^{\scriptscriptstyle I}= & {} \varepsilon _{r,i,A}^{\scriptscriptstyle I} = \varepsilon _{r,i}^{\scriptscriptstyle I} \nonumber \\= & {} \frac{ 1}{ E_\mathrm{m}} \left( 1-\nu _\mathrm{m} \right) \sigma _{r,m,A}^{\scriptscriptstyle I} = \frac{C_q}{E} S_z \end{aligned}$$

(34)

The identity of Eqs. (33) and (34) together with Eqs. (27) and (31) demonstrates the constancy of the strain field inside the inhomogeneity. This homogeneous strain distribution causes again an ellipsoidal deformation, Fig. 9, which can be described after integration of Eqs. (32) and (33) by the displacements at the surface c by

$$\begin{aligned} v_{z,m,c}^{\scriptscriptstyle I}(S_z) = \frac{C_p z_c}{E_\mathrm{m}} S_z \end{aligned}$$

(35)

and

$$\begin{aligned} v_{r,m,c}^{\scriptscriptstyle I}(S_z) = \frac{C_q r_c}{E_\mathrm{m}} S_z \end{aligned}$$

(36)

leading at the pole and the equator , Fig. 10, to

$$\begin{aligned} v_{z,m,A}^{\scriptscriptstyle I}(S_z)= & {} \frac{R C_p}{E_\mathrm{m}} S_z \end{aligned}$$

(37)

$$\begin{aligned} v_{r,m,B}^{\scriptscriptstyle I}(S_z)= & {} \frac{R C_q}{E_\mathrm{m}} S_z \end{aligned}$$

(38)

Fig. 9

Body with a spherical cave unloaded (a), loaded and deformed by an axial stress $S_z$ shown in a $r-z$-plane (b) and the equatorial plane $z=0$ (c)

Fig. 10

Body with a spherical cave under radial loading $S_z$ affine displacements of the cave surface in the $r-z$-plane

3.2 Axial-symmetrical radial loading stress $S_r$

The significant stresses for the axial-symmetrical radial loading case $S_r$ can be realized by superposition of a biaxial load case with load stresses $S_x = S_y =S_r$. At the pole this leads to

$$\begin{aligned} \sigma _{r,m,A}^{\scriptscriptstyle I} = \frac{ 3}{2}\cdot \frac{8}{ 7-5 \nu _\mathrm{m}} S_r \end{aligned}$$

(39)

At the equator , the following stress components arise

$$\begin{aligned} \sigma _{z,m,B}^{\scriptscriptstyle I}= & {} -\frac{ 3}{ 2}\cdot \frac{2}{ 7-5 \nu _\mathrm{m}} S_r \end{aligned}$$

(40)

$$\begin{aligned} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I}= & {} \frac{ 3}{ 2}\cdot \frac{8-10 \nu _\mathrm{m}}{ 7-5 \nu _\mathrm{m}} S_r \end{aligned}$$

(41)

In the radial load case, the composed stress factors give

$$\begin{aligned} \sigma _{z,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I}= & {} -\frac{3}{2} (1-\nu _\mathrm{m})\left[ \frac{2+10 \nu _\mathrm{m}}{7-5 \nu _\mathrm{m}}\right] S_r = 2 C_q S_r \end{aligned}$$

(42)

$$\begin{aligned} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{z,m,B}^{\scriptscriptstyle I}= & {} \frac{3}{2} (1-\nu _\mathrm{m})\left[ \frac{8}{7-5 \nu _\mathrm{m}}\right] S_r = (C_p + C_q ) S_r \end{aligned}$$

(43)

The strain states at and are correlated with the stress states according to Eqs. (21)–(23) by

$$\begin{aligned} \varepsilon _{z,m,B}^{\scriptscriptstyle I}= & {} \varepsilon _{z,i,B}^{\scriptscriptstyle I} = \varepsilon _{z,i}^{\scriptscriptstyle I} \nonumber \\= & {} \frac{ 1}{ E_\mathrm{m}} \left( \sigma _{z,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{\varphi ,m,B}^{\scriptscriptstyle I} \right) = \frac{2 C_q}{E} S_r \end{aligned}$$

(44)

$$\begin{aligned} \varepsilon _{\varphi ,m,B}^{\scriptscriptstyle I}= & {} \varepsilon _{\varphi ,i,B}^{\scriptscriptstyle I} = \varepsilon _{\varphi ,i}^{\scriptscriptstyle I} \nonumber \\= & {} \frac{ 1}{ E_\mathrm{m}} \left( \sigma _{\varphi ,m,B}^{\scriptscriptstyle I} - \nu _\mathrm{m} \sigma _{z,m,B}^{\scriptscriptstyle I} \right) = \frac{(C_p + C_q)}{E} S_r \end{aligned}$$

(45)

$$\begin{aligned} \varepsilon _{r,m,A}^{\scriptscriptstyle I}= & {} \varepsilon _{r,i,A}^{\scriptscriptstyle I} = \varepsilon _{r,i}^{\scriptscriptstyle I} \nonumber \\= & {} \frac{ 1}{ E_\mathrm{m}} \left( 1-\nu _\mathrm{m} \right) \sigma _{r,m,A}^{\scriptscriptstyle I} = \frac{(C_p + C_q)}{E} S_r \end{aligned}$$

(46)

Integrating Eqs. (44) and (45) delivers the proportional displacements of the ellipsoidal deformation of the sphere, Fig. 11

$$\begin{aligned} v_{z,m,c}^{\scriptscriptstyle I}(S_r)= & {} \frac{2 C_q z_c}{E_\mathrm{m}} S_r \end{aligned}$$

(47)

$$\begin{aligned} v_{r,m,c}^{\scriptscriptstyle I}(S_r)= & {} \frac{(C_p + C_q) r_c}{E_\mathrm{m}} S_r \end{aligned}$$

(48)

and at the pole and the equator , Fig. 12

$$\begin{aligned} v_{z,m,A}^{\scriptscriptstyle I}(S_r)= & {} \frac{2R C_q}{E_\mathrm{m}} S_r \end{aligned}$$

(49)

$$\begin{aligned} v_{r,m,B}^{\scriptscriptstyle I}(S_r)= & {} \frac{R (C_p + C_q)}{E_\mathrm{m}} S_r \end{aligned}$$

(50)

Fig. 11

Body with a spherical cave unloaded (a), loaded and deformed by a radial stress $S_r$ shown in a $r-z$-plane (b) and the equatorial plane $z=0$, c axissymmetrical coordinate system r - z

Fig. 12

Body with a spherical cave under radial loading $S_r$ affine displacements of the cave surface in the $r-z$-plane

4 Load cases stress in the interface between matrix and spherical inhomogeneity

To solve the problem of an elastic solid with an elastic inhomogeneous region of different Young’s modulus and Poisson’s ratio under remote loading, the method of equivalent eigenstrain may be chosen as in [13]. But in this work for the sake of mathematical simplicity, a strategy is pursued to get the solution by a superposition of the solutions of three loading cases:

• (A) The solid with cave under outer loading.

• (B) The solid with cave under a traction on the cave’s surface. When the reaction of the traction is applied on the surface of the inhomogeneity, it is under a homogeneous state of stress, $\sigma _z^*$. Therefore, the traction is $t_z^* = \sigma _z^* \cdot n_z$ where $n_z$ is the z-component of the unit normal vector on the sphere’s surface.

• (C) The solid with cave under another traction on the cave’s surface. When the reaction of this traction is applied on the surface of the inhomogeneity, it is under a homogeneous rotationally symmetric state of stress, $\sigma _r^*$. Therefore, the traction is $t_r^* = \sigma _r^* \cdot n_r$ where $n_r$ is the r-component of the unit normal vector on the sphere’s surface.

The relevant stresses $\sigma _z^*$ or $\sigma _r^*$ have to be determined from the displacements of all parts of the superposed system satisfying the condition of compatible deformations while considering the different Young’s moduli and Poisson’s ratios in matrix and inhomogeneity. The solutions for the special loading cases of the solid with cave under such tractions on the cave surface as noted in cases (B) and (C) explained in the list above can be derived in advance. This requires the superposition of the solution of the homogeneous solid and the solid with cave, both under outer loading but opposed load direction

$$\begin{aligned} \varGamma ^{OI} = \varGamma ^O - \varGamma ^I. \end{aligned}$$

(51)

As a result of the sign change in the loading of the two systems, the stress field in some distance of the interface tends to zero. The stresses in the matrix are concentrated to the neighborhood of the interface.

4.1 Axial loading stress $S_z$

The superposition according to Eq. (51) is performed here for the displacements of the inner surface at the pole and the equator inserting Eqs. (7), (8), (37) and (38) results in

$$\begin{aligned} v_{z,m,A}^{\scriptscriptstyle OI}(S_z)= & {} \frac{R}{ E_\mathrm{m}} S_z - \frac{R C_p}{E_\mathrm{m}} S_z = \frac{R (1- C_p)}{E_\mathrm{m}} S_z \end{aligned}$$

(52)

$$\begin{aligned} v_{r,m,B}^{\scriptscriptstyle OI}(S_z)= & {} -\frac{R \nu _\mathrm{m}}{ E_\mathrm{m}} S_z - \frac{R C_q}{E_\mathrm{m}} S_z = - \frac{R (\nu _\mathrm{m} + C_q)}{E_\mathrm{m}} S_z \end{aligned}$$

(53)

In the following derivations of Sect. 5, the load case shown in Fig. 13c is treated as an independent load, case B in above list. The stresses $S_z$ appearing in Eqs. (52) and (53) are therefore renamed to $\sigma _z^*$.

$$\begin{aligned} v_{z,m,A}^{\scriptscriptstyle OI}(\sigma _z^*)= & {} \frac{R(1 - C_p)}{E_\mathrm{m}} \sigma _z^* \end{aligned}$$

(54)

$$\begin{aligned} v_{r,m,B}^{\scriptscriptstyle OI}(\sigma _z^*)= & {} - \frac{R(\nu _\mathrm{m} + C_q)}{E_\mathrm{m}} \sigma _z^*. \end{aligned}$$

(55)

Unnecessary to mention that the superposition according to Fig. (13) and Eq. (51) can be performed for any stress-, strain-, or displacement-field variable. The stress fields of the loading cases according to Fig. 13a, b are available in analytic form, see e.g., [12], and so are the fields for the load case according to Fig. 13c. Nevertheless, it is sufficient here to restrict to the two values of Eqs. (54) and (55).

4.2 Axial-symmetrical radial loading stress $S_r$

In strict analogy, see Fig. 14, the superposition of the axial-symmetrical load case $S_r$ after Eq. (51) produces the displacements of the interface with Eqs. (15), (16), (49) and (50) as

$$\begin{aligned} v_{z,m,A}^{\scriptscriptstyle OI}(S_r)= & {} -\frac{2 R \nu _\mathrm{m}}{ E_\mathrm{m}} S_r - \frac{2 R C_q}{ E_\mathrm{m}} S_r = -\frac{2 R(\nu _\mathrm{m} + C_q)}{ E_\mathrm{m}} S_r \end{aligned}$$

(56)

$$\begin{aligned} v_{r,m,B}^{\scriptscriptstyle OI}(S_r)= & {} \frac{(1 - \nu _\mathrm{m}) R}{E_\mathrm{m}} S_r - \frac{R (C_p + C_q)}{ E_\mathrm{m}} S_r = \frac{R (1-\nu _\mathrm{m} - C_p - C_q)}{ E_\mathrm{m}} S_r \end{aligned}$$

(57)

and after renaming $S_r$ to $\sigma _r^*$

$$\begin{aligned} v_{z,m,A}^{\scriptscriptstyle OI}(\sigma _r^*)= & {} -\frac{2 R(\nu _\mathrm{m}+ C_q )}{E_\mathrm{m}} \sigma _r^* \end{aligned}$$

(58)

$$\begin{aligned} v_{r,m,B}^{\scriptscriptstyle OI}(\sigma _r^*)= & {} \frac{R(1-\nu _\mathrm{m} -C_p - C_q)}{E_\mathrm{m}} \sigma _r^* \end{aligned}$$

(59)

Fig. 13

Scheme to the superposition according to Eq. (51) for axial loading a homogeneous body, b body with cave, c body with cave under inner and inhomogeneity under outer stress $t_z = S_z \cdot n_z$

Fig. 14

Scheme to the superposition according to Eq. (51) for radial loading a homogeneous body, b body with cave, c body with cave under inner and inhomogeneity under outer stress $t_r = S_r \cdot n_r$

5 Infinite solid with a spherical inhomogeneity under axial load $S_z$ and axial-symmetrical radial load $S_r$

The correlation between deformation kinematics and stress-strain-states in an infinite solid with a spherical inhomogeneity offer an opportunity for the analysis of the general problem with non-matching stiffness of matrix and inhomogeneity. For this purpose, the system is separated fictitiously into three parts, Fig. 15,

• (a) the solid with spherical cave under an outer uniform load $S_j$,

• (b) the spherical inhomogeneity under tractions on its surface causing constant stresses $\sigma _z^*$, $\sigma _r^*$ inside, and

• (c) the solid with spherical cave where the same tractions re-act on the cave surface.

Compatible displacements of the interface between matrix and inhomogeneity are provided by an appropriate choice of the inner stress components $\sigma _z^*$ and $\sigma _r^*$, considering the different material properties in inhomogeneity and matrix.

In respect of the general geometrical affinity in the ellipsoidal deformations, the condition of compatibility (according to the method of compatible deformations of a twofold statically indetermined system) may be formulated on the basis of an equation system referring to the displacements at the pole and at the equator , Fig. 15. In general form, the conditions are given by

Fig. 15

Superposition scheme after Eqs. (62) and (63) to derive the inner stress $\sigma _z^*$ and $\sigma _r^*$ ensuring compatible deformations between matrix and inhomogeneity

(60)

(61)

where $v_{z,m,A}^I (S_j)$ and $v_{r,m,B}^I (S_j)$ are the displacements of the cave surface under the outer axial load $S_z$ or $S_r$. These displacements have to be compensated by the displacements of the inhomogeneity under the unknown inner stress $\sigma _z^*$ and $\sigma _r^*$ after Eqs. (7), (8), (15) and (16)

$$\begin{aligned} v_{z,i,A}^{\scriptscriptstyle O}(\sigma _z^*,\sigma _r^*)= & {} \frac{\textstyle R}{\textstyle E_\mathrm{i}} \sigma _z^* - \frac{\textstyle 2\nu _i R}{\textstyle E_\mathrm{i}} \sigma _r^* \end{aligned}$$

(62)

$$\begin{aligned} v_{r,i,B}^{O}(\sigma _z^*,\sigma _r^*)= & {} -\frac{\textstyle \nu _i R}{\textstyle E_\mathrm{i}} \sigma _z^* + \frac{\textstyle (1-\nu _\mathrm{i}) R}{\textstyle E_\mathrm{i}} \sigma _r^* \end{aligned}$$

(63)

and the displacements of the inner stress on the cave surface of the solid regarding Eqs. (54), (55), (58) and (59)

$$\begin{aligned} v_{z,m,A}^{\scriptscriptstyle OI}(\sigma _z^*,\sigma _r^*)= & {} \frac{\textstyle R (1-C_p)}{\textstyle E_\mathrm{m}} \sigma _z^* - \frac{\textstyle 2 R ( \nu _\mathrm{m} + C_q)}{\textstyle E_\mathrm{m}} \sigma _r^* \end{aligned}$$

(64)

$$\begin{aligned} v_{r,m,B}^{OI}(\sigma _z^*,\sigma _r^*)= & {} -\frac{\textstyle R (\nu _\mathrm{m} + C_q)}{\textstyle E_\mathrm{m}} \sigma _z^* + \frac{\textstyle R ( 1-\nu _\mathrm{m} - C_p - C_q )}{E_\mathrm{m}} \sigma _r^* \end{aligned}$$

(65)

Inserting all quantities in Eqs. (60) and (61) leads to an equation system for the determination of the two inner unknown stress components $\sigma _z^*$ and $\sigma _r^*$ in dependence of the load stress $S_z$ or $S_r$ and the material parameters $E_\mathrm{i}$ and $\nu _\mathrm{i}$ of the inhomogeneity and $E_\mathrm{m}$ and $\nu _\mathrm{m}$ of the matrix, respectively

(66)

(67)

where $f_{S,A}$ and $f_{S,B}$ are load case depending factors.

Division by R and multiplication by $E_\mathrm{i}$ after introducing of the quantity $\phi = E_\mathrm{i}/E_\mathrm{m}$ and performing a couple of algebraic re-arrangements the equation system is re-written as

(68)

(69)

Introducing the expressions

$$\begin{aligned} \psi _1= & {} -1 - \phi \Biggl [ \frac{ 13-2\nu _\mathrm{m} -15\nu _\mathrm{m}^2}{ 2(7-5\nu _\mathrm{m})} \Biggr ] = -1 + \phi ( 1 - C_p ) \end{aligned}$$

(70)

$$\begin{aligned} \psi _2= & {} \nu _\mathrm{i} - \phi \Biggl [ \frac{ 3 - 2\nu _\mathrm{m} - 5\nu _\mathrm{m}^2}{ {2(7-5\nu _\mathrm{m})}} \Biggr ] = \nu _\mathrm{i} - \phi \cdot ( \nu _\mathrm{m} + C_q ) \end{aligned}$$

(71)

$$\begin{aligned} \psi _3= & {} -1+\nu _\mathrm{i} - \phi \Biggl [ \frac{ 5 -5\nu _\mathrm{m}^2}{ 7-5\nu _\mathrm{m}} \Biggr ] = -1+\nu _\mathrm{i} + \phi \cdot ( 1 - \nu _\mathrm{m} - C_p - C_q ) \end{aligned}$$

(72)

reduces the equation system to

(73)

(74)

5.1 Solution of the axial loading case $S_z$

The load factors of this load case are

$$\begin{aligned} f_{S,A}= & {} C_p = \frac{3}{2} (1-\nu _\mathrm{m})\left[ \frac{9+5 \nu _\mathrm{m}}{7-5 \nu _\mathrm{m}}\right] \end{aligned}$$

(75)

$$\begin{aligned} f_{S,B}= & {} C_q = -\frac{3}{2} (1-\nu _\mathrm{m})\left[ \frac{1+5 \nu _\mathrm{m}}{7-5 \nu _\mathrm{m}}\right] \end{aligned}$$

(76)

After completion the equation system reads

(77)

(78)

The solution of the equations yields

$$\begin{aligned} \sigma _z^*= & {} \frac{\textstyle \phi \Bigl [ 2 \psi _2 C_q - \psi _3 C_p \Bigr ]}{\textstyle \psi _1 \psi _3-2 \psi _2^2} S_z \end{aligned}$$

(79)

$$\begin{aligned} \sigma _r^*= & {} \frac{\textstyle \phi \Bigl [ \psi _2 C_p - \psi _1 C_q \Bigr ]}{\textstyle \psi _1 \psi _3-2 \psi _2^2} S_z \end{aligned}$$

(80)

or expressed in a handbook-compatible formulation

$$\begin{aligned} \sigma _z^*= & {} K_z(S_z)\cdot S_z = K_z^z \cdot S_z \end{aligned}$$

(81)

$$\begin{aligned} \sigma _r^*= & {} K_r(S_z)\cdot S_z = K_r^z \cdot S_z \end{aligned}$$

(82)

with

$$\begin{aligned} K_z^z= & {} \frac{\textstyle \phi \Bigl [ 2 \psi _2 C_q - \psi _3 C_p \Bigr ]}{\textstyle \psi _1 \psi _3-2 \psi _2^2} \end{aligned}$$

(83)

$$\begin{aligned} K_r^z= & {} \frac{\textstyle \phi \Bigl [ \psi _2 C_p - \psi _1 C_q \Bigr ]}{\textstyle \psi _1 \psi _3-2 \psi _2^2} \end{aligned}$$

(84)

Fig. 16

Diagram of $K_z$-values for axial loading $S_z$

Fig. 17

Diagram of $K_r$-values for axial loading $S_z$

Plots of $K_z$ and $K_r$ are shown in the diagrams in Figs. 16 and 17. Besides the reference curve with $\nu _\mathrm{i} = \nu _\mathrm{m} = 0.3$ two other curves with extreme Poisson’s ratio combinations of $\nu _\mathrm{i} = 0.5$ and $\nu _\mathrm{m} = 0.1$ or $\nu _\mathrm{i} = 0.1$ and $\nu _\mathrm{m} = 0.5$ are given, showing the bandwidth of theoretical values. The solution was confirmed by a series of numerical calculations by the finite element method, the results of the latter are indicated with symbols in Figs. 16 and 17 .

5.2 Solution of the axial-symmetrical radial loading case $S_r$

In this load case, the load factors become

$$\begin{aligned} f_{S,A}= & {} 2 C_q = 3 (1-\nu _\mathrm{m}) \frac{9+5 \nu _\mathrm{m}}{ 7-5 \nu _m}\end{aligned}$$

(85)

$$\begin{aligned} f_{S,B}= & {} C_p+C_q = 3 \frac{ 1-\nu _\mathrm{m}}{ 7-5 \nu _\mathrm{m}}, \end{aligned}$$

(86)

and after inserting in Eqs. (73) and (74), the equation system arises

(87)

(88)

From these equations, the sought-after stress components $\sigma _z^*$ and $\sigma _r^*$ result in

$$\begin{aligned} \sigma _z^*= & {} \frac{\textstyle \phi \Bigl [ 2 \psi _2 (C_p+C_q) - 2 \psi _3 C_q \Bigr ]}{\textstyle \psi _1 \psi _3 - 2 \psi _2^2} S_r \end{aligned}$$

(89)

$$\begin{aligned} \sigma _r^*= & {} \frac{\textstyle \phi \Bigl [ 2 \psi _2 C_q - \psi _1 (C_p+C_q) \Bigr ]}{\textstyle \psi _1 \psi _3 - 2 \psi _2^2 } S_r \end{aligned}$$

(90)

or formulated in K-values

$$\begin{aligned} \sigma _z^*= & {} K_z(S_r)\cdot S_r = K_z^r \cdot S_r \end{aligned}$$

(91)

$$\begin{aligned} \sigma _r^*= & {} K_r(S_r)\cdot S_r = K_r^r \cdot S_r \end{aligned}$$

(92)

with

$$\begin{aligned} K_z^r= & {} \frac{\textstyle \phi \Bigl [ 2 \psi _2 (C_p+C_q) - 2 \psi _3 C_q \Bigr ]}{\textstyle \psi _1 \psi _3 - 2 \psi _2^2} \end{aligned}$$

(93)

$$\begin{aligned} K_r^r= & {} \frac{\textstyle \phi \Bigl [ 2 \psi _2 C_q - \psi _1 (C_p+C_q) \Bigr ]}{\textstyle \psi _1 \psi _3 - 2 \psi _2^2 } \end{aligned}$$

(94)

Fig. 18

Diagram of $K_z$-values for radial loading $S_r$

Fig. 19

Diagram of $K_r$-values for radial loading $S_r$

Graphs of $K_z(S_r)$ and $K_r(S_r)$ are given in Figs. 18 and 19. Again curves of extreme Poisson’s ratios show the variety of theoretically possible values in comparison with usual Poisson’s ratios for steel as $\nu _\mathrm{i} = 0.3$ and $\nu _\mathrm{m} = 0.3$.

6 Transformation of the stress state in the inhomogeneity to the stress state at the interface layer of the matrix

As inhomogeneity and matrix have different elastic material parameters, the knowledge of the inhomogeneity stress state alone is not sufficient to asses the failure of the component. The highest stress concentrations in the matrix are located at the interface between inhomogeneity and matrix. To include the assessment of the matrix, it seems sufficient to transform the stresses of the inhomogeneity to the stresses at the matrix layer of the interface.

The stress state of the inhomogeneity can be transferred to the adjacent layer of the matrix, Fig. 20, by the transition conditions of the stress components in normal and tangential direction considering actio-reactio principle and compatibility of deformations. The normal and tangential direction of a given point of the surface C is determined by a vertical angle $\theta$. Because of the axis-symmetrical system, the stress component in circumferential direction is

$$\begin{aligned} \sigma _{\varphi ,i} = \sigma _{r,i} = const. \end{aligned}$$

(95)

inside the inhomogeneity. The inhomogeneity stresses $\sigma _{n,i}$, $\sigma _{t,i}$ and $\tau _{nt,i}$ are correlated with the components $\sigma _{z,i}$ and $\sigma _{r,i}$ by the known transformation relations

Fig. 20

Transformation of the inhomogeneity stress state to the stress components of the matrix at the interface layer

$$\begin{aligned} \sigma _{n,i}= & {} \frac{\textstyle \sigma _{r,i} + \sigma _{z,i} }{\textstyle 2 } + \frac{\textstyle \sigma _{r,i} - \sigma _{z,i} }{\textstyle 2 } \text{ cos } (2 \theta ) \end{aligned}$$

(96)

$$\begin{aligned} \sigma _{t,i}= & {} \frac{\textstyle \sigma _{r,i} + \sigma _{z,i} }{\textstyle 2 } - \frac{\textstyle \sigma _{r,i} - \sigma _{z,i} }{\textstyle 2 } \text{ cos } (2 \theta ) \end{aligned}$$

(97)

$$\begin{aligned} \tau _{nt,i}= & {} - \frac{\textstyle \sigma _{r,i} - \sigma _{z,i} }{\textstyle 2 } \text{ sin } (2 \theta ) \end{aligned}$$

(98)

or expressed by factors $K_z^j$ and $K_r^j$ of the relevant load case j

$$\begin{aligned} \sigma _{n,i}= & {} \left[ \frac{\textstyle K_r^j + K_z^j }{\textstyle 2 } + \frac{\textstyle K_r^j - K_z^j }{\textstyle 2 } \text{ cos }(2 \theta ) \right] S_j \end{aligned}$$

(99)

$$\begin{aligned} \sigma _{t,i}= & {} \left[ \frac{\textstyle K_r^j + K_z^j }{\textstyle 2 } - \frac{\textstyle K_r^j - K_z^j }{\textstyle 2 } \text{ cos }(2 \theta ) \right] S_j \end{aligned}$$

(100)

$$\begin{aligned} \tau _{nt,i}= & {} - \left[ \frac{\textstyle K_r^j - K_z^j}{\textstyle 2 } \text{ sin } (2 \theta ) \right] S_j \end{aligned}$$

(101)

A more direct calculation of the sum $K_r + K_z$ and difference $K_r - K_z$ can be chosen by special K-factors $K_{r+z}$ and $K_{r-z}$. In the axial loading case, $S_z$

$$\begin{aligned} K_{r+z}(S_z) = \frac{\textstyle K_r^z+ K_z^z}{\textstyle 2 }= & {} \frac{\textstyle \phi \Bigl [ (\psi _2\ - \psi _3)C_p - (\psi _1 - 2 \psi _2) C_q \Bigr ]}{\textstyle 2(\psi _1 \psi _3-2 \psi _2^2)} \end{aligned}$$

(102)

$$\begin{aligned} K_{r-z}(S_z) = \frac{\textstyle K_r^z - K_z^z }{\textstyle 2 }= & {} \frac{\textstyle \phi \Bigl [ (\psi _2\ + \psi _3C_p - (\psi _1 + 2 \psi _2) C_q \Bigr ]}{\textstyle 2(\psi _1 \psi _3-2 \psi _2^2)} \end{aligned}$$

(103)

for the axialsymmetrical loading $S_r$ by

$$\begin{aligned} K_{r+z}(S_r) = \frac{\textstyle K_r^r + K_z^r }{\textstyle 2 }= & {} \frac{\textstyle \phi \Bigl [ 2 (\psi _2 - \psi _3)C_q - (\psi _1 - 2\psi _2) (C_p+C_q) \Bigr ]}{\textstyle 2(\psi _1 \psi _3-2\psi _2^2)} \end{aligned}$$

(104)

$$\begin{aligned} K_{r-z}(S_r) = \frac{\textstyle K_r^r - K_z^r }{\textstyle 2 }= & {} \frac{\textstyle \phi \Bigl [ (2 (\psi _2 + \psi _3 )C_q - (\psi _1 + 2 \psi _2)(C_p+C_q) \Bigr ]}{\textstyle 2(\psi _1 \psi _3-2 \psi _2^2)} \end{aligned}$$

(105)

Now, the stress components on the i surface inside the inhomogeneity become

$$\begin{aligned} \sigma _{n,i}= & {} \left[ K_{r+z}(S_j) + K_{r-z}(S_j) \text{ cos }(2 \theta ) \right] S_j \end{aligned}$$

(106)

$$\begin{aligned} \sigma _{t,i}= & {} \left[ K_{r+z}(S_j) - K_{r-z}(S_j) \text{ cos }(2 \theta ) \right] S_j \end{aligned}$$

(107)

$$\begin{aligned} \tau _{nt,i}= & {} - \left[ K_{r-z}(S_j) \text{ sin }(2 \theta ) \right] S_j \end{aligned}$$

(108)

Fig. 21

Comparison of analytically calculated notch stresses $\sigma _{t,m,c}$ for $\theta = 0$ with numerically obtained as well as literature [14] values, normalized by the applied load $S_z$

Fig. 22

Stress functions ${\bar{\sigma }}_t$, ${\bar{\sigma }}_\varphi$ in tangential and perimeter direction and according to the maximum distortion strain energy criterion ${\bar{\sigma }}_e$ for axial loading $S_z$

Fig. 23

Stress functions ${\bar{\sigma }}_t$, ${\bar{\sigma }}_\varphi$ in tangential and perimeter direction and according to the maximum distortion strain energy criterion ${\bar{\sigma }}_e$ for radial loading $S_r$

Fig. 24

Curves of normalized stress component ${{\bar{\sigma }}}_z(r)$, for $\theta = 0$, for various $\varPhi$-values under axial loading $S_z$

To the stress components on the matrix side of the interface, actio-reactio principle implies

$$\begin{aligned} \sigma _{n,m,c}= & {} \sigma _{n,i} \end{aligned}$$

(109)

$$\begin{aligned} \tau _{nt,m,c}= & {} \tau _{nt,i}, \end{aligned}$$

(110)

while for both of the other stress components, it has to be noticed

$$\begin{aligned} \sigma _{t,m,c}\ne & {} \sigma _{t,i} \end{aligned}$$

(111)

$$\begin{aligned} \sigma _{\varphi ,m,c}\ne & {} \sigma _{\varphi ,i} \end{aligned}$$

(112)

Compatible deformations postulate

$$\begin{aligned} \varepsilon _{t,m,c}= & {} \varepsilon _{t,i} \end{aligned}$$

(113)

$$\begin{aligned} \varepsilon _{\varphi ,m,c}= & {} \varepsilon _{\varphi ,i} \end{aligned}$$

(114)

whereas the strain component in normal direction changes

$$\begin{aligned} \varepsilon _{n,m,c} \ne \varepsilon _{n,i}. \end{aligned}$$

(115)

Using Eqs. (95)–(97), (99) and (100), the missing stress components can be determined by the stress–strain equations

$$\begin{aligned} \varepsilon _{t,i}= & {} \frac{1}{E_\mathrm{i}}\Bigl [ \sigma _{t,i} - \nu _\mathrm{i} ( \sigma _{n,i} + \sigma _{\varphi ,i} ) \Bigr ] \end{aligned}$$

(116)

$$\begin{aligned} \varepsilon _{t,m,c}= & {} \frac{1}{E_\mathrm{m}}\Bigl [ \sigma _{t,m,c} - \nu _\mathrm{m} ( \sigma _{n,m,c} + \sigma _{\varphi ,m,c} ) \Bigr ] \end{aligned}$$

(117)

$$\begin{aligned} \varepsilon _{\varphi ,i}= & {} \frac{1}{E_\mathrm{i}}\Bigl [ \sigma _{\varphi ,i} - \nu _\mathrm{i} ( \sigma _{n,i} + \sigma _{t,i} ) \Bigr ] \end{aligned}$$

(118)

$$\begin{aligned} \varepsilon _{\varphi ,m,c}= & {} \frac{1}{E_\mathrm{m}}\Bigl [ \sigma _{\varphi ,m,c} - \nu _\mathrm{m} ( \sigma _{n,m,c} + \sigma _{ti,m,c} ) \Bigr ] . \end{aligned}$$

(119)

As $\varepsilon _{t,m,c} = \varepsilon _{t,i}$ and $\varepsilon _{\varphi ,m,c} = \varepsilon _{\varphi ,i}$, the relations can be used for the following equation system

$$\begin{aligned} \sigma _{t,m,c} - \nu _\mathrm{m}\sigma _{\varphi ,m,c}= & {} \frac{E_\mathrm{m}}{E_\mathrm{i}}\Bigl [ \sigma _{t,i} - \nu _\mathrm{i} ( \sigma _{n,i} + \sigma _{\varphi ,i} ) \Bigr ] + \nu _\mathrm{m}\sigma _{n,m,c} \end{aligned}$$

(120)

$$\begin{aligned} \sigma _{\varphi ,m,c} - \nu _\mathrm{m}\sigma _{t,m,c}= & {} \frac{E_\mathrm{m}}{E_\mathrm{i}}\Bigl [ \sigma _{\varphi ,i} - \nu _\mathrm{i} ( \sigma _{n,i} + \sigma _{t,i} ) \Bigr ] +\nu _\mathrm{m}\sigma _{n,m,c} . \end{aligned}$$

(121)

The solution leads to

$$\begin{aligned} \sigma _{t,m,c} = \frac{1}{1-\nu _\mathrm{m}^2}\Biggl [ \frac{E_\mathrm{m}}{E_\mathrm{i}}\Bigl [ \sigma _{t,i} - \nu _\mathrm{i} ( \sigma _{\varphi ,i} + \sigma _{n,i} ) \Bigr ] + \nu _\mathrm{m} \frac{E_\mathrm{m}}{E_\mathrm{i}}\Bigl [ \sigma _{\varphi ,i} - \nu _\mathrm{i} ( \sigma _{t,i} + \sigma _{n,i} ) \Bigr ] + \nu _\mathrm{m}(1+\nu _\mathrm{m})\sigma _{n,m,c} \Biggr ] \end{aligned}$$

(122)

$$\begin{aligned} \sigma _{\varphi ,m,c} = \frac{1}{1-\nu _\mathrm{m}^2}\Biggl [ \frac{E_\mathrm{m}}{E_\mathrm{i}}\Bigl [ \sigma _{\varphi ,i} - \nu _\mathrm{i} ( \sigma _{t,i} + \sigma _{n,i} ) \Bigr ] + \nu _\mathrm{m} \frac{E_\mathrm{m}}{E_\mathrm{i}}\Bigl [ \sigma _{t,i} - \nu _\mathrm{i} ( \sigma _{\varphi ,i} + \sigma _{n,i} ) \Bigr ] + \nu _\mathrm{m}(1+\nu _\mathrm{m})\sigma _{n,m,c} \Biggr ]\nonumber \\ \end{aligned}$$

(123)

The stress component $\sigma _{t,m,c}$ of Eq. (122), normalized by the applied load $S_z$, allows for $\theta = 0$ a comparison with Mura’s results given in curve plots, page 191 in [14]. In Fig. 21, the course of Eq. (122) in dependency of $\phi = E_\mathrm{i}/E_\mathrm{m}$ is compared with the results of Mura as well as with some values from finite element analyses. The results described by Eq. (122) are identical to Mura’s results within the accuracy of his graphics. This is not too surprising as both approaches deliver exact solutions.

A material-specific failure theory will require to derive an appropriate equivalent stress. For example, the maximum distortion strain energy criterion is described by the equivalent stress $\sigma _e$ according to von Mises

$$\begin{aligned} \sigma _e = \sqrt{\frac{1}{2}\biggl [ (\sigma _n-\sigma _t)^2+(\sigma _t-\sigma _\varphi )^2+(\sigma _\varphi -\sigma _n)^2 +6\tau _{nt}^2 \biggr ]} = \sqrt{3\cdot J_2'} \end{aligned}$$

(124)

where $J_2'$ is the second invariant of the stress deviator.

The calculated stress components are plotted in the diagrams of Fig. 22 for axial loading by $S_z$ and of Fig. 23 for axis-symmetrical radial loading $S_r$ both in their dependence of the vertical angle $\theta$. The left-side diagrams apply to soft inhomogeneities with $\phi = E_\mathrm{i}/E_\mathrm{m} = 0.5$, the right-side ones to hard inhomogeneities with $\phi = E_\mathrm{i}/E_\mathrm{m} = 2.0$. In each chart the graphs of a stress component of the inhomogeneities (solid line) is confronted that at the interface of the matrix (dashed line) demonstrating the deviations as a result of the differing Youngs moduli of inhomogeneities and matrix.

The equivalent stress $\sigma _e$ shown in the bottom diagrams might be chosen for an evaluation of the material’s strength capacity. Soft inhomogeneities with $\phi = E_\mathrm{i}/E_\mathrm{m} < 1$ move the stress peaks of $\sigma _e$ to the matrix side, while hard inhomogeneities $\phi = E_\mathrm{i}/E_\mathrm{m} > 1$ have an attractive effect with higher stress levels relieving the matrix. But absolute statements require the knowledge of and the comparison with the strength limits of both material constituents and the interface itself.

It is remarkable that the equivalent stress of the inhomogeneities in Fig. 22 for the load case $S_z$ is identical to that of Fig. 23 for the load case $S_r$. The background of this equivalence is that the stress state caused by a single load $S_x$ (generating an equivalent stress as by $S_z$) remains unchanged by a superposition of a second load $S_y$, whereas the stress components change.

Non-local failure hypotheses not only require information for stress or strain values at the critical location, e.g., at the interface for matrix failure, on which the focus has been placed so far. Only by applying such non-local hypotheses can, for example, the fatigue strength of materials and components be described realistically, see e.g., [15, 16]. As mentioned in Sect. 4.1, all field variables are available in analytical form, provided the input, $\sigma _z^*$ and $\sigma _r^*$, is known. Only a more or less virtuoso superposition of Neuber’s solution equations [12] for the spherical cavities becomes necessary. Figure 24 shows the curves for the stress component $\sigma _z(r)$, for $\theta = 0$, normalized by the applied load $S_z$, for various $\varPhi$-values. The dot-in-circle markers $\odot$ indicate that FE calculations have been performed. The graphs of the results of the converged numerical solution cannot be distinguished from the graph of the analytical solution, independent of any reasonable resolution of the graphics.

7 Conclusions

Up to now, the known solutions for a spherical inhomogeneity in an infinite solid have found little attention in practical failure assessments because of their disregard in the handbooks for engineering design. This lack may be attributed to the complicated mathematical methods of derivation and the incommodious depiction of the solutions. The exact solution can, however, also be presented in a more engineering oriented way of analysis considering the special deformation characteristics of the spherical inhomogeneity problem. The method used is based only on the special solution for a spherical cave from Neuber’s solution [12] for the axial-symmetrical deep ellipsoidal inner notch published 1937. Theoretically at that time, the precondition to solve the corresponding inhomogeneity problem was given.

As soon as the analytical solution for a remote homogenous loading with $S_z$ is known, the solutions for $S_x$- or $S_y$-loading can be obtained by simple permutation of indexes. The three solutions can further be superposed to provide the solution for an arbitrary remote homogeneous principal stress loading case. Any given remote homogeneous loading situation can be transformed to a principal stress loading case. After solving the latter, back-transformation of the field variables into the coordinate system of the given stress components provides the solution for this case, too. In this sense, the presented solution is comprehensive.

The present result is a compact formula including three simple influence factors depending on Young’s moduli and Poisson’s ratios which describes the stress state in the inhomogeneity in form of stress concentration factors. The stress state at the interface of the matrix can also be expressed in terms of concentration factors. It is expected that the clearly structured derivation supports the publication in handbooks and the application in practice.