Inflation with non-minimal kinetic and Gauss–Bonnet couplings

Abstract

The Mukhanov–Sasaki equation is deduced from linear perturbations for a general scalar-tensor model with non-minimal coupling to curvature, to the Gauss–Bonnet invariant and non-minimal kinetic coupling to curvature. The general formulas for the power spectra of the primordial scalar and tensor fluctuations are obtained for arbitrary coupling functions. The results have been applied to models with power-law, exponential, natural and double-well potentials. It was found that the presence of these non-minimal couplings affect the inflationary observables leading to values favored by the latest observations, while some interesting results like sub-planckian symmetry breaking scale in natural inflation and sub-planckian v.e.v. of the scalar filed in the double-well potential were obtained. The consistency with the reheating process was discussed and some numerical cases were shown. The equivalence of the model to a sector of generalized Galileons was shown and the functions that establish the correspondence were found.

1 Introduction

The theory of cosmic inflation [1,2,3,4,5,6] that has been favored by the latest observational data [7,8,9,10] is by now the most likely scenario for the early universe, since it provides the explanation to flatness, horizon and monopole problems, among others, for the standard hot Bing Bang cosmology [11,12,13,14,15,16]. Inflation also provides a detailed account of fluctuations that constitute the seeds for the large scale structure and the currently observed CMB anisotropies [17,18,19,20,21,22,23,24,25], as well as predicts a nearly scale invariant power spectrum.

There are currently many inflationary scenarios in direct proportion to the numerous existing models, being the minimally coupled scalar field the simplest one [3, 4] and continuing with several non-minimal extensions inspired on quantization on curved spaces arguments or on fundamental theories like string theory or supergravity. To those non-minimal scenarios belong inflation by non-minimally coupled scalar field [26,27,28], kinetic inflation [29], vector inflation [30,31,32], inflaton potential in supergravity [33,34,35,36], string theory inspired inflation [37,38,39,40,41], Dirac-Born-Infeld inflation model [42,43,44,45], $\alpha$-attractor models originated in supergravity [46,47,48,49]. Another class of ghost-free models has been recently considered, named “Galileon” models [50, 51]. A remarkable property of these models is that they contain higher derivatives of the scalar field and the metric but the corresponding field equations contain derivatives no higher than two. The effect of these Galileon terms is mostly reflected in the modification of the kinetic term compared to the standard canonical scalar field, which in turn can relax the physical constraints on the potential. For the Higgs potential, for instance, in the framework of Galilean models one of the effects of the higher derivative terms is the reduction of the self coupling of the Higgs boson, so that the spectra of primordial density perturbations are consistent with the present observational data [52,53,54]. Different aspects aspects of Galilean-inflation have been considered in [52,53,54,55,56,57,58,59].

An interesting class of models that belong to the generalized Galilean-type theories are models with non-minimal derivative couplings to curvature (particularly to the Einstein tensor) and non-minimal coupling to the Gauss–Bonnet four dimensional invariant. In the appendices B and C we show the correspondence of these models with the generalized Galileons. This correspondence determines the $G_i(X,\phi )$ functions of the generalized Galilean theory that give the equivalence with the corresponding terms in the scalar-tensor theory.

Non-minimal kinetic coupling (NMKC) to curvature and non-minimal coupling of the scalar field to the Gauss–Bonnet (GB) invariant appear from higher-order corrections to the low-energy bosonic string action [60, 61], and the effect of such corrections on the background evolution has been studied in connection with non-singular pre big-gang scenarios [62,63,64]. It is then expected that, in a high curvature regime typical of the inflationary period, these non-minimal couplings may become important and could affect the slow-roll dynamics and therefore the inflationary observables. The early time inflation with non-minimal kinetic coupling (NMKC) has been analyzed in [65,66,67,68,69,70,71,72,73,74,75,76,77,78], where it was shown that the additional gravitational friction provided by this coupling leads to successful inflation in various cosmological scenarios. The study of slow-roll inflation in scalar-tensor models with Gauss–Bonnet (GB) coupling has been done in [79,80,81,82,83,84,85,86,87,88]. The combined effect of the NMKC and GB coupling in the slow-roll inflation have been studied in [89,90,91,92] where some cosmological scenarios have been analyzed.

On the other hand, it is expected that the end of the slow-roll is followed by a reheating phase which eventually leads to the production of ordinary matter and connects the inflation with the hot big-bang phase [93,94,95,96,97,98,99]. This phase, that is one of the most poorly known processes after the end of inflation, can be a source of significant uncertainties for the inflationary predictions, in part due to the unreliability in determining the magnitude of the energy scale involved in the reheating process. Using the approximation of constant equation of state during reheating, some relations can be derived between reheating characteristics like its equation of state parameter, its energy scale and the inflationary indices. This allows to do some analysis of the consistency between the slow-roll phase and the reheating process, which in the present paper is illustrated with some of the models we have considered.

In this paper we make a general study of the slow-roll inflation in the frame of scalar-tensor model with NMKC to curvature and non-minimal coupling to the Gauss–Bonnet 4-dimensional invariant. We obtain the general formulas for the power spectra of scalar and tensor perturbations by deducing the Muhkanov-Sasaki equation within the first-order formalism, without resorting to the second-order action for these perturbations. The analytic formulas for the slow-roll parameters for the general scalar-tensor model with NMKC and GB couplings have been found. Then, we consider general models where the coupling functions are related to the scalar field potential and analyze the specific cases of power-law, exponential, natural and double-well potentials. The paper is organized as follows. In the next section we introduce the model, the background field equations and define the slow-roll parameters. In Sect. 3 we deduce the Mukhanov–sasaki equation from linear perturbations for scalar and tensor modes. In Sect. 4 we perform the slow-roll analysis for general relationships between the couplings and the potential and study models with power-law, exponential, natural and double-well potentials. In Sect. 5 we analyze the consistency of the slow-roll inflation with the reheating process and show some numerical cases. A discussion is given in Sect. 6. In appendix A we deduce the first-order perturbations for all the terms in the model in the Newtonian Gauge. In appendixes B and C we show the correspondence of the present model with the generalized Galileons.

2 The model and background equations

We consider the scalar-tensor model with non-minimal coupling of the scalar field to curvature, non-minimal kinetic coupling of the scalar field to the Einstein’s tensor and coupling of the scalar field to the Gauss–Bonnet (GB) 4-dimensional invariant

$$\begin{aligned} S= & {} \int d^4x\sqrt{-g}\left[ \frac{1}{2}F(\phi )R-\frac{1}{2}\partial _{\mu } \phi \partial ^{\mu }\phi -V(\phi )\right. \nonumber \\&\left. +F_1(\phi )G_{\mu \nu }\partial ^{\mu }\phi \partial ^{\nu }\phi -F_2(\phi )\mathcal{G}\right] \end{aligned}$$

(2.1)

where $G_{\mu \nu }$ is the Einstein’s tensor, $\mathcal{G}$ is the GB 4-dimensional invariant given by

$$\begin{aligned}&\mathcal{G}=R^2-4R_{\mu \nu }R^{\mu \nu }+R_{\mu \nu \lambda \rho }R^{\mu \nu \lambda \rho } \end{aligned}$$

(2.2)

$$\begin{aligned}&F(\phi )=\frac{1}{\kappa ^2}+f(\phi ), \end{aligned}$$

(2.3)

and $\kappa ^2=M_p^{-2}=8\pi G$. One remarkable characteristic of this model is that it yields second-order field equations and can avoid Ostrogradsky instabilities. Using the general results of Appendix B, expanded on the flat FRW background

$$\begin{aligned} ds^2=-dt^2+a(t)^2\left( dx^2+dy^2+dz^2\right) \end{aligned}$$

(2.4)

one finds the following equations

$$\begin{aligned}&3H^2F\left( 1-\frac{3F_1{\dot{\phi }}^2}{F}-\frac{8H\dot{F_2}}{F}\right) =\frac{1}{2}{\dot{\phi }}^2+V-3H{\dot{F}} \end{aligned}$$

(2.5)

$$\begin{aligned}&2{\dot{H}}F\left( 1-\frac{F_1{\dot{\phi }}^2}{F}-\frac{8H\dot{F_2}}{F}\right) =-{\dot{\phi }}^2\nonumber \\&\quad -{\ddot{F}}+H{\dot{F}}+8H^2\ddot{F_2}-8H^3\dot{F_2}\nonumber \\&\quad -6H^2F_1{\dot{\phi }}^2+4HF_1{\dot{\phi }}\ddot{\phi } +2H{\dot{F}}_1{\dot{\phi }}^2 \end{aligned}$$

(2.6)

$$\begin{aligned}&\ddot{\phi }+3H{\dot{\phi }}+V'-3F'\left( 2H^2+{\dot{H}}\right) \nonumber \\&\quad +24H^2\left( H^2+{\dot{H}}\right) F_2'+18H^3F_1{\dot{\phi }}\nonumber \\&\quad +12H{\dot{H}}F_1{\dot{\phi }}+6H^2F_1\ddot{\phi }+3H^2F_1'{\dot{\phi }}^2=0 \end{aligned}$$

(2.7)

where ($'$) denotes derivative with respect to the scalar field. In order to perform the slow-roll analysis for this model and taking into account the different couplings, we consider the following slow-roll parameters

$$\begin{aligned}&\epsilon _0=-\frac{{\dot{H}}}{H^2},\;\;\; \epsilon _1=\frac{{\dot{\epsilon }}_0}{H\epsilon _0}, \end{aligned}$$

(2.8)

$$\begin{aligned}&\ell _0=\frac{{\dot{F}}}{HF},\;\;\; \ell _1=\frac{{\dot{\ell }}_0}{H\ell _0}, \end{aligned}$$

(2.9)

$$\begin{aligned}&k_0=\frac{3F_1{\dot{\phi }}^2}{F},\;\;\; k_1=\frac{{\dot{k}}_0}{Hk_0}, \end{aligned}$$

(2.10)

$$\begin{aligned}&\Delta _0=\frac{8H\dot{F_2}}{F},\;\;\; \Delta _1=\frac{{\dot{\Delta }}_0}{H\Delta _0}, \end{aligned}$$

(2.11)

which must satisfy $\epsilon _0,\epsilon _1,...<<1$ during inflation. From the cosmological equations (2.5) and (2.6) and using the slow-roll parameters (2.8)–(2.11) we find the following expressions for ${\dot{\phi }}^2$ and V

$$\begin{aligned} V= & {} H^2F\Bigg [3-\frac{5}{2}\Delta _0-2k_0-\epsilon _0+\frac{5}{2}\ell _0 +\frac{1}{2}\ell _0\left( \ell _1-\epsilon _0+\ell _0\right) \nonumber \\&-\frac{1}{2}\Delta _0\left( \Delta _1-\epsilon _0+\ell _0\right) -\frac{1}{3}k_0\left( k_1+\ell _0-\epsilon _0\right) \Bigg ] \end{aligned}$$

(2.12)

$$\begin{aligned} {\dot{\phi }}^2= & {} H^2F\Bigg [2\epsilon _0+\ell _0-\Delta _0-2k_0+\Delta _0 \left( \Delta _1-\epsilon _0+\ell _0\right) \nonumber \\&\quad - \ell _0\left( \ell _1-\epsilon _0+\ell _0\right) +\frac{2}{3}k_0\left( k_1+\ell _0-\epsilon _0\right) \Bigg ] \end{aligned}$$

(2.13)

It is useful to define the variable Y from Eq. (2.13) as

$$\begin{aligned} Y=\frac{{\dot{\phi }}^2}{H^2F} \end{aligned}$$

(2.14)

where it follows that $Y = \mathcal{O}(\varepsilon )$. The cosmological equations (2.5)–(2.7) can be simplified under the slow-roll conditions $\ddot{\phi }<<3H{\dot{\phi }}$ and $\ell _i, k_i, \Delta _i<<1$ as follows

$$\begin{aligned}&3H^2F\simeq V, \end{aligned}$$

(2.15)

$$\begin{aligned}&2{\dot{H}}F\simeq -{\dot{\phi }}^2+H{\dot{F}}-6H^2F_1{\dot{\phi }}^2-8H^3{\dot{F}}_2, \end{aligned}$$

(2.16)

$$\begin{aligned}&3H{\dot{\phi }}+V'-6H^2F'+18H^3F_1{\dot{\phi }}+24H^4F'_2\simeq 0 \end{aligned}$$

(2.17)

where the potential V gives the dominant contribution to the Hubble parameter, while Eqs. (2.16) and (2.17) determine the dynamics of the scalar field in the slow-roll approximation. The number of e-folds is determined from

$$\begin{aligned} N=\int _{\phi _i}^{\phi _e}\frac{H}{{\dot{\phi }}}d\phi =\int _{\phi _i}^{\phi _e}\frac{H^2+6H^4F_1}{2H^2F'-8H^4F'_2-\frac{1}{3}V'}d\phi \nonumber \\ \end{aligned}$$

(2.18)

where $\phi _i$ and $\phi _e$ are the values of the scalar field at the beginning and end of inflation respectively, and the expression for ${\dot{\phi }}$ was taken from (2.17). The criteria for choosing the initial values will be discussed below.

3 The Mukhanov–Sasaki equation from linear perturbations

3.1 Scalar perturbations

The Mukhanov–Sasaki equation for scalar perturbations can be obtained from the linear perturbations in the Newtonian gauge. As will be shown, the final expression matches exactly the one obtained by the second perturbations in the uniform gauge ($\delta \phi =0$). We will use the following metric with scalar perturbations

$$\begin{aligned} d{s^2} = - (1 + 2\Phi )d{t^2} + {a^2}(t)\left[ {(1 - 2\Psi ){\delta _{ij}} } \right] d{x^i}d{x^j} \end{aligned}$$

(3.1)

The details of the first-order perturbations are given in appendix A. The comovil curvature perturbation which is a gauge invariant quantity [23, 25] is given by

$$\begin{aligned} \mathcal{{R}} = - \Psi - \frac{H}{{{{\dot{\phi }}} }}\delta \phi \end{aligned}$$

(3.2)

Taking the derivative with respect to time one finds:

$$\begin{aligned} \mathcal{{\dot{R}}} = - {{\dot{\Psi }}} - \frac{{{\dot{H}}}}{{{{\dot{\phi }}} }}\delta \phi + \frac{{H\ddot{\phi }}}{{{{{{\dot{\phi }}} }^2}}}\delta \phi - \frac{H}{{{{\dot{\phi }}} }}\delta {{\dot{\phi }}} \end{aligned}$$

(3.3)

The next steep is algebraically large. From the system of equations $\delta T_0^0=0$, $\delta T_i^0=0$ and $\delta T_j^i - \frac{1}{3}\delta _j^i\delta T_k^k=0$ (see Appendix A) we obtain the expressions for ${{{\dot{\Psi }}} }$, $\delta {{\dot{\phi }}}$ and $\Phi$, which are replaced in (3.3). To simplify the (very large) resulting expression, we use the background equations (2.6) and (2.7) in order to eliminate ${\ddot{\phi }}$ and $V'(\phi )$. After some algebra it is obtained:

$$\begin{aligned} \mathcal{{\dot{R}}} = 2{w_1}\frac{\Delta }{{{a^2}}}\Pi \end{aligned}$$

(3.4)

where

$$\begin{aligned} {w_1}= & {} \frac{{(H + \frac{{\dot{F} + {W_a}}}{{2F + {W_b}}})(F + \frac{1}{2}{W_b})}}{{({{{{\dot{\phi }}} }^2} + 3\frac{{{{(\dot{F} + {W_a})}^2}}}{{2F + {W_b}}} + {W_c})}}\,\,, \end{aligned}$$

(3.5)

$$\begin{aligned} \Pi= & {} - \Psi + \frac{1}{{{{\dot{\phi }}} }}\left( {\frac{{\dot{F} + {W_a}}}{{2F + {W_b}}}} \right) \,\,, \end{aligned}$$

(3.6)

with

$$\begin{aligned}&{W_a} = - 8{{\dot{F}}_2}{H^2} - 4{{{{\dot{\phi }}} }^2}{F_1}H\\&{W_b} = - 16{{\dot{F}}_2}H - 2{{{{\dot{\phi }}} }^2}F_1\\&{W_c} = 6{{{{\dot{\phi }}} }^2}{F_1}{H^2}\\ \end{aligned}$$

A second relationship between $\mathcal{{ R}}$ y $\Pi$ can be obtained by eliminating ${ \Psi }$, $\delta \phi$, $\Phi$ from the system of equations for $\delta T_i^0=0$ and $\delta T_j^i - \frac{1}{3}\delta _j^i\delta T_k^k=0$, and the expressions (3.2) and (3.6). The final expression can be simplified by using the background equation (2.6). After a tedious algebraic process it is obtained:

$$\begin{aligned} \frac{1}{{{w_2}}}\frac{d}{{dt}}\left( {{w_2}\Pi } \right) = \frac{1}{2}{w_3}\mathcal{{R}} \end{aligned}$$

(3.7)

where

$$\begin{aligned} {w_2}= & {} \frac{{a(F + \frac{1}{2}{W_b})}}{{(H + \frac{{\dot{F} + {W_a}}}{{2F + {W_b}}})}},\,\,\,\,\,\,\,\,\,\,\nonumber \\ {w_3}= & {} \frac{{{{{{\dot{\phi }}} }^2} + 3\frac{{{{(\dot{F} + {W_a})}^2}}}{{2F + {W_b}}} + {W_c} + {W_d} + \frac{{\dot{F} + {W_a}}}{{2F + {W_b}}}{W_e} + {{\left( {\frac{{\dot{F} + {W_a}}}{{2F + {W_b}}}} \right) }^2}{W_f}}}{{(H + \frac{{\dot{F} + {W_a}}}{{2F + {W_b}}})(F + \frac{1}{2}{W_b})}}\nonumber \\ \end{aligned}$$

(3.8)

with

$$\begin{aligned} {W_d}= & {} 4{{{{\dot{\phi }}} }^2}{F_1}{\dot{H}} \\ {W_e}= & {} - 32{{\dot{F}}_2}{\dot{H}} - 4{{\dot{\phi }}} ({{\dot{\phi }}} {{\dot{F}}_1} - 2{{\dot{\phi }}} {F_1}H + 2{F_1}\ddot{\phi }) \\ {W_f}= & {} 16({{{\ddot{F}}}_2} - {{\dot{F}}_2}H) - 4{{{{\dot{\phi }}} }^2}{F_1} \end{aligned}$$

The equations (3.4) and (3.7) can be rewritten with the help of the following definitions

$$\begin{aligned} c_S^2 = {w_1}{w_3}\,,\,\,\,\,\,\,z = \sqrt{\frac{{a{w_2}}}{{{w_1}}}} \,\,,\,\,\,\,\,u = z\mathcal{{R}}\,\,,\,\,\,\,\,\,v = \sqrt{\frac{{{w_2}}}{{a{w_3}}}} \Pi \nonumber \\ \end{aligned}$$

(3.9)

Taking into account the above definitions and in the conformal time $dt = ad\eta$ (“prima” means derivative with respect to conformal time), it is obtained that the equations (3.4) y (3.7) can be rewritten in the following form:

$$\begin{aligned}&{\left( {\frac{u}{z}} \right) ^\prime } = 2\frac{{{c_S}}}{z}\Delta v \end{aligned}$$

(3.10)

$$\begin{aligned}&\frac{2}{{c_S^2z}}{\left( {{c_S}zv} \right) ^\prime } = u \end{aligned}$$

(3.11)

Deriving (3.10) with respect to conformal time, one obtains:

$$\begin{aligned} \frac{{u''}}{z} - 2\frac{{z'u'}}{{{z^2}}} + 2\frac{{{{z'}^2}}}{{{z^3}}} - \frac{{z''u}}{{{z^2}}} = - 4\frac{{z'}}{{{z^3}}}\Delta \left( {{c_S}zv} \right) + \frac{2}{{{z^2}}}\Delta {\left( {{c_S}zv} \right) ^\prime } \end{aligned}$$

Using (3.10) y (3.11), the above expression can be rewritten in the following form:

$$\begin{aligned} \frac{{u''}}{z} - 2\frac{{z'u'}}{{{z^2}}} + 2\frac{{{{z'}^2}}}{{{z^3}}} - \frac{{z''u}}{{{z^2}}} = - 2\frac{{z'}}{z}{\left( {\frac{u}{z}} \right) ^\prime } + \frac{{c_S^2}}{z}\Delta u \end{aligned}$$

Multiplying the above equation by z and simplifying, gives

$$\begin{aligned} u'' - c_S^2\Delta u - \frac{{z''}}{z}u = 0 \end{aligned}$$

(3.12)

It is worth noticing that in this deduction the gauge invariant quantity $\mathcal{{R}}$ was used, and therefore this quantity is not affected by the gauge fixing. This is the reason why the Mukhanov–Sasaki equation matches the one obtained in the uniform field gauge ($\delta \phi =0$) with second order perturbations. In fact, in the uniform field gauge, $\mathcal{{R}} = - \Psi$, what simplifies the calculations in relation to (3.2).

The equation (3.12) is the Mukhanov–Sasaki equation obtained in general form from the linear perturbations, which matches exactly the one obtained from quadratic perturbations [89] and also coincides with the results reported in [100] (see also [58] for generalized Galileons). To show this one can write the quantities $W_a,\; W_b,...$ in terms of the slow-roll parameters as follows

$$\begin{aligned}&W_a=-HF\left( \Delta _0+\frac{4}{3}k_0\right) , \end{aligned}$$

(3.13)

$$\begin{aligned}&W_b=-F\left( 2\Delta _0+\frac{2}{3}k_0\right) , \end{aligned}$$

(3.14)

$$\begin{aligned}&W_c=2H^2F k_0, \end{aligned}$$

(3.15)

$$\begin{aligned}&W_d=-\frac{4}{3}H^2F\epsilon _0k_0, \end{aligned}$$

(3.16)

$$\begin{aligned}&W_e=4HF\left( \frac{2}{3}k_0+\epsilon _0\Delta _0-\frac{1}{3}k_0\left( k_1+\ell _0\right) \right) , \end{aligned}$$

(3.17)

$$\begin{aligned}&W_f=-2F\left( \Delta _0+\frac{2}{3}k_0+\Delta _0\left( \epsilon _0+\ell _0+\Delta _1\right) \right) , \end{aligned}$$

(3.18)

where we used

$$\begin{aligned} {\ddot{F}}_2=\frac{F\Delta _0}{8}\left( \Delta _1+\epsilon _0+\ell _0\right) , \end{aligned}$$

(3.19)

and

$$\begin{aligned} \frac{{{{\dot{F}}_1}{{{{\dot{\phi }}} }^2}}}{{HF}} + \frac{{2{F_1}{{\dot{\phi }}} \ddot{\phi }}}{{HF}} = \frac{1}{3}{k_0}{k_1} + \frac{1}{3}{k_0}{l_0}. \end{aligned}$$

(3.20)

Using these results in (3.5) and (3.8) we find the velocity of the scalar perturbations defined in (3.9), as

$$\begin{aligned} c_S^2 = 1 + \frac{\frac{1}{2}{{W^2}\left( {{\Delta _0}({\varepsilon _0} + {l_0} +{\Delta _1} )-\Delta _0 - \frac{2}{3}{k_0}} \right) + \frac{2}{3}W\left( {{2k_0}-k_0\left( {{l_0}+ {k_1} } \right) + 3{\Delta _0}{\varepsilon _0}} \right) - \frac{4}{3}{k_0}{\varepsilon _0}}}{{Y + 2{k_0} + \frac{3}{2}{W^2}(1 - {\Delta _0} - \frac{1}{3}{k_0})}} \end{aligned}$$

(3.21)

where

$$\begin{aligned} W = \frac{\ell _0-\Delta _0-\frac{4}{3}k_0}{1-\Delta _0-\frac{1}{3}k_0}. \end{aligned}$$

(3.22)

This is the same result that was obtained for $c_S^2$ using the second order formalism. Expanding up to second order in slow-roll parameters we find for $c_S^2$

$$\begin{aligned} c_S^2 \approx 1 + \frac{{{W^2}\left( { - \frac{1}{2}{\Delta _0} - \frac{1}{3}{k_0}} \right) + W\left( {\frac{4}{3}{k_0}\left( {1 + {\Delta _0} + \frac{1}{3}{k_0}} \right) - \frac{2}{3}{k_0}({k_1} + {l_0}) + 2{\Delta _0}{\varepsilon _0}} \right) - \frac{4}{3}{k_0}{\varepsilon _0}}}{{2{\varepsilon _0} + {l_0} - {\Delta _0}}}, \end{aligned}$$

(3.23)

where

$$\begin{aligned} W \approx {l_0} - {\Delta _0} - \frac{4}{3}{k_0}. \end{aligned}$$

To find the variable z in terms of the slow-roll parameters we first write $w_1$ and $w_2$ using (3.13)-(3.15) as

$$\begin{aligned}&w_1=\frac{1+\frac{1}{2}W\left( 1-\Delta _0-\frac{1}{3}k_0\right) }{H\left( Y+2k_0+\frac{3}{2}W^2(1-\Delta _0-\frac{1}{3}k_0\right) }, \end{aligned}$$

(3.24)

$$\begin{aligned}&w_2=\frac{aF}{H}\left( \frac{1-\Delta _0-\frac{1}{3}k_0}{1+\frac{1}{2} W}\right) . \end{aligned}$$

(3.25)

Then, from (3.9) follows

$$\begin{aligned} z=\sqrt{\frac{aw_2}{w_1}}=a\left( \frac{F\left( Y+2k_0+\frac{3}{2}W^2\left( 1-\Delta _0-\frac{1}{3}k_0\right) \right) }{\left( 1+\frac{1}{2}W\right) ^2}\right) ^{1/2}. \end{aligned}$$

(3.26)

which can be written as

$$\begin{aligned} z=a\sqrt{2{\mathcal{G}_S}}, \end{aligned}$$

(3.27)

where $\mathcal{G}_S$ is half the expression under the square root in (3.26). This quantity is equal to that obtained in the second order formalism [89]. Expanding up to second order in slow roll parameters it is found for $\mathcal{G}_S$

$$\begin{aligned} \begin{aligned} {\mathcal{G}_S} \approx F\Bigg [&\left( {{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}} \right) \left( {1 - W} \right) + \frac{1}{2}{\Delta _0}\left( {{\Delta _1} - {\varepsilon _0} + {l_0}} \right) \\&- \frac{1}{2}{l_0}\left( {{l_1} - {\varepsilon _0} + {l_0}} \right) + \frac{1}{3}{k_0}\left( {{k_1} + {l_0} - {\varepsilon _0}} \right) + \frac{3}{4}{W^2}\Bigg ] \end{aligned} \end{aligned}$$

(3.28)

Taking into account that $c_S^2$ can also be written as $c_S^2=\mathcal{F}_S/\mathcal{G}_S$, we consider the following change of variables as suggested in [58]

$$\begin{aligned}&{z_S} = \sqrt{2} a{\left( {{\mathcal{F}_S}{\mathcal{G}_S}} \right) ^{1/4}} = \sqrt{{c_S}} z\\&{{\tilde{u}}} = {z_S}\mathcal{R} = \sqrt{{c_S}} u\\&d{y_S} = {c_S}d\eta , \end{aligned}$$

after some algebra, the equation (3.12) can be rewritten in terms of these variables, giving

$$\begin{aligned} {{\tilde{u}}}'' - \Delta {{\tilde{u}}} - \frac{{{{z_S''}}}}{{{z_S}}}{{\tilde{u}}} = 0 \end{aligned}$$

(3.29)

where “prima” indicates derivative with respect to $y_S$. This shows that the equation resulting from the the second order action for the scalar perturbations [58, 89] can be obtained from (3.12) after the change of variables.

The next step is to derive de power spectrum using Eq. (3.12). Taking the derivative of z with respect to the conformal time it is obtained:

$$\begin{aligned}&\frac{{z'}}{z} = aH\left( {1 + \frac{1}{2}{g_S}} \right) \end{aligned}$$

(3.30)

$$\begin{aligned}&\frac{{z''}}{z} = {a^2}{H^2}\left[ {\left( {1 + \frac{1}{2}{g_S}} \right) \left( {2 + \frac{{{\dot{H}}}}{{{H^2}}} + \frac{1}{2}{g_S}} \right) + \frac{1}{2}\frac{1}{H}\frac{{d{g_S}}}{{dt}}} \right] \nonumber \\ \end{aligned}$$

(3.31)

where

$$\begin{aligned} {g_S} = \frac{{{{\dot{\mathcal{G}}}_S}}}{{H{\mathcal{G}_S}}} \end{aligned}$$

Expanding $g_S$ and $\frac{1}{H}\frac{{d{g_S}}}{{dt}}$ up to second order in slow-roll parameters gives

$$\begin{aligned}&{g_S} \approx {l_0} + \frac{{{\varepsilon _0}{\varepsilon _1} + \frac{1}{2}{l_0}{l_1} - \frac{1}{2}{\Delta _0}{\Delta _1}}}{{{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}}} - \frac{{\left( {{\varepsilon _0}{\varepsilon _1} + \frac{1}{2}{l_0}{l_1} - \frac{1}{2}{\Delta _0}{\Delta _1}} \right) \left( {{l_0} - {\Delta _0} - \frac{4}{3}{k_0}} \right) }}{{{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}}}\\&\quad - \frac{{\left( {{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}} \right) \left( {{l_0}{l_1} - {\Delta _0}{\Delta _1} - \frac{4}{3}{k_0}{k_1}} \right) - \frac{1}{2}{\Delta _0}{\Delta _1}\left( {{\Delta _1} - {\varepsilon _0} + {l_0}} \right) - \frac{1}{2}{\Delta _0}\left( {{\Delta _1}{\Delta _2} - {\varepsilon _0}{\varepsilon _1} + {l_0}{l_1}} \right) }}{{{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}}}\\&\quad - \frac{{\frac{1}{2}{l_0}{l_1}\left( {{l_1} - {\varepsilon _0} + {l_0}} \right) + \frac{1}{2}{l_0}\left( {{l_1}{l_2} - {\varepsilon _0}{\varepsilon _1} + {l_0}{l_1}} \right) - \frac{1}{3}{k_0}{k_1}\left( {{k_1} + {l_0} - {\varepsilon _0}} \right) - \frac{1}{3}{k_0}\left( {{k_1}{k_2} + {l_0}{l_1} - {\varepsilon _0}{\varepsilon _1}} \right) }}{{{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}}}\\&\quad + \frac{{\frac{3}{2}\left( {{l_0} - {\Delta _0} - \frac{4}{3}{k_0}} \right) \left( {{l_0}{l_1} - {\Delta _0}{\Delta _1} - \frac{4}{3}{k_0}{k_1}} \right) }}{{{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}}} \\&\frac{1}{H}\frac{{d{g_S}}}{{dt}} \approx {l_0}{l_1} + \frac{{\left( {{\varepsilon _0}\varepsilon _1^2 + {\varepsilon _0}{\varepsilon _1}{\varepsilon _2} + \frac{1}{2}{l_0}l_1^2 + \frac{1}{2}{l_0}{l_1}{l_2} - \frac{1}{2}{\Delta _0}\Delta _1^2 - \frac{1}{2}{\Delta _0}{\Delta _1}{\Delta _2}} \right) \left( {{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}} \right) }}{{{{\left( {{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}} \right) }^2}}}\\&\quad - \frac{{{{\left( {{\varepsilon _0}{\varepsilon _1} + \frac{1}{2}{l_0}{l_1} - \frac{1}{2}{\Delta _0}{\Delta _1}} \right) }^2}}}{{{{\left( {{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}} \right) }^2}}} \end{aligned}$$

where

$$\begin{aligned} {\varepsilon _2} = \frac{{{{{{\dot{\varepsilon }}} }_1}}}{{H{\varepsilon _1}}},\,\,\,\,\,\,\,{l_2} = \frac{{{{\dot{l}}_1}}}{{H{l_1}}},\,\,\,\,\,{\Delta _2} = \frac{{{{{{\dot{\Delta }}} }_1}}}{{H{\Delta _1}}},\,\,\,\,\,\,\,{k_2} = \frac{{{{\dot{k}}_1}}}{{H{k_1}}} \end{aligned}$$

match exactly with the respective expressions obtained from the generalized Galileons using second order perturbations. Note also that in the first order approximation in slow-roll parameters, the last term in (3.31) can be neglected. Thus, up to first order

$$\begin{aligned}&\frac{{z'}}{z}\approx aH\left( {1 + \frac{1}{2}{l_0} + \frac{1}{2}\frac{{{\varepsilon _0}{\varepsilon _1} + \frac{1}{2}{l_0}{l_1} - \frac{1}{2}{\Delta _0}{\Delta _1}}}{{{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}}}} \right) \end{aligned}$$

(3.32)

$$\begin{aligned}&\frac{{z''}}{z} \approx {a^2}{H^2}\left[ {2 - {\varepsilon _0} + \frac{3}{2}{l_0} + \frac{3}{2}\left( {\frac{{{\varepsilon _0}{\varepsilon _1} + \frac{1}{2}{l_0}{l_1} - \frac{1}{2}{\Delta _0}{\Delta _1}}}{{{\varepsilon _0} + \frac{1}{2}{l_0} - \frac{1}{2}{\Delta _0}}}} \right) } \right] \nonumber \\ \end{aligned}$$

(3.33)

This result allows to calculate the spectral index. Solving the equation (3.12) in Fourier components with $\frac{{z''}}{z}$ given by (3.33), and imposing the Bunch-Davies vacuum state [101, 102] we find the power spectrum of the curvature perturbation as

$$\begin{aligned} \mathcal{P}_S=\frac{\mathcal{A_S}H^2}{(2\pi )^2\mathcal{G}_S c_S^3}, \end{aligned}$$

(3.34)

where

$$\begin{aligned} \mathcal{A}_S=\frac{1}{2}2^{2\mu _s-3}\Big |\frac{\Gamma (\mu _s)}{\Gamma (3/2)}\Big |^2. \end{aligned}$$

The spectral index is

$$\begin{aligned} n_s-1=\frac{d \ln \mathcal{P}_S}{d\ln k}\Big |_{c_Sk=aH}=-2\epsilon _0-\ell _0-\frac{2\epsilon _0\epsilon _1+\ell _0\ell _1-\Delta _0\Delta _1}{2\epsilon _0+\ell _0-\Delta _0} \end{aligned}$$

(3.35)

which is evaluated at the horizon crossing, $c_S k = aH$ (k is the comovil wavenumber).

4 Tensor perturbations

The tensor perturbations affect only the traceless part of the spatial metric and the traceless part of the stress tensor. Then the amplitudes of tensor perturbations and $\pi ^T_{ij}$ (the dissipative correction to the stress tensor) are automatically gauge invariant. In order to calculate the power spectrum of tensor perturbations, we consider the following perturbed metric

$$\begin{aligned} d{s^2} = - d{t^2} + {a^2}(t)\left( {{\delta _{ij}} + {h_{ij}}} \right) d{x^i}d{x^j} \end{aligned}$$

(3.36)

where $h_{ij}$ is the tensor perturbation which satisfies ${h_{ii}}=0$, ${h_{ij}}={h_{ji}}$ and ${{\partial _i}}{h_{ij}}=0$. The spatial component of the perturbed field equation (up to first order) gives the following result for the tensorial modes

$$\begin{aligned}&\left( { - \frac{1}{2}F + \frac{1}{2}{F_1}{{{{\dot{\phi }}} }^2} + 4H{{\dot{F}}_2}} \right) {\ddot{h}}_j^i \nonumber \\&\quad + \left( {\frac{1}{2}F + \frac{1}{2}{F_1}{{{{\dot{\phi }}} }^2} - 4{{{\ddot{F}}}_2}} \right) \frac{{\Delta h_j^i}}{{{a^2}}}\nonumber \\&\quad + \left( {3H\left( { - \frac{1}{2}F + \frac{1}{2}{F_1}{{{{\dot{\phi }}} }^2} + 4H{{\dot{F}}_2}} \right) - \frac{1}{2}\dot{F} }\right. \nonumber \\&\quad \left. + {{F_1}{{\dot{\phi }}} \ddot{\phi }+ \frac{1}{2}{{\dot{F}}_1}{{{{\dot{\phi }}} }^2} + 4{\dot{H}}{{\dot{F}}_2} + 4H{{{\ddot{F}}}_2}} \right) {\dot{h}}_j^i=0. \end{aligned}$$

(3.37)

The above expression can be rewritten in the following form

$$\begin{aligned}&{\ddot{h}}_j^i + \left[ {3H + \frac{{\dot{F} - 2{F_1}{{\dot{\phi }}} \ddot{\phi }- {{\dot{F}}_1}{{{{\dot{\phi }}} }^2} - 8{\dot{H}}{{\dot{F}}_2} - 8H{{{\ddot{F}}}_2}}}{{F - {F_1}{{{{\dot{\phi }}} }^2} - 8H{{\dot{F}}_2}}}} \right] \nonumber \\&{\dot{h}}_j^i - \left[ {\frac{{F + {F_1}{{{{\dot{\phi }}} }^2} - 8{{{\ddot{F}}}_2}}}{{F - {F_1}{{{{\dot{\phi }}} }^2} - 8H{{\dot{F}}_2}}}} \right] \frac{{\Delta h_j^i}}{{{a^2}}} = 0 \end{aligned}$$

(3.38)

Let us define the following quantities

$$\begin{aligned}&{\mathcal{G}_T} = F - {F_1}{{{{\dot{\phi }}} }^2} - 8H{{\dot{F}}_2}=F\left( 1-\frac{1}{3}k_0-\Delta _0\right) \end{aligned}$$

(3.39)

$$\begin{aligned}&{\mathcal{F}_T} = F + {F_1}{{{{\dot{\phi }}} }^2} - 8{{{\ddot{F}}}_2}=F\left( 1+\frac{1}{3}k_0-\Delta _0\left( \epsilon _0+\ell _0+\Delta _1\right) \right) \nonumber \\ \end{aligned}$$

(3.40)

that allow to write the above equation in compact form as

$$\begin{aligned} {\ddot{h}}_j^i + \left[ {3H + \frac{{{{\dot{\mathcal{G}}}_T}}}{{{\mathcal{G}_T}}}} \right] {\dot{h}}_j^i - \left[ {\frac{{{\mathcal{F}_T}}}{{{\mathcal{G}_T}}}} \right] \frac{{\Delta h_j^i}}{{{a^2}}} = 0, \end{aligned}$$

(3.41)

which can be rewritten in the following form

$$\begin{aligned} \frac{1}{{{a^3}{\mathcal{G}_T}}}\frac{d}{{dt}}\left[ {{a^3}{\mathcal{G}_T}{\dot{h}}_j^i} \right] - \left[ {\frac{{{\mathcal{F}_T}}}{{{\mathcal{G}_T}}}} \right] \frac{{\Delta h_j^i}}{{{a^2}}} = 0. \end{aligned}$$

(3.42)

Introducing the variable $v_j^i \equiv {z_T}h_j^i$ with ${z_T} \equiv a\sqrt{{\mathcal{G}_T}}$, the above equation can be rewritten as

$$\begin{aligned} \frac{1}{{{z_T}}}{\left[ {z_T^2{{\left( {\frac{{v_j^i}}{{{z_T}}}} \right) }^\prime }} \right] ^\prime } - \left[ {\frac{{{\mathcal{F}_T}}}{{{\mathcal{G}_T}}}} \right] \Delta v_j^i = 0, \end{aligned}$$

(3.43)

where “prima” indicates differentiation with respect to conformal time $\eta$, with $dt = ad\eta$. Taking the derivatives and simplifying it is obtained

$$\begin{aligned} {\left( {v_j^i} \right) ^{\prime \prime }} - c_T^2v_j^i - \frac{{{z_T}^{\prime \prime }}}{{{z_T}}}v_j^i = 0, \end{aligned}$$

(3.44)

where

$$\begin{aligned} c_T^2 = \frac{{{\mathcal{F}_T}}}{{{\mathcal{G}_T}}}. \end{aligned}$$

(3.45)

Following the same process as for scalar modes we find the power spectra for the tensor fluctuations created by inflation as

$$\begin{aligned} \mathcal{P}_T= 16A_T\frac{H^2}{(2\pi )^2}\frac{\mathcal{G}_T^{1/2}}{\mathcal{F}_T^{3/2}}=\frac{16A_T H^2}{(2\pi )^2\mathcal{G}_T c_T^3} \end{aligned}$$

(3.46)

where

$$\begin{aligned} A_T=\frac{1}{2}2^{2\mu _T-3}\Big |\frac{\Gamma (\mu _T)}{\Gamma (3/2)}\Big |^2. \end{aligned}$$

For the tensor spectral index it is found

$$\begin{aligned} n_T=\frac{d \ln \mathcal{P}_T}{d\ln k}\Big |_{c_Sk=aH}=-2\epsilon _0-\ell _0. \end{aligned}$$

(3.47)

Another important quantity is the relative contribution to the power spectra of tensor and scalar perturbations, defined as the tensor/scalar ratio r

$$\begin{aligned} r=\frac{\mathcal{P}_T}{\mathcal{P}_S}\simeq 16\frac{\mathcal{G}_S}{\mathcal{G}_T} \end{aligned}$$

(3.48)

where in the last approximation we used the fact that $A_T/A_S\simeq 1$ and $c_T\simeq c_S\simeq 1$ during inflation, when $\epsilon _0,\ell _0, \Delta _0,...<<1$ holds. Using the results for $\mathcal{G}_S$ (3.28) and $\mathcal{G}_T$ (3.39), up to first order in slow-roll parameters we find

$$\begin{aligned} r=8\left( \frac{2\epsilon _0+\ell _0-\Delta _0}{1-\frac{1}{3}k_0-\Delta _0}\right) \simeq 8\left( 2\epsilon _0+\ell _0-\Delta _0\right) , \end{aligned}$$

(3.49)

which is the consistency relation in presence of non-minimal kinetic and GB couplings, that modifies the standard relation $r=16\epsilon _0$. An observational deviation from the standard consistency relation could be a signal of interactions beyond the simple canonical scalar field.

5 Slow-roll analysis

From Eqs. (2.15)–(2.17) and the equations that define the slow-roll parameters (2.8)–(2.11) one can express the slow-roll parameters and the main inflationary observables in terms of the scalar field potential $V(\phi )$ and the couplings F, $F_1$, $F_2$. In the following analysis we will consider the effect of the kinetic and GB couplings with

$$\begin{aligned} F=\frac{1}{\kappa ^2}=M_P^2. \end{aligned}$$

From the equations (2.15)–(2.17) we find in terms of the scalar field $H(\phi ), {\dot{H}}(\phi ), {\ddot{H}}(\phi ), {\dot{\phi }}$ and $\ddot{\phi }$, which are used to find $\epsilon _0, \epsilon _1,...$ from (2.8)–(2.11). After some algebra we find the following expressions for $\epsilon _0$, $\Delta _0$, $k_0$

$$\begin{aligned}&\epsilon _0=\frac{V'\left( 8V^2F_2'+3M_p^4V'\right) }{6V^2\left( M_p^2+2F_1 V\right) },\;\; k_0=\frac{F_1\left( 8V^2F_2'+3M_p^4V'\right) ^2}{9M_p^4V\left( M_p^2+2F_1 V\right) ^2},\;\; \nonumber \\&\Delta _0= -\frac{8F_2'\left( 8V^2F_2'+3M_p^4V'\right) }{9M_p^4\left( M_p^2+2F_1 V\right) } \end{aligned}$$

(4.1)

taking the time derivative of these magnitudes and replacing ${\dot{\phi }}$ and $\ddot{\phi }$ we find for $\epsilon _1$, $k_1$ and $\Delta _1$ the following result

$$\begin{aligned} \epsilon _1= & {} -\frac{2}{3V^2V'\left( M_p^2+2F_1 V\right) ^2}\nonumber \\&\times \Big [-3M_p^6V'^3-3M_p^4V^2V'\left( F_1' V'-2F_1V''\right) \nonumber \\&+3V\left( -3M_p^4F_1V'^3+M_p^6V'V''\right) \nonumber \\&+V^3\left( -8F_1F_2'V'^2+4M_p^2\left( V'F_2''+F_2'V''\right) \right) \nonumber \\&+V^4\left( -8F_1'F_2'V'+8F_1\left( V'F_2''+F_2'V''\right) \right) \Big ], \end{aligned}$$

(4.2)

$$\begin{aligned} k_1= & {} \frac{1}{3F_1V^2\left( M_p^2+2F_1 V\right) ^2}\nonumber \\&\times \Big [3M_p^6F_1V'^2+16F_1V^4\left( F_1'F_2'-2F_1F_2''\right) \nonumber \\&-8V^3\left( M_p^2F_1'F_2'+2F_1\left( F_1F_2'V'+M_p^2F_2''\right) \right) \nonumber \\&-6M_p^2F_1V^2\big (-M_p^2F_1'V'\nonumber \\&+4F_2'V'+2M_p^2F_1V''\big )\nonumber \\&-3V\left( M_p^6F_1'V'+2M_p^4F_1\left( -3F_1V'^2+M_p^2V''\right) \right) \Big ], \end{aligned}$$

(4.3)

$$\begin{aligned} \Delta _1= & {} \frac{1}{3M_p^2VF_2'\left( M_p^2+2F_1 V\right) ^2}\nonumber \\&\times \Big [-16M_p^4VF_2'\left( F_2'V'+VF_2''\right) \nonumber \\&+16M^2V^2F_2'\left( -F_1F_2'V'+V\left( F_1'F_2'-2F_1F_2''\right) \right) \nonumber \\&-3M_p^8\left( V'F_2''+F_2'V''\right) \nonumber \\&+M_p^6\left( 6F_1F_2'V'^2+6V \left( F_1'F_2'V'-F_1\left( V'F_2''+F_2'V''\right) \right) \right) \Big ],\nonumber \\ \end{aligned}$$

(4.4)

where “prima” indicates derivative with respect to $\phi$. Using these results we find the analytical expressions, in terms of the scalar field, for the scalar spectral index $n_s$ and the tensor-to-scalar ratio r as follows

$$\begin{aligned} \begin{aligned} n_s=&\frac{1}{3V^2\left( M_p^2+2F_1 V\right) ^2}\Big [4V^4\left( 3F_1^2-4F_1'F_2'+8F_1F_2''\right) \\&+4M_p^2V^2\left( 3F_1V+2F_2'V'+4VF_2''\right) \\&+M_p^6\left( -9V'^2+6VV''\right) \\ {}&+3M_p^4V\left( -8F_1V'^2+V\left( 1-2F_1'V'+4F_1V''\right) \right) \Big ], \end{aligned} \end{aligned}$$

(4.5)

and

$$\begin{aligned} r=\frac{8\left( 8V^2F_2'+3M_p^4V'\right) ^2}{9M_p^4V^2\left( M_p^2+2F_1V\right) }. \end{aligned}$$

(4.6)

These magnitudes must be evaluated at the value that the scalar field takes at the horizon crossing. Note that $n_s$ and r reduce to the corresponding expressions for the standard minimally coupled scalar field (given $F_1=0, \; F_2=0$)

$$\begin{aligned} n_s=1-3M_p^2\left( \frac{V'}{V}\right) ^2+2M_p^2\frac{V''}{V} \end{aligned}$$

(4.7)

and

$$\begin{aligned} r=8M_p^2\left( \frac{V'}{V}\right) ^2 \end{aligned}$$

(4.8)

It can be seen that all above magnitudes depend on $V,\; F_1,\;F_2$ only through combinations

$$\begin{aligned} \frac{V'}{V}, \;\; F_1V,\;\; F_2V', \end{aligned}$$

which can be used to discuss some general aspects of inflation in the frame of scalar-tensor models with kinetic and GB couplings. $\epsilon _0$, can be rewritten as follows

$$\begin{aligned} \epsilon _0=\frac{8VF_2'+3M_p^4 V'/V}{6\left( M_p^2+2F_1V\right) }\left( \frac{V'}{V}\right) , \end{aligned}$$

(4.9)

and similarly for $\epsilon _1, k_0,...$ given in (4.2–(4.4). The scalar spectral index and tensor-to-scalar ratio can be rewritten the form

$$\begin{aligned} n_s= & {} \frac{1}{3\left( M_p^2+2F_1 V\right) ^2}\Bigg \{4\Big [3(F_1V)^2-4(F_2'V)\left( (F_1V)'-(F_1V)\left( \frac{V'}{V}\right) \right) \nonumber \\&+ 8(F_1V)\left( (F_2'V)'-(F_2'V)\left( \frac{V'}{V}\right) \right) \Big ]+4M_p^2\Big [3(F_1V)+2(F_2'V)\left( \frac{V'}{V}\right) \nonumber \\&+4(F_2'V)'-4(F_2'V)\left( \frac{V'}{V}\right) \Big ]+3M_p^4\Big [1-8(F_1V)\left( \frac{V'}{V}\right) ^2-2(F_1V)'\left( \frac{V'}{V}\right) \nonumber \\&+ 2(F_1V)\left( \frac{V'}{V}\right) ^2+4(F_1V)\left( \frac{V'}{V}\right) '+4(F_1V)\left( \frac{V'}{V}\right) ^2\Big ] +M_p^6\left( 6\left( \frac{V'}{V}\right) '-3\left( \frac{V'}{V}\right) ^2\right) \Bigg \} \end{aligned}$$

(4.10)

$$\begin{aligned} r=\frac{8}{9M_p^4\left( M_p^2+2F_1 V\right) }\left( 8F_2'V+3M_p^4\left( \frac{V'}{V}\right) \right) ^2. \end{aligned}$$

(4.11)

The number of e-foldings (2.18) takes the form

$$\begin{aligned} N=-\int _{\phi _i}^{\phi _e}\frac{3\left( M_p^2+2F_1V\right) }{8F_2'V+3M_p^4\left( \frac{V'}{V}\right) }d\phi . \end{aligned}$$

(4.12)

All above magnitudes should be evaluated at the beginning of inflation or the horizon crossing, when $c_Sk=aH$. From this last equation it follows the dependence of the scalar field at the beginning of inflation on the coupling constants associated to the kinetic and GB terms as well as the potential. Only after the form of these interactions are given one can analyze different asymptotic behavior of the model but still, we can make some general considerations.

So for example the kinetic coupling appears only in the denominator in $\epsilon _0$, which in the case of chaotic inflation (which usually takes place for large scalar field) could allow small field inflation ($\phi <M_p$). At first glance it can also be seen that the strong coupling limit for the GB term is not allowed since $\epsilon _0$ could grow unlimitedly. The tensor/scalar ratio can also take lower values at strong kinetic coupling limit as follows from (4.11), which could improve the results for power-law (chaotic) potentials. On the other hand, it is clear that by establishing relationships between the potential and the coupling functions $F_1$ and $F_2$ one can extract interesting results. For a more detailed analysis we will consider some special cases.

5.1 Inverse proportionality between V and the couplings

We consider the relations

$$\begin{aligned} F_1(\phi )V(\phi )=const.=\beta M_p^2,\;\;\; F_2'(\phi )V(\phi )=-\eta M_p^4\frac{V'(\phi )}{V(\phi )}. \end{aligned}$$

(4.13)

The last relation is equivalent to $F_2(\phi )V(\phi )=\eta M_p^4$. This restriction has been frequently used in the study of slow-roll inflation with scalar-tensor couplings and gives viable theoretical predictions for $n_s$ and r [103,104,105,106,107,108,109]. Note that from the definition of $k_0$ in Eq. (2.10) and Eq. (2.13) follows

$$\begin{aligned} F_1\sim \frac{k_0}{3(2\epsilon _0+\cdots ) H^2}\sim \frac{1}{H^2}, \end{aligned}$$

(4.14)

valid during slow-roll inflation and assuming that the slow-roll parameters are of the same order or are approximately constant during most of the time of inflation. Hence, taking into account the approximation $3H^2\approx \kappa ^2 V$, valid during potential-driven inflation [see Eq. (2.15)], it follows from (4.14) that the choice $F_1\propto V^{-1}$ seems suitable for inflation.

With this choice of $F_1$ and $F_2$ the corresponding contributions to the Lagrangian during inflation are of the size

$$\begin{aligned} F_1 R\left( \partial \phi \right) ^2\sim \frac{\beta M_p^2}{V}H_i^2\left( \partial \phi \right) ^2\sim \frac{\beta M_p^2 H_i^2}{V_0}\left( \partial \phi \right) ^2 \end{aligned}$$

(4.15)

and

$$\begin{aligned} F_2 R^2\sim \frac{\eta M^4 H_i^4}{V}\sim \frac{\eta M_p^4 H_i^4}{V_i}, \end{aligned}$$

(4.16)

where $H_i$ and $V_i$ are the Hubble parameter and the scale of the potential during inflation. Assuming the typical values for $H_i$ and $V_i$, $H_i\sim 10^{-5}M_p$, $V_i\sim 10^{-10}M_p^4$ we find $F_1 R\left( \partial \phi \right) ^2\sim \beta \left( \partial \phi \right) ^2$ and $F_2 R^2\sim 10^{-10}\eta M_p^4$. Then values of $\eta \sim 1$ and $\beta >1$ (or even $>>1$ whenever $\beta \left( \partial \phi \right) ^2<<V_i$) lead to inflationary dynamics driven by the potential.

In order to have a consistent reheating process at the end of inflation where the scalar field can oscillate at the minimum of the potential, when needed, we can add a small constant correction to the relations (4.13) in the form $F_1(V+\alpha )=\beta M_p^2$ and $F_2(V+\alpha )=\eta M_p^4$, where $\alpha<<V$ during inflation. In this way we can avoid possible divergences in the coupling functions during oscillations around the minimum of the potential.

Using (4.13) the slow-roll parameters take the following simple form (we are going to use $\kappa ^2=M_p^{-2}=1$ for simplicity and recover $M_p^2$ when needed)

$$\begin{aligned}&\epsilon _0= \frac{3-8\eta }{6(1+2\beta )}\left( \frac{V'^2}{V^2}\right) ,\;\;\Delta _0= \frac{8\eta \left( 3-8\eta \right) }{9(1+2\beta )}\left( \frac{V'^2}{V^2}\right) ,\nonumber \\&k_0= \frac{\beta \left( 3-8\eta \right) ^2}{9(1+2\beta )^2}\left( \frac{V'^2}{V^2}\right) \nonumber \\&\epsilon _1=\Delta _1=k_1=\frac{2\left( 3-8\eta \right) }{3\left( 1+2\beta \right) }\left( \frac{V'^2-VV''}{V^2}\right) \end{aligned}$$

(4.17)

For $n_s$ and r the following expressions are obtained

$$\begin{aligned}&n_s=\frac{3\left( 8\eta -3\right) V'^2+V\left[ \left( 6-16\eta \right) V''+3\left( 2\beta +1\right) V\right] }{3\left( 2\beta +1\right) V^2} \nonumber \\\end{aligned}$$

(4.18)

$$\begin{aligned}&r=\frac{8\left( 3-8\eta \right) }{9\left( 1+2\beta \right) }\left( \frac{V'^2}{V^2}\right) . \end{aligned}$$

(4.19)

For the number of e-folds form (4.12) we find

$$\begin{aligned} N=-\frac{3(1+2\beta )}{3-8\eta }\int _{\phi _i}^{\phi _e}\left( \frac{V}{V'}\right) d\phi . \end{aligned}$$

(4.20)

Then the slow-roll dynamics becomes determined by the form of the potential. The following cases are of interest.

Power-law potential

Let us consider potential

$$\begin{aligned} V=\frac{\lambda }{n}\phi ^n \end{aligned}$$

(4.21)

In the canonical model this potential includes the simplest chaotic models characterized by large values of the inflaton field. The slow-roll parameters are

$$\begin{aligned}&\epsilon _0=\frac{\left( 3-8\eta \right) n^2}{6\left( 2\beta +1\right) \phi ^2},\;\; \Delta _0=\frac{16\eta }{3}\epsilon _0,\;\; k_0=\frac{\beta \left( 3-8\eta \right) ^2n^2}{9\left( 2\beta +1\right) ^2\phi ^2}\nonumber \\&\epsilon _1=\Delta _1=k_1=\frac{2\left( 3-8\eta \right) n}{3\left( 2\beta +2\right) \phi ^2}. \end{aligned}$$

(4.22)

The inflaton field at the beginning and at the end of inflation takes the values (recovering $\kappa$)

$$\begin{aligned} \phi _i=\sqrt{\frac{n(4N+n)(3-8\eta )}{6(1+2\beta )}}M_p,\;\;\; \phi _e=\sqrt{\frac{3-8\eta }{6(1+2\beta )}}M_p \end{aligned}$$

(4.23)

valid for $\eta <3/8$. Note that the inflaton can take values $\phi <M_p$ if the the kinetic coupling constant $\beta$ is large enough or in the case $\eta$ close to 3/8. For the observables $n_s$ and r we find

$$\begin{aligned} n_s=\frac{4N-n-4}{4N+n},\;\;\; r=\frac{16n(3-8\eta )}{3(4N+n)}. \end{aligned}$$

(4.24)

While $n_s$ remains the same as in the standard minimal case, the tensor/scalar ratio is influenced by the GB coupling and can take values in the range consistent with observations ($r<0.05$) [9]. This favors the simplest inflationary model corresponding to $n=2$ (assuming for instance $\eta =1/4$, then for 60 e-foldings gives $r\approx 0.044$). As will be shown in Sect. 6, if the subsequent reheating process is taken into account, then in the approximation of instantaneous reheating the $\phi ^2$ and $\phi ^4$ potentials become favored since $n_s$ and r can take values well inside the region favored by the latest observations.

Exponential potential

The exponential potential is given by

$$\begin{aligned} V=V_0 e^{-\lambda \phi /M_p}, \end{aligned}$$

(4.25)

where $V_0$ is fixed by COBE normalization and $\lambda$ is a free parameter. With the couplings (4.13) this potential has been considered in [90]. In the canonical model the inflation is of power-law type since the scale factor evolves as $a\propto t^{2/\lambda ^2}$, and the slow-roll parameters are constant ($\epsilon _0=\lambda ^2/2$, which for consistency requires $\lambda ^2<<1$) and therefore there is no way out of inflation. This result also holds for the couplings satisfying the conditions (4.13), as follows from (4.17). However it predicts the following results for the inflationary observables $n_s$ and r [90]

$$\begin{aligned} n_s=\frac{6\beta +8\eta \lambda ^2-3\lambda ^2+3}{6\beta +3},\;\;\; r=\frac{8\left( 8\eta -3\right) ^2\lambda ^2}{9\left( 2\beta +1\right) } \end{aligned}$$

(4.26)

that can give values compatible with observations. Taking for instance $\lambda =2/3,\; \beta =6/7,\; \eta =0.3$ gives $n_s\approx 0.967$ and $r\approx 0.052$. This would make sense if there were a mechanism of exit from inflation that does not alter the results of perturbations.

Natural inflation potential

In natural inflation the effective potential for the axion scalar field takes the form [110, 111]

$$\begin{aligned} V=\Lambda ^4\left( 1+\cos \left( \frac{\phi }{f}\right) \right) , \end{aligned}$$

(4.27)

where $\Lambda$ is the scale of the potential which is fixed by appropriate normalization of the scalar perturbations and f is the axion scale that controls the slope of the potential. this model gives consistent results with CMB for $f\gtrsim 5M_p$ [9], while theoretical requirements of consistency demand $f<M_p$ (f is the symmetry breaking scale of the shift symmetry (see [110])). Some mechanisms have been proposed in order to obtain natural inflation in terms of axions in sub-Planckian scale [54, 112,113,114,115]. If one assumes a non-standard coupling of the axion field in the form of coupling to the GB term and kinetic coupling to curvature that satisfy the relations (4.13), then the symmetry properties of the potential remain preserved and, as will be shown, the axion field can lead to inflation while maintaining $f<M_p$. The scalar field at the end and at the beginning of inflation are

$$\begin{aligned}&\phi _e=2f\arctan \left[ f\sqrt{\frac{6(2\beta +1)}{3-8\eta }}\right] ,\nonumber \\&\phi _i=2f\arcsin \left[ \frac{e^{-\frac{(3-8\eta )N}{6f^2(2\beta +1)}}}{\sqrt{1+\frac{3-8\eta }{6f^2(2\beta +1)}}}\right] . \end{aligned}$$

(4.28)

Note that for $\eta$ the physically allowable values are $\eta <3/8$. Taking into account the periodicity, $0\le \phi /f\le 2\pi$, from these expressions it follows that the size of $\phi _i,\; \phi _e$ is of the same order of f. Then, if the scale of symmetry breaking is sub Planckian, the inflation occurs in the small field regime. The slow-roll indices at the horizon crossing take the values

$$\begin{aligned}&\epsilon _0=\frac{(3-8\eta )e^{-\frac{(3-8\eta )N}{3f^2(2\beta +1)}}}{6f^2(2\beta +1)\left( 1-e^{-\frac{(3-8\eta )N}{3f^3(2\beta +1)}}\right) -8\eta +3},\nonumber \\&\Delta _0=\frac{16\eta }{3}\epsilon _0,\quad k_0=\frac{2\beta (3-8\eta )}{3(2\beta +1)}\epsilon _0\nonumber \\&\epsilon _1=\Delta _1=k_1=\frac{3-8\eta }{3f^2(2\beta +1)\left[ 1-\frac{e^{-\frac{(3-8\eta )N}{3f^2(2\beta +1)}}}{1+\frac{3-8\eta }{6f^2(2\beta +1)}}\right] }. \end{aligned}$$

(4.29)

Note that making $\beta$ large enough and/or $\eta$ close to 3/8 we can make the slow-roll parameters as small as necessary under the condition $f<M_p$. The scalar spectral index and the tensor/scalar ratio as functions of the scalar field from (4.17) are

$$\begin{aligned}&n_s=\frac{2\left[ \left( 3f^2(2\beta +1)-8\eta +3\right) \cos \left( \phi /f\right) +3\left( f^2(2\beta +1)+8\eta -3\right) \right] cos^2\left( \phi /(2f)\right) }{3f^2(2\beta +1)\left( \cos \left( \phi /f\right) +1\right) ^2} \end{aligned}$$

(4.30)

$$\begin{aligned}&r=\frac{8\left( 8\eta -3\right) ^2\tan ^2\left( \frac{\phi }{2f}\right) }{9f^2\left( 2\beta +1\right) } \end{aligned}$$

(4.31)

and evaluating them at the horizon crossing gives

$$\begin{aligned}&n_s=\frac{18f^4(2\beta +1)^2\left[ e^{-\frac{(3-8\eta )N}{3f^2(2\beta +1)}}-1\right] +3f^2(2\beta +1)(3-8\eta )\left[ 2e^{-\frac{(3-8\eta )N}{3f^2(2\beta +1)}}+1\right] +(8\eta -3)^2}{3f^2(2\beta +1)\left[ 6f^2(2\beta +1)\left( e^{-\frac{(3-8\eta )N}{3f^2(2\beta +1)}}-1\right) +8\eta -3\right] } \end{aligned}$$

(4.32)

$$\begin{aligned}&r=\frac{16(8\eta -3)^2e^{-\frac{(3-8\eta )N}{3f^2(2\beta +1)}}}{3\left[ 6f^2(2\beta +1)\left( 1-e^{-\frac{(3-8\eta )N}{3f^2(2\beta +1)}}\right) -8\eta +3\right] }. \end{aligned}$$

(4.33)

In the region $\beta>>1$ the spectral index takes values close to the asymptotic limit

$$\begin{aligned} n_s=\frac{2N-3}{2N+1} \end{aligned}$$

(4.34)

for $50\le N\le 70$ $n_s$ varies in the interval $0.960\le n_s\le 0.972$ which is consistent with observations. The corresponding limit for r is

$$\begin{aligned} r=\frac{16(3-8\eta )}{6N+3}, \end{aligned}$$

(4.35)

which in the interval $50\le N\le 70$ is very small when $\eta$ is very close to 3/8. Imposing an upper bound for r, for instance for $r <0.05$, then in the interval $50\le N\le 70$ $\eta$ must take values in the interval $3.9\times 10^{-4}(957-6N)<\eta <3/8$. For $N=60$ and $\eta =1/3$ we find $r\approx 0.015$. The scalar field at the beginning and at the end of inflation behaves as

$$\begin{aligned} \lim _{\beta \rightarrow \infty }\phi _i=2f,\;\; \lim _{\beta \rightarrow \infty } \phi _e=\pi f. \end{aligned}$$

(4.36)

Then in the strong kinetic coupling limit the inflation can be realized with small fields and at sub Planckian symmetry breaking scales.

On the other hand, neglecting the kinetic coupling, setting $\beta =0$, we can analyze the effect of the GB coupling on the slow-roll dynamics driven by the natural potential (4.27). $n_s$ and r in this case are given by the following expressions

$$\begin{aligned}&n_s=\frac{18f^4\left[ e^{-\frac{(3-8\eta )N}{3f^2}}-1\right] +3f^2(3-8\eta )\left[ 2e^{-\frac{(3-8\eta )N}{3f^2}}+1\right] +(8\eta -3)^2}{3f^2\left[ 6f^2\left( e^{-\frac{(3-8\eta )N}{3f^2}}-1\right) +8\eta -3\right] }\nonumber \\ \end{aligned}$$

(4.37)

$$\begin{aligned}&r=\frac{16(8\eta -3)^2e^{-\frac{(3-8\eta )N}{3f^2}}}{3\left[ 6f^2\left( 1-e^{-\frac{(3-8\eta )N}{3f^2}}\right) -8\eta +3\right] }. \end{aligned}$$

(4.38)

In the limit $\eta \rightarrow 3/8$ we find

$$\begin{aligned} n_s=\frac{2N-3}{2N+1}, \end{aligned}$$

(4.39)

which is the same limit obtained for $\beta>>1$, but the signatures of gravitational waves disappear since

$$\begin{aligned} \lim _{\eta \rightarrow 3/8}r=0. \end{aligned}$$

The initial conditions for the inflaton become

$$\begin{aligned} \lim _{\eta \rightarrow 3/8}\phi _i=2f,\;\; \lim _{\eta \rightarrow 3/8} \phi _e=\pi f. \end{aligned}$$

(4.40)

For small values $f<<1$ we can neglect the exponential terms in the expression (4.37) for $n_s$, leading to

$$\begin{aligned} n_s=1-\frac{3-8\eta }{3f^2} \end{aligned}$$

(4.41)

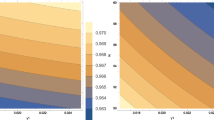
Thus to obtain $n_s=0.966$ with $f=10^{-2}$ we find $\eta =0.374999$, i.e. $\eta$ must be very close to the critical value 3/8. On the other hand, the exponential in the numerator of the expression (4.38) rapidly tends to zero and $r\propto e^{-\frac{(3-8\eta )N}{3f^2}}$. Taking for instance $f\sim 10^{-2}$ then $r\sim 10^{-695}$ and there will be no signal of gravitational waves. As will be shown bellow this problem does not exist if kinetic coupling is considered. So natural inflation with additional GB interaction can be realized for the symmetry breaking scale $f\lesssim 10^{-2}M_p$ but at the expense of having no signals of GW. A very weak signal of gravitational waves is present in the interval $0.3\le f\le 1$. In Fig. 1 we show some curves in the $n_s-r$ plane for $N=60$.

Fig. 1

$n_s$ vs r for the potential (4.27) with additional GB coupling for some values of f in the interval $0.3\le f\le 1$ and $N=60$. The curves correspond to the narrow interval $0.374<\eta <0.37459$. While $n_s$ is in the region favored by observational data, r is very small although it is within the region delimited by current observations

If only the kinetic coupling is present, $n_s$ and r become

$$\begin{aligned}&n_s=\frac{18f^4(2\beta +1)^2\left[ e^{-\frac{N}{f^2(2\beta +1)}}-1\right] +9f^2(2\beta +1)\left[ 2e^{-\frac{N}{f^2(2\beta +1)}}+1\right] +9}{3f^2(2\beta +1)\left[ 6f^2(2\beta +1)\left( e^{-\frac{N}{f^2(2\beta +1)}}-1\right) -3\right] }, \nonumber \\\end{aligned}$$

(4.42)

$$\begin{aligned}&r=\frac{48e^{-\frac{N}{f^2(2\beta +1)}}}{6f^2(2\beta +1)\left( 1-e^{-\frac{N}{f^2(2\beta +1)}}\right) +3}. \end{aligned}$$

(4.43)

From the last expression it follows that for r not to be excessively small the product $f^2\beta$ must be of the order $f^2\beta \lesssim \mathcal{O}(N)$. If $f^2\beta > \mathcal{O}(N)$ then r increases taking values over 0.1 and approaching the limit $r=16/(2N+1)$ as $f^2\beta>>1$. This would leave r outside the region delimited by the observations. In Fig. 2 we show some numerical results

Fig. 2

$n_s$ vs r for the potential (4.27) with non-minimal kinetic coupling ($\eta =0,\; \beta \ne 0$) for f in the interval $10^{-3}M_p\le f\le 10^{-2}M_p$, $\beta =2\times 10^7$ and $N=50,\; 60,\; 70$. for N between 60 and 70 $n_s$ can take values in the region favored by observational data. The scale of symmetry breaking f is of the order of the GUT scale ($10^{16}$ Gev)

Therefore the natural inflation with the inflaton kinetic term non-minimally coupled to curvature leads to successful inflation with symmetry breaking scale $f\sim 10^{16}$ Gev which is the GUT scale. Hence the problem of super-Planckian values of f can be successfully addressed with the inclusion of additional friction encoded in the non-minimal KC. This problem can not be solved with the inclusion of the Galileon term $G_3$ [54]. This scale can not be achieved with the only GB coupling without affecting the tensor/scalar ratio, which at such low scales disappears.

It is clear form above results that the combined effect of the GB and non-minimal kinetic coupling can lead to wider range for $n_s$ and r within the the region of consistency with the latest observations. Fig. 3 shows a numerical study for inflation in the interval $10^7\le \beta \le 10^8$, in Fig. 4 we study the interval $1/4\le \eta \le 1/3$ and Fig. 5 shows results for the symmetry breaking interval $0.001\le f\le 0.01$.

Fig. 3

$n_s$ vs r for $\beta$ in the interval $10^7\le \beta \le 10^8$ for $N=60$ and $\eta =1/3,\; 1/4,\; 1/5$. Note that $n_s$ basically does not change along this interval while r is significantly more susceptible to changes in $\eta$. For all curves $f=0.001$

Fig. 4

$n_s$ vs r for $\eta$ in the interval $1/4\le \eta \le 1/3$ for $N=60$ and $\beta =10^7,\; 2\times 10^7,\; 5\times 10^7$. The scale f for all curves is $f=0.001$

Fig. 5

$n_s$ vs r for f in the interval $0.01\le f\le 0.001$ and $N=60$. In all curves $n_s\approx 0.967$ while r is also constant along the studied interval for each curve, but it varies from one curve to another depending on $\beta$ and $\eta$

To illustrate the behavior of the slow-roll parameters for this model, in Fig. 6 we show the evolution of the slow-roll parameters during inflation period for $\beta =5\times 10^{7}$, $\eta =0.35$ and $f=10^{-3}M_p$.

Fig. 6

The variation of $\epsilon _0,\; \epsilon _1,\ldots$ during inflation, for $\beta =5\times 10^{7}$, $\eta =0.35$ and $f=10^{-3}M_p$. This behavior is typical of all cases considered and lead to appropriate results for the inflationary indices

All curves in Figs. 3, 4 and 5 fall within the region delimited by current observational data. We can conclude that the non-minimal kinetic coupling increases the signal of primordial GW compared to the GB coupling and also allows successful inflation for a range of the symmetry breaking scale of the order of the GUT scale ($\sim 10^{16}$ Gev). Compared to the cases $\eta =0$ and $\beta =0$ we can conclude that the combined effect of both couplings allows a wider range of parameter values leading to inflationary observables well inside the region quoted by the latest observations. In all cases the spectral index was found in a very good interval, $n_s\sim 0.96--0.97$, and the tensor/scalar ratio can take values bellow the bound 0.05 without getting too small.

We can apply the COBE normalization to estimate the scale $\Lambda$ of the potential. For the amplitude of perturbations N e-folds before the end of inflation we find from (3.34)

$$\begin{aligned} \mathcal{P}_S=\frac{H^2}{2(2\pi )^2\mathcal{G}_S}=\frac{H^2}{(2\pi )^2M_p^2}\frac{1}{2\epsilon _0-\Delta _0} \end{aligned}$$

(4.44)

where we used the approximation $\mathcal{A_S}\approx 1/2$ and $c_S\approx 1$ during horizon crossing. For $\mathcal{G}_s$ up to first order from (3.28) was also used, which is given by ($\kappa ^2=1$)

$$\begin{aligned} \mathcal{G}_s=\epsilon _0-\frac{1}{2}\Delta _0. \end{aligned}$$

(4.45)

In terms of the scalar field we find

$$\begin{aligned} \mathcal{P}_S=\frac{3f^2(2\beta +1)\Lambda ^4\left( 1+\cos [\phi /f]\right) \cot ^2[\phi /(2f)]}{4\pi ^2\left( 3-8\eta \right) ^2M_p^4}\Big |_{\phi =\phi _i} \end{aligned}$$

(4.46)

Replacing $\phi _i$ from (4.28) we find

$$\begin{aligned} \mathcal{P}_S=\frac{e^{\frac{(3-8\eta )N}{3f^2(2\beta +1)}} \left[ 6f^2(2\beta +1)\left( e^{-\frac{(3-8\eta )N}{3f^2(2\beta +1)}} -1\right) +8\eta -3\right] ^2\Lambda ^4}{4\pi ^2(3-8\eta )^2 \left( 6f^2(2\beta +1)-8\eta +3\right) M_p^4} \end{aligned}$$

(4.47)

Applying the COBE normalization, $\mathcal{P}_S\simeq 2.5\times 10^{-9}$ we can find the scale $\Lambda$ as function of f and the coupling parameters for a given number of e-foldings before the end of inflation. Taking for instance $N=60,\; \beta =10^7,\; \eta =1/3$, for $f=0.001 M_p$ we find $\Lambda \simeq 5\times 10^{-3}M_p$, which is the order of the GUT scale. This gives for the axion mass scale $m_{\phi }^2=\Lambda ^4/f^2\sim 10^{-6}M_p^2$. Note that for all above cases $\beta>>1$ and also $\beta>>\eta$, and therefore $\frac{(3-8\eta )N}{6f^2\beta }<<1$ we find that the scale $\Lambda$ does not depend on $\eta$ and can be approximated by

$$\begin{aligned} \Lambda \sim \left( \frac{12\pi ^2\beta f^2}{N^2}\mathcal{P}_S\right) ^{1/4} \end{aligned}$$

(4.48)

For f varying in the interval $10^{-4}M_p-10^{-2}M_p$ $\Lambda$ varies almost in the same interval preserving approximately the same order of f. According to this, for the above numerical cases the axion mass is approximately $m_{\phi }^2\sim \Lambda ^2\sim f^2$, i.e. is of the order of the symmetry breaking scale.

Double-well inflation

The potential is given by

$$\begin{aligned} V=M^4\left[ \left( \frac{\phi }{\phi _0}\right) ^2-1\right] ^{2}, \end{aligned}$$

(4.49)

where the scale M is determined by the COBE normalization, and $\phi _0$ corresponds to the vev. The shape of this potential is that of the Mexican hat and it gives the best illustration of spontaneous symmetry breaking [116]. If the scalar field is minimally coupled, then successful inflation with this potential consistent with observations demands super-Planckian values of $\phi _0$ [98, 117]. If we consider non-minimal kinetic and GB couplings that satisfy (4.13), then as will be shown, the restriction of super-Planckian values can be relaxed while the inflationary observables remain in the range of values consistent with observations. The slow-roll parameters take the form

$$\begin{aligned}&\epsilon _0=\frac{8(3-8\eta )M_p^2\phi ^2}{3(1+2\beta )\left( \phi ^2-\phi _0^2\right) ^2},\;\; \Delta _0=\frac{16\eta }{3}\epsilon _0,\;\; \nonumber \\&k_0=\frac{2}{3}\beta \left( 3-8\eta \right) \epsilon _0\nonumber \\&\epsilon _1=\Delta _1=k_1=\frac{8\left( 3-8\eta \right) M_p^2\left( \phi ^2+\phi _0^2\right) }{3\left( 1+2\beta \right) \left( \phi ^2-\phi _0^2\right) ^2} \end{aligned}$$

(4.50)

It is worth noticing that the functional dependence of the slow-roll parameters with respect to the scalar field is the same as in the case of canonical case except for the coefficients, that makes the difference in the physical restrictions on the parameters. The slow-roll goes from the left to the right towards the minimum of the potential at $\phi _0$ and the slow-roll parameters are increasing functions for $\phi$ in the interval $[0,\phi _0]$. But at $\phi =0$

$$\begin{aligned} \epsilon _1,\Delta _1,k_1=\frac{8\left( 3-8\eta \right) M_p^2}{3\left( 1+2\beta \right) \phi _0^2}. \end{aligned}$$

Then, in order to be consistent with the slow-roll dynamics $\epsilon _1,\Delta _1,k_1<1$, which leads to

$$\begin{aligned} \phi _0^2>\frac{3-8\eta }{3(1+2\beta )}M_p^2. \end{aligned}$$

(4.51)

Note that the coefficient of $M_p^2$ can be made much smaller that 1 for and $\beta>>1$ ($\eta$ can not be very close to 3/8 as discussed bellow). Then, the vev of the scalar field can be much less than $M_p$ due to the non-minimal kinetic coupling.

In terms of the scalar field, the scalar spectral index and the tensor/scalar ratio are given by the simple expressions

$$\begin{aligned}&n_s=1-\frac{\left( 3-8\eta \right) M_p^2\left( 3\phi ^2+\phi _0^2\right) }{3\left( 1+2\beta \right) \left( \phi ^2-\phi _0^2\right) ^2} \end{aligned}$$

(4.52)

$$\begin{aligned}&r=\frac{128\left( 3-8\eta \right) ^2M_p^2\phi ^2}{9\left( 1+2\beta \right) \left( \phi ^2-\phi _0^2\right) ^2} \end{aligned}$$

(4.53)

The end of inflation ($\epsilon _0=1$) occurs at the following value of the scalar field

$$\begin{aligned} \phi _e= & {} \frac{1}{3(1+2\beta )}\left[ 4(3-8\eta )M_p^2+3(1+2\beta ) \phi _0^2\right. \nonumber \\&\left. -2\sqrt{2}\sqrt{(3-8\eta )M_p^2 \left( 2(3-8\eta )M_p^2+3(1+2\beta )\phi _0^2\right) }\right] \nonumber \\ \end{aligned}$$

(4.54)

After the integration of the e-folds number, that can be performed exactly, one obtains the following expression for the scalar field N e-folds before the end of inflation

$$\begin{aligned} \phi _i=\sqrt{-W\left[ -\frac{M_p^2}{\phi _0^2}\exp \left( -\frac{8\left( 3-8\eta \right) \left( N-N_e\right) M_p^2}{3\left( 1+2\beta \right) \phi _0^2}\right) \right] }\phi _0, \end{aligned}$$

(4.55)

where

$$\begin{aligned} N_e=\frac{3\left( 1+2\beta \right) \left( \phi ^2-\phi _0^2\ln \left[ \phi ^2/M_p^2\right] \right) }{8\left( 8\eta -3\right) M_p^2}\Big |_{\phi _e}, \end{aligned}$$

(4.56)

with $\phi _e$ given by (4.54).

The properties of the Lambert function W imply a restriction on his argument in order for the results to be real. Since the argument in W is negative, then for the argument in the interval $[-1/e,0]$, W takes values in the interval $[-1,0]$ which imply the following restriction on $\phi _0$

$$\begin{aligned} 0\le \frac{8\left( 3-8\eta \right) \left( N-N_e\right) M_p}{3\left( 1+2\beta \right) \phi _0}\le 1-2\ln \left( \frac{\phi _0}{M_p}\right) \end{aligned}$$

(4.57)

The calculation of the observables $n_s$ and r at Hubble crossing gives

$$\begin{aligned}&ns=1-\frac{8\left( 3-8\eta \right) M_p^2\left( 1-3W\left[ -\frac{M_p^2}{\phi _0^2}\exp \left( -\frac{8(N-N_e)(3-8\eta )M_p^2}{3(1+2\beta )\phi _0^2}\right) \right] \right) }{3(1+2\beta )\phi _0^2\left( 1+W\left[ -\frac{M_p^2}{\phi _0^2}\exp \left( -\frac{8(N-N_e)(3-8\eta )M_p^2}{3(1+2\beta )\phi _0^2}\right) \right] \right) ^2} \nonumber \\\end{aligned}$$

(4.58)

$$\begin{aligned}&r=-\frac{128\left( 3-8\eta \right) ^2M_p^2 W\left[ -\frac{M_p^2}{\phi _0^2}\exp \left( -\frac{8(N-N_e)(3-8\eta )M_p^2}{3(1+2\beta )\phi _0^2}\right) \right] }{9(1+2\beta )\phi _0^2\left( 1+W\left[ -\frac{M_p^2}{\phi _0^2}\exp \left( -\frac{8(N-N_e)(3-8\eta )M_p^2}{3(1+2\beta )\phi _0^2}\right) \right] \right) ^2}. \nonumber \\ \end{aligned}$$

(4.59)

Limiting ourselves to the case when only the GB coupling is present, i.e. $\beta =0$, we find that in the region of small $\phi _0$ ($0.01M_p<\phi _0<0.1M_p$) it is possible to find suitable values for $n_s$ ($n_s\sim 0.064-0.968$) but $\eta$ must be extremely close to the critical value 3/8 ($\eta =0.3749999$) which renders extremely small r ($r\sim 10^{-8}$). For even smaller values of $\phi _0$, $n_s$ acquires values inconsistent with observations and r reduces practically to zero, unless we consider values for $\eta$ even closer to 3/8 but in this case any signal of gravitational waves disappears. For $\phi _0>M_p$ (in fact for $\eta >10$) there is a wider range of $\eta$ values that lead to successful inflation with suitable range for $n_s$ and r, but in this case as in the canonical model the scale of symmetry breaking becomes super Planckian. On the other hand for negative $\eta$, $-1< \eta <0$, we can find values of $n_s$ and r favored by observations but always for super Planckian values of $\phi _0$. $\eta <-1$ leads to large values of r disfavored by observations. Resuming, the inflation with sub Planckian $\phi _0$ can be realized with GB coupling but at the cost of very weak ($r\sim 10^{-8}$) or no signals of primordial gravitational waves. With super Planckian scale of symmetry breaking inflation is always possible with suitable values of $n_s$ and r.

To have another appreciation and make a close estimate of the regions of suitability of the model we can follow the behavior of the Lambert function in (4.58) and (4.59). It can be checked numerically that for $\beta =0$ and $\phi _0<<M_p$, for instance $\phi _0\sim 10^{-2}-10^{-4}M_p$, independently of $\eta$ (as long as $\eta$ is not extremely close to 3/8) it follows that $W\approx 0$ from which we can conclude that

$$\begin{aligned} n_s\approx 1-\frac{8(3-8\eta )M_p^2}{3\phi _0^2},\;\;\; r\approx 0, \end{aligned}$$

(4.60)

from which it becomes clear that the GB coupling can not lead to successful inflation with the symmetry breaking below the Planck scale, unless $\eta$ is extremely close to its critical value 3/8, which can lead to suitable $n_s$ but without signals of gravitational waves.

Considering only the non-minimal kinetic coupling in Figs. 7 and 8 we show some curves in the ($n_s-r$)-plane for different regions $\beta$ and $\phi _0$. These results show that it is possible to realize successful inflation with $n_s$ and r in the regions favored by observations, with the symmetry breaking scale of the order of the GUT scale ($\phi _0\sim 10^{-3}M_p$).

Fig. 7

$n_s$ vs r for $\beta$ in the interval $10^8\le \beta \le 10^9$ for $N=50,60,70$ and $\phi _0=10^{-3}M_p$. Note that larger number of e-folds moves r well inside the region quoted by latest observations

Fig. 8

$n_s$ vs r for $\phi _0$ in the interval $10^{-4}M_p\le \phi _0\le 10^{-3}M_p$ for $N=50,60,70$ and $\beta =10^{10}$. All curves pass through zones of the region favored by observations

In the strong coupling limit the inflationary magnitudes can be simplified and take the following form that numerically give results very close to those obtained with the exact expressions. From (4.54) and (4.55) the following expression is obtained for $\phi _i$ in the regime $\beta>>1$

$$\begin{aligned} \phi _i=\sqrt{-W\left[ -\exp \left( -1-\frac{4NM_p^2}{\beta \phi _0^2}\right) \right] }\phi _0, \end{aligned}$$

(4.61)

which leads to the following results for the inflationary indices

$$\begin{aligned}&n_s=1-\frac{8\left( 1-3W\left[ -\exp \left( -1-\frac{4NM_p^2}{\beta \phi _0^2}\right) \right] \right) M_p^2}{\left( 2\beta +1\right) \left( 1+W\left[ -\exp \left( -1-\frac{4NM_p^2}{\beta \phi _0^2}\right) \right] \right) ^2\phi _0^2} \nonumber \\\end{aligned}$$

(4.62)

$$\begin{aligned}&r=-\frac{128 W\left[ -\exp \left( -1-\frac{4NM_p^2}{\beta \phi _0^2}\right) \right] M_p^2}{\left( 2\beta +1\right) \left( 1+W\left[ -\exp \left( -1-\frac{4NM_p^2}{\beta \phi _0^2}\right) \right] \right) ^2\phi _0^2}. \nonumber \\\end{aligned}$$

(4.63)

In the large $\beta$ limit we find

$$\begin{aligned} n_s=\frac{N-2}{N},\;\;\; r=\frac{8}{N} \end{aligned}$$

(4.64)

which for $N=60$ give $n_s\approx 0.967,\; r\approx 0.133$. Since the function (4.63) is an increasing function with respect to $\beta$ and $\phi _0$, then $r=\frac{8}{N}$ is the upper limit for r in this model. It should be noted that at $\beta \rightarrow \infty$ from (4.55) follows $\phi _i\rightarrow \phi _0$ which from (4.52) and (4.53) gives that $n_s,\; r$ apparently blow up, but also $\beta \rightarrow \infty$ which amounts to finite $n_s$ and r. This becomes clear when $N_e$ is replaced in (4.58) and (4.59). The above numerical analysis shows that the scalar field with the double well potential (4.49) and non-minimal kinetic coupling term gives inflationary indices in the region favored by observations with small field inflation and the symmetry breaking scale of the order of GUT scale.

The effect of both GB and NMKC is illustrated in Figs. 9, 10 and 11, where different regions of the parameters is considered.

The above results show that coupling of scalar field to curvature and specially the NMKC could be important in the slow-roll dynamics leading to inflationary indices in the region favored by observations. For the double well potential this becomes possible with a scale of symmetry breaking of the order of the GUT scale or bellow.

5.2 Constant NMKC and GB coupling $\propto V^{-1}$

The effect of constant NMKC in inflation in various cosmological scenarios has been studied in [65,66,67,68,69, 71,72,73,74,75,76,77,78]. We propose the following class of couplings

$$\begin{aligned} F_1=\frac{\beta }{M_p^2},\;\;\; F_2(\phi )=\frac{\eta M_p^4}{V(\phi )}, \end{aligned}$$

(4.65)

which give the following slow-roll parameters

Fig. 9

$n_s$ vs r for $\phi _0$ in the interval $2\times 10^{-4}M_p\le \phi _0\le 2\times 10^{-3}M_p$ for $N=50,60,70$, $\eta =0.3$ and $\beta =10^9$. All curves fall well inside the region favored by latest observations

$$\begin{aligned}&\epsilon _0=\frac{(3-8\eta )M_p^6V'^2}{6V^2\left( 2\beta V+M_p^4\right) },\;\; \Delta _0=\frac{16\eta }{3}\epsilon _0,\;\; k_0=\frac{\beta (3-8\eta )^2M_p^6 V'^2}{9V\left( 2\beta V+M_p^4\right) ^2}\nonumber \\&\epsilon _1=\Delta _1=\frac{2(3-8\eta )M_p^6\left( V'^2-2V'' V\right) \left( 2\beta V+M_p^4\right) }{3V^2(2\beta V+M_p^4)^2},\;\; \nonumber \\&k_1=\frac{(3-8\eta )M_p^6\left( V'^2-2V'' V\right) \left( 2\beta V+M_p^4\right) }{3V^2(2\beta V+M_p^4)^2}. \end{aligned}$$

(4.66)

For the inflationary indices $n_s$ and r we obtain

$$\begin{aligned}&n_s=\frac{V\left( 2\beta V+M_p^4\right) \left[ 2(3-8\eta )M_p^6V''+3V(2\beta V+M_p^4)\right] -(3-8\eta )M_p^6V'^2(8\beta V+3M_p^4)}{3V^2\left( 2\beta V+M_p^4\right) ^2} \end{aligned}$$

(4.67)

$$\begin{aligned}&r=\frac{8(3-8\eta )^2M_p^6V'^2}{9V^2(2\beta V+M_p^4)} \end{aligned}$$

(4.68)

For the number of e-folds form (4.12) we find

$$\begin{aligned} N=-\int _{\phi _i}^{\phi _e}\frac{3V\left( 2\beta V+M_p^4\right) }{(3-8\eta )M_p^6 V'}d\phi . \end{aligned}$$

(4.69)

Note that for consistency at the end of inflation the coefficient of $\Delta _0$ in (4.66) must be of the order 1, i.e. $16\eta /3\sim \mathcal{O}(1)$. Note also that unlike the previous models, the slow-roll parameters and therefore the inflationary indices for models of the type (4.65) depend on the scale of the potential. For the models (4.65) we can appreciate the contribution of the couplings $F_1$ and $F_2$ to the Lagrangian during inflation as follows

$$\begin{aligned} F_1 R\left( \partial \phi \right) ^2\sim \frac{\beta }{M_p^2}H_i^2\left( \partial \phi \right) ^2\sim 10^{-10}\beta \left( \partial \phi \right) ^2 \end{aligned}$$

(4.70)

and

$$\begin{aligned} F_2 R^2\sim \frac{\eta M^4 H_i^4}{V}\sim \frac{\eta M_p^4 H_i^4}{V_i}\sim 10^{-10}\eta M_p^4 \end{aligned}$$

(4.71)

where we assumed the typical values, $H_i\sim 10^{-5}M_p$, $V_i\sim 10^{-10}M_p^4$. Then values of $\eta \sim 1$ and $\beta>>1$ (whenever $10^{-10}\beta \left( \partial \phi \right) ^2<<V_i$) lead to inflationary dynamics driven by the potential. Bellow we analyze some cases that are of interest.

Fig. 10

$n_s$ vs r for $\phi _0$ in the interval $3\times 10^{-4}M_p\le \phi _0\le 3\times 10^{-3}M_p$ for $N=60$, $\beta =10^9$ and $\eta =0.2,0.3,0.35$. All curves run though values favored by latest observations

Power-law potential

The power-law potential with dimensionless self-coupling $\lambda$ is given by

$$\begin{aligned} V=\frac{\lambda M_p^4}{n}\left( \frac{\phi }{M_p}\right) ^n, \end{aligned}$$

(4.72)

where $\lambda$ is fixed by COBE normalization. This potential leads to the following slow-roll parameters

$$\begin{aligned}&\epsilon _0=\frac{(3-8\eta )n^3M_p^{n+2}}{6\phi ^2\left( 2\beta \lambda \phi ^n+nM_p^n\right) },\;\; \Delta _0=\frac{16\eta }{3}\epsilon _0,\;\; \nonumber \\&k_0=\frac{\beta \lambda (3-8\eta )^2M_p^{n+2}\phi ^n}{9\phi ^2\left( 2\beta \lambda \phi ^n+nM_p^n\right) ^2}\nonumber \\&\quad \epsilon _1=\Delta _1=\frac{2n^2(3-8\eta )M_p^{n+2}\left( (n+2)\beta \lambda \phi ^n+nM_p^n\right) }{3\phi ^2\left( 2\beta \lambda \phi ^n+nM_p^n\right) ^2}\nonumber \\&\quad k_1=\frac{n^2(3-8\eta )M_p^{n+2}\left[ 4\beta \lambda \phi ^n+2n(\beta \lambda \phi ^n+M_p^n)-n^2M_p^n\right] }{3\phi ^2\left( 2\beta \lambda \phi ^n+nM_p^n\right) ^2},\nonumber \\ \end{aligned}$$

(4.73)

that give the following observables in terms of the scalar field

$$\begin{aligned}&n_s=1-\frac{(3-8\eta )n^2M_p^{n+2}\left( 4\beta \lambda \phi ^n(n+1)+n(n+2)M_p^n\right) }{3\phi ^2\left( 2\beta \lambda \phi ^n+nM_p^n\right) ^2} \nonumber \\ \end{aligned}$$

(4.74)

$$\begin{aligned}&r=\frac{8n^3(3-8\eta )^2M_p^{n+2}}{9\phi ^2\left( 2\beta \lambda \phi ^n+nM_p^n\right) } \end{aligned}$$

(4.75)

which are evaluated at the horizon crossing, $\phi =\phi _i$.

We can consider some cases that allow analytical approach (the case $n=2$ has been discussed in [89]). In absence of kinetic coupling the fields at the beginning and at the end of inflation are

$$\begin{aligned} \phi _i=\sqrt{\frac{n(4N+n)(3-8\eta )}{6}}M_p,\;\;\; \phi _e=\sqrt{\frac{3-8\eta }{6}}M_p \end{aligned}$$

(4.76)

where $\eta <3/8$. For the inflationary indices we find the same results of the power-law potential for the model (4.13), namely

$$\begin{aligned} n_s=\frac{4N-n-4}{4N+n},\;\;\; r=\frac{16n(3-8\eta )}{3(4N+n)}. \end{aligned}$$

(4.77)

that have been already discussed.

Fig. 11

$n_s$ vs r for $\phi _0$ in the interval $3\times 10^{-4}M_p\le \phi _0\le 3\times 10^{-3}M_p$ for $N=60$, $\eta =0.25$ and $\beta =10^9, 10^{10},10^{11}$. All curves follow the same trajectory but start at different points depending on $\beta$

In absence of GB coupling we need to fix n in order to find analytical expressions. For $n=2$ the scalar field takes the values

$$\begin{aligned} \phi _i&=\frac{M_p}{\sqrt{2\beta \lambda }}\sqrt{\sqrt{2(4\beta \lambda (4N+1)+\sqrt{8\beta \lambda +1}+1)}-2},\;\;\nonumber \\ \phi _e&=\frac{M_p}{\sqrt{2\beta \lambda }}\sqrt{\sqrt{8\beta \lambda +1}-1}. \end{aligned}$$

(4.78)

From (4.74) and (4.75) we find

$$\begin{aligned}&n_s=1-\frac{8\beta \lambda \left( 3\sqrt{2}\sqrt{4\beta \lambda (4N+1)+\sqrt{8\beta \lambda +1}+1}-2\right) }{\left( 4\beta \lambda (4N+1)+\sqrt{8\beta \lambda +1}+1\right) \left( \sqrt{2(4\beta \lambda (4N+1)+\sqrt{8\beta \lambda +1}+1)}-2\right) } \end{aligned}$$

(4.79)

$$\begin{aligned}&r=\frac{64\sqrt{2}\beta \lambda }{\sqrt{4\beta \lambda (4N+1)+\sqrt{8\beta \lambda +1}+1}\left( \sqrt{2(4\beta \lambda (4N+1)+\sqrt{8\beta \lambda +1}+1)}-2\right) } \end{aligned}$$

(4.80)

In the limit $\beta>>1$ these magnitudes approach the values

$$\begin{aligned} n_s=\frac{4N-5}{4N+1},\;\;\; r=\frac{16}{4N+1} \end{aligned}$$

(4.81)

Taking into account the results (4.77) (for $\beta =0$) we find that the inflationary indices take values in the intervals

$$\begin{aligned}&\frac{2N-3}{2N+1}<n_s<\frac{4N-5}{4N+1} \end{aligned}$$

(4.82)

$$\begin{aligned}&\frac{16}{4N+1}<r<\frac{16}{2N+1} \end{aligned}$$

(4.83)

Thus, for $N=60$: $0.967<n_s<0.975$ and $0.066<r<0.132$. For $N=50$: $0.96<n_s<0.97$ and $0.0796<r<0.158$.

Considering the two couplings we find the following asymptotic behavior at $\beta>>1$

$$\begin{aligned} n_s=\frac{4N-5}{4N+1},\;\;\; r=\frac{16(3-8\eta )}{3(4N+1)} \end{aligned}$$

(4.84)

comparing to (4.77) that correspond to $\beta =0$ it can be seen that for $0<\beta <\infty$ the values of $n_s$ remain in the same interval (4.82) and r takes values in the following interval

$$\begin{aligned} \frac{16\left( 3-8\eta \right) }{3\left( 4N+1\right) }<r<\frac{16 \left( 3-8\eta \right) }{3\left( 2N+1\right) } \end{aligned}$$

(4.85)

so the GB coupling affects only r in the large $\beta$ regime. So it is clear that $50\le N\le 60$ gives suitable values for $n_s$ and for r we can always choose $\eta$ in such a way that satisfies the bound $r<0.05$.

For $n=4$ the algebraic expressions for the fields are too large, but in the regime $\beta>>1$ the following limits for $n_s$ and r are found

$$\begin{aligned} n_s=\frac{3N-4}{3N+1},\;\;\; r=\frac{16}{3N+1}. \end{aligned}$$

(4.86)

From (4.77) (for $\eta =0$) we find that the inflationary indices for $0<\beta <\infty$ take values

$$\begin{aligned}&\frac{N-2}{N+1}<n_s<\frac{3N-4}{3N+1} \end{aligned}$$

(4.87)

$$\begin{aligned}&\frac{16}{3N+1}<r<\frac{16}{N+1} \end{aligned}$$

(4.88)

which give the intervals for $N=60$: $0.951<n_s<0.972$ and $0.088<r<0.262$. For $N=50$: $0.941<n_s<0.967$ and $0.106<r<0.314$. For $n=70$: $0.958<n_s<0.976$ and $0.076<r<0.225$. It is clear that the only interval that marginally saves r corresponds to 70 e-folds. Taking into account the GB coupling, it is found that the behavior of $n_s$ remains unchanged in the interval $0<\beta <\infty$, while r varies in the following interval

$$\begin{aligned} \frac{16(3-8\eta )}{3(3N+1)}<r<\frac{16(3-8\eta )}{3(N+1)}, \end{aligned}$$

(4.89)

so that theoretically for $n=4$, r can satisfy the bound $r<0.05$ by choosing an appropriate $\eta <3/8$.

Exponential potential

$$\begin{aligned} V=V_0e^{-\lambda \phi /M_p}. \end{aligned}$$

(4.90)

The slow-roll parameters for this model with couplings (4.65) are

$$\begin{aligned}&\epsilon _0=\frac{\left( 3-8\eta \right) \lambda ^2M_p^4e^{\lambda \phi /M_p}}{6\left( M_p^4 e^{\lambda \phi /M_p}+2\beta V_0\right) },\;\;\Delta _0=\frac{16\eta }{3}\epsilon _0,\;\;\nonumber \\&k_0=\frac{\left( 3-8\eta \right) ^2\lambda ^2\beta V_0 M_p^4e^{\lambda \phi /M_p}}{9\left( M_p^4 e^{\lambda \phi /M_p}+2\beta V_0\right) ^2}\nonumber \\&\quad \epsilon _1=\Delta _1=\frac{2\left( 3-8\eta \right) \lambda ^2\beta V_0 M_p^4e^{\lambda \phi /M_p}}{3\left( M_p^4 e^{\lambda \phi /M_p}+2\beta V_0\right) ^2}\nonumber \\&\quad k_1=\frac{\left( 3-8\eta \right) \lambda ^2M_p^4\left( 2\beta V_0 -M_p^4e^{\lambda \phi /M_p}\right) e^{\lambda \phi /M_p}}{3\left( M_p^4 e^{\lambda \phi /M_p}+2\beta V_0\right) ^2}.\nonumber \\ \end{aligned}$$

(4.91)

For the scalar fields the following expressions are found

$$\begin{aligned} \phi _i= & {} \frac{1}{6\lambda }\Big [6\ln \left[ \frac{12\beta V_0}{\left( (3-8\eta )\lambda ^2-6\right) M_p^4}\right] \nonumber \\&+6W\left[ \frac{1}{6}\left( (3-8\eta )\lambda ^2-6\right) e^{-1+\frac{1}{6}(3-8\eta )(2N+1)\lambda ^2}\right] \nonumber \\&-(3-8\eta )(2N+1)\lambda ^2+6\Big ]M_p, \end{aligned}$$

(4.92)

$$\begin{aligned} \phi _e= & {} \frac{1}{\lambda }\ln \left[ \frac{12\beta V_0}{\left( (3-8\eta )\lambda ^2-6\right) M_p^4}\right] M_p, \end{aligned}$$

(4.93)

which imposes the following restriction on $\eta$ and $\lambda$ to avoid negative arguments in the logarithmic function

$$\begin{aligned} \eta <\frac{3\lambda ^2-6}{8\lambda ^2}. \end{aligned}$$

(4.94)

So that the upper limit of $\eta$ depends on $\lambda$ and in the limit $\lambda>>1$ this limit is the critical value 3/8. The inflationary indexes con be expressed analytically in terms of the parameters as follows

$$\begin{aligned}&n_s=1-\frac{(3-8\eta )\lambda ^2\left( 2W\left[ \frac{1}{6} \left( (3-8\eta )\lambda ^2-6\right) e^{-1+\frac{1}{6}(3-8\eta )(2N+1)\lambda ^2}\right] +1\right) }{\nonumber }\\&\qquad \qquad {3\left( W\left[ \frac{1}{6}\left( (3-8\eta )\lambda ^2-6\right) e^{-1+\frac{1}{6}(3-8\eta )(2N+1)\lambda ^2}\right] +1\right) ^2} \end{aligned}$$

(4.95)

$$\begin{aligned}&r=\frac{8(3-8\eta )\lambda ^2}{9\left( W\left[ \frac{1}{6} \left( (3-8\eta )\lambda ^2-6\right) e^{-1+\frac{1}{6}(3-8\eta )(2N+1) \lambda ^2}\right] +1\right) } \end{aligned}$$

(4.96)

A remarkable property of $n_s$ and r in this model is that they do not depend on $\beta$. Note that if $\beta =0$ then the slow-roll parameters become constant. Then the principal role of $\beta$ is to provide the graceful exit from inflation, apart from setting the initial conditions on the scalar field as seen in (4.92) and (4.93), which allows small-field inflation. Note also from (4.95) and (4.96) that as $\eta$ approaches its critical value 3/8 the spectral index approaches the value $n_s=\frac{2N-1}{2N}$, very close to the scale invariance for $N\sim 60-70$, and the signal of gravitational waves disappears. In Figs. 12 and 13 we show some trajectories in the ($n_s-r$)-plane.

Fig. 12

$n_s$ vs r for $\eta =0.2,\lambda =3$ (dotted), $\eta =0.25,\lambda =10$ (dashed) and $\eta =0.35,\lambda =100$ (dot-dashed) in the N- e-fold interval $50\le N \le 70$. $n_s$ increases while r decreases with N. All curves are in the region favored by latest observations

To estimate which values of $\lambda$ and $\eta$ are more suitable for inflation we can look at the slow-roll parameters at the end of inflation, which are given by

$$\begin{aligned}&\epsilon _0=1,\;\; \epsilon _1=2-\frac{12}{(3-8\eta )\lambda ^2},\;\; \Delta _0=\frac{16\eta }{3},\;\;\nonumber \\&\Delta _1=2-\frac{12}{(3-8\eta )\lambda ^2}\nonumber \\&\quad k_0=1-\frac{8\eta }{3}-\frac{2}{\lambda ^2},\;\; k_1=2-\frac{24}{(3-8\eta )\lambda ^2}. \end{aligned}$$

(4.97)

Note that if $\lambda>>1$ then $\epsilon _1,\Delta _1, k_1\approx 2$ and $\delta _0, k_0\sim \epsilon _0$ (provided $\eta \sim 0.1 - 0.3$). To keep them of the order $\mathcal{O}(1)$ one can choose $\eta , \lambda$ that satisfy the relation $\eta \approx \frac{3(\lambda ^2-5)}{8\lambda ^2}$.

Natural inflation potential

This potential that has been discussed above (4.27) [110, 111]

$$\begin{aligned} V=\Lambda ^4\left( 1+\cos \left( \frac{\phi }{f}\right) \right) , \end{aligned}$$

(4.98)

with the NMKC and GB couplings defined in (4.65) leads to the following slow-roll parameters in terms of the scalar field (setting $M_p=1$ and $\alpha =\beta \Lambda ^4$)

$$\begin{aligned}&\epsilon _0=\frac{(3-8\eta )\tan ^2\left( \frac{\phi }{2f}\right) }{6f^2\left[ 2\alpha \cos \left( \frac{\phi }{f}\right) +2\alpha +1\right] }, \;\; \Delta _0=\frac{16\eta }{3}\epsilon _0,\;\; \\&k_0=\frac{2\alpha \left( 3-8\eta \right) ^2\sin ^2 \left( \frac{\phi }{2f}\right) }{9f^2\left[ 2\alpha \cos \left( \frac{\phi }{f}\right) +2\alpha +1\right] ^2},\nonumber \\ \end{aligned}$$

$$\begin{aligned}&\quad \epsilon _1=\Delta _1=\frac{(3-8\eta )\left[ 4\alpha \cos \left( \frac{\phi }{f}\right) -\alpha \cos \left( \frac{2\phi }{f}\right) +5\alpha +2\right] \sec ^2\left( \frac{\phi }{2f}\right) }{6f^2\left[ 2\alpha \cos \left( \frac{\phi }{f}\right) +2\alpha +1\right] ^2},\nonumber \\&\quad k_1=\frac{(3-8\eta )\left[ 6\alpha -2\alpha \cos \left( \frac{\phi }{f}\right) +1\right] }{3f^2\left[ 2\alpha \cos \left( \frac{\phi }{f}\right) +2\alpha +1\right] ^2}. \end{aligned}$$

(4.99)

For the scalar spectral index and the tensor-to-scalar ratio it is found

$$\begin{aligned}&n_s=\frac{\sec ^2\left( \frac{\phi }{2f}\right) }{6f^2\left[ 2\alpha \cos \left( \frac{\phi }{f}\right) +2\alpha +1\right] ^2}\Big [\left[ 3f^2\left( 15\alpha ^2+8\alpha +1\right) \right. \nonumber \\&\quad \left. -(4\beta -1)(3-8\eta )\right] \cos \left( \frac{\phi }{f}\right) \nonumber \\&\quad + 2\alpha \left[ 3f^2(3\alpha +1)-8\eta +3\right] \cos \left( \frac{2\phi }{f}\right) \nonumber \\&\quad +3\left[ f^2\alpha ^2\cos \left( \frac{3\phi }{f}\right) +f^2\left( 10\alpha ^2+6\alpha +1\right) \right. \nonumber \\&\quad \left. -(2\alpha +1)(3-8\eta )\right] \Big ] \end{aligned}$$

(4.100)

$$\begin{aligned}&r=\frac{8\left( 3-8\eta \right) ^2\tan ^2\left( \frac{\phi }{2f}\right) }{9f^2\left[ 2\alpha \cos \left( \frac{\phi }{f}\right) +2\alpha +1\right] } \end{aligned}$$

(4.101)

where the scalar field is evaluated at the horizon crossing, $\phi =\phi _1$. From $\epsilon _0=1$ we find the field at the end of inflation

Fig. 13

$n_s$ vs r for $N=60$ and $\lambda =2$ (dotted), $\lambda =5$ (dashed) and $\lambda =10$ (dot-dashed) with $\eta$ in the interval $0.1\le \eta \le 0.35$

$$\begin{aligned}&\phi _e=2f\arctan \left[ \sqrt{\frac{48f^2\alpha +6f^2-8\eta +3-\sqrt{(6f^2-8\eta +3)^2+96f^2\alpha (3-8\eta )}}{\sqrt{(6f^2-8\eta +3)^2+96f^2\alpha (3-8\eta )}-6f^2+8\eta -3}}\right] \end{aligned}$$

(4.102)

For the number of e-foldings the following expression is obtained

$$\begin{aligned} N=\frac{6f^2\alpha }{3-8\eta }\left( I\left[ \phi _e\right] -I\left[ \phi _i\right] \right) , \end{aligned}$$

(4.103)

where

$$\begin{aligned} I\left[ \phi \right] =\cos \left( \frac{\phi }{f}\right) +\frac{4\alpha +1}{\alpha }\ln \left[ \sin \left( \frac{\phi }{f}\right) \right] \end{aligned}$$

(4.104)

This equation cannot be solved analytically with respect to $\phi _i$. We can numerically evaluate $n_s$ and r in terms of the e-foldings and the model parameters. In Fig. 14 we plot some $(n_s,r)$ curves for f in the range $0.001M_p\le f\le 0.1M_p$.

Using the COBE normalization we find the following expression for $\Lambda$ using (4.46) and (4.99) (recovering $M_p$)

$$\begin{aligned} \Lambda =\frac{\sqrt{2\pi \left( 3-8\eta \right) }M_p^{5/2}\mathcal{P}_S^{1/4}}{\left[ 3f^2\left( \cos \left( \frac{\phi }{f}\right) +1\right) \left[ 2\alpha \cos \left( \frac{\phi }{f}\right) +2\alpha +M_p^4\right] \cot ^2\left( \frac{\phi }{f}\right) \right] ^{1/4}\Big |_{\phi =\phi _i}} \end{aligned}$$

(4.105)

The behavior of $\Lambda$ and V for the curves of Fig. 14 is ploted in Fig. 15. This numerical behavior shows that $\Lambda$ is of the order of the GUT scale for $f\sim 10^{-3}M_p$ and the potential is in the expected scale according to COBE normalization.

In Fig. 16 we illustrate the typical behavior of the slow-roll parameters that lead to the trajectories in Fig. 14.

Double-Well Inflation

The potential

$$\begin{aligned} V=M^4\left[ \left( \frac{\phi }{\phi _0}\right) ^2-1\right] ^{2}, \end{aligned}$$

(4.106)

Has been discussed in the previous case. The slow-roll parameters with the couplings defined in (4.65) are given by

$$\begin{aligned}&\epsilon _0=\frac{8\left( 3-8\eta \right) M_p^6\phi _0^4\phi ^2}{3\left( \phi ^2-\phi _0^2\right) ^2\left[ M_p^4\phi _0^4+2\beta V_0\left( \phi ^2-\phi _0^2\right) ^2\right] },\;\; \Delta _0=\frac{16\eta }{3}\epsilon _0\nonumber \\&k_0=\frac{16\beta M^6 V_0\left( 3-8\eta \right) ^2\phi _0^4\phi ^2}{9\left[ M_p^4 \phi _0^4+2\beta V_0\left( \phi ^2-\phi _0^2\right) ^2\right] ^2},\nonumber \\&\epsilon _1=\Delta _1=\frac{8\left( 3-8\eta \right) M^6\phi _0^4\left[ \phi _0^4 M^4 \left( \phi ^2+\phi _0^2\right) +2\beta V_0\left( \phi ^2-\phi _0^2\right) ^2\left( 3\phi ^2+\phi _0^2\right) \right] }{3\left( \phi ^2- \phi _0^2\right) ^2\left[ M_p^4\phi _0^4+2\beta V_0\left( \phi ^2-\phi _0^2\right) ^2\right] ^2},\nonumber \\&k_1=-\frac{8\left( 3-8\eta \right) M^6\phi _0^4\left[ M_p^4\phi _0^4-2\beta V_0\left( 3\phi ^4-2 \phi _0^2\phi ^2-\phi _0^4 \right) \right] }{3\left( \phi ^2-\phi _0^2\right) \left[ \phi _0^4M_p^4+2\beta V_0\left( \phi ^2-\phi _0^2\right) ^2\right] ^2}. \end{aligned}$$

(4.107)

Fig. 14

$n_s$ vs r for $N=60$ and $0.001\le f\le 0.1$ ($M_p=1$). As $\eta$ gets closer to 3/8, r gets smaller and is suppressed for $\eta =3/8$

Fig. 15

The scale $\Lambda$ and the potential vs f for $N=60$ and $0.001\le f\le 0.1$, corresponding to the curves in Fig. 13. The scale $\Lambda$ from COBE normalization is of the order of the GUT scale for $f\sim 10^{-3}M_p$

For the spectral index and the tensor-to-scalar ratio we find

$$\begin{aligned} n_s= & {} \frac{1}{3\left( \phi ^2-\phi _0^2\right) ^2\left[ M_p^4\phi _0^4+2\beta V_0\left( \phi ^2-\phi _0^2\right) ^2\right] ^2}\nonumber \\&\quad \times \Big [12\beta ^2V_0^2 \left( \phi ^2-\phi _0^2\right) ^6 +3M^8\phi _0^8\left( \phi ^2-\phi _0^2\right) ^2\nonumber \\&- 8\left( 3-8\eta \right) M_p^{10}\phi _0^8\left( 3\phi ^2+\phi _0^2\right) +4\beta V_0 M_p^4\phi _0^4\nonumber \\&\quad \times \left[ 3\left( \phi ^2-\phi _0^2\right) ^4-4\left( 3-8\eta \right) M_p^2\left( \phi ^2-\phi _0^2\right) ^2\left( 5\phi ^2 +\phi _0^2\right) \right] \nonumber \\ \end{aligned}$$

(4.108)

$$\begin{aligned} r= & {} \frac{128\left( 3-8\eta \right) ^2M_p^6\phi _0^4\phi ^2}{9\left( \phi ^2-\phi _0^2\right) ^2\left[ M_p^4\phi _0^4 +2\beta V_0\left( \phi ^2-\phi _0^2\right) ^2\right] } \end{aligned}$$

(4.109)

For the number of e-folds we find

$$\begin{aligned} N=\frac{1}{\left( 8\eta -3\right) M_p^6\phi _0^4} \left( I_1\left[ \phi _e\right] -I_1\left[ \phi _i\right] \right) , \end{aligned}$$

(4.110)

where

$$\begin{aligned}&I_1\left[ \phi \right] =\left[ 3M_p^4\phi _0^4+\beta V_0\left( 2\phi ^4-9\phi _0^2\phi ^2 +18\phi _0^4\right) \right] \nonumber \\&\quad \phi ^2-6\left( 2\beta V_0+M_p^4\right) \phi _0^6\ln \left( \phi /M_p\right) \end{aligned}$$

(4.111)

The remaining expressions are too long and the scalar field at the horizon crossing cannot be found explicitly, allowing only numerical analysis. The case $\beta =0$ that can be treated analytically is the same as the model (4.13) already analyzed. In the numerical example shown in Fig. 17 we plot the results of the model for $n_s$ and r.

The curves corresponding to $N=50$ and $N=60$ are clearly more favored by observational data. Note also that along the large interval $1\le \beta \le 10^{10}$ for each curve, the inflationary observables $n_s$ and r suffer only a small variation of the order of $10^{-3}$. The scalar spectral index is a growing function of $\beta$ while r decreases with $\beta$. Numerical analysis shows that $\eta$ does not have much impact on $n_s$ but it does affect the value of r. Thus for $\phi _0=0.001$ and $\beta =10^7$, r decreases from 0.0983 for $\eta =0$ to 0 for $\eta =3/8$.

Fig. 16

The variation of $\epsilon _0,\; \epsilon _1,\ldots$ during inflation, for $\alpha =5\times 10^{6}$, $\eta =0.2$ and $f=10^{-3}M_p$. Note that $\alpha =\beta V_0$, where $V_0$ is fixed by COBE normalization

Fig. 17

$n_s$ vs r for $\eta =0.2$, $\phi _0=10^{-3}M_p$ and $1\le \beta \le 10^{10}$. The three curves correspond to $N=50,60,70$. On average, over the $\beta$-interval, $n_s$ and r vary only in $\sim 10^{-3}$

6 Consistency with the reheating process

After the end of inflation the Universe enters into the next phase called pre/reheating [93,94,95,96,97,98,99] that originates, according to one of the simplest mechanisms, from the oscillations of the scalar field around the minimum of the potential, which eventually leads to the production of ordinary matter. During this period the Universe expands under matter domination passing trough period of radiation domination followed by matter domination, which lasts until a redshift of the order one, giving way to the current dark energy dominated era. The reheating phase, which allows us to understand how inflation is connected to the hot big-bang phase, represents one of the most poorly known processes after the end of inflation and can lead to important uncertainties for the inflationary predictions. This is due in part to the fact that there are not strict constraints on the reheating energy scale.

In order to understand and illustrate how the inflation predictions depend on the details of the reheating era, one can use the approximation of constant equation of state during reheating which allows to derive relations between some reheating characteristics like its equation of state parameter, its energy scale and the inflationary indices. These new constraints could in principle break degeneracies between different models of inflation that give the same predictions for $n_s$ and r.

Let $\rho _{rh}$ and $p_{rh}$ be the energy density and pressure of the effective fluid that originates during reheating and dominates the Universe . The continuity equation for this fluid gives

$$\begin{aligned} \rho _{rh}(N)=\rho _e \exp \left[ -3\int _{Ne}^{N}\left( 1+w_{rh}(N')\right) dN'\right] , \end{aligned}$$

(5.1)

where $w_{rh}=p_{rh}/\rho _{rh}$ is the EoS during reheating. A useful quantity is the mean EoS $\tilde{w_{rh}}$ defined as

$$\begin{aligned} {\bar{w}}_{rh}=\frac{1}{\Delta N}\int _{N_e}^{N_{rh}}w_{rh}(N')dN' \end{aligned}$$

(5.2)

where $\Delta N=N_{rh}-N_e$ is the total number of e-folds during reheating. A useful phenomenological parameter that encodes the deviations of the reheating from the pure radiation era is defined as [94, 95]

$$\begin{aligned} R_{rad}=\frac{a_e}{a_{rh}}\left( \frac{\rho _e}{\rho _{rh}}\right) ^{1/4}, \end{aligned}$$

(5.3)

where $\rho _{rh}$ represents the energy density at the end of reheating era, $\rho _{rh}=\rho _{rh}(N_{rh})$. Taking the logarithm and using (5.1) we can write

$$\begin{aligned} \ln R_{rad}=-\Delta N+\frac{3}{4}\Delta N\left( 1+{\bar{w}}_{rh}\right) =\frac{1}{4}\Delta N\left( 3{\bar{w}}_{rh}-1\right) \end{aligned}$$

(5.4)

using $\Delta N$ from (5.2) we find

$$\begin{aligned} \ln R_{rad}=\frac{1-3{\bar{w}}_{rh}}{12\left( 1+{\bar{w}}_{rh}\right) }\ln \left( \frac{\rho _{rh}}{\rho _e}\right) \end{aligned}$$

(5.5)

The label $``*''$ will be used to make explicitly that the magnitudes are evaluated at the horizon crossing. Thus, at the horizon crossing the equality

$$\begin{aligned} \frac{k_{*}}{a(N_{*})H(N_{*})}=1 \end{aligned}$$

(5.6)

takes place, which can be written as

$$\begin{aligned} \frac{k_{*}}{a_0}\left( 1+z_e\right) e^{\Delta N_{*}}=H_{*} \end{aligned}$$

(5.7)

where $H_{*}=H(N_{*})$ and $\Delta N_{*}=N_e-N_{*}=\ln \left( a_e/a_{*}\right)$ is the number of e-folds before the end of inflation (see (2.18) where $N_{*}$ and $N_e$ correspond to the integral evaluated in its lower and upper limits respectively). On the other hand $H_{*}$ can be obtained from the amplitude of the scalar power spectrum (3.34) which is evaluated at the horizon crossing and is directly related to the COBE normalization

$$\begin{aligned} \mathcal{P}_S=\frac{H_{*}^2}{(2\pi )^2M_p^2}\frac{1}{2\epsilon _{0*}-\Delta _{0*}} \end{aligned}$$

(5.8)

where $\epsilon _0$ and $\Delta _0$ are given by

$$\begin{aligned}&\epsilon _0=\frac{V'(\phi )\left[ 8V(\phi )^2F_2'(\phi )+3M_p^4V'(\phi )\right] }{6V(\phi )^2\left[ M_p^2+2F_1(\phi ) V(\phi )\right] }\Big |_{\phi =\phi _{*}}, \end{aligned}$$

(5.9)

$$\begin{aligned}&\Delta _0= -\frac{8F_2'(\phi )\left[ 8V(\phi )^2F_2'(\phi )+3M_p^4V'(\phi )\right] }{9M_p^4\left[ M_p^2+2F_1(\phi ) V(\phi )\right] }\Big |_{\phi =\phi _{*}}.\nonumber \\ \end{aligned}$$

(5.10)

The redshift at which the inflation ends can be expressed in terms of $R_{rad}$ from (5.3) as [97,98,99]

$$\begin{aligned} 1+z_e=\frac{1}{R_{rad}}\left( \frac{\rho _e}{Q_{rh}\rho _{\gamma }}\right) ^{1/4} \end{aligned}$$

(5.11)

where $\rho _{\gamma }=3H_0^2M_p^2\Omega _{\gamma }$ is the current energy density of radiation and $Q_{rh}$ measures the change of relativistic degrees of freedom from reheating to current epoch. By replacing (5.11) in (5.7) we find

$$\begin{aligned} \Delta N_{*}=\ln R_{rad}+\ln \left( \frac{H_{*}}{M_p}\right) -\frac{1}{4}\ln \left( \frac{\rho _e}{M_p^4}\right) -N_0 \end{aligned}$$

(5.12)

where

$$\begin{aligned} N_0=\ln \left( \frac{k_{*}/a_0}{\left( Q_{rh}\rho _{\gamma }\right) ^{1/4}}\right) . \end{aligned}$$

The density $\rho _e$ can be obtained using the Friedman equation (2.15) and the expression (2.12) for the potential up to first order in slow-roll parameters

$$\begin{aligned}&\rho _e=\frac{3V_e}{3-\epsilon _{0e}-\frac{5}{2}\Delta _{0e}-2k_{0e}}=3M_p^2H_{*}^2\left( \frac{V_e}{V_{*}}\right) \nonumber \\&\qquad \times \frac{3-\epsilon _{0*}-5/2\Delta _{0*}-2k_{0*}}{3-\epsilon _{0e}-5/2\Delta _{0e}-2k_{0e}}\approx \nonumber \\&\quad \approx \left( \frac{V_e}{V_{*}}\right) \frac{9M_p^2H_{*}^2}{3-\epsilon _{0e}-5/2\Delta _{0e}-2k_{0e}} \end{aligned}$$

(5.13)

where we used the fact that $\epsilon _{0*},\Delta _{0*}, k_{0*}<<1$. In this form $\rho _e$ does not depend on the normalization of the potential. Replacing (5.13) in (5.12) we find

$$\begin{aligned} \Delta N_{*}&=\ln R_{rad}-\frac{1}{4}\ln \left[ \frac{9}{\left( 2\epsilon _{0*}-\Delta _{0*}\right) \left( 3-\epsilon _{0e}-\frac{5}{2}\Delta _{0e}-2k_{0e}\right) }\frac{V_e}{V_{*}}\right] \nonumber \\&\quad +\frac{1}{4}\ln \left( 4\pi ^2\mathcal{P}_S\right) -N_0 \end{aligned}$$

(5.14)

Using $\ln R_{rad}$ from (5.5) and (5.13) gives the final expression

$$\begin{aligned} \begin{aligned} \Delta N_{*}=&\frac{1-3{\bar{w}}_{rh}}{12(1+{\bar{w}}_{rh})}\ln \left( \rho _{rh}\right) +\frac{1+3{\bar{w}}_{rh}}{6(1+{\bar{w}}_{rh})}\ln \left( 4\pi ^2\mathcal{P}_S\right) -\\&\frac{1}{3+3{\bar{w}}_{rh}}\ln \left[ \frac{9}{\left( 2\epsilon _{0*}-\Delta _{0*}\right) ^{\frac{1+3{\bar{w}}_{rh}}{2}}\left( 3-\epsilon _{0e}-\frac{5}{2}\Delta _{0e}-2k_{0e}\right) }\left( \frac{V_e}{V_{*}}\right) \right] -N_0 \end{aligned} \end{aligned}$$

(5.15)

Once one performs the integration in Eq. (2.18) we find $\Delta N_{*}=\Delta N(\phi _{*})$ ($\phi _{*}=\phi _i$), which after being replaced in the l.h.s of (5.15) turns this equation into an algebraic equation whose solution determines $\phi _{*}$ (which in turn gives us the number of e-folds required before the end of inflation). The difficulty lies in specifying $\rho _{rh}$ and ${\bar{w}}_{rh}$ that depend on the process of reheating which is the less known post-inflationary phase.

A crude appreciation of $\Delta N_{*}$ can be obtained if one assumes instantaneous reheating, i.e. $\rho _{rh}=\rho _e$, in which case as follows from (5.3) and (5.4) $R_{rad}=1$ and ${\bar{w}}_{rh}=1/3$ and therefore $\Delta N_{*}$ will depend only on quantities defined during inflation. In this case from (5.15) it follows that

$$\begin{aligned} \Delta N_{*}=\frac{1}{4}\ln \left( 4\pi ^2\mathcal{P}_S\right) -\frac{1}{4}\ln \left[ \frac{9}{\left( 2\epsilon _{0*}-\Delta _{0*}\right) \left( 3-\epsilon _{0e}-\frac{5}{2}\Delta _{0e}-2k_{0e}\right) }\left( \frac{V_e}{V_{*}}\right) \right] -N_0 \end{aligned}$$

(5.16)

Further analysis requires the specification of the inflationary model, that is to define $V(\phi )$, $F_1(\phi )$ and $F_2(\phi )$.

In order to apply the above results to at least show the consistency with the subsequent reheating process, we can consider here an additional simplification (apart from assuming instantaneous reheating) by assuming that there is not significant drop in energy density during the lasts stages of inflation, so that $V_{*}\approx V_e$. This leads to the number of e-foldings from (5.16) [93]

$$\begin{aligned} \Delta N_{*}&\approx \frac{1}{4}\ln \left( 4\pi ^2\mathcal{P}_S\right) -\frac{1}{4}\ln \left[ \frac{3}{\left( 2\epsilon _{0*}-\Delta _{0*}\right) }\right] -N_0\nonumber \\&\approx 63.3 -\frac{1}{4}\ln \left[ \frac{3}{\left( 2\epsilon _{0*}-\Delta _{0*}\right) }\right] \end{aligned}$$

(5.17)

where for the numerical estimation in the second equality we have based on [93], and we have neglected $\epsilon _{0e},\ldots$ which is equivalent to setting $\rho _e=V_e$ in (5.12). So, the above estimation still keeps trace of the non-minimal couplings. Note that the smaller $(2\epsilon _{0*}-\Delta _{0*})$, the more significant the contribution of this term can be. In terms of $\phi _{*}$ we can write the following equation

$$\begin{aligned} \Delta N_{*}\approx 63.3 -\frac{1}{4}\ln \left[ \frac{27M_p^4V^2(\phi _{*})\left( 2F_1(\phi _{*})V(\phi _{*})+M_p^2\right) }{\left[ 8V^2(\phi _{*})F_2'(\phi _{*})+3M_p^4V'(\phi _{*})\right] ^2}\right] \end{aligned}$$

(5.18)

To illustrate some cases let us consider the power-law potential in the model (4.13) where the scalar spectral index depends only on the power n and the proposed number of e-foldings N, favoring only the model $n=2$ as follows from (4.24). Taking into account the Eq. (5.18) in Fig. rvsnskin16 we show the behavior of $n_s$ and r for the cases $n=2$ and $n=4$, showing that both models become favored by observations.

Along the trajectories in Fig. 18 the number of e-folds $\Delta N_{*}$ does not present major variations, being equal to 61.3 for $n=2$ and 61.7 for $n=4$.

In Fig. 19 we show some $(n_s,r)$ trajectories for the natural potential in the model (4.13).

Fig. 18

$n_s$ vs r for $\phi ^2$ and $\phi ^4$ potentials, where the number of e-folds satisfies the consistency with instantaneous reheating (5.18). For $n=2$, $\eta$ was taken in the interval $0.34\le \eta \le 0.35$ and $\beta =0.5$, and for $n=4$, $0.31\le \eta \le 0.33$ and $\beta =0.3$. Note that both curves satisfy the current observational bounds

Fig. 19

$n_s$ vs r for the natural potential (4.27) in the $\beta$-interval $10^5\le \eta \le 10^8$ and assuming $f=10^{-3}M_p$. The curves correspond to $\eta =0.15,\; 0.2,\; 0.25$. All curves are in the region favored by observations. The right panel shows the corresponding to each curve number of e-folds, that satisfies the consistency of slow-roll results with the instantaneous reheating (5.18)

7 Discussion

The analysis of general slow-roll inflation for a scalar-tensor model with non-minimal kinetic and Gauss–Bonnet couplings was performed and the results were applied to study some inflationary scenarios. The Mukhanov–Sasaki equation and the general expression for the power spectra have been deduced within the first-order formalism without resorting to second-order action. The correspondence of this model with a sector of generalized Galileons was shown and the functions $G_i(X,\phi )$ that give the equivalence with the corresponding terms in the scalar-tensor model were found.

From the general expressions for the slow-roll parameters and the inflationary indices, it was found that these magnitudes depend on the scalar field only through the ratio $V'/V$ ($V''/V=(V'/V)'+(V'/V)^2$) and the products $F_1V$ and $F'_2V$. This feature can facilitate the analysis in some cases depending on the relationships between $F_1$, $F_2$ and V, and two classes of couplings were considered that, for some models, lead to exact analytical results in the slow-roll approximation. The first one considers models where the coupling functions $F_1$ and $F_2$ have an inverse relation with the potential, which significantly simplifies the expressions for the slow-roll indices and the derived magnitudes as seen in (4.17)–(4.20)).

It was shown in the present study that the couplings $F_1, F_2\propto V^{-1}$ lead to inflationary indices well inside the region favored by observations [9] for scalar potentials that otherwise would not achieve it. An important consequence of considering these couplings is that the inflationary indices, as seen in [see (4.17)–(4.20)], do not depend on the scale of the potential. For the power-law models the most favored model is the quadratic potential and for the exponential potential there is no graceful exit from inflation although very acceptable values can be obtained for $n_s$ and r. In natural inflation with the potential (4.27), in the strong coupling limit $n_s$ increases towards the values $n_s=(2N-3)/(2N+1)$ which gives suitable values in the interval $50\le N\le 70$, while r depends on $\eta$ as $r=16(3-8\eta )/(6N+3))$ and can satisfy a suitable bound for appropriate $\eta$-interval. It was also found that the successful inflation can be realized with small fields leading to symmetry breaking scale below the Planck scale, which can be of the order of the GUT scale ($\sim 10^{16}$ Gev). If only GB coupling is considered, then for $f<<1$ suitable values for $n_s$ can be obtained for $\eta$ very close to 3/8 but at the expense of having no signals of GW. With the only NMKC successful inflation with symmetry breaking scale $f\sim 10^{16}$ Gev can be achieved as shown in Fig. rvsnskin2.

For the double-well potential (4.49) the functional dependence of the slow-roll parameters with respect to the scalar field is the same as in the case of canonical case except for the coefficients, that makes the difference in the physical restrictions on the parameters. The NMKC allows inflation with the vev $\phi _0<<M_p$. When only the GB coupling is present, the inflation with sub Planckian $\phi _0$ can be realized as long as $\eta$ is extremely close to its critical value 3/8 but at the cost of very weak ($r\sim 10^{-8}$) or no signals of primordial gravitational waves. Considering only the NMKC as shown in Fig. rvsnskin7 it is possible to realize successful inflation, with $n_s$ and r in the regions favored by observations, with the symmetry breaking scale of the order of the GUT scale.

In the second type of models the GB coupling maintains the same form $F_2\propto V^{-1}$ while the kinetic coupling function $F_1$ is assumed constant. As follows from (4.66)–(4.69) the inflationary observables depend on the scale of the potential. This imply that only after fixing the scale of the potential by COBE normalization we can determine the numerical value of $\beta$. The power-law potential in the regime $\eta =0$ and $0<\beta <\infty$ leads to intervals $0.967<n_s<0.975$ and $0.066<r<0.132$ for $N=60$ as follows from (4.82), (4.83). For the power-law potential, as follows from (4.82)–(4.89) for $n=2,4$, it was found that the interval of variation of $n_s$ is not affected by the GB coupling while for r the GB coupling leads to values that satisfy the bound $r<0.05$. For the exponential potential the results are plotted in Figs. 12 and 13, showing that the inflationary indices fall well inside the region favored by observations. Numerical analysis for natural inflation and the double-well inflation potential show also successful small-field inflation with the scale of symmetry breaking bellow the Planck scale. The behavior of the slow-roll parameters during inflation was illustrated for the natural inflation model, but similar behavior takes place for all the models considered.

When the reheating phase was taken into account it was obtained that, at least in the instantaneous reheating approximation, the slow-roll results were consistent with the reheating phase which was illustrated numerically for power-law and natural inflation. Particularly interesting is that this consistency improves the behavior of $\phi ^2$ and $\phi ^4$ inflation in the model (4.13) where $n_s$ and r moved to the region favored by the latest observations, as seen in Fig. 18.

Resuming, the inclusion of non-minimal kinetic and GB couplings in single scalar field inflationary scenarios can lead to significant effects. It was shown that the inflationary indices can take values favored by the latest observations, which cannot be attained with a canonical scalar field in some models. Additionally, some interesting results like small-field successful inflation with power-law potential, sub-planckian scale of symmetry breaking in natural inflation and sub-planckian v.e.v for the scalar filed in double-well potential can be achieved. It was also shown that $N\sim 60$ is consistent with the reheating process and that taking account of it can improve in some models the behavior of the inflationary observables.

Appendices

First order perturbations

We start from the full action

$$\begin{aligned} S= & {} \int {{d^4}x\sqrt{ - g} \bigg [ {\frac{1}{2}F(\phi )R - \frac{1}{2}{\partial _\mu }\phi {\partial ^\mu }\phi - V(\phi )}} \nonumber \\&{{+ {F_{1}(\phi )}{G_{\mu \nu }}{\nabla ^\mu }\phi {\nabla ^\nu }\phi - {F_2}(\phi )\mathcal{G}}\bigg ] } \end{aligned}$$

(A.1)

that can be splitted in the following manner

$$\begin{aligned} S = {S_{NMC}} + {S_\phi } + {S_{GB}} + {S_K}, \end{aligned}$$

(A.2)

where

$$\begin{aligned}&{S_{NMC}} = \int {{d^4}x\sqrt{ - g} \left( {\frac{1}{{2}}} F(\phi )R \right) }\\&{S_\phi } = \int {{d^4}x\sqrt{ - g} \left( { - \frac{{1}}{2}{\partial _\mu }\phi {\partial ^\mu }\phi - V(\phi )} \right) }\\&{S_{GB}} = - \int {{d^4}x\sqrt{ - g} } {{F_2}(\phi )\mathcal {G}}.\\&{S_K} = \int {{d^4}x\sqrt{ - g} {{F_1}(\phi ){G_{\mu \nu }}{\partial ^\mu }\phi {\partial ^\nu }\phi }} \end{aligned}$$

Then, the variation with respect to the metric gives the field equation that can be expressed as

$$\begin{aligned} T_{\nu }^{\mu }= {T_{\mu \nu }^{\left( \phi \right) } + T_{\mu \nu }^{GB} + T_{\mu \nu }^K} +T_{\mu \nu }^{NMC}=0, \end{aligned}$$

(A.3)

where

$$\begin{aligned} T_{\mu \nu }^{NMC}= & {} - \frac{2}{{\sqrt{ - g} }}\frac{{\delta {S_{NMC}}}}{{\delta {g^{\mu \nu }}}} \quad T_{\mu \nu }^{\left( \phi \right) } \\= & {} - \frac{2}{{\sqrt{ - g} }}\frac{{\delta {S_\phi }}}{{\delta {g^{\mu \nu }}}}\quad T_{\mu \nu }^{GB} \\= & {} - \frac{2}{{\sqrt{ - g} }}\frac{{\delta {S_{GB}}}}{{\delta {g^{\mu \nu }}}}\quad T_{\mu \nu }^K = - \frac{2}{{\sqrt{ - g} }}\frac{{\delta {S_K}}}{{\delta {g^{\mu \nu }}}}, \end{aligned}$$

with the explicit expressions for the energy-momentum tensors given by:

$$\begin{aligned} T_{\mu \nu }^{(\phi )}= & {} {\nabla _\mu }\phi {\nabla _\nu }\phi - \frac{1}{2}{g_{\mu \nu }}{\nabla _\lambda }\phi {\nabla ^\lambda }\phi - {g_{\mu \nu }}V(\phi ), \end{aligned}$$

(A.4)

$$\begin{aligned} T_{\mu \nu }^{NMC}= & {} { - {g_{\mu \nu }}\left[ {{\nabla _\sigma }{\nabla ^\sigma }{F(\phi )}} \right] + \left[ {{\nabla _\mu }{\nabla _\nu }{F(\phi ) }} \right] }- { {F(\phi ) }} G_{\mu \nu }, \end{aligned}$$

(A.5)

$$\begin{aligned} T_{\mu \nu }^{GB}= & {} -4\Big ([{\nabla _\mu }{\nabla _\nu }{F_2}(\phi )]R - {g_{\mu \nu }}[{\nabla _\rho }{\nabla ^\rho }{F_2}(\phi )]R \nonumber \\&- 2[{\nabla ^\rho }{\nabla _\mu }{F_2}(\phi )]{R_{\nu \rho }} - 2[{\nabla ^\rho }{\nabla _\nu }{F_2}(\phi )]{R_{\mu \rho }} \nonumber \\&+ 2[{\nabla _\rho }{\nabla ^\rho }{F_2}(\phi )]{R_{\mu \nu }} + 2{g_{\mu \nu }}[{\nabla ^\rho }{\nabla ^\sigma }{F_2}(\phi )]{R_{\rho \sigma }} \nonumber \\&- 2[{\nabla ^\rho }{\nabla ^\sigma }{F_2}(\phi )]{R_{\mu \rho \nu \sigma }}\Big ), \end{aligned}$$

(A.6)

$$\begin{aligned} T_{\mu \nu }^K= & {} \left( {{R_{\mu \nu }} - \frac{1}{2}R{g_{\mu \nu }}} \right) {F_1}(\phi ){\nabla _\lambda }\phi {\nabla ^\lambda }\phi \nonumber \\&+ {g_{\mu \nu }}{\nabla _\lambda }{\nabla ^\lambda }\left( {{F_1}(\phi ){\nabla _\gamma }\phi {\nabla ^\gamma }\phi } \right) \nonumber \\&-{{\nabla _\nu }{\nabla _\mu }}\left( {{F_1}\left( \phi \right) {\nabla _\lambda }\phi {\nabla ^\lambda }\phi } \right) + R{F_1}\left( \phi \right) {\nabla _\mu }\phi {\nabla _\nu }\phi \nonumber \\&- 2{F_1}\left( \phi \right) \left( {{R_{\mu \lambda }}{\nabla ^\lambda }\phi {\nabla _\nu }\phi + {R_{\nu \lambda }}{\nabla ^\lambda }\phi {\nabla _\mu }\phi } \right) \nonumber \\&+ {g_{\mu \nu }}{R_{\lambda \gamma }}{F_1}\left( \phi \right) {\nabla ^\lambda }\phi {\nabla ^\gamma }\phi \nonumber \\&+{\nabla _\lambda }{\nabla _\mu }\left( {{F_1}\left( \phi \right) {\nabla ^\lambda }\phi {\nabla _\nu }\phi } \right) + {\nabla _\lambda }{\nabla _\nu }\left( {{F_1}\left( \phi \right) {\nabla ^\lambda }\phi {\nabla _\mu }\phi } \right) \nonumber \\&- {\nabla _\lambda }{\nabla ^\lambda }\left( {{F_1}\left( \phi \right) {\nabla _\mu }\phi {\nabla _\nu }\phi } \right) - {g_{\mu \nu }}{\nabla _\lambda }{\nabla _\gamma }\left( {{F_1}\left( \phi \right) {\nabla ^\lambda }\phi {\nabla ^\gamma }\phi } \right) .\nonumber \\ \end{aligned}$$

(A.7)

And the equation of motion for the scalar field is given by

$$\begin{aligned}&\frac{1}{2}F'(\phi )R + {\nabla _\mu }{\nabla ^\mu }\phi - V'(\phi ) - {F_1}'(\phi ){G_{\mu \nu }}{\nabla ^\mu }\phi {\nabla ^\nu }\phi \nonumber \\&\qquad - 2{F_1}(\phi ){G_{\mu \nu }}{\nabla ^\mu }{\nabla ^\nu }\phi - {F_2}'(\phi )\mathcal{G} = 0 \end{aligned}$$

(A.8)

Linear perturbations

To calculate the linear perturbations we use the metric in the Newtonian Gauge:

$$\begin{aligned} d{s^2} = - (1 + 2\Phi )d{t^2} + {a^2}(t)\left[ {(1 - 2\Psi ){\delta _{ij}} } \right] d{x^i}d{x^j}. \end{aligned}$$

(A.9)

The perturbed first order field equation can be written as:

$$\begin{aligned} \delta T_{\nu } ^{\mu }= \delta T_\nu ^{\mu (\phi )} + \delta T_\nu ^{\mu (NMC)} + \delta T_\nu ^{\mu (GB)}+ \delta T_\nu ^{\mu (K)}=0, \end{aligned}$$

where the explicit expressions for each perturbation are given by [89]:

1. For the minimally-coupled scalar field:

$$\begin{aligned} \begin{aligned}&\delta T_0^{0(\phi )} = {{{{\dot{\phi }}} }^2}\Phi - {{\dot{\phi }}} \delta {{\dot{\phi }}} - V'\delta \phi , \\ {}&\delta T_i^{0(\phi )} = {\partial _i}\left( { - {{\dot{\phi }}} \delta \phi } \right) ,\\&\delta T_j^{i(\phi )} - \frac{1}{3}\delta _j^i\delta T_k^{k(\phi )} = 0, \\&\delta T_k^{k(\phi )} - \delta T_0^{0(\phi )} = - 4\Phi {{{{\dot{\phi }}} }^2} + 4{{\dot{\phi }}} \delta {{\dot{\phi }}} - 2V'\delta \phi . \end{aligned} \end{aligned}$$

(A.10)

2. For the non-minimal coupling:

$$\begin{aligned}&\delta T_0^{0(NM)} = - 2F\left( {H(3H\Phi + 3{{\dot{\Psi }}} ) - \frac{\Delta }{{{a^2}}}\Psi } \right) \\&\quad - \dot{F}(3{{\dot{\Psi }}} + 6H\Phi ) + 3{H^2}\delta F + 3H\delta \dot{F} - \left( {\frac{\Delta }{{{a^2}}}} \right) \delta F,\\&\delta T_i^{0(NM)} = {\partial _i}\left( {2F(H\Phi + {{\dot{\Psi }}} ) + \dot{F}\Phi - \delta \dot{F} + H\delta F} \right) ,\\&\delta T_j^{i(NM)} - \frac{1}{3}\delta _j^i\delta T_k^{k(NM)} = \frac{1}{{{a^2}}}\\&\quad \left( {{\partial _i}{\partial _j} - \frac{1}{3}{\delta _{ij}}\Delta } \right) \left( {F\left( { - \Psi + \Phi } \right) + \delta F} \right) ,\\&\delta T_k^{k(NM)} - \delta T_0^{0(NM)} = - 2F\left( (3H{{\dot{\Phi }}} + 3\ddot{\Psi }) \right. \\&\quad + 2H(3H\Phi + 3{{\dot{\Psi }}} ) + 6{\dot{H}}\Phi \\&\left. + \frac{\Delta }{{{a^2}}}\Phi \right) - \dot{F}(3{{\dot{\Psi }}} + 6H\Phi )\\&\quad - 3\dot{F}{{\dot{\Phi }}} - 6{\ddot{F}}\Phi + 6({\dot{H}} + {H^2})\delta F + 3\delta {\ddot{F}} \\&\quad + 3H\delta \dot{F} - \left( {\frac{\Delta }{{{a^2}}}} \right) \delta F. \end{aligned}$$

3. For the non-minimal kinetic coupling:

$$\begin{aligned}&\delta T_0^{0(K)} = - 2{{\dot{\phi }}} \left( - {F_1}{{\dot{\phi }}} \left( { - \frac{\Delta }{{{a^2}}}\Psi + 18\Phi {H^2} + 9H{{\dot{\Psi }}} )} \right) \right. \nonumber \\&\quad \left. - 2{F_1}H\frac{\Delta }{{{a^2}}}\delta \phi + 9{H^2}{F_1}\delta {{\dot{\phi }}} + \frac{9}{2}{H^2}{{\dot{\phi }}} \delta {F_1} \right) ,\nonumber \\&\delta T_i^{0(K)} = {\partial _i}\bigg [ { - 2{{\dot{\phi }}} \bigg ( { - 2H{F_1}\delta {{\dot{\phi }}} + 3{H^2}{F_1}\delta \phi - H{{\dot{\phi }}} \delta {F_1} }}\nonumber \\&{{+ {F_1}{{\dot{\phi }}} \left( {{{\dot{\Psi }}} + 3H\Phi } \right) } \bigg )} \bigg ],\nonumber \\&\delta T_j^{i(K)} - \frac{1}{3}\delta _j^i\delta T_k^{k(K)} = \frac{1}{{{a^2}}}\left( {{\partial _i}{\partial _j} - \frac{1}{3}{\delta _{ij}}\Delta } \right) \nonumber \\&\quad [ - {{{{\dot{\phi }}} }^2}\delta {F_1} - 2({F_1}\ddot{\phi }+ H{F_1}{{\dot{\phi }}} )\delta \phi + {F_1}{{{{\dot{\phi }}} }^2}( - \Psi - \Phi )],\nonumber \\&\delta T_k^{k(K)} - \delta T_0^{0(K)} = - 12H{{\dot{F}}_1}{{\dot{\phi }}} \delta {{\dot{\phi }}} - 12{\dot{H}}{F_1}{{\dot{\phi }}} \delta {{\dot{\phi }}} - 12H{F_1}{{\dot{\phi }}} \delta \ddot{\phi }\nonumber \\&\quad + 2{F_1}{{{{\dot{\phi }}} }^2}\frac{\Delta }{{{a^2}}}\Phi + 2{{{{\dot{\phi }}} }^2}\frac{\Delta }{{{a^2}}}\delta {F_1} + 4{F_1}{{{{\dot{\phi }}} }^2}\frac{\Delta }{{{a^2}}}\Psi \nonumber \\&\quad - 6{\dot{H}}{{{{\dot{\phi }}} }^2}\delta {F_1} - 6H{{{{\dot{\phi }}} }^2}\delta {{\dot{F}}_1} + 2{{\dot{F}}_1}{{{{\dot{\phi }}} }^2}(12H\Phi + 3{{\dot{\Psi }}} ) \nonumber \\&\quad + 2{F_1}{{{{\dot{\phi }}} }^2}(12{\dot{H}}\Phi + 9H{{\dot{\Phi }}} + 3\ddot{\Psi }) \nonumber \\&\quad + 4{F_1}\ddot{\phi }\frac{\Delta }{{{a^2}}}\delta \phi - 12{F_1}H\ddot{\phi }\delta {{\dot{\phi }}} - 12H{{\dot{\phi }}} \ddot{\phi }\delta {F_1} \nonumber \\&\quad + 4{F_1}{{\dot{\phi }}} \ddot{\phi }(12H\Phi + 3{{\dot{\Psi }}} ). \end{aligned}$$

(A.11)

4. For the Gauss–Bonnet coupling:

$$\begin{aligned} \delta T^{0 GB}_0= & {} 24H^3\dot{\delta F_2(\phi )}-96H^3\dot{F_2(\phi )} \Phi -72H^2\dot{F_2(\phi )}{\dot{\Psi }}\nonumber \\&-\frac{8}{a^2}H^2\nabla ^2\delta F_2(\phi )+\frac{16}{a^2}H\dot{F_2(\phi )}\nabla ^2\Psi ,\nonumber \\ \delta T^{i GB}_j= & {} \frac{8}{a^2}\partial _i\partial _j \left[ -\left( F_2''(\phi ){\dot{\phi }}^2+F_2'(\phi )\ddot{\phi }\right) \Psi +HF_2'(\phi ){\dot{\phi }}\Phi \right. \nonumber \\&\left. +\left( H^2+{\dot{H}}\right) F_2'(\phi )\delta \phi \right] \nonumber \\&+8\Big [H^2\ddot{\delta F_2(\phi )}-\frac{1}{a^2}H^2F_2'(\phi )\nabla ^2\delta \phi \nonumber \\&\quad -\frac{1}{a^2}{\dot{H}}F_2'(\phi )\nabla ^2\delta \phi +2H^3\dot{\delta F_2(\phi )}+2H{\dot{H}}\dot{\delta F_2(\phi )} \nonumber \\&-\frac{1}{a^2}H\dot{F_2(\phi )}\nabla ^2\Phi - 8H^3\dot{F_2(\phi )}\Phi -8H{\dot{H}}\dot{F_2(\phi )}\Phi \nonumber \\&\quad +\frac{1}{a^2}\ddot{F_2(\phi )}\nabla ^2\Psi -4H^2\ddot{F_2(\phi )}\Phi \nonumber \\&-3H^2\dot{F_2(\phi )}{\dot{\Phi }}-6H^2\dot{F_2(\phi )}{\dot{\Psi }} -2{\dot{H}}\dot{F_2(\phi )}{\dot{\Psi }}\nonumber \\&\quad -2H\ddot{F_2(\phi )}{\dot{\Psi }} -2H\dot{F_2(\phi )}\ddot{\Psi }\Big ]\delta _{ij},\nonumber \\&\delta T^{k GB}_k =\frac{16}{a^2}\ddot{F_2(\phi )}\nabla ^2\Psi \nonumber \\&\quad -\frac{16}{a^2}H\dot{F_2(\phi )}\nabla ^2\Phi -\frac{16}{a^2}\left( H^2+{\dot{H}}\right) \nabla ^2\delta F_2(\phi )\nonumber \\&\quad +24H^2\ddot{\delta F_2(\phi )}\nonumber \\&\quad + 48H^3\dot{\delta F_2(\phi )}+48H{\dot{H}}\dot{\delta F_2(\phi )} -192H^3\dot{F_2(\phi )}\Phi \nonumber \\&\quad -192H{\dot{H}}\dot{F_2(\phi )}\Phi -96H^2\ddot{F_2(\phi )}\Phi \nonumber \\&\quad -72H^2\dot{F_2(\phi )}{\dot{\Phi }} -144H^2\dot{F_2(\phi )}{\dot{\Psi }}-48{\dot{H}}\dot{F_2(\phi )} {\dot{\Psi }}\nonumber \\&\quad -48H\ddot{F_2(\phi )}{\dot{\Psi }}-48H\dot{F_2(\phi )}\ddot{\Psi },\nonumber \\ \delta T^{0 GB}_i= & {} 8\partial _i\left[ H^3\delta F_2(\phi )-H^2\dot{\delta F_2(\phi )}+2H\dot{F_2(\phi )}{\dot{\Psi }}\right. \nonumber \\&\quad \left. +3H^2\dot{F_2(\phi )}\Phi \right] ,\nonumber \\ \delta T^{i GB}_0= & {} \frac{8}{a^2}\partial _i\left[ H^2\dot{\delta F_2(\phi )}-H^3\delta F_2(\phi )-2H\dot{F_2(\phi )}{\dot{\Psi }}\right. \nonumber \\&\quad \left. -3H^2\dot{F_2(\phi )}\Phi \right] . \end{aligned}$$

(A.12)

5. Linear perturbation of the equation of motion (A.8)

$$\begin{aligned}&3H\delta {{\dot{\phi }}} + 18{F_1}{H^3}\delta {{\dot{\phi }}} + 12{F_1}H{\dot{H}}\delta {{\dot{\phi }}} \\&\quad + \delta \ddot{\phi }+ 6{F_1}{H^2}\delta \ddot{\phi }- 6H{{\dot{\phi }}} \Phi - 72{F_1}{H^3}{{\dot{\phi }}} \Phi \\&\quad - 48{F_1}H{\dot{H}}{{\dot{\phi }}} \Phi - 2\ddot{\phi }\Phi \\&\quad - 24{F_1}{H^2}\ddot{\phi }\Phi - {{\dot{\phi }}} {{\dot{\Phi }}} - 18{F_1}{H^2}{{\dot{\phi }}} {{\dot{\Phi }}} \\&\quad - 3{{\dot{\phi }}} {{\dot{\Psi }}} - 54{F_1}{H^2}{{\dot{\phi }}} {{\dot{\Psi }}} - 12{F_1}{\dot{H}}{{\dot{\phi }}} {{\dot{\Psi }}} \\&\quad - 12{F_1}H\ddot{\phi }{{\dot{\Psi }}} - 12{F_1}H{{\dot{\phi }}} \ddot{\Psi }\\&\quad - \frac{{\Delta \delta \phi }}{{{a^2}}} - \frac{{6{F_1}{H^2}\Delta \delta \phi }}{{{a^2}}} - \frac{{4{F_1}{\dot{H}}\Delta \delta \phi }}{{{a^2}}} \\&\quad - \frac{{4{F_1}H{{\dot{\phi }}} \Delta \Phi }}{{{a^2}}} + \frac{{4{F_1}H{{\dot{\phi }}} \Delta \Psi }}{{{a^2}}} \\&\quad + \frac{{4{F_1}\ddot{\phi }\Delta \Psi }}{{{a^2}}} + 12{H^2}\Phi F' \\&\quad + 6{\dot{H}}\Phi F' + 3H{{\dot{\Phi }}} F' + 12H{{\dot{\Psi }}} F' + 3\ddot{\Psi }F' \\&\quad + \frac{{\Delta \Phi F'}}{{{a^2}}} - \frac{{2\Delta \Psi F'}}{{{a^2}}} + 18{H^3}{{\dot{\phi }}} \delta \phi {F_1}' \\&\quad + 12H{\dot{H}}{{\dot{\phi }}} \delta \phi {F_1}'\\&\quad + 6{H^2}\ddot{\phi }\delta \phi {F_1}' + 6{H^2}{{\dot{\phi }}} \delta {{\dot{\phi }}} {F_1}' - 12{H^2}{{{{\dot{\phi }}} }^2}\Phi {F_1}' \\&\quad - 6H{{{{\dot{\phi }}} }^2}{{\dot{\Psi }}} {F_1}' + \frac{{2{{{{\dot{\phi }}} }^2}\Delta \Psi {F_1}'}}{{{a^2}}} - 96{H^4}\Phi {F_2}' - 96{H^2}{\dot{H}}\Phi {F_2}' \\&\quad - 24{H^3}{{\dot{\Phi }}} {F_2}' - 96{H^3}{{\dot{\Psi }}} {F_2}' - 48H{\dot{H}}{{\dot{\Psi }}} {F_2}' - 24{H^2}\ddot{\Psi }{F_2}'\nonumber \\&\quad - \frac{{8{H^2}\Delta \Phi {F_2}'}}{{{a^2}}} + \frac{{16{H^2}\Delta \Psi {F_2}'}}{{{a^2}}} + \frac{{16{\dot{H}}\Delta \Psi {F_2}'}}{{{a^2}}}\\&\quad - 6{H^2}\delta \phi F'' - 3{\dot{H}}\delta \phi F'' + 3{H^2}{{{{\dot{\phi }}} }^2}\delta \phi {F_1}'' \\&\quad + 24{H^4}\delta \phi {F_2}'' +24{H^2}{\dot{H}}\delta \phi {F_2}'' + \delta \phi V'' = 0 \end{aligned}$$

Correspondence between the NMKC and generalized Galileons

The action for the non-minimal kinetic term is given by

$$\begin{aligned} {S} = \int {{d^4}} x\sqrt{ - g} {F_1}(\phi ){G_{\mu \nu }}{\nabla ^\mu }\phi {\nabla ^\nu }\phi \end{aligned}$$

(B.1)

It will be proven that this action is equivalent equivalent (up to surface terms) to the following model of generalized Galileons:

$$\begin{aligned} S_{gal}= & {} \int {d^4}x\sqrt{ - g} \left[ K - {G_3}\square \phi + {G_4}R + {G_4}_{,X}\left[ {{\left( {\square \phi } \right) }^2} \right. \right. \nonumber \\&\left. \left. - {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2} \right] \right] \end{aligned}$$

(B.2)

where K y $G_i$ are functions of $\phi$ y $X = - \frac{1}{2}{\nabla _\mu }\phi {\nabla ^\nu }\phi$ given by

$$\begin{aligned} K= & {} 2{F_1}''(\phi ){X^2} \nonumber \\ {G_3}= & {} 3{F_1}'(\phi )X \nonumber \\ {G_4}= & {} {F_1}(\phi )X \end{aligned}$$

(B.3)

In fact, replacing the Einstein tensor, ${G_{\mu \nu }} = {R_{\mu \nu }} - \frac{1}{2}R{g_{\mu \nu }}$, in (B.1), it follows that

$$\begin{aligned} S= & {} \int {{d^4}x\sqrt{ - g} {F_1}(\phi )\left( {{R_{\mu \nu }} - \frac{1}{2}R{g_{\mu \nu }}} \right) } {\nabla ^\mu }\phi {\nabla ^\nu }\phi \\= & {} \int {{d^4}x\sqrt{ - g} \left[ {{F_1}(\phi ){R_{\mu \nu }}{\nabla ^\mu }\phi {\nabla ^\nu }\phi + R{F_1}(\phi )X} \right] } \end{aligned}$$

Taking into account the commutator of covariant derivatives:

$$\begin{aligned} \left[ {{\nabla _\lambda },{\nabla _\nu }} \right] {\nabla ^\lambda }\phi = R_{\mu \lambda \nu }^\lambda {\nabla ^\mu }\phi = {R_{\mu \nu }}{\nabla ^\mu }\phi , \end{aligned}$$

the action (B.1) can be written as

$$\begin{aligned} S&= \int {{d^4}x\sqrt{ - g} \left[ {{F_1}(\phi ){\nabla ^\nu }\phi \left[ {{\nabla _\lambda },{\nabla _\nu }} \right] {\nabla ^\lambda }\phi + R{F_1}(\phi )X} \right] }\\&=\int {{d^4}x\sqrt{ - g} \bigg [ {{F_1}(\phi ){\nabla ^\nu }\phi {\nabla _\lambda }{\nabla _\nu }{\nabla ^\lambda }\phi - {F_1}(\phi ){\nabla ^\nu }\phi {\nabla _\nu }{\nabla _\lambda }{\nabla ^\lambda }\phi }}\nonumber \\&\quad {{+ R{F_1}(\phi )X} \bigg ]} \end{aligned}$$

After integration by parts in the second term and omitting surface integrals, it is found

$$\begin{aligned} S= & {} \int {d^4}x\sqrt{ - g} \left[ {F_1}(\phi ){\nabla ^\nu }\phi {\nabla _\lambda }{\nabla _\nu }{\nabla ^\lambda }\phi \right. \\&\quad + {F_1}'(\phi ){\nabla _\nu }\phi {\nabla ^\nu }\phi {\nabla _\lambda }{\nabla ^\lambda }\phi \\&\quad \left. + {F_1}(\phi ){{\left( {\square \phi } \right) }^2} + R{F_1}(\phi )X \right] \end{aligned}$$

where ${\left( {\square \phi } \right) ^2} = \left( {{\nabla _\lambda }{\nabla ^\lambda }\phi } \right) \left( {{\nabla _\nu }{\nabla ^\nu }\phi } \right)$. Integrating again by parts in the first term and omitting surface integrals, gives

$$\begin{aligned} S =&\int {d^4}x\sqrt{ - g} \Big [ - {F_1}'(\phi ){\nabla _\lambda } \phi {\nabla ^\nu }\phi {\nabla _\nu }{\nabla ^\lambda } \phi \\&\quad - {F_1}(\phi ){\nabla _\lambda }{\nabla ^\nu }\phi {\nabla _\nu }{\nabla ^\lambda }\phi + {F_1}'(\phi ){\nabla _\nu }\phi {\nabla ^\nu }\phi {\nabla _\lambda }{\nabla ^\lambda }\phi \\&\quad + {F_1}(\phi ){{\left( {\square \phi } \right) }^2} + R{F_1}(\phi )X \Big ] \end{aligned}$$

In order to simplify the expressions we use the notation ${\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) ^2} \equiv {\nabla _\mu }{\nabla _\nu }\phi {\nabla ^\mu }{\nabla ^\nu }\phi = {\nabla _\lambda }{\nabla ^\nu }\phi {\nabla _\nu }{\nabla ^\lambda }\phi$, which allows to write the action as follows

$$\begin{aligned} S =&\int {d^4}x\sqrt{ - g} \Big [ - {F_1}'(\phi ){\nabla _\lambda }\phi {\nabla ^\nu }\phi {\nabla _\nu }{\nabla ^\lambda }\phi \\&\quad + {F_1}'(\phi ){\nabla _\nu }\phi {\nabla ^\nu }\phi {\nabla _\lambda }{\nabla ^\lambda }\phi + R{F_1}(\phi )X \\&\quad + {F_1}(\phi )\left( {{{\left( {\square \phi } \right) }^2} - {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2}} \right) \Big ] \end{aligned}$$

This expression can be rewritten in the following form

$$\begin{aligned} S =&\int {d^4}x\sqrt{ - g} \Bigg [ - \frac{1}{2}{F_1}'(\phi ){\nabla _\lambda }\phi {\nabla ^\nu }\phi {\nabla _\nu }{\nabla ^\lambda }\phi \\&\quad - \frac{1}{2}{F_1}'(\phi ){\nabla _\lambda }\phi {\nabla ^\nu }\phi {\nabla _\nu }{\nabla ^\lambda }\phi - \frac{1}{2}{F_1}'(\phi ){\nabla _\nu }\phi {\nabla ^\nu }\phi {\nabla _\lambda }{\nabla ^\lambda }\phi \\&\quad + \frac{3}{2}{F_1}'(\phi ){\nabla _\nu }\phi {\nabla ^\nu }\phi {\nabla _\lambda }{\nabla ^\lambda }\phi \\&\quad + {F_1}(\phi )\left[ {{{\left( {\square \phi } \right) }^2} - {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2}} \right] + R{F_1}(\phi )X \Bigg ] \end{aligned}$$

After integrating by parts in the first term and simplifying it is found

$$\begin{aligned} S =&\int {d^4}x\sqrt{ - g} \Bigg [ \frac{1}{2}{F_1}''(\phi ){\nabla _\nu }\phi {\nabla _\lambda }\phi {\nabla ^\nu }\phi {\nabla ^\lambda }\phi \\&\quad + \frac{3}{2}{F_1}'(\phi ){\nabla _\nu }\phi {\nabla ^\nu }\phi {\nabla _\lambda }{\nabla ^\lambda }\phi + R{F_1}(\phi )X \\&+ {F_1}(\phi )\left( {{{\left( {\square \phi } \right) }^2} - {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2}}\right) \Bigg ] \end{aligned}$$

Using the notation $X = - \frac{1}{2}{\nabla _\mu }\phi {\nabla ^\nu }\phi$ y $\square = {\nabla _\lambda }{\nabla ^\lambda }$, this expression can be rewritten as

$$\begin{aligned} S= & {} \int {{d^4}x\sqrt{ - g} \bigg [ {2{F_1}''(\phi ){X^2} - 3{F_1}'(\phi )X\square \phi }} \\&{{+ {F_1}(\phi )\left[ {{{\left( {\square \phi } \right) }^2} - {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2}} \right] + R{F_1}(\phi )X} \bigg ]} \end{aligned}$$

Taking into account the functions defined in (B.3) it can be seen that the action takes the final form

$$\begin{aligned} S&= \int {{d^4}x\sqrt{ - g} \bigg [ {K - {G_3}\square \phi + {G_4}R }}\nonumber \\ {}&\quad {{+ {G_4}_{,X}\left[ {{{\left( {\square \phi } \right) }^2} - {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2}} \right] } \bigg ]} \end{aligned}$$

(B.4)

which is the same action (B.2) and demonstrates the equivalence of the actions (B.1) and (B.2).

Correspondence between the GB coupling and generalized Galileons

We start with the action for the GB coupling

$$\begin{aligned} S&= \int {{d^4}x\sqrt{ - g} {f}(\phi )\mathcal{G}} = \int {{d^4}x\sqrt{ - g} {f}(\phi )\bigg [ {{R^2} - 4{R_{\mu \nu }}{R^{\mu \nu }} }}\nonumber \\ {}&{{+ {R_{\mu \nu \rho \sigma }}{R^{\mu \nu \rho \sigma }}} \bigg ]} \end{aligned}$$

(C.1)

whose corresponding energy-momentum tensor is the following (A.6)

$$\begin{aligned} T_{(f)}^{\mu \nu } =&\, 4\Big ([{\nabla ^\nu }{\nabla ^\mu }{f}]R - {g^{\mu \nu }}[{\nabla ^\rho }{\nabla _\rho }{f}]R - 2[{\nabla _\rho }{\nabla ^\mu }{f}]{R^{\rho \nu }}\nonumber \\&+ 2{g^{\mu \nu }}[{\nabla ^\rho }{\nabla ^\sigma }{f}]{R_{\rho \sigma }} \nonumber \\&+ 2[{\nabla ^\rho }{\nabla _\rho }{f}]{R^{\mu \nu }} - 2[{\nabla _\rho }{\nabla ^\nu }{f}]{R^{\rho \mu }} - 2[{\nabla _\rho }{\nabla _\sigma }{f}]{R^{\mu \rho \nu \sigma }}\Big ) \end{aligned}$$

(C.2)

Next we evaluate the divergence of this tensor, namely ${\nabla _\mu }T_{(f)}^{\mu \nu }$. This calculation is tedious and we present here some steeps that allow to reproduce the results. It should be taken into account that for an arbitrary vector $V^\mu$ and scalar $\varphi$, it follows

$$\begin{aligned}&({\nabla _\alpha }{\nabla _\beta } - {\nabla _\beta }{\nabla _\alpha }){V^\mu } = R_{\lambda \alpha \beta }^\mu {V^\lambda },\\&({\nabla _\lambda }{\nabla _\nu }{\nabla ^\lambda } - {\nabla _\nu }{\nabla _\lambda }{\nabla ^\lambda })\varphi = {R_{\mu \nu }}{\nabla ^\mu }\varphi \end{aligned}$$

After some algebraic manipulations it is obtained

$$\begin{aligned} {\nabla _\mu }T_{(f)}^{\mu \nu }&= 4(R{R^{\mu \nu }} - 2{R^{\sigma \nu }}R_\sigma ^\mu + 2{R_{\rho \sigma }}{R^{\mu \rho \sigma \nu }}){\nabla _\mu }f \nonumber \\&\quad - 8\left( {{\nabla _\mu }{\nabla _\rho }{\nabla _\sigma }f} \right) {R^{\mu \rho \nu \sigma }}. \end{aligned}$$

(C.3)

From

$$\begin{aligned}{\nabla _\mu }{\nabla _\rho }{\nabla _\sigma }f - {\nabla _\rho }{\nabla _\mu }{\nabla _\sigma }f = - R_{\sigma \mu \rho }^\lambda {\nabla _\lambda }f, \end{aligned}$$

follows

$$\begin{aligned}{R^{\mu \rho \nu \sigma }}\left( {{\nabla _\mu }{\nabla _\rho }{\nabla _\sigma }f - {\nabla _\rho }{\nabla _\mu }{\nabla _\sigma }f} \right) = - R_{\sigma \mu \rho }^\lambda {R^{\mu \rho \nu \sigma }}{\nabla _\lambda }f,\end{aligned}$$

which imply

$$\begin{aligned}2{R^{\mu \rho \nu \sigma }}\left( {{\nabla _\mu }{\nabla _\rho }{\nabla _\sigma }f} \right) = - R_{\sigma \mu \rho }^\lambda {R^{\mu \rho \nu \sigma }}{\nabla _\lambda }f.\end{aligned}$$

Substituting this expression in (C.3) it is found

$$\begin{aligned} {\nabla _\mu }T_{(f)}^{\mu \nu } = 4(R{R^{\mu \nu }} - 2{R^{\sigma \nu }}R_\sigma ^\mu + 2{R_{\rho \sigma }}{R^{\mu \rho \sigma \nu }} + R_{\sigma \lambda \rho }^\mu {R^{\lambda \rho \nu \sigma }}){\nabla _\mu }f \end{aligned}$$

(C.4)

This expression can be written in more compact form if using the Banch-Lanczos identity in 4 dimensions:

$$\begin{aligned} {g^{\mu \nu }}\mathcal{G} = 4(R{R^{\mu \nu }} - 2{R^{\sigma \nu }}R_\sigma ^\mu + 2{R_{\rho \sigma }}{R^{\mu \rho \sigma \nu }} + R_{\sigma \lambda \rho }^\mu {R^{\nu \sigma \lambda \rho }}) \end{aligned}$$

In this way, it is obtained that

$$\begin{aligned} {\nabla _\mu }T_{(f)}^{\mu \nu } = \mathcal{G}{\nabla ^\nu }f \end{aligned}$$

(C.5)

Notice that this expression is an identity, which is also consistent with the field equations. Solving for $\mathcal{G}$ from this identity we find

$$\begin{aligned}\mathcal{G} = \frac{1}{{{\nabla ^\alpha }f{\nabla _\alpha }f}}{\nabla _\nu }f{\nabla _\mu }T_{(f)}^{\mu \nu }\end{aligned}$$

Particularly, if $f=\phi$, it gives

$$\begin{aligned} \mathcal{G} = \frac{1}{{{\nabla ^\alpha }\phi {\nabla _\alpha }\phi }}{\nabla _\nu }\phi {\nabla _\mu }T_{(\phi )}^{\mu \nu } = - \frac{1}{{2X}}{\nabla _\nu }\phi {\nabla _\mu }T_{(\phi )}^{\mu \nu } \end{aligned}$$

(C.6)

where $X = - \frac{1}{2}{\nabla ^\alpha }\phi {\nabla _\alpha }\phi$. Substituting (C.6) in the initial action gives

$$\begin{aligned}S = \int {{d^4}x\sqrt{ - g} \left( { - \frac{f}{{2X}}{\nabla _\nu }\phi {\nabla _\mu }T_{(\phi )}^{\mu \nu }} \right) } \end{aligned}$$

To better visualise, we expand explicitly this action

$$\begin{aligned} S =&\int {{d^4}x\sqrt{ - g} } \Bigg [- { \frac{{2f}}{X}} {\nabla _\mu }\big ([{\nabla ^\nu }{\nabla ^\mu }{\phi }]R\big ){\nabla _\nu }\phi \nonumber \\&+ { \frac{{2f}}{X}} {\nabla _\mu }\big ( [{\nabla ^\rho }{\nabla _\rho }{\phi }]R\big ){\nabla ^\mu }\phi \nonumber \\&+ { \frac{{4f}}{X}} {\nabla _\mu }\big ([{\nabla _\rho }{\nabla ^\mu }{\phi }]{R^{\rho \nu }}\big ){\nabla _\nu }\phi \nonumber \\&- { \frac{{4f}}{X}} {\nabla _\mu }\big ([{\nabla ^\rho }{\nabla ^\sigma }{\phi }]{R_{\rho \sigma }}\big ){\nabla ^\mu }\phi \nonumber \\&- { \frac{{4f}}{X}} {\nabla _\mu }\big ([{\nabla ^\rho }{\nabla _\rho }{\phi }]{R^{\mu \nu }}\big ){\nabla _\nu }\phi \nonumber \\&+ { \frac{{4f}}{X}} {\nabla _\mu }\big ([{\nabla _\rho }{\nabla ^\nu }{\phi }]{R^{\rho \mu }}\big ){\nabla _\nu }\phi \nonumber \\&+ { \frac{{4f}}{X}} {\nabla _\mu }\big ([{\nabla _\rho }{\nabla _\sigma }{\phi }]{R^{\mu \rho \nu \sigma }}\big ){\nabla _\nu }\phi \Bigg .] \end{aligned}$$

(C.7)

Integrating by parts in the first four terms, we obtain

$$\begin{aligned} S =&\int {{d^4}x\sqrt{ - g} } \Bigg [\frac{{2f'}}{X}{\nabla _\mu }\phi {\nabla _\nu }\phi [{\nabla ^\nu }{\nabla ^\mu }\phi ]R \nonumber \\&+ 2f{\nabla _\nu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla ^\nu }{\nabla ^\mu }\phi ]R \nonumber \\&+ \frac{{2f}}{X}[{\nabla _\mu }{\nabla _\nu }\phi ][{\nabla ^\nu }{\nabla ^\mu }\phi ]R \nonumber \\&- \frac{{2f'}}{X}{\nabla _\mu }\phi {\nabla ^\mu }\phi [{\nabla ^\rho }{\nabla _\rho }\phi ]R \nonumber \\&- 2f{\nabla ^\mu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla ^\rho }{\nabla _\rho }\phi ]R \nonumber \\&\quad - \frac{{2f}}{X}[{\nabla _\mu }{\nabla ^\mu }\phi ][{\nabla ^\rho }{\nabla _\rho }\phi ]R \nonumber \\&- \frac{{4f'}}{X}{\nabla _\mu }\phi {\nabla _\nu }\phi [{\nabla _\rho }{\nabla ^\mu }\phi ]{R^{\rho \nu }} \nonumber \\&- 4f{\nabla _\nu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla _\rho }{\nabla ^\mu }\phi ]{R^{\rho \nu }}\nonumber \\&- \frac{{4f}}{X}[{\nabla _\mu }{\nabla _\nu }\phi ][{\nabla _\rho }{\nabla ^\mu }\phi ]{R^{\rho \nu }} \nonumber \\&+ \frac{{4f'}}{X}{\nabla _\mu }\phi {\nabla ^\mu }\phi [{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }} \nonumber \\&+ 4f{\nabla ^\mu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }} \nonumber \\&+ \frac{{4f}}{X}[{\nabla _\mu }{\nabla ^\mu }\phi ][{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }} \nonumber \\&- \frac{{4f}}{X}{\nabla _\mu }([{\nabla ^\rho }{\nabla _\rho }\phi ]{R^{\mu \nu }}){\nabla _\nu }\phi \nonumber \\&+ \frac{{4f}}{X}{\nabla _\mu }([{\nabla _\rho }{\nabla ^\nu }\phi ]{R^{\rho \mu }}){\nabla _\nu }\phi \nonumber \\&+ \frac{{4f}}{X}{\nabla _\mu }([{\nabla _\rho }{\nabla _\sigma }\phi ]{R^{\mu \rho \nu \sigma }}){\nabla _\nu }\phi \Bigg ] \end{aligned}$$

(C.8)

In order to rewrite some terms, it is useful to take into account the following relations

$$\begin{aligned}&\frac{1}{X}{\nabla _\mu }\phi {\nabla ^\mu }\phi = - 2\\&{\nabla _\nu }\left( {\ln X} \right) = - \frac{1}{X}\left[ {{\nabla _\nu }{\nabla _\mu }\phi } \right] {\nabla ^\mu }\phi \end{aligned}$$

Using these equations, the action (C.8) takes the form

$$\begin{aligned} S =&\int {{d^4}x\sqrt{ - g} } \Bigg [ - 2f'{\nabla ^\nu }\phi {\nabla _\nu }\left( {\ln X} \right) R\nonumber \\&+ 2f{\nabla _\nu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla ^\nu }{\nabla ^\mu }\phi ]R \nonumber \\&+ \frac{{2f}}{X}[{\nabla _\mu }{\nabla _\nu }\phi ][{\nabla ^\nu }{\nabla ^\mu }\phi ]R \nonumber \\&+4f' [{\nabla ^\rho }{\nabla _\rho }\phi ]R - 2f{\nabla ^\mu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla ^\rho }{\nabla _\rho }\phi ]R \nonumber \\&- \frac{{2f}}{X}[{\nabla _\mu }{\nabla ^\mu }\phi ][{\nabla ^\rho }{\nabla _\rho }\phi ]R \nonumber \\&+ 4f'{\nabla _\nu }\phi {\nabla _\rho }\left( {\ln X} \right) {R^{\rho \nu }} - 4f{\nabla _\nu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla _\rho }{\nabla ^\mu }\phi ]{R^{\rho \nu }}\nonumber \\&- \frac{{4f}}{X}[{\nabla _\mu }{\nabla _\nu }\phi ][{\nabla _\rho }{\nabla ^\mu }\phi ]{R^{\rho \nu }} \nonumber \\&- 8f'[{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }} + 4f{\nabla ^\mu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }} \nonumber \\&+ \frac{{4f}}{X}[{\nabla _\mu }{\nabla ^\mu }\phi ][{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }} \nonumber \\&- \frac{{4f}}{X}{\nabla _\mu }([{\nabla ^\rho }{\nabla _\rho }\phi ]{R^{\mu \nu }}){\nabla _\nu }\phi + \frac{{4f}}{X}{\nabla _\mu }([{\nabla _\rho }{\nabla ^\nu }\phi ]{R^{\rho \mu }}){\nabla _\nu }\phi \nonumber \\&+ \frac{{4f}}{X}{\nabla _\mu }([{\nabla _\rho }{\nabla _\sigma }\phi ]{R^{\mu \rho \nu \sigma }}){\nabla _\nu }\phi \Bigg ] \end{aligned}$$

(C.9)

To continue, notice that

$$\begin{aligned} - 2f'{\nabla ^\nu }\phi {\nabla _\nu }\left( {\ln X} \right) R= & {} - 4f''X\ln XR + 2f'\ln X\square \phi R \nonumber \\&+ 2f'\ln X{\nabla ^\nu }\phi {\nabla _\nu }R + {\text {t.d}} \nonumber \\ \end{aligned}$$

(C.10)

$$\begin{aligned} 4f'[{\nabla ^\rho }{\nabla _\rho }\phi ]R= & {} 8f''XR - 4f'{\nabla _\rho }\phi {\nabla ^\rho }R + {\text {t.d}} \nonumber \\ \end{aligned}$$

(C.11)

$$\begin{aligned}&4f'{\nabla _\nu }\phi {\nabla _\rho }\left( {\ln X} \right) {R^{\rho \nu }}= - 4f''\ln X{\nabla _\rho }\phi {\nabla _\nu }\phi {R^{\rho \nu }} \nonumber \\&\quad - 4f'\ln X[{\nabla _\rho }{\nabla _\nu }\phi ]{R^{\rho \nu }} - 2f'\ln X{\nabla _\nu }\phi {\nabla ^\nu }R + {\text {t.d}}\nonumber \\ \end{aligned}$$

(C.12)

$$\begin{aligned}&- 8f'[{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }}= - 8f'''{\nabla _\lambda }\phi {\nabla ^\sigma }\phi [{\nabla _\sigma }{\nabla ^\lambda }\phi ] \nonumber \\&\quad - 8f''[{\nabla _\lambda }{\nabla ^\sigma }\phi ][{\nabla _\sigma }{\nabla ^\lambda }\phi ] - 16f'''X\square \phi +8f''{\left( {\square \phi } \right) ^2} \nonumber \\&\quad + 4f'{\nabla ^\sigma }\phi {\nabla _\sigma }R + {\text {t.d}} \end{aligned}$$

(C.13)

where t.d. indicates terms associated to total derivatives. It is convenient to expand some terms in (C.12) and (C.13) as follows

$$\begin{aligned} - 4f''\ln X{\nabla _\rho }\phi {\nabla _\nu }\phi {R^{\rho \nu }} =&\, 4f'''\ln X{\nabla _\lambda }\phi [{\nabla _\rho }{\nabla ^\lambda }\phi ]{\nabla ^\rho }\phi \nonumber \\&\quad + 4f''{\nabla _\lambda }\left( {\ln X} \right) [{\nabla _\rho }{\nabla ^\lambda }\phi ]{\nabla ^\rho }\phi \nonumber \\&+ 4f''\ln X[{\nabla _\rho }{\nabla ^\lambda }\phi ][{\nabla _\lambda }{\nabla ^\rho }\phi ] \nonumber \\&\quad + 8f'''X\ln X\square \phi \nonumber \\&\quad - 4f''{\nabla _\rho }\left( {\ln X} \right) {\nabla ^\rho }\phi \square \phi \nonumber \\&- 4f''\ln X{\left( {\square \phi } \right) ^2} + {\text {t.d}} \end{aligned}$$

(C.14)

$$\begin{aligned} - 8f'''{\nabla _\lambda }\phi {\nabla ^\sigma }\phi [{\nabla _\sigma }{\nabla ^\lambda }\phi ] =&16f''''{X^2}\ln X - 8f'''X\ln X\square \phi \nonumber \\&\quad + 8f'''\ln X[{\nabla _\lambda }{\nabla _\alpha }\phi ]{\nabla ^\lambda }\phi {\nabla ^\alpha }\phi + {\text {t.d}} \end{aligned}$$

(C.15)

$$\begin{aligned} - 16f'''X\square \phi =&- 28f'''X\square \phi + 24f''''{X^2} \nonumber \\&\quad - 24f''''{X^2}\ln X + 12f'''X\ln X\square \phi \nonumber \\&- 12f'''\ln X[{\nabla _\lambda }{\nabla _\alpha }\phi ]{\nabla ^\lambda }\phi {\nabla ^\alpha }\phi + {\text {t.d}} \end{aligned}$$

(C.16)

Replacing (C.14), (C.15) and (C.16) in (C.10), (C.11), (C.12) and (C.13), and substituting in the action, we obtain

$$\begin{aligned} S =&\int {{d^4}x\sqrt{ - g} } \Bigg [K - {G_3}\square \phi + {G_4}R + {G_{4X}}\bigg [ {{{\left( {\square \phi } \right) }^2}} \nonumber \\&\quad {- {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2}} \bigg ] + {G_5}{G_{\mu \nu }}[{\nabla ^\mu }{\nabla ^\nu }\phi ] \nonumber \\&+ 4f''\left[ {{{\left( {\square \phi } \right) }^2} - {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2}} \right] + 2f{\nabla _\nu }\phi {\nabla _\mu }\nonumber \\&\times \left( {\frac{1}{X}} \right) [{\nabla ^\nu }{\nabla ^\mu }\phi ]R + \frac{{2f}}{X}[{\nabla _\mu }{\nabla _\nu }\phi ][{\nabla ^\nu }{\nabla ^\mu }\phi ]R \nonumber \\&- 2f{\nabla ^\mu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla ^\rho }{\nabla _\rho }\phi ]R - \frac{{2f}}{X}[{\nabla _\mu }{\nabla ^\mu }\phi ][{\nabla ^\rho }{\nabla _\rho }\phi ]R \nonumber \\&+ 4f''{\nabla _\lambda }\left( {\ln X} \right) [{\nabla _\rho }{\nabla ^\lambda }\phi ]{\nabla ^\rho }\phi \nonumber \\&- 4f''{\nabla _\rho }\left( {\ln X} \right) {\nabla ^\rho }\phi \square \phi - 4f{\nabla _\nu }\phi {\nabla _\mu }\nonumber \\&\times \left( {\frac{1}{X}} \right) [{\nabla _\rho }{\nabla ^\mu }\phi ]{R^{\rho \nu }} - \frac{{4f}}{X}[{\nabla _\mu }{\nabla _\nu }\phi ][{\nabla _\rho }{\nabla ^\mu }\phi ]{R^{\rho \nu }} \nonumber \\&+ 4f{\nabla ^\mu }\phi {\nabla _\mu }\left( {\frac{1}{X}} \right) [{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }}\nonumber \\&+ \frac{{4f}}{X}[{\nabla _\mu }{\nabla ^\mu }\phi ][{\nabla ^\rho }{\nabla ^\sigma }\phi ]{R_{\rho \sigma }} \nonumber \\&- \frac{{4f}}{X}{\nabla _\mu }([{\nabla ^\rho }{\nabla _\rho }\phi ]{R^{\mu \nu }}){\nabla _\nu }\phi \nonumber \\&+ \frac{{4f}}{X}{\nabla _\mu }([{\nabla _\rho }{\nabla ^\nu }\phi ]{R^{\rho \mu }}){\nabla _\nu }\phi \nonumber \\&+ \frac{{4f}}{X}{\nabla _\mu }([{\nabla _\rho }{\nabla _\sigma }\phi ]{R^{\mu \rho \nu \sigma }}){\nabla _\nu }\phi \Bigg ] \end{aligned}$$

(C.17)

where the notation ${\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) ^2} \equiv [{\nabla _\mu }{\nabla _\nu }\phi ] [{\nabla ^\mu }{\nabla ^\nu }\phi ]$ has been used and the functions K, $G_3$, $G_4$ y $G_5$ have been defined in the following way

$$\begin{aligned} K= & {} 8f''''{X^2}(3 - \ln X) \\ {G_3}= & {} 4f'''X(7 - 3\ln X) \\ {G_4}= & {} 4f''X(2 - \ln X) \\ {G_5}= & {} - 4f'\ln X \end{aligned}$$

where ${G_{iX}} = \partial {G_i}/\partial X$. After multiple integration by parts in the action (C.17) and tedious algebraic manipulations, it is possible to cancel all counter terms in (C.17) and reproduce the action in terms of generalized Galileons, given by

$$\begin{aligned} S =&\int {{d^4}x\sqrt{ - g} }\Bigg [K - {G_3}\square \phi + {G_4}R \nonumber \\&\quad + {G_{4X}}\left[ {{{\left( {\square \phi } \right) }^2} - {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2}} \right] + {G_5}{G_{\mu \nu }}[{\nabla ^\mu }{\nabla ^\nu }\phi ] \nonumber \\&\quad - \frac{{{G_{5X}}}}{6}\left[ {{{\left( {\square \phi } \right) }^3} - 3\left( {\square \phi } \right) {{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^2} + 2{{\left( {{\nabla _\mu }{\nabla _\nu }\phi } \right) }^3}} \right] \Bigg ] \end{aligned}$$

(C.18)