A-type Quiver Varieties and ADHM Moduli Spaces

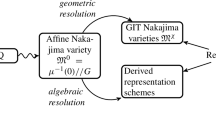
Abstract

We study quantum geometry of Nakajima quiver varieties of two different types—framed A-type quivers and ADHM quivers. While these spaces look completely different we find a surprising connection between equivariant K-theories thereof with a nontrivial match between their equivariant parameters. In particular, we demonstrate that quantum equivariant K-theory of $A_n$ quiver varieties in a certain $n\rightarrow \infty$ limit reproduces equivariant K-theory of the Hilbert scheme of points on $\mathbb {C}^2$. We analyze the correspondence from the point of view of enumerative geometry, representation theory and integrable systems. We also propose a conjecture which relates spectra of quantum multiplication operators in K-theory of the ADHM moduli spaces with the solution of the elliptic Ruijsenaars–Schneider model.

Appendix A. tRS Difference Equation for \(T^*\mathbb {P}^1\)

Let us illustrate (2.16) for $X_2=T^*\mathbb {P}^1$. The vertex function is given by

$$\begin{aligned} V=\frac{e^{\frac{\log \zeta _2\cdot \log a_1\cdots a_n}{\log q}}}{2\pi i}\int \limits _C \frac{ds}{s}\,e^{\frac{\log \zeta _1/\zeta _2\cdot \log s}{\log q}} \frac{\varphi \left( \hbar \frac{s}{a_1}\right) }{\varphi \left( \frac{s}{a_1}\right) }\frac{\varphi \left( \hbar \frac{s}{a_2}\right) }{\varphi \left( \frac{s}{a_2}\right) }. \end{aligned}$$

(A.1)

For $X_2$ there are two tRS operators

$$\begin{aligned} T_1(\varvec{\zeta })&= \frac{\hbar \zeta _1-\zeta _2}{\zeta _1-\zeta _2} p_1 + \frac{\hbar \zeta _2-\zeta _1}{\zeta _2-\zeta _1} p_2,\nonumber \\ T_2(\varvec{\zeta })&= p_1 p_2. \end{aligned}$$

(A.2)

By acting with these operators on the above function we get

$$\begin{aligned} T_1(\varvec{\zeta }) \mathrm {V}&= \mathrm {V}^{\left( T_1(s)\right) },\nonumber \\ T_2(\varvec{\zeta }) \mathrm {V}&= a_1 a_2 \mathrm {V}, \end{aligned}$$

(A.3)

where the first tRS class is given by¹⁰

$$\begin{aligned} T_1(s) = \frac{\hbar \zeta _1-\zeta _2}{\zeta _1-\zeta _2} s + \frac{\hbar \zeta _2-\zeta _1}{\zeta _2-\zeta _1} \frac{a_1 a_2}{s}, \end{aligned}$$

(A.4)

and is a linear combination of the tautological bundle $\mathscr {V}$ and $\Lambda ^2\mathscr {W}\otimes \mathscr {V}^*$ over $X_2$ with coefficients dependent on quantum parameter $z=\frac{\zeta _1}{\zeta _2}$ and the equivariant parameters.

In order to prove that $\mathrm {V}^{\left( T_1(s)\right) }=(a_1+a_2)\mathrm {V}^{(1)}$ we shall use the following integral (see also [NPZ], Appendix D)

$$\begin{aligned} I_2=\int \limits _C \frac{ds}{s}\left[ \frac{1}{s}\left( 1-\frac{s}{a_1}\right) \left( 1-\frac{s}{a_2}\right) \right] \,e^{\frac{\log z \cdot \log s}{\log q}} \frac{\varphi \left( \hbar \frac{s}{a_1}\right) }{\varphi \left( \frac{s}{a_1}\right) }\frac{\varphi \left( \hbar \frac{s}{a_2}\right) }{\varphi \left( \frac{s}{a_2}\right) }, \end{aligned}$$

(A.5)

where contour C is chosen in such a way that shift $s\rightarrow q^{-1}s$ does not pick up any poles. This can be straightforwardly generalized to the n-particle tRS model. Thus integral $I_2$ in the shifted variable is equal to itself which leads us to

$$\begin{aligned} 0=\int \limits _C \frac{ds}{s}\frac{1}{z \hbar }\left[ (1-\hbar z)s+(\hbar - z)\frac{a_1 a_2}{s}-(a_1+a_2)(1-z)\right] \,e^{\frac{\log z \cdot \log s}{\log q}} \frac{\varphi \left( \hbar \frac{s}{a_1}\right) }{\varphi \left( \frac{s}{a_1}\right) }\frac{\varphi \left( \hbar \frac{s}{a_2}\right) }{\varphi \left( \frac{s}{a_2}\right) },\nonumber \\ \end{aligned}$$

(A.6)

from where the statement follows since the expression in the square brackets must vanish.